Difference between revisions of "Reihan Azril Ramadhan"
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == My Concious Effort on Numerical Method Learning and Its Application in Hydrogen Storage Design == | ||
| + | <youtube width="200" height="100">v=WJLslRTNoqM&ab</youtube> | ||
| + | |||
== Introduction == | == Introduction == | ||
Perkenalkan nama saya Reihan Azril Ramadhan dari jurusan Teknik Perkapalan angkatan 2021 | Perkenalkan nama saya Reihan Azril Ramadhan dari jurusan Teknik Perkapalan angkatan 2021 | ||
| Line 80: | Line 83: | ||
== Final Report Hydrogen Storage == | == Final Report Hydrogen Storage == | ||
| − | import math | + | Pada kali ini saya akan membuat finalisasi dari desain hydrogen storage rancangan saya. Dengan spesifikasi yang ditentukan seperti volume tabung sebesar 1 liter, tekanan 8 bar, serta untuk biaya yang dikeluarkan tidak boleh lebih dari Rp 500.000,00. |
| + | |||
| + | == Menentukan Dimensi == | ||
| + | |||
| + | Langkah pertama adalah menetukan dimensi atau ukuran dari tabung yang akan dibuat. Untuk menentukannya saya menggunakan metode numerik agar lebih praktis. | ||
| + | |||
| + | import math | ||
| − | def calculate_lowest_surface_area(volume): | + | def calculate_lowest_surface_area(volume): |
lowest_surface_area = float('inf') # Initialize with infinity | lowest_surface_area = float('inf') # Initialize with infinity | ||
optimal_radius = 0 | optimal_radius = 0 | ||
| Line 100: | Line 109: | ||
return optimal_radius, optimal_height, lowest_surface_area | return optimal_radius, optimal_height, lowest_surface_area | ||
| − | # Test the function for a 1 liter volume | + | # Test the function for a 1 liter volume |
| − | volume = 1000 # cubic centimeters | + | volume = 1000 # cubic centimeters |
| − | radius, height, surface_area = calculate_lowest_surface_area(volume) | + | radius, height, surface_area = calculate_lowest_surface_area(volume) |
| − | print(f"Optimal radius: {radius} cm") | + | print(f"Optimal radius: {radius} cm") |
| − | print(f"Optimal height: {height} cm") | + | print(f"Optimal height: {height} cm") |
| − | print(f"Lowest surface area: {surface_area} cm²") | + | print(f"Lowest surface area: {surface_area} cm²") |
| + | |||
| + | Diperoleh nilai dari radius, height, serta lowest surface area adalah sebesar : | ||
| + | |||
| + | Optimal radius: 5 cm | ||
| + | Optimal height: 12.732395447351626 cm | ||
| + | Lowest surface area: 557.0796326794897 cm² | ||
| + | |||
| + | == Pemilihan Material == | ||
| + | |||
| + | Langkah kedua adalah menentukan material yang akan dipakai. Setelah melakukan riset, saya memutuskan untuk menggunakan material AISI 1020. Saya menggunakan bahan ini karena harganya yang murah dan memiliki yield strength yang tinggi, yaitu sebesar 350 MPa. Berikut adalah list harga dari AISI | ||
| + | |||
| + | [[File:AISI 1020.jpg]] | ||
| + | |||
| + | Langkah selanjutnya adalah menghitung Hoop Stress, untuk mengetahui apakah bahan tersebut sanggup menahan tekanan yang berasal dari dalam dan luar. Saya mematok ketebalan disekitar 1mm-3mm. | ||
| + | |||
| + | # Given values | ||
| + | yield_stress = 350 * 10**6 # Pa | ||
| + | radius = 5 # cm | ||
| + | pressure = 800000 # Pa | ||
| + | atmospheric_pressure = 101325 # Pa | ||
| + | |||
| + | # Conversion factors | ||
| + | cm_to_m = 0.01 | ||
| + | |||
| + | # Convert radius to meters | ||
| + | radius_m = radius * cm_to_m | ||
| + | |||
| + | # Iterate over thickness range from 1 mm to 3 mm | ||
| + | for thickness_mm in range(1, 4): | ||
| + | thickness = thickness_mm * cm_to_m | ||
| + | |||
| + | # Calculate the hoop stress | ||
| + | hoop_stress = calculate_hoop_stress(pressure, radius_m, thickness) | ||
| − | + | # Check if the hoop stress exceeds the yield stress | |
| + | if hoop_stress > yield_stress: | ||
| + | print(f"For a thickness of {thickness_mm} mm, the hoop stress ({hoop_stress / 10**6} MPa) exceeds the yield stress.") | ||
| + | else: | ||
| + | print(f"For a thickness of {thickness_mm} mm, the hoop stress is {hoop_stress / 10**6} MPa.") | ||
| − | + | Dan diperoleh nilai Hoop Stress dari tiap ketebalan adalah sebagai berikut : | |
| − | |||
| − | |||
| − | |||
| − | + | For a thickness of 1 mm, the hoop stress is 4.0 MPa. | |
| − | + | For a thickness of 2 mm, the hoop stress is 2.0 MPa. | |
| − | + | For a thickness of 3 mm, the hoop stress is 1.3333333333333335 MPa. | |
| − | |||
| − | + | == Menentukan Harga == | |
| − | |||
| − | + | Dengan dimensi plat yang tersedia adalah 12 x 24 cm, harga dari plat nya adalah sebesar Rp 94.000,00. Kemudian adalah mencari regulator untuk tabung tersebut. Setelah melakukan riset, saya memutuskan akan menggunakan regulator : | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:regulator.jpg]] | |
| − | + | Harga dari regulator tersebut adalah Rp 126.258,00. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Agar tidak berkarat, saya akan melapisi tabung dengan cat anti karat. Berikut adalah harga dari cat : | |
| − | |||
| − | |||
| − | + | [[File:kucing.jpg]] | |
| − | |||
| − | |||
| − | |||
| − | + | Harga dari cat anti karat tersebut adalah Rp 78.000,00. | |
| − | |||
| + | Langkah Terakhir adalah menjumlahkan total biaya yang dibutuhkan. Berikut adalah list nya : | ||
| + | Plat AISI 1020 = Rp 94.000,00 | ||
| + | Regulator = Rp 126.258,00 | ||
| + | Cat Anti Karat = Rp 78.000,00 | ||
| + | Total = '''Rp 298.258,00''' | ||
| + | == Kesimpulan == | ||
| − | + | Nama alat : Hydrogen Storage Tube | |
| − | + | Volume : 1 L | |
| − | + | Pressure : 8 bar | |
| − | + | Radius : 5 cm | |
| − | + | Height : 12.732395447351626 cm | |
| − | + | Thickness : 1 mm | |
| − | + | Surface Area : 557.0796326794897 cm² | |
| + | Materials : AISI 1020 | ||
| + | Price : '''Rp 298.258,00''' | ||
Latest revision as of 18:52, 15 June 2023
Contents
My Concious Effort on Numerical Method Learning and Its Application in Hydrogen Storage Design
Introduction
Perkenalkan nama saya Reihan Azril Ramadhan dari jurusan Teknik Perkapalan angkatan 2021
Resume Minggu 1
Resume Minggu 1
Di sini kita belajar bahwa setiap individu, seperti seorang siswa, harus memiliki hati nurani atau kesadaran untuk berpikir secara optimal untuk mencapai hasil yang terbaik dalam memecahkan masalah. Pak Dai juga menekankan kepada mahasiswanya agar memanfaatkan potensi yang dimiliki dengan sebaik mungkin dan menekankan kepada mahasiswanya agar tidak hanya menggunakan waktu untuk belajar selama perkuliahan tetapi juga belajar dengan mandiri. Pak Dai juga menjelaskan metode pengujian yang nantinya digunakan di kelas yang dia ajar. Metode ujiannya adalah “Blank Paper Assignment” dimana mahasiswa diberi kesempatan untuk menulis dan membuat materi serta soal yang dibuat oleh mahasiswa itu sendiri berdasarkan semua ilmu yang didapat selama perkuliahan. Pak DAI mengharapkan mahasiswa memahami materi yang disampaikan dalam perkuliahan, yang nantinya akan di aplikasikan pada pekerjaan yang ditugaskan. Pak Dai memperkenalkan studi kasus dan pendekatan analogi untuk menggugah mahasiswa belajar lebih giat dan mendekatkan diri kepada Tuhan Yang Maha Esa, sehingga perkuliahan harus selalu mengingat bahwa tidak ada yang sempurna dan pasti kecuali Yang Maha Kuasa.
Desain Optimasi Sistem Penyimpanan Hidrogen 1
Spesifikasi tabung penyimpanan hidrogen : - Volume : 1 Liter - Tekanan : 8 Bar - Biaya Maksimum : Rp. 500.000,00
Berdasarkan spesifikasi tabung penyimpanan hidrogen yang diberikan, saya sadar bahwa hal-hal tersebut belum cukup untuk mulai membuat atau mendesign tabung penyimpanan yang diminta. Untuk lebih memperdalam lagi apa saja yang diperlukan, saya menggunakan ChatGPT.
Berikut adalah langkah-langkah yang lebih rinci dalam membuat dan mengoptimalkan tabung penyimpanan hidrogen:
Perencanaan dan Desain: - Tentukan kapasitas dan tekanan yang diinginkan untuk tabung penyimpanan hidrogen. - Pertimbangkan kebutuhan aplikasi, seperti mobilitas atau penyimpanan stasioner, dan berapa lama hidrogen harus disimpan. - Rancang tabung dengan dimensi yang sesuai dan pertimbangkan faktor keamanan, kekuatan, dan berat. - Pilih bahan yang cocok untuk tabung, seperti serat karbon diperkuat dengan polimer (carbon fiber reinforced polymer/CFRP), serat karbon, baja, atau aluminium.
Proses Manufaktur: - Pilih metode pembuatan yang sesuai, seperti pembalutan serat karbon atau metode filament winding. - Persiapkan cetakan dengan lapisan pemisah dan aplikasikan resin polimer sesuai dengan instruksi pabrikan. - Lakukan proses pembalutan serat karbon dengan benang serat karbon yang sesuai. - Keringkan dan tambal tabung sesuai kebutuhan. - Gunakan oven atau mesin curing yang sesuai untuk mengeras dan memperkuat tabung.
Pengujian dan Verifikasi: - Lakukan pengujian untuk memastikan bahwa tabung memenuhi standar keamanan dan kualitas. - Beberapa pengujian yang mungkin dilakukan meliputi pengujian tekanan hidrostatis, pengujian kekuatan, pengujian kebocoran, dan pengujian ketahanan terhadap deformasi. - Pastikan tabung memenuhi standar industri yang berlaku, seperti ISO 11439 atau standar nasional setempat.
Inspeksi dan Sertifikasi: - Lakukan inspeksi visual untuk memeriksa adanya cacat atau kerusakan pada tabung. - Kirim tabung untuk sertifikasi dan verifikasi oleh otoritas yang kompeten sesuai dengan regulasi dan standar yang berlaku.
Pengoptimalan Performa: - Pertimbangkan teknologi insulasi termal yang efektif untuk mengurangi kebocoran dan mempertahankan kualitas hidrogen. - Gunakan teknologi penyerap hidrogen atau material adsorpsi fisik untuk meningkatkan kapasitas penyimpanan. - Rancang sistem pengendalian tekanan dan katup yang sesuai untuk tabung penyimpanan hidrogen. - Lakukan penelitian dan pengembangan terus-menerus untuk memperbaiki desain dan material tabung.
Pastikan untuk berkonsultasi dengan ahli teknik dan mematuhi standar keamanan serta regulasi yang berlaku di wilayah Anda saat membuat dan mengoptimalkan tabung penyimpanan hidrogen. Penting juga untuk mengikuti praktik terbaik dalam industri penyimpanan hidrogen yang terus berkembang.
Untuk mengoptimalkan tabung penyimpanan hidrogen, Anda dapat mempertimbangkan beberapa langkah berikut:
Material dan Struktur Tabung: - Pilih material dengan kekuatan dan kekakuan yang tinggi, seperti serat karbon diperkuat dengan polimer (CFRP) atau serat karbon. - Rancang struktur tabung dengan efisiensi tinggi untuk memaksimalkan kapasitas penyimpanan dan meminimalkan berat tabung. - Pertimbangkan material baru atau teknologi inovatif dalam pengembangan tabung, seperti komposit nanokarbon atau material penyerap hidrogen.
Optimasi Desain Tabung: - Rancang geometri yang sesuai untuk tabung, dengan mempertimbangkan faktor keamanan, tekanan, dan beban struktural. - Pertimbangkan metode konstruksi yang efisien, seperti proses pembalutan serat karbon (carbon fiber wrapping) atau metode filament winding, untuk memaksimalkan kekuatan dan
kekakuan struktural.
- Gunakan teknik optimasi komputer untuk merancang tabung dengan parameter yang optimal, seperti ukuran, tebal dinding, dan penempatan serat karbon.
Isolasi Termal dan Penahan Panas: - Terapkan isolasi termal yang efektif pada tabung untuk mengurangi kebocoran panas dan mempertahankan kualitas hidrogen. - Pilih bahan isolasi dengan konduktivitas termal yang rendah, seperti busa polimer termal atau perlapisan khusus. - Pastikan isolasi meliputi seluruh permukaan tabung untuk meminimalkan hilangnya energi termal.
Sistem Pengendalian dan Pengurangan Kebocoran: - Rancang sistem pengendalian tekanan dan katup yang cermat untuk memastikan stabilitas tekanan hidrogen dalam tabung. - Pertimbangkan penggunaan sistem pemantauan tekanan dan suhu secara real-time untuk mendeteksi kebocoran atau kondisi yang tidak normal. - Gunakan teknologi segel yang andal dan tahan terhadap hidrogen untuk mengurangi risiko kebocoran.
Perawatan dan Pemeliharaan Rutin: - Lakukan inspeksi rutin dan pemeliharaan terhadap tabung penyimpanan hidrogen untuk memastikan kinerja yang optimal. - Ikuti panduan produsen dan rekomendasi perawatan untuk menjaga tabung dalam kondisi yang baik. - Lakukan pengujian berkala untuk memeriksa kebocoran, deformasi, atau kerusakan pada tabung.
Selain itu, penting untuk terus mengikuti perkembangan dalam teknologi penyimpanan hidrogen dan berpartisipasi dalam penelitian dan pengembangan untuk meningkatkan performa tabung penyimpanan hidrogen.
Final Report Hydrogen Storage
Pada kali ini saya akan membuat finalisasi dari desain hydrogen storage rancangan saya. Dengan spesifikasi yang ditentukan seperti volume tabung sebesar 1 liter, tekanan 8 bar, serta untuk biaya yang dikeluarkan tidak boleh lebih dari Rp 500.000,00.
Menentukan Dimensi
Langkah pertama adalah menetukan dimensi atau ukuran dari tabung yang akan dibuat. Untuk menentukannya saya menggunakan metode numerik agar lebih praktis.
import math
def calculate_lowest_surface_area(volume):
lowest_surface_area = float('inf') # Initialize with infinity
optimal_radius = 0
optimal_height = 0
# Iterate over possible radius values
for radius in range(1, int(math.sqrt(volume / math.pi)) + 1):
height = volume / (math.pi * radius**2)
surface_area = 2 * math.pi * radius * (radius + height)
# Check if the current surface area is lower than the lowest recorded so far
if surface_area < lowest_surface_area:
lowest_surface_area = surface_area
optimal_radius = radius
optimal_height = height
return optimal_radius, optimal_height, lowest_surface_area
# Test the function for a 1 liter volume
volume = 1000 # cubic centimeters
radius, height, surface_area = calculate_lowest_surface_area(volume)
print(f"Optimal radius: {radius} cm")
print(f"Optimal height: {height} cm")
print(f"Lowest surface area: {surface_area} cm²")
Diperoleh nilai dari radius, height, serta lowest surface area adalah sebesar :
Optimal radius: 5 cm Optimal height: 12.732395447351626 cm Lowest surface area: 557.0796326794897 cm²
Pemilihan Material
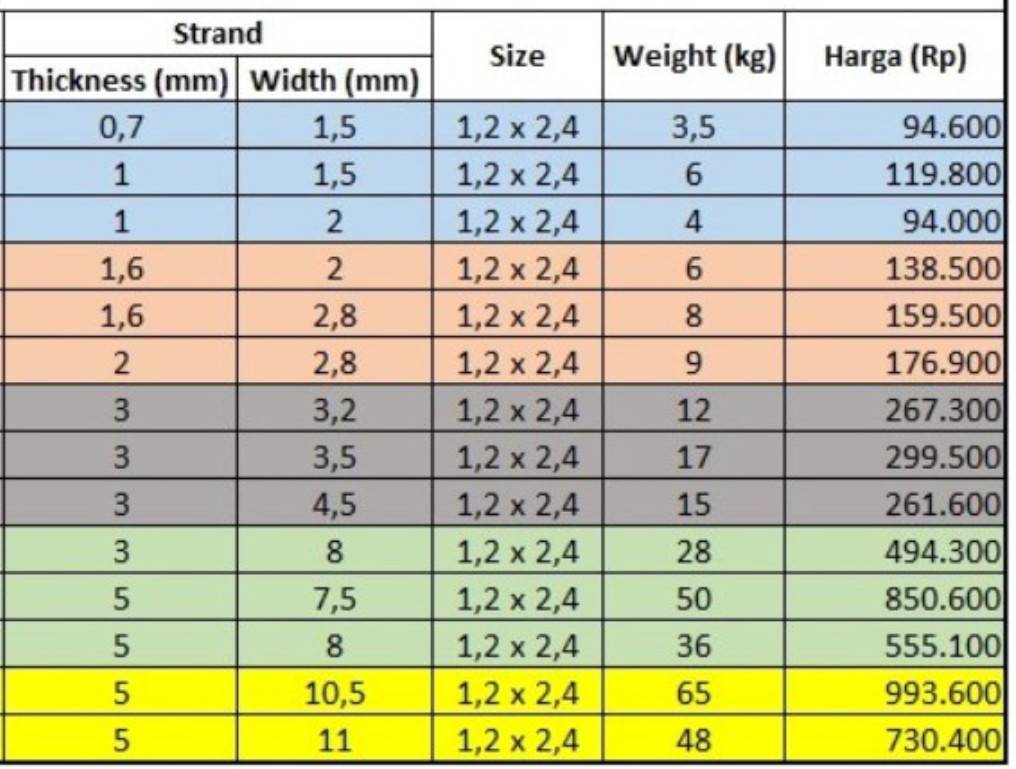
Langkah kedua adalah menentukan material yang akan dipakai. Setelah melakukan riset, saya memutuskan untuk menggunakan material AISI 1020. Saya menggunakan bahan ini karena harganya yang murah dan memiliki yield strength yang tinggi, yaitu sebesar 350 MPa. Berikut adalah list harga dari AISI
Langkah selanjutnya adalah menghitung Hoop Stress, untuk mengetahui apakah bahan tersebut sanggup menahan tekanan yang berasal dari dalam dan luar. Saya mematok ketebalan disekitar 1mm-3mm.
# Given values yield_stress = 350 * 10**6 # Pa radius = 5 # cm pressure = 800000 # Pa atmospheric_pressure = 101325 # Pa
# Conversion factors cm_to_m = 0.01
# Convert radius to meters radius_m = radius * cm_to_m
# Iterate over thickness range from 1 mm to 3 mm for thickness_mm in range(1, 4): thickness = thickness_mm * cm_to_m
# Calculate the hoop stress hoop_stress = calculate_hoop_stress(pressure, radius_m, thickness)
# Check if the hoop stress exceeds the yield stress
if hoop_stress > yield_stress:
print(f"For a thickness of {thickness_mm} mm, the hoop stress ({hoop_stress / 10**6} MPa) exceeds the yield stress.")
else:
print(f"For a thickness of {thickness_mm} mm, the hoop stress is {hoop_stress / 10**6} MPa.")
Dan diperoleh nilai Hoop Stress dari tiap ketebalan adalah sebagai berikut :
For a thickness of 1 mm, the hoop stress is 4.0 MPa. For a thickness of 2 mm, the hoop stress is 2.0 MPa. For a thickness of 3 mm, the hoop stress is 1.3333333333333335 MPa.
Menentukan Harga
Dengan dimensi plat yang tersedia adalah 12 x 24 cm, harga dari plat nya adalah sebesar Rp 94.000,00. Kemudian adalah mencari regulator untuk tabung tersebut. Setelah melakukan riset, saya memutuskan akan menggunakan regulator :
Harga dari regulator tersebut adalah Rp 126.258,00.
Agar tidak berkarat, saya akan melapisi tabung dengan cat anti karat. Berikut adalah harga dari cat :
Harga dari cat anti karat tersebut adalah Rp 78.000,00.
Langkah Terakhir adalah menjumlahkan total biaya yang dibutuhkan. Berikut adalah list nya : Plat AISI 1020 = Rp 94.000,00 Regulator = Rp 126.258,00 Cat Anti Karat = Rp 78.000,00 Total = Rp 298.258,00
Kesimpulan
Nama alat : Hydrogen Storage Tube Volume : 1 L Pressure : 8 bar Radius : 5 cm Height : 12.732395447351626 cm Thickness : 1 mm Surface Area : 557.0796326794897 cm² Materials : AISI 1020 Price : Rp 298.258,00