Difference between revisions of "Frisca Nuradha Fresilliya"
Frisca Nur (talk | contribs) (→Design & Optimization of Pressurized Hydrogen Storage (01/06/23)) |
Frisca Nur (talk | contribs) |
||
| (32 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
i am studying about numerical method that so fun <3 | i am studying about numerical method that so fun <3 | ||
| − | == Resume 26/05/23 | + | == Resume 26/05/23 = |
'''Numerical Methods in Engineering''' | '''Numerical Methods in Engineering''' | ||
| − | Definision : | + | '''Definision :''' |
| + | |||
Numerical methods are widely used in engineering to solve complex mathematical problems and simulate real-world phenomena. | Numerical methods are widely used in engineering to solve complex mathematical problems and simulate real-world phenomena. | ||
| − | Case study of this week : | + | '''Case study of this week :''' |
| + | |||
1- Liter hydrogen storage optimization project. | 1- Liter hydrogen storage optimization project. | ||
| − | The discustions: | + | '''The discustions:''' |
| − | |||
| − | 2. Consciousness relevant to this case? | + | '''1.''' (x+1)(x-1)/(x-1) = 2, if we do subtitution, in mathematics, division by zero is undefined. It is not possible to divide any number by zero and obtain a meaningful result. If you attempt to divide 1 by 0 in a mathematical operation or calculator, you would typically encounter an error or an undefined result. But, if we do elimination, we get the answer is 2. So, in this case we must be have a change between undifined or 2. |
| + | |||
| + | '''2.''' Consciousness relevant to this case? | ||
The definition of Conscious Mathematic is an approach or philosophy in mathematic that consolidated with conciousness concept, consideration, and observation by human. So, in my opinion, this case is relevant with consciousness. Because, we can approach an exact number that in this case is 2. | The definition of Conscious Mathematic is an approach or philosophy in mathematic that consolidated with conciousness concept, consideration, and observation by human. So, in my opinion, this case is relevant with consciousness. Because, we can approach an exact number that in this case is 2. | ||
| − | 3. We need "Tafakur" to grasp this case. | + | '''3.''' We need "Tafakur" to grasp this case. |
"Tafakur" means thinking, reflection, and contemplation to grasp this live."Tafakur" gives us to aware with philosophy. So, if we have a change between 2 choise, we need "Tafakur" to get a best choise. | "Tafakur" means thinking, reflection, and contemplation to grasp this live."Tafakur" gives us to aware with philosophy. So, if we have a change between 2 choise, we need "Tafakur" to get a best choise. | ||
| − | Conclusion: | + | '''Conclusion:''' |
The case in number 1, (x+1)(x-1)/(x-1) = 2, is my choise answer. I conscious and use "Tafakur" to get this answer. Not only in this case, but also in a problem of live we need both of them (conscious and "tafakur"). | The case in number 1, (x+1)(x-1)/(x-1) = 2, is my choise answer. I conscious and use "Tafakur" to get this answer. Not only in this case, but also in a problem of live we need both of them (conscious and "tafakur"). | ||
| − | == Design & Optimization of Pressurized Hydrogen Storage (01/06/23) | + | == Progress of Design & Optimization of Pressurized Hydrogen Storage (01/06/23)= |
| Line 65: | Line 68: | ||
'''Remember''', hydrogen storage systems can be complex, and it's crucial to consult with experts in the field to ensure the design and optimization process is carried out safely and effectively. | '''Remember''', hydrogen storage systems can be complex, and it's crucial to consult with experts in the field to ensure the design and optimization process is carried out safely and effectively. | ||
| + | |||
| + | == Final Report Design & Optimization of Pressurized Hydrogen Storage (07/06/23)== | ||
| + | |||
| + | To optimize hydrogen storage for 1 liter at a pressure of 8 bar, we need to consider various factors such as the type of storage material, design considerations, and cost constraints. Here's a simplified example of how you could approach the optimization process: | ||
| + | |||
| + | '''Step 1: Define the optimization goal''' | ||
| + | In this case, let's assume that the optimization goal is to maximize the hydrogen storage capacity while keeping the cost within Rp 500,000. | ||
| + | |||
| + | [[File:H1.fig.005.jpg|200x200px]] | ||
| + | |||
| + | '''Step 2: Research storage materials and designs''' | ||
| + | There are several options for hydrogen storage, including compressed gas cylinders, metal hydrides, and carbon-based materials. Research each option to determine their capacity, compatibility with high pressure, and cost. This is a example of materials at cylinder | ||
| + | |||
| + | [[File:H2.jpg|200x200px]] | ||
| + | |||
| + | '''Step 3: Calculation the storage''' | ||
| + | |||
| + | '''Calculation of high of the cylinder:''' | ||
| + | [[File:V1.png|200x200px]] | ||
| + | |||
| + | To optimize hydrogen storage for 1 liter at a pressure of 8 bar within a cost of Rp 500,000, you can use Python and apply a brute-force approach to evaluate different storage options. Here's an example code that demonstrates the optimization process: | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | # Define storage options and their characteristics | ||
| + | storage_options = [ | ||
| + | {"name": "Compressed Gas Cylinder", "capacity_liters": 10, "pressure_bar": 200, "cost_rp": 100000}, | ||
| + | {"name": "Metal Hydride", "capacity_liters": 5, "pressure_bar": 100, "cost_rp": 150000}, | ||
| + | {"name": "Carbon-Based Material", "capacity_liters": 15, "pressure_bar": 150, "cost_rp": 200000}, | ||
| + | # Add more storage options as needed | ||
| + | ] | ||
| + | |||
| + | # Define optimization parameters | ||
| + | target_capacity_liters = 1 | ||
| + | target_pressure_bar = 8 | ||
| + | max_cost_rp = 500000 | ||
| + | |||
| + | # Initialize variables to track the best option found | ||
| + | best_option = None | ||
| + | best_option_score = 0 | ||
| + | |||
| + | # Iterate over storage options | ||
| + | for option in storage_options: | ||
| + | # Check if the option meets the target pressure and capacity requirements | ||
| + | if option["capacity_liters"] >= target_capacity_liters and option["pressure_bar"] >= target_pressure_bar: | ||
| + | # Calculate the cost per liter | ||
| + | cost_per_liter = option["cost_rp"] / option["capacity_liters"] | ||
| + | |||
| + | # Check if the option's cost per liter is within the budget and update the best option if necessary | ||
| + | if cost_per_liter <= max_cost_rp and option["capacity_liters"] > best_option_score: | ||
| + | best_option = option | ||
| + | best_option_score = option["capacity_liters"] | ||
| + | |||
| + | # Print the best option found | ||
| + | if best_option is not None: | ||
| + | print("Best Option:") | ||
| + | print("Name:", best_option["name"]) | ||
| + | print("Capacity (liters):", best_option["capacity_liters"]) | ||
| + | print("Pressure (bar):", best_option["pressure_bar"]) | ||
| + | print("Cost (Rp):", best_option["cost_rp"]) | ||
| + | else: | ||
| + | print("No suitable options found within the given constraints.") | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | In this code, we define a list of storage options with their characteristics such as capacity, pressure, and cost. We then iterate over these options and evaluate if they meet the target pressure and capacity requirements while considering the cost constraint. The option with the highest capacity that satisfies all the conditions is considered the best option. | ||
| + | |||
| + | Please note that this code is a basic illustration and assumes the given data structure for storage options. You may need to adapt it to your specific data format and include additional conditions or optimization criteria as per your requirements. | ||
| + | |||
| + | |||
| + | '''Step 4: Select the most cost-effective option''' | ||
| + | Choose the storage option that provides the highest hydrogen storage capacity within the cost constraint of Rp 500,000. This will depend on the specific cost and capacity values you find during your research. | ||
| + | |||
| + | We need to know the specific cost and capacity values for the storage system. Without this information, I can provide you with an example code that demonstrates how you can perform calculations based on cost and capacity inputs. | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | def calculate_hydrogen_capacity(cost_constraint): | ||
| + | # Assuming the cost and capacity values in Rp | ||
| + | cost_per_capacity = 1000 # Cost per unit of capacity in Rp | ||
| + | |||
| + | # Calculate the maximum hydrogen storage capacity | ||
| + | max_capacity = cost_constraint // cost_per_capacity | ||
| + | |||
| + | return max_capacity | ||
| + | |||
| + | # Example usage | ||
| + | cost_constraint = 500000 # Cost constraint in Rp | ||
| + | max_hydrogen_capacity = calculate_hydrogen_capacity(cost_constraint) | ||
| + | print("Maximum Hydrogen Storage Capacity:", max_hydrogen_capacity, "units") | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | '''Step 5: Optimize further if necessary''' | ||
| + | If the chosen option is within the cost constraint but does not maximize the hydrogen storage capacity, you can consider optimizing other factors. For example, you could explore ways to increase the pressure or volume of the storage system without exceeding the cost constraint. | ||
| + | |||
| + | To visualize the relationship between volume and pressure in hydrogen storage, you can create a graph using Python libraries such as Matplotlib. Here's an example code that generates a simple graph: | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | # Define the pressure and volume data | ||
| + | pressure = [1, 5, 10, 15, 20] # Example pressure values | ||
| + | volume = [10, 8, 6, 4, 2] # Example volume values | ||
| + | |||
| + | # Plot the data | ||
| + | plt.plot(pressure, volume, marker='o') | ||
| + | plt.title("Hydrogen Storage: Volume vs Pressure") | ||
| + | plt.xlabel("Pressure (bar)") | ||
| + | plt.ylabel("Volume (liters)") | ||
| + | |||
| + | # Add gridlines | ||
| + | plt.grid(True) | ||
| + | |||
| + | # Display the graph | ||
| + | plt.show() | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | '''Step 6: Verify safety and feasibility''' | ||
| + | Ensure that the chosen storage option is safe, feasible, and complies with relevant regulations and standards. This is crucial to prevent any potential hazards associated with hydrogen storage. | ||
| + | |||
| + | '''Conclusion:''' | ||
| + | |||
| + | '''1.''' We must have a several assumptions variabel, for example (R), that need to be calculate a high of cylinder. | ||
| + | |||
| + | '''2.''' We need material that have best quality with a range total cost Rp500.000. | ||
| + | |||
| + | '''3.''' We must have a consideration with the increase the pressure or volume of the storage system. | ||
| + | |||
| + | '''4.''' Don't forget to think about Verify safety and feasibility. | ||
| + | |||
| + | == Video Presentation = | ||
| + | <youtube width="200" height="100">0KNrH-M5QRY</youtube> | ||
Latest revision as of 00:25, 16 June 2023
Contents
= Introduction
Hello, I am Ica. This is my air.eng.ui.id account. Now, with Mr.DAI, i am studying about numerical method that so fun <3
= Resume 26/05/23
Numerical Methods in Engineering
Definision :
Numerical methods are widely used in engineering to solve complex mathematical problems and simulate real-world phenomena.
Case study of this week :
1- Liter hydrogen storage optimization project.
The discustions:
1. (x+1)(x-1)/(x-1) = 2, if we do subtitution, in mathematics, division by zero is undefined. It is not possible to divide any number by zero and obtain a meaningful result. If you attempt to divide 1 by 0 in a mathematical operation or calculator, you would typically encounter an error or an undefined result. But, if we do elimination, we get the answer is 2. So, in this case we must be have a change between undifined or 2.
2. Consciousness relevant to this case? The definition of Conscious Mathematic is an approach or philosophy in mathematic that consolidated with conciousness concept, consideration, and observation by human. So, in my opinion, this case is relevant with consciousness. Because, we can approach an exact number that in this case is 2.
3. We need "Tafakur" to grasp this case. "Tafakur" means thinking, reflection, and contemplation to grasp this live."Tafakur" gives us to aware with philosophy. So, if we have a change between 2 choise, we need "Tafakur" to get a best choise.
Conclusion: The case in number 1, (x+1)(x-1)/(x-1) = 2, is my choise answer. I conscious and use "Tafakur" to get this answer. Not only in this case, but also in a problem of live we need both of them (conscious and "tafakur").
= Progress of Design & Optimization of Pressurized Hydrogen Storage (01/06/23)
Specification of Hydrogen Storage
Volume : 1 Liter
Pressure : 8 bar Cost : Rp500.000
How to design this Hydrogen Storage?
To design and optimize a pressurized hydrogen storage system with a volume of 1 liter, several factors need to be considered, including pressure, material selection, safety, and efficiency. Here are some steps to help you with the design process:
Determine the target pressure: The pressure at which you want to store hydrogen will depend on your specific application. Higher pressures generally allow for more hydrogen storage, but they also require stronger and more expensive materials. Determine the appropriate pressure range based on your requirements.
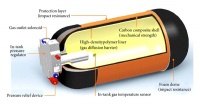
Select a suitable material: The choice of material for the storage vessel is critical to ensure safety, weight, and cost considerations. Common materials used for hydrogen storage include carbon fiber composites, metal hydrides, and high-strength metals like aluminum or steel. Consider the material's strength, weight, compatibility with hydrogen, and cost when making your selection.
Design the storage vessel: Determine the dimensions and shape of the storage vessel to achieve a volume of 1 liter. Consider factors such as the internal pressure, material thickness, and any necessary reinforcements to ensure structural integrity. It's important to consult with a qualified engineer or expert in pressure vessel design to ensure compliance with relevant safety standards and regulations.
Optimize the storage system: To optimize the storage system, consider the following factors:
a. Heat management: Hydrogen storage can generate heat during filling and discharging processes. Implement effective heat management techniques, such as incorporating heat exchangers or cooling systems, to enhance the overall efficiency and safety of the system.
b. Insulation: Insulate the storage vessel to minimize heat transfer and improve the system's overall efficiency. Select appropriate insulation materials to reduce the energy losses associated with hydrogen storage.
c. Safety features: Incorporate safety features into the design, such as pressure relief valves and rupture discs, to prevent overpressure situations and ensure the system can handle unexpected pressure spikes.
d. Leakage prevention: Hydrogen has small molecular size, and leakage can be a concern. Ensure proper sealing mechanisms and regularly check for leaks to maintain system integrity.
e. System weight: Consider the weight of the storage system, especially if portability is a requirement. Optimize the design and material selection to achieve a balance between weight and other performance factors.
f. Testing and validation: Once the design is complete, perform thorough testing and validation to ensure the system meets safety and performance requirements. This may involve pressure testing, leak detection, and compliance with applicable standards and regulations.
Remember, hydrogen storage systems can be complex, and it's crucial to consult with experts in the field to ensure the design and optimization process is carried out safely and effectively.
Final Report Design & Optimization of Pressurized Hydrogen Storage (07/06/23)
To optimize hydrogen storage for 1 liter at a pressure of 8 bar, we need to consider various factors such as the type of storage material, design considerations, and cost constraints. Here's a simplified example of how you could approach the optimization process:
Step 1: Define the optimization goal In this case, let's assume that the optimization goal is to maximize the hydrogen storage capacity while keeping the cost within Rp 500,000.
Step 2: Research storage materials and designs There are several options for hydrogen storage, including compressed gas cylinders, metal hydrides, and carbon-based materials. Research each option to determine their capacity, compatibility with high pressure, and cost. This is a example of materials at cylinder
Step 3: Calculation the storage
Calculation of high of the cylinder:

To optimize hydrogen storage for 1 liter at a pressure of 8 bar within a cost of Rp 500,000, you can use Python and apply a brute-force approach to evaluate different storage options. Here's an example code that demonstrates the optimization process:
# Define storage options and their characteristics
storage_options = [
{"name": "Compressed Gas Cylinder", "capacity_liters": 10, "pressure_bar": 200, "cost_rp": 100000},
{"name": "Metal Hydride", "capacity_liters": 5, "pressure_bar": 100, "cost_rp": 150000},
{"name": "Carbon-Based Material", "capacity_liters": 15, "pressure_bar": 150, "cost_rp": 200000},
# Add more storage options as needed
]
# Define optimization parameters
target_capacity_liters = 1
target_pressure_bar = 8
max_cost_rp = 500000
# Initialize variables to track the best option found
best_option = None
best_option_score = 0
# Iterate over storage options
for option in storage_options:
# Check if the option meets the target pressure and capacity requirements
if option["capacity_liters"] >= target_capacity_liters and option["pressure_bar"] >= target_pressure_bar:
# Calculate the cost per liter
cost_per_liter = option["cost_rp"] / option["capacity_liters"]
# Check if the option's cost per liter is within the budget and update the best option if necessary
if cost_per_liter <= max_cost_rp and option["capacity_liters"] > best_option_score:
best_option = option
best_option_score = option["capacity_liters"]
# Print the best option found
if best_option is not None:
print("Best Option:")
print("Name:", best_option["name"])
print("Capacity (liters):", best_option["capacity_liters"])
print("Pressure (bar):", best_option["pressure_bar"])
print("Cost (Rp):", best_option["cost_rp"])
else:
print("No suitable options found within the given constraints.")In this code, we define a list of storage options with their characteristics such as capacity, pressure, and cost. We then iterate over these options and evaluate if they meet the target pressure and capacity requirements while considering the cost constraint. The option with the highest capacity that satisfies all the conditions is considered the best option.
Please note that this code is a basic illustration and assumes the given data structure for storage options. You may need to adapt it to your specific data format and include additional conditions or optimization criteria as per your requirements.
Step 4: Select the most cost-effective option
Choose the storage option that provides the highest hydrogen storage capacity within the cost constraint of Rp 500,000. This will depend on the specific cost and capacity values you find during your research.
We need to know the specific cost and capacity values for the storage system. Without this information, I can provide you with an example code that demonstrates how you can perform calculations based on cost and capacity inputs.
def calculate_hydrogen_capacity(cost_constraint):
# Assuming the cost and capacity values in Rp
cost_per_capacity = 1000 # Cost per unit of capacity in Rp
# Calculate the maximum hydrogen storage capacity
max_capacity = cost_constraint // cost_per_capacity
return max_capacity
# Example usage
cost_constraint = 500000 # Cost constraint in Rp
max_hydrogen_capacity = calculate_hydrogen_capacity(cost_constraint)
print("Maximum Hydrogen Storage Capacity:", max_hydrogen_capacity, "units")Step 5: Optimize further if necessary If the chosen option is within the cost constraint but does not maximize the hydrogen storage capacity, you can consider optimizing other factors. For example, you could explore ways to increase the pressure or volume of the storage system without exceeding the cost constraint.
To visualize the relationship between volume and pressure in hydrogen storage, you can create a graph using Python libraries such as Matplotlib. Here's an example code that generates a simple graph:
import matplotlib.pyplot as plt
# Define the pressure and volume data
pressure = [1, 5, 10, 15, 20] # Example pressure values
volume = [10, 8, 6, 4, 2] # Example volume values
# Plot the data
plt.plot(pressure, volume, marker='o')
plt.title("Hydrogen Storage: Volume vs Pressure")
plt.xlabel("Pressure (bar)")
plt.ylabel("Volume (liters)")
# Add gridlines
plt.grid(True)
# Display the graph
plt.show()Step 6: Verify safety and feasibility Ensure that the chosen storage option is safe, feasible, and complies with relevant regulations and standards. This is crucial to prevent any potential hazards associated with hydrogen storage.
Conclusion:
1. We must have a several assumptions variabel, for example (R), that need to be calculate a high of cylinder.
2. We need material that have best quality with a range total cost Rp500.000.
3. We must have a consideration with the increase the pressure or volume of the storage system.
4. Don't forget to think about Verify safety and feasibility.