Difference between revisions of "Vincent Collin"
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Introduction]] | [[Introduction]] | ||
| − | Halo, saya Vincent Collin dengan NPM 2106632352 | + | [https://www.youtube.com/watch?v=kpWXZmQ3FsI&feature=youtu.be Design & Optimization Hydrogen Storage Made by Vincent Collin 2106632352] |
| + | <youtube width="200" hegiht="100">v=kpWXZmQ3FsI</youtube> | ||
| + | |||
| + | [[File:Pinsen.jpg]] | ||
| + | |||
| + | Halo, saya Vincent Collin dengan NPM 2106632352. | ||
Sekarang saya berkuliah di UI dengan jurusan Teknik Perkapalan. | Sekarang saya berkuliah di UI dengan jurusan Teknik Perkapalan. | ||
| Line 51: | Line 56: | ||
== Final Report of Design & Optimization Hydrogen Storage == | == Final Report of Design & Optimization Hydrogen Storage == | ||
| + | Volume | ||
| + | ---- | ||
| + | |||
Dengan adanya 3 batasan yang ditentukan untuk design dan optimasi hydrogen storage ini, yaitu : Volume, Tekanan, dan Biaya. Maka saya dapat memulai desain sekaligus mengoptimasi volume dari hydrogen storage ini. Dengan bantuan software Pycharm, saya dapat mengcoding optimasi volume terlebih dahulu. Berikut adalah hasil kodingannya serta hasilnya. | Dengan adanya 3 batasan yang ditentukan untuk design dan optimasi hydrogen storage ini, yaitu : Volume, Tekanan, dan Biaya. Maka saya dapat memulai desain sekaligus mengoptimasi volume dari hydrogen storage ini. Dengan bantuan software Pycharm, saya dapat mengcoding optimasi volume terlebih dahulu. Berikut adalah hasil kodingannya serta hasilnya. | ||
| − | import math | + | import math |
| + | |||
| + | def objective(r, h): | ||
| + | volume = math.pi * r ** 2 * h | ||
| + | target_volume = 1000 # dalam cm^3 sehingga perhitungan dalam cm. | ||
| + | diff = abs(volume - target_volume) | ||
| + | |||
| + | return diff | ||
| + | |||
| + | initial_radius = 1 | ||
| + | initial_tinggi = 1 | ||
| + | |||
| + | # Batasan radius dan tinggi | ||
| + | min_radius = 0 | ||
| + | max_radius = 50 | ||
| + | min_tinggi = 0 | ||
| + | max_tinggi = 50 | ||
| + | |||
| + | # Menginisialisasi nilai terbaik | ||
| + | best_radius = initial_radius | ||
| + | best_tinggi = initial_tinggi | ||
| + | best_diff = objective(initial_radius, initial_tinggi) | ||
| + | |||
| + | # Melakukan grid search | ||
| + | for radius in range(min_radius, max_radius + 1): | ||
| + | for tinggi in range(min_tinggi, max_tinggi + 1): | ||
| + | diff = objective(radius, tinggi) | ||
| + | |||
| + | # Memperbarui nilai terbaik jika ditemukan perbedaan terkecil | ||
| + | if diff < best_diff: | ||
| + | best_radius = radius | ||
| + | best_tinggi = tinggi | ||
| + | best_diff = diff | ||
| + | |||
| + | # Mendapatkan hasil optimasi dan luas permukaan | ||
| + | optimized_radius = best_radius | ||
| + | optimized_tinggi = best_tinggi | ||
| + | surface_area = 2 * math.pi * best_radius * (best_tinggi + best_radius) | ||
| + | |||
| + | print("Optimasi Tabung Hidrogen:") | ||
| + | print("Jari-jari teroptimasi:", optimized_radius, "cm") | ||
| + | print("Tinggi teroptimasi:", optimized_tinggi, "cm") | ||
| + | print("luas permukaan:", surface_area, "cm^2") | ||
| + | |||
| + | [[File:Python Optimasi Volume.jpg]] '''Dengan begitu, didapatlah jari jari sebesar 4 cm dan tinggi sebesar 20 cm (dengan rata-rata lebar mobil 1,8 m dan panjangnya 4 m, maka tabung tersebut dapat muat dalam mobil).''' | ||
| + | |||
| + | '''Ketebalan''' | ||
| + | ---- | ||
| + | |||
| + | Berdasarkan riset yang telah dilakukan, selanjutnya adalah memilih material yang ingin digunakan. Pada study case ini saya ingin menggunakan metal hydride yang salah satu contohnya adalah Aluminium Alloy yang dapat digunakan untuk menyimpan hidrogen. properti Aluminium Alloy dapat dilihat pada link berikut: [https://en.wikipedia.org/wiki/5052_aluminium_alloy]. Dengan begitu kita dapat mencari ketebalan material untuk tabung tersebut dengan coding berikut: | ||
| + | |||
| + | import math | ||
| + | |||
| + | def calculate_thickness(radius, pressure, tensile_strength): | ||
| + | # Menghitung ketebalan tabung berdasarkan persamaan tegangan | ||
| + | thickness = (pressure * radius) / (tensile_strength) | ||
| + | return thickness | ||
| + | |||
| + | radius = 4 | ||
| + | pressure = 0.8 # MPa | ||
| + | |||
| + | # Nilai tensile strength Material | ||
| + | tensile_strength = 228 # Dalam MPa | ||
| + | |||
| + | # Menghitung ketebalan tabung teroptimasi | ||
| + | optimized_thickness = calculate_thickness(radius, pressure, tensile_strength) | ||
| + | |||
| + | print("Optimasi Ketebalan Tabung Hidrogen:") | ||
| + | print("Ketebalan teroptimasi:", optimized_thickness, "cm") | ||
| + | |||
| + | [[File:Optimasi Ketebalan.jpg]] '''Dengan begitu didapatkan juga ketebalan minimal material yang digunakan sebesar 0.01403509 cm.''' | ||
| + | |||
| + | Akan tetapi ketebalan 0.01403509 cm itu terlalu spesifik oleh karena itu, dicarilah beberapa ketebalan yang dijual dan didapatlah perkiraan ketebalan sekitar 0,2 mm atau 0,02 cm hingga 8 mm referensi terdapat pada link berikut [https://store.buymetal.com/aluminum/sheet-plate/5052-h32/aluminum-sheet-5052-h32-0.125.html]. Akan tetapi saya akan menggunakan ketebalan 0,5 mm hingga 5 mm untuk diiterasi apakah material kuat atau tidaknya. Berikut adalah kodingnya: | ||
| + | |||
| + | r = 4 | ||
| + | p = 800000 | ||
| + | t = 0.02 | ||
| + | |||
| + | while t < 0.5: | ||
| + | hoop = (p * r)/(t) | ||
| + | print('Untuk ketebalan', t, 'maka hoop stress =', hoop, "Pa") | ||
| + | t += 0.02 | ||
| + | if hoop > 228000000: #Yield Strength of Aluminium Alloys 5052 | ||
| + | break | ||
| + | |||
| + | [[File:Loop Ketebalan (hoop).jpg]] '''Terbukti bahwa pada ketebalan 0,3 cm material kuat menahan stress yang ada''' | ||
| − | + | '''Budget''' | |
| − | + | ---- | |
| − | |||
| − | |||
| − | + | Dengan budget Rp 500.000, maka dapat diperkiraan harga untuk pembuatan tabung tersebut. Dengan plat aluminium alloy 5052 yang berharga $32.76 / plate ukuran 24" X 12" X 0.125", maka saya dapat menghitung estimasi harga untuk 1 tabung. Berikut adalah hasil kodingnya | |
| − | + | import math | |
| − | + | density_aluminium = 2.68 # Density of aluminium in g/cm^3 | |
| − | # | + | best_radius = 4 # cm |
| − | + | best_tinggi = 20 #cm | |
| − | + | surface_area = 2 * math.pi * best_radius * (best_tinggi + best_radius) | |
| − | |||
| − | |||
| − | # | + | pressure = 0.8 # MPa |
| − | + | tensile_strength = 228 # MPa | |
| − | + | thickness = 0.3 # cm | |
| − | |||
| − | + | weight = (surface_area * thickness * density_aluminium) | |
| − | |||
| − | |||
| − | |||
| − | + | cost_per_plate = 489696 | |
| − | + | volume_plate = 60.96 * 30.48 * thickness | |
| − | + | weight_plate = volume_plate * density_aluminium | |
| − | + | cost_per_weight = cost_per_plate / weight_plate | |
| − | + | cost = weight * cost_per_weight | |
| − | + | budget = 500000 | |
| − | + | n = budget/cost | |
| − | + | rounded = math.floor(n) | |
| − | print(" | + | print("Cost of 1 Hydrogen Storage", cost) |
| − | + | print("Jumlah tabung hidrogen yang dapat dibuat dengan budget adalah", rounded) | |
| − | print(" | ||
| − | [[File: | + | [[File:Pekiraan.jpg]] '''Dengan begitu didapatlah perkiraan cost untuk 1 hydrogen storage adalah 158970.9380714146 dan dengan budget 500k IDR didapatkan 3 tabung hidrogen dengan ukuran radius 4 cm, tinggi 20 cm, dan ketebalan 0,3 cm.''' |
Latest revision as of 16:19, 15 June 2023
Introduction Design & Optimization Hydrogen Storage Made by Vincent Collin 2106632352
Halo, saya Vincent Collin dengan NPM 2106632352.
Sekarang saya berkuliah di UI dengan jurusan Teknik Perkapalan.
Resume Pertemuan 26/05/2023
Pada pertemuan minggu ini, saya mempelajari bahwa metode numerik adalah suatu metode penyelesaian suatu masalah dengan menggunakan pendekatan pendekatan tertentu. Biasanya metode ini melakukan iterasi berkali kali untuk mendapatkan hasil yang lebih akurat. Nilai yang didapat menggunakan metode numerik bukan merupakan nilai yang exact atau absolut, tidak seperti metode analitikal dimana hasilnya exact yang didapat dari rumus. Di dalam Indonesia, kita wajib menganut kepercayaan atau agama masing masing. Sehingga atheis tidak boleh ada di Indonesia karena akan melanggar dasar negara yang ada. Akan tetapi keberadaan agnostik dapat menyebabkan orang untuk bingung memegang kepercayaannya atau tidak. Akan tetapi, sebagai orang percaya kita perlu mempertanyakan kembali apakah kita benar benar percaya akan adanya Tuhan didunia ini. Dan pastinya sebagian besar akan berpikir bahwa Tuhan itu ada di dunia ini.
Design & Optimization of Pressurized Hydrogen Storage
Study Case Design & Optimization of Pressurized Hydrogen Storage Capacity = 1 L Pressure = 8 bar Cost should not exceed 500k IDR
Dalam mendesain tabung hidrogen ini saya mencoba untuk menggunakan tools yang ada salah satunya adalah ChatGPT. Saya menggunakan chat GPT untuk mencari informasi yang saya butuhkan. Berikut adalah hasil respon dan pencarian informasi dari ChatGPT.
Hal yang perlu diperhatikan dalam mendesain tabung hidrogen
1. Kebutuhan System : Volume, tekanan, kapasitas, cara kerja, berapa lama dapat bertahan selama digunakan, safety dan lainnya.
2. Budget yang ada: Maksimal budget.
3. Properti Material: Berdasarkan karakteristik dari hidrogen yang mudah terbakar, maka diperlukan material yang cocok seperti metal hydride
4. Keselamatan: Mempertimbangkan keamanan dari tabung hidrogen dengan tingginya potensi berbahaya dari hidrogen
5. Efisiensi Sistem: Setelah mendesain, kembali memastikan apakah sistem tabung hidrogen ini sudah efisien untuk digunakan.
6. Integrasi sistem: Memperhatikan sistem lain yang mendukung kelancaran sistem tabung hidrogen.
7. Analisa Harga: Kembali mengkonsiderasi harga yang diperlukan dalam mendesain agar sesuai dengan budget yang ada.
8. Terus memantau peraturan dan research terbaru dari tabung hidrogen.
Material Selection Ada beberapa material yang cocok digunakan untuk tabung hidrogen ini diantaranya sebagai berikut:
1. Compressed Gas Storage: Terbuat dari baja atau bahan komposit. Tetapi mencapai kapasitas penyimpanan yang tinggi dengan volume yang kecil akan menjadi tantangan dengan material ini.
2. Metal Hydrides: Senyawa yang terbentuk dari kombinasi logam dan hidrogen. Dapat menyimpan dan melepaskan hidrogen dengan rekasi yang reversibel. Beberapa metal hidrida memiliki kapasitas penyimpanan hidrogen yang tinggi, memungkinkan penyimpanan yang efisien dalam volume kecil. Namun, mereka dapat lebih mahal dibandingkan dengan pilihan lainnya.
3. Carbon Materials: memiliki kemampuan untuk menyerap molekul hidrogen ke permukaannya. Bahan-bahan karbon ini dapat menyimpan hidrogen melalui proses yang disebut fisiorpsi. Bahan berbasis karbon menawarkan kapasitas penyimpanan yang sedang dan dapat menjadi pilihan yang ekonomis.
4. Metal-Organic Frameworks (MOFs): MOFs adalah bahan berpori yang terbuat dari ion-ion logam yang terhubung oleh ligan organik. Mereka memiliki luas permukaan internal yang tinggi, yang memungkinkan penyimpanan hidrogen yang efisien. MOFs dapat disesuaikan untuk mengoptimalkan kapasitas adsorpsi hidrogen dan sifat desorpsi. Namun, biaya sintesis dan skalabilitas bisa menjadi faktor pembatas.
5. Chemical Hydrides: menyimpan hidrogen melalui ikatan kimia. Bahan-bahan ini menawarkan kapasitas penyimpanan hidrogen yang tinggi, tetapi seringkali membutuhkan suhu tinggi atau reaktan tambahan untuk pelepasan hidrogen. Biaya dan praktikabilitas regenerasi bisa menjadi pertimbangan.
Final Report of Design & Optimization Hydrogen Storage
Volume
Dengan adanya 3 batasan yang ditentukan untuk design dan optimasi hydrogen storage ini, yaitu : Volume, Tekanan, dan Biaya. Maka saya dapat memulai desain sekaligus mengoptimasi volume dari hydrogen storage ini. Dengan bantuan software Pycharm, saya dapat mengcoding optimasi volume terlebih dahulu. Berikut adalah hasil kodingannya serta hasilnya.
import math
def objective(r, h):
volume = math.pi * r ** 2 * h
target_volume = 1000 # dalam cm^3 sehingga perhitungan dalam cm.
diff = abs(volume - target_volume)
return diff
initial_radius = 1 initial_tinggi = 1
# Batasan radius dan tinggi min_radius = 0 max_radius = 50 min_tinggi = 0 max_tinggi = 50
# Menginisialisasi nilai terbaik best_radius = initial_radius best_tinggi = initial_tinggi best_diff = objective(initial_radius, initial_tinggi)
# Melakukan grid search
for radius in range(min_radius, max_radius + 1):
for tinggi in range(min_tinggi, max_tinggi + 1):
diff = objective(radius, tinggi)
# Memperbarui nilai terbaik jika ditemukan perbedaan terkecil
if diff < best_diff:
best_radius = radius
best_tinggi = tinggi
best_diff = diff
# Mendapatkan hasil optimasi dan luas permukaan optimized_radius = best_radius optimized_tinggi = best_tinggi surface_area = 2 * math.pi * best_radius * (best_tinggi + best_radius)
print("Optimasi Tabung Hidrogen:")
print("Jari-jari teroptimasi:", optimized_radius, "cm")
print("Tinggi teroptimasi:", optimized_tinggi, "cm")
print("luas permukaan:", surface_area, "cm^2")
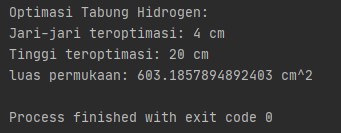 Dengan begitu, didapatlah jari jari sebesar 4 cm dan tinggi sebesar 20 cm (dengan rata-rata lebar mobil 1,8 m dan panjangnya 4 m, maka tabung tersebut dapat muat dalam mobil).
Dengan begitu, didapatlah jari jari sebesar 4 cm dan tinggi sebesar 20 cm (dengan rata-rata lebar mobil 1,8 m dan panjangnya 4 m, maka tabung tersebut dapat muat dalam mobil).
Ketebalan
Berdasarkan riset yang telah dilakukan, selanjutnya adalah memilih material yang ingin digunakan. Pada study case ini saya ingin menggunakan metal hydride yang salah satu contohnya adalah Aluminium Alloy yang dapat digunakan untuk menyimpan hidrogen. properti Aluminium Alloy dapat dilihat pada link berikut: [1]. Dengan begitu kita dapat mencari ketebalan material untuk tabung tersebut dengan coding berikut:
import math
def calculate_thickness(radius, pressure, tensile_strength):
# Menghitung ketebalan tabung berdasarkan persamaan tegangan
thickness = (pressure * radius) / (tensile_strength)
return thickness
radius = 4 pressure = 0.8 # MPa
# Nilai tensile strength Material tensile_strength = 228 # Dalam MPa
# Menghitung ketebalan tabung teroptimasi optimized_thickness = calculate_thickness(radius, pressure, tensile_strength)
print("Optimasi Ketebalan Tabung Hidrogen:")
print("Ketebalan teroptimasi:", optimized_thickness, "cm")
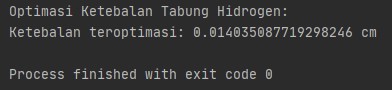 Dengan begitu didapatkan juga ketebalan minimal material yang digunakan sebesar 0.01403509 cm.
Dengan begitu didapatkan juga ketebalan minimal material yang digunakan sebesar 0.01403509 cm.
Akan tetapi ketebalan 0.01403509 cm itu terlalu spesifik oleh karena itu, dicarilah beberapa ketebalan yang dijual dan didapatlah perkiraan ketebalan sekitar 0,2 mm atau 0,02 cm hingga 8 mm referensi terdapat pada link berikut [2]. Akan tetapi saya akan menggunakan ketebalan 0,5 mm hingga 5 mm untuk diiterasi apakah material kuat atau tidaknya. Berikut adalah kodingnya:
r = 4 p = 800000 t = 0.02
while t < 0.5:
hoop = (p * r)/(t)
print('Untuk ketebalan', t, 'maka hoop stress =', hoop, "Pa")
t += 0.02
if hoop > 228000000: #Yield Strength of Aluminium Alloys 5052
break
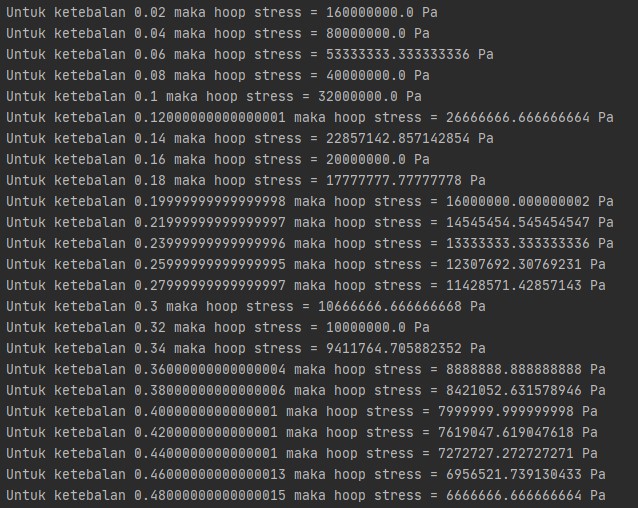 Terbukti bahwa pada ketebalan 0,3 cm material kuat menahan stress yang ada
Terbukti bahwa pada ketebalan 0,3 cm material kuat menahan stress yang ada
Budget
Dengan budget Rp 500.000, maka dapat diperkiraan harga untuk pembuatan tabung tersebut. Dengan plat aluminium alloy 5052 yang berharga $32.76 / plate ukuran 24" X 12" X 0.125", maka saya dapat menghitung estimasi harga untuk 1 tabung. Berikut adalah hasil kodingnya
import math density_aluminium = 2.68 # Density of aluminium in g/cm^3
best_radius = 4 # cm best_tinggi = 20 #cm surface_area = 2 * math.pi * best_radius * (best_tinggi + best_radius)
pressure = 0.8 # MPa tensile_strength = 228 # MPa thickness = 0.3 # cm
weight = (surface_area * thickness * density_aluminium)
cost_per_plate = 489696 volume_plate = 60.96 * 30.48 * thickness weight_plate = volume_plate * density_aluminium cost_per_weight = cost_per_plate / weight_plate cost = weight * cost_per_weight
budget = 500000 n = budget/cost rounded = math.floor(n)
print("Cost of 1 Hydrogen Storage", cost)
print("Jumlah tabung hidrogen yang dapat dibuat dengan budget adalah", rounded)
 Dengan begitu didapatlah perkiraan cost untuk 1 hydrogen storage adalah 158970.9380714146 dan dengan budget 500k IDR didapatkan 3 tabung hidrogen dengan ukuran radius 4 cm, tinggi 20 cm, dan ketebalan 0,3 cm.
Dengan begitu didapatlah perkiraan cost untuk 1 hydrogen storage adalah 158970.9380714146 dan dengan budget 500k IDR didapatkan 3 tabung hidrogen dengan ukuran radius 4 cm, tinggi 20 cm, dan ketebalan 0,3 cm.
