Difference between revisions of "User:Muhammad Adriel Justicio"
(→Final Report Hydrogen Storage Optimization) |
(→Final Report Hydrogen Storage Optimization) |
||
| (11 intermediate revisions by the same user not shown) | |||
| Line 33: | Line 33: | ||
== Final Report Hydrogen Storage Optimization == | == Final Report Hydrogen Storage Optimization == | ||
| + | |||
| + | '''UKURAN TABUNG''' | ||
Dengan optimasi hidrogen yang memiliki kapasitas maksimal 1 liter dan biaya maksimal produksi sebesar Rp. 500.000, maka diperlukan pemrograman untuk menghitung ukuran tabung yang optimal juga | Dengan optimasi hidrogen yang memiliki kapasitas maksimal 1 liter dan biaya maksimal produksi sebesar Rp. 500.000, maka diperlukan pemrograman untuk menghitung ukuran tabung yang optimal juga | ||
| + | |||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
import numpy as np | import numpy as np | ||
| Line 83: | Line 89: | ||
print('Optimal Surface Area:', optimal_surface_area, 'cm^2') | print('Optimal Surface Area:', optimal_surface_area, 'cm^2') | ||
| + | |||
| + | </syntaxhighlight> | ||
Sehingga mendapatkan hasil | Sehingga mendapatkan hasil | ||
Optimal Radius: 5.419262767614773 cm | Optimal Radius: 5.419262767614773 cm | ||
| + | |||
Optimal Height: 10.83851313481415 cm | Optimal Height: 10.83851313481415 cm | ||
| + | |||
Optimal Surface Area: 553.5810444881138 cm^2 | Optimal Surface Area: 553.5810444881138 cm^2 | ||
| + | |||
| + | |||
| + | '''MATERIAL''' | ||
| + | |||
| + | Selanjutnya, pada pemilihan material saya menggunakan material stainless steel AISI 316, dikarenakan material ini umumnya memiliki ketahanan korosi dan sifat mekanik yang bagus juga memiliki harga yang lumayan terjangkau, sehingga sangat cocok untuk pembuatan tangki hidrogen. | ||
| + | |||
| + | Untuk detail properti material akan ditammpilkan sebagai berikut | ||
| + | [[File:Aisi316.png]] | ||
| + | |||
| + | |||
| + | |||
| + | '''KETEBALAN TANGKI''' | ||
| + | |||
| + | Melalui gambar diatas diketahui bahwa Yield Strength dari AISI 316 sebesar 205 Mpa sehingga untuk mengetahui ketebalan dinding tangki dan hoop stress diperlukan kode seperti berikut: | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | r = 5.42e-2 | ||
| + | p = 800000 | ||
| + | t = 2.9e-3 | ||
| + | while t < 12e-3: | ||
| + | hoop = (r * p)/(t) | ||
| + | print('for thickness', t, 'hoop stress =', hoop, "Pa") | ||
| + | t += 1e-3 | ||
| + | if hoop > 205e9: | ||
| + | break | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | Berdasarkan kode diatas kita mendapatkan | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | for thickness 0.0029 hoop stress = 14951724.137931036 Pa | ||
| + | for thickness 0.0039 hoop stress = 11117948.717948718 Pa | ||
| + | for thickness 0.0049 hoop stress = 8848979.591836736 Pa | ||
| + | for thickness 0.0059 hoop stress = 7349152.542372881 Pa | ||
| + | for thickness 0.0069 hoop stress = 6284057.971014493 Pa | ||
| + | for thickness 0.0079 hoop stress = 5488607.594936708 Pa | ||
| + | for thickness 0.008900000000000002 hoop stress = 4871910.11235955 Pa | ||
| + | for thickness 0.009900000000000003 hoop stress = 4379797.979797979 Pa | ||
| + | for thickness 0.010900000000000003 hoop stress = 3977981.6513761454 Pa | ||
| + | for thickness 0.011900000000000004 hoop stress = 3643697.478991595 Pa | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | Dari nilai diatas dapat diketahui bahwa semua nilai ketebalan 2,9 mm hingga 12 mm dengan penambahan 1 mm masih memenuhi batas dari yield strength. | ||
| + | |||
| + | |||
| + | '''BUDGET''' | ||
| + | |||
| + | Tahap terakhir dari optimasi ialah estimasi budget dimana harus tidak melebihi Rp. 500.000,00. Berdasarkan material yang digunakan yaitu, AISI 316, kita dapat menghitung biaya melalui tabel harga berikut : | ||
| + | |||
| + | [[File:Hargaplat.png]] | ||
| + | melalui data diatas , kita bisa lihat dari range tebal 3 mm sampai 12 mm saya memilih ketebalan 6 mm . | ||
| + | |||
| + | |||
| + | |||
| + | '''CONCLUSION''' | ||
| + | |||
| + | Untuk mendesain secara optimal hydorgen storage ini, perlu untuk melakukan perhitungan dimensi radius, dimana pada kasus ini didapatkan sebesar Radius: 5.419262767614773 cm, Height: 10.83851313481415 cm, Surface Area: 553.5810444881138 cm^2. Setelah itu kita perlu untuk mencari material yang tepat dimana Stainless Steel AISI 316 cocok untuk kasus ini. Lalu, diperolehlah range ketebalan dari plat AISI tersebut, sehingga didapatkan bahwa ketebalan 6 mm merupakan ketebalan yang paling optimal dan biayanya tidak lebih dari budget yang sudah ditentukan. | ||
Latest revision as of 22:31, 12 June 2023
BIO
Nama : Muhammad Adriel Justicio
NPM : 2106728156
Kelas : Metode Numerik 02
Tugas Hydrogen Storage Optimization
Hydrogen storage optimization refers to the process of maximizing the efficiency, capacity, and safety of hydrogen storage systems. So, here is the step to optimize it :
1) Define requirements and objectives: Determine the specific requirements for the hydrogen storage system, such as desired storage capacity, operating conditions, safety considerations, and any specific performance targets.
2) Assess available storage technologies: Evaluate various hydrogen storage technologies, such as compressed gas storage, cryogenic liquid storage, metal hydrides, or chemical storage options. Understand the advantages, limitations, costs, and safety aspects of each technology.
3) Analyze system constraints: Identify any limitations or constraints that may impact the design, such as space availability, weight restrictions, infrastructure compatibility, and regulatory requirements. Consider factors like transportation, refueling, and integration with existing systems.
4) Perform modeling and simulation: Use mathematical modeling and simulation tools to analyze and optimize the design. This includes evaluating different system configurations, storage materials, pressure levels, temperature control, and operational strategies to maximize storage capacity, efficiency, and safety.
5) Conduct techno-economic analysis: Assess the economic feasibility of the designed storage system. Consider the costs associated with materials, fabrication, installation, operation, maintenance, and any required safety measures. Compare the economic benefits with the desired objectives and available budget.
6) Evaluate safety measures: Ensure that the storage system design incorporates appropriate safety measures to mitigate potential risks, such as leak detection, pressure relief mechanisms, and protection against overheating or overpressure.
7) Prototype and testing: Build a prototype based on the optimized design and perform rigorous testing to validate its performance and safety. Test the storage system under various operating conditions, such as temperature fluctuations, pressure changes, and mechanical stress.
8) Continual improvement and optimization: Analyze the test results and gather feedback to identify areas for improvement. Iterate the design, simulation, and testing process to optimize the storage system further, considering technological advancements and emerging research in the field.
9) Deployment and monitoring: Once the optimized storage system is ready, deploy it in the desired application or infrastructure. Monitor its performance, efficiency, and safety over time, and make any necessary adjustments or improvements based on real-world usage and feedback.
Collaboration with specialists in hydrogen storage, materials science, engineering, and safety regulations is crucial at every stage to ensure the development of a well-designed and optimized hydrogen storage system.
Final Report Hydrogen Storage Optimization
UKURAN TABUNG
Dengan optimasi hidrogen yang memiliki kapasitas maksimal 1 liter dan biaya maksimal produksi sebesar Rp. 500.000, maka diperlukan pemrograman untuk menghitung ukuran tabung yang optimal juga
import numpy as np
from scipy.optimize import minimize
def calculateSurfaceArea(radius, height):
return 2 * np.pi * radius * height + 2 * np.pi * radius**2
def calculateVolume(radius, height):
return np.pi * radius**2 * height
# Set constant variables
target_volume = 1000 # Constant volume (in cubic centimeters)
# Define the objective function to minimize
def objectiveFunction(x):
radius, height = x
surface_area = calculateSurfaceArea(radius, height)
return surface_area
# Define the constraint function
def constraintFunction(x):
radius, height = x
volume = calculateVolume(radius, height)
return volume - target_volume
# Set initial guess for optimization variables
initial_guess = [1.0, 1.0]
# Define the bounds for the variables
bounds = [(0, None), (0, None)]
# Define the optimization problem
constraint = {'type': 'eq', 'fun': constraintFunction}
# Solve the optimization problem
result = minimize(objectiveFunction, initial_guess, method='SLSQP', bounds=bounds, constraints=constraint)
# Extract the optimized variables
optimal_radius, optimal_height = result.x
# Calculate the optimized surface area
optimal_surface_area = calculateSurfaceArea(optimal_radius, optimal_height)
# Display the results
print('Optimal Radius:', optimal_radius, 'cm')
print('Optimal Height:', optimal_height, 'cm')
print('Optimal Surface Area:', optimal_surface_area, 'cm^2')Sehingga mendapatkan hasil
Optimal Radius: 5.419262767614773 cm
Optimal Height: 10.83851313481415 cm
Optimal Surface Area: 553.5810444881138 cm^2
MATERIAL
Selanjutnya, pada pemilihan material saya menggunakan material stainless steel AISI 316, dikarenakan material ini umumnya memiliki ketahanan korosi dan sifat mekanik yang bagus juga memiliki harga yang lumayan terjangkau, sehingga sangat cocok untuk pembuatan tangki hidrogen.
Untuk detail properti material akan ditammpilkan sebagai berikut
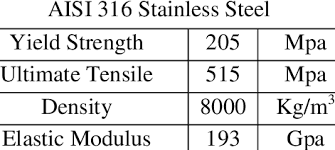
KETEBALAN TANGKI
Melalui gambar diatas diketahui bahwa Yield Strength dari AISI 316 sebesar 205 Mpa sehingga untuk mengetahui ketebalan dinding tangki dan hoop stress diperlukan kode seperti berikut:
r = 5.42e-2
p = 800000
t = 2.9e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9:
break
Berdasarkan kode diatas kita mendapatkan
for thickness 0.0029 hoop stress = 14951724.137931036 Pa
for thickness 0.0039 hoop stress = 11117948.717948718 Pa
for thickness 0.0049 hoop stress = 8848979.591836736 Pa
for thickness 0.0059 hoop stress = 7349152.542372881 Pa
for thickness 0.0069 hoop stress = 6284057.971014493 Pa
for thickness 0.0079 hoop stress = 5488607.594936708 Pa
for thickness 0.008900000000000002 hoop stress = 4871910.11235955 Pa
for thickness 0.009900000000000003 hoop stress = 4379797.979797979 Pa
for thickness 0.010900000000000003 hoop stress = 3977981.6513761454 Pa
for thickness 0.011900000000000004 hoop stress = 3643697.478991595 Pa
Dari nilai diatas dapat diketahui bahwa semua nilai ketebalan 2,9 mm hingga 12 mm dengan penambahan 1 mm masih memenuhi batas dari yield strength.
BUDGET
Tahap terakhir dari optimasi ialah estimasi budget dimana harus tidak melebihi Rp. 500.000,00. Berdasarkan material yang digunakan yaitu, AISI 316, kita dapat menghitung biaya melalui tabel harga berikut :
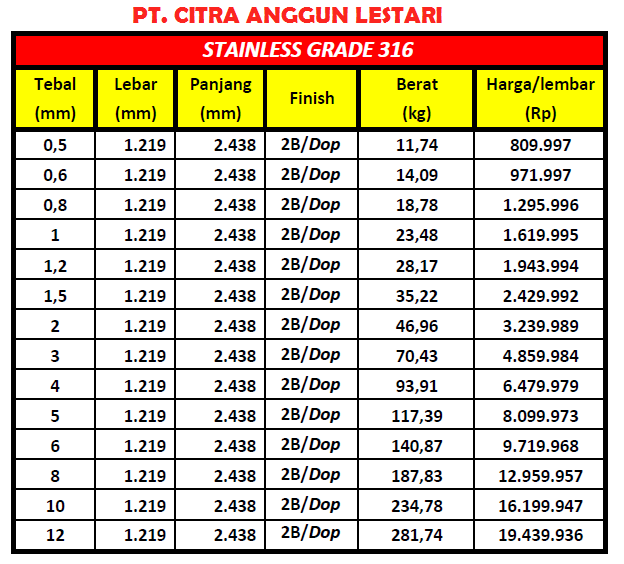 melalui data diatas , kita bisa lihat dari range tebal 3 mm sampai 12 mm saya memilih ketebalan 6 mm .
melalui data diatas , kita bisa lihat dari range tebal 3 mm sampai 12 mm saya memilih ketebalan 6 mm .
CONCLUSION
Untuk mendesain secara optimal hydorgen storage ini, perlu untuk melakukan perhitungan dimensi radius, dimana pada kasus ini didapatkan sebesar Radius: 5.419262767614773 cm, Height: 10.83851313481415 cm, Surface Area: 553.5810444881138 cm^2. Setelah itu kita perlu untuk mencari material yang tepat dimana Stainless Steel AISI 316 cocok untuk kasus ini. Lalu, diperolehlah range ketebalan dari plat AISI tersebut, sehingga didapatkan bahwa ketebalan 6 mm merupakan ketebalan yang paling optimal dan biayanya tidak lebih dari budget yang sudah ditentukan.