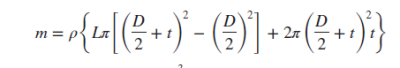Difference between revisions of "Tugas 2 Metnum Dani (Case Study)"
Danisharif (talk | contribs) |
Danisharif (talk | contribs) (→Kode yang digunakan (Python)) |
||
| Line 46: | Line 46: | ||
== Kode yang digunakan (Python) == | == Kode yang digunakan (Python) == | ||
| − | #Import library python untuk membantu menyelesaikan nonlinear programming\ | + | # Import library python untuk membantu menyelesaikan nonlinear programming\ |
from gekko import GEKKO | from gekko import GEKKO | ||
| Line 52: | Line 52: | ||
import numpy as np | import numpy as np | ||
| − | #menyatakan variabel untuk l dan d dengan lb adalah batas bawah dan ub adalah batas atas (berlaku sebagai constrain) | + | # menyatakan variabel untuk l dan d dengan lb adalah batas bawah dan ub adalah batas atas (berlaku sebagai constrain) |
m = GEKKO() | m = GEKKO() | ||
| Line 63: | Line 63: | ||
| − | #Melakukan optimasi variabel l dan d | + | # Melakukan optimasi variabel l dan d |
m.solve() | m.solve() | ||
| Line 74: | Line 74: | ||
| − | #Menyatakan fungsi dari persamaan optimasi storage | + | # Menyatakan fungsi dari persamaan optimasi storage |
| − | #Menghitung massa | + | # Menghitung massa |
def mass (l, d, rho = 2700, t = 0.01) | def mass (l, d, rho = 2700, t = 0.01) | ||
| Line 85: | Line 85: | ||
| − | #Menghitung panjang welding | + | # Menghitung panjang welding |
def weld_length(d : float, t =0.01): | def weld_length(d : float, t =0.01): | ||
| Line 94: | Line 94: | ||
| − | #Menghitung Cost total storage | + | # Menghitung Cost total storage |
def cost(mass, weld_length, material_cost = 2, weld_cost = 15): | def cost(mass, weld_length, material_cost = 2, weld_cost = 15): | ||
Latest revision as of 04:26, 6 June 2023
Contents
[hide]Menentukan Material Tank Storage'
Material yang tepat untuk tank storage hidrogen adalah aluminium dengan keterangan :
p (density) = 2700 kg/m^3
C_m (material cost) = 2 $/kg
C_w (welding cost) = 15 $/m (diasumsikan diperlukan welding pada setiap tutup dan dasar tank
Menentukan dimensi
d = 0.08 m
l = 0.15 m
v ≤ 0.001 → (πd^2 l)/4 = 0.00076 m^3
t = 0.001 m
Menghitung Constrain
d_max = d + 2t = 0.1 → d_max ≤ 0.1
l_max = l + 2t = 0.017 → l_max ≤ 0.17
v_max ≤ 0.001 m^3
Persamaan Optimasi Tank
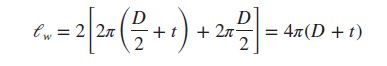 (menentukan panjang welding yang dibutuhkan)
(menentukan panjang welding yang dibutuhkan)
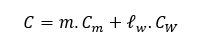 (menghitung cost yang dibutuhkan)
(menghitung cost yang dibutuhkan)
Kode yang digunakan (Python)
# Import library python untuk membantu menyelesaikan nonlinear programming\
from gekko import GEKKO
import numpy as np
# menyatakan variabel untuk l dan d dengan lb adalah batas bawah dan ub adalah batas atas (berlaku sebagai constrain)
m = GEKKO()
d = m.Var(value=0.08, lb=0, ub=0.1)
l = m.Var(value=0.15, lb=0, ub=0.17)
m.Equation(np.pi*(d**2)*l*0.25<=0.001)
# Melakukan optimasi variabel l dan d
m.solve()
print(l.value[0])
print(d.value[0])
-Output adalah nilai l = 0.079164178354, dan nilai d = 0.042635773839
# Menyatakan fungsi dari persamaan optimasi storage
# Menghitung massa
def mass (l, d, rho = 2700, t = 0.01)
mass = rho(l*np.pi(((d*0.5 + t)**2.0) - (d*0.5)**2.0) + 2.0*t*np.pi*((d*0.5 + t)**2.0))
return mass
# Menghitung panjang welding
def weld_length(d : float, t =0.01):
weld_length = (4*np.pi(d + t))
return weld_length
# Menghitung Cost total storage
def cost(mass, weld_length, material_cost = 2, weld_cost = 15):
cost = float(material_cost*mass(l.value[0], d.value[0]) + weld_cost*weld_length(d.value[0]))
return print(f'Least Cost Tank Optimization is, {cost}$')
- Output = Least Cost Tank Optimization is 103.435$
Berdasarkan perhitungan dengan bantuan bahasa pemrograman python, dibutuhkan biaya 103.435$ untuk mendesain storage 0.001 m^3 atau 1 liter dengan material aluminium dengan massa 10.626 kg serta panjang 0.792 m dan diameter 0.426 m