Difference between revisions of "Ivan Kusno"
Ivan Kusno (talk | contribs) (→Material Thickness to Strength) |
Ivan Kusno (talk | contribs) (→My Conscious Efforts on Numerical Method Learning & Its Application in Hydrogen Storage Design Optimization) |
||
| (17 intermediate revisions by the same user not shown) | |||
| Line 74: | Line 74: | ||
'''The Result: ''' | '''The Result: ''' | ||
| − | [(2006.2857142857142, 1), (1025.142857142857, 2), (723.2380952380953, 3), (600.5714285714286, 4), (557.1428571428571, 5), | + | [(2006.2857142857142, 1), (1025.142857142857, 2), (723.2380952380953, 3), (600.5714285714286, 4), (557.1428571428571, 5), (559.6190476190477, 6), (593.7142857142858, 7), (652.2857142857142, 8), (731.3650793650793, 9), (828.5714285714286, 10), (942.3896103896104, 11), (1071.8095238095239, 12), (1216.131868131868, 13), (1374.857142857143, 14), (1547.6190476190475, 15)] |
| − | (559.6190476190477, 6), (593.7142857142858, 7), (652.2857142857142, 8), (731.3650793650793, 9), (828.5714285714286, 10), | ||
| − | (942.3896103896104, 11), (1071.8095238095239, 12), (1216.131868131868, 13), (1374.857142857143, 14), (1547.6190476190475, 15)] | ||
Ranging from '''5 to 6''' cm of the radius, we could get the minimum surface area. To have more precise calculation, we'll use smaller range of iteration. Below are the code: | Ranging from '''5 to 6''' cm of the radius, we could get the minimum surface area. To have more precise calculation, we'll use smaller range of iteration. Below are the code: | ||
| Line 92: | Line 90: | ||
'''The Final Result:''' | '''The Final Result:''' | ||
| − | (minimum surface area, radian): (553.6553471797575, 5.419999999999991) | + | (minimum surface area, radian): (553.6553471797575, 5.419999999999991) |
Thus the minimum surface area 553.7 cm^2 occurs on radius of '''5.42 cm''' | Thus the minimum surface area 553.7 cm^2 occurs on radius of '''5.42 cm''' | ||
| Line 112: | Line 110: | ||
'''The Result''' | '''The Result''' | ||
| − | (Thickness, Pressure): | + | (Thickness, Pressure)(m, Pa): |
[(0.0011, 43360000.0), (0.0012000000000000001, 39418181.81818181), (0.0013000000000000002, 36133333.33333333), (0.0014000000000000002, 33353846.15384615), (0.0015000000000000002, 30971428.571428567), (0.0016000000000000003, 28906666.66666666), (0.0017000000000000003, 27099999.999999996), (0.0018000000000000004, 25505882.35294117), (0.0019000000000000004, 24088888.888888884), (0.0020000000000000005, 22821052.63157894), (0.0021000000000000003, 21679999.999999996), (0.0022, 20647619.047619045), (0.0023, 19709090.909090906), (0.0024, 18852173.91304348), (0.0024999999999999996, 18066666.666666668), (0.0025999999999999994, 17344000.000000004), (0.0026999999999999993, 16676923.07692308), (0.002799999999999999, 16059259.259259263), (0.002899999999999999, 15485714.285714291), (0.0029999999999999988, 14951724.13793104), (0.0030999999999999986, 14453333.33333334)] | [(0.0011, 43360000.0), (0.0012000000000000001, 39418181.81818181), (0.0013000000000000002, 36133333.33333333), (0.0014000000000000002, 33353846.15384615), (0.0015000000000000002, 30971428.571428567), (0.0016000000000000003, 28906666.66666666), (0.0017000000000000003, 27099999.999999996), (0.0018000000000000004, 25505882.35294117), (0.0019000000000000004, 24088888.888888884), (0.0020000000000000005, 22821052.63157894), (0.0021000000000000003, 21679999.999999996), (0.0022, 20647619.047619045), (0.0023, 19709090.909090906), (0.0024, 18852173.91304348), (0.0024999999999999996, 18066666.666666668), (0.0025999999999999994, 17344000.000000004), (0.0026999999999999993, 16676923.07692308), (0.002799999999999999, 16059259.259259263), (0.002899999999999999, 15485714.285714291), (0.0029999999999999988, 14951724.13793104), (0.0030999999999999986, 14453333.33333334)] | ||
| + | |||
| + | Thus, for thickness 1.1 mm, required material that has 43.4 MPa yield strength. The addition of thickness could lowered required material strength, for thickness 3.1 mm, only required 14.45 MPa yield strength. | ||
| + | |||
| + | The '''selection of thickness''' '''will depend on material selection''' based on cost and availability in market | ||
| + | |||
| + | |||
| + | == Material Selection == | ||
| + | |||
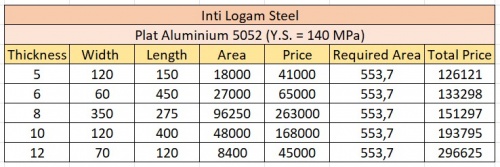
| + | Material selection depends on availability on market. With various choices in market, one of the most suitable choice for hydrogen storage is Aluminium 5052 (AA) that has 140 MPa yield strength with relative affordable price. | ||
| + | |||
| + | [[File:Aluminium 5052 Price.jpg|500px]] | ||
| + | |||
| + | With budget Rp 500,000, is far than enough to purchase sufficient strength for the hydrogen storage. But to have the optimal cost to strength, '''thickness of 8 mm is recommended''' to be chosen, with cost not far above thickness of 6 mm, but has 33% more strength since engineering aspects require safety factor to prevent material failure during application and usage. | ||
| + | |||
| + | |||
| + | == '''My Conscious Efforts on Numerical Method Learning & Its Application in Hydrogen Storage Design Optimization''' == | ||
| + | '''Presentasi Akhir''' | ||
| + | |||
| + | Ivan Kusno | ||
| + | |||
| + | 2106709314 | ||
| + | |||
| + | Metode Numerik-02 | ||
| + | |||
| + | <youtube width="200" height="100">v=6QOkxVa-GT8</youtube> | ||
Latest revision as of 17:34, 12 June 2023
Contents
- 1 Introduction
- 2 Tugas Designing & Calculation of Hydrogen Storage Optimization
- 3 Final Report of Hydrogen Storage Optimization
- 4 Geometry Optimization
- 5 Material Thickness to Strength
- 6 Material Selection
- 7 My Conscious Efforts on Numerical Method Learning & Its Application in Hydrogen Storage Design Optimization
Introduction
Nama: Ivan Kusno
NPM: 2106709314
Metode Numerik 02
Tugas Designing & Calculation of Hydrogen Storage Optimization
Aspects of designing hydrogen storage to be considered
Incorporating calculations related to pressure, cost, and design size can further enhance the optimization process for hydrogen storage. Consider the following aspects:
1. Pressure calculation: Determine the required pressure for the storage system based on the specific application and storage method. Calculate the pressure vessel thickness and volume based on safety factors and desired storage capacity. Consider the material properties and regulatory requirements to ensure the vessel can withstand the calculated pressure.
2. Cost analysis: Evaluate the costs associated with different storage methods, materials, and system designs. Consider factors such as material costs, manufacturing expenses, maintenance requirements, and any additional infrastructure needed for storage. Compare the cost-effectiveness of various options to make informed decisions during the optimization process.
3. Design size optimization: Assess the size and dimensions of the storage system to maximize capacity while considering space limitations and practicality. Calculate the required volume based on storage capacity, pressure, and temperature conditions. Optimize the design to minimize the footprint and ensure efficient use of available space.
4. Energy efficiency analysis: Calculate the energy requirements for compression, cooling, or other processes involved in the storage system. Assess the energy losses and efficiency of different storage methods and designs. Consider energy input and output to optimize the overall energy efficiency of the system.
5. Performance modeling: Utilize mathematical modeling and simulation tools to predict the performance of the storage system under different operating conditions. Incorporate parameters such as pressure, temperature, storage duration, and usage patterns to analyze the system's behavior and identify opportunities for improvement.
6. By integrating these calculations into the optimization process, you can make informed decisions regarding pressure requirements, cost-effectiveness, design size, and energy efficiency. This holistic approach will help optimize hydrogen storage systems for maximum performance and practicality.
Steps in achieving desirable result in designing hydrogen storage
The task of hydrogen storage optimization involves maximizing the effectiveness and capacity of systems used for storing hydrogen. This can be achieved through the following steps:
1. Understand your storage requirements: Gain a clear understanding of the specific needs for hydrogen storage, including capacity, pressure, and temperature range. Take into account the intended application and any limitations or constraints that may exist.
2. Select the appropriate storage method: Evaluate different methods of hydrogen storage, such as compressed gas, liquid hydrogen, metal hydrides, or chemical hydrides. Each method has its own advantages and disadvantages in terms of capacity, energy density, safety, and cost.
3. Optimize the design of the storage system: Consider factors such as the material of the storage vessel, insulation, and pressure containment. Design the storage system in a way that minimizes leaks, ensures safety, and maximizes capacity. Utilize advanced materials and manufacturing techniques to enhance the efficiency of storage.
4. Optimize the operating conditions: Explore the optimal pressure and temperature ranges for hydrogen storage based on the chosen storage method. Higher pressures and lower temperatures generally result in improved storage capacity, but they may also have cost and safety implications. Conduct experiments or simulations to determine the best operating conditions.
5. Enhance storage materials: Conduct research and development to discover new materials that offer higher hydrogen storage capacities and improved kinetics. For example, metal-organic frameworks (MOFs) and carbon-based materials like graphene have shown promise in improving hydrogen storage efficiency. Collaborate with researchers and experts in the field to explore cutting-edge materials.
6. Implement monitoring and control systems for the storage system: Install sensors and monitoring systems to ensure the safe and efficient operation of the hydrogen storage system. Utilize real-time data to optimize storage conditions and promptly detect any abnormalities or leaks.
7. Consider system integration: Take into account the integration of hydrogen storage into larger systems, such as fuel cell vehicles or renewable energy storage systems. Optimize the interface between the storage system and the end-use application to maximize overall efficiency.
8. Conduct comprehensive safety assessments: Prioritize safety in hydrogen storage optimization. Perform thorough safety assessments, including risk analysis, to identify potential hazards and implement appropriate safety measures. Adhere to industry standards and regulations to ensure safe storage and handling practices.
9. Continuously improve through research and development: Stay updated with the latest advancements in hydrogen storage technologies and materials. Collaborate with researchers, universities, and industry experts to leverage their knowledge and expertise. Invest in research and development to continually optimize and innovate hydrogen storage systems.
Final Report of Hydrogen Storage Optimization
Requirements : Designing hydrogen storage at 8 bar with capacity of 1 liter and budget of Rp 500.000
Design variables : Geometry size, material thickness to strength, material selection
Constraints : Price not exceeding Rp 500.000
Objectives : Smallest surface area, thinnest material and withstand 8 bar pressure.
Geometry Optimization
The geometry optimization is to minimize the surface area of the hydrogen storage in order to save material needs. The volume of the storage is fix with 1 liter size but could have numerous combination of radius and height. In order to minimize the surface area, using python will help the long work. Below are the code:
pi=22/7
height = 1000/(pi*radian**2)
mylist = []
for radian in range (1,16):
sur_area = ((2*pi*radian) * height) + ((pi*radian**2)*2)
mylist.append((sur_area,radian))
print(mylist)
The Result:
[(2006.2857142857142, 1), (1025.142857142857, 2), (723.2380952380953, 3), (600.5714285714286, 4), (557.1428571428571, 5), (559.6190476190477, 6), (593.7142857142858, 7), (652.2857142857142, 8), (731.3650793650793, 9), (828.5714285714286, 10), (942.3896103896104, 11), (1071.8095238095239, 12), (1216.131868131868, 13), (1374.857142857143, 14), (1547.6190476190475, 15)]
Ranging from 5 to 6 cm of the radius, we could get the minimum surface area. To have more precise calculation, we'll use smaller range of iteration. Below are the code:
mylist = []
r = 5
while True:
sur_area = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
mylist.append((sur_area, r))
r += 0.01
if r > 6:
break
print('minimum surface area, radian:', min(mylist))
The Final Result:
(minimum surface area, radian): (553.6553471797575, 5.419999999999991)
Thus the minimum surface area 553.7 cm^2 occurs on radius of 5.42 cm
Material Thickness to Strength
The biggest stress in thin wall tube is circumferential stress, so the calculation of the material thickness to the circumferential stress should satisfy its strength in order to ensure the storage is safe. Below are the code to iterate several thickness to required strength:
r = 5.42e-2
p = 800000
t = 1e-3
mylist = []
while t < 3e-3:
circumferential = (r * p)/(t)
t += 0.1e-3
mylist.append((t,circumferential))
print('(Thickness, Pressure):',mylist)
The Result (Thickness, Pressure)(m, Pa):
[(0.0011, 43360000.0), (0.0012000000000000001, 39418181.81818181), (0.0013000000000000002, 36133333.33333333), (0.0014000000000000002, 33353846.15384615), (0.0015000000000000002, 30971428.571428567), (0.0016000000000000003, 28906666.66666666), (0.0017000000000000003, 27099999.999999996), (0.0018000000000000004, 25505882.35294117), (0.0019000000000000004, 24088888.888888884), (0.0020000000000000005, 22821052.63157894), (0.0021000000000000003, 21679999.999999996), (0.0022, 20647619.047619045), (0.0023, 19709090.909090906), (0.0024, 18852173.91304348), (0.0024999999999999996, 18066666.666666668), (0.0025999999999999994, 17344000.000000004), (0.0026999999999999993, 16676923.07692308), (0.002799999999999999, 16059259.259259263), (0.002899999999999999, 15485714.285714291), (0.0029999999999999988, 14951724.13793104), (0.0030999999999999986, 14453333.33333334)]
Thus, for thickness 1.1 mm, required material that has 43.4 MPa yield strength. The addition of thickness could lowered required material strength, for thickness 3.1 mm, only required 14.45 MPa yield strength.
The selection of thickness will depend on material selection based on cost and availability in market
Material Selection
Material selection depends on availability on market. With various choices in market, one of the most suitable choice for hydrogen storage is Aluminium 5052 (AA) that has 140 MPa yield strength with relative affordable price.
With budget Rp 500,000, is far than enough to purchase sufficient strength for the hydrogen storage. But to have the optimal cost to strength, thickness of 8 mm is recommended to be chosen, with cost not far above thickness of 6 mm, but has 33% more strength since engineering aspects require safety factor to prevent material failure during application and usage.
My Conscious Efforts on Numerical Method Learning & Its Application in Hydrogen Storage Design Optimization
Presentasi Akhir
Ivan Kusno
2106709314
Metode Numerik-02