Difference between revisions of "User:Rafaelshia"
Rafaelshia (talk | contribs) (→PEKAN 2) |
Rafaelshia (talk | contribs) (→PEKAN 2) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 63: | Line 63: | ||
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| − | [[File:500px- | + | [[File:500px-Hasil_optimasi.png]] |
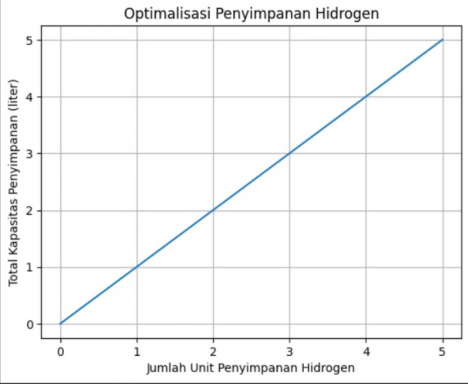
| − | + | Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini : | |
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Harga dan kapasitas | ||
| + | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen | ||
| + | kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit | ||
| + | |||
| + | # Anggaran maksimal | ||
| + | budget_maksimal = 500000 | ||
| + | |||
| + | # Fungsi tujuan | ||
| + | def fungsi_tujuan(x): | ||
| + | return -x | ||
| + | |||
| + | # Kendala | ||
| + | def kendala(x): | ||
| + | return budget_maksimal - (harga_per_unit * x[0]) | ||
| + | |||
| + | kendala_anggaran = [{'type': 'ineq', 'fun': kendala}] | ||
| + | |||
| + | # Nilai awal | ||
| + | x0 = [0] | ||
| + | |||
| + | # Batasan | ||
| + | batas = [(0, None)] | ||
| + | |||
| + | # Membuat fungsi untuk menampilkan hasil | ||
| + | def tampilkan_hasil(solusi): | ||
| + | print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi") | ||
| + | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | ||
| + | print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
| + | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| + | |||
| + | # Menyelesaikan masalah optimisasi | ||
| + | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran) | ||
| + | |||
| + | # Menampilkan hasil | ||
| + | tampilkan_hasil(solusi) | ||
| + | |||
| + | # Menghasilkan grafik | ||
| + | anggaran = np.linspace(0, 10, 100) # Range anggaran | ||
| + | kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran | ||
| + | biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran | ||
| + | |||
| + | plt.figure() | ||
| + | plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan') | ||
| + | plt.plot(anggaran, biaya, label='Total Biaya') | ||
| + | plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal') | ||
| + | plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal') | ||
| + | plt.xlabel('Anggaran') | ||
| + | plt.ylabel('Kapasitas/Biaya') | ||
| + | plt.title('Optimisasi Penyimpanan Hidrogen') | ||
| + | plt.legend() | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | [[File:500px-graph.png]] | ||
Latest revision as of 09:56, 5 June 2023
Introduction
Hi semua! Perkenalkan nama saya Rafael Sinema Hia biasa dipanggil Rafael dengan NPM 2106707183. Saya merupakan mahasiswa Departemen Teknik Mesin FTUI yang saat ini mengikuti kelas Metode Numerik - 01
Hydrogen Storage Optimization
Progress Pekan 1
Tugas : Optimasi tangki hidrogen dengan kapasitas 1 liter, pressure 8 bar, dan biaya produksi maksimal Rp. 500.000
Beberapa faktor yang dapat diperhatikan dalam merancang tangki hidrogen 1. Pilihan Material Tangki: Memilih bahan yang cocok untuk tangki hidrogen. Umumnya, tangki hidrogen dibuat dari baja khusus, aluminium, atau komposit serat karbon. Bahan-bahan ini harus memiliki kekuatan dan ketahanan yang memadai untuk menahan tekanan hidrogen yang tinggi serta tahan terhadap korosi.
2. Kekuatan dan Keamanan: Pastikan tangki dirancang dengan kekuatan yang cukup untuk menahan tekanan hidrogen yang diinginkan tanpa mengalami deformasi atau kebocoran. Keamanan harus menjadi prioritas utama dalam desain tangki hidrogen dengan menyertakan fitur-fitur seperti katup pengaman tekanan berlebihan, perangkat pelindung termal, dan pemisahan antara ruang hidrogen dan lingkungan luar untuk mengurangi risiko kebakaran atau ledakan.
3. Efisiensi Ruang: Desain tangki yang optimal harus memperhatikan efisiensi ruang untuk memaksimalkan kapasitas penyimpanan hidrogen dalam ukuran yang sesuai. Ini dapat mencakup penggunaan desain geometri yang efisien, seperti tangki silinder atau tabung berbentuk silinder, atau penggunaan tangki komposit yang dapat menyesuaikan bentuk dan ukuran dengan lebih baik.
4. Isolasi Termal: Tangki hidrogen harus memiliki isolasi termal yang memadai untuk mengurangi kehilangan energi dan menjaga suhu yang stabil di dalam tangki. Hal ini penting untuk mencegah hidrogen menjadi cair atau menguap secara berlebihan, terutama jika menggunakan tangki cair.
5. Sistem Pengisian dan Pengosongan: Desain tangki hidrogen yang baik harus mempertimbangkan sistem pengisian dan pengosongan yang efisien dan aman. Ini melibatkan pemilihan dan pemasangan katup dan konektor yang sesuai untuk memastikan proses pengisian dan pengosongan dapat dilakukan dengan mudah dan dengan risiko minimal.
6. Pemantauan dan Kontrol: Tangki hidrogen ideal harus dilengkapi dengan sistem pemantauan dan kontrol yang memadai. Hal ini akan memungkinkan pengguna untuk memantau tekanan, suhu, tingkat hidrogen, dan kondisi tangki secara real-time, serta memberikan peringatan atau tindakan perbaikan jika terdeteksi masalah.
7. Sertifikasi dan Standar: Pastikan desain tangki hidrogen memenuhi semua sertifikasi, pedoman, dan standar keamanan yang berlaku. Ini termasuk sertifikasi keamanan industri dan keselamatan seperti ISO 15869, ISO 11439, atau standar lainnya yang relevan.
Beberapa faktor tersebut sangat mempengaruhi keselamatan dan keamanan penggunaan dari tangki hidrogen.
PEKAN 2
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1
# Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini :
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(x):
return budget_maksimal - (harga_per_unit * x[0])
kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]
# Nilai awal
x0 = [0]
# Batasan
batas = [(0, None)]
# Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)
# Menampilkan hasil
tampilkan_hasil(solusi)
# Menghasilkan grafik
anggaran = np.linspace(0, 10, 100) # Range anggaran
kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran
biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran
plt.figure()
plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan')
plt.plot(anggaran, biaya, label='Total Biaya')
plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal')
plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal')
plt.xlabel('Anggaran')
plt.ylabel('Kapasitas/Biaya')
plt.title('Optimisasi Penyimpanan Hidrogen')
plt.legend()
plt.grid(True)
plt.show()