Difference between revisions of "Aria Panungku Gandanegara"
| (14 intermediate revisions by 2 users not shown) | |||
| Line 65: | Line 65: | ||
'''Stress Analysis''' | '''Stress Analysis''' | ||
| − | [[File: | + | [[File:Tabung 1 liter.jpg]] |
| + | |||
| + | |||
| + | [[File:Safety_factor.jpg]] | ||
| + | |||
| + | Demikianlah hasil dari analisis stress analysis ini. Dengan menggunakan metode yang tepat dan data yang tersedia, setelah berhasil menghitung dan menganalisis ketegangan dalam struktur yang relevan. Hasil ini memberikan pemahaman yang lebih baik tentang bagaimana tegangan dan deformasi bekerja dalam tabung hidrogen tersebut. | ||
| + | |||
| + | == Pressurized hydrogen storage optimization == | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def calculate_volume(r, h): | ||
| + | volume = math.pi * r**2 * h | ||
| + | return volume | ||
| + | |||
| + | def calculate_pressure(volume, r): | ||
| + | pressure = (volume * 1e-3) / (math.pi * r**2) | ||
| + | return pressure | ||
| + | |||
| + | def objective(x): | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | volume = calculate_volume(r, h) | ||
| + | return -volume # Negatifkan volume untuk maksimisasi | ||
| + | |||
| + | # Batasan geometri: jari-jari (r) harus lebih kecil dari setengah diameter dan tinggi (h) lebih kecil dari tinggi awal | ||
| + | def constraint(x): | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | return [6 - r, 8.8464 - h] | ||
| + | |||
| + | # Batasan tekanan: tekanan harus kurang dari atau sama dengan 8 bar | ||
| + | def pressure_constraint(x): | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | volume = calculate_volume(r, h) | ||
| + | pressure = calculate_pressure(volume, r) | ||
| + | return pressure - 8 # Batasan tekanan maksimum 8 bar | ||
| + | |||
| + | # Inisialisasi nilai awal untuk jari-jari dan tinggi tabung | ||
| + | x0 = [6, 8.8464] | ||
| + | |||
| + | # Definisikan batasan dan jenis batasan (<=) | ||
| + | constraint1 = {'type': 'ineq', 'fun': constraint} | ||
| + | constraint2 = {'type': 'ineq', 'fun': pressure_constraint} | ||
| + | |||
| + | # Panggil fungsi minimize untuk mencari solusi optimisasi | ||
| + | sol = minimize(objective, x0, constraints=[constraint1, constraint2]) | ||
| + | |||
| + | # Ambil hasil optimisasi | ||
| + | optimized_r = sol.x[0] | ||
| + | optimized_h = sol.x[1] | ||
| + | optimized_volume = calculate_volume(optimized_r, optimized_h) | ||
| + | optimized_pressure = calculate_pressure(optimized_volume, optimized_r) | ||
| + | |||
| + | print("Jari-jari optimal:", optimized_r, "cm") | ||
| + | print("Tinggi optimal:", optimized_h, "cm") | ||
| + | print("Volume optimal:", optimized_volume, "cm^3") | ||
| + | print("Tekanan optimal:", optimized_pressure, "bar") | ||
| + | |||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Dari kode di atas, kita berhasil menemukan nilai optimal untuk jari-jari tabung sebesar 6 cm dan tinggi tabung sebesar 8,8464 cm. Dengan parameter tersebut, volume tabung yang optimal adalah 1000.504226 cm^3, sedangkan tekanan maksimal yang dihasilkan adalah sebesar 0,00884 bar. | ||
| + | lalu untuk luas permukaan tabung | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | |||
| + | def calculate_surface_area(diameter, tinggi): | ||
| + | r = diameter / 2 | ||
| + | luas_lingkaran = math.pi * r**2 | ||
| + | luas_selimut = 2 * math.pi * r * tinggi | ||
| + | luas_permukaan = 2 * luas_lingkaran + luas_selimut | ||
| + | return luas_permukaan | ||
| + | |||
| + | diameter = 8 # cm | ||
| + | tinggi = 8.8464 # cm | ||
| + | |||
| + | luas_permukaan = calculate_surface_area(diameter, tinggi) | ||
| + | |||
| + | print("Luas Permukaan Tabung:", luas_permukaan, "cm^2") | ||
| + | |||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Berdasarkan hasil dari penggunaan kode dan penerapan rumus untuk menghitung luas permukaan tabung, ditemukan bahwa luas permukaan tabung tersebut adalah sebesar 559.6960 cm^2. Hasil ini menunjukkan ukuran total area yang meliputi kedua tutup tabung dan selimutnya. Luas permukaan tabung memiliki peran penting dalam berbagai aplikasi dan perhitungan, seperti dalam memahami pertukaran panas, penyerapan cahaya, atau pemodelan mekanika fluida. Dengan mengetahui luas permukaan tabung, kita dapat melakukan analisis lebih lanjut terkait sifat-sifat fisik dan kinerja tabung tersebut. | ||
| + | |||
| + | |||
| + | [[File:tabelll12.jpg]] | ||
| + | |||
| + | [[File:harga_pas.jpg]] | ||
| + | |||
| + | Berdasarkan anggaran yang telah ditentukan sebesar Rp 500.000, dengan mempertimbangkan range harga tangki dengan ketebalan yang tepat sebesar 8 mm seharga Rp. 244.072,23, maka sisa anggaran yang tersedia dapat dialokasikan untuk membeli katup dan pengatur tekanan. Dengan demikian, pengguna dapat memenuhi kebutuhan tangki dengan ketebalan yang sesuai dan masih memiliki sisa anggaran untuk membeli komponen tambahan yang diperlukan. | ||
| + | |||
| + | Link Video youtube presentasi : | ||
| + | [[Media:https://youtu.be/k9iJaQvKDWQ]] | ||
Latest revision as of 03:53, 12 June 2023
Hydrogen Optimization
Karena permintaan akan sumber energi yang bersih dan berkelanjutan terus meningkat, penyimpanan hidrogen memainkan peran penting dalam memungkinkan penggunaan hidrogen secara luas sebagai pembawa energi. Merancang sistem penyimpanan hidrogen yang optimal sangat penting untuk mengatasi tantangan yang terkait dengan transportasi, distribusi, dan pemanfaatan hidrogen. Esai ini mengeksplorasi pertimbangan utama dan teknologi yang terlibat dalam merancang sistem penyimpanan hidrogen yang efisien dan aman, menyoroti pentingnya optimalisasi penyimpanan dalam memajukan ekonomi hidrogen.
Pertimbangan untuk Desain Penyimpanan Hidrogen yang Optimal:
Kepadatan Energi: Memaksimalkan kepadatan energi penyimpanan hidrogen sangat penting untuk memastikan pemanfaatan ruang yang efisien dan memfasilitasi transportasi jarak jauh. Metode penyimpanan kepadatan tinggi memungkinkan lebih banyak hidrogen disimpan dalam volume atau massa tertentu, meminimalkan jejak penyimpanan dan memungkinkan aplikasi praktis di berbagai sektor.
Keselamatan: Pertimbangan keselamatan sangat penting dalam merancang sistem penyimpanan hidrogen. Hidrogen sangat mudah terbakar, dan setiap solusi penyimpanan harus mengatasi masalah keamanan secara efektif. Desain harus menggabungkan fitur keselamatan yang sesuai, seperti mekanisme pelepas tekanan, sistem deteksi kebocoran, dan bahan penahan yang kuat, untuk mencegah kecelakaan dan memastikan penyimpanan hidrogen yang aman.
Efisiensi Penyimpanan: Efisiensi sistem penyimpanan hidrogen mengacu pada rasio energi yang disimpan dengan energi yang dibutuhkan untuk penyimpanan. Merancang teknologi penyimpanan dengan efisiensi tinggi membantu meminimalkan kehilangan energi selama penyimpanan dan meningkatkan proses konversi energi secara keseluruhan. Metode penyimpanan yang efisien juga berkontribusi untuk mengurangi biaya produksi dan pemanfaatan hidrogen.
Skalabilitas dan Fleksibilitas: Sistem penyimpanan hidrogen yang optimal harus dapat diskalakan untuk mengakomodasi berbagai permintaan dan skenario pasokan. Itu juga harus dapat disesuaikan dengan aplikasi yang berbeda, mulai dari penyimpanan stasioner untuk pembangkit listrik hingga penyimpanan bergerak untuk transportasi. Skalabilitas dan fleksibilitas memungkinkan integrasi penyimpanan hidrogen dengan infrastruktur yang ada dan memfasilitasi transisi ke sistem energi berbasis hidrogen.
Teknologi Penyimpanan Hidrogen:
Penyimpanan Gas Terkompresi: Mengompresi gas hidrogen dan menyimpannya dalam silinder atau tangki bertekanan tinggi adalah salah satu metode penyimpanan yang paling banyak digunakan. Teknologi ini menawarkan kepadatan energi yang relatif tinggi dan sangat cocok untuk aplikasi stasioner dan seluler. Namun, hal itu membutuhkan bahan penahan yang kuat dan dapat menyebabkan kehilangan energi selama proses kompresi dan dekompresi.
Penyimpanan Hidrogen Cair: Mendinginkan gas hidrogen ke suhu yang sangat rendah (-253°C) memungkinkannya mencair, menghasilkan pengurangan volume yang signifikan. Penyimpanan hidrogen cair menawarkan kepadatan energi yang tinggi dan umumnya digunakan dalam eksplorasi ruang angkasa dan aplikasi industri tertentu. Namun, itu membutuhkan peralatan kriogenik untuk mempertahankan suhu rendah dan menimbulkan tantangan dalam hal pendidihan dan isolasi.
Penyimpanan Hidrogen Solid-State: Penyimpanan solid-state melibatkan penggunaan bahan yang dapat menyerap dan melepaskan hidrogen, yang dikenal sebagai bahan penyimpanan hidrogen atau hidrida. Bahan-bahan ini menyimpan hidrogen melalui adsorpsi kimia atau fisik, menyediakan opsi penyimpanan yang aman dan reversibel. Teknologi penyimpanan solid-state terus berkembang dan menawarkan potensi kapasitas penyimpanan yang tinggi dan peningkatan keamanan.
Penyimpanan Hidrogen Kimia: Penyimpanan hidrogen kimia melibatkan pengubahan hidrogen menjadi senyawa kimia untuk penyimpanan dan transportasi yang lebih mudah. Contohnya termasuk hidrogenasi senyawa organik dan penyimpanan hidrogen reversibel dalam hidrida logam. Penyimpanan bahan kimia dapat memberikan kepadatan energi yang tinggi tetapi seringkali membutuhkan langkah pemrosesan tambahan untuk pelepasan hidrogen.
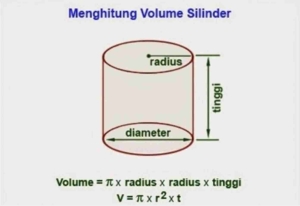
Mengitung Dimensi Tangki
Dari gambar tersebut kita isa menentukan volume tangki dan menggunakan persamaan volume untuk mencari tingi dari tangki tersebut. jika ktia asumsikan diameter tangki adalah sebesar 12cm maka kita dapat menentukan tingginya dengan =
h = 1000/3,14 x 6 x 6 h = 8,846433
maka dari itu, tinggi sebesar 8,846433 cm dengan diameter 6 cm dapat menampung 1 liter hidrogen.
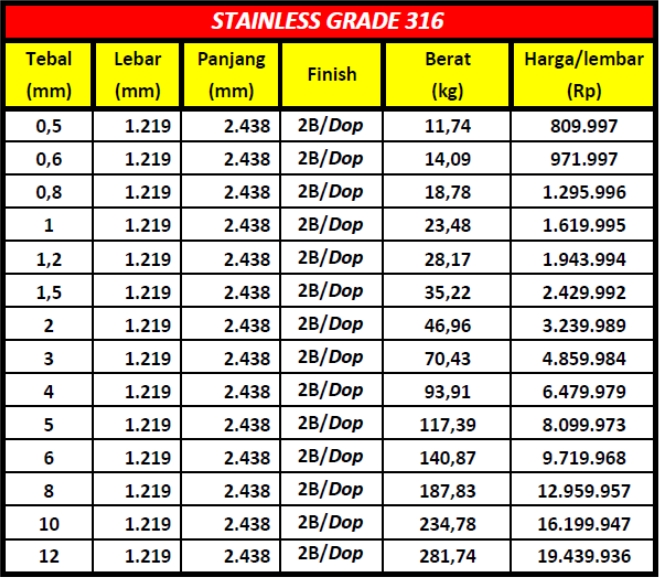
32Pemilihan material Material yang digunakan dengan budget 500.000 adalah ASTM A36 sheet metal : Yield Strength (Sy)2; 36 Ksi Allowable Stress Value : 2/3 x Sy = 24 Ksi / 165,474 Mpa
Rumus Ketebalan untuk arah tegang :
t = PR/(SE - 0,6P)
t < 0,5R
t < 0,385SE
dimana : E = kekuatan efisiensi P = tekanan dalam R = radius dalam S = tegangan pada bahan T = ketebalan silinder
rumus ketebalan untuk arah tegangan longitudinal : t = PR/(SE + 0,4P) t < 0,5R P < 1,25SE
toleransi = 1 mm = 0,039 inchi3 t = 117x(1,6+0,039) / (24000x0,6)-(0,6x117) = 0,0133 + toleransi3 = 0,052 inch t = 1,32 mm (keliling) ; t = 1,2 mm (Longitudinal) Jadi, ketebalan lembaran logam minimal adalah 1,4 mm
Stress Analysis
Demikianlah hasil dari analisis stress analysis ini. Dengan menggunakan metode yang tepat dan data yang tersedia, setelah berhasil menghitung dan menganalisis ketegangan dalam struktur yang relevan. Hasil ini memberikan pemahaman yang lebih baik tentang bagaimana tegangan dan deformasi bekerja dalam tabung hidrogen tersebut.
Pressurized hydrogen storage optimization
import math
from scipy.optimize import minimize
def calculate_volume(r, h):
volume = math.pi * r**2 * h
return volume
def calculate_pressure(volume, r):
pressure = (volume * 1e-3) / (math.pi * r**2)
return pressure
def objective(x):
r = x[0]
h = x[1]
volume = calculate_volume(r, h)
return -volume # Negatifkan volume untuk maksimisasi
# Batasan geometri: jari-jari (r) harus lebih kecil dari setengah diameter dan tinggi (h) lebih kecil dari tinggi awal
def constraint(x):
r = x[0]
h = x[1]
return [6 - r, 8.8464 - h]
# Batasan tekanan: tekanan harus kurang dari atau sama dengan 8 bar
def pressure_constraint(x):
r = x[0]
h = x[1]
volume = calculate_volume(r, h)
pressure = calculate_pressure(volume, r)
return pressure - 8 # Batasan tekanan maksimum 8 bar
# Inisialisasi nilai awal untuk jari-jari dan tinggi tabung
x0 = [6, 8.8464]
# Definisikan batasan dan jenis batasan (<=)
constraint1 = {'type': 'ineq', 'fun': constraint}
constraint2 = {'type': 'ineq', 'fun': pressure_constraint}
# Panggil fungsi minimize untuk mencari solusi optimisasi
sol = minimize(objective, x0, constraints=[constraint1, constraint2])
# Ambil hasil optimisasi
optimized_r = sol.x[0]
optimized_h = sol.x[1]
optimized_volume = calculate_volume(optimized_r, optimized_h)
optimized_pressure = calculate_pressure(optimized_volume, optimized_r)
print("Jari-jari optimal:", optimized_r, "cm")
print("Tinggi optimal:", optimized_h, "cm")
print("Volume optimal:", optimized_volume, "cm^3")
print("Tekanan optimal:", optimized_pressure, "bar")Dari kode di atas, kita berhasil menemukan nilai optimal untuk jari-jari tabung sebesar 6 cm dan tinggi tabung sebesar 8,8464 cm. Dengan parameter tersebut, volume tabung yang optimal adalah 1000.504226 cm^3, sedangkan tekanan maksimal yang dihasilkan adalah sebesar 0,00884 bar. lalu untuk luas permukaan tabung
import math
def calculate_surface_area(diameter, tinggi):
r = diameter / 2
luas_lingkaran = math.pi * r**2
luas_selimut = 2 * math.pi * r * tinggi
luas_permukaan = 2 * luas_lingkaran + luas_selimut
return luas_permukaan
diameter = 8 # cm
tinggi = 8.8464 # cm
luas_permukaan = calculate_surface_area(diameter, tinggi)
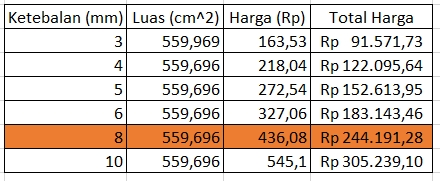
print("Luas Permukaan Tabung:", luas_permukaan, "cm^2")Berdasarkan hasil dari penggunaan kode dan penerapan rumus untuk menghitung luas permukaan tabung, ditemukan bahwa luas permukaan tabung tersebut adalah sebesar 559.6960 cm^2. Hasil ini menunjukkan ukuran total area yang meliputi kedua tutup tabung dan selimutnya. Luas permukaan tabung memiliki peran penting dalam berbagai aplikasi dan perhitungan, seperti dalam memahami pertukaran panas, penyerapan cahaya, atau pemodelan mekanika fluida. Dengan mengetahui luas permukaan tabung, kita dapat melakukan analisis lebih lanjut terkait sifat-sifat fisik dan kinerja tabung tersebut.
Berdasarkan anggaran yang telah ditentukan sebesar Rp 500.000, dengan mempertimbangkan range harga tangki dengan ketebalan yang tepat sebesar 8 mm seharga Rp. 244.072,23, maka sisa anggaran yang tersedia dapat dialokasikan untuk membeli katup dan pengatur tekanan. Dengan demikian, pengguna dapat memenuhi kebutuhan tangki dengan ketebalan yang sesuai dan masih memiliki sisa anggaran untuk membeli komponen tambahan yang diperlukan.
Link Video youtube presentasi : Media:https://youtu.be/k9iJaQvKDWQ