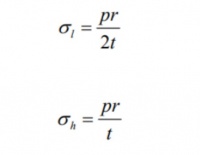Difference between revisions of "Ibrahim Ardhi Pancamakarim"
(→Geometry Constrain Calculation) |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Ibrahim Ardhi.jpg|300x300px]] | [[File:Ibrahim Ardhi.jpg|300x300px]] | ||
| − | Hello, my name is Ibrahim Ardhi (2106651105), and I am currently pursuing a Bachelor's degree in Mechanical Engineering, University of Indonesia. As a future engineer, I am excited to embark my studies and to keep gain knowledge. Remember, stay | + | Hello, my name is Ibrahim Ardhi (2106651105), and I am currently pursuing a Bachelor's degree in Mechanical Engineering, University of Indonesia. As a future engineer, I am excited to embark my studies and to keep gain knowledge. Remember, stay conscious! |
| + | |||
| + | =='''Consciousness'''== | ||
| + | Consciousness is a fundamental aspect of human existence. It has to do with your ability to perceive yourself, your environment, and your mental state. It is a complex phenomenon that includes many aspects such as self-awareness, awareness, thoughts, emotions, and the ability to observe oneself. Human consciousness enables us to experience the world, make decisions, and interact in meaningful ways with others. It is the basis of our identity and shapes our understanding of reality. Through awareness, we can reflect on our own thoughts and feelings, reflect on the past and future, and think critically. | ||
=='''Design & Optimization of Pressurized Hydrogen Storage'''== | =='''Design & Optimization of Pressurized Hydrogen Storage'''== | ||
| Line 62: | Line 65: | ||
Remember, a comprehensive risk assessment should be conducted by individuals with expertise in hydrogen storage systems and safety protocols. They can provide further insights into the specific risks associated with your design and help develop appropriate risk mitigation strategies. | Remember, a comprehensive risk assessment should be conducted by individuals with expertise in hydrogen storage systems and safety protocols. They can provide further insights into the specific risks associated with your design and help develop appropriate risk mitigation strategies. | ||
| − | ==Geometry Constrain Calculation== | + | =='''Geometry Constrain Calculation'''== |
To optimize hydrogen storage with a capacity of 1 liter, a pressure of 8 bar, and a maximum budget of 500,000, these calculations can be done using Python or manually. The following is the calculation using Python: | To optimize hydrogen storage with a capacity of 1 liter, a pressure of 8 bar, and a maximum budget of 500,000, these calculations can be done using Python or manually. The following is the calculation using Python: | ||
| Line 104: | Line 107: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
From the code above, we obtain the following data: | From the code above, we obtain the following data: | ||
| + | |||
Optimal Radius: 54.19 mm | Optimal Radius: 54.19 mm | ||
| + | |||
Optimal Height: 108.38 mm | Optimal Height: 108.38 mm | ||
| + | |||
Minimum Surface Area: 55358.10 mm² | Minimum Surface Area: 55358.10 mm² | ||
This code is performing an optimization calculation for a geometric problem. Specifically, it aims to minimize the surface area of a cylinder subject to a volume constraint. The cylinder represents a hydrogen storage tank with a given volume capacity. The objective function calculates the surface area of the cylinder, which is to be minimized. The constraint function ensures that the volume of the cylinder meets a specified value (in this case, 1000 units). The `minimize` function from the `scipy.optimize` module is used to find the optimal values for the radius and height of the cylinder that satisfy the volume constraint while minimizing the surface area. The code then prints the optimal values for the radius and height, as well as the minimum surface area achieved. | This code is performing an optimization calculation for a geometric problem. Specifically, it aims to minimize the surface area of a cylinder subject to a volume constraint. The cylinder represents a hydrogen storage tank with a given volume capacity. The objective function calculates the surface area of the cylinder, which is to be minimized. The constraint function ensures that the volume of the cylinder meets a specified value (in this case, 1000 units). The `minimize` function from the `scipy.optimize` module is used to find the optimal values for the radius and height of the cylinder that satisfy the volume constraint while minimizing the surface area. The code then prints the optimal values for the radius and height, as well as the minimum surface area achieved. | ||
| + | |||
| + | =='''Material Strength Constraint Code'''== | ||
| + | |||
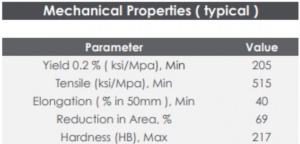
| + | [[File:Materialstregthanalysisronna.jpg|300x300px]] | ||
| + | |||
| + | In a pressurized storage system, the material strength and plate thickness of the tank must be able to withstand the pressure exerted by the gas in all directions on the tank walls. Specifically, this 1-liter hydrogen tank has a maximum pressure limit of 8 bar. The plate thickness of the tank can be calculated using the following hoop stress equation. | ||
| + | |||
| + | [[File:Formula_hoop_equation.jpg|200x200px]] | ||
| + | |||
| + | The range of plate thickness should not be less than 1/5 of the tank radius. According to Section VIII D.1 of the ASME BPV Code, the minimum plate thickness of the tank should be 1/16 inch or 1.59 mm, disregarding corrosion, material, or dimensional considerations. In this calculation, we will iterate from a minimum radius of 2.7 mm to 11.05 mm, with an increment of 1 mm for each iteration. | ||
| + | |||
| + | Therefore, the material that will be used in the construction of this hydrogen tank is AISI 316 austenitic stainless steel. | ||
| + | |||
| + | '''Iteration Process''' | ||
| + | Phyton Code | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | r = 5.42e-2 | ||
| + | p = 800000 | ||
| + | t = 2.9e-3 | ||
| + | |||
| + | while t < 12e-3: | ||
| + | hoop = (r * p)/(t) | ||
| + | print('for thickness', t, 'hoop stress =', hoop, "Pa") | ||
| + | t += 1e-3 | ||
| + | if hoop > 205e9: | ||
| + | break | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | '''Result''' | ||
| + | |||
| + | for thickness 0.004099999999999999 hoop stress = 10770731.707317077 Pa | ||
| + | for thickness 0.004199999999999999 hoop stress = 10514285.714285716 Pa | ||
| + | for thickness 0.004299999999999999 hoop stress = 10269767.441860467 Pa | ||
| + | for thickness 0.004399999999999999 hoop stress = 10036363.636363639 Pa | ||
| + | for thickness 0.0045 hoop stress = 9813333.333333334 Pa | ||
| + | for thickness 0.0046 hoop stress = 9600000.0 Pa | ||
| + | for thickness 0.0047 hoop stress = 9395744.680851063 Pa | ||
| + | for thickness 0.0048000000000000004 hoop stress = 9200000.0 Pa | ||
| + | for thickness 0.004900000000000001 hoop stress = 9012244.897959182 Pa | ||
| + | for thickness 0.005000000000000001 hoop stress = 8831999.999999998 Pa | ||
| + | for thickness 0.005100000000000001 hoop stress = 8658823.529411763 Pa | ||
| + | for thickness 0.0052000000000000015 hoop stress = 8492307.69230769 Pa | ||
| + | for thickness 0.005300000000000002 hoop stress = 8332075.47169811 Pa | ||
| + | for thickness 0.005400000000000002 hoop stress = 8177777.777777774 Pa | ||
| + | for thickness 0.005500000000000002 hoop stress = 8029090.909090905 Pa | ||
| + | for thickness 0.0056000000000000025 hoop stress = 7885714.285714282 Pa | ||
| + | for thickness 0.005700000000000003 hoop stress = 7747368.421052628 Pa | ||
| + | for thickness 0.005800000000000003 hoop stress = 7613793.103448272 Pa | ||
| + | for thickness 0.005900000000000003 hoop stress = 7484745.76271186 Pa | ||
| + | for thickness 0.006000000000000004 hoop stress = 7359999.999999995 Pa | ||
| + | for thickness 0.006100000000000004 hoop stress = 7239344.262295078 Pa | ||
| + | for thickness 0.006200000000000004 hoop stress = 7122580.645161286 Pa | ||
| + | for thickness 0.006300000000000004 hoop stress = 7009523.809523805 Pa | ||
| + | for thickness 0.006400000000000005 hoop stress = 6899999.999999995 Pa | ||
| + | for thickness 0.006500000000000005 hoop stress = 6793846.153846148 Pa | ||
| + | for thickness 0.006600000000000005 hoop stress = 6690909.090909085 Pa | ||
| + | for thickness 0.006700000000000005 hoop stress = 6591044.776119398 Pa | ||
| + | for thickness 0.006800000000000006 hoop stress = 6494117.6470588185 Pa | ||
| + | for thickness 0.006900000000000006 hoop stress = 6399999.999999994 Pa | ||
| + | for thickness 0.007000000000000006 hoop stress = 6308571.428571423 Pa | ||
| + | |||
| + | |||
| + | The provided code calculates the hoop stress by examining various thickness values between 2.9 mm and 12 mm. It includes a condition that stops the iteration if the total hoop stress exceeds the yield strength of AISI 316 stainless steel. The results indicate that all thickness values from 2.9 mm to 12 mm, incremented by 1 mm, meet the yield strength criteria. The code produces the following calculation results, demonstrating that the hoop stress remains significantly below the yield strength of 205 MPa. | ||
| + | |||
| + | =='''Cost Constraint Code'''== | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Price and capacity | ||
| + | price_per_unit = 100000 # Price per unit of hydrogen storage | ||
| + | capacity_per_unit = 1 # Capacity of hydrogen storage per unit | ||
| + | |||
| + | # Maximum budget | ||
| + | max_budget = 500000 | ||
| + | |||
| + | # Objective function | ||
| + | def objective_function(x): | ||
| + | return -x * capacity_per_unit | ||
| + | |||
| + | # Constraint function | ||
| + | def budget_constraint(purchase_amount): | ||
| + | return max_budget - (price_per_unit * purchase_amount) | ||
| + | |||
| + | budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint} | ||
| + | |||
| + | # Initial value | ||
| + | x0 = 0 | ||
| + | |||
| + | # Bounds | ||
| + | bounds = [(0, None)] | ||
| + | |||
| + | # Solve the optimization problem | ||
| + | solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq]) | ||
| + | |||
| + | # Print the results | ||
| + | print("Status:", "Optimal" if solution.success else "No solution found") | ||
| + | print("Number of hydrogen storage units to be purchased:", solution.x[0]) | ||
| + | print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters") | ||
| + | print("Total cost:", solution.x[0] * price_per_unit, "Rupiah") | ||
| + | |||
| + | |||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Price and capacity | ||
| + | price_per_unit = 100000 # Price per unit of hydrogen storage | ||
| + | capacity_per_unit = 1 # Capacity of hydrogen storage per unit | ||
| + | |||
| + | # Maximum budget | ||
| + | max_budget = 500000 | ||
| + | |||
| + | # Objective function | ||
| + | def objective_function(x): | ||
| + | return -x * capacity_per_unit | ||
| + | |||
| + | # Constraint function | ||
| + | def budget_constraint(purchase_amount): | ||
| + | return max_budget - (price_per_unit * purchase_amount) | ||
| + | |||
| + | budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint} | ||
| + | |||
| + | # Initial value | ||
| + | x0 = 0 | ||
| + | |||
| + | # Bounds | ||
| + | bounds = [(0, None)] | ||
| + | |||
| + | # Solve the optimization problem | ||
| + | solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq]) | ||
| + | |||
| + | # Print the results | ||
| + | print("Status:", "Optimal" if solution.success else "No solution found") | ||
| + | print("Number of hydrogen storage units to be purchased:", solution.x[0]) | ||
| + | print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters") | ||
| + | print("Total cost:", solution.x[0] * price_per_unit, "Rupiah") | ||
| + | </syntaxhighlight> | ||
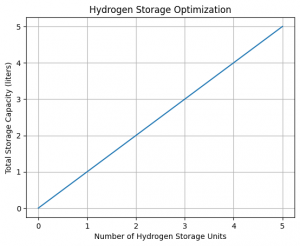
| + | This code shows us that the optimal results for creating a hydrogen storage system with a budget of Rp500.000,00 is to make 5 tanks with a capacity of 1 liters each. | ||
| + | |||
| + | We can also make a graph through this code above: | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | # Price and capacity | ||
| + | price_per_unit = 100000 # Price per unit of hydrogen storage | ||
| + | capacity_per_unit = 1 # Capacity of hydrogen storage per unit | ||
| + | |||
| + | # Maximum budget | ||
| + | max_budget = 500000 | ||
| + | |||
| + | # Initialize variables | ||
| + | best_unit_count = 0 | ||
| + | best_total_capacity = 0 | ||
| + | best_total_cost = 0 | ||
| + | |||
| + | # Initialize lists for the graph | ||
| + | unit_count_list = [] | ||
| + | total_capacity_list = [] | ||
| + | |||
| + | # Iterate to find the optimal solution | ||
| + | for unit_count in range(int(max_budget / price_per_unit) + 1): | ||
| + | total_capacity = unit_count * capacity_per_unit | ||
| + | total_cost = unit_count * price_per_unit | ||
| + | |||
| + | if total_capacity > best_total_capacity and total_cost <= max_budget: | ||
| + | best_unit_count = unit_count | ||
| + | best_total_capacity = total_capacity | ||
| + | best_total_cost = total_cost | ||
| + | |||
| + | # Add data to the list for the graph | ||
| + | unit_count_list.append(unit_count) | ||
| + | total_capacity_list.append(total_capacity) | ||
| + | |||
| + | # Print the results | ||
| + | print("Number of hydrogen storage units to be purchased:", best_unit_count) | ||
| + | print("Total storage capacity:", best_total_capacity, "liters") | ||
| + | print("Total cost:", best_total_cost, "Rupiah") | ||
| + | |||
| + | # Display the graph | ||
| + | plt.plot(unit_count_list, total_capacity_list) | ||
| + | plt.xlabel('Number of Hydrogen Storage Units') | ||
| + | plt.ylabel('Total Storage Capacity (liters)') | ||
| + | plt.title('Hydrogen Storage Optimization') | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | </syntaxhighlight> | ||
| + | The graph are shown below: | ||
| + | |||
| + | [[File:Graphic.png|300x300px]] | ||
| + | |||
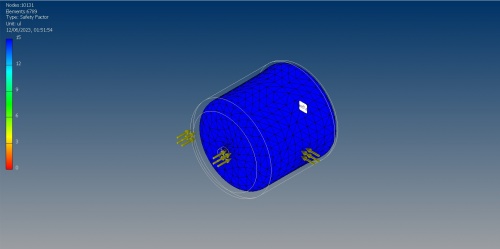
| + | ='''Stress Analysis'''= | ||
| + | [[File:Safety Factor.jpg|500x500px]] | ||
| + | |||
| + | After performing stress analysis using Inventor,the results appear blue and not red, it can indicate that the tank is still within the safe limits. | ||
| + | |||
| + | =='''Conclusion'''== | ||
| + | Overall, by considering design optimization, safety measures, cost-effective choices, and conducting thorough testing, it is possible to develop an efficient and budget-friendly pressurized hydrogen storage system. Consulting with experts in the field and following relevant regulations and standards will further ensure a successful and safe design. | ||
| + | |||
| + | [https://www.youtube.com/watch?v=GRzeFGtD418 My Presentation] | ||
Latest revision as of 02:47, 12 June 2023
Hello, my name is Ibrahim Ardhi (2106651105), and I am currently pursuing a Bachelor's degree in Mechanical Engineering, University of Indonesia. As a future engineer, I am excited to embark my studies and to keep gain knowledge. Remember, stay conscious!
Contents
Consciousness
Consciousness is a fundamental aspect of human existence. It has to do with your ability to perceive yourself, your environment, and your mental state. It is a complex phenomenon that includes many aspects such as self-awareness, awareness, thoughts, emotions, and the ability to observe oneself. Human consciousness enables us to experience the world, make decisions, and interact in meaningful ways with others. It is the basis of our identity and shapes our understanding of reality. Through awareness, we can reflect on our own thoughts and feelings, reflect on the past and future, and think critically.
Design & Optimization of Pressurized Hydrogen Storage
Optimizing a 1-liter hydrogen storage design within a limited budget requires careful consideration of various factors. Here are a few suggestions to help you achieve an efficient and cost-effective solution:
1. Choose a Cost-Effective Storage Material:
Look for affordable options such as lightweight plastic or composite materials for the storage container. Consider their compatibility with hydrogen and their ability to withstand the required pressure.
2. Cylinder Design:
Optimize for a smaller-sized cylinder to accommodate 1 liter of hydrogen. This will help minimize material costs while meeting the pressure requirement. Consider lightweight materials that are cost-effective, such as aluminum or composite cylinders.
3. Safety Considerations:
Ensure the chosen storage system includes essential safety features such as pressure relief valves and adequate ventilation. These measures are crucial to prevent over-pressurization and ensure the safe storage of hydrogen.
4. Cost-Effective Components:
Select affordable valves, fittings, and seals that meet the pressure requirements and are compatible with the storage material. Research suppliers and compare prices to get the best deal within your budget.
5. Efficient Manufacturing:
Explore cost-effective manufacturing methods, such as injection molding for plastic components or standardized assembly processes. Streamlining the manufacturing process can help reduce costs.
6. System Integration:
Ensure the components of the storage system are properly integrated and sealed to prevent leaks and ensure efficient operation. Test the system for any potential leaks or weaknesses that may impact performance and safety.
7. Performance Testing:
Once the storage system is designed and assembled, conduct performance tests to ensure it meets the required specifications. Evaluate factors such as pressure retention, durability, and overall functionality.
It's important to note that optimizing a hydrogen storage design within a limited budget requires careful consideration of various factors, including material costs, component selection, and manufacturing processes. It may also be helpful to consult with experts or professionals in the field who have experience with hydrogen storage systems to ensure that the design meets safety standards and functional requirements.
It is also crucial to conduct a thorough risk assessment. Here is a list of potential risks to consider during the assessment:
Fire and Explosion: Hydrogen is highly flammable, so there is a risk of fire or explosion if there is a leakage or ignition source. Assess the system's design and materials to ensure they minimize the risk of fire and explosion.
Pressure Overload: If the storage system cannot handle the designated 8-bar pressure limit, there is a risk of rupture or failure. Evaluate the structural integrity of the chosen materials and design to ensure they can withstand the required pressure.
Material Compatibility: Some materials may not be compatible with hydrogen and can lead to embrittlement or other adverse effects. Assess the compatibility of all components, including storage containers, valves, and fittings, to avoid material degradation or failure.
Leakage: Hydrogen is a small molecule that can easily escape through tiny gaps or poorly sealed connections. Assess the system for potential leakage points and ensure proper sealing and connection integrity.
Ventilation: Hydrogen is lighter than air and can accumulate in enclosed spaces, leading to the risk of an explosive atmosphere. Evaluate the ventilation system to ensure adequate air circulation and prevent hydrogen buildup.
Handling and Transport: Risks may arise during the handling and transportation of the hydrogen storage system. Evaluate the potential hazards associated with moving or installing the system, including manual handling, drop risks, or transportation accidents.
Regulatory Compliance: Ensure that the design and implementation of the hydrogen storage system comply with local, national, and international safety regulations and standards. Stay informed about applicable codes and guidelines to mitigate legal and compliance risks.
Maintenance and Inspection: Establish regular maintenance and inspection procedures to monitor the condition of the storage system over time. This helps identify potential risks, such as corrosion, degradation, or component failures, and allows for timely intervention.
Training and Safety Procedures: Provide adequate training to individuals involved in the installation, operation, and maintenance of the hydrogen storage system. Develop comprehensive safety procedures and protocols to mitigate human error and ensure safe practices.
Emergency Response: Have an emergency response plan in place to address any hydrogen-related incidents promptly. Include procedures for evacuation, containment, and contacting emergency services.
Remember, a comprehensive risk assessment should be conducted by individuals with expertise in hydrogen storage systems and safety protocols. They can provide further insights into the specific risks associated with your design and help develop appropriate risk mitigation strategies.
Geometry Constrain Calculation
To optimize hydrogen storage with a capacity of 1 liter, a pressure of 8 bar, and a maximum budget of 500,000, these calculations can be done using Python or manually. The following is the calculation using Python:
import math
from scipy.optimize import minimize
# Define the objective function
def calculate_surface_area(x):
radius, height = x
return 2 * math.pi * (radius**2) + 2 * math.pi * radius * height
# Define the volume constraint function
def check_volume_constraint(x):
radius, height = x
return math.pi * (radius**2) * height - 1000
# Initial estimation for the radius and height (in mm)
initial_guess = [10, 100]
# Define the bounds for the radius and height (in mm)
bounds = [(0, None), (0, None)]
# Define the volume constraint as an equality constraint
volume_constraint = {'type': 'eq', 'fun': check_volume_constraint}
# Minimize the surface area while satisfying the volume constraint
result = minimize(calculate_surface_area, initial_guess, method='SLSQP', bounds=bounds, constraints=volume_constraint)
# Extract the optimal radius, height, and minimum surface area
optimal_radius = result.x[0] * 10 # Convert back to millimeters
optimal_height = result.x[1] * 10 # Convert back to millimeters
min_surface_area = result.fun * 100 # Convert to square millimeters
# Print the results (in mm)
print(f"\n\nOptimal Radius: {optimal_radius:.2f} mm")
print(f"Optimal Height: {optimal_height:.2f} mm")
print(f"Minimum Surface Area: {min_surface_area:.2f} mm²\n\n")From the code above, we obtain the following data:
Optimal Radius: 54.19 mm
Optimal Height: 108.38 mm
Minimum Surface Area: 55358.10 mm²
This code is performing an optimization calculation for a geometric problem. Specifically, it aims to minimize the surface area of a cylinder subject to a volume constraint. The cylinder represents a hydrogen storage tank with a given volume capacity. The objective function calculates the surface area of the cylinder, which is to be minimized. The constraint function ensures that the volume of the cylinder meets a specified value (in this case, 1000 units). The `minimize` function from the `scipy.optimize` module is used to find the optimal values for the radius and height of the cylinder that satisfy the volume constraint while minimizing the surface area. The code then prints the optimal values for the radius and height, as well as the minimum surface area achieved.
Material Strength Constraint Code
In a pressurized storage system, the material strength and plate thickness of the tank must be able to withstand the pressure exerted by the gas in all directions on the tank walls. Specifically, this 1-liter hydrogen tank has a maximum pressure limit of 8 bar. The plate thickness of the tank can be calculated using the following hoop stress equation.
The range of plate thickness should not be less than 1/5 of the tank radius. According to Section VIII D.1 of the ASME BPV Code, the minimum plate thickness of the tank should be 1/16 inch or 1.59 mm, disregarding corrosion, material, or dimensional considerations. In this calculation, we will iterate from a minimum radius of 2.7 mm to 11.05 mm, with an increment of 1 mm for each iteration.
Therefore, the material that will be used in the construction of this hydrogen tank is AISI 316 austenitic stainless steel.
Iteration Process Phyton Code
r = 5.42e-2
p = 800000
t = 2.9e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9:
breakResult
for thickness 0.004099999999999999 hoop stress = 10770731.707317077 Pa for thickness 0.004199999999999999 hoop stress = 10514285.714285716 Pa for thickness 0.004299999999999999 hoop stress = 10269767.441860467 Pa for thickness 0.004399999999999999 hoop stress = 10036363.636363639 Pa for thickness 0.0045 hoop stress = 9813333.333333334 Pa for thickness 0.0046 hoop stress = 9600000.0 Pa for thickness 0.0047 hoop stress = 9395744.680851063 Pa for thickness 0.0048000000000000004 hoop stress = 9200000.0 Pa for thickness 0.004900000000000001 hoop stress = 9012244.897959182 Pa for thickness 0.005000000000000001 hoop stress = 8831999.999999998 Pa for thickness 0.005100000000000001 hoop stress = 8658823.529411763 Pa for thickness 0.0052000000000000015 hoop stress = 8492307.69230769 Pa for thickness 0.005300000000000002 hoop stress = 8332075.47169811 Pa for thickness 0.005400000000000002 hoop stress = 8177777.777777774 Pa for thickness 0.005500000000000002 hoop stress = 8029090.909090905 Pa for thickness 0.0056000000000000025 hoop stress = 7885714.285714282 Pa for thickness 0.005700000000000003 hoop stress = 7747368.421052628 Pa for thickness 0.005800000000000003 hoop stress = 7613793.103448272 Pa for thickness 0.005900000000000003 hoop stress = 7484745.76271186 Pa for thickness 0.006000000000000004 hoop stress = 7359999.999999995 Pa for thickness 0.006100000000000004 hoop stress = 7239344.262295078 Pa for thickness 0.006200000000000004 hoop stress = 7122580.645161286 Pa for thickness 0.006300000000000004 hoop stress = 7009523.809523805 Pa for thickness 0.006400000000000005 hoop stress = 6899999.999999995 Pa for thickness 0.006500000000000005 hoop stress = 6793846.153846148 Pa for thickness 0.006600000000000005 hoop stress = 6690909.090909085 Pa for thickness 0.006700000000000005 hoop stress = 6591044.776119398 Pa for thickness 0.006800000000000006 hoop stress = 6494117.6470588185 Pa for thickness 0.006900000000000006 hoop stress = 6399999.999999994 Pa for thickness 0.007000000000000006 hoop stress = 6308571.428571423 Pa
The provided code calculates the hoop stress by examining various thickness values between 2.9 mm and 12 mm. It includes a condition that stops the iteration if the total hoop stress exceeds the yield strength of AISI 316 stainless steel. The results indicate that all thickness values from 2.9 mm to 12 mm, incremented by 1 mm, meet the yield strength criteria. The code produces the following calculation results, demonstrating that the hoop stress remains significantly below the yield strength of 205 MPa.
Cost Constraint Code
from scipy.optimize import minimize
# Price and capacity
price_per_unit = 100000 # Price per unit of hydrogen storage
capacity_per_unit = 1 # Capacity of hydrogen storage per unit
# Maximum budget
max_budget = 500000
# Objective function
def objective_function(x):
return -x * capacity_per_unit
# Constraint function
def budget_constraint(purchase_amount):
return max_budget - (price_per_unit * purchase_amount)
budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint}
# Initial value
x0 = 0
# Bounds
bounds = [(0, None)]
# Solve the optimization problem
solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq])
# Print the results
print("Status:", "Optimal" if solution.success else "No solution found")
print("Number of hydrogen storage units to be purchased:", solution.x[0])
print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters")
print("Total cost:", solution.x[0] * price_per_unit, "Rupiah")
from scipy.optimize import minimize
# Price and capacity
price_per_unit = 100000 # Price per unit of hydrogen storage
capacity_per_unit = 1 # Capacity of hydrogen storage per unit
# Maximum budget
max_budget = 500000
# Objective function
def objective_function(x):
return -x * capacity_per_unit
# Constraint function
def budget_constraint(purchase_amount):
return max_budget - (price_per_unit * purchase_amount)
budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint}
# Initial value
x0 = 0
# Bounds
bounds = [(0, None)]
# Solve the optimization problem
solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq])
# Print the results
print("Status:", "Optimal" if solution.success else "No solution found")
print("Number of hydrogen storage units to be purchased:", solution.x[0])
print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters")
print("Total cost:", solution.x[0] * price_per_unit, "Rupiah")This code shows us that the optimal results for creating a hydrogen storage system with a budget of Rp500.000,00 is to make 5 tanks with a capacity of 1 liters each.
We can also make a graph through this code above:
import matplotlib.pyplot as plt
# Price and capacity
price_per_unit = 100000 # Price per unit of hydrogen storage
capacity_per_unit = 1 # Capacity of hydrogen storage per unit
# Maximum budget
max_budget = 500000
# Initialize variables
best_unit_count = 0
best_total_capacity = 0
best_total_cost = 0
# Initialize lists for the graph
unit_count_list = []
total_capacity_list = []
# Iterate to find the optimal solution
for unit_count in range(int(max_budget / price_per_unit) + 1):
total_capacity = unit_count * capacity_per_unit
total_cost = unit_count * price_per_unit
if total_capacity > best_total_capacity and total_cost <= max_budget:
best_unit_count = unit_count
best_total_capacity = total_capacity
best_total_cost = total_cost
# Add data to the list for the graph
unit_count_list.append(unit_count)
total_capacity_list.append(total_capacity)
# Print the results
print("Number of hydrogen storage units to be purchased:", best_unit_count)
print("Total storage capacity:", best_total_capacity, "liters")
print("Total cost:", best_total_cost, "Rupiah")
# Display the graph
plt.plot(unit_count_list, total_capacity_list)
plt.xlabel('Number of Hydrogen Storage Units')
plt.ylabel('Total Storage Capacity (liters)')
plt.title('Hydrogen Storage Optimization')
plt.grid(True)
plt.show()The graph are shown below:
Stress Analysis
After performing stress analysis using Inventor,the results appear blue and not red, it can indicate that the tank is still within the safe limits.
Conclusion
Overall, by considering design optimization, safety measures, cost-effective choices, and conducting thorough testing, it is possible to develop an efficient and budget-friendly pressurized hydrogen storage system. Consulting with experts in the field and following relevant regulations and standards will further ensure a successful and safe design.