Difference between revisions of "Muhammad Alvito Bintang Safero"
(→Design and Optimization of 1-Litre Pressurized Hydrogen Storage with 8 Bar Pressure Capability) |
|||
| (42 intermediate revisions by the same user not shown) | |||
| Line 47: | Line 47: | ||
== '''Design and Optimization of 1-Litre Pressurized Hydrogen Storage with 8 Bar Pressure Capability''' == | == '''Design and Optimization of 1-Litre Pressurized Hydrogen Storage with 8 Bar Pressure Capability''' == | ||
| + | Due to the ever-increasing stringency of environmental policy requirements, hydrogen fuel cell vehicles (HFCVs), which are intended to serve as a substitute for conventional automobiles, are continuously evolving as a new promising technology. It is essential to conduct hazard identification as an early phase in the development of HFCVs in order to describe possible hazards and identify potential safety concerns. The onboard hydrogen storage and supply system is an essential component of HFCVs, serving to store hydrogen and provide it to the fuel cell system to guarantee its proper functioning. Designing a 1-litre pressurized hydrogen storage system with the ability to hold a pressure of 8 bars within a budget of 500,000 Indonesian Rupiah (IDR) presents a challenge. In this essay, we will explore the considerations and possibilities of designing an efficient and cost-effective hydrogen storage system that meets the pressure requirement while staying within the given budget constraints. | ||
| − | + | ||
| + | [[Material Selection:]] | ||
| + | |||
| + | In order to build this hydrogen storage, the material I choose is ASTM A36 sheet metal with yield strength of 36,000 psi and allowable stress value = 2/3 x Sy = 24.000 psi . | ||
[[Tank Design:]] | [[Tank Design:]] | ||
| − | |||
| − | [[ | + | '''To optimize a tube with a volume of 1 liter (1000 cm3), we can look for a combination of radius and height that produces the smallest surface area. In this case, we will use an optimization algorithm approach to find the best solution. Here are examples of coding using Python and the scipy optimization module:''' |
| − | + | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | |||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def objective(x): | ||
| + | # x[0] = radius, x[1] = height | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | surface_area = 2 * math.pi * r * (r + h) | ||
| + | return surface_area | ||
| + | |||
| + | def constraint(x): | ||
| + | # x[0] = radius, x[1] = height | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | volume = math.pi * r**2 * h | ||
| + | return volume - 1000 # Constraint: Volume = 1000 cm³ | ||
| − | + | # Inisialisasi nilai awal | |
| + | x0 = [1, 1] | ||
| − | + | # Mendefinisikan batasan | |
| + | volume_constraint = {'type': 'eq', 'fun': constraint} | ||
| − | + | # Menyelesaikan optimisasi dengan batasan | |
| + | result = minimize(objective, x0, constraints=volume_constraint) | ||
| + | # Mendapatkan jari-jari dan tinggi teroptimasi | ||
| + | radius = result.x[0] | ||
| + | height = result.x[1] | ||
| − | [[ | + | # Menghitung luas permukaan teroptimasi |
| − | + | min_surface_area = objective(result.x) | |
| + | |||
| + | # Menampilkan hasil | ||
| + | print("Jari-jari teroptimasi:", radius) | ||
| + | print("Tinggi teroptimasi:", height) | ||
| + | print("Luas permukaan teroptimasi:", min_surface_area) | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | '''Jari-jari teroptimasi: 5.41926305506462''' | ||
| + | |||
| + | '''Tinggi teroptimasi: 10.838511985088449''' | ||
| + | |||
| + | '''Luas permukaan teroptimasi: 553.5810444905989''' | ||
| + | |||
| + | In the example above, we use the minimize function of the scipy module to solve optimization problems with limitations. The objective function is the object function that seeks the area of the surface, while the constraint function is a volume limit. We give the initial value x0 for fingers and heights, and the optimization results are stored in the result variable. As a result, we can obtain optimized radius, optimized heights, and optimized surface areas that are then displayed. | ||
| + | |||
| + | |||
| + | |||
| + | '''Thickness formula for longitudinal stress direction :''' | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | print ("with reference to some data that we have obtained, we can determine the minimum\nthickness of the vessel, with the following data :\n ") | ||
| + | |||
| + | print ("the value of E : 0.85 (double welded butt joint) ") | ||
| + | |||
| + | print ("the value of P (psi) : 116 psi") | ||
| + | |||
| + | print ("the value of R (inch) : 2.133568131915205335 inch ") | ||
| + | |||
| + | print ("the value of S (psi) : 24000 psi ") | ||
| + | |||
| + | print ("the value of corrosion allowance (inch) : 0.039 inch \n") | ||
| + | |||
| + | E = 0.85 | ||
| + | P = 116 | ||
| + | R = 2.133568131915205335 | ||
| + | S = 24000 | ||
| + | corrosion_allowance = 0.039 | ||
| + | |||
| + | # Calculate t circumferential | ||
| + | t_circumferential = P * (R + corrosion_allowance) / ((S * E) - (E * P)) | ||
| + | final_t_circumferential = t_circumferential + corrosion_allowance | ||
| + | |||
| + | # Calculate t longitudinal | ||
| + | t_longitudinal = P * (R + corrosion_allowance) / ((2 * S * E) + (0.4 * P)) | ||
| + | final_t_longitudinal = t_longitudinal + corrosion_allowance | ||
| + | |||
| + | if final_t_circumferential > final_t_longitudinal: | ||
| + | minimum_thickness = final_t_circumferential | ||
| + | else: | ||
| + | minimum_thickness = final_t_longitudinal | ||
| + | |||
| + | print ("then the following results were found : \n") | ||
| + | |||
| + | print(f"Final T Circumferential = {final_t_circumferential:.4f} inch") | ||
| + | print(f"Final T Longitudinal = {final_t_longitudinal:.4f} inch\n") | ||
| + | print(f"Hence, minimum thickness is {minimum_thickness:.4f} inch\n") | ||
| + | |||
| + | the value of E : 0.85 | ||
| + | |||
| + | the value of P (psi) : 116 psi | ||
| + | |||
| + | the value of R (inch) : 2.133568131915205335 inch | ||
| + | |||
| + | the value of S (psi) : 24000 psi | ||
| + | |||
| + | the value of corrosion allowance (inch) : 0.039 inch | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | '''Then the following results were found :''' | ||
| + | |||
| + | Final T Circumferential = 0.0514 inch | ||
| + | |||
| + | Final T Longitudinal = 0.0452 inch | ||
| + | |||
| + | Hence, minimum thickness is 0.0514 inch or 0,131 cm | ||
| + | |||
| + | '''So, for the storage of hydrogen of 1 Liter I used the calculation of:''' | ||
| + | |||
| + | Radius 5.42 + 0.131 = 5.551 cm | ||
| + | |||
| + | Height 10.85 + 0.131 = 10.981 cm | ||
| + | |||
| + | V = 3.14 x 5.551 x 5.551 x 10.981 = 1,062.464 cm^3 | ||
| + | |||
| + | '''Hydrogen inside the storage''' | ||
| + | |||
| + | V = 3.14 x 5.42 x 5.42 x 10.85 = 1,000.825 cm^3 | ||
| + | |||
| + | |||
| + | [[Hydrogen Storage]] | ||
| + | |||
| + | [[File:Screenshot_2023-06-10_235658.png|500x500px]] | ||
| + | |||
| + | |||
| + | [[Von Mises Stress]] | ||
| + | |||
| + | [[File:Screenshot_2023-06-10_235955.png|500x500px]] | ||
| + | |||
| + | |||
| + | [[Safety Factor]] | ||
| + | |||
| + | [[File:Screenshot 2023-06-11 000309.png|500x500px]] | ||
| + | |||
| + | |||
| + | [[Cost:]] | ||
| + | |||
| + | This hydrogen storage surface area is 576.31 cm^2. Using the material of ASTM A36, the material price is approximately Rp 50,000 [https://www.tokopedia.com/rizqibarokahsteel/jual-plate-bar-astm-a36-3-200-200mm-1-pcs].Added to the cost of welding about Rp 125,000. Total cost of 1 hydrogen storage is 50,000 + 125,000 = Rp 175,000 | ||
| + | |||
| + | |||
| + | [[Conclusion:]] | ||
| − | + | Mr. Dai gave us challenge to design a 1-litre pressurized hydrogen storage system with the ability to hold a pressure of 8 bars within a budget of Rp 500,000. From all the calculations above, it comes to a conclusion. | |
| − | + | The material I choose for this hydrogen storage is ASTM A36. With the help of coding using python, I found to optimize the tank design. Its surface area is 576.31 cm^2. The hydrogen inside the tank is V = 3.14 x 5.42 x 5.42 x 10.85 = 1,000.825 cm^3 and with the wall thickness which 0.0514 inch or 0,131 cm is V = 3.14 x 5.551 x 5.551 x 10.981 = 1,062.464 cm^3. And last, the cost production for this hydrogen storage is approximately Rp 175,000. | |
| + | Last but not least, as a result of this essay. I hope it will be a reference that can be used for hydrogen storage development in hydrogen fuel cell vehicles (HFCVs) and leads to a better future. | ||
| − | |||
| − | |||
| − | + | [[Video Presentation:]] | |
| − | + | https://www.youtube.com/@alvitobintang8873 | |
Latest revision as of 22:14, 11 June 2023
Consciousness
If we subtitute X = 1 in the equation (X^2 -1) /(X-1). This will result in 0/0 meaning undefined. Why so? Division is a mathematical operation that divides a number with another number to produce a certain value. To prove whether 0/0 is undefined. We can use the “Reductio Ad Absurdum” technique. The essence of “Reductio Ad Absurdum” reasoning is to prove that the proposition “P” is correct by taking the first step to consider the negation p, which is “~p”, to be the correct proposition. The second step deduces a contradiction based on the assumption that “~p” is true. Since the assumptions that have been established produce contradictions and contradiction are irrational, then the probability “~p” is true is rejected and it is concluded that p is true.
First assuming 0/0 is defined by producing a certain value. For a and b € R. 0/0 = a -> 0 = 0 x a (correct). 0/0 = b -> 0 = 0 x b (correct). Because a 0/0 division produces an unspecified and uncertain value and this contradicts the statement that 0/0 is defined by producing a certain certain value. Therefore, the assumption 0/0 defined is denegated to be 0/0 undefined.
We need to find answers by other methods. As a factoring method. (X^2 -1) /(X-1) = (X+1) (X-1)/(X-1). Then we can eliminate (X-1) and leave (X+1). Subtitute X = 1 to X + 1. The answer is 2.
Is Consciousness relevant to the previous case ? Do narate it ! why is that so?
In my opinion, consciousness arises from the complex computational processes that occur in the brain, which can be explained and understood through mathematical models. According to this perspective, brain nerve networks and their interactions can be explained mathematically, and consciousness is the emerging property of these computational processes.
However, it is important to note that mathematics, as a formal system, is not synonymous with consciousness itself. While mathematical models can help us understand and describe certain aspects of cognitive processes, they do not fully capture the subjective nature of conscious experience.
In short, while mathematics can be a valuable tool to understand and model certain aspects of brain function, it does not provide a complete explanation for consciousness.
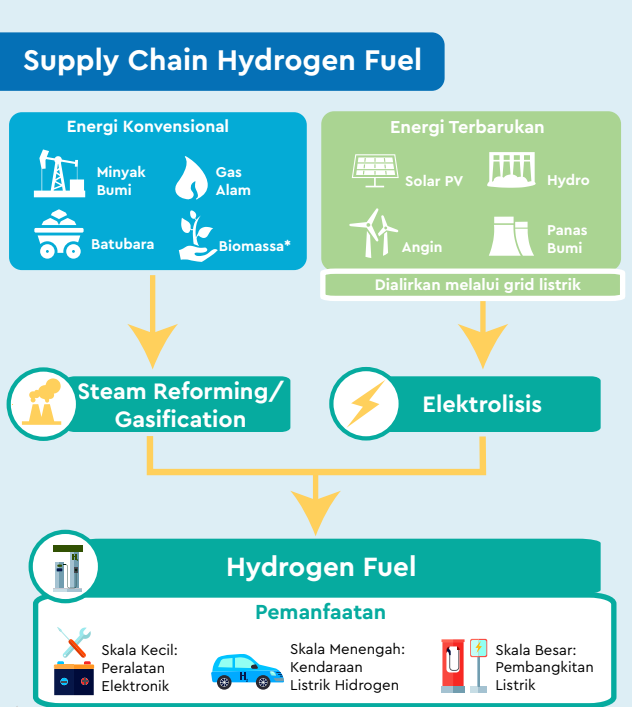
Hydrogen Fuel
Hydrogen fuel is a non-emission fuel used as a fuel for power generation along with oxygen using a unit called hydrogen fuel cell. Hydrogen Fuel Cell works similarly to a battery, where a fuel cell has anode (-) and cathode (+) poles. Hydrogen (H2) is transferred to the anode pole which will subsequently break the hydrogen molecule into electrons and hydrogen ions. The flow of electrons on the external circuit will produce electricity. Meanwhile, hydrogen ions will react with oxygen (O2) which will produce water vapor. (H2O). The by-product of this reaction is only water vapor, so hydrogen fuel is a very clean type of energy. There are several methods for producing hydrogen as fuel. Currently, the most commonly used method is steam reforming using natural gas. In addition, there are several other methods such as gasification, electrolysis, as well as biological processes.
Steam Reformation In this process, the methane contained in natural gas is extracted and reacted with steam to produce hydrogen. About 95% of the hydrogen available on the market is produced by this process.
Gasification
In the process of gasification, coal or biomass materials are reacted with oxygen and steam to produce gas synthesis. Subsequently, hydrogen molecules are separated from gas synthesis using a separation system.
Electrolysis
The process of electrolysis uses a tool called an electrolyzer. The main concept of this process is the separation of hydrogen molecules as well as oxygen from water by reactions caused by electric flow.
The biological process
Microbes such as bacteria and microalgae can produce hydrogen by biological reactions using sunlight or organic matter. The technology is still in the research and development phase.
Design and Optimization of 1-Litre Pressurized Hydrogen Storage with 8 Bar Pressure Capability
Due to the ever-increasing stringency of environmental policy requirements, hydrogen fuel cell vehicles (HFCVs), which are intended to serve as a substitute for conventional automobiles, are continuously evolving as a new promising technology. It is essential to conduct hazard identification as an early phase in the development of HFCVs in order to describe possible hazards and identify potential safety concerns. The onboard hydrogen storage and supply system is an essential component of HFCVs, serving to store hydrogen and provide it to the fuel cell system to guarantee its proper functioning. Designing a 1-litre pressurized hydrogen storage system with the ability to hold a pressure of 8 bars within a budget of 500,000 Indonesian Rupiah (IDR) presents a challenge. In this essay, we will explore the considerations and possibilities of designing an efficient and cost-effective hydrogen storage system that meets the pressure requirement while staying within the given budget constraints.
In order to build this hydrogen storage, the material I choose is ASTM A36 sheet metal with yield strength of 36,000 psi and allowable stress value = 2/3 x Sy = 24.000 psi .
To optimize a tube with a volume of 1 liter (1000 cm3), we can look for a combination of radius and height that produces the smallest surface area. In this case, we will use an optimization algorithm approach to find the best solution. Here are examples of coding using Python and the scipy optimization module:
import math
from scipy.optimize import minimize
def objective(x):
# x[0] = radius, x[1] = height
r = x[0]
h = x[1]
surface_area = 2 * math.pi * r * (r + h)
return surface_area
def constraint(x):
# x[0] = radius, x[1] = height
r = x[0]
h = x[1]
volume = math.pi * r**2 * h
return volume - 1000 # Constraint: Volume = 1000 cm³
# Inisialisasi nilai awal
x0 = [1, 1]
# Mendefinisikan batasan
volume_constraint = {'type': 'eq', 'fun': constraint}
# Menyelesaikan optimisasi dengan batasan
result = minimize(objective, x0, constraints=volume_constraint)
# Mendapatkan jari-jari dan tinggi teroptimasi
radius = result.x[0]
height = result.x[1]
# Menghitung luas permukaan teroptimasi
min_surface_area = objective(result.x)
# Menampilkan hasil
print("Jari-jari teroptimasi:", radius)
print("Tinggi teroptimasi:", height)
print("Luas permukaan teroptimasi:", min_surface_area)Jari-jari teroptimasi: 5.41926305506462
Tinggi teroptimasi: 10.838511985088449
Luas permukaan teroptimasi: 553.5810444905989
In the example above, we use the minimize function of the scipy module to solve optimization problems with limitations. The objective function is the object function that seeks the area of the surface, while the constraint function is a volume limit. We give the initial value x0 for fingers and heights, and the optimization results are stored in the result variable. As a result, we can obtain optimized radius, optimized heights, and optimized surface areas that are then displayed.
Thickness formula for longitudinal stress direction :
print ("with reference to some data that we have obtained, we can determine the minimum\nthickness of the vessel, with the following data :\n ")
print ("the value of E : 0.85 (double welded butt joint) ")
print ("the value of P (psi) : 116 psi")
print ("the value of R (inch) : 2.133568131915205335 inch ")
print ("the value of S (psi) : 24000 psi ")
print ("the value of corrosion allowance (inch) : 0.039 inch \n")
E = 0.85
P = 116
R = 2.133568131915205335
S = 24000
corrosion_allowance = 0.039
# Calculate t circumferential
t_circumferential = P * (R + corrosion_allowance) / ((S * E) - (E * P))
final_t_circumferential = t_circumferential + corrosion_allowance
# Calculate t longitudinal
t_longitudinal = P * (R + corrosion_allowance) / ((2 * S * E) + (0.4 * P))
final_t_longitudinal = t_longitudinal + corrosion_allowance
if final_t_circumferential > final_t_longitudinal:
minimum_thickness = final_t_circumferential
else:
minimum_thickness = final_t_longitudinal
print ("then the following results were found : \n")
print(f"Final T Circumferential = {final_t_circumferential:.4f} inch")
print(f"Final T Longitudinal = {final_t_longitudinal:.4f} inch\n")
print(f"Hence, minimum thickness is {minimum_thickness:.4f} inch\n")
the value of E : 0.85
the value of P (psi) : 116 psi
the value of R (inch) : 2.133568131915205335 inch
the value of S (psi) : 24000 psi
the value of corrosion allowance (inch) : 0.039 inchThen the following results were found :
Final T Circumferential = 0.0514 inch
Final T Longitudinal = 0.0452 inch
Hence, minimum thickness is 0.0514 inch or 0,131 cm
So, for the storage of hydrogen of 1 Liter I used the calculation of:
Radius 5.42 + 0.131 = 5.551 cm
Height 10.85 + 0.131 = 10.981 cm
V = 3.14 x 5.551 x 5.551 x 10.981 = 1,062.464 cm^3
Hydrogen inside the storage
V = 3.14 x 5.42 x 5.42 x 10.85 = 1,000.825 cm^3
This hydrogen storage surface area is 576.31 cm^2. Using the material of ASTM A36, the material price is approximately Rp 50,000 [1].Added to the cost of welding about Rp 125,000. Total cost of 1 hydrogen storage is 50,000 + 125,000 = Rp 175,000
Mr. Dai gave us challenge to design a 1-litre pressurized hydrogen storage system with the ability to hold a pressure of 8 bars within a budget of Rp 500,000. From all the calculations above, it comes to a conclusion.
The material I choose for this hydrogen storage is ASTM A36. With the help of coding using python, I found to optimize the tank design. Its surface area is 576.31 cm^2. The hydrogen inside the tank is V = 3.14 x 5.42 x 5.42 x 10.85 = 1,000.825 cm^3 and with the wall thickness which 0.0514 inch or 0,131 cm is V = 3.14 x 5.551 x 5.551 x 10.981 = 1,062.464 cm^3. And last, the cost production for this hydrogen storage is approximately Rp 175,000.
Last but not least, as a result of this essay. I hope it will be a reference that can be used for hydrogen storage development in hydrogen fuel cell vehicles (HFCVs) and leads to a better future.