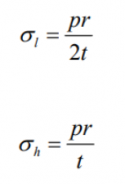Difference between revisions of "Farras Hafizh Al Farisi"
(→Geometrical Constraints) |
(→Material Selection) |
||
| (51 intermediate revisions by 2 users not shown) | |||
| Line 12: | Line 12: | ||
==Factors Involved in Designing and Optimizing a Pressurized Hydrogen Storage== | ==Factors Involved in Designing and Optimizing a Pressurized Hydrogen Storage== | ||
| + | : [[File: Hydrogen_Storage_Example_Farras Hafizh.jpg|450px|thumb|middle| Simple example of a pressurized hydrogen tank (source: doosanmobility.com)]] | ||
: | : | ||
: Designing and optimizing a pressurized hydrogen storage involves several factors and processes to ensure its safety, efficiency, and performance. Here are some key considerations in the design and optimization process: | : Designing and optimizing a pressurized hydrogen storage involves several factors and processes to ensure its safety, efficiency, and performance. Here are some key considerations in the design and optimization process: | ||
| Line 49: | Line 50: | ||
==Material Selection== | ==Material Selection== | ||
| + | : [[File: Austenitic_Stainless_Steel_Farras_Hafizh.jpg|200px|thumb|middle| AISI 316 Austenitic Stainless Steel (source: gpss.com)]] | ||
| + | : [[File: Micrographs of AISI 316L Austenitic Stainless Steel_Farras Hafizh.jpeg|200px|thumb|middle| Grain Structures of AISI 316 Austenitic Stainless Steel (source: researchgate.com)]] | ||
: By carefully considering the materials available for pressurized hydrogen storage, our selection has led us to choose '''AISI 316 austenitic stainless steel'''. This decision is rooted in the unique properties and advantages offered by this particular material. Here are some reasons for considering AISI 316 stainless steel for pressurized hydrogen storage: | : By carefully considering the materials available for pressurized hydrogen storage, our selection has led us to choose '''AISI 316 austenitic stainless steel'''. This decision is rooted in the unique properties and advantages offered by this particular material. Here are some reasons for considering AISI 316 stainless steel for pressurized hydrogen storage: | ||
:'''1) Corrosion Resistance''' | :'''1) Corrosion Resistance''' | ||
| Line 58: | Line 61: | ||
:'''4) Established Industrial Usage''' | :'''4) Established Industrial Usage''' | ||
: AISI 316 stainless steel is widely used in various industries, including chemical processing, oil and gas, and marine applications. It has a well-established track record and extensive knowledge base regarding its behavior in different environments, making it a trusted material choice for engineering applications. | : AISI 316 stainless steel is widely used in various industries, including chemical processing, oil and gas, and marine applications. It has a well-established track record and extensive knowledge base regarding its behavior in different environments, making it a trusted material choice for engineering applications. | ||
| − | |||
==Constraints== | ==Constraints== | ||
| Line 110: | Line 112: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | : From the coding results, it can be inferred that by minimizing the surface area, the optimal dimensions for the cylindrical tank are achieved with a '''height-to-radius ratio of 2:1'''. Specifically, the tank has a '''height of 10.84 cm and a radius of 5.42 cm'''. These measurements result in a '''surface area of 553.58 cm^2''', which is the smallest possible area for the given volume and pressure requirements. | ||
| + | : [[File: Farras_Pressurized_Hydrogen_Storage_Coding_Result.png|300px| Coding Result of Pressurized Hydrogen Storage Optimization (source: Personal Analysis)]] | ||
| + | |||
| + | ====End Cap Geometry==== | ||
| + | : Using a purely cylindrical geometry for the storage tank may pose risks due to stress concentration at the corners. To minimize stress concentration and reduce surface area while maintaining the same volume, it is more efficient to adopt a torispherical end cap shape. This shape can be achieved by adding a fillet with a radius equal to half the tank's radius. The filleting creates a smooth curvature and helps reduce stress concentration. Adjustments in the geometrical parameters are necessary to compensate for the volume reduction caused by the filleting. By calculating the percentage reduction in the cross-sectional area, we can inversely apply it to the required volume to obtain the new increased volume constraint. | ||
| + | : [[File: Hasil_perhitungan_Geometry_End_Cap.png|500px| Fillet Radius of Tank's End Cap Calculation (source: Personal Analysis)]] | ||
| + | : The calculation results mentioned earlier reveal that the fillet radius obtained for the tank's end caps is '''2.56443 cm''' | ||
===Material Strength Constraints=== | ===Material Strength Constraints=== | ||
| + | |||
| + | ====Formula Used==== | ||
| + | : In the context of a pressurized container, ensuring that the thickness and strength of the container material can endure the applied pressure on the walls is crucial. Regarding the specific requirements, the '''1-liter hydrogen tank has a maximum pressure limit of 8 bar'''. | ||
| + | |||
| + | : Within a thin-walled cylindrical component, two main types of stress exist: '''circumferential (hoop) stress and longitudinal stress'''. Although radial stress is present, it :can be disregarded since the radius is significantly larger than the wall thickness. The formulas provided below can be used to calculate the hoop stress and longitudinal stress. | ||
| + | |||
| + | : [[File: Hoop_Long_Stress_Farras_Hafizh.png|125px|center| Hoop Long Stress Formula (source: Personal Analysis)]] | ||
| + | |||
| + | ====Mechanical Properties of AISI 316 Austenitic Stainless Steel==== | ||
| + | |||
| + | :[[File: Mechanical_Properties_316.png|500px|thumb|left| Mechanical Properties of AISI 316 Austenitic Stainless Steel (source: Researchgate.com)]] | ||
| + | : The range of acceptable wall thickness is not arbitrary and should not exceed one-fifth of the vessel radius. According to ASME BPV Code Section VIII D.1, the '''minimum wall thickness should be at least 1/16 in (1.59 mm)''', regardless of corrosion allowance, material, or dimensions. | ||
| + | |||
| + | : Based on data obtained from Ferrobend, which provides information on the mechanical properties of AISI 316 stainless steel, we will employ both a conservative and less conservative approach by setting our limit at the yield strength and maximum tensile strength to represent failure. | ||
| + | |||
| + | : In this calculation, we will iterate from a minimum radius of '''2.9 mm to 12 mm''' with increments of '''1 mm in each iteration'''. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ====Iteration Process==== | ||
| + | |||
| + | <syntaxhighlight lang=xml> | ||
| + | |||
| + | r = 5.42e-2 | ||
| + | p = 800000 | ||
| + | t = 2.9e-3 | ||
| + | |||
| + | while t < 12e-3: | ||
| + | hoop = (r * p)/(t) | ||
| + | print('for thickness', t, 'hoop stress =', hoop, "Pa") | ||
| + | t += 1e-3 | ||
| + | if hoop > 205e9: | ||
| + | break | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | : The provided code calculates the hoop stress for various thickness values ranging from 2.9 mm to 12 mm, with a constraint that stops the iteration if the total hoop stress exceeds the yield strength of AISI 316 stainless steel. Based on the results, '''all thickness values ranging from 2.9 mm to 12 mm at 1 mm increments satisfy the yield strength constraint'''. Here are the calculation results from the code, which indicate that '''the hoop stress is significantly below the yield strength of 205 MPa'''. | ||
| + | |||
| + | : [[File: Calculation_of_Material_Strength.png|500px| Calculation of Material Strength (source: Personal Analysis)]] | ||
===Budget Constraints=== | ===Budget Constraints=== | ||
| + | |||
| + | : To ensure compliance with the cost constraint of '''not exceeding Rp500.000''',-, we need to evaluate the selected geometrical parameters. As a small-sized thin-walled vessel, '''sheet-metal manufacturing''' is the likely method for production. Therefore, we will '''procure materials in the form of sheet metal or plates'''. | ||
| + | |||
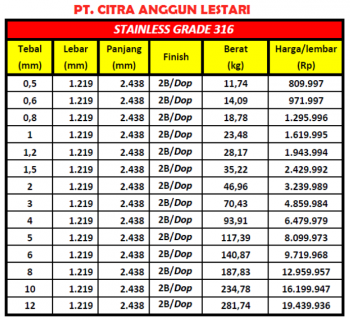
| + | :[[File: Pricing AISI 316 PT Citra Anggun Lestari Farras Hafizh.png|350px|thumb|left| AISI 316 Steel Plates Pricing from PT Citra Anggun Lestari (source: Personal Analysis)]] | ||
| + | |||
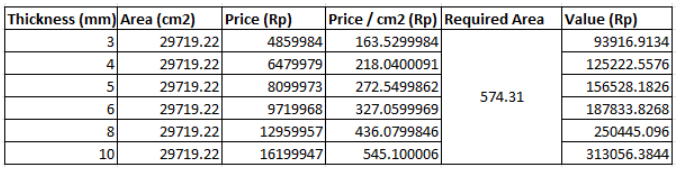
| + | :[[File: Detailed_Pricing_Calculation_Farras_Hafizh.png|750px|middle| AISI 316 Steel Plates Pricing Calculation (source: Personal Analysis)]] | ||
| + | |||
| + | |||
| + | : The table above presents a narrowed range of thicknesses within our area of interest. Since steel plates are not commonly available in small surface areas like our application, we conducted a cost per area analysis based on data from PT Citra Anggun Lestari. Fortunately, all possible thickness values satisfy the cost constraint. In selecting the thickness, we also consider '''minimizing weight while maintaining sufficient strength'''. As a result, '''the optimal choice is a 6 mm wall thickness'''. | ||
Latest revision as of 06:35, 9 June 2023
Contents
Introduction
- Halo semua, saya Farras Hafizh Al Farisi dengan NPM 2106635846 mahasiswa Metode Numerik 01.
- Berikut merupakan kumpulan tulisan saya selama mempelajari Metode Numerik serta selama mengakumulasi pemahaman mengenai makna mendalam Consciousness.
Pressurized Hydrogen Storage Optimization
Pressurized Hydrogen Storage
- Pressurized hydrogen storage involves compressing hydrogen gas and storing it in specially designed tanks or cylinders. These tanks are built to withstand high pressures, typically ranging from a few hundred to several thousand pounds per square inch (psi). Pressurized storage offers advantages such as simplicity, portability, and fast refueling times. However, it also presents challenges related to weight, safety, and limited storage capacity. Tank materials must be robust, and strict testing is necessary to prevent leaks or ruptures. Alternative storage methods like cryogenic storage and hydrogen carriers are being explored to address these limitations and optimize hydrogen storage and utilization.
Factors Involved in Designing and Optimizing a Pressurized Hydrogen Storage
- Designing and optimizing a pressurized hydrogen storage involves several factors and processes to ensure its safety, efficiency, and performance. Here are some key considerations in the design and optimization process:
- Storage Capacity
- The required storage capacity of hydrogen must be determined based on the anticipated demand and usage. Factors such as the desired duration of storage, refill frequency, and system requirements play a role in determining the storage capacity.
- Material Selection
- The choice of materials for the storage tank is crucial. Factors such as material strength, corrosion resistance, hydrogen compatibility, weight, and cost need to be considered. The selected material should meet safety standards, regulatory requirements, and be suitable for the specific application.
- Pressure Requirements
- Determining the optimal operating pressure is critical to balance storage capacity, tank weight, and safety. Higher pressures allow for more hydrogen storage within a given volume, but it increases material requirements and safety considerations. The pressure requirements should align with the intended use and regulatory standards.
- Safety Considerations
- Safety is paramount in hydrogen storage design. Factors such as material integrity, leak prevention, pressure relief mechanisms, and appropriate safety measures need to be incorporated. Standards and guidelines from regulatory bodies, such as the International Organization for Standardization (ISO) and national safety codes, should be followed.
- Structural Design
- The structural design of the storage tank must ensure its mechanical integrity and resistance to external loads, vibrations, and impacts. Finite element analysis (FEA) and other engineering calculations are performed to determine the optimal tank shape, thickness, reinforcement, and support structures.
- Thermal Management
- Hydrogen storage systems may require thermal management to control temperature variations. Insulation, cooling, or heating mechanisms are employed to maintain the desired hydrogen temperature range and prevent thermal stresses.
- Cost Optimization
- Optimization techniques, such as mathematical modeling and numerical methods, can be applied to minimize costs while meeting performance and safety requirements. This includes optimizing material usage, tank size, manufacturing processes, and other relevant parameters.
- Regulatory Compliance
- Compliance with relevant regulations, standards, and codes is essential in the design and operation of pressurized hydrogen storage. It ensures safety, environmental protection, and compatibility with industry norms.
- Hydrogen Purity
- The required purity level of hydrogen for the specific application should be considered. Impurities in the hydrogen stream can impact the integrity and performance of the storage system. Depending on the application, purification processes may be needed to remove impurities.
- Fill and Discharge Rates
- The desired fill and discharge rates of hydrogen affect the design and optimization of the storage system. Factors such as the available infrastructure, operational requirements, and efficiency considerations influence the sizing of valves, piping, and other components.
- System Integration
- Pressurized hydrogen storage systems are often integrated with other components and subsystems, such as hydrogen production units, fuel cells, or transportation systems. Seamless integration and compatibility with these systems are important to ensure overall system performance.
- Environmental Considerations
- Environmental factors, including temperature variations, exposure to corrosive substances, and seismic activity, should be taken into account during the design process. Adequate protection and design measures, such as coatings, seismic restraints, and environmental monitoring, may be required.
- Manufacturing and Fabrication Methods
- The manufacturing and fabrication techniques employed impact the quality, cost, and scalability of the storage system. Selection of appropriate manufacturing methods, such as welding, forming, or composite layup, needs to be aligned with the chosen materials and desired characteristics.
Final Report of Design and Optimization of Pressurized Hydrogen Storage
Requirements
- The specific requirements are 1 liter (1000 cm^3) of Hydrogen with 8 bar (800 kPa) Pressure with a maximum cost of Rp 500.000
Material Selection
- By carefully considering the materials available for pressurized hydrogen storage, our selection has led us to choose AISI 316 austenitic stainless steel. This decision is rooted in the unique properties and advantages offered by this particular material. Here are some reasons for considering AISI 316 stainless steel for pressurized hydrogen storage:
- 1) Corrosion Resistance
- Hydrogen can cause embrittlement and corrosion in some materials, leading to reduced structural integrity and potential safety hazards. AISI 316 stainless steel offers superior corrosion resistance, particularly in environments with high levels of hydrogen. This property helps ensure the long-term durability and safety of the storage system.
- 2) Strength and Pressure Resistance
- Pressurized hydrogen storage systems require materials with high strength to withstand the internal pressure. AISI 316 stainless steel possesses good mechanical properties, including high tensile strength and yield strength, allowing it to withstand the required pressure levels while maintaining structural integrity.
- 3) Compatibility with Hydrogen
- AISI 316 stainless steel has demonstrated compatibility with hydrogen gas in various studies and practical applications. It exhibits low permeability to hydrogen, reducing the risk of hydrogen loss and ensuring efficient containment within the storage system.
- 4) Established Industrial Usage
- AISI 316 stainless steel is widely used in various industries, including chemical processing, oil and gas, and marine applications. It has a well-established track record and extensive knowledge base regarding its behavior in different environments, making it a trusted material choice for engineering applications.
Constraints
- Pressurized hydrogen storage plays a crucial role in various applications, ranging from energy storage to fuel cell technology. Designing an optimized storage system requires careful consideration of multiple factors to ensure efficiency, safety, and cost-effectiveness. In this context, incorporating three key constraints - geometrical, material strength, and budget constraints - forms the foundation of an effective optimization model.
- 1) Geometrical Constraint
- The geometrical constraint ensures that the design of the storage system meets specific volume requirements. By setting a constraint on the volume or dimensions of the storage tank, you can optimize the geometrical parameters such as radius and height to ensure the tank can accommodate the desired volume of 1 liter (1000 cm^3). This constraint ensures that the storage tank is appropriately sized and fits within the available space.
- 2) Material Strength Constraint
- The material strength constraint focuses on selecting a material that can withstand the high-pressure environment of the hydrogen storage system. Hydrogen is stored under high pressure (8 bar or 800 kPa), and selecting a material with appropriate strength characteristics is crucial for the safety and integrity of the storage system. By incorporating this constraint, you ensure that the selected material, such as AISI 316 austenitic stainless steel, possesses the necessary mechanical properties to withstand the pressure and prevent any material failures or leaks.
- 3) Budget Constraint
- The budget constraint places a limitation on the cost of the pressurized hydrogen storage system. By including this constraint, you ensure that the optimization model considers the cost-effectiveness of the design. The budget constraint helps in selecting cost-efficient materials and optimizing the geometrical parameters to meet the required specifications while staying within the allocated budget of Rp 500.000. This constraint ensures that the final design is financially feasible and aligns with the available resources.
Geometrical Constraints
- The code provided utilizes an optimization algorithm implemented in Python, utilizing the powerful capabilities of the NumPy and SciPy libraries. The objective of the code is to determine the optimal values for the radius and height of the storage tank by minimizing the surface area, while considering the specified volume of hydrogen. The incorporation of NumPy allows for efficient mathematical operations and array manipulation, while SciPy provides advanced optimization techniques and algorithms
Base Geometry
import numpy as np
from scipy.optimize import minimize
# Define the objective function
def objective(x):
radius, height = x
surface_area = 2 * np.pi * radius * (radius + height)
return surface_area
# Define the volume constraint function
def volume_constraint(x):
radius, height = x
volume = np.pi * radius**2 * height
return volume - 1000
# Define the optimization problem
x0 = [1.0, 10.0]
bounds = [(0, None), (0, None)]
constraint = {'type': 'eq', 'fun': volume_constraint}
problem = minimize(objective, x0, bounds=bounds, constraints=constraint)
# Extract the optimized results
optimized_radius = problem.x[0]
optimized_height = problem.x[1]
optimized_surface_area = problem.fun
# Print the optimized results
print("Optimization Results:")
print(f"Radius: {optimized_radius:.2f} cm")
print(f"Height: {optimized_height:.2f} cm")
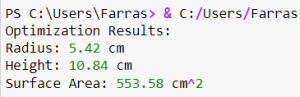
print(f"Surface Area: {optimized_surface_area:.2f} cm^2")- From the coding results, it can be inferred that by minimizing the surface area, the optimal dimensions for the cylindrical tank are achieved with a height-to-radius ratio of 2:1. Specifically, the tank has a height of 10.84 cm and a radius of 5.42 cm. These measurements result in a surface area of 553.58 cm^2, which is the smallest possible area for the given volume and pressure requirements.
-
End Cap Geometry
- Using a purely cylindrical geometry for the storage tank may pose risks due to stress concentration at the corners. To minimize stress concentration and reduce surface area while maintaining the same volume, it is more efficient to adopt a torispherical end cap shape. This shape can be achieved by adding a fillet with a radius equal to half the tank's radius. The filleting creates a smooth curvature and helps reduce stress concentration. Adjustments in the geometrical parameters are necessary to compensate for the volume reduction caused by the filleting. By calculating the percentage reduction in the cross-sectional area, we can inversely apply it to the required volume to obtain the new increased volume constraint.
-
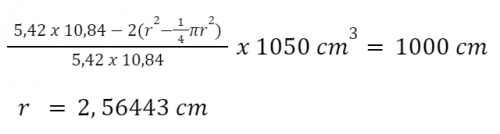
- The calculation results mentioned earlier reveal that the fillet radius obtained for the tank's end caps is 2.56443 cm
Material Strength Constraints
Formula Used
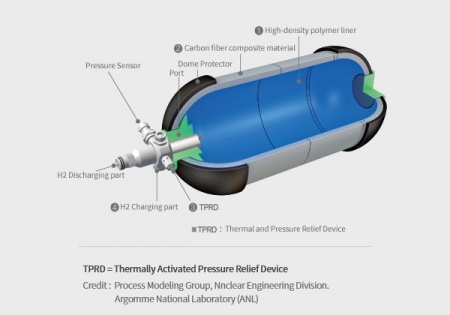
- In the context of a pressurized container, ensuring that the thickness and strength of the container material can endure the applied pressure on the walls is crucial. Regarding the specific requirements, the 1-liter hydrogen tank has a maximum pressure limit of 8 bar.
- Within a thin-walled cylindrical component, two main types of stress exist: circumferential (hoop) stress and longitudinal stress. Although radial stress is present, it :can be disregarded since the radius is significantly larger than the wall thickness. The formulas provided below can be used to calculate the hoop stress and longitudinal stress.
Mechanical Properties of AISI 316 Austenitic Stainless Steel
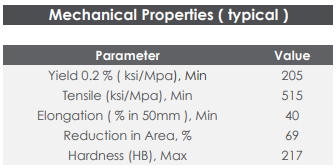
- The range of acceptable wall thickness is not arbitrary and should not exceed one-fifth of the vessel radius. According to ASME BPV Code Section VIII D.1, the minimum wall thickness should be at least 1/16 in (1.59 mm), regardless of corrosion allowance, material, or dimensions.
- Based on data obtained from Ferrobend, which provides information on the mechanical properties of AISI 316 stainless steel, we will employ both a conservative and less conservative approach by setting our limit at the yield strength and maximum tensile strength to represent failure.
- In this calculation, we will iterate from a minimum radius of 2.9 mm to 12 mm with increments of 1 mm in each iteration.
Iteration Process
r = 5.42e-2
p = 800000
t = 2.9e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9:
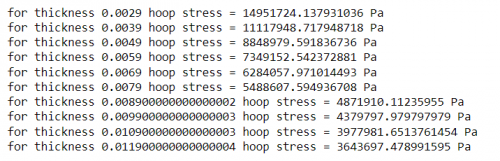
break- The provided code calculates the hoop stress for various thickness values ranging from 2.9 mm to 12 mm, with a constraint that stops the iteration if the total hoop stress exceeds the yield strength of AISI 316 stainless steel. Based on the results, all thickness values ranging from 2.9 mm to 12 mm at 1 mm increments satisfy the yield strength constraint. Here are the calculation results from the code, which indicate that the hoop stress is significantly below the yield strength of 205 MPa.
Budget Constraints
- To ensure compliance with the cost constraint of not exceeding Rp500.000,-, we need to evaluate the selected geometrical parameters. As a small-sized thin-walled vessel, sheet-metal manufacturing is the likely method for production. Therefore, we will procure materials in the form of sheet metal or plates.
- The table above presents a narrowed range of thicknesses within our area of interest. Since steel plates are not commonly available in small surface areas like our application, we conducted a cost per area analysis based on data from PT Citra Anggun Lestari. Fortunately, all possible thickness values satisfy the cost constraint. In selecting the thickness, we also consider minimizing weight while maintaining sufficient strength. As a result, the optimal choice is a 6 mm wall thickness.