Difference between revisions of "Kausar Nur Budirahardjo"
| (16 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
hello my name is Kausar Nur (2106651710) and i'm currently pursuing a Bachelor's degree in Mechanical Engineering, University of Indonesia. As a future engineer, I am excited to embark my studies and to keep gain knowledge. Remember, stay concious! | hello my name is Kausar Nur (2106651710) and i'm currently pursuing a Bachelor's degree in Mechanical Engineering, University of Indonesia. As a future engineer, I am excited to embark my studies and to keep gain knowledge. Remember, stay concious! | ||
| + | |||
| + | Sebagai mahasiswa Teknik Mesin yang merupakan calon-calon insinyur berkualitas, kita harus melakukan pendekatan secara menyeluruh pada segala faktor yang berpengaruh dalam mendesain suatu komponen, terutama efisiensi dan optimisasi yang urgensinya sangat penting. Melalui kelas Metode Numerik dengan tugas mendesain dan mengoptimalkan pressurized hydrogen storage ini, kita dapat belajar untuk berpola pikir layaknya seorang insinyur. Secara tidak langsung, hal ini juga melatih consciousness kita. | ||
| Line 61: | Line 63: | ||
7. Certification and Testing: Compressed hydrogen storage tanks must undergo rigorous testing and certification processes to ensure compliance with safety standards. These tests evaluate the tank's structural integrity, leak resistance, and endurance under various conditions. | 7. Certification and Testing: Compressed hydrogen storage tanks must undergo rigorous testing and certification processes to ensure compliance with safety standards. These tests evaluate the tank's structural integrity, leak resistance, and endurance under various conditions. | ||
| + | |||
| + | ---- | ||
| + | Designing compressed hydrogen storage tanks involves several calculations to determine parameters such as tank volume, pressure, and weight. Here are some key calculations involved: | ||
| + | |||
| + | 1. Storage Capacity: The storage capacity of the tank is determined by the desired amount of hydrogen to be stored. This calculation depends on the application requirements, such as the range or duration of hydrogen supply needed. The storage capacity is typically measured in kilograms (kg) or liters (L). | ||
| + | |||
| + | 2. Tank Volume: The tank volume calculation depends on the storage capacity and the density of hydrogen at the operating pressure and temperature. The ideal gas law equation, PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the ideal gas constant, and T is the temperature, can be used to calculate the volume of hydrogen gas at specific conditions. | ||
| + | |||
| + | 3. Tank Pressure: The tank pressure depends on factors such as the application requirements, safety regulations, and industry standards. It is important to ensure that the tank can withstand the desired pressure without compromising safety. The pressure calculation may involve considering factors such as the maximum working pressure, safety margins, and pressure relief mechanisms. | ||
| + | |||
| + | 4. Tank Weight: The weight of the tank is influenced by various factors, including the tank material, design, and safety features. The weight calculation involves considering the weight of the tank structure, internal components, and any additional insulation or protective layers. | ||
| + | |||
| + | 5. Hydrogen Density: The density of hydrogen gas varies with pressure and temperature. To calculate the density, the ideal gas law can be rearranged to solve for density (ρ): ρ = (P * M) / (R * T), where P is the pressure, M is the molar mass of hydrogen, R is the ideal gas constant, and T is the temperature. This calculation helps determine the volume of hydrogen required to achieve the desired storage capacity. | ||
| + | |||
| + | It is important to note that these calculations are based on specific conditions and assumptions, and the actual design and calculations for compressed hydrogen storage tanks require careful consideration of safety factors, regulatory requirements, and industry standards. Consulting experts in hydrogen storage and adhering to applicable guidelines is crucial to ensure accurate and safe tank design. | ||
| + | |||
| + | ---- | ||
| + | == Perhitungan Tangki == | ||
| + | |||
| + | untuk mencari tinggi dari tabung sendiri maka kita bisa memakai rumus | ||
| + | |||
| + | V = πr^2h | ||
| + | |||
| + | dimana Vnya yaitu 1 liter atau setara 1000 cm^3 | ||
| + | |||
| + | lalu π nya 3,14 | ||
| + | |||
| + | untuk diameter kita memakai asumsi semisal 12 cm maka r nya 6 cm | ||
| + | |||
| + | 1000 = (π)(6)^2(h) | ||
| + | maka h kita dapat h ≈ 8,8464 cm | ||
| + | |||
| + | 1. Pemilihan Material | ||
| + | Material yang digunakan adalah sheet metal ASTM A36 dengan yield strength 248 MPa | ||
| + | |||
| + | Allowable Stress = 2/3 x 248 = 165,3 MPa | ||
| + | |||
| + | 2. Minimum Ketebalan | ||
| + | |||
| + | [[File:Screen Shot 2023-06-12 at 00.30.49.png|650px]] | ||
| + | |||
| + | E = 0,60 | ||
| + | |||
| + | P = 8 bar = 116 Psi | ||
| + | |||
| + | R = 100 mm = 3,93 inch | ||
| + | |||
| + | S = 24000 ksi | ||
| + | |||
| + | Corrosion allowance = 1 mm = 0,039 inch | ||
| + | |||
| + | t = 116x(3,93+0,039) / (24000x0,6)-(0,6x116) = 0,03212 + corrosion allowance | ||
| + | |||
| + | t = 0,07112 in atau 1,8 mm | ||
| + | |||
| + | == Bentuk Model == | ||
| + | |||
| + | [[File:MessageImage 1686505374382.jpg|550px]] | ||
| + | |||
| + | |||
| + | == Pressurized hydrogen storage optimization == | ||
| + | |||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def calculate_volume(r, h): | ||
| + | volume = math.pi * r**2 * h | ||
| + | return volume | ||
| + | |||
| + | def calculate_pressure(volume, r): | ||
| + | pressure = (volume * 1e-3) / (math.pi * r**2) | ||
| + | return pressure | ||
| + | |||
| + | def objective(x): | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | volume = calculate_volume(r, h) | ||
| + | return -volume # Negatifkan volume untuk maksimisasi | ||
| + | |||
| + | # Batasan geometri: jari-jari (r) harus lebih kecil dari setengah diameter dan tinggi (h) lebih kecil dari tinggi awal | ||
| + | def constraint(x): | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | return [6 - r, 8.8464 - h] | ||
| + | |||
| + | # Batasan tekanan: tekanan harus kurang dari atau sama dengan 8 bar | ||
| + | def pressure_constraint(x): | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | volume = calculate_volume(r, h) | ||
| + | pressure = calculate_pressure(volume, r) | ||
| + | return pressure - 8 # Batasan tekanan maksimum 8 bar | ||
| + | |||
| + | # Inisialisasi nilai awal untuk jari-jari dan tinggi tabung | ||
| + | x0 = [6, 8.8464] | ||
| + | |||
| + | # Definisikan batasan dan jenis batasan (<=) | ||
| + | constraint1 = {'type': 'ineq', 'fun': constraint} | ||
| + | constraint2 = {'type': 'ineq', 'fun': pressure_constraint} | ||
| + | |||
| + | # Panggil fungsi minimize untuk mencari solusi optimisasi | ||
| + | sol = minimize(objective, x0, constraints=[constraint1, constraint2]) | ||
| + | |||
| + | # Ambil hasil optimisasi | ||
| + | optimized_r = sol.x[0] | ||
| + | optimized_h = sol.x[1] | ||
| + | optimized_volume = calculate_volume(optimized_r, optimized_h) | ||
| + | optimized_pressure = calculate_pressure(optimized_volume, optimized_r) | ||
| + | |||
| + | print("Jari-jari optimal:", optimized_r, "cm") | ||
| + | print("Tinggi optimal:", optimized_h, "cm") | ||
| + | print("Volume optimal:", optimized_volume, "cm^3") | ||
| + | print("Tekanan optimal:", optimized_pressure, "bar") | ||
| + | |||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Hasil coding : | ||
| + | |||
| + | Diameter tangki oksigen (cm): 6 cm | ||
| + | |||
| + | Tinggi tangki oksigen (cm): 8,8464 cm | ||
| + | |||
| + | Luas permukaan tangki oksigen (cm^2): 1000.504226 cm^3 | ||
| + | |||
| + | Tekanan Optimal : 0,00884 bar | ||
| + | |||
| + | |||
| + | Lalu melakukan perhitungan luas permukaan tabung dengan menggunakan code : | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | |||
| + | def calculate_surface_area(diameter, tinggi): | ||
| + | r = diameter / 2 | ||
| + | luas_lingkaran = math.pi * r**2 | ||
| + | luas_selimut = 2 * math.pi * r * tinggi | ||
| + | luas_permukaan = 2 * luas_lingkaran + luas_selimut | ||
| + | return luas_permukaan | ||
| + | |||
| + | diameter = 12 # cm | ||
| + | tinggi = 8.8464 # cm | ||
| + | |||
| + | luas_permukaan = calculate_surface_area(diameter, tinggi) | ||
| + | |||
| + | print("Luas Permukaan Tabung:", luas_permukaan, "cm^2") | ||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Hasi Coding : | ||
| + | |||
| + | luas permukaan tabung 559.6960 cm^2 | ||
| + | |||
| + | == Budget Constraint == | ||
| + | |||
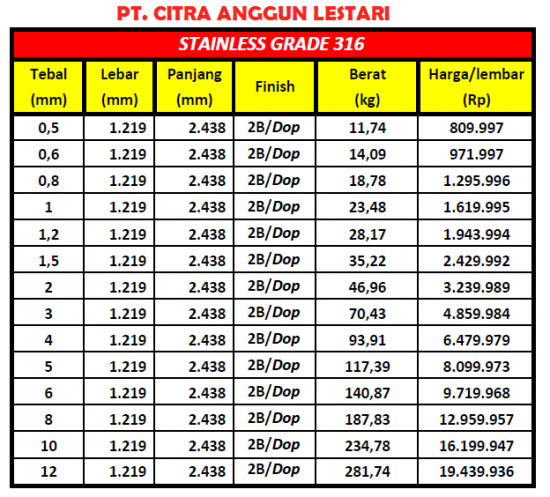
| + | [[File:Sus316.png|550px]] | ||
| + | [[File:MessageImage 1686509511951.jpg|550px]] | ||
| + | |||
| + | Dengan mempertimbangkan anggaran yang telah ditentukan sebesar Rp 300.000, ketebalan yang tepat untuk tangki tersebut adalah 8 mm. Dengan demikian, sisa anggaran dapat dialokasikan untuk membeli katup dan pengatur tekanan. | ||
| + | |||
| + | == Final Remarks == | ||
| + | |||
| + | Optimisasi desain tangki ini diperoleh ukuran tangki, yaitu radius sebesar 6 cm, tinggi sebesar 8,8464 cm, luas permukaan sebesar 559,6960 cm^2. selanjutnya tangki tersebut menggunakan material dengan batasan biaya sebesar RP 300.000 dan diperoleh ukuran ketebalan dinding tangki hidrogen sebesar 8 mm dan sisa biayanya dapat dialokasikan untuk membeli katup. | ||
Latest revision as of 01:51, 12 June 2023
hello my name is Kausar Nur (2106651710) and i'm currently pursuing a Bachelor's degree in Mechanical Engineering, University of Indonesia. As a future engineer, I am excited to embark my studies and to keep gain knowledge. Remember, stay concious!
Sebagai mahasiswa Teknik Mesin yang merupakan calon-calon insinyur berkualitas, kita harus melakukan pendekatan secara menyeluruh pada segala faktor yang berpengaruh dalam mendesain suatu komponen, terutama efisiensi dan optimisasi yang urgensinya sangat penting. Melalui kelas Metode Numerik dengan tugas mendesain dan mengoptimalkan pressurized hydrogen storage ini, kita dapat belajar untuk berpola pikir layaknya seorang insinyur. Secara tidak langsung, hal ini juga melatih consciousness kita.
Design & Optimization of Pressurized Hydrogen Storage
A 1-liter hydrogen storage design that is budget-friendly must carefully take into account a number of variables. Here are some ideas to assist you in finding a workable and affordable solution: 1. Choose a Cost-Effective Storage Material For the storage container, look for economical solutions such lightweight plastic or composite materials. Think about how they react with hydrogen and whether they can endure the necessary pressure. 2. Cylinder Design A smaller cylinder should be optimized to hold 1 liter of hydrogen. This will save material costs while still maintaining the required pressure. Think about inexpensive, lightweight materials like aluminum or composite cylinders. 3. Safety Considerations Make sure the storage system you choose has all the necessary safety precautions, like pressure relief valves and enough ventilation. To avoid overpressurization and maintain the secure storage of hydrogen, certain precautions are essential. 4. Cost-Effective Components Choose reasonably priced valves, fittings, and seals that are compatible with the storage material and meet the necessary pressure requirements. To find the best bargain within your price range, research vendors and compare pricing. 5. Efficient Manufacturing Investigate low-cost manufacturing strategies like standardized assembly procedures or injection molding for plastic parts. Costs can be decreased by streamlining the manufacturing process. 6. System Integration Make sure the storage system's components are correctly integrated and sealed to avoid leaks and guarantee effective performance. Check the system for any flaws or leaks that can affect performance and security. 7. Performance Testing Perform performance tests to make sure the storage system satisfies the necessary requirements after it has been created and put together. Consider aspects including pressure retention, robustness, and overall functionality.
It's crucial to keep in mind that optimizing a hydrogen storage system on a tight budget necessitates careful consideration of a number of aspects, including material pricing, component selection, and manufacturing methods. To make sure that the design complies with safety standards and functional needs, it could also be beneficial to speak with specialists or professionals in the industry who have experience with hydrogen storage systems.
Hydrogen as a vehicle fuel offers several advantages. It produces zero emissions, reducing air pollution and combating climate change. Hydrogen fuel cells are energy efficient, providing improved fuel economy and longer driving range. Refueling hydrogen vehicles is fast, taking only minutes. Hydrogen can be produced from various sources, promoting versatility and integration with renewable energy. It can serve as energy storage, enabling the integration of intermittent renewable energy sources. Utilizing hydrogen reduces dependence on fossil fuels and increases energy security. Challenges remain, but ongoing research aims to overcome them and make hydrogen a viable and widespread vehicle fuel option.
While hydrogen fuel has numerous advantages, there are also several challenges associated with its widespread adoption:
1. Infrastructure: One of the primary challenges is the lack of a widespread hydrogen infrastructure. Building an extensive network of hydrogen refueling stations requires significant investment and coordination among governments, energy companies, and vehicle manufacturers. Without a well-developed infrastructure, the accessibility and convenience of refueling hydrogen vehicles can be limited.
2. Production and Distribution: The production of hydrogen can be energy-intensive and costly. Currently, most hydrogen is produced from natural gas through a process called steam methane reforming, which generates carbon emissions unless carbon capture and storage technologies are employed. The scaling up of renewable hydrogen production methods, such as electrolysis powered by renewable energy sources, is necessary to ensure a sustainable and low-carbon supply. Additionally, transporting and distributing hydrogen requires dedicated infrastructure due to its low energy density and high reactivity, further adding to the complexity and cost.
3. Storage and Safety: Hydrogen has a low energy density, which means it requires large storage tanks to store sufficient amounts for practical use in vehicles. Finding suitable materials for safe and efficient hydrogen storage remains a technical challenge. Additionally, hydrogen is highly flammable and requires careful handling and storage to ensure safety. Public perception and concerns regarding hydrogen safety also need to be addressed.
4. Cost: The cost of hydrogen fuel cell vehicles and hydrogen production remains relatively high compared to conventional internal combustion engine vehicles. Advancements in technology and economies of scale are necessary to reduce costs and make hydrogen fuel cell vehicles more affordable and competitive in the market.
5. Energy Efficiency: While hydrogen fuel cells offer high energy efficiency, the overall efficiency of the hydrogen production process (including production, storage, and conversion) is l
ower compared to battery-electric vehicles (BEVs). The conversion of electricity to hydrogen through electrolysis and then back to electricity in fuel cells results in energy losses at each step. However, ongoing research aims to improve the overall efficiency of the hydrogen energy system.
Addressing these challenges requires continued research, development, and investment in hydrogen technologies, infrastructure, and supportive policies. Collaboration between governments, industries, and research institutions is crucial for overcoming these hurdles and realizing the full potential of hydrogen as a vehicle fuel.
The manufacturing requirements for hydrogen fuel involve two main aspects: hydrogen production and fuel cell manufacturing. Hydrogen can be produced through methods such as steam methane reforming or electrolysis, the latter being a cleaner option when powered by renewable energy. Fuel cell manufacturing includes processes such as stack assembly, membrane electrode assembly (MEA) manufacturing, and balance of plant (BOP) component production. Specialized equipment, expertise, and quality control are necessary to ensure high-performance fuel cells. Advancements in manufacturing techniques and economies of scale are important for reducing costs and improving efficiency in hydrogen fuel cell production.
Designing and calculating compressed hydrogen storage tanks involves several considerations to ensure safety, efficiency, and compliance with industry standards. Here are some key aspects to consider:
1. Tank Material: Selecting the appropriate tank material is crucial for hydrogen storage. Common materials used include carbon fiber composite, aluminum, or steel. Carbon fiber composite tanks are lightweight and have high strength-to-weight ratios, making them popular for automotive applications. Aluminum and steel tanks are more common for stationary or industrial use.
2. Tank Design: The tank design should account for factors such as pressure requirements, storage capacity, weight limitations, and space constraints. The shape and size of the tank can vary depending on the application and available space. Common tank designs include cylindrical, spherical, or prismatic shapes.
3. Pressure Rating: Compressed hydrogen storage tanks are typically designed to withstand high-pressure conditions. The pressure rating depends on the application, regulations, and safety standards. Common pressure ratings range from 350 bar (5,076 psi) to 700 bar (10,152 psi) for automotive applications.
4. Safety Considerations: Safety is of paramount importance when designing compressed hydrogen storage tanks. The tank design should incorporate safety features such as pressure relief devices, burst disks, and leak detection systems. Compliance with standards like ISO 15869 or SAE J2579 is essential to ensure the tanks meet safety requirements.
5. Tank Volume and Capacity: The tank volume and storage capacity depend on the specific application and desired range or duration of hydrogen supply. The volume and capacity calculations should consider factors such as required vehicle range, hydrogen consumption rate, and available refueling infrastructure.
6. Hydrogen Density and Temperature Effects: Compressed hydrogen's density is influenced by pressure and temperature. The ideal gas law, which relates pressure, volume, and temperature, is used to calculate the density of compressed hydrogen at various conditions. Understanding the effects of temperature on hydrogen density is important for accurate calculations.
7. Certification and Testing: Compressed hydrogen storage tanks must undergo rigorous testing and certification processes to ensure compliance with safety standards. These tests evaluate the tank's structural integrity, leak resistance, and endurance under various conditions.
Designing compressed hydrogen storage tanks involves several calculations to determine parameters such as tank volume, pressure, and weight. Here are some key calculations involved:
1. Storage Capacity: The storage capacity of the tank is determined by the desired amount of hydrogen to be stored. This calculation depends on the application requirements, such as the range or duration of hydrogen supply needed. The storage capacity is typically measured in kilograms (kg) or liters (L).
2. Tank Volume: The tank volume calculation depends on the storage capacity and the density of hydrogen at the operating pressure and temperature. The ideal gas law equation, PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the ideal gas constant, and T is the temperature, can be used to calculate the volume of hydrogen gas at specific conditions.
3. Tank Pressure: The tank pressure depends on factors such as the application requirements, safety regulations, and industry standards. It is important to ensure that the tank can withstand the desired pressure without compromising safety. The pressure calculation may involve considering factors such as the maximum working pressure, safety margins, and pressure relief mechanisms.
4. Tank Weight: The weight of the tank is influenced by various factors, including the tank material, design, and safety features. The weight calculation involves considering the weight of the tank structure, internal components, and any additional insulation or protective layers.
5. Hydrogen Density: The density of hydrogen gas varies with pressure and temperature. To calculate the density, the ideal gas law can be rearranged to solve for density (ρ): ρ = (P * M) / (R * T), where P is the pressure, M is the molar mass of hydrogen, R is the ideal gas constant, and T is the temperature. This calculation helps determine the volume of hydrogen required to achieve the desired storage capacity.
It is important to note that these calculations are based on specific conditions and assumptions, and the actual design and calculations for compressed hydrogen storage tanks require careful consideration of safety factors, regulatory requirements, and industry standards. Consulting experts in hydrogen storage and adhering to applicable guidelines is crucial to ensure accurate and safe tank design.
Contents
Perhitungan Tangki
untuk mencari tinggi dari tabung sendiri maka kita bisa memakai rumus
V = πr^2h
dimana Vnya yaitu 1 liter atau setara 1000 cm^3
lalu π nya 3,14
untuk diameter kita memakai asumsi semisal 12 cm maka r nya 6 cm
1000 = (π)(6)^2(h) maka h kita dapat h ≈ 8,8464 cm
1. Pemilihan Material Material yang digunakan adalah sheet metal ASTM A36 dengan yield strength 248 MPa
Allowable Stress = 2/3 x 248 = 165,3 MPa
2. Minimum Ketebalan
E = 0,60
P = 8 bar = 116 Psi
R = 100 mm = 3,93 inch
S = 24000 ksi
Corrosion allowance = 1 mm = 0,039 inch
t = 116x(3,93+0,039) / (24000x0,6)-(0,6x116) = 0,03212 + corrosion allowance
t = 0,07112 in atau 1,8 mm
Bentuk Model
Pressurized hydrogen storage optimization
import math
from scipy.optimize import minimize
def calculate_volume(r, h):
volume = math.pi * r**2 * h
return volume
def calculate_pressure(volume, r):
pressure = (volume * 1e-3) / (math.pi * r**2)
return pressure
def objective(x):
r = x[0]
h = x[1]
volume = calculate_volume(r, h)
return -volume # Negatifkan volume untuk maksimisasi
# Batasan geometri: jari-jari (r) harus lebih kecil dari setengah diameter dan tinggi (h) lebih kecil dari tinggi awal
def constraint(x):
r = x[0]
h = x[1]
return [6 - r, 8.8464 - h]
# Batasan tekanan: tekanan harus kurang dari atau sama dengan 8 bar
def pressure_constraint(x):
r = x[0]
h = x[1]
volume = calculate_volume(r, h)
pressure = calculate_pressure(volume, r)
return pressure - 8 # Batasan tekanan maksimum 8 bar
# Inisialisasi nilai awal untuk jari-jari dan tinggi tabung
x0 = [6, 8.8464]
# Definisikan batasan dan jenis batasan (<=)
constraint1 = {'type': 'ineq', 'fun': constraint}
constraint2 = {'type': 'ineq', 'fun': pressure_constraint}
# Panggil fungsi minimize untuk mencari solusi optimisasi
sol = minimize(objective, x0, constraints=[constraint1, constraint2])
# Ambil hasil optimisasi
optimized_r = sol.x[0]
optimized_h = sol.x[1]
optimized_volume = calculate_volume(optimized_r, optimized_h)
optimized_pressure = calculate_pressure(optimized_volume, optimized_r)
print("Jari-jari optimal:", optimized_r, "cm")
print("Tinggi optimal:", optimized_h, "cm")
print("Volume optimal:", optimized_volume, "cm^3")
print("Tekanan optimal:", optimized_pressure, "bar")Hasil coding :
Diameter tangki oksigen (cm): 6 cm
Tinggi tangki oksigen (cm): 8,8464 cm
Luas permukaan tangki oksigen (cm^2): 1000.504226 cm^3
Tekanan Optimal : 0,00884 bar
Lalu melakukan perhitungan luas permukaan tabung dengan menggunakan code :
import math
def calculate_surface_area(diameter, tinggi):
r = diameter / 2
luas_lingkaran = math.pi * r**2
luas_selimut = 2 * math.pi * r * tinggi
luas_permukaan = 2 * luas_lingkaran + luas_selimut
return luas_permukaan
diameter = 12 # cm
tinggi = 8.8464 # cm
luas_permukaan = calculate_surface_area(diameter, tinggi)
print("Luas Permukaan Tabung:", luas_permukaan, "cm^2")Hasi Coding :
luas permukaan tabung 559.6960 cm^2
Budget Constraint
Dengan mempertimbangkan anggaran yang telah ditentukan sebesar Rp 300.000, ketebalan yang tepat untuk tangki tersebut adalah 8 mm. Dengan demikian, sisa anggaran dapat dialokasikan untuk membeli katup dan pengatur tekanan.
Final Remarks
Optimisasi desain tangki ini diperoleh ukuran tangki, yaitu radius sebesar 6 cm, tinggi sebesar 8,8464 cm, luas permukaan sebesar 559,6960 cm^2. selanjutnya tangki tersebut menggunakan material dengan batasan biaya sebesar RP 300.000 dan diperoleh ukuran ketebalan dinding tangki hidrogen sebesar 8 mm dan sisa biayanya dapat dialokasikan untuk membeli katup.