Difference between revisions of "Phyton Code"
| (27 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Untuk | + | Untuk menentukan ukuran pelat yang akan digunakan berdasarkan volume yang dibutuhkan, yaitu 1 liter, namun menggunakan luas pelat seminimal mungkin menggunakan perhitungan sebagai berikut: |
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def hitung_luas_permukaan(x): | ||
| + | radius, tinggi = x | ||
| + | luas_permukaan = 2 * np.pi * radius * (radius + tinggi) | ||
| + | return luas_permukaan | ||
| + | |||
| + | def hitung_volume(x): | ||
| + | radius, tinggi = x | ||
| + | volume = np.pi * radius**2 * tinggi | ||
| + | return volume | ||
| + | |||
| + | def optimasi_silinder(): | ||
| + | tebakan_awal = [1.0, 10.0] | ||
| + | batasan = [(0, None), (0, None)] | ||
| + | kendala = {'type': 'eq', 'fun': lambda x: hitung_volume(x) - 1050} | ||
| + | |||
| + | hasil = minimize(hitung_luas_permukaan, tebakan_awal, method='SLSQP', bounds=batasan, constraints=kendala) | ||
| + | |||
| + | print("Hasil Optimisasi:") | ||
| + | print("Radius: {:.2f} cm".format(hasil.x[0])) | ||
| + | print("Tinggi: {:.2f} cm".format(hasil.x[1])) | ||
| + | print("Luas Permukaan: {:.2f} cm^2".format(hasil.fun)) | ||
| + | |||
| + | optimasi_silinder() | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Dari coding di atas di dapatkan hasil sebagai berikut : | ||
| + | |||
| + | [[File:alvino124.png|300x10000px]] | ||
| + | Untuk menentukan proses iterasi dari ketebalan tangki tersebut dapat dilakukan dengan coding sebagai berikut : | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | r = 5.42e-2 | ||
| + | p = 800000 | ||
| + | t = 2.9e-3 | ||
| + | |||
| + | while t < 12e-3: | ||
| + | hoop = (r * p)/(t) | ||
| + | print('for thickness', t, 'hoop stress =', hoop, "Pa") | ||
| + | t += 1e-3 | ||
| + | if hoop > 205e9: | ||
| + | break | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | [[File:cccalvino.png|500x300px]] | ||
| + | |||
| + | Coding di atas menentukan tegangan lingkaran dengan mengevaluasi berbagai nilai ketebalan dalam rentang 2,9 mm hingga 12 mm. Kode tersebut menggabungkan sebuah batasan yang menghentikan iterasi jika total tegangan lingkaran melebihi kekuatan luluh dari baja tahan karat '''AISI 316'''. Hasilnya menunjukkan bahwa semua nilai ketebalan dari 2,9 mm hingga 12 mm, dengan penambahan 1 mm, memenuhi persyaratan kekuatan luluh. Kode tersebut menghasilkan hasil perhitungan berikut, yang menunjukkan bahwa tegangan lingkaran tetap jauh di bawah kekuatan luluh sebesar 205 MPa. | ||
| + | |||
| + | Untuk mengoptimisasi penyimpanan hidrogen pada tekanan 8 bar dengan kapasitas 1 liter dan anggaran maksimal Rp500.000, dapat diselesaikan dengan phyton code dibawah : | ||
<syntaxhighlight lang="xml"> | <syntaxhighlight lang="xml"> | ||
| Line 42: | Line 99: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | Kode di atas menggunakan fungsi tujuan untuk memaksimalkan jumlah unit penyimpanan hidrogen yang akan dibeli. Kendala anggaran diatur menggunakan fungsi kendala, yang memastikan bahwa total biaya tidak melebihi anggaran maksimal yang diberikan. Output akan menampilkan jumlah unit yang harus dibeli, total kapasitas penyimpanan, dan total biaya yang dibutuhkan. Di bawah ini merupakan hasil dari phyton code tersebut : | ||
| + | |||
| + | [[File:Hasil_optimasi.png|500x300px]] | ||
| + | |||
| + | Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini : | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Harga dan kapasitas | ||
| + | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen | ||
| + | kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit | ||
| + | |||
| + | # Anggaran maksimal | ||
| + | budget_maksimal = 500000 | ||
| + | |||
| + | # Fungsi tujuan | ||
| + | def fungsi_tujuan(x): | ||
| + | return -x | ||
| + | |||
| + | # Kendala | ||
| + | def kendala(x): | ||
| + | return budget_maksimal - (harga_per_unit * x[0]) | ||
| + | |||
| + | kendala_anggaran = [{'type': 'ineq', 'fun': kendala}] | ||
| + | |||
| + | # Nilai awal | ||
| + | x0 = [0] | ||
| + | |||
| + | # Batasan | ||
| + | batas = [(0, None)] | ||
| + | |||
| + | # Membuat fungsi untuk menampilkan hasil | ||
| + | def tampilkan_hasil(solusi): | ||
| + | print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi") | ||
| + | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | ||
| + | print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
| + | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| + | |||
| + | # Menyelesaikan masalah optimisasi | ||
| + | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran) | ||
| + | |||
| + | # Menampilkan hasil | ||
| + | tampilkan_hasil(solusi) | ||
| + | |||
| + | # Menghasilkan grafik | ||
| + | anggaran = np.linspace(0, 10, 100) # Range anggaran | ||
| + | kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran | ||
| + | biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran | ||
| + | |||
| + | plt.figure() | ||
| + | plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan') | ||
| + | plt.plot(anggaran, biaya, label='Total Biaya') | ||
| + | plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal') | ||
| + | plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal') | ||
| + | plt.xlabel('Anggaran') | ||
| + | plt.ylabel('Kapasitas/Biaya') | ||
| + | plt.title('Optimisasi Penyimpanan Hidrogen') | ||
| + | plt.legend() | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Kode di atas menghitung jumlah optimal unit penyimpanan hidrogen yang akan dibeli berdasarkan harga per unit, kapasitas per unit, dan anggaran maksimal yang diberikan. Kode ini memberikan solusi terbaik dengan kapasitas total tertinggi yang tetap berada dalam anggaran. Hasilnya kemudian dicetak, termasuk jumlah unit, kapasitas total, dan biaya total. Selain itu, kode ini juga membuat grafik yang menunjukkan hubungan antara kapasitan dan anggaran optimisasi penyimpanan hidrogen | ||
| + | |||
| + | [[File:grafikdats.png|800x400px]] | ||
| + | |||
| + | Untuk menentukan ketebalan yang tepat untuk tangki tersebut dengan memperhatikan budget dapat dilihat dari tabel di bawah | ||
| + | |||
| + | [[File:316alv.png|800x400px]] | ||
| + | [[File:tabelhargaalv.jpg|500x300px]] | ||
| + | |||
| + | Ketebalan yang tepat untuk tangki tersebut dengan memperhatikan budget yang telah diberikan yaitu Rp500.000 adalah ketebalan 8 mm. Jadi anggaran yang tersisa dapat kita gunakan untuk katup dan pengatur ruangan | ||
Latest revision as of 01:34, 12 June 2023
Untuk menentukan ukuran pelat yang akan digunakan berdasarkan volume yang dibutuhkan, yaitu 1 liter, namun menggunakan luas pelat seminimal mungkin menggunakan perhitungan sebagai berikut:
import numpy as np
from scipy.optimize import minimize
def hitung_luas_permukaan(x):
radius, tinggi = x
luas_permukaan = 2 * np.pi * radius * (radius + tinggi)
return luas_permukaan
def hitung_volume(x):
radius, tinggi = x
volume = np.pi * radius**2 * tinggi
return volume
def optimasi_silinder():
tebakan_awal = [1.0, 10.0]
batasan = [(0, None), (0, None)]
kendala = {'type': 'eq', 'fun': lambda x: hitung_volume(x) - 1050}
hasil = minimize(hitung_luas_permukaan, tebakan_awal, method='SLSQP', bounds=batasan, constraints=kendala)
print("Hasil Optimisasi:")
print("Radius: {:.2f} cm".format(hasil.x[0]))
print("Tinggi: {:.2f} cm".format(hasil.x[1]))
print("Luas Permukaan: {:.2f} cm^2".format(hasil.fun))
optimasi_silinder()Dari coding di atas di dapatkan hasil sebagai berikut :
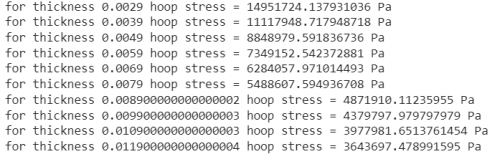
 Untuk menentukan proses iterasi dari ketebalan tangki tersebut dapat dilakukan dengan coding sebagai berikut :
Untuk menentukan proses iterasi dari ketebalan tangki tersebut dapat dilakukan dengan coding sebagai berikut :
r = 5.42e-2
p = 800000
t = 2.9e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9:
breakCoding di atas menentukan tegangan lingkaran dengan mengevaluasi berbagai nilai ketebalan dalam rentang 2,9 mm hingga 12 mm. Kode tersebut menggabungkan sebuah batasan yang menghentikan iterasi jika total tegangan lingkaran melebihi kekuatan luluh dari baja tahan karat AISI 316. Hasilnya menunjukkan bahwa semua nilai ketebalan dari 2,9 mm hingga 12 mm, dengan penambahan 1 mm, memenuhi persyaratan kekuatan luluh. Kode tersebut menghasilkan hasil perhitungan berikut, yang menunjukkan bahwa tegangan lingkaran tetap jauh di bawah kekuatan luluh sebesar 205 MPa.
Untuk mengoptimisasi penyimpanan hidrogen pada tekanan 8 bar dengan kapasitas 1 liter dan anggaran maksimal Rp500.000, dapat diselesaikan dengan phyton code dibawah :
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(x):
return budget_maksimal - (harga_per_unit * x[0])
kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]
# Nilai awal
x0 = [0]
# Batasan
batas = [(0, None)]
# Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)
# Menampilkan hasil
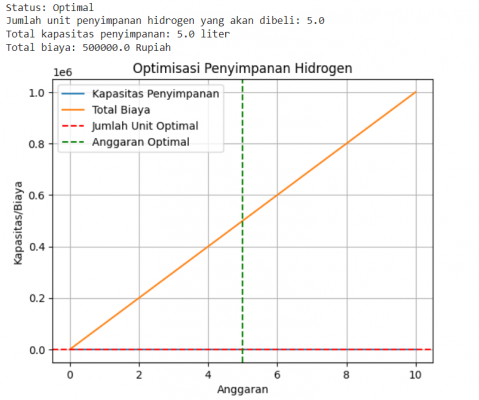
tampilkan_hasil(solusi)Kode di atas menggunakan fungsi tujuan untuk memaksimalkan jumlah unit penyimpanan hidrogen yang akan dibeli. Kendala anggaran diatur menggunakan fungsi kendala, yang memastikan bahwa total biaya tidak melebihi anggaran maksimal yang diberikan. Output akan menampilkan jumlah unit yang harus dibeli, total kapasitas penyimpanan, dan total biaya yang dibutuhkan. Di bawah ini merupakan hasil dari phyton code tersebut :
Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini :
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(x):
return budget_maksimal - (harga_per_unit * x[0])
kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]
# Nilai awal
x0 = [0]
# Batasan
batas = [(0, None)]
# Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)
# Menampilkan hasil
tampilkan_hasil(solusi)
# Menghasilkan grafik
anggaran = np.linspace(0, 10, 100) # Range anggaran
kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran
biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran
plt.figure()
plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan')
plt.plot(anggaran, biaya, label='Total Biaya')
plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal')
plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal')
plt.xlabel('Anggaran')
plt.ylabel('Kapasitas/Biaya')
plt.title('Optimisasi Penyimpanan Hidrogen')
plt.legend()
plt.grid(True)
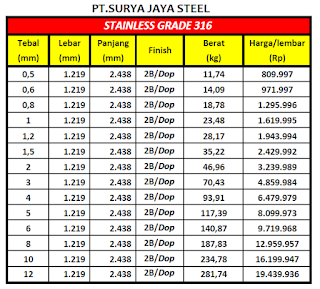
plt.show()Kode di atas menghitung jumlah optimal unit penyimpanan hidrogen yang akan dibeli berdasarkan harga per unit, kapasitas per unit, dan anggaran maksimal yang diberikan. Kode ini memberikan solusi terbaik dengan kapasitas total tertinggi yang tetap berada dalam anggaran. Hasilnya kemudian dicetak, termasuk jumlah unit, kapasitas total, dan biaya total. Selain itu, kode ini juga membuat grafik yang menunjukkan hubungan antara kapasitan dan anggaran optimisasi penyimpanan hidrogen
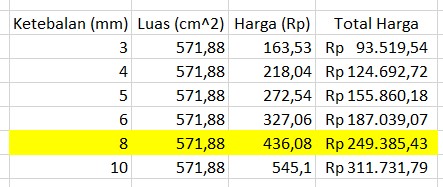
Untuk menentukan ketebalan yang tepat untuk tangki tersebut dengan memperhatikan budget dapat dilihat dari tabel di bawah
Ketebalan yang tepat untuk tangki tersebut dengan memperhatikan budget yang telah diberikan yaitu Rp500.000 adalah ketebalan 8 mm. Jadi anggaran yang tersisa dapat kita gunakan untuk katup dan pengatur ruangan