Difference between revisions of "Teddy Tumenggung"
(→Design & Optimization of Pressurized Hydrogen Storage) |
(→Video My Concious Effort on Numerical Method Learning and Its Application in Hydrogen Storage Design) |
||
| (22 intermediate revisions by the same user not shown) | |||
| Line 29: | Line 29: | ||
'''Determine the required storage capacity''' | '''Determine the required storage capacity''' | ||
| + | |||
In case we need to calculate the amount of hydrogen to store based on specific application. Consider factors such as daily demand, peak usage, and storage duration. This will help to determine the size and number of storage tanks required. | In case we need to calculate the amount of hydrogen to store based on specific application. Consider factors such as daily demand, peak usage, and storage duration. This will help to determine the size and number of storage tanks required. | ||
'''Select the storage tank type''' | '''Select the storage tank type''' | ||
| + | |||
There are several types of storage tanks for pressurized hydrogen, including steel cylinders, composite cylinders, and cryogenic tanks. | There are several types of storage tanks for pressurized hydrogen, including steel cylinders, composite cylinders, and cryogenic tanks. | ||
'''Assess the storage pressure''' | '''Assess the storage pressure''' | ||
| + | |||
We need to determine the appropriate storage pressure for application. Higher pressure allows for more hydrogen to be stored in a given volume but requires stronger and more expensive storage tanks. | We need to determine the appropriate storage pressure for application. Higher pressure allows for more hydrogen to be stored in a given volume but requires stronger and more expensive storage tanks. | ||
'''Analyze safety considerations''' | '''Analyze safety considerations''' | ||
| + | |||
Safety is paramount when designing a hydrogen storage system. Evaluate the safety features required for your specific application, such as pressure relief devices, leak detection systems, and adequate ventilation. Ensure compliance with applicable safety standards and regulations to minimize the risk of accidents. | Safety is paramount when designing a hydrogen storage system. Evaluate the safety features required for your specific application, such as pressure relief devices, leak detection systems, and adequate ventilation. Ensure compliance with applicable safety standards and regulations to minimize the risk of accidents. | ||
| + | |||
| + | |||
| + | |||
| + | '''Geometry Optimization''' | ||
| + | |||
| + | Geometry Optimization calculations for storage space | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | import math | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def surface_area(x): | ||
| + | # x[0] represents the radius, x[1] represents the height | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | |||
| + | # Calculate the surface area of the cylindrical container | ||
| + | surface_area = 2 * math.pi * r * (r + h) | ||
| + | |||
| + | return surface_area | ||
| + | |||
| + | def volume_constraint(x): | ||
| + | # x[0] represents the radius, x[1] represents the height | ||
| + | r = x[0] | ||
| + | h = x[1] | ||
| + | |||
| + | # Calculate the volume of the cylindrical container | ||
| + | volume = math.pi * r**2 * h | ||
| + | |||
| + | # Constraint: volume should be equal to 1 liter (1000 cubic centimeters) | ||
| + | return volume - 1000 | ||
| + | |||
| + | # Initial guess for radius and height | ||
| + | x0 = [1.0, 1.0] | ||
| + | |||
| + | # Define the optimization problem | ||
| + | problem = { | ||
| + | 'type': 'eq', | ||
| + | 'fun': volume_constraint | ||
| + | } | ||
| + | |||
| + | # Solve the optimization problem | ||
| + | result = minimize(surface_area, x0, constraints=problem) | ||
| + | |||
| + | # Extract the optimal values | ||
| + | optimal_radius = result.x[0] | ||
| + | optimal_height = result.x[1] | ||
| + | optimal_surface_area = result.fun | ||
| + | |||
| + | # Print the results | ||
| + | print(f"Optimal Radius: {optimal_radius:.2f} cm") | ||
| + | print(f"Optimal Height: {optimal_height:.2f} cm") | ||
| + | print(f"Minimum Surface Area: {optimal_surface_area:.2f} cm^2") | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Based on the results obtained from the code, it can be inferred that the optimal configuration for a cylindrical tank, achieved by minimizing the surface area, corresponds to a height-radius ratio of 2:1. In particular, the tank has a height of 10.84 cm and a radius of 5.42 cm. These dimensions yield a surface area of 553.58 cm², which represents the smallest achievable area while satisfying the specified volume and pressure requirements. | ||
| + | |||
| + | '''Thickness Calculation''' | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | |||
| + | def calculate_thickness(material, capacity, pressure): | ||
| + | if material == "AISI 316": | ||
| + | tensile_strength = 290 # MPa | ||
| + | safety_factor = 3 | ||
| + | else: | ||
| + | return "Invalid material" | ||
| + | |||
| + | volume = capacity * 1000 # Convert capacity from liters to cubic centimeters | ||
| + | pressure_pa = pressure * 0.1 # Convert pressure from bar to MegaPascal | ||
| + | |||
| + | thickness = (pressure_pa * volume * safety_factor) / (2 * math.pi * tensile_strength) | ||
| + | thickness_mm = thickness * 10 # Convert thickness from centimeters to millimeters | ||
| + | |||
| + | return thickness_mm | ||
| + | |||
| + | AISI_316_thickness = calculate_thickness("AISI 316", 1, 8) | ||
| + | |||
| + | print("Optimized thickness for AISI 316:", AISI_316_thickness, "mm") | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | The optimal thickness for a hydrogen tube with a 1 L capacity and 0.8 mPa pressure is split between AISI 316 thickness: 13.17 mm | ||
| + | '''Surface Area Calculation''' | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import math | ||
| + | |||
| + | def calculate_surface_area(radius, height): | ||
| + | # Calculate the surface area of the tube | ||
| + | base_area = math.pi * radius**2 | ||
| + | lateral_area = 2 * math.pi * radius * height | ||
| + | surface_area = 2 * base_area + lateral_area | ||
| + | |||
| + | return surface_area | ||
| + | |||
| + | def calculate_lowest_surface_area(height, radius, pressure, thickness): | ||
| + | # Convert pressure from bar to Pascal | ||
| + | pressure_pa = pressure * 100000 | ||
| + | |||
| + | # Convert thickness from mm to cm | ||
| + | thickness_cm = thickness / 10 | ||
| + | |||
| + | # Adjust the radius and height by subtracting the thickness | ||
| + | adjusted_radius = radius - thickness_cm | ||
| + | adjusted_height = height - (2 * thickness_cm) | ||
| + | |||
| + | # Calculate the surface area of the adjusted tube | ||
| + | surface_area = calculate_surface_area(adjusted_radius, adjusted_height) | ||
| + | |||
| + | return surface_area | ||
| + | |||
| + | # Define the input parameters | ||
| + | height = 10.84 # cm | ||
| + | radius = 5.42 # cm | ||
| + | pressure = 8 # bar | ||
| + | thickness = 13.17 # mm | ||
| + | |||
| + | # Calculate the lowest surface area | ||
| + | lowest_surface_area = calculate_lowest_surface_area(height, radius, pressure, thickness) | ||
| + | |||
| + | # Display the result | ||
| + | print(f"Luas permukaan terendah untuk tabung hidrogen dengan tinggi 10.84 cm, jari-jari 5.42 cm, tekanan 8 bar, dan ketebalan AISI 316 {thickness} mm:") | ||
| + | print(f"Luas Permukaan Terendah: {lowest_surface_area} cm^2") | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | The lowest surface area for a hydrogen storage with a height of 10.84 cm, a radius of 5.42 cm, a pressure of 8 bar, and a material AISI 316 thickness of 13.17 mm has | ||
| + | Lowest Surface Area: 317.3249037627396 cm^2 | ||
| + | |||
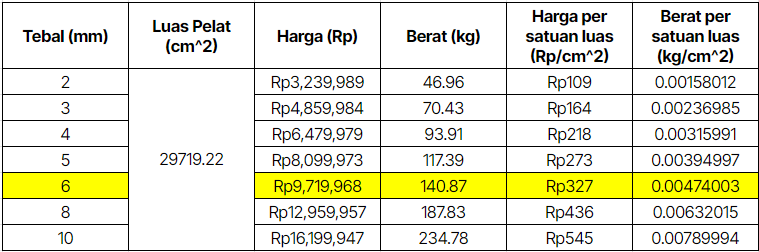
| + | '''Cost Calculation''' | ||
| + | |||
| + | [[File:Cost_Aluminium_316.png]] | ||
| + | |||
| + | The cost required to design a hydrogen storage tube based on the previous calculations requires a fund of Rp 224.862 which is the funds required do not exceed the maximum figure that has been determined | ||
| + | |||
| + | ==Video My Concious Effort on Numerical Method Learning and Its Application in Hydrogen Storage Design== | ||
| + | |||
| + | <youtube width="200" height="100">v=Dtsu9WMR5bU</youtube> | ||
Latest revision as of 00:50, 16 June 2023
Contents
Introduction
Introduction Assalamualaikum Warahmatullahi Wabarakatuh, Perkenalkan saya Teddy Tumenggung mahasiswa Teknik Perkapalan 2021 dengan NPM 2106704194. Saya lahir di Jakarta pada tanggal 01 Januari 2003 dan berdomisili di Kabupaten Bogor.
Perkuliahan 26/05/23
Pertemuan Pertama merupakan kelas pertama Metode Numerik dengan dosen Dr. Ir. Ahmad Indra Siswantara atau dipanggil dengan Pak DAI. Kelas dimulai dengan beliau memperkenalkan diri terlebih dahulu kepada mahasiswanya. Dilanjutkan dengan membahas seberapa tertariknya mahasiswa dengan mata kuliah Metode Numerik ini dengan menunjuk ke beberapa mahasiswa yang ada dikelas. Beliau mengaskan kepada mahasiswanya untuk memanfaatkan potensi yang dimiliki sebaik mungkin dan menekankan kepada mahasiswanya untuk memanfaatkan waktu sebaik mungkin untuk belajar dengan mandiri tidak hanya pada saat perkuliahan dan juga berinteraksi dengan dosen. Lalu beliau mencoba untuk mengajak mahasiswa untuk lebih memahami Metode Numerik dengan memberikan contoh soal serta memberikan penugasan agar mahasiswa lebih memahami penerapan Metode Numerik ini dalam kehidupan aktual.
Design & Optimization of Pressurized Hydrogen Storage
Specification
Volume : 1 Liter
Pressure : 8 bar
cost : Rp 500.000
Hydrogen is the most abundant gas in nature, which is around 75%. This makes people think about making hydrogen as a renewable energy. Hydrogen is considered a renewable energy source because it can be produced using abundant natural resources such as water and solar energy. One of the advantages of hydrogen as a renewable energy is that when it is used as a fuel, the reaction produces only water as a by-product, without the emission of greenhouse gases or other pollutants. In order to use energy sourced from hydrogen, of course we need a storage. With my limitations in designing I concius that I need help in this case to get information using GPT Chat and another resource. To designing pressurized hydrogen storage requires considering the following factors:
1. Pressure levels
2. Storage methods
3. Materials
4. Integration with renewable energy
And there are several steps in designing this hydrogen storage
Determine the required storage capacity
In case we need to calculate the amount of hydrogen to store based on specific application. Consider factors such as daily demand, peak usage, and storage duration. This will help to determine the size and number of storage tanks required.
Select the storage tank type
There are several types of storage tanks for pressurized hydrogen, including steel cylinders, composite cylinders, and cryogenic tanks.
Assess the storage pressure
We need to determine the appropriate storage pressure for application. Higher pressure allows for more hydrogen to be stored in a given volume but requires stronger and more expensive storage tanks.
Analyze safety considerations
Safety is paramount when designing a hydrogen storage system. Evaluate the safety features required for your specific application, such as pressure relief devices, leak detection systems, and adequate ventilation. Ensure compliance with applicable safety standards and regulations to minimize the risk of accidents.
Geometry Optimization
Geometry Optimization calculations for storage space
import math
from scipy.optimize import minimize
def surface_area(x):
# x[0] represents the radius, x[1] represents the height
r = x[0]
h = x[1]
# Calculate the surface area of the cylindrical container
surface_area = 2 * math.pi * r * (r + h)
return surface_area
def volume_constraint(x):
# x[0] represents the radius, x[1] represents the height
r = x[0]
h = x[1]
# Calculate the volume of the cylindrical container
volume = math.pi * r**2 * h
# Constraint: volume should be equal to 1 liter (1000 cubic centimeters)
return volume - 1000
# Initial guess for radius and height
x0 = [1.0, 1.0]
# Define the optimization problem
problem = {
'type': 'eq',
'fun': volume_constraint
}
# Solve the optimization problem
result = minimize(surface_area, x0, constraints=problem)
# Extract the optimal values
optimal_radius = result.x[0]
optimal_height = result.x[1]
optimal_surface_area = result.fun
# Print the results
print(f"Optimal Radius: {optimal_radius:.2f} cm")
print(f"Optimal Height: {optimal_height:.2f} cm")
print(f"Minimum Surface Area: {optimal_surface_area:.2f} cm^2")Based on the results obtained from the code, it can be inferred that the optimal configuration for a cylindrical tank, achieved by minimizing the surface area, corresponds to a height-radius ratio of 2:1. In particular, the tank has a height of 10.84 cm and a radius of 5.42 cm. These dimensions yield a surface area of 553.58 cm², which represents the smallest achievable area while satisfying the specified volume and pressure requirements.
Thickness Calculation
import math
def calculate_thickness(material, capacity, pressure):
if material == "AISI 316":
tensile_strength = 290 # MPa
safety_factor = 3
else:
return "Invalid material"
volume = capacity * 1000 # Convert capacity from liters to cubic centimeters
pressure_pa = pressure * 0.1 # Convert pressure from bar to MegaPascal
thickness = (pressure_pa * volume * safety_factor) / (2 * math.pi * tensile_strength)
thickness_mm = thickness * 10 # Convert thickness from centimeters to millimeters
return thickness_mm
AISI_316_thickness = calculate_thickness("AISI 316", 1, 8)
print("Optimized thickness for AISI 316:", AISI_316_thickness, "mm")The optimal thickness for a hydrogen tube with a 1 L capacity and 0.8 mPa pressure is split between AISI 316 thickness: 13.17 mm Surface Area Calculation
import math
def calculate_surface_area(radius, height):
# Calculate the surface area of the tube
base_area = math.pi * radius**2
lateral_area = 2 * math.pi * radius * height
surface_area = 2 * base_area + lateral_area
return surface_area
def calculate_lowest_surface_area(height, radius, pressure, thickness):
# Convert pressure from bar to Pascal
pressure_pa = pressure * 100000
# Convert thickness from mm to cm
thickness_cm = thickness / 10
# Adjust the radius and height by subtracting the thickness
adjusted_radius = radius - thickness_cm
adjusted_height = height - (2 * thickness_cm)
# Calculate the surface area of the adjusted tube
surface_area = calculate_surface_area(adjusted_radius, adjusted_height)
return surface_area
# Define the input parameters
height = 10.84 # cm
radius = 5.42 # cm
pressure = 8 # bar
thickness = 13.17 # mm
# Calculate the lowest surface area
lowest_surface_area = calculate_lowest_surface_area(height, radius, pressure, thickness)
# Display the result
print(f"Luas permukaan terendah untuk tabung hidrogen dengan tinggi 10.84 cm, jari-jari 5.42 cm, tekanan 8 bar, dan ketebalan AISI 316 {thickness} mm:")
print(f"Luas Permukaan Terendah: {lowest_surface_area} cm^2")The lowest surface area for a hydrogen storage with a height of 10.84 cm, a radius of 5.42 cm, a pressure of 8 bar, and a material AISI 316 thickness of 13.17 mm has Lowest Surface Area: 317.3249037627396 cm^2
Cost Calculation
The cost required to design a hydrogen storage tube based on the previous calculations requires a fund of Rp 224.862 which is the funds required do not exceed the maximum figure that has been determined