Difference between revisions of "Naufal Alif Indratma"
Naufal.alif (talk | contribs) |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | == '''Introduction''' == | ||
| + | [[File:Alif.jpg|300px]] | ||
| + | |||
Naufal Alif Indratma | Naufal Alif Indratma | ||
| Line 6: | Line 9: | ||
Metode Numerik - 02 | Metode Numerik - 02 | ||
| + | |||
| + | I am concious of myself and the world around me | ||
| + | == '''Pressurized Hydrogen Storage Optimization''' == | ||
| + | Berikut beberapa tips cara mengoptimalkan desain sistem penyimpanan hidrogen 1 liter untuk menyimpan hidrogen pada tekanan 8 bar dengan budget Rp500.000: | ||
| + | |||
| + | 1. '''Pilih bahan penyimpanan yang tepat'''. Ada sejumlah bahan berbeda yang dapat digunakan untuk menyimpan hidrogen, masing-masing dengan kelebihan dan kekurangannya sendiri. Beberapa bahan yang paling umum termasuk hidrida logam, tabung nano karbon, dan kerangka organik logam. Bahan terbaik untuk aplikasi Anda akan bergantung pada sejumlah faktor, termasuk tekanan, suhu, dan biaya yang diperlukan. | ||
| + | |||
| + | 2. '''Pertimbangkan bentuk bejana penyimpanan'''. Bentuk bejana penyimpanan dapat berdampak signifikan pada efisiensinya. Misalnya, bejana bulat akan lebih efisien daripada bejana silinder dengan volume yang sama. | ||
| + | |||
| + | 3. '''Minimalkan luas permukaan bejana penyimpanan'''. Luas permukaan bejana penyimpanan terpapar ke lingkungan, dan ini dapat menyebabkan hilangnya hidrogen. Meminimalkan luas permukaan akan membantu mengurangi kerugian ini. | ||
| + | |||
| + | 4. '''Gunakan insulasi'''. Insulasi dapat membantu mengurangi kehilangan panas dari bejana penyimpanan, yang dapat meningkatkan efisiensi. | ||
| + | |||
| + | 5. '''Gunakan pengatur tekanan'''. Pengatur tekanan dapat membantu memastikan bahwa tekanan di bejana penyimpanan tidak melebihi batas pengoperasian yang aman. | ||
| + | |||
| + | Dengan mengikuti tips ini, Anda dapat mengoptimalkan desain sistem penyimpanan hidrogen dan meningkatkan efisiensinya. | ||
| + | |||
| + | Berikut adalah beberapa pertimbangan tambahan yang mungkin relevan dengan aplikasi spesifik Anda: | ||
| + | |||
| + | * Berat sistem penyimpanan penting jika akan portabel. | ||
| + | * Ketahanan sistem penyimpanan penting jika akan terkena lingkungan yang keras. | ||
| + | * Kemudahan pemeliharaan sistem penyimpanan penting jika akan digunakan di lokasi yang jauh. | ||
| + | |||
| + | Dengan hati-hati mempertimbangkan semua faktor ini, Anda dapat merancang sistem penyimpanan hidrogen yang memenuhi kebutuhan khusus Anda. | ||
| + | |||
| + | == '''Final Report of Design & Optimization of Pressurized Hydrogen Storage''' == | ||
| + | |||
| + | ---- | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | import math | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def calculate_tank_properties(diameter, height): | ||
| + | # Menghitung volume tangki | ||
| + | volume_m3 = (math.pi * (diameter**2) * height) / 4 | ||
| + | |||
| + | # Menghitung luas permukaan tangki | ||
| + | radius = diameter / 2 | ||
| + | surface_area = 2 * math.pi * radius * (radius + height) | ||
| + | |||
| + | # Konversi diameter, tinggi, dan luas permukaan ke dalam satuan cm | ||
| + | diameter_cm = diameter * 100 | ||
| + | height_cm = height * 100 | ||
| + | surface_area_cm2 = surface_area * 10000 | ||
| + | |||
| + | return diameter_cm, height_cm, surface_area_cm2 | ||
| + | |||
| + | def cost_function(x): | ||
| + | diameter = x[0] | ||
| + | height = x[1] | ||
| + | |||
| + | # Menghitung luas permukaan tangki | ||
| + | _, _, surface_area_cm2 = calculate_tank_properties(diameter, height) | ||
| + | |||
| + | # Menghitung biaya berdasarkan luas permukaan | ||
| + | # Anggap harga material adalah Rp 100 per cm^2 | ||
| + | cost = surface_area_cm2 * 100 | ||
| + | |||
| + | return cost | ||
| + | |||
| + | # Mendefinisikan batasan ukuran tangki | ||
| + | diameter_bounds = (0.1, 100) # batasan diameter antara 0.1 cm dan 100 cm | ||
| + | height_bounds = (0.1, 100) # batasan tinggi antara 0.1 cm dan 100 cm | ||
| + | |||
| + | # Mendefinisikan nilai awal diameter dan tinggi | ||
| + | x0 = [1, 1] # nilai awal diameter 1 cm, tinggi 1 cm | ||
| + | |||
| + | # Melakukan optimisasi dengan menggunakan metode minimize dari library scipy | ||
| + | result = minimize(cost_function, x0, bounds=(diameter_bounds, height_bounds)) | ||
| + | |||
| + | # Mengambil nilai diameter dan tinggi yang dioptimasi | ||
| + | diameter_opt = result.x[0] | ||
| + | height_opt = result.x[1] | ||
| + | |||
| + | # Menghitung luas permukaan tangki yang dioptimasi | ||
| + | diameter_cm, height_cm, surface_area_cm2 = calculate_tank_properties(diameter_opt, height_opt) | ||
| + | |||
| + | print("Diameter tangki oksigen (cm):", diameter_cm) | ||
| + | print("Tinggi tangki oksigen (cm):", height_cm) | ||
| + | print("Luas permukaan tangki oksigen (cm^2):", surface_area_cm2) | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | [[File:Alvin2.jpg|300x300px|thumb|right]] | ||
| + | |||
| + | based on the calculation (coding python) that has been done above using the calculate_tank_properties function to calculate the volume of the tank. It was found that the diameter and height needed to make a cylinder with a capacity of 1 liter and a pressure of 8 bar are as follows: | ||
| + | Diameter = 10 cm | ||
| + | Height = 30 cm | ||
| + | Surface area = 2514.238898038469 cm² | ||
| + | For oxygen tanks with a capacity of 1 liter and a pressure of 8 bar, plates with a thickness of between 1 mm and 3 mm are generally used. | ||
| + | |||
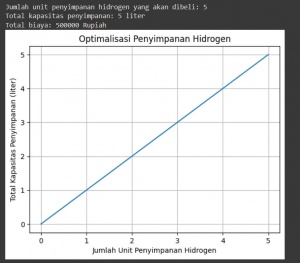
| + | The code above uses the objective function to maximize the number of hydrogen storage units to buy. The budget constraint is set using the constraint function, which ensures that the total cost does not exceed the given maximum budget. The output will display the number of units that must be purchased, the total storage capacity, and the total cost required. | ||
| + | |||
| + | The code is focused on optimizing hydrogen storage considering the given capacity and budget constraints. The main goal is to find the number of hydrogen storage units to be purchased to achieve the maximum total storage capacity, while complying with the specified maximum budget constraints. | ||
| + | |||
| + | Within the code, it is iterated to try every possible number of units purchased within the budget constraint. Each unit quantity is tested to calculate the total storage capacity and the associated total cost. If the resulting total capacity exceeds the previous best total capacity and the total cost is still within the budget limit, then the optimal solution is updated. | ||
| + | |||
| + | Additionally, the code creates a graph showing the relationship between the number of hydrogen storage units to be purchased and the total storage capacity acquired. This graph provides a visual representation of how total capacity changes as additional hydrogen storage units are added. | ||
| + | |||
| + | So the main focus of the code is to find the optimal solution to maximize hydrogen storage capacity taking into account the maximum budget constraints, as well as providing a visual understanding via graphs. | ||
| + | |||
| + | == '''Final Video on my concious efforts in learning and application in numerical method''' == | ||
| + | |||
| + | <youtube width="200" height="100">uUBgSKyXnGc</youtube> | ||
Latest revision as of 23:48, 12 June 2023
Contents
Introduction
Naufal Alif Indratma
2106728124
Teknik Mesin
Metode Numerik - 02
I am concious of myself and the world around me
Pressurized Hydrogen Storage Optimization
Berikut beberapa tips cara mengoptimalkan desain sistem penyimpanan hidrogen 1 liter untuk menyimpan hidrogen pada tekanan 8 bar dengan budget Rp500.000:
1. Pilih bahan penyimpanan yang tepat. Ada sejumlah bahan berbeda yang dapat digunakan untuk menyimpan hidrogen, masing-masing dengan kelebihan dan kekurangannya sendiri. Beberapa bahan yang paling umum termasuk hidrida logam, tabung nano karbon, dan kerangka organik logam. Bahan terbaik untuk aplikasi Anda akan bergantung pada sejumlah faktor, termasuk tekanan, suhu, dan biaya yang diperlukan.
2. Pertimbangkan bentuk bejana penyimpanan. Bentuk bejana penyimpanan dapat berdampak signifikan pada efisiensinya. Misalnya, bejana bulat akan lebih efisien daripada bejana silinder dengan volume yang sama.
3. Minimalkan luas permukaan bejana penyimpanan. Luas permukaan bejana penyimpanan terpapar ke lingkungan, dan ini dapat menyebabkan hilangnya hidrogen. Meminimalkan luas permukaan akan membantu mengurangi kerugian ini.
4. Gunakan insulasi. Insulasi dapat membantu mengurangi kehilangan panas dari bejana penyimpanan, yang dapat meningkatkan efisiensi.
5. Gunakan pengatur tekanan. Pengatur tekanan dapat membantu memastikan bahwa tekanan di bejana penyimpanan tidak melebihi batas pengoperasian yang aman.
Dengan mengikuti tips ini, Anda dapat mengoptimalkan desain sistem penyimpanan hidrogen dan meningkatkan efisiensinya.
Berikut adalah beberapa pertimbangan tambahan yang mungkin relevan dengan aplikasi spesifik Anda:
- Berat sistem penyimpanan penting jika akan portabel.
- Ketahanan sistem penyimpanan penting jika akan terkena lingkungan yang keras.
- Kemudahan pemeliharaan sistem penyimpanan penting jika akan digunakan di lokasi yang jauh.
Dengan hati-hati mempertimbangkan semua faktor ini, Anda dapat merancang sistem penyimpanan hidrogen yang memenuhi kebutuhan khusus Anda.
Final Report of Design & Optimization of Pressurized Hydrogen Storage
import math
from scipy.optimize import minimize
def calculate_tank_properties(diameter, height):
# Menghitung volume tangki
volume_m3 = (math.pi * (diameter**2) * height) / 4
# Menghitung luas permukaan tangki
radius = diameter / 2
surface_area = 2 * math.pi * radius * (radius + height)
# Konversi diameter, tinggi, dan luas permukaan ke dalam satuan cm
diameter_cm = diameter * 100
height_cm = height * 100
surface_area_cm2 = surface_area * 10000
return diameter_cm, height_cm, surface_area_cm2
def cost_function(x):
diameter = x[0]
height = x[1]
# Menghitung luas permukaan tangki
_, _, surface_area_cm2 = calculate_tank_properties(diameter, height)
# Menghitung biaya berdasarkan luas permukaan
# Anggap harga material adalah Rp 100 per cm^2
cost = surface_area_cm2 * 100
return cost
# Mendefinisikan batasan ukuran tangki
diameter_bounds = (0.1, 100) # batasan diameter antara 0.1 cm dan 100 cm
height_bounds = (0.1, 100) # batasan tinggi antara 0.1 cm dan 100 cm
# Mendefinisikan nilai awal diameter dan tinggi
x0 = [1, 1] # nilai awal diameter 1 cm, tinggi 1 cm
# Melakukan optimisasi dengan menggunakan metode minimize dari library scipy
result = minimize(cost_function, x0, bounds=(diameter_bounds, height_bounds))
# Mengambil nilai diameter dan tinggi yang dioptimasi
diameter_opt = result.x[0]
height_opt = result.x[1]
# Menghitung luas permukaan tangki yang dioptimasi
diameter_cm, height_cm, surface_area_cm2 = calculate_tank_properties(diameter_opt, height_opt)
print("Diameter tangki oksigen (cm):", diameter_cm)
print("Tinggi tangki oksigen (cm):", height_cm)
print("Luas permukaan tangki oksigen (cm^2):", surface_area_cm2)based on the calculation (coding python) that has been done above using the calculate_tank_properties function to calculate the volume of the tank. It was found that the diameter and height needed to make a cylinder with a capacity of 1 liter and a pressure of 8 bar are as follows: Diameter = 10 cm Height = 30 cm Surface area = 2514.238898038469 cm² For oxygen tanks with a capacity of 1 liter and a pressure of 8 bar, plates with a thickness of between 1 mm and 3 mm are generally used.
The code above uses the objective function to maximize the number of hydrogen storage units to buy. The budget constraint is set using the constraint function, which ensures that the total cost does not exceed the given maximum budget. The output will display the number of units that must be purchased, the total storage capacity, and the total cost required.
The code is focused on optimizing hydrogen storage considering the given capacity and budget constraints. The main goal is to find the number of hydrogen storage units to be purchased to achieve the maximum total storage capacity, while complying with the specified maximum budget constraints.
Within the code, it is iterated to try every possible number of units purchased within the budget constraint. Each unit quantity is tested to calculate the total storage capacity and the associated total cost. If the resulting total capacity exceeds the previous best total capacity and the total cost is still within the budget limit, then the optimal solution is updated.
Additionally, the code creates a graph showing the relationship between the number of hydrogen storage units to be purchased and the total storage capacity acquired. This graph provides a visual representation of how total capacity changes as additional hydrogen storage units are added.
So the main focus of the code is to find the optimal solution to maximize hydrogen storage capacity taking into account the maximum budget constraints, as well as providing a visual understanding via graphs.