Difference between revisions of "Zefanya Valeryan H.H. (Metode Numerik)"
(→My Conscious Efforts in Numerical Method Learning & It's Application in Hydrogen Storage Optimization) |
|||
| (38 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== BIODATA== | == BIODATA== | ||
| − | [[File:Banner_Metnum. | + | [[File:Banner_Metnum-2.png|Right|800px]] |
| Line 38: | Line 38: | ||
Penulis | Penulis | ||
| + | |||
| + | =Pressurized Hydrogen Storage Optimization= | ||
| + | ==Pressurized Hydrogen Storage== | ||
| + | : | ||
| + | : Pressurized hydrogen storage involves compressing hydrogen gas and storing it in specially designed tanks or cylinders. These tanks are built to withstand high pressures, typically ranging from a few hundred to several thousand pounds per square inch (psi). Pressurized storage offers advantages such as simplicity, portability, and fast refueling times. However, it also presents challenges related to weight, safety, and limited storage capacity. Tank materials must be robust, and strict testing is necessary to prevent leaks or ruptures. Alternative storage methods like cryogenic storage and hydrogen carriers are being explored to address these limitations and optimize hydrogen storage and utilization. | ||
| + | |||
| + | |||
| + | ==Factors Involved in Designing and Optimizing a Pressurized Hydrogen Storage== | ||
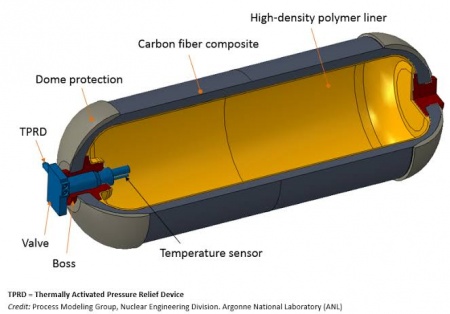
| + | : [[File: 16859845860772405471272770780537.jpg|450px|thumb|middle| Pressurized hydrogen tank (source: Department of Energy)]] | ||
| + | : | ||
| + | : Designing and optimizing a pressurized hydrogen storage involves several factors and processes to ensure its safety, efficiency, and performance. Here are some key considerations in the design and optimization process: | ||
| + | : | ||
| + | : '''Storage Capacity''' | ||
| + | : The required storage capacity of hydrogen must be determined based on the anticipated demand and usage. Factors such as the desired duration of storage, refill frequency, and system requirements play a role in determining the storage capacity. | ||
| + | :'''Material Selection''' | ||
| + | : The choice of materials for the storage tank is crucial. Factors such as material strength, corrosion resistance, hydrogen compatibility, weight, and cost need to be considered. The selected material should meet safety standards, regulatory requirements, and be suitable for the specific application. | ||
| + | :'''Pressure Requirements''' | ||
| + | : Determining the optimal operating pressure is critical to balance storage capacity, tank weight, and safety. Higher pressures allow for more hydrogen storage within a given volume, but it increases material requirements and safety considerations. The pressure requirements should align with the intended use and regulatory standards. | ||
| + | :'''Safety Considerations''' | ||
| + | : Safety is paramount in hydrogen storage design. Factors such as material integrity, leak prevention, pressure relief mechanisms, and appropriate safety measures need to be incorporated. Standards and guidelines from regulatory bodies, such as the International Organization for Standardization (ISO) and national safety codes, should be followed. | ||
| + | :'''Structural Design''' | ||
| + | : The structural design of the storage tank must ensure its mechanical integrity and resistance to external loads, vibrations, and impacts. Finite element analysis (FEA) and other engineering calculations are performed to determine the optimal tank shape, thickness, reinforcement, and support structures. | ||
| + | :'''Thermal Management''' | ||
| + | : Hydrogen storage systems may require thermal management to control temperature variations. Insulation, cooling, or heating mechanisms are employed to maintain the desired hydrogen temperature range and prevent thermal stresses. | ||
| + | :'''Cost Optimization''' | ||
| + | : Optimization techniques, such as mathematical modeling and numerical methods, can be applied to minimize costs while meeting performance and safety requirements. This includes optimizing material usage, tank size, manufacturing processes, and other relevant parameters. | ||
| + | :'''Regulatory Compliance''' | ||
| + | : Compliance with relevant regulations, standards, and codes is essential in the design and operation of pressurized hydrogen storage. It ensures safety, environmental protection, and compatibility with industry norms. | ||
| + | :'''Hydrogen Purity''' | ||
| + | : The required purity level of hydrogen for the specific application should be considered. Impurities in the hydrogen stream can impact the integrity and performance of the storage system. Depending on the application, purification processes may be needed to remove impurities. | ||
| + | :'''Fill and Discharge Rates''' | ||
| + | : The desired fill and discharge rates of hydrogen affect the design and optimization of the storage system. Factors such as the available infrastructure, operational requirements, and efficiency considerations influence the sizing of valves, piping, and other components. | ||
| + | :'''System Integration''' | ||
| + | : Pressurized hydrogen storage systems are often integrated with other components and subsystems, such as hydrogen production units, fuel cells, or transportation systems. Seamless integration and compatibility with these systems are important to ensure overall system performance. | ||
| + | :'''Environmental Considerations''' | ||
| + | : Environmental factors, including temperature variations, exposure to corrosive substances, and seismic activity, should be taken into account during the design process. Adequate protection and design measures, such as coatings, seismic restraints, and environmental monitoring, may be required. | ||
| + | :'''Manufacturing and Fabrication Methods''' | ||
| + | : The manufacturing and fabrication techniques employed impact the quality, cost, and scalability of the storage system. Selection of appropriate manufacturing methods, such as welding, forming, or composite layup, needs to be aligned with the chosen materials and desired characteristics. | ||
| + | |||
| + | =Final Report of Design and Optimization of Pressurized Hydrogen Storage= | ||
| + | |||
| + | ==Requirements== | ||
| + | : The specific requirements are '''1 liter''' of Hydrogen with '''8 bar''' Pressure with a maximum cost of '''Rp 500.000,00''' | ||
| + | |||
| + | |||
| + | ==Material Selection== | ||
| + | : By carefully considering the materials available for pressurized hydrogen storage, our selection has led us to choose '''AISI 316 austenitic stainless steel'''. This decision is rooted in the unique properties and advantages offered by this particular material. Here are some reasons for considering AISI 316 stainless steel for pressurized hydrogen storage: | ||
| + | :'''1) Corrosion Resistance''' | ||
| + | : Hydrogen can cause embrittlement and corrosion in some materials, leading to reduced structural integrity and potential safety hazards. AISI 316 stainless steel offers superior corrosion resistance, particularly in environments with high levels of hydrogen. This property helps ensure the long-term durability and safety of the storage system. | ||
| + | :'''2) Strength and Pressure Resistance''' | ||
| + | : Pressurized hydrogen storage systems require materials with high strength to withstand the internal pressure. AISI 316 stainless steel possesses good mechanical properties, including high tensile strength and yield strength, allowing it to withstand the required pressure levels while maintaining structural integrity. | ||
| + | :'''3) Compatibility with Hydrogen''' | ||
| + | : AISI 316 stainless steel has demonstrated compatibility with hydrogen gas in various studies and practical applications. It exhibits low permeability to hydrogen, reducing the risk of hydrogen loss and ensuring efficient containment within the storage system. | ||
| + | :'''4) Established Industrial Usage''' | ||
| + | : AISI 316 stainless steel is widely used in various industries, including chemical processing, oil and gas, and marine applications. It has a well-established track record and extensive knowledge base regarding its behavior in different environments, making it a trusted material choice for engineering applications. | ||
| + | |||
| + | ==Constraints== | ||
| + | : Pressurized hydrogen storage plays a crucial role in various applications, ranging from energy storage to fuel cell technology. Designing an optimized storage system requires careful consideration of multiple factors to ensure efficiency, safety, and cost-effectiveness. In this context, incorporating three key constraints - geometrical, material strength, and budget constraints - forms the foundation of an effective optimization model. | ||
| + | :'''1) Geometrical Constraint''' | ||
| + | : The geometrical constraint ensures that the design of the storage system meets specific volume requirements. By setting a constraint on the volume or dimensions of the storage tank, you can optimize the geometrical parameters such as radius and height to ensure the tank can accommodate the desired volume of 1 liter (1000 cm^3). This constraint ensures that the storage tank is appropriately sized and fits within the available space. | ||
| + | :'''2) Material Strength Constraint''' | ||
| + | : The material strength constraint focuses on selecting a material that can withstand the high-pressure environment of the hydrogen storage system. Hydrogen is stored under high pressure (8 bar or 800 kPa), and selecting a material with appropriate strength characteristics is crucial for the safety and integrity of the storage system. By incorporating this constraint, you ensure that the selected material, such as AISI 316 austenitic stainless steel, possesses the necessary mechanical properties to withstand the pressure and prevent any material failures or leaks. | ||
| + | :'''3) Budget Constraint''' | ||
| + | : The budget constraint places a limitation on the cost of the pressurized hydrogen storage system. By including this constraint, you ensure that the optimization model considers the cost-effectiveness of the design. The budget constraint helps in selecting cost-efficient materials and optimizing the geometrical parameters to meet the required specifications while staying within the allocated budget of Rp 500.000. This constraint ensures that the final design is financially feasible and aligns with the available resources. | ||
| + | |||
| + | |||
| + | ===Geometrical Constraints=== | ||
| + | : The code provided utilizes an optimization algorithm implemented in Python, utilizing the powerful capabilities of the NumPy and SciPy libraries. The objective of the code is to determine the optimal values for the radius and height of the storage tank by minimizing the surface area, while considering the specified volume of hydrogen. The incorporation of NumPy allows for efficient mathematical operations and array manipulation, while SciPy provides advanced optimization techniques and algorithms | ||
| + | |||
| + | ====Base Geometry==== | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Define the objective function | ||
| + | def objective(x): | ||
| + | radius, height = x | ||
| + | surface_area = 2 * np.pi * radius * (radius + height) | ||
| + | return surface_area | ||
| + | |||
| + | # Define the volume constraint function | ||
| + | def volume_constraint(x): | ||
| + | radius, height = x | ||
| + | volume = np.pi * radius**2 * height | ||
| + | return volume - 1000 | ||
| + | |||
| + | # Define the optimization problem | ||
| + | x0 = [1.0, 10.0] | ||
| + | bounds = [(0, None), (0, None)] | ||
| + | constraint = {'type': 'eq', 'fun': volume_constraint} | ||
| + | problem = minimize(objective, x0, bounds=bounds, constraints=constraint) | ||
| + | |||
| + | # Extract the optimized results | ||
| + | optimized_radius = problem.x[0] | ||
| + | optimized_height = problem.x[1] | ||
| + | optimized_surface_area = problem.fun | ||
| + | |||
| + | # Print the optimized results | ||
| + | print("Optimization Results:") | ||
| + | print(f"Radius: {optimized_radius:.2f} cm") | ||
| + | print(f"Height: {optimized_height:.2f} cm") | ||
| + | print(f"Surface Area: {optimized_surface_area:.2f} cm^2") | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | : Dari hasil pengkodean, dapat disimpulkan bahwa dengan meminimalkan luas permukaan, dimensi optimal untuk tangki silinder dicapai dengan rasio tinggi-jari-jari 2:1. Secara spesifik, tangki tersebut memiliki tinggi 10,84 cm dan radius 5,42 cm. Pengukuran ini menghasilkan luas permukaan 553,58 cm^2, yang merupakan luas terkecil yang mungkin untuk kebutuhan volume dan tekanan tertentu. | ||
| + | |||
| + | ====End Cap Geometry==== | ||
| + | : Using a purely cylindrical geometry for the storage tank may pose risks due to stress concentration at the corners. To minimize stress concentration and reduce surface area while maintaining the same volume, it is more efficient to adopt a torispherical end cap shape. This shape can be achieved by adding a fillet with a radius equal to half the tank's radius. The filleting creates a smooth curvature and helps reduce stress concentration. Adjustments in the geometrical parameters are necessary to compensate for the volume reduction caused by the filleting. | ||
| + | |||
| + | Dengan menghitung persentase pengurangan luas penampang, kita dapat menerapkannya secara terbalik ke volume yang diperlukan untuk mendapatkan batasan volume baru yang ditingkatkan. | ||
| + | : [[File: Hasil_perhitungan_Geometry_End_Cap.png|500px| Fillet Radius of Tank's End Cap Calculation (source: Personal Analysis)]] | ||
| + | : Hasil perhitungan mengungkapkan bahwa jari-jari fillet yang diperoleh untuk tutup ujung tangki adalah '''2.56443 cm''' | ||
| + | |||
| + | ===Material Strength Constraints=== | ||
| + | |||
| + | ====Mechanical Properties of AISI 316 Austenitic Stainless Steel==== | ||
| + | |||
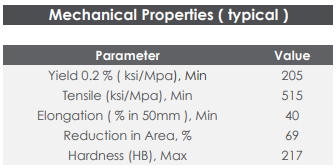
| + | :[[File: Mechanical_Properties_316.png|500px|thumb|left| Mechanical Properties of AISI 316 Austenitic Stainless Steel (source: Researchgate.com)]] | ||
| + | : The range of acceptable wall thickness is not arbitrary and should not exceed one-fifth of the vessel radius. According to ASME BPV Code Section VIII D.1, the '''minimum wall thickness should be at least 1/16 in (1.59 mm)''', regardless of corrosion allowance, material, or dimensions. | ||
| + | |||
| + | : Based on data obtained from Ferrobend, which provides information on the mechanical properties of AISI 316 stainless steel, we will employ both a conservative and less conservative approach by setting our limit at the yield strength and maximum tensile strength to represent failure. | ||
| + | |||
| + | : Dalam perhitungan ini, kita akan melakukan iterasi dari radius minimal 2,9 mm hingga 12 mm dengan inkremen 1 mm di setiap iterasi.'''. | ||
| + | |||
| + | ====Iteration Process==== | ||
| + | |||
| + | <syntaxhighlight lang=xml> | ||
| + | |||
| + | r = 5.42e-2 | ||
| + | p = 800000 | ||
| + | t = 2.9e-3 | ||
| + | |||
| + | while t < 12e-3: | ||
| + | hoop = (r * p)/(t) | ||
| + | print('for thickness', t, 'hoop stress =', hoop, "Pa") | ||
| + | t += 1e-3 | ||
| + | if hoop > 205e9: | ||
| + | break | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
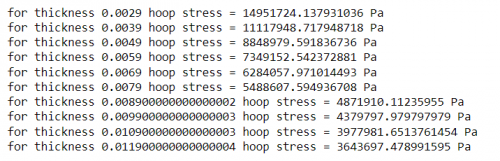
| + | : Kode tadi untuk menghitung hoop stress untuk berbagai nilai ketebalan mulai dari 2,9 mm hingga 12 mm, dengan constraint yang menghentikan iterasi jika total hoop stress melebihi yield strength stainless steel AISI 316. Berdasarkan hasil, '''semua nilai ketebalan mulai dari 2,9 mm hingga 12 mm dengan kenaikan 1 mm memenuhi batasan yield strength. Berikut adalah hasil perhitungan dari kode yang menunjukkan bahwa tegangan hoop jauh di bawah yield strength 205 MPa.'''. | ||
| + | |||
| + | : [[File: Calculation_of_Material_Strength.png|500px| Calculation of Material Strength (source: Personal Analysis)]] | ||
| + | |||
| + | ==Budget Constraint== | ||
| + | |||
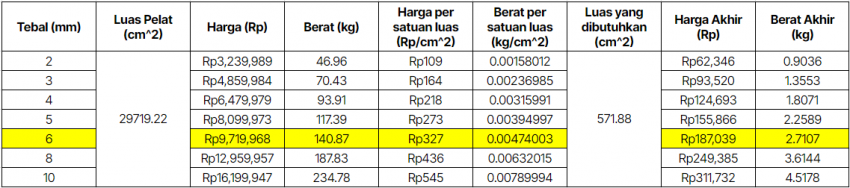
| + | Setelah menemukan parameter geometrik, tahap terakhir dari optimasi ini adalah membandingkannya dengan batas biaya yang tidak boleh melebihi Rp500.000,00. Berdasarkan material yang dipilih sebelumnya yaitu AISI 316, kita harus memilih ketebalan dinding tangki yang sesuai dengan kisaran anggaran. Berikut daftar harga beserta perhitungannya. | ||
| + | |||
| + | |||
| + | [[File:CostConstraints_Alif.png|850px|center]] | ||
| + | |||
| + | Berdasarkan perhitungan ini, dengan mengoptimalkan kendala anggaran, bobot minimum yang masuk akal, namun tetap mempertahankan kekuatan yang masuk akal, dipilih ketebalan 6 mm untuk dinding tangki hidrogen ini. | ||
| + | |||
| + | |||
| + | ==My Conscious Efforts in Numerical Method Learning & It's Application in Hydrogen Storage Optimization== | ||
| + | |||
| + | <youtube width="200" height="100">CxJBYW9A-2o</youtube> | ||
| + | |||
| + | Zefanya Valeryan Harbangan Hutabarat | ||
| + | |||
| + | 2106630611 | ||
| + | |||
| + | Metode Numerik - 02 | ||
Latest revision as of 23:11, 12 June 2023
Contents
- 1 BIODATA
- 2 Pressurized Hydrogen Storage Optimization
- 3 Final Report of Design and Optimization of Pressurized Hydrogen Storage
BIODATA
Nama :
Zefanya Valeryan Harbangan Hutabarat
NPM :
2106630611
TTL :
Depok, 31 Januari 2003
Program Studi :
Teknik Mesin
KATA PENGANTAR
Puji syukur saya panjatkan ke hadirat Tuhan Yang Maha Esa. Atas rahmat dan berkat-Nya, penulis dapat menjalani perkuliahannya di jurusan teknik mesin di Universitas Indonesia.
Tidak lupa penulis mengucapkan rasa terima kasih kepada Bapak Dr. Ir. Ahmad Indra Siswantara selaku dosen untuk mata kuliah metode numerik yang telah membantu penulis dalam mengerjakan laman ini. Penulis juga mengucapkan terima kasih kepada teman-teman serta asisten dosen yang telah memberikan masukan serta pengetahuan dalam pembuatan laman ini.
Laman ini berisikan catatan serta tugas saya selama menjalani mata kuliah mekanika fluida dasar. Bagi para mahasiswa yang mencari sumber pengetahuan tentang mekanika fluida dasar, maka laman ini dapat menjadi salah satu sarana pembelajaran.
Penulis menyadari adanya kekurangan pada laman ini. Oleh karena itu, saran dan kritik senantiasa diharapkan demi perbaikan laman ini. Penulis juga berharap agar laman ini dapat memberikan pengetahuan tentang mekanika fluida dasar kepada orang banyak.
Depok, 25 Mei 2023
Penulis
Pressurized Hydrogen Storage Optimization
Pressurized Hydrogen Storage
- Pressurized hydrogen storage involves compressing hydrogen gas and storing it in specially designed tanks or cylinders. These tanks are built to withstand high pressures, typically ranging from a few hundred to several thousand pounds per square inch (psi). Pressurized storage offers advantages such as simplicity, portability, and fast refueling times. However, it also presents challenges related to weight, safety, and limited storage capacity. Tank materials must be robust, and strict testing is necessary to prevent leaks or ruptures. Alternative storage methods like cryogenic storage and hydrogen carriers are being explored to address these limitations and optimize hydrogen storage and utilization.
Factors Involved in Designing and Optimizing a Pressurized Hydrogen Storage
- Designing and optimizing a pressurized hydrogen storage involves several factors and processes to ensure its safety, efficiency, and performance. Here are some key considerations in the design and optimization process:
- Storage Capacity
- The required storage capacity of hydrogen must be determined based on the anticipated demand and usage. Factors such as the desired duration of storage, refill frequency, and system requirements play a role in determining the storage capacity.
- Material Selection
- The choice of materials for the storage tank is crucial. Factors such as material strength, corrosion resistance, hydrogen compatibility, weight, and cost need to be considered. The selected material should meet safety standards, regulatory requirements, and be suitable for the specific application.
- Pressure Requirements
- Determining the optimal operating pressure is critical to balance storage capacity, tank weight, and safety. Higher pressures allow for more hydrogen storage within a given volume, but it increases material requirements and safety considerations. The pressure requirements should align with the intended use and regulatory standards.
- Safety Considerations
- Safety is paramount in hydrogen storage design. Factors such as material integrity, leak prevention, pressure relief mechanisms, and appropriate safety measures need to be incorporated. Standards and guidelines from regulatory bodies, such as the International Organization for Standardization (ISO) and national safety codes, should be followed.
- Structural Design
- The structural design of the storage tank must ensure its mechanical integrity and resistance to external loads, vibrations, and impacts. Finite element analysis (FEA) and other engineering calculations are performed to determine the optimal tank shape, thickness, reinforcement, and support structures.
- Thermal Management
- Hydrogen storage systems may require thermal management to control temperature variations. Insulation, cooling, or heating mechanisms are employed to maintain the desired hydrogen temperature range and prevent thermal stresses.
- Cost Optimization
- Optimization techniques, such as mathematical modeling and numerical methods, can be applied to minimize costs while meeting performance and safety requirements. This includes optimizing material usage, tank size, manufacturing processes, and other relevant parameters.
- Regulatory Compliance
- Compliance with relevant regulations, standards, and codes is essential in the design and operation of pressurized hydrogen storage. It ensures safety, environmental protection, and compatibility with industry norms.
- Hydrogen Purity
- The required purity level of hydrogen for the specific application should be considered. Impurities in the hydrogen stream can impact the integrity and performance of the storage system. Depending on the application, purification processes may be needed to remove impurities.
- Fill and Discharge Rates
- The desired fill and discharge rates of hydrogen affect the design and optimization of the storage system. Factors such as the available infrastructure, operational requirements, and efficiency considerations influence the sizing of valves, piping, and other components.
- System Integration
- Pressurized hydrogen storage systems are often integrated with other components and subsystems, such as hydrogen production units, fuel cells, or transportation systems. Seamless integration and compatibility with these systems are important to ensure overall system performance.
- Environmental Considerations
- Environmental factors, including temperature variations, exposure to corrosive substances, and seismic activity, should be taken into account during the design process. Adequate protection and design measures, such as coatings, seismic restraints, and environmental monitoring, may be required.
- Manufacturing and Fabrication Methods
- The manufacturing and fabrication techniques employed impact the quality, cost, and scalability of the storage system. Selection of appropriate manufacturing methods, such as welding, forming, or composite layup, needs to be aligned with the chosen materials and desired characteristics.
Final Report of Design and Optimization of Pressurized Hydrogen Storage
Requirements
- The specific requirements are 1 liter of Hydrogen with 8 bar Pressure with a maximum cost of Rp 500.000,00
Material Selection
- By carefully considering the materials available for pressurized hydrogen storage, our selection has led us to choose AISI 316 austenitic stainless steel. This decision is rooted in the unique properties and advantages offered by this particular material. Here are some reasons for considering AISI 316 stainless steel for pressurized hydrogen storage:
- 1) Corrosion Resistance
- Hydrogen can cause embrittlement and corrosion in some materials, leading to reduced structural integrity and potential safety hazards. AISI 316 stainless steel offers superior corrosion resistance, particularly in environments with high levels of hydrogen. This property helps ensure the long-term durability and safety of the storage system.
- 2) Strength and Pressure Resistance
- Pressurized hydrogen storage systems require materials with high strength to withstand the internal pressure. AISI 316 stainless steel possesses good mechanical properties, including high tensile strength and yield strength, allowing it to withstand the required pressure levels while maintaining structural integrity.
- 3) Compatibility with Hydrogen
- AISI 316 stainless steel has demonstrated compatibility with hydrogen gas in various studies and practical applications. It exhibits low permeability to hydrogen, reducing the risk of hydrogen loss and ensuring efficient containment within the storage system.
- 4) Established Industrial Usage
- AISI 316 stainless steel is widely used in various industries, including chemical processing, oil and gas, and marine applications. It has a well-established track record and extensive knowledge base regarding its behavior in different environments, making it a trusted material choice for engineering applications.
Constraints
- Pressurized hydrogen storage plays a crucial role in various applications, ranging from energy storage to fuel cell technology. Designing an optimized storage system requires careful consideration of multiple factors to ensure efficiency, safety, and cost-effectiveness. In this context, incorporating three key constraints - geometrical, material strength, and budget constraints - forms the foundation of an effective optimization model.
- 1) Geometrical Constraint
- The geometrical constraint ensures that the design of the storage system meets specific volume requirements. By setting a constraint on the volume or dimensions of the storage tank, you can optimize the geometrical parameters such as radius and height to ensure the tank can accommodate the desired volume of 1 liter (1000 cm^3). This constraint ensures that the storage tank is appropriately sized and fits within the available space.
- 2) Material Strength Constraint
- The material strength constraint focuses on selecting a material that can withstand the high-pressure environment of the hydrogen storage system. Hydrogen is stored under high pressure (8 bar or 800 kPa), and selecting a material with appropriate strength characteristics is crucial for the safety and integrity of the storage system. By incorporating this constraint, you ensure that the selected material, such as AISI 316 austenitic stainless steel, possesses the necessary mechanical properties to withstand the pressure and prevent any material failures or leaks.
- 3) Budget Constraint
- The budget constraint places a limitation on the cost of the pressurized hydrogen storage system. By including this constraint, you ensure that the optimization model considers the cost-effectiveness of the design. The budget constraint helps in selecting cost-efficient materials and optimizing the geometrical parameters to meet the required specifications while staying within the allocated budget of Rp 500.000. This constraint ensures that the final design is financially feasible and aligns with the available resources.
Geometrical Constraints
- The code provided utilizes an optimization algorithm implemented in Python, utilizing the powerful capabilities of the NumPy and SciPy libraries. The objective of the code is to determine the optimal values for the radius and height of the storage tank by minimizing the surface area, while considering the specified volume of hydrogen. The incorporation of NumPy allows for efficient mathematical operations and array manipulation, while SciPy provides advanced optimization techniques and algorithms
Base Geometry
import numpy as np
from scipy.optimize import minimize
# Define the objective function
def objective(x):
radius, height = x
surface_area = 2 * np.pi * radius * (radius + height)
return surface_area
# Define the volume constraint function
def volume_constraint(x):
radius, height = x
volume = np.pi * radius**2 * height
return volume - 1000
# Define the optimization problem
x0 = [1.0, 10.0]
bounds = [(0, None), (0, None)]
constraint = {'type': 'eq', 'fun': volume_constraint}
problem = minimize(objective, x0, bounds=bounds, constraints=constraint)
# Extract the optimized results
optimized_radius = problem.x[0]
optimized_height = problem.x[1]
optimized_surface_area = problem.fun
# Print the optimized results
print("Optimization Results:")
print(f"Radius: {optimized_radius:.2f} cm")
print(f"Height: {optimized_height:.2f} cm")
print(f"Surface Area: {optimized_surface_area:.2f} cm^2")- Dari hasil pengkodean, dapat disimpulkan bahwa dengan meminimalkan luas permukaan, dimensi optimal untuk tangki silinder dicapai dengan rasio tinggi-jari-jari 2:1. Secara spesifik, tangki tersebut memiliki tinggi 10,84 cm dan radius 5,42 cm. Pengukuran ini menghasilkan luas permukaan 553,58 cm^2, yang merupakan luas terkecil yang mungkin untuk kebutuhan volume dan tekanan tertentu.
End Cap Geometry
- Using a purely cylindrical geometry for the storage tank may pose risks due to stress concentration at the corners. To minimize stress concentration and reduce surface area while maintaining the same volume, it is more efficient to adopt a torispherical end cap shape. This shape can be achieved by adding a fillet with a radius equal to half the tank's radius. The filleting creates a smooth curvature and helps reduce stress concentration. Adjustments in the geometrical parameters are necessary to compensate for the volume reduction caused by the filleting.
Dengan menghitung persentase pengurangan luas penampang, kita dapat menerapkannya secara terbalik ke volume yang diperlukan untuk mendapatkan batasan volume baru yang ditingkatkan.
-
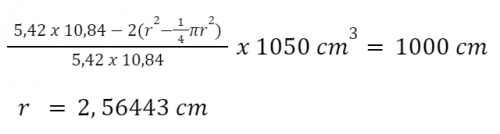
- Hasil perhitungan mengungkapkan bahwa jari-jari fillet yang diperoleh untuk tutup ujung tangki adalah 2.56443 cm
Material Strength Constraints
Mechanical Properties of AISI 316 Austenitic Stainless Steel
- The range of acceptable wall thickness is not arbitrary and should not exceed one-fifth of the vessel radius. According to ASME BPV Code Section VIII D.1, the minimum wall thickness should be at least 1/16 in (1.59 mm), regardless of corrosion allowance, material, or dimensions.
- Based on data obtained from Ferrobend, which provides information on the mechanical properties of AISI 316 stainless steel, we will employ both a conservative and less conservative approach by setting our limit at the yield strength and maximum tensile strength to represent failure.
- Dalam perhitungan ini, kita akan melakukan iterasi dari radius minimal 2,9 mm hingga 12 mm dengan inkremen 1 mm di setiap iterasi..
Iteration Process
r = 5.42e-2
p = 800000
t = 2.9e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9:
break- Kode tadi untuk menghitung hoop stress untuk berbagai nilai ketebalan mulai dari 2,9 mm hingga 12 mm, dengan constraint yang menghentikan iterasi jika total hoop stress melebihi yield strength stainless steel AISI 316. Berdasarkan hasil, semua nilai ketebalan mulai dari 2,9 mm hingga 12 mm dengan kenaikan 1 mm memenuhi batasan yield strength. Berikut adalah hasil perhitungan dari kode yang menunjukkan bahwa tegangan hoop jauh di bawah yield strength 205 MPa..
Budget Constraint
Setelah menemukan parameter geometrik, tahap terakhir dari optimasi ini adalah membandingkannya dengan batas biaya yang tidak boleh melebihi Rp500.000,00. Berdasarkan material yang dipilih sebelumnya yaitu AISI 316, kita harus memilih ketebalan dinding tangki yang sesuai dengan kisaran anggaran. Berikut daftar harga beserta perhitungannya.
Berdasarkan perhitungan ini, dengan mengoptimalkan kendala anggaran, bobot minimum yang masuk akal, namun tetap mempertahankan kekuatan yang masuk akal, dipilih ketebalan 6 mm untuk dinding tangki hidrogen ini.
My Conscious Efforts in Numerical Method Learning & It's Application in Hydrogen Storage Optimization
Zefanya Valeryan Harbangan Hutabarat
2106630611
Metode Numerik - 02