Difference between revisions of "Salmanisa Kinanti Armadani"
(→Question Number 3) |
(→Presentation) |
||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
== Question Number 1 == | == Question Number 1 == | ||
'''''What will be (x^2-1)/(x-1) if x=1?''''' | '''''What will be (x^2-1)/(x-1) if x=1?''''' | ||
| Line 5: | Line 4: | ||
Answer : If we substitute x = 1 into the expression (x^2 - 1)/(x - 1), we get an indeterminate form of 0/0. This is because both the numerator and the denominator become 0 when x = 1. What's the result of 0 / 0? It's "undefined". | Answer : If we substitute x = 1 into the expression (x^2 - 1)/(x - 1), we get an indeterminate form of 0/0. This is because both the numerator and the denominator become 0 when x = 1. What's the result of 0 / 0? It's "undefined". | ||
Why? If we divided a ∕ b it means a number which multiplied by b will produce a. For example, the reason 1 ∕ 0 is undefined is because there isn't any number x that results in 0 ⋅ x = 1. | Why? If we divided a ∕ b it means a number which multiplied by b will produce a. For example, the reason 1 ∕ 0 is undefined is because there isn't any number x that results in 0 ⋅ x = 1. | ||
| − | For the case 0 ∕ 0 it's different, because for any value of any x will result in 0 ⋅ x = 0. In other words, the result of dividing 0∕0 is undefined. Formally, it is called indefinite form because there are some functions whose function value is 0/0 | + | For the case 0 ∕ 0 it's different, because for any value of any x will result in 0 ⋅ x = 0. In other words, the result of dividing 0∕0 is undefined. Formally, it is called indefinite form because there are some functions whose function value is 0 / 0 |
| − | but the limit value is not single; there are limits to real numbers, infinity, negative infinity, or limits that doesn't exist | + | but the limit value is not single; there are limits to real numbers, infinity, negative infinity, or limits that doesn't exist [http://p4tkmatematika.org/file/ARTIKEL/Artikel%20Matematika/Bentuk%20Tak%20Tentu_sumardyono.pdf] |
| − | |||
Another answer but not related to mathematics, let say the numerator (0) is what we give and the denominator (0) is what we what do expect to return and the result is undefined. I believe if we give something but we don't talk about it and think of it as nothing (0), and in return we expect nothing (0), the result or the blessing that we'll get will be undefined because it is something more than we can expect (Q.S Al Baqarah ayat 261) | Another answer but not related to mathematics, let say the numerator (0) is what we give and the denominator (0) is what we what do expect to return and the result is undefined. I believe if we give something but we don't talk about it and think of it as nothing (0), and in return we expect nothing (0), the result or the blessing that we'll get will be undefined because it is something more than we can expect (Q.S Al Baqarah ayat 261) | ||
| Line 27: | Line 25: | ||
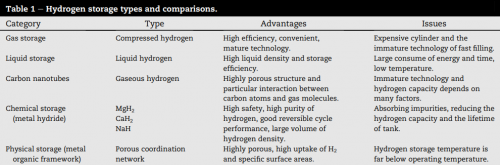
I'll attach a table that show some ways to storage hydrogen in this section. | I'll attach a table that show some ways to storage hydrogen in this section. | ||
| − | [[File:Hydrogen_Storages.png|500px|thumb| | + | [[File:Hydrogen_Storages.png|500px|thumb|center|Hydrogen Storages Types]] |
| + | |||
| + | So, how to optimize it? First, choose in what form the hydrogen will be stored. Different materials can be used to store hydrogen, each with varying storage capacities. Investigate advanced storage materials. Hydrogen can be stored at high pressures to increase the amount that can be stored within a given volume. So, utilizing storage tanks designed to withstand high pressures, such as composite or metal hydride tanks, can help maximize the hydrogen storage capacity. | ||
| + | |||
| + | |||
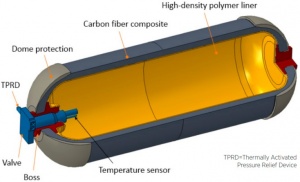
| + | Here's the design if we want to make a storage tanks from composite. | ||
| + | [[File:Composite_Hydrogen_Tanks.jpg|300px|thumb|center|Composite Hydrogen Tanks]] | ||
| + | |||
| + | Last, temperature-dependent hydrogen storage techniques imply the addition of a heat management system, which adds costs, complexity, and possibly mass. Ideally, this technique should be avoided, and operation near ambient temperature throughout refueling, standby, and discharge is desirable. Another important aspect to consider is the operating pressure. Pressure vessels must be reinforced with high strength materials that are subject to strict regulation and testing, which negatively impacts gravimetric density and costs. The final important thermodynamic property is efficiency. If hydrogen is used in an effort to capture renewable energy and displace hydrocarbons, then efficiency should be as high as possible to make optimal use of available renewable energy.[https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6630991/] | ||
| + | |||
| + | |||
| + | To calculate pressurized tank's optimization, use this code (this code is in Python format) ; | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | Fungsi objektif yang akan dioptimalkan (minimalkan) | ||
| + | def objective_function(x): | ||
| + | # x adalah array yang berisi variabel yang dioptimalkan | ||
| + | # Misalnya, x[0] adalah volume tangki, x[1] adalah tekanan maksimum, dll. | ||
| + | |||
| + | # Menghitung biaya produksi berdasarkan variabel yang dioptimalkan | ||
| + | volume = x[0] | ||
| + | tekanan = x[1] | ||
| + | biaya = ... # Hitung biaya produksi berdasarkan volume dan tekanan | ||
| + | |||
| + | return biaya | ||
| + | |||
| + | Batasan dan kendala yang harus dipatuhi | ||
| + | def constraint_function(x): | ||
| + | # x adalah array yang berisi variabel yang dioptimalkan | ||
| + | # Misalnya, x[0] adalah volume tangki, x[1] adalah tekanan maksimum, dll. | ||
| + | |||
| + | # Cek apakah variabel memenuhi batasan | ||
| + | batasan1 = ... # Misalnya, x[0] <= volume_maksimum | ||
| + | batasan2 = ... # Misalnya, x[1] >= tekanan_minimum | ||
| + | |||
| + | # Menggabungkan semua batasan menjadi array | ||
| + | constraints = np.array([batasan1, batasan2]) | ||
| + | |||
| + | return constraints | ||
| + | |||
| + | Variabel awal atau tebakan awal | ||
| + | x0 = np.array([volume_awal, tekanan_awal, ...]) # Misalnya, volume_awal dan tekanan_awal adalah tebakan awal | ||
| + | |||
| + | |||
| + | Mendefinisikan batasan dan kendala | ||
| + | constraint = {'type': 'ineq', 'fun': constraint_function} | ||
| + | |||
| + | |||
| + | Melakukan optimasi | ||
| + | result = minimize(objective_function, x0, constraints=constraint) | ||
| + | |||
| + | |||
| + | Menampilkan hasil optimasi | ||
| + | |||
| + | print("Hasil Optimasi:") | ||
| + | |||
| + | print("Volume tangki:", result.x[0]) | ||
| + | |||
| + | print("Tekanan maksimum:", result.x[1]) | ||
| + | |||
| + | print("Biaya produksi:", result.fun) | ||
| − | + | == Presentation == | |
| + | Here's the presentation of this topic![https://www.youtube.com/watch?v=Aq5FY7yKv1I] | ||
Latest revision as of 03:42, 12 June 2023
Question Number 1
What will be (x^2-1)/(x-1) if x=1?
Answer : If we substitute x = 1 into the expression (x^2 - 1)/(x - 1), we get an indeterminate form of 0/0. This is because both the numerator and the denominator become 0 when x = 1. What's the result of 0 / 0? It's "undefined". Why? If we divided a ∕ b it means a number which multiplied by b will produce a. For example, the reason 1 ∕ 0 is undefined is because there isn't any number x that results in 0 ⋅ x = 1. For the case 0 ∕ 0 it's different, because for any value of any x will result in 0 ⋅ x = 0. In other words, the result of dividing 0∕0 is undefined. Formally, it is called indefinite form because there are some functions whose function value is 0 / 0 but the limit value is not single; there are limits to real numbers, infinity, negative infinity, or limits that doesn't exist [1]
Another answer but not related to mathematics, let say the numerator (0) is what we give and the denominator (0) is what we what do expect to return and the result is undefined. I believe if we give something but we don't talk about it and think of it as nothing (0), and in return we expect nothing (0), the result or the blessing that we'll get will be undefined because it is something more than we can expect (Q.S Al Baqarah ayat 261)
Question Number 2
Is consciousness relevant to the previous case? Do narrate it!
Answer : Consciousness is our awareness of ourself and our surroundings. It means our own personal experience of perceiving, thinking, emoting, and acting. Self-consciousness, that is, being conscious of our selves as thinking entities [2]. Based on this definition, so I think yes, it is related to the previous case because we need to be fully conscious while thinking about the solution of (x^2-1)/(x-1) if x=1. Also, I think the result of the previous question can be defined as something not related to mathematics. Let say the numerator (0) is what we give and the denominator (0) is what we what do expect to return and the result is undefined. I believe if we give something but we don't talk about it and think of it as nothing (0), and in return we expect nothing (0), the result or the blessing that we'll get will be undefined because it is something more than we can expect (Q.S Al Baqarah ayat 261), and of course it's related to consciousness. We have to be fully conscious to do good things wholeheartedly, sincerely.
Question Number 3
How to optimize 1 liter of pressured hydrogen storage?
Answer :
Hydrogen storage is a key enabling technology for the advancement of hydrogen and fuel cell technologies in applications including stationary power, portable power, and transportation. Hydrogen has the highest energy per mass of any fuel; however, its low ambient temperature density results in a low energy per unit volume, therefore requiring the development of advanced storage methods that have potential for higher energy density ([3]
There is amount of ways for storing hydrogen fuel in different forms. Compared with the above several methods, compressed gas storage is more popular due to its technical simplicity, high reliability, acceptable efficiency and affordability. Hydrogen may be stored as gas or a liquid in pure, molecular form without any significant physical or chemical bonding to other materials; molecular hydrogen may be adsorbed onto or into a material, held by relatively weak physical van der Waals bonds; atomic hydrogen may be chemically bonded (absorbed) [4]
I'll attach a table that show some ways to storage hydrogen in this section.
So, how to optimize it? First, choose in what form the hydrogen will be stored. Different materials can be used to store hydrogen, each with varying storage capacities. Investigate advanced storage materials. Hydrogen can be stored at high pressures to increase the amount that can be stored within a given volume. So, utilizing storage tanks designed to withstand high pressures, such as composite or metal hydride tanks, can help maximize the hydrogen storage capacity.
Here's the design if we want to make a storage tanks from composite.
Last, temperature-dependent hydrogen storage techniques imply the addition of a heat management system, which adds costs, complexity, and possibly mass. Ideally, this technique should be avoided, and operation near ambient temperature throughout refueling, standby, and discharge is desirable. Another important aspect to consider is the operating pressure. Pressure vessels must be reinforced with high strength materials that are subject to strict regulation and testing, which negatively impacts gravimetric density and costs. The final important thermodynamic property is efficiency. If hydrogen is used in an effort to capture renewable energy and displace hydrocarbons, then efficiency should be as high as possible to make optimal use of available renewable energy.[5]
To calculate pressurized tank's optimization, use this code (this code is in Python format) ;
import numpy as np from scipy.optimize import minimize
Fungsi objektif yang akan dioptimalkan (minimalkan)
def objective_function(x):
# x adalah array yang berisi variabel yang dioptimalkan # Misalnya, x[0] adalah volume tangki, x[1] adalah tekanan maksimum, dll. # Menghitung biaya produksi berdasarkan variabel yang dioptimalkan volume = x[0] tekanan = x[1] biaya = ... # Hitung biaya produksi berdasarkan volume dan tekanan return biaya
Batasan dan kendala yang harus dipatuhi
def constraint_function(x):
# x adalah array yang berisi variabel yang dioptimalkan # Misalnya, x[0] adalah volume tangki, x[1] adalah tekanan maksimum, dll. # Cek apakah variabel memenuhi batasan batasan1 = ... # Misalnya, x[0] <= volume_maksimum batasan2 = ... # Misalnya, x[1] >= tekanan_minimum # Menggabungkan semua batasan menjadi array constraints = np.array([batasan1, batasan2]) return constraints
Variabel awal atau tebakan awal
x0 = np.array([volume_awal, tekanan_awal, ...]) # Misalnya, volume_awal dan tekanan_awal adalah tebakan awal
Mendefinisikan batasan dan kendala
constraint = {'type': 'ineq', 'fun': constraint_function}
Melakukan optimasi
result = minimize(objective_function, x0, constraints=constraint)
Menampilkan hasil optimasi
print("Hasil Optimasi:")
print("Volume tangki:", result.x[0])
print("Tekanan maksimum:", result.x[1])
print("Biaya produksi:", result.fun)
Presentation
Here's the presentation of this topic![6]