Difference between revisions of "Ronna Hamimah"
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Ronna Hamimah.jpg|300x300px]] | [[File:Ronna Hamimah.jpg|300x300px]] | ||
| − | Hello there! My name is Ronna Hamimah (2106635543) , and I am a dedicated student pursuing a degree in Mechanical Engineering at University of Indonesia. With a passion for unraveling the complexities of machines and systems, I have immersed myself in the fascinating world of engineering. As a student, I strive for excellence in both my academic pursuits and practical applications | + | =='''Introduction'''== |
| + | Hello there! My name is '''Ronna Hamimah (2106635543)''' , and I am a dedicated student pursuing a degree in Mechanical Engineering at University of Indonesia. With a passion for unraveling the complexities of machines and systems, I have immersed myself in the fascinating world of engineering. As a student, I strive for excellence in both my academic pursuits and practical applications | ||
| + | |||
| + | =='''Conciousness'''== | ||
| + | Consciousness plays a pivotal role when it comes to studying effectively. It involves being fully present and engaged in the learning process, actively absorbing and comprehending the material at hand. By cultivating consciousness during studying, individuals can enhance their focus, attention, and overall retention of information. It allows for a deeper level of understanding, as one becomes attuned to the nuances and connections within the subject matter. Furthermore, consciousness helps individuals identify their own learning styles and adapt their study methods accordingly, maximizing their efficiency and productivity. By being conscious of their progress, strengths, and weaknesses, students can also make informed decisions on how to allocate their time and resources effectively. In essence, consciousness while studying empowers learners to take ownership of their education and facilitates a more meaningful and impactful learning experience. | ||
| + | |||
| + | =='''Hydrogen'''== | ||
| + | Hydrogen serves as an excellent '''medium for energy storage, transportation, and conversion''', aiming to develop '''clean and emission-free energy concepts'''. Various sources, using different technologies, can be utilized to produce hydrogen. Hydrogen can be derived from compounds such as fossil fuels, biomass, and water. Thermochemical processes allow for hydrogen production from biomass and fossil fuels like coal, petroleum, and natural gas. | ||
| + | |||
| + | Hydrogen, acquired through these methods, can be stored as an energy carrier in gas, liquid, or solid metal forms. High pressure is necessary to store hydrogen as a gas, while cryogenic systems are required for storing it as a liquid. Hydrogen can also be stored in solid form. | ||
| + | |||
| + | == '''Design & Optimization of Pressurized Hydrogen Storage'''== | ||
| + | |||
| + | Optimizing a 1-liter hydrogen storage design within a limited budget requires careful consideration of various factors. Here are a few suggestions to help you achieve a design concept and optimization for storing hydrogen at 8 bar pressure with a capacity of 1 liter and a maximum budget of Rp500,000. | ||
| + | |||
| + | '''1. Material Selection''' | ||
| + | |||
| + | Choose lightweight materials that can withstand high-pressure conditions while remaining cost-effective. Composite materials, such as carbon fiber reinforced polymers (CFRP) or aluminum alloys, could be potential options. | ||
| + | |||
| + | '''2. Tank Design''' | ||
| + | |||
| + | Opt for a cylindrical shape with reinforced walls to minimize material usage while maintaining structural integrity. Conduct thorough stress analysis to ensure the tank can withstand the desired pressure of 8 bar. | ||
| + | |||
| + | [[File:Tankdesain.jpg|300x300px]] | ||
| + | |||
| + | '''3. Safety Measures''' | ||
| + | |||
| + | Implement necessary safety features, such as pressure relief valves and rupture discs, to prevent over-pressurization and ensure the integrity of the tank. | ||
| + | |||
| + | '''4. Insulation''' | ||
| + | |||
| + | To reduce heat transfer and minimize energy loss, consider incorporating efficient insulation materials, such as foams or vacuum insulation panels. | ||
| + | |||
| + | '''5. Regulators and Valves''' | ||
| + | |||
| + | Include efficient pressure regulators and valves to control the release of hydrogen and maintain a stable pressure within the storage system. | ||
| + | |||
| + | '''6. Cost Analysis''' | ||
| + | |||
| + | Evaluate different suppliers, materials, and manufacturing methods to find the most cost-effective options within your budget. Consider both initial costs and long-term maintenance expenses. | ||
| + | |||
| + | '''7. Testing and Certification''' | ||
| + | |||
| + | Ensure the hydrogen storage design complies with industry standards and safety regulations. Perform thorough testing, including burst tests and leak checks, to verify the integrity of the storage system. | ||
| + | |||
| + | |||
| + | Conducting a comprehensive risk assessment is an essential part of designing any hydrogen storage system. Hydrogen is a highly flammable gas, and ensuring the safety of the storage system is of paramount importance. Here are some key aspects to consider during the '''risk assessment''': | ||
| + | |||
| + | '''1. Fire and Explosion Hazards:''' | ||
| + | |||
| + | Hydrogen is highly flammable and can form explosive mixtures with air. Assess the potential for ignition sources, such as electrical equipment, static electricity, or open flames, and implement appropriate safety measures to mitigate the risks. | ||
| + | |||
| + | '''2. Ventilation:''' | ||
| + | |||
| + | Adequate ventilation is crucial to prevent the accumulation of hydrogen gas, which can create an explosive atmosphere. Ensure that the storage system is properly ventilated to disperse any leaked hydrogen gas. | ||
| + | |||
| + | '''3. Pressure Management:''' | ||
| + | |||
| + | Hydrogen storage systems operate under pressure. Assess the risks associated with over-pressurization or sudden pressure releases, and include pressure relief valves, burst discs, or other pressure safety devices to prevent catastrophic failures. | ||
| + | |||
| + | '''4. Material Compatibility:''' | ||
| + | |||
| + | Evaluate the compatibility of storage materials (e.g., cylinders, seals, valves) with hydrogen gas. Hydrogen can cause embrittlement in certain metals, potentially leading to failures. Use materials that are specifically designed for hydrogen storage or have been certified for compatibility. | ||
| + | |||
| + | '''5. Leak Detection and Monitoring:''' | ||
| + | |||
| + | Implement systems for detecting and monitoring hydrogen leaks. This can include gas sensors, hydrogen detectors, or leak detection solutions. Early detection of leaks allows for timely intervention and prevents the build-up of hydrogen gas. | ||
| + | |||
| + | '''6. Training and Safety Procedures:''' | ||
| + | |||
| + | Provide adequate training to personnel involved in handling, storing, and maintaining the hydrogen storage system. Develop clear safety procedures, emergency response plans, and protocols for handling hydrogen-related incidents. | ||
| + | |||
| + | '''7. Compliance with Regulations:''' | ||
| + | |||
| + | Ensure compliance with relevant safety regulations, codes, and standards for hydrogen storage systems. Familiarize yourself with local, national, and international guidelines to ensure the system meets all necessary requirements. | ||
| + | |||
| + | =='''Material of The Tank'''== | ||
| + | The material that will be used in the construction of this hydrogen tank is '''AISI 316 austenitic stainless steel'''. Austenitic stainless steel is also one of the primary choices for manufacturers of industrial hydrogen storage. This indicates that austenitic stainless steel has been tested for availability, durability, strength, machinability, compatibility with hydrogen gas (non-reactive with hydrogen), and so on. | ||
| + | |||
| + | =='''Material Strength Constraints Analysis'''== | ||
| + | Ensuring the durability of the container material and its ability to withstand the pressure exerted on its walls are of utmost importance in the case of a pressurized container. The 1-liter hydrogen tank, with a maximum pressure limit of 8 bar, has specific requirements that need to be met. | ||
| + | In a cylindrical component with thin walls, there are two primary types of stress: circumferential (hoop) stress and longitudinal stress. While there is also radial stress, it can be disregarded due to the significantly larger radius compared to the wall thickness. | ||
| + | |||
| + | [[File:Formula_hoop_equation.jpg|300x300px]] | ||
| + | |||
| + | The provided formulas above can be utilized for calculating the '''hoop stress''' and '''longitudinal stress'''. | ||
| + | |||
| + | [[File:Materialstregthanalysisronna.jpg|300x300px]] | ||
| + | |||
| + | To ensure structural integrity, the plate thickness for the tank should be at least one-fifth of the tank radius. According to ASME BPV Code Section VIII D.1, the minimum plate thickness for the tank is specified as 1/16 inch or 1.59 mm, without considering factors like corrosion, material properties, or dimensional considerations. For the purpose of this calculation, we will iterate through a range of tank radii, starting from a minimum radius of 2.7 mm up to 11.05 mm, with an increment of 1 mm for each iteration. | ||
| + | |||
| + | '''Iteration Process''' | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | r = 5.42e-2 | ||
| + | p = 800000 | ||
| + | t = 2.9e-3 | ||
| + | |||
| + | while t < 12e-3: | ||
| + | hoop = (r * p)/(t) | ||
| + | print('for thickness', t, 'hoop stress =', hoop, "Pa") | ||
| + | t += 1e-3 | ||
| + | if hoop > 205e9: | ||
| + | break | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | '''Results''' | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | for thickness 0.004099999999999999 hoop stress = 10770731.707317077 Pa | ||
| + | for thickness 0.004199999999999999 hoop stress = 10514285.714285716 Pa | ||
| + | for thickness 0.004299999999999999 hoop stress = 10269767.441860467 Pa | ||
| + | for thickness 0.004399999999999999 hoop stress = 10036363.636363639 Pa | ||
| + | for thickness 0.0045 hoop stress = 9813333.333333334 Pa | ||
| + | for thickness 0.0046 hoop stress = 9600000.0 Pa | ||
| + | for thickness 0.0047 hoop stress = 9395744.680851063 Pa | ||
| + | for thickness 0.0048000000000000004 hoop stress = 9200000.0 Pa | ||
| + | for thickness 0.004900000000000001 hoop stress = 9012244.897959182 Pa | ||
| + | for thickness 0.005000000000000001 hoop stress = 8831999.999999998 Pa | ||
| + | for thickness 0.005100000000000001 hoop stress = 8658823.529411763 Pa | ||
| + | for thickness 0.0052000000000000015 hoop stress = 8492307.69230769 Pa | ||
| + | for thickness 0.005300000000000002 hoop stress = 8332075.47169811 Pa | ||
| + | for thickness 0.005400000000000002 hoop stress = 8177777.777777774 Pa | ||
| + | for thickness 0.005500000000000002 hoop stress = 8029090.909090905 Pa | ||
| + | for thickness 0.0056000000000000025 hoop stress = 7885714.285714282 Pa | ||
| + | for thickness 0.005700000000000003 hoop stress = 7747368.421052628 Pa | ||
| + | for thickness 0.005800000000000003 hoop stress = 7613793.103448272 Pa | ||
| + | for thickness 0.005900000000000003 hoop stress = 7484745.76271186 Pa | ||
| + | for thickness 0.006000000000000004 hoop stress = 7359999.999999995 Pa | ||
| + | for thickness 0.006100000000000004 hoop stress = 7239344.262295078 Pa | ||
| + | for thickness 0.006200000000000004 hoop stress = 7122580.645161286 Pa | ||
| + | for thickness 0.006300000000000004 hoop stress = 7009523.809523805 Pa | ||
| + | for thickness 0.006400000000000005 hoop stress = 6899999.999999995 Pa | ||
| + | for thickness 0.006500000000000005 hoop stress = 6793846.153846148 Pa | ||
| + | for thickness 0.006600000000000005 hoop stress = 6690909.090909085 Pa | ||
| + | for thickness 0.006700000000000005 hoop stress = 6591044.776119398 Pa | ||
| + | for thickness 0.006800000000000006 hoop stress = 6494117.6470588185 Pa | ||
| + | for thickness 0.006900000000000006 hoop stress = 6399999.999999994 Pa | ||
| + | for thickness 0.007000000000000006 hoop stress = 6308571.428571423 Pa | ||
| + | </syntaxhighlight> | ||
| + | The given code computes the hoop stress using different thickness values ranging from 2.9 mm to 12 mm. It includes a condition that terminates the iteration if the total hoop stress surpasses the yield strength of AISI 316 stainless steel. The results demonstrate that '''all thickness values within the range of 2.9 mm to 12 mm, incremented by 1 mm,''' comply with the yield strength constraint. The calculations from the code reveal that '''the hoop stress remains well below the yield strength of 205 MPa, indicating a significant safety margin'''. | ||
| + | |||
| + | =='''Geometry Constraints Analysis'''== | ||
| + | The code above optimizes the dimensions (radius and height) of a cylindrical structure to minimize its surface area while satisfying a volume constraint. This can be useful in various engineering and design applications where minimizing surface area or optimizing geometrical parameters is desired. | ||
| + | <syntaxhighlight lang="xml"> | ||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def calculate_surface_area(x): | ||
| + | radius, height = x | ||
| + | surface_area = 2 * np.pi * radius * (radius + height) | ||
| + | return surface_area | ||
| + | |||
| + | def calculate_volume(x): | ||
| + | radius, height = x | ||
| + | volume = np.pi * radius**2 * height | ||
| + | return volume | ||
| + | |||
| + | def optimize_cylinder(): | ||
| + | initial_guess = [1.0, 10.0] | ||
| + | bounds = [(0, None), (0, None)] | ||
| + | constraint = {'type': 'eq', 'fun': lambda x: calculate_volume(x) - 1050} | ||
| + | |||
| + | result = minimize(calculate_surface_area, initial_guess, method='SLSQP', bounds=bounds, constraints=constraint) | ||
| + | |||
| + | print("Optimization Results:") | ||
| + | print("Radius: {:.2f} cm".format(result.x[0])) | ||
| + | print("Height: {:.2f} cm".format(result.x[1])) | ||
| + | print("Surface Area: {:.2f} cm^2".format(result.fun)) | ||
| + | |||
| + | optimize_cylinder() | ||
| + | </syntaxhighlight> | ||
| + | Based on the provided code, the following information can be obtained: | ||
| + | the code Optimization Results: | ||
| + | Radius: '''5.51 cm''' | ||
| + | Height: '''11.02 cm''' | ||
| + | Surface Area: '''571.88 cm^2''' | ||
| + | |||
| + | =='''Cost Constraints Analysis'''== | ||
| + | To optimize the storage of hydrogen at 8 bar pressure with a 1-liter capacity and a maximum budget of Rp500,000, we can approach it as an optimization problem by using a phyton's code below: | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Price and capacity | ||
| + | price_per_unit = 100000 # Price per unit of hydrogen storage | ||
| + | capacity_per_unit = 1 # Capacity of hydrogen storage per unit | ||
| + | |||
| + | # Maximum budget | ||
| + | max_budget = 500000 | ||
| + | |||
| + | # Objective function | ||
| + | def objective_function(x): | ||
| + | return -x * capacity_per_unit | ||
| + | |||
| + | # Constraint function | ||
| + | def budget_constraint(purchase_amount): | ||
| + | return max_budget - (price_per_unit * purchase_amount) | ||
| + | |||
| + | budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint} | ||
| + | |||
| + | # Initial value | ||
| + | x0 = 0 | ||
| + | |||
| + | # Bounds | ||
| + | bounds = [(0, None)] | ||
| + | |||
| + | # Solve the optimization problem | ||
| + | solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq]) | ||
| + | |||
| + | # Print the results | ||
| + | print("Status:", "Optimal" if solution.success else "No solution found") | ||
| + | print("Number of hydrogen storage units to be purchased:", solution.x[0]) | ||
| + | print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters") | ||
| + | print("Total cost:", solution.x[0] * price_per_unit, "Rupiah") | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | This code will calculate the optimal number of hydrogen storage units to be purchased within the given budget, considering a storage capacity of 1 liter per unit and a price per unit of Rp100,000. The optimization problem is solved using the SLSQP method, and the results are printed, including the status, the number of units to be purchased, the total storage capacity, and the total cost in Rupiah. | ||
| + | |||
| + | From the code above, we obtain the following information: | ||
| + | |||
| + | Status: Optimal | ||
| + | Number of hydrogen storage units to be purchased: 5.0 | ||
| + | Total storage capacity: 5.0 liters | ||
| + | Total cost: 500000.0 Rupiah | ||
| + | |||
| + | |||
| + | We can also use phyton to show '''graphic''' between total storage and hydrogen storage optimazation: | ||
| + | |||
| + | <syntaxhighlight lang="xml"> | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | # Price and capacity | ||
| + | unit_price = 100000 # Price per unit of hydrogen storage | ||
| + | unit_capacity = 1 # Capacity per unit of hydrogen storage | ||
| + | |||
| + | # Maximum budget | ||
| + | max_budget = 500000 | ||
| + | |||
| + | # Initialize variables | ||
| + | best_unit_count = 0 | ||
| + | best_total_capacity = 0 | ||
| + | best_total_cost = 0 | ||
| + | |||
| + | # Initialize lists for the graph | ||
| + | unit_count_list = [] | ||
| + | total_capacity_list = [] | ||
| + | |||
| + | # Iteration to find the optimal solution | ||
| + | for unit_count in range(int(max_budget / unit_price) + 1): | ||
| + | total_capacity = unit_count * unit_capacity | ||
| + | total_cost = unit_count * unit_price | ||
| + | |||
| + | if total_capacity > best_total_capacity and total_cost <= max_budget: | ||
| + | best_unit_count = unit_count | ||
| + | best_total_capacity = total_capacity | ||
| + | best_total_cost = total_cost | ||
| + | |||
| + | # Add data to the lists for the graph | ||
| + | unit_count_list.append(unit_count) | ||
| + | total_capacity_list.append(total_capacity) | ||
| + | |||
| + | # Display the results | ||
| + | print("Number of hydrogen storage units to be purchased:", best_unit_count) | ||
| + | print("Total storage capacity:", best_total_capacity, "liters") | ||
| + | print("Total cost:", best_total_cost, "Rupiah") | ||
| + | |||
| + | # Display the graph | ||
| + | plt.plot(unit_count_list, total_capacity_list) | ||
| + | plt.xlabel('Number of Hydrogen Storage Units') | ||
| + | plt.ylabel('Total Storage Capacity (liters)') | ||
| + | plt.title('Hydrogen Storage Optimization') | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | </syntaxhighlight> | ||
| + | This code calculates the optimal number of hydrogen storage units to be purchased based on the given price per unit, capacity per unit, and maximum budget. It iterates through the possible number of units within the budget and calculates the corresponding total storage capacity and cost. It keeps track of the best solution with the highest total capacity while staying within the budget. The results are then printed, including the number of units, total capacity, and total cost. Additionally, the code plots a graph showing the '''relationship between the number of units and the total storage capacity'''. | ||
| + | [[File:Graphic.png|300x300px]] | ||
| + | |||
| + | =='''Final Remarks'''== | ||
| + | It is highly recommended to involve experienced professionals with expertise in hydrogen safety and risk assessment during the design and implementation of a hydrogen storage system. They can provide valuable insights and help identify and mitigate potential risks associated with the specific storage design and application. Remember that optimizing a hydrogen storage design requires a multidisciplinary approach involving mechanical engineering, materials science, and safety considerations. It's advisable to consult with experts in the field and conduct a detailed feasibility study to achieve the best results within your budget. | ||
| + | |||
| + | =='''Youtube'''== | ||
| + | [https://www.youtube.com/watch?v=pSy7j6OGCww My Presentation] | ||
Latest revision as of 19:06, 15 June 2023
Contents
Introduction
Hello there! My name is Ronna Hamimah (2106635543) , and I am a dedicated student pursuing a degree in Mechanical Engineering at University of Indonesia. With a passion for unraveling the complexities of machines and systems, I have immersed myself in the fascinating world of engineering. As a student, I strive for excellence in both my academic pursuits and practical applications
Conciousness
Consciousness plays a pivotal role when it comes to studying effectively. It involves being fully present and engaged in the learning process, actively absorbing and comprehending the material at hand. By cultivating consciousness during studying, individuals can enhance their focus, attention, and overall retention of information. It allows for a deeper level of understanding, as one becomes attuned to the nuances and connections within the subject matter. Furthermore, consciousness helps individuals identify their own learning styles and adapt their study methods accordingly, maximizing their efficiency and productivity. By being conscious of their progress, strengths, and weaknesses, students can also make informed decisions on how to allocate their time and resources effectively. In essence, consciousness while studying empowers learners to take ownership of their education and facilitates a more meaningful and impactful learning experience.
Hydrogen
Hydrogen serves as an excellent medium for energy storage, transportation, and conversion, aiming to develop clean and emission-free energy concepts. Various sources, using different technologies, can be utilized to produce hydrogen. Hydrogen can be derived from compounds such as fossil fuels, biomass, and water. Thermochemical processes allow for hydrogen production from biomass and fossil fuels like coal, petroleum, and natural gas.
Hydrogen, acquired through these methods, can be stored as an energy carrier in gas, liquid, or solid metal forms. High pressure is necessary to store hydrogen as a gas, while cryogenic systems are required for storing it as a liquid. Hydrogen can also be stored in solid form.
Design & Optimization of Pressurized Hydrogen Storage
Optimizing a 1-liter hydrogen storage design within a limited budget requires careful consideration of various factors. Here are a few suggestions to help you achieve a design concept and optimization for storing hydrogen at 8 bar pressure with a capacity of 1 liter and a maximum budget of Rp500,000.
1. Material Selection
Choose lightweight materials that can withstand high-pressure conditions while remaining cost-effective. Composite materials, such as carbon fiber reinforced polymers (CFRP) or aluminum alloys, could be potential options.
2. Tank Design
Opt for a cylindrical shape with reinforced walls to minimize material usage while maintaining structural integrity. Conduct thorough stress analysis to ensure the tank can withstand the desired pressure of 8 bar.
3. Safety Measures
Implement necessary safety features, such as pressure relief valves and rupture discs, to prevent over-pressurization and ensure the integrity of the tank.
4. Insulation
To reduce heat transfer and minimize energy loss, consider incorporating efficient insulation materials, such as foams or vacuum insulation panels.
5. Regulators and Valves
Include efficient pressure regulators and valves to control the release of hydrogen and maintain a stable pressure within the storage system.
6. Cost Analysis
Evaluate different suppliers, materials, and manufacturing methods to find the most cost-effective options within your budget. Consider both initial costs and long-term maintenance expenses.
7. Testing and Certification
Ensure the hydrogen storage design complies with industry standards and safety regulations. Perform thorough testing, including burst tests and leak checks, to verify the integrity of the storage system.
Conducting a comprehensive risk assessment is an essential part of designing any hydrogen storage system. Hydrogen is a highly flammable gas, and ensuring the safety of the storage system is of paramount importance. Here are some key aspects to consider during the risk assessment:
1. Fire and Explosion Hazards:
Hydrogen is highly flammable and can form explosive mixtures with air. Assess the potential for ignition sources, such as electrical equipment, static electricity, or open flames, and implement appropriate safety measures to mitigate the risks.
2. Ventilation:
Adequate ventilation is crucial to prevent the accumulation of hydrogen gas, which can create an explosive atmosphere. Ensure that the storage system is properly ventilated to disperse any leaked hydrogen gas.
3. Pressure Management:
Hydrogen storage systems operate under pressure. Assess the risks associated with over-pressurization or sudden pressure releases, and include pressure relief valves, burst discs, or other pressure safety devices to prevent catastrophic failures.
4. Material Compatibility:
Evaluate the compatibility of storage materials (e.g., cylinders, seals, valves) with hydrogen gas. Hydrogen can cause embrittlement in certain metals, potentially leading to failures. Use materials that are specifically designed for hydrogen storage or have been certified for compatibility.
5. Leak Detection and Monitoring:
Implement systems for detecting and monitoring hydrogen leaks. This can include gas sensors, hydrogen detectors, or leak detection solutions. Early detection of leaks allows for timely intervention and prevents the build-up of hydrogen gas.
6. Training and Safety Procedures:
Provide adequate training to personnel involved in handling, storing, and maintaining the hydrogen storage system. Develop clear safety procedures, emergency response plans, and protocols for handling hydrogen-related incidents.
7. Compliance with Regulations:
Ensure compliance with relevant safety regulations, codes, and standards for hydrogen storage systems. Familiarize yourself with local, national, and international guidelines to ensure the system meets all necessary requirements.
Material of The Tank
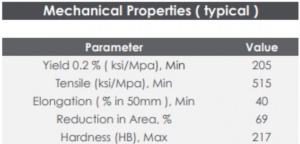
The material that will be used in the construction of this hydrogen tank is AISI 316 austenitic stainless steel. Austenitic stainless steel is also one of the primary choices for manufacturers of industrial hydrogen storage. This indicates that austenitic stainless steel has been tested for availability, durability, strength, machinability, compatibility with hydrogen gas (non-reactive with hydrogen), and so on.
Material Strength Constraints Analysis
Ensuring the durability of the container material and its ability to withstand the pressure exerted on its walls are of utmost importance in the case of a pressurized container. The 1-liter hydrogen tank, with a maximum pressure limit of 8 bar, has specific requirements that need to be met. In a cylindrical component with thin walls, there are two primary types of stress: circumferential (hoop) stress and longitudinal stress. While there is also radial stress, it can be disregarded due to the significantly larger radius compared to the wall thickness.
The provided formulas above can be utilized for calculating the hoop stress and longitudinal stress.
To ensure structural integrity, the plate thickness for the tank should be at least one-fifth of the tank radius. According to ASME BPV Code Section VIII D.1, the minimum plate thickness for the tank is specified as 1/16 inch or 1.59 mm, without considering factors like corrosion, material properties, or dimensional considerations. For the purpose of this calculation, we will iterate through a range of tank radii, starting from a minimum radius of 2.7 mm up to 11.05 mm, with an increment of 1 mm for each iteration.
Iteration Process
r = 5.42e-2
p = 800000
t = 2.9e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9:
breakResults
for thickness 0.004099999999999999 hoop stress = 10770731.707317077 Pa
for thickness 0.004199999999999999 hoop stress = 10514285.714285716 Pa
for thickness 0.004299999999999999 hoop stress = 10269767.441860467 Pa
for thickness 0.004399999999999999 hoop stress = 10036363.636363639 Pa
for thickness 0.0045 hoop stress = 9813333.333333334 Pa
for thickness 0.0046 hoop stress = 9600000.0 Pa
for thickness 0.0047 hoop stress = 9395744.680851063 Pa
for thickness 0.0048000000000000004 hoop stress = 9200000.0 Pa
for thickness 0.004900000000000001 hoop stress = 9012244.897959182 Pa
for thickness 0.005000000000000001 hoop stress = 8831999.999999998 Pa
for thickness 0.005100000000000001 hoop stress = 8658823.529411763 Pa
for thickness 0.0052000000000000015 hoop stress = 8492307.69230769 Pa
for thickness 0.005300000000000002 hoop stress = 8332075.47169811 Pa
for thickness 0.005400000000000002 hoop stress = 8177777.777777774 Pa
for thickness 0.005500000000000002 hoop stress = 8029090.909090905 Pa
for thickness 0.0056000000000000025 hoop stress = 7885714.285714282 Pa
for thickness 0.005700000000000003 hoop stress = 7747368.421052628 Pa
for thickness 0.005800000000000003 hoop stress = 7613793.103448272 Pa
for thickness 0.005900000000000003 hoop stress = 7484745.76271186 Pa
for thickness 0.006000000000000004 hoop stress = 7359999.999999995 Pa
for thickness 0.006100000000000004 hoop stress = 7239344.262295078 Pa
for thickness 0.006200000000000004 hoop stress = 7122580.645161286 Pa
for thickness 0.006300000000000004 hoop stress = 7009523.809523805 Pa
for thickness 0.006400000000000005 hoop stress = 6899999.999999995 Pa
for thickness 0.006500000000000005 hoop stress = 6793846.153846148 Pa
for thickness 0.006600000000000005 hoop stress = 6690909.090909085 Pa
for thickness 0.006700000000000005 hoop stress = 6591044.776119398 Pa
for thickness 0.006800000000000006 hoop stress = 6494117.6470588185 Pa
for thickness 0.006900000000000006 hoop stress = 6399999.999999994 Pa
for thickness 0.007000000000000006 hoop stress = 6308571.428571423 PaThe given code computes the hoop stress using different thickness values ranging from 2.9 mm to 12 mm. It includes a condition that terminates the iteration if the total hoop stress surpasses the yield strength of AISI 316 stainless steel. The results demonstrate that all thickness values within the range of 2.9 mm to 12 mm, incremented by 1 mm, comply with the yield strength constraint. The calculations from the code reveal that the hoop stress remains well below the yield strength of 205 MPa, indicating a significant safety margin.
Geometry Constraints Analysis
The code above optimizes the dimensions (radius and height) of a cylindrical structure to minimize its surface area while satisfying a volume constraint. This can be useful in various engineering and design applications where minimizing surface area or optimizing geometrical parameters is desired.
import numpy as np
from scipy.optimize import minimize
def calculate_surface_area(x):
radius, height = x
surface_area = 2 * np.pi * radius * (radius + height)
return surface_area
def calculate_volume(x):
radius, height = x
volume = np.pi * radius**2 * height
return volume
def optimize_cylinder():
initial_guess = [1.0, 10.0]
bounds = [(0, None), (0, None)]
constraint = {'type': 'eq', 'fun': lambda x: calculate_volume(x) - 1050}
result = minimize(calculate_surface_area, initial_guess, method='SLSQP', bounds=bounds, constraints=constraint)
print("Optimization Results:")
print("Radius: {:.2f} cm".format(result.x[0]))
print("Height: {:.2f} cm".format(result.x[1]))
print("Surface Area: {:.2f} cm^2".format(result.fun))
optimize_cylinder()Based on the provided code, the following information can be obtained: the code Optimization Results: Radius: 5.51 cm Height: 11.02 cm Surface Area: 571.88 cm^2
Cost Constraints Analysis
To optimize the storage of hydrogen at 8 bar pressure with a 1-liter capacity and a maximum budget of Rp500,000, we can approach it as an optimization problem by using a phyton's code below:
from scipy.optimize import minimize
# Price and capacity
price_per_unit = 100000 # Price per unit of hydrogen storage
capacity_per_unit = 1 # Capacity of hydrogen storage per unit
# Maximum budget
max_budget = 500000
# Objective function
def objective_function(x):
return -x * capacity_per_unit
# Constraint function
def budget_constraint(purchase_amount):
return max_budget - (price_per_unit * purchase_amount)
budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint}
# Initial value
x0 = 0
# Bounds
bounds = [(0, None)]
# Solve the optimization problem
solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq])
# Print the results
print("Status:", "Optimal" if solution.success else "No solution found")
print("Number of hydrogen storage units to be purchased:", solution.x[0])
print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters")
print("Total cost:", solution.x[0] * price_per_unit, "Rupiah")This code will calculate the optimal number of hydrogen storage units to be purchased within the given budget, considering a storage capacity of 1 liter per unit and a price per unit of Rp100,000. The optimization problem is solved using the SLSQP method, and the results are printed, including the status, the number of units to be purchased, the total storage capacity, and the total cost in Rupiah.
From the code above, we obtain the following information:
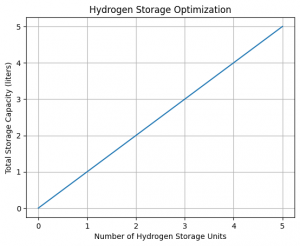
Status: Optimal Number of hydrogen storage units to be purchased: 5.0 Total storage capacity: 5.0 liters Total cost: 500000.0 Rupiah
We can also use phyton to show graphic between total storage and hydrogen storage optimazation:
import matplotlib.pyplot as plt
# Price and capacity
unit_price = 100000 # Price per unit of hydrogen storage
unit_capacity = 1 # Capacity per unit of hydrogen storage
# Maximum budget
max_budget = 500000
# Initialize variables
best_unit_count = 0
best_total_capacity = 0
best_total_cost = 0
# Initialize lists for the graph
unit_count_list = []
total_capacity_list = []
# Iteration to find the optimal solution
for unit_count in range(int(max_budget / unit_price) + 1):
total_capacity = unit_count * unit_capacity
total_cost = unit_count * unit_price
if total_capacity > best_total_capacity and total_cost <= max_budget:
best_unit_count = unit_count
best_total_capacity = total_capacity
best_total_cost = total_cost
# Add data to the lists for the graph
unit_count_list.append(unit_count)
total_capacity_list.append(total_capacity)
# Display the results
print("Number of hydrogen storage units to be purchased:", best_unit_count)
print("Total storage capacity:", best_total_capacity, "liters")
print("Total cost:", best_total_cost, "Rupiah")
# Display the graph
plt.plot(unit_count_list, total_capacity_list)
plt.xlabel('Number of Hydrogen Storage Units')
plt.ylabel('Total Storage Capacity (liters)')
plt.title('Hydrogen Storage Optimization')
plt.grid(True)
plt.show()This code calculates the optimal number of hydrogen storage units to be purchased based on the given price per unit, capacity per unit, and maximum budget. It iterates through the possible number of units within the budget and calculates the corresponding total storage capacity and cost. It keeps track of the best solution with the highest total capacity while staying within the budget. The results are then printed, including the number of units, total capacity, and total cost. Additionally, the code plots a graph showing the relationship between the number of units and the total storage capacity.
Final Remarks
It is highly recommended to involve experienced professionals with expertise in hydrogen safety and risk assessment during the design and implementation of a hydrogen storage system. They can provide valuable insights and help identify and mitigate potential risks associated with the specific storage design and application. Remember that optimizing a hydrogen storage design requires a multidisciplinary approach involving mechanical engineering, materials science, and safety considerations. It's advisable to consult with experts in the field and conduct a detailed feasibility study to achieve the best results within your budget.