Difference between revisions of "Momen inersia dengan integrasi"
| (13 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
r adalah jarak tegak lurus terhadap sumbu rotasi. | r adalah jarak tegak lurus terhadap sumbu rotasi. | ||
| − | Analisis | + | '''Analisis''' |
Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh | Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh | ||
| Line 22: | Line 22: | ||
Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:[[File:Inersia_aditif.png]] | Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:[[File:Inersia_aditif.png]] | ||
| − | Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut: | + | Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:[[File:Inersia_pejal.png]] |
di mana | di mana | ||
| + | |||
V adalah volume yang ditempati objek | V adalah volume yang ditempati objek | ||
| + | |||
ρ adalah fungsi kerapatan spasial objek | ρ adalah fungsi kerapatan spasial objek | ||
| + | |||
r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut. | r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut. | ||
| − | Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk: | + | Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:[[File:Inersia_dimensi.png]] |
di mana | di mana | ||
| + | |||
M adalah massa | M adalah massa | ||
| − | R adalah jari-jari objek dari pusat massa | + | |
| + | R adalah jari-jari objek dari pusat massa | ||
| + | |||
k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait. | k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait. | ||
| − | Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh: | + | Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. |
| + | Contoh: | ||
k = 1, cincin tipis atau silinder tipis di sekeliling pusat | k = 1, cincin tipis atau silinder tipis di sekeliling pusat | ||
| + | |||
k = 2/5, bola pejal di sekitar pusat | k = 2/5, bola pejal di sekitar pusat | ||
| + | |||
k = 1/2, silinder atau piringan pejal di sekitar pusat. | k = 1/2, silinder atau piringan pejal di sekitar pusat. | ||
| Line 49: | Line 58: | ||
𝐷= 𝑥, 𝑐≤𝑦≤𝑑, 𝑦 ≤𝑥≤𝜓 𝑦 , dimana 𝜙 dan 𝜓 kontinu pada [𝑐,𝑑] ……(gambar.2) | 𝐷= 𝑥, 𝑐≤𝑦≤𝑑, 𝑦 ≤𝑥≤𝜓 𝑦 , dimana 𝜙 dan 𝜓 kontinu pada [𝑐,𝑑] ……(gambar.2) | ||
Rapat massa di setiap titik pada keping (𝑥,) pada keping 𝐷 adalah (𝑥,𝑦) di mana 𝛿 merupakan fungsi kontinu pada D. | Rapat massa di setiap titik pada keping (𝑥,) pada keping 𝐷 adalah (𝑥,𝑦) di mana 𝛿 merupakan fungsi kontinu pada D. | ||
| − | Kedua keping datar tersebut diperlihatkan pada gambar | + | Kedua keping datar tersebut diperlihatkan pada gambar |
| + | |||
| + | [[File:Inersia_2keping.png]] | ||
| − | |||
Rumus Massa, Momen Terhadap Sumbu Koordinat dan Pusat Massa Keping D | Rumus Massa, Momen Terhadap Sumbu Koordinat dan Pusat Massa Keping D | ||
Buatlah jaring Δ untuk keping 𝐷 yang terdiri dari 𝑛 buah persegi panjang yang semuanya beririsan dengan daerah 𝐷 seperti diperlihatkan pada gambar dibawah ini | Buatlah jaring Δ untuk keping 𝐷 yang terdiri dari 𝑛 buah persegi panjang yang semuanya beririsan dengan daerah 𝐷 seperti diperlihatkan pada gambar dibawah ini | ||
| + | |||
| + | [[File:Gambar_inersia3.png]] | ||
Gambar 3 | Gambar 3 | ||
| + | |||
| + | [[File:Gambar_inersia4.png]] | ||
Gambar 4 | Gambar 4 | ||
| Line 65: | Line 79: | ||
Definisi Massa dan Pusat Massa Suatu Keping Datar dalam Koordinat Kartesius | Definisi Massa dan Pusat Massa Suatu Keping Datar dalam Koordinat Kartesius | ||
Massa keping 𝐷 didefinisikan sebagai limit dari jumlah Riemann ini, yaitu | Massa keping 𝐷 didefinisikan sebagai limit dari jumlah Riemann ini, yaitu | ||
| + | |||
| + | [[File:Inersia_kartesius.png]] | ||
| + | Momen Massa Keping D Terhadap Sumbu X | ||
| − | + | Momen massa keping terhadap sumbu X didefinisikan sebagai limit jumlah Riemann dari momen massa sistem n partikel terhadap sumbu X, yaitu | |
| − | + | [[File:Inersia_x.png]] | |
| − | Momen massa keping terhadap sumbu X didefinisikan sebagai limit jumlah Riemann dari momen massa sistem n partikel terhadap sumbu X, yaitu | ||
Momen Massa Keping D Terhadap Sumbu Y | Momen Massa Keping D Terhadap Sumbu Y | ||
| + | |||
Momen massa keping terhadap sumbu Y didefinisikan sebagai limit jumlah Riemann dari momen massa sistem n partikel terhadap sumbu Y, yaitu | Momen massa keping terhadap sumbu Y didefinisikan sebagai limit jumlah Riemann dari momen massa sistem n partikel terhadap sumbu Y, yaitu | ||
| − | + | [[File:Inersia_y.png]] | |
Pusat Massa Keping D | Pusat Massa Keping D | ||
| + | |||
Pusat massa keping adalah titik (X ,Y ), dimana | Pusat massa keping adalah titik (X ,Y ), dimana | ||
| − | + | [[File:Pusat_masa.png]] | |
C. STUDI KASUS | C. STUDI KASUS | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Diketahui suatu keping 𝐷 yang dibatasi oleh suatu grafik fungsi 𝑦 = 𝑥1/2, grafik 𝑥=9 dan sumbu 𝑋. Jika rapat massa di setiap titik (𝑥,) pada 𝐷 adalah 𝛿 𝑥, =1+𝑥𝑦, tentukan momen inersia dari keping 𝐷 terhadap sumbu 𝑋, sumbu 𝑦, dan titik O. Kemudian tentukan juga jari-jari kitaran keping 𝐷 terhadap sumbu 𝑌. | ||
D. PENYELESAIAN SECARA MANUAL | D. PENYELESAIAN SECARA MANUAL | ||
| − | + | [[File:Fungsi_luas.png]] | |
Gambar 5. Luasan Benda dengan fungsi 𝑦 = 𝑥1/2 | Gambar 5. Luasan Benda dengan fungsi 𝑦 = 𝑥1/2 | ||
| + | |||
Apabila daerah D dipartisi terhadap sumbu X, sehingga daerah integrasi | Apabila daerah D dipartisi terhadap sumbu X, sehingga daerah integrasi | ||
| Line 105: | Line 118: | ||
= ∫_0^9▒〖1/3 x^(3/2)+1/4 x^2 〗 | = ∫_0^9▒〖1/3 x^(3/2)+1/4 x^2 〗 | ||
| − | + | Momen inersia keping 𝑫 terhadap sumbu X | |
I_y=∫▒∫_D▒〖x^2 δ(x,y)〗 dA= ∫_0^9▒∫_0^(x^(1/2))▒〖x^2 (1+xy)dy dx〗 | I_y=∫▒∫_D▒〖x^2 δ(x,y)〗 dA= ∫_0^9▒∫_0^(x^(1/2))▒〖x^2 (1+xy)dy dx〗 | ||
| Line 113: | Line 126: | ||
Jadi Momen Inersia total = Ix+Iy | Jadi Momen Inersia total = Ix+Iy | ||
| − | |||
| − | |||
| − | |||
| Line 141: | Line 151: | ||
Hasil running simulasi denganEES disajikan pada gambar berikut: | Hasil running simulasi denganEES disajikan pada gambar berikut: | ||
| + | |||
| + | [[File:Input_ees.png]] | ||
Gambar 6. Input pada equtions window | Gambar 6. Input pada equtions window | ||
| − | + | ||
| + | [[File:solusi_ees.png]] | ||
Gambar 7. Hasil simulasi pada solution window | Gambar 7. Hasil simulasi pada solution window | ||
Latest revision as of 03:20, 14 April 2019
Oleh : Andi Cahyo Prasetyo
NPM : 1806244332
A. PENDAHULUAN
Momen inersia adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi daripada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain.
Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:
I=∫(r^2) dm di mana : m adalah massa r adalah jarak tegak lurus terhadap sumbu rotasi.
Analisis
Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh
![]()
Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik: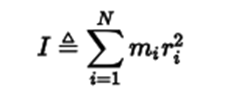
Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut: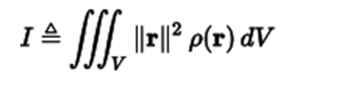
di mana
V adalah volume yang ditempati objek
ρ adalah fungsi kerapatan spasial objek
r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut.
Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk: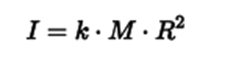
di mana
M adalah massa
R adalah jari-jari objek dari pusat massa
k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait.
Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh: k = 1, cincin tipis atau silinder tipis di sekeliling pusat
k = 2/5, bola pejal di sekitar pusat
k = 1/2, silinder atau piringan pejal di sekitar pusat.
B. MASSA DAN PUSAT MASSA SUATU KEPING DATAR DALAM SISTEM KOORDINAT KARTESIUS
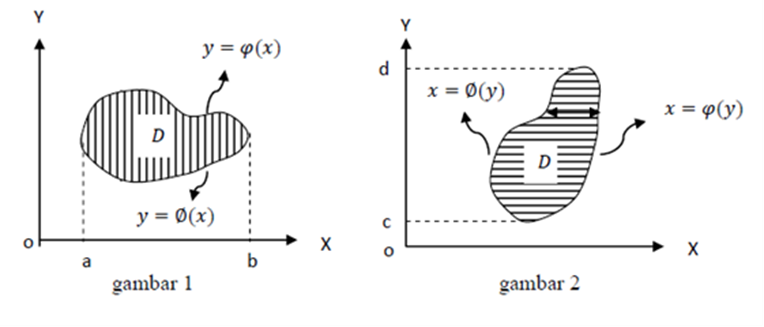
Menentukan massa, pusat massa, dan momen inersia suatu keping datar dengan rapat masa yang tak homogen. Rapat massa keeping di setiap titiknya bergantung pada letak titik tersebut, yaitu merupakan fungsi dua peubah. Kerapatan massa keping datar yaitu besar massa per satuan luas, dapat dinyatakan sebagai fungsi dalam 𝑥 dan 𝑦 biasanya disimbolkan dengan (𝑥,). Contoh : sebuah keping datar dengan rapat massa tak homogen yang berbentuk daerah 𝐷. 𝐷= 𝑥, 𝑎≤𝑥≤𝑏, 𝑥 ≤𝑦≤𝜓 𝑥 , dimana 𝜙 dan 𝜓 kontinu pada 𝑎,𝑏 ……(gambar.1) atau 𝐷= 𝑥, 𝑐≤𝑦≤𝑑, 𝑦 ≤𝑥≤𝜓 𝑦 , dimana 𝜙 dan 𝜓 kontinu pada [𝑐,𝑑] ……(gambar.2) Rapat massa di setiap titik pada keping (𝑥,) pada keping 𝐷 adalah (𝑥,𝑦) di mana 𝛿 merupakan fungsi kontinu pada D. Kedua keping datar tersebut diperlihatkan pada gambar
Rumus Massa, Momen Terhadap Sumbu Koordinat dan Pusat Massa Keping D
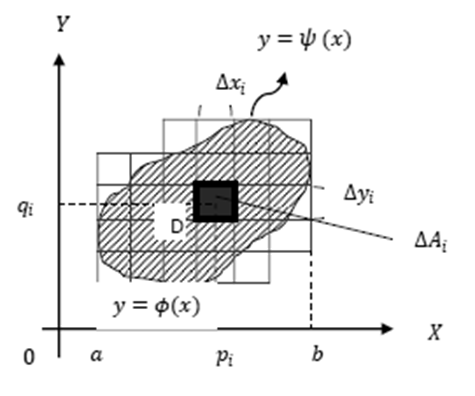
Buatlah jaring Δ untuk keping 𝐷 yang terdiri dari 𝑛 buah persegi panjang yang semuanya beririsan dengan daerah 𝐷 seperti diperlihatkan pada gambar dibawah ini
Gambar 3
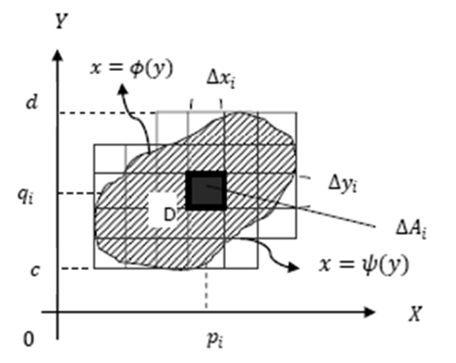
Gambar 4
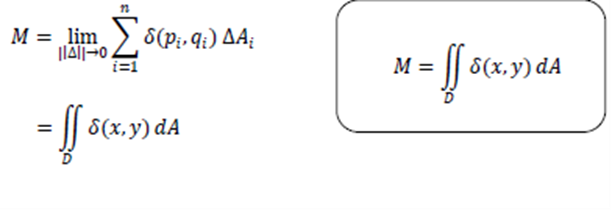
Komponen jaring yang ke-i adalah ∆𝐴𝑖= ∆𝑥𝑖∆𝑦 Ukuran jaring ke-i didefinisikan sebagai persegi panjang diagonal terbesar dari persegi panjang Δ𝐴𝑖 ditulis dengan lambang |𝐴|. Pilihlah titik (𝑝𝑖,) pada komponen jaring ke-i. Keping 𝐷 dapat dipandang sebagai sistem 𝑛 partikel yang terletak di titik 𝑝𝑖, ,𝑖 =1,2,…,𝑛. Jika massa partikel ke-i adalah Δ𝑚𝑖, maka ∆𝑚 = (𝑝𝑖, 𝑞𝑖)∆𝐴𝑖
Definisi Massa dan Pusat Massa Suatu Keping Datar dalam Koordinat Kartesius Massa keping 𝐷 didefinisikan sebagai limit dari jumlah Riemann ini, yaitu
Momen Massa Keping D Terhadap Sumbu X
Momen massa keping terhadap sumbu X didefinisikan sebagai limit jumlah Riemann dari momen massa sistem n partikel terhadap sumbu X, yaitu
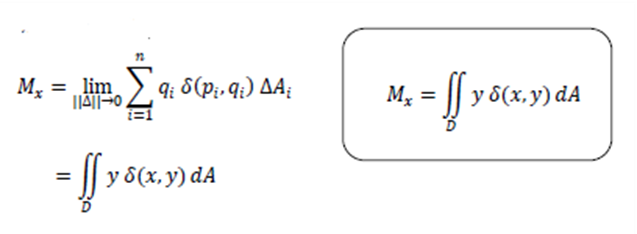
Momen Massa Keping D Terhadap Sumbu Y
Momen massa keping terhadap sumbu Y didefinisikan sebagai limit jumlah Riemann dari momen massa sistem n partikel terhadap sumbu Y, yaitu
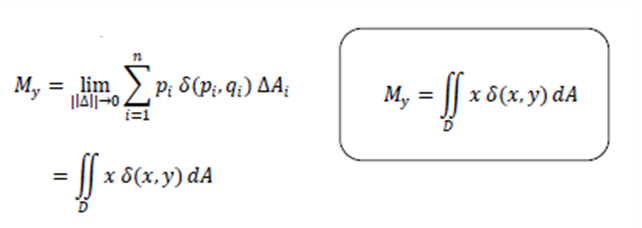
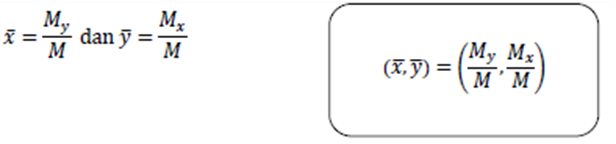
Pusat Massa Keping D
Pusat massa keping adalah titik (X ,Y ), dimana
C. STUDI KASUS
Diketahui suatu keping 𝐷 yang dibatasi oleh suatu grafik fungsi 𝑦 = 𝑥1/2, grafik 𝑥=9 dan sumbu 𝑋. Jika rapat massa di setiap titik (𝑥,) pada 𝐷 adalah 𝛿 𝑥, =1+𝑥𝑦, tentukan momen inersia dari keping 𝐷 terhadap sumbu 𝑋, sumbu 𝑦, dan titik O. Kemudian tentukan juga jari-jari kitaran keping 𝐷 terhadap sumbu 𝑌.
D. PENYELESAIAN SECARA MANUAL
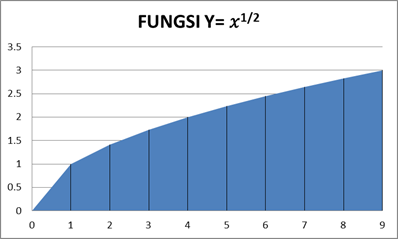 Gambar 5. Luasan Benda dengan fungsi 𝑦 = 𝑥1/2
Gambar 5. Luasan Benda dengan fungsi 𝑦 = 𝑥1/2
Apabila daerah D dipartisi terhadap sumbu X, sehingga daerah integrasi
D = { (x,y)│0 ≤ x ≤ 9, dan 0 ≤y ≤ x1/2
Momen inersia keping 𝑫 terhadap sumbu y I_x=∫▒∫_D▒〖y^2 δ(x,y)〗 dA= ∫_0^9▒∫_0^(x^(1/2))▒〖y^2 (1+xy)dy dx〗
= ∫_0^9▒∫_0^(x^(1/2))▒〖y^2 (1+xy^3 )dy dx〗= ∫_0^9▒〖[1/3 y^3+1/4 〖xy〗^3 ] (y=x^(1/2))¦(y=0)〗 dx = ∫_0^9▒〖1/3 x^(3/2)+1/4 x^2 〗
Momen inersia keping 𝑫 terhadap sumbu X
I_y=∫▒∫_D▒〖x^2 δ(x,y)〗 dA= ∫_0^9▒∫_0^(x^(1/2))▒〖x^2 (1+xy)dy dx〗
= ∫_0^9▒∫_0^(x^(1/2))▒〖x^2 (1+x^3 y)dy dx〗= ∫_0^9▒〖[x^2 y+1/2 x^3 y^2 ] x^(1/2)¦0〗 dx = ∫_0^9▒〖x^(5/2)+1/2 x^4 〗
Jadi Momen Inersia total = Ix+Iy
E. PENYELESAIAN DENGAN EES ENGINEERING SOLVER
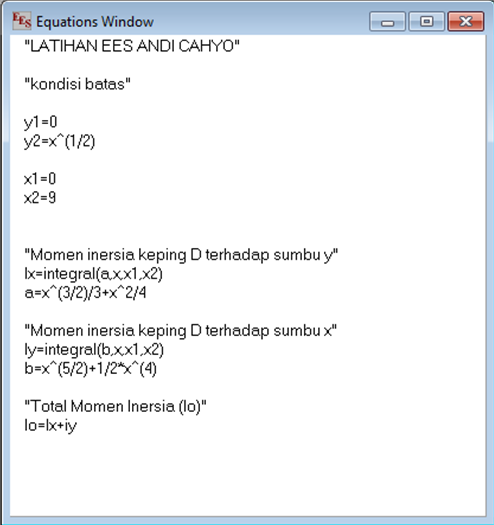
Input Coding adalah sebagai berikut: "LATIHAN EES ANDI CAHYO" "kondisi batas" y1=0 y2=x^(1/2)
x1=0 x2=9
"Momen inersia keping D terhadap sumbu y" Ix=integral(a,x,x1,x2) a=x^(3/2)/3+x^2/4
"Momen inersia keping D terhadap sumbu x" Iy=integral(b,x,x1,x2) b=x^(5/2)+1/2*x^(4)
"Total Momen Inersia (Io)" Io=Ix+iy
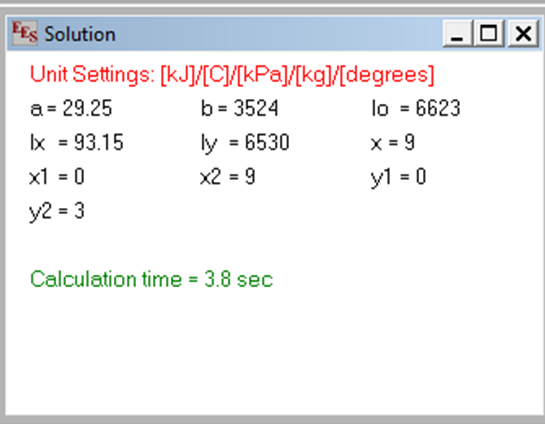
Hasil running simulasi denganEES disajikan pada gambar berikut:
Gambar 6. Input pada equtions window
Gambar 7. Hasil simulasi pada solution window