Difference between revisions of "Menghitung momen inersia penampang"

From ccitonlinewiki
Jump to: navigation, search
(Created page with "TUGAS KOMPUTASI TEKNIK DI SUSUN OLEH ARIA WIRA YUDA NPM. 1806155270 PROGRAM STUDI MAGISTER TEKNIK MESIN FAKULTAS TEKNIK UNIVERSITAS INDONESIA DEPOK Momen Inersia...")
 
 
(3 intermediate revisions by the same user not shown)
Line 35: Line 35:
  
 
[[File:momenme.jpg]]
 
[[File:momenme.jpg]]
 +
 +
Persegi di atas berukuran b x h, dengan sumbu x terletak pada sumbu netral atau garis berat. Berdasarkan formula dasar Ix = ∫ y2 dA ,
 +
 +
maka kita harus meninjau sebuah elemen kecil  . Elemen ini mempunyai ukuran dx dan dy. Sehingga bisa kita tuliskan
 +
 +
dA = dx . dy
 +
 +
Jika kita kumpulkan semua elemen dA yang mempunyai nilai y yang sama, maka elemen dA, kini menjadi:
 +
 +
dA = b . dy, sehingga  Ix= ∫ by2 dy
 +
 +
Karena b bernilai konstan untuk setiap nilai y, kita keluarkan saja b dari kurungan tersebut,
 +
 +
Ix= b ∫ y2 dy
 +
 +
Pertanyaannya adalah, buatlah program ESS untuk menghitung inersia sembarang profil.
 +
 +
Untuk menjawab ini, penulis terlebih dahulu menetapkan asumsi awal, antara lain:
 +
 +
b : konstan (diambil nilai 1)
 +
 +
y_low : batas bawah integral arah y mulai dari 0 sampai -20, dengan interval -0,1 dimasukkan dalam tabel"
 +
 +
y_up : batas atas integral arah y mulai dari 0 sampai 20, dengan interval 0,1 dimasukkan dalam tabel"
 +
 +
Ix : momen inersia terhadap sumbu x, dimana Ix= b ∫ y2 dy
 +
 +
Hasil perhitungan akan ditampilkan dalam bentuk tabel, dimana untuk mengatur “dy” pengguna dapat merubahnya di window TABLE, lalu ALTER PARAMETRIC TABLE VALUES dan menghasilkan nilai momen inersia sesuai dengan nilai “dy”.
 +
 +
Algoritma
 +
 +
Untuk memudahkan perhitungan, terlebih dilakukan dengan membuat algoritma.
 +
 +
[[File:algome.jpg]]
 +
 +
Coding ESS:
 +
 +
[[File:codeme.jpg]]
 +
 +
Menetapkan parameter tabel
 +
 +
[[File:newme.jpg]]
 +
 +
[[File:new1me.jpg]]
 +
 +
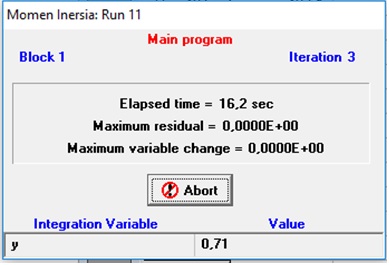
Run Program:
 +
 +
[[File:runme.jpg]]
 +
 +
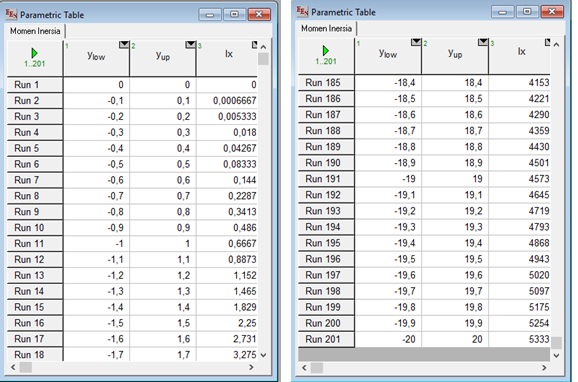
Hasilnya
 +
 +
[[File:hasilme.jpg]]
 +
 +
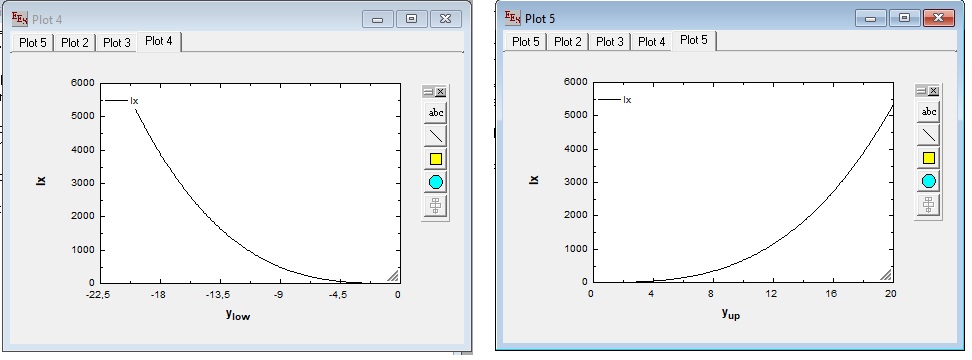
[[File:plotme.jpg]]
 +
 +
selesai

Latest revision as of 01:46, 1 April 2019

TUGAS

KOMPUTASI TEKNIK

DI SUSUN OLEH

ARIA WIRA YUDA

NPM. 1806155270


PROGRAM STUDI MAGISTER TEKNIK MESIN

FAKULTAS TEKNIK

UNIVERSITAS INDONESIA

DEPOK

Momen Inersia Penampang

Pendahuluan

Momen inersia penampang adalah salah satu parameter geometri yang sangat penting dalam analisis struktur. Keberadaanya sangat penting dalam perancangan suatu komponen, benda, maupun bangunan atau struktur.

Momen Inersia linier yaitu momen inersia terhadap suatu garis lurus atau sumbu. Jika terhadap sumbu x adalah Ix dan jika terhadap sumbu y adalah Iy

Momen inersia terhadap sumbu x adalah: Ix= ∫ y2 dA

Momen inersia terhadap sumbu y adalah: Iy = ∫ x2 dA

Dari formula dasar itulah kita bisa menurunkan formula momen inersia untuk bentuk geometri apapun.

Bentuk Persegi

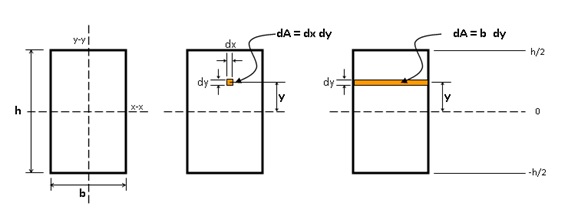
Momenme.jpg

Persegi di atas berukuran b x h, dengan sumbu x terletak pada sumbu netral atau garis berat. Berdasarkan formula dasar Ix = ∫ y2 dA ,

maka kita harus meninjau sebuah elemen kecil . Elemen ini mempunyai ukuran dx dan dy. Sehingga bisa kita tuliskan

dA = dx . dy

Jika kita kumpulkan semua elemen dA yang mempunyai nilai y yang sama, maka elemen dA, kini menjadi:

dA = b . dy, sehingga Ix= ∫ by2 dy

Karena b bernilai konstan untuk setiap nilai y, kita keluarkan saja b dari kurungan tersebut,

Ix= b ∫ y2 dy

Pertanyaannya adalah, buatlah program ESS untuk menghitung inersia sembarang profil.

Untuk menjawab ini, penulis terlebih dahulu menetapkan asumsi awal, antara lain:

b : konstan (diambil nilai 1)

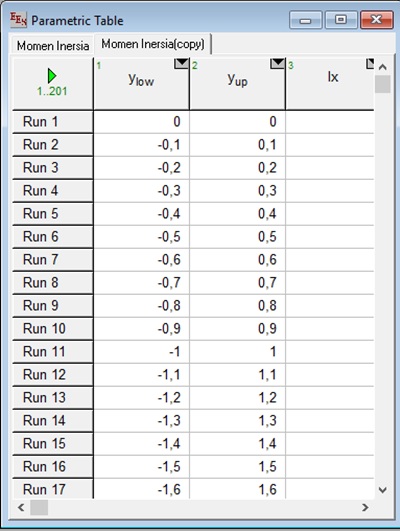
y_low : batas bawah integral arah y mulai dari 0 sampai -20, dengan interval -0,1 dimasukkan dalam tabel"

y_up : batas atas integral arah y mulai dari 0 sampai 20, dengan interval 0,1 dimasukkan dalam tabel"

Ix : momen inersia terhadap sumbu x, dimana Ix= b ∫ y2 dy

Hasil perhitungan akan ditampilkan dalam bentuk tabel, dimana untuk mengatur “dy” pengguna dapat merubahnya di window TABLE, lalu ALTER PARAMETRIC TABLE VALUES dan menghasilkan nilai momen inersia sesuai dengan nilai “dy”.

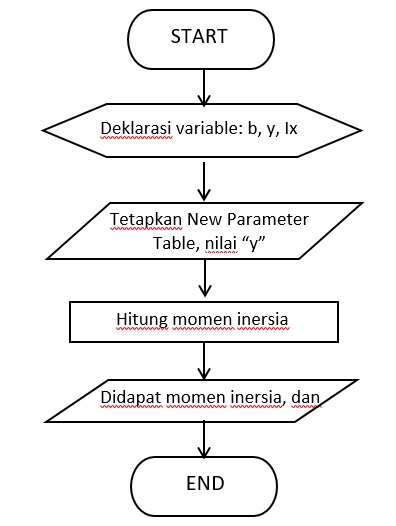
Algoritma

Untuk memudahkan perhitungan, terlebih dilakukan dengan membuat algoritma.

Algome.jpg

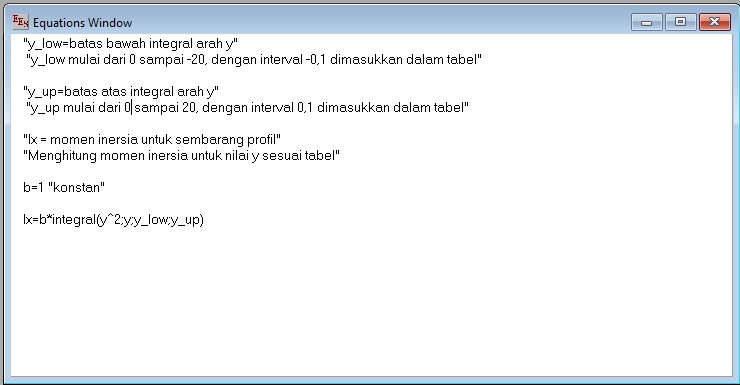
Coding ESS:

Codeme.jpg

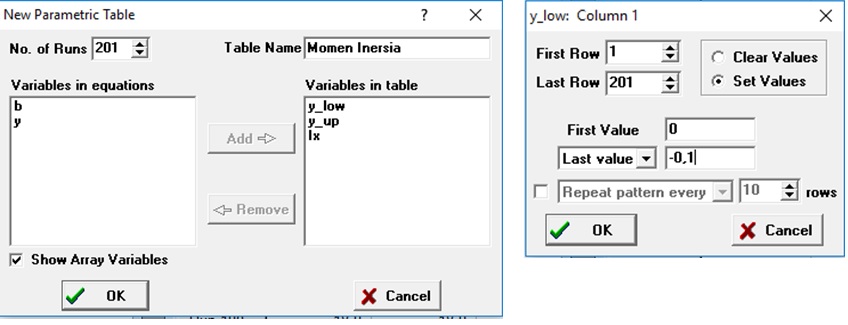
Menetapkan parameter tabel

Newme.jpg

New1me.jpg

Run Program:

Runme.jpg

Hasilnya

Hasilme.jpg

Plotme.jpg

selesai

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Menghitung_momen_inersia_penampang&oldid=5754"