Difference between revisions of "Muhammad Hasfi Rizki Nur"
(→Tugas Besar (23 Desember 2020)) |
(→Ujian Akhir Semester (13 Januari 2021)) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 975: | Line 975: | ||
'''Kesimpulan''' | '''Kesimpulan''' | ||
*Nilai luas area penampang optimum untuk material SS304 adalah 283,81 mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 6m dan tebal 60mm. | *Nilai luas area penampang optimum untuk material SS304 adalah 283,81 mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 6m dan tebal 60mm. | ||
| + | |||
*Material optimum yang dapat digunakan untuk luas penampang 270mm^2 adalah material dengan nilai elastisitas 15324000000000 N/m^2 atau material yang paling mendekati adalah SS316L. | *Material optimum yang dapat digunakan untuk luas penampang 270mm^2 adalah material dengan nilai elastisitas 15324000000000 N/m^2 atau material yang paling mendekati adalah SS316L. | ||
| + | |||
| + | == Ujian Akhir Semester (13 Januari 2021) == | ||
| + | |||
| + | |||
| + | Berikut jawaban Ujian Akhir Semester (UAS) mata kuliah Metode Numerik yang saya kerjakan pada tanggal 13 januari 2021. | ||
| + | |||
| + | |||
| + | [[File:hasfiuas1.jpg|600px|centre]] | ||
| + | [[File:hasfiuas2.jpg|600px|centre]] | ||
| + | [[File:hasfiuas3.jpg|600px|centre]] | ||
| + | [[File:hasfiuas4.jpg|600px|centre]] | ||
| + | [[File:hasfiuas5.jpg|600px|centre]] | ||
| + | |||
| + | |||
| + | Jawaban nomor 7 dilakukan menggunakan aplikasi OpenModelica. Berikut code yang saya simulasikan di aplikasi tersebut: | ||
| + | |||
| + | |||
| + | [[File:hasfiuas6.jpg|800px|centre]] | ||
| + | [[File:hasfiuas7.jpg|800px|centre]] | ||
| + | [[File:hasfiuas8.jpg|800px|centre]] | ||
| + | [[File:hasfiuas9.jpg|800px|centre]] | ||
| + | [[File:hasfiuas10.jpg|800px|centre]] | ||
| + | |||
| + | |||
| + | Dari simulasi pada aplikasi OpenModelica didapatkan hasil sebagai berikut: | ||
| + | |||
| + | |||
| + | [[File:hasfiuas11.jpg|300px]][[File:hasfiuas12.jpg|300px]][[File:hasfiuas13.jpg|300px]] | ||
Latest revision as of 16:29, 14 January 2021
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Biodata Diri
Nama: Muhammad Hasfi Rizki Nur
NPM : 1806201163
TTL : Jakarta, 26 Oktober 2000
Saya mahasiswa prodi Teknik Mesin Universitas Indonesia angkatan 2018. Saat ini saya sedang menempuh kuliah pada semester kelima.
Alasan saya memilih prodi ini adalah saya tertarik belajar dan bekerja di bidang energi dan ingin memberikan dampak yang baik kepada perkembangan teknologi energi di Indonesia.
Contents
Pertemuan 1 (11 November 2020)
Materi pertemuan pertama
Pada pertemuan pertama, Bapak Ahmad Indra memberikan penjelasan bagaiman mengoperasikan situs wiki air dan memberikan 4 poin tujuan pembelajaran Metode Numerik saat ini. Keempat poin tersebut adalah:
- Mempelajari dan memahami konsep dasar dari pelajaran Metode Numerik.
- Mampu menerapkan pemahaman konsep kedalam permodelan numerik.
- Mengaplikasikan metode numerik dengan output yang berasal dari persoalan seputar Teknik Mesin.
- Mengevaluasi diri sendiri sehingga menjadi orang yang lebih beradab sesuai Sila kedua dari Pancasila.
Tugas Video
Diberikan tugas berupa menjelaskan perangkat lunak OpenModelica dan pengoperasikannya. Berikut video yang sudah saya buat:
Pertemuan 2 (18 November 2020)
Pada kegiatan pembelajaran mata kuliah metode numerik hari ini. Bapak Ahmad Indra mengawali dengan mereview tugas yang diberikan pada pertemuan minggu lalu. Review tersebut mengenai software Open Modelica dan perhitungan yang masing - masing mahasiswa lakukan.
Berikut ini adalah contoh penerapan aplikasi OpenModelica untuk membuat 4 algoritma metode numerik dalam mencari roots of equation (akar persamaan) dari:
f(x) = exp^(-x)-(x)
f'(x) = -exp^(-x)-1
error maksimum = 0.0000001
1) Newton Raphson (Terbuka)
model Newton_Raphson_Algorithm parameter Real g=1; //guess parameter Integer N=20; //max iteration parameter Real er=0.0000001; //error maximum Real a[N]; Real y[N];//function Real ER[N]; //error Real sol; //solution algorithm a[1]:=g; y[1]:=a[1]-(exp(-a[1])-a[1])/(-exp(-a[1])-1); ER[1]:=abs(1-a[1]/y[1]); for i in 2:N loop a[i]:=y[i-1]; y[i]:=a[i]-(exp(-a[i])-a[i])/(-exp(-a[i])-1); ER[i]:=abs(1-y[i-1]/y[i]); if ER[i]<er then sol:=y[i]; break; end if; end for; end Newton_Raphson_Algorithm;
2) Secant (Terbuka)
model Secant_Algorithm parameter Real a=0; //guess parameter Real b=1; //guess parameter Integer N=10; //max iteration parameter Real er=0.0000001; //error maximum Real A[N]; Real B[N]; Real y[N]; Real ER[N]; Real sol; //solution algorithm A[1]:=a; B[1]:=b; y[1]:=B[1]-(exp(-B[1])-B[1])*(A[1]-B[1])/((exp(-A[1])-A[1])-(exp(-B[1])-B[1])); ER[1]:=abs(1-B[1]/y[1]); for i in 2:N loop A[i]:=B[i-1]; B[i]:=y[i-1]; y[i]:=B[i]-(exp(-B[i])-B[i])*(A[i]-B[i])/((exp(-A[i])-A[i])-(exp(-B[i])-B[i])); ER[i]:=abs(1-y[i-1]/y[i]); if ER[i]<er then sol:=y[i]; break; end if; end for; end Secant_Algorithm;
3) Bisection (Tertutup)
model Bisection_Algorithm parameter Real a=0; //guess bawah parameter Real b=1; //guess atas parameter Integer N=50; //max iteration parameter Real er=0.0000001; //error maximum Real fa=(exp(-a)-a); Real fb=(exp(-b)-b); Real A[N]; Real B[N]; Real fy[N]; Real y[N]; Real ER[N]; Real sol; //solution algorithm if fa*fb<0 then A[1]:=a; B[1]:=b; y[1]:=(A[1]+B[1])/2; fy[1]:=exp(-y[1])-y[1]; ER[1]:=1; for i in 2:N loop if fy[i-1]>0 then A[i]:=y[i-1]; B[i]:=B[i-1]; else A[i]:=A[i-1]; B[i]:=y[i-1]; end if; y[i]:=(A[i]+ B[i])/2; fy[i]:=exp(-y[i])-y[i]; ER[i]:=abs(1-y[i-1]/y[i]); if ER[i]<er then sol:=y[i]; break; end if; end for; end if; end Bisection_Algorithm;
4) Regula Falsi (Tertutup)
model Regula_Falsi_Algorithm parameter Real a=0; //guess bawah parameter Real b=1; //guess atas parameter Integer N=20; //max iteration parameter Real er=0.0000001; //error maximum Real A[N]; Real B[N]; Real fa[N]; Real fb[N]; Real fy[N]; Real y[N]; Real ER[N]; Real sol; //solution algorithm A[1]:=a; B[1]:=b; fa[1]:=exp(-A[1])-A[1]; fb[1]:=exp(-B[1])-B[1]; if fa[1]*fb[1]<0 then y[1]:=(A[1]*fb[1]-B[1]*fa[1])/(fb[1]-fa[1]); fy[1]:=exp(-y[1])-y[1]; ER[1]:=1; for i in 2:N loop if fy[i-1]>0 then A[i]:=y[i-1]; B[i]:=B[i-1]; else A[i]:=A[i-1]; B[i]:=y[i-1]; end if; fa[i]:=exp(-A[i])-A[i]; fb[i]:=exp(-B[i])-B[i]; y[i]:=(A[i]*fb[i]-B[i]*fa[i])/(fb[i]-fa[i]); fy[i]:=exp(-y[i])-y[i]; ER[i]:=abs(1-y[i-1]/y[i]); if ER[i]<er then sol:=y[i]; break; end if; end for; end if; end Regula_Falsi_Algorithm;
Tugas Video
Berikut video yang sudah saya buat: https://youtu.be/Q8-usKi9NsM
Pertemuan 3 (25 November 2020)
Pada awal-awal Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, pertama ada Computation Fluid Dynamics (CFD), lalu FInite Element Analysis (FEA), dan Metode Stokastik. CFD dan FEA berbasis ilmu fisika, kemudian metode stokastik berbasis data dan statistik. Ada lima langkah yang Pak Dai paparkan dalam mengaplikasikan metode numerik ke permasalahan teknik :
- Riset masalah tekniknya terlebih dahulu
- Menganalisis masalah (mendefinisikan variabel yang mau dicari dan mencari parameter fisikanya)
- Membuat model matematika
- Membuat model numerik
- Setelah itu cari penyelesaian dengan bantuan komputer untuk mendapatkan output yang diinginkan
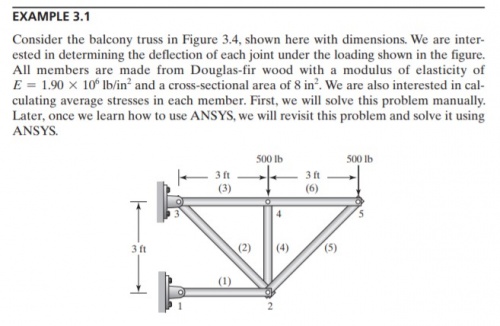
Soal Latihan Trusses Problem
Code
|
Persamaan model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
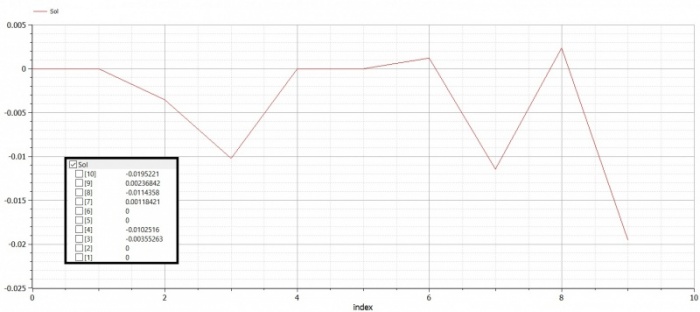
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
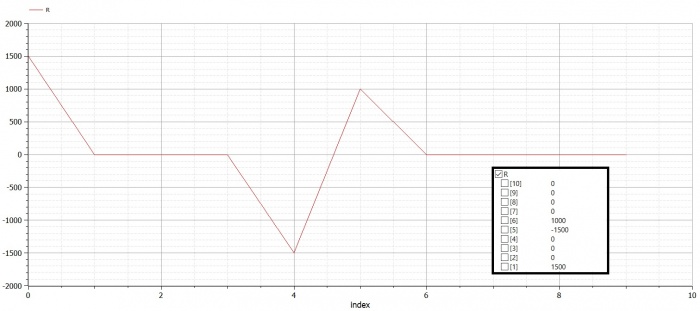
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
|
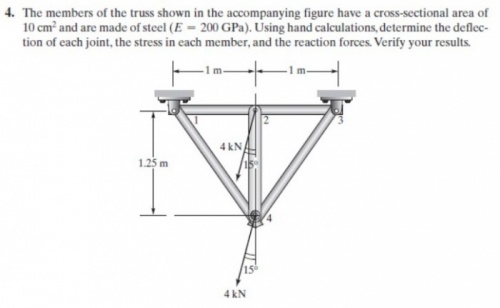
Tugas Trusses Problem
code
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
Pertemuan 4 (2 Desember 2020)
Kuis: Membuat Flowchart dan Diagram
Tugas
Pertemuan 5 (16 Desember 2020)
Pada minggu ini topiknya adalah optimasi sistem menggunakan OpenModelica. Sebelum pertemuan Bu Chandra memberikan contoh kasus optimasi dan juga pesudocode nya. Contoh kasus tersebut adalah optimasi metode bracket. Berikut code dalam penerapan di aplikasi OpenModelica:
FungsiObjek.mo function FungsiObjek input Real x; output Real y; algorithm y:= 2*Modelica.Math.sin(x)-x^2/10; end FungsiObjek;
BracketOptimal.mo
model BracketOptimal
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end BracketOptimal;
Tugas Besar (23 Desember 2020)
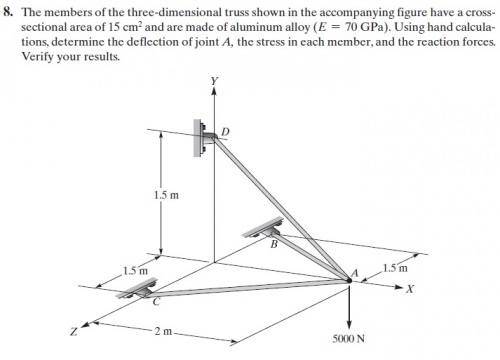
Soal Tugas Besar
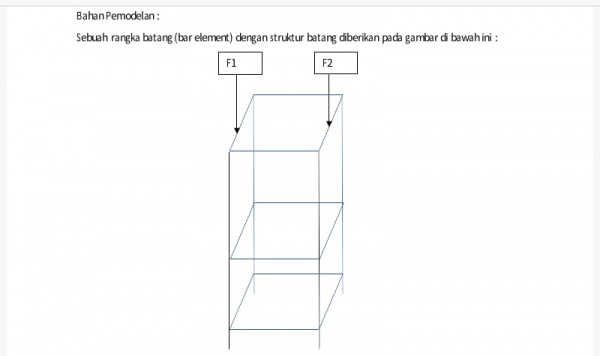
Untuk tugas besar mata kuliah Metode Numerik terdapat sebuah permodelan rangka kontruksi. Mahasiswa diminta untuk mencari harga pengadaan rangka tersebut secara optimal dengan pertimbangan dimensi dan material.
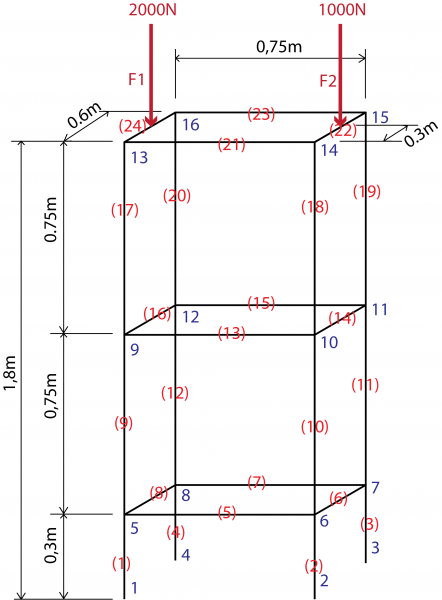
Definisi Node dan Elemen
Penyelesaian dari soal tugas besar ini harus diawali dengan pendefinisian elemen dan node pada rangka.
Asumsi dan constraint
Asumsi yang saya lakukan pada permodelan ini:
- Bersifat trusses (beban akan terdistribusi hanya pada node).
- Safety factor = 2.
- Batas displacement = 0,001 m (sesaat sebelum buckling pada truss paling atas).
- h trusses = 0,6 m (setiap lantai).
constraint atau batasan pada kasus ini:
- Node 1,2,3,4 fixed.
- F1 dan F2 terdistribusi ke node sekitaranya.
- Node 13 & 16 = 1000N.
- Node 14 & 15 = 500N.
Penyelesaian
Dalam kasus pada soal yaitu mencari dimensi area dan material yang paling optimal untuk pembentukan rangka, maka diperlukan pencarian data dari material dan variasi dimensi yang akan diuji. Saya menggunakan data excel dari teman saya yaitu Josiah, Christopher dan Fahmi sehingga mendapat data sebagai berikut
Penyelesaian dilakukan dengan dua metode yaitu:
- Pencarian material yang optimal dengan satu data dimensi (fixed area)
- Pencarian dimensi yang optimal dengan satu data material (fixed material)
Code
|
Stress analysis model TugasBesarMuhammadHasfi //define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa)
parameter Real Area= (nilai area) ; //Luas Siku (Dimension=30x30x3mm)
parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa)
//define connection
parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end TugasBesarMuhammadHasfi;
|
|
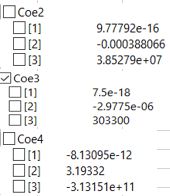
Curve fitting model callcurve
parameter Real [8] X={1.11e-4,1.41e-4,1.71e-4,2.31e-4,3.04e-4,3.75e-4,7.44e-4,8.64e-4};
parameter Real [8] Y={273700 ,318800 ,381200 ,512800 ,683700 ,838000 ,1663100,1986400};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
Function function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting; |
|
Optimalisasi (metode golden ratio) model Opt_Gold
parameter Real[3] y={-834.974,0.356007,2.39937e-5};
parameter Real xlo=111e-6;
parameter Real xhi=3.75e-4;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for; end Opt_Gold; |
Perhitungan
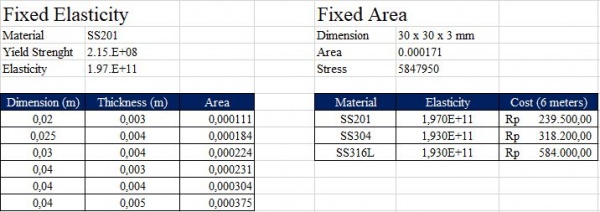
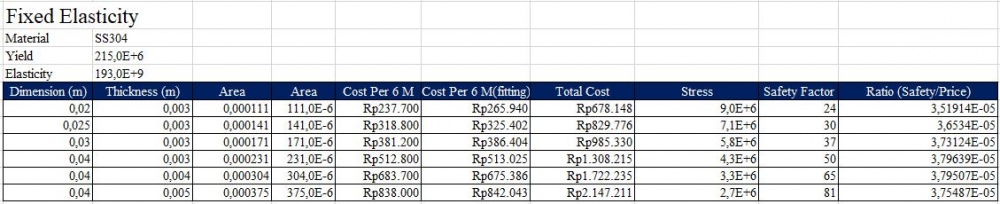
A. Fixed Elasticity
Berikut perhitungan dalam menentukan Safety Factor/Cost ratio. Rasio ini diperlukan unuk mengetahui dimensi apa yang optimal dalam pembentukan rangka yang ada. Curve fitting juga diperlukan dalam perhitungan untuk melengkapi data SS304 yang masih belum diketahui.
B. Fixed Area
Dalam menentukan material yang optimal digunakan dimensi tetap yaitu 30x30x3mm serta dilakukan curve fitting.
Kesimpulan
- Nilai luas area penampang optimum untuk material SS304 adalah 283,81 mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 6m dan tebal 60mm.
- Material optimum yang dapat digunakan untuk luas penampang 270mm^2 adalah material dengan nilai elastisitas 15324000000000 N/m^2 atau material yang paling mendekati adalah SS316L.
Ujian Akhir Semester (13 Januari 2021)
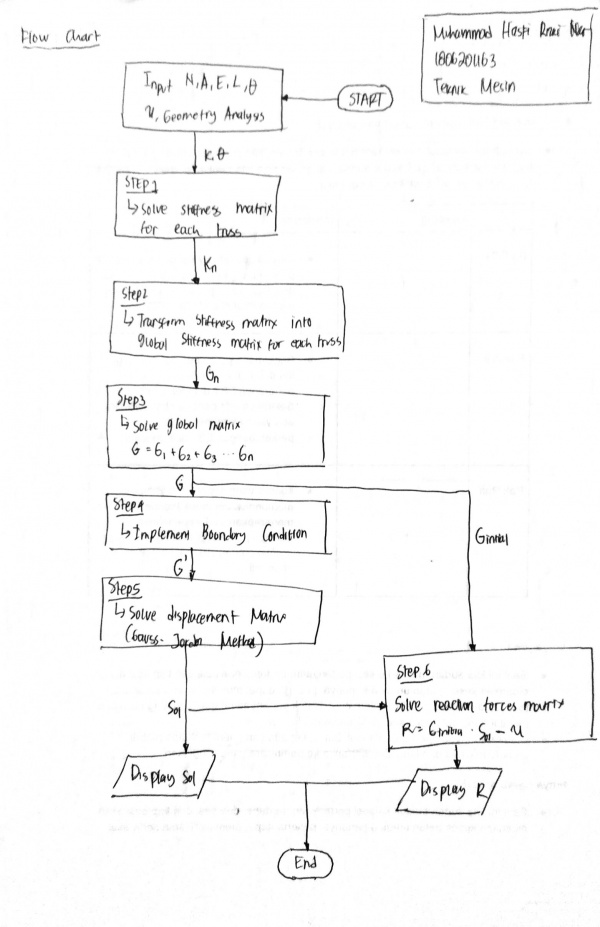
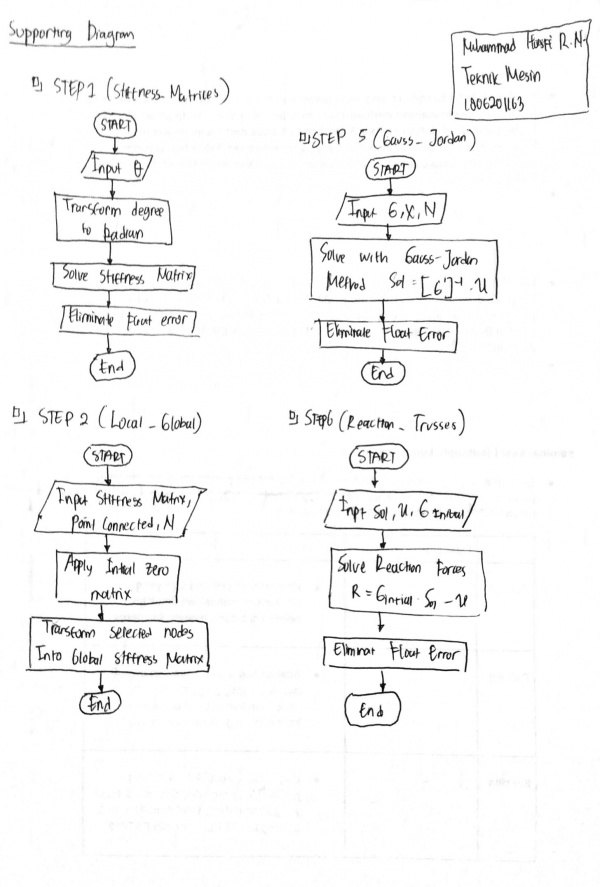
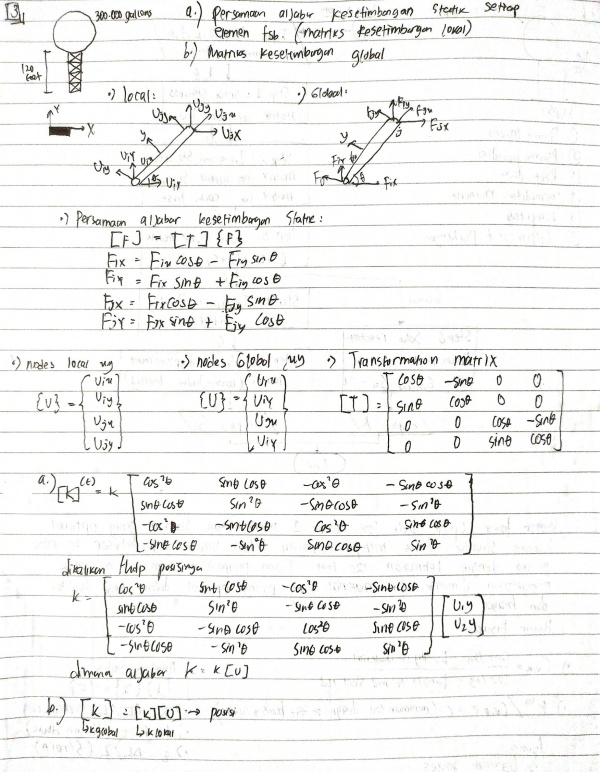
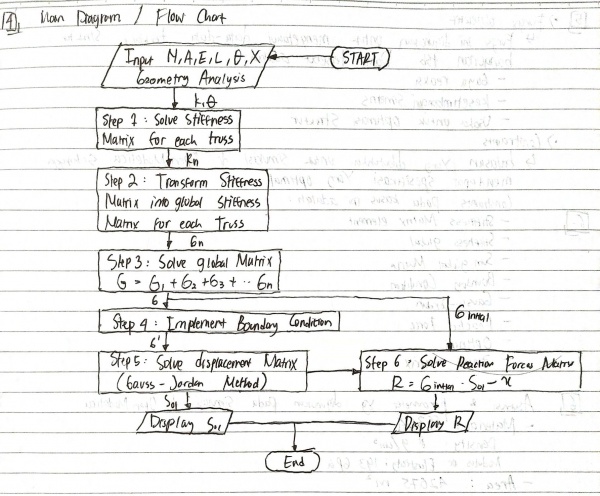
Berikut jawaban Ujian Akhir Semester (UAS) mata kuliah Metode Numerik yang saya kerjakan pada tanggal 13 januari 2021.
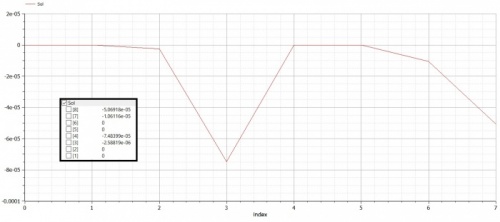
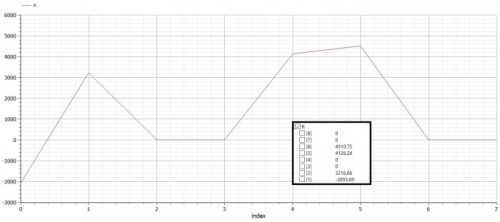
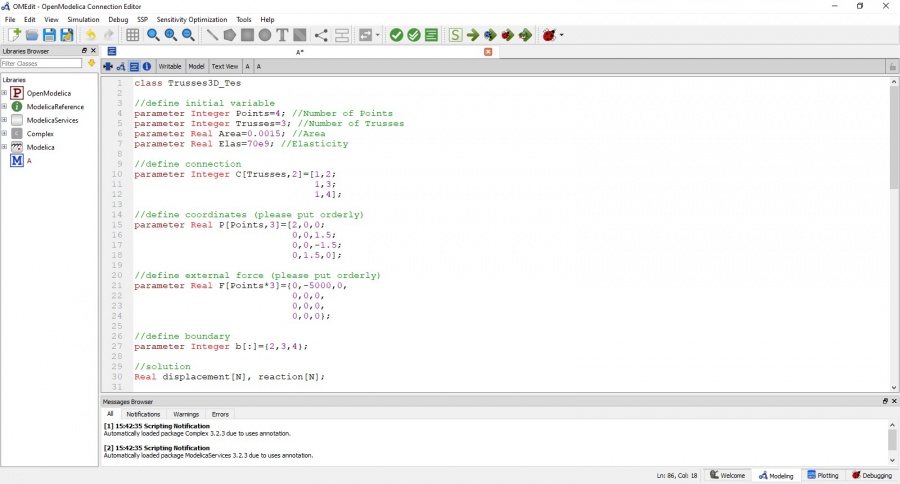
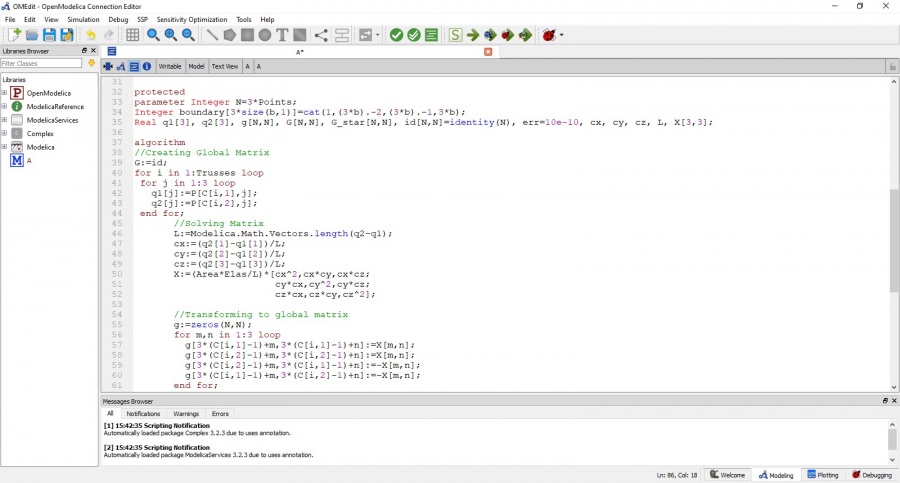
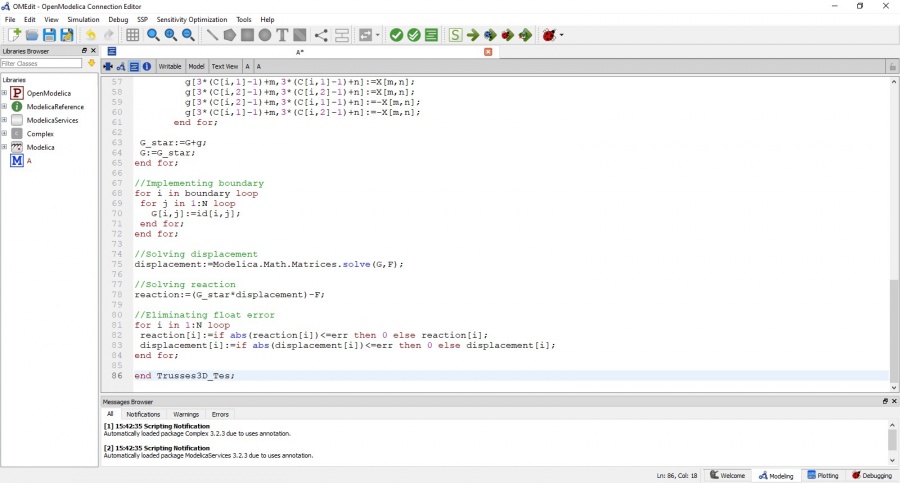
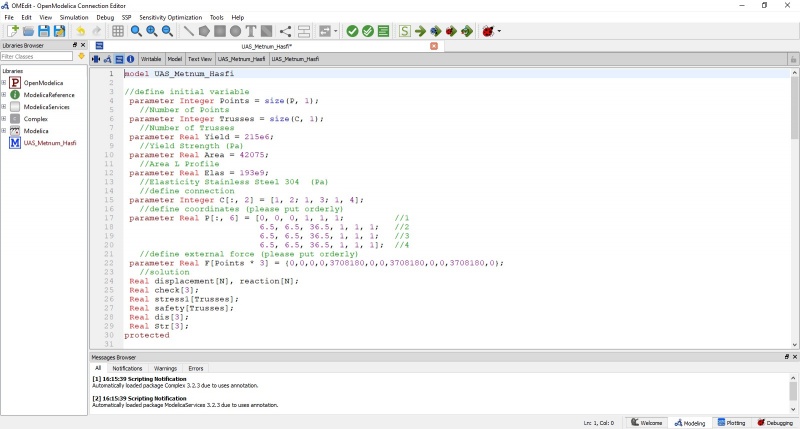
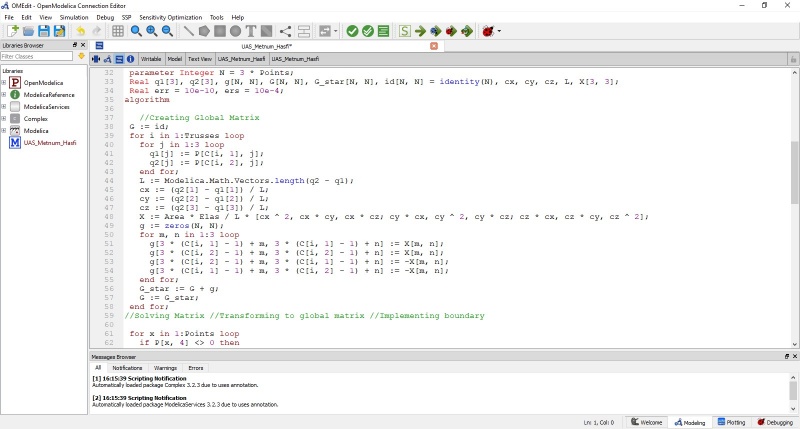
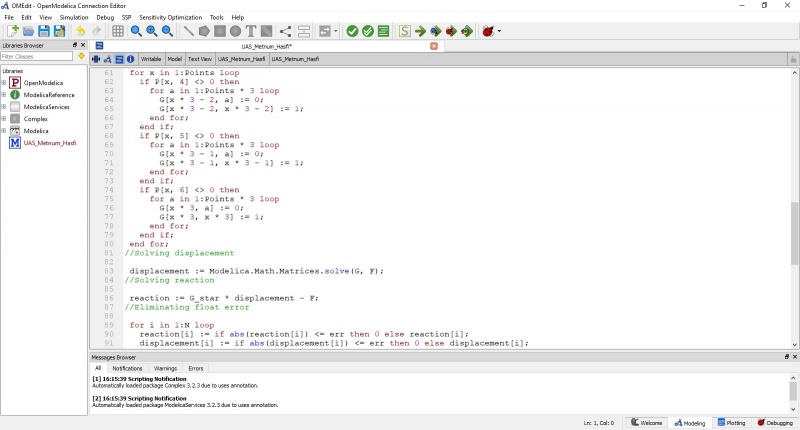
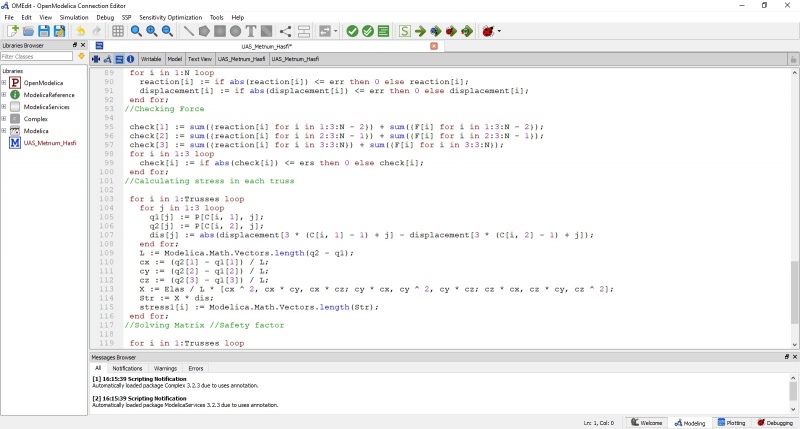
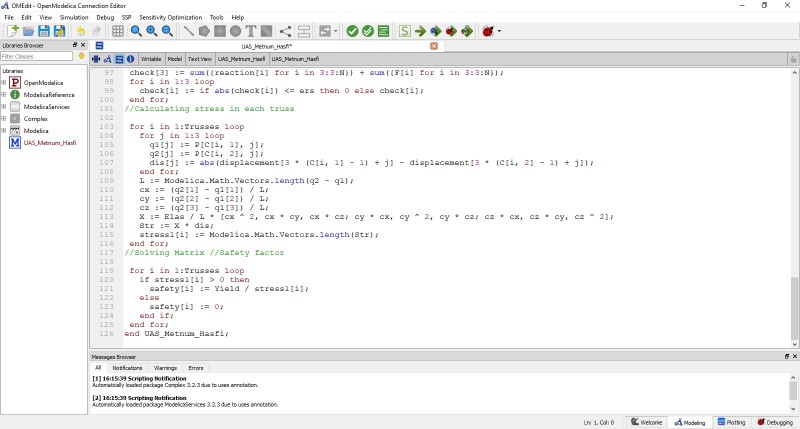
Jawaban nomor 7 dilakukan menggunakan aplikasi OpenModelica. Berikut code yang saya simulasikan di aplikasi tersebut:
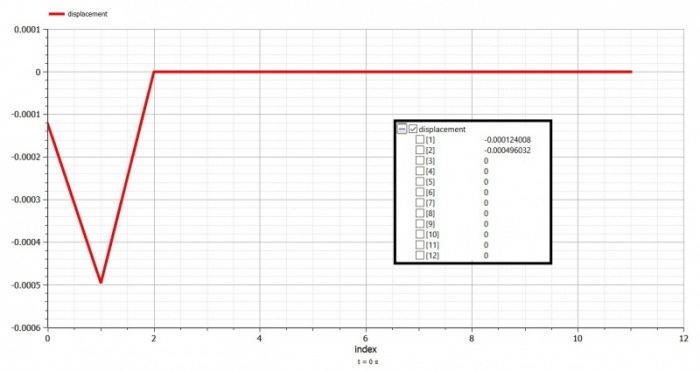
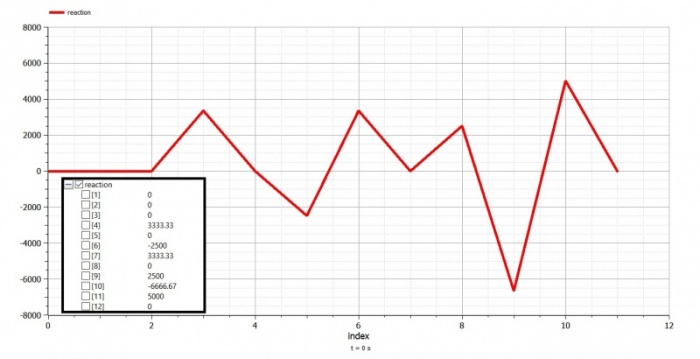
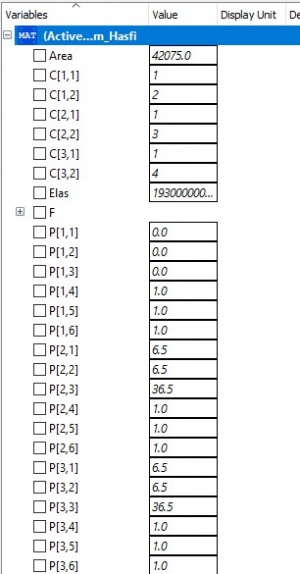
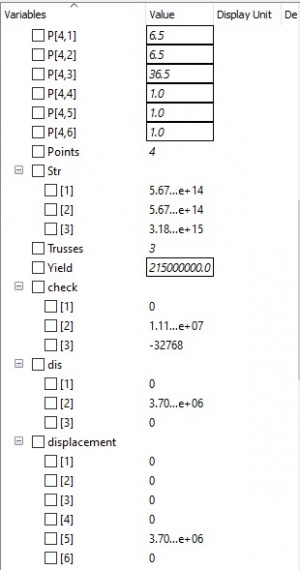
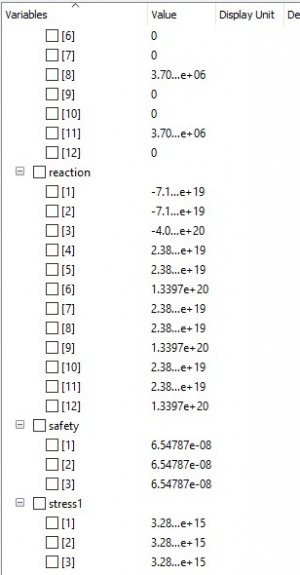
Dari simulasi pada aplikasi OpenModelica didapatkan hasil sebagai berikut: