Difference between revisions of "Metnum03-Bimo Adinugroho"
(→Tugas Besar Metode Numerik) |
(→Ujian Akhir Semester) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 56: | Line 56: | ||
[[File:Soal3.jpeg|300px|center]] | [[File:Soal3.jpeg|300px|center]] | ||
| − | |||
| − | |||
Pada algoritma Ahmad Muhammad Fahmi, metode yang digunakan untuk penyelesaian sama dengan ''flowchart'' yang sudah saya buat untuk Quiz. Penyelesaian kedua soal ini memiliki ''parameter input'': | Pada algoritma Ahmad Muhammad Fahmi, metode yang digunakan untuk penyelesaian sama dengan ''flowchart'' yang sudah saya buat untuk Quiz. Penyelesaian kedua soal ini memiliki ''parameter input'': | ||
| − | + | A (Luas Permukaan), E (Modulus Elastisitas), node, load | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Pada algoritma ini dibuat terlebih dahulu beberapa ''function'' untuk mempermudah pemanggilan pada ''class''. Disini terdapat ''function'' yaitu Stiffness Matrix Global, Sum Stiffness Matrix Global, Boundary Stiffness Matrix Global, Gauss Jordan, Reaction Force, dan Check Force. | Pada algoritma ini dibuat terlebih dahulu beberapa ''function'' untuk mempermudah pemanggilan pada ''class''. Disini terdapat ''function'' yaitu Stiffness Matrix Global, Sum Stiffness Matrix Global, Boundary Stiffness Matrix Global, Gauss Jordan, Reaction Force, dan Check Force. | ||
| Line 512: | Line 504: | ||
'''1. Mendefinisikan karakteristik dari Truss''' | '''1. Mendefinisikan karakteristik dari Truss''' | ||
| − | Dari soal diminta untuk mencari material pada struktur tersebut yang paling optimal. Besi siku(angle bar akan menjadi strukturnya. Membandingkan optimasi material dan optimasi luas penampang. Struktur pada kasus ini memiliki dimensi 0. | + | Dari soal diminta untuk mencari material pada struktur tersebut yang paling optimal. Besi siku(angle bar akan menjadi strukturnya. Membandingkan optimasi material dan optimasi luas penampang. Struktur pada kasus ini memiliki dimensi 0.75m x 0.6m x 1.8m. Pada bagian atas diberikan dua gaya yang memengaruhi struktur |
F1 : 2000 N | F1 : 2000 N | ||
| Line 523: | Line 515: | ||
'''3. Mencari data profil besi siku yang digunakan''' | '''3. Mencari data profil besi siku yang digunakan''' | ||
| + | |||
| + | [[File:Hargamaterialbm.jpeg]] | ||
'''4. Melakukan simulasi pada OpenModelica''' | '''4. Melakukan simulasi pada OpenModelica''' | ||
| − | |||
| − | |||
//define initial variable | //define initial variable | ||
| Line 537: | Line 529: | ||
//define connection | //define connection | ||
parameter Integer C[:,2]=[1,5; | parameter Integer C[:,2]=[1,5; | ||
| − | + | 2,6; | |
| − | + | 3,7; | |
| − | + | 4,8; | |
| − | + | 5,6; //1st floor | |
| − | + | 6,7; //1st floor | |
| − | + | 7,8; //1st floor | |
| − | + | 5,8; //1st floor | |
| − | + | 5,9; | |
| − | + | 6,10; | |
| − | + | 7,11; | |
| − | + | 8,12; | |
| − | + | 9,10; //2nd floor | |
| − | + | 10,11;//2nd floor | |
| − | + | 11,12;//2nd floor | |
| − | + | 9,12; //2nd floor | |
| − | + | 9,13; | |
| − | + | 10,14; | |
| − | + | 11,15; | |
| − | + | 12,16; | |
| − | + | 13,14;//3rd floor | |
| − | + | 14,15;//3rd floor | |
| − | + | 15,16;//3rd floor | |
| − | + | 13,16];//3rd floor | |
//define coordinates (please put orderly) | //define coordinates (please put orderly) | ||
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| − | + | -0.3,-0.375,0,1,1,1; //2 | |
| − | + | -0.3,0.375,0,1,1,1; //3 | |
| − | + | 0.3,0.375,0,1,1,1; //4 | |
| − | + | ||
| − | + | 0.3,-0.375,0.6,0,0,0; //5 | |
| − | + | -0.3,-0.375,0.6,0,0,0; //6 | |
| − | + | -0.3,0.375,0.6,0,0,0; //7 | |
| − | + | 0.3,0.375,0.6,0,0,0; //8 | |
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| − | + | 0.3,-0.375,1.8,0,0,0; //13 | |
| − | + | -0.3,-0.375,1.8,0,0,0; //14 | |
| − | + | -0.3,0.375,1.8,0,0,0; //15 | |
| − | + | 0.3,0.375,1.8,0,0,0]; //16 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
//define external force (please put orderly) | //define external force (please put orderly) | ||
parameter Real F[Points*3]={0,0,0, | parameter Real F[Points*3]={0,0,0, | ||
| Line 608: | Line 600: | ||
Real dis[3]; | Real dis[3]; | ||
Real Str[3]; | Real Str[3]; | ||
| − | + | ||
protected | protected | ||
parameter Integer N=3*Points; | parameter Integer N=3*Points; | ||
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| − | Real err=10e-10, ers=10e- | + | Real err=10e-10, ers=10e-6; |
algorithm | algorithm | ||
| Line 619: | Line 611: | ||
for i in 1:Trusses loop | for i in 1:Trusses loop | ||
for j in 1:3 loop | for j in 1:3 loop | ||
| − | + | q1[j]:=P[C[i,1],j]; | |
| − | + | q2[j]:=P[C[i,2],j]; | |
end for; | end for; | ||
| − | + | ||
| − | + | //Solving Matrix | |
| − | + | L:=Modelica.Math.Vectors.length(q2-q1); | |
| − | + | cx:=(q2[1]-q1[1])/L; | |
| − | + | cy:=(q2[2]-q1[2])/L; | |
| − | + | cz:=(q2[3]-q1[3])/L; | |
| − | + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | |
| − | + | cy*cx,cy^2,cy*cz; | |
| − | + | cz*cx,cz*cy,cz^2]; | |
| − | + | ||
| − | + | //Transforming to global matrix | |
| − | + | g:=zeros(N,N); | |
| − | + | for m,n in 1:3 loop | |
| − | + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | |
| − | + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | |
| − | + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | |
| − | + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | |
| − | + | end for; | |
| − | + | ||
G_star:=G+g; | G_star:=G+g; | ||
G:=G_star; | G:=G_star; | ||
end for; | end for; | ||
| − | + | ||
//Implementing boundary | //Implementing boundary | ||
for x in 1:Points loop | for x in 1:Points loop | ||
| − | + | if P[x,4] <> 0 then | |
| − | + | for a in 1:Points*3 loop | |
| − | + | G[(x*3)-2,a]:=0; | |
| − | + | G[(x*3)-2,(x*3)-2]:=1; | |
| − | + | end for; | |
| − | + | end if; | |
| − | + | if P[x,5] <> 0 then | |
| − | + | for a in 1:Points*3 loop | |
| − | + | G[(x*3)-1,a]:=0; | |
| − | + | G[(x*3)-1,(x*3)-1]:=1; | |
| − | + | end for; | |
| − | + | end if; | |
| − | + | if P[x,6] <> 0 then | |
| − | + | for a in 1:Points*3 loop | |
| − | + | G[x*3,a]:=0; | |
| − | + | G[x*3,x*3]:=1; | |
| − | + | end for; | |
| − | + | end if; | |
end for; | end for; | ||
| Line 685: | Line 677: | ||
for i in 1:3 loop | for i in 1:3 loop | ||
| − | + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | |
end for; | end for; | ||
//Calculating stress in each truss | //Calculating stress in each truss | ||
for i in 1:Trusses loop | for i in 1:Trusses loop | ||
| − | for j in 1:3 loop | + | for j in 1:3 loop |
| − | + | q1[j]:=P[C[i,1],j]; | |
| − | + | q2[j]:=P[C[i,2],j]; | |
| − | + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | |
| − | end for; | + | end for; |
| − | + | ||
| − | + | //Solving Matrix | |
| − | + | L:=Modelica.Math.Vectors.length(q2-q1); | |
| − | + | cx:=(q2[1]-q1[1])/L; | |
| − | + | cy:=(q2[2]-q1[2])/L; | |
| − | + | cz:=(q2[3]-q1[3])/L; | |
| − | + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | |
| − | + | cy*cx,cy^2,cy*cz; | |
| − | + | cz*cx,cz*cy,cz^2]; | |
| − | + | ||
| − | + | Str:=(X*dis); | |
| − | + | stress1[i]:=Modelica.Math.Vectors.length(Str); | |
end for; | end for; | ||
//Safety factor | //Safety factor | ||
for i in 1:Trusses loop | for i in 1:Trusses loop | ||
| − | + | if stress1[i]>0 then | |
| − | + | safety[i]:=Yield/stress1[i]; | |
| − | + | else | |
| − | + | safety[i]:=0; | |
| − | + | end if; | |
end for; | end for; | ||
| Line 723: | Line 715: | ||
'''6. Mendapatkan kurva hasil optimasi yang telah dilakukan dan menganalisanya''' | '''6. Mendapatkan kurva hasil optimasi yang telah dilakukan dan menganalisanya''' | ||
| + | |||
| + | |||
| + | |||
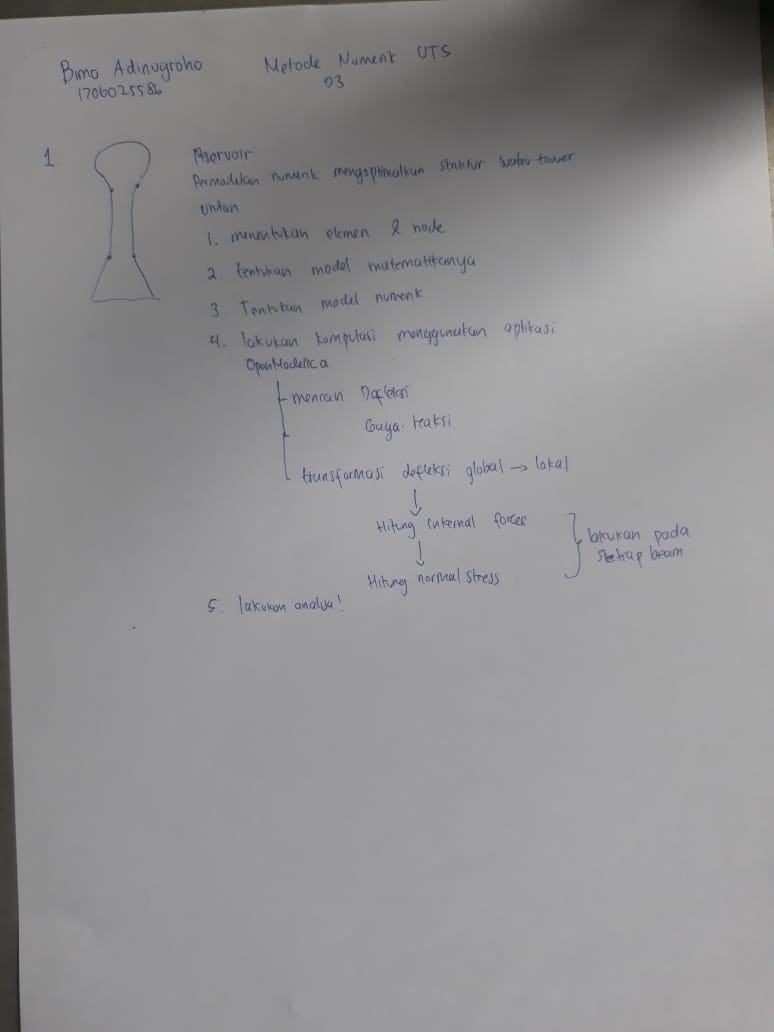
| + | == Ujian Akhir Semester == | ||
| + | |||
| + | [[File:UASbm1.jpeg]] | ||
| + | |||
| + | [[File:UASbm2.jpeg]] | ||
| + | |||
| + | [[File:UASbm3.jpeg]] | ||
| + | |||
| + | [[File:UASbm4.jpeg]] | ||
Latest revision as of 17:42, 13 January 2021
بِسْمِ اللّهِ الرَّحْمَنِ الرَّحِيْمِ
Kelas Metode Numerik 03
Nama : Bimo Adinugroho
NPM : 1706025586
Contents
Pertemuan Pertama
Pertemuan pertama pada kelas metode numerik dengan Pak Dai saya diminta untuk menginstall aplikasi OpenModelica. Fungsi dari aplikasi ini untuk mensimulaikan suatu sistem yang didistribusikan dalam bentuk kode dan biner untuk penelitian. Pada pertemuan tersebut Pak Dai belum menjelaskan menggunakan aplikasi tersebut secara dalam, melainkan Pak Dai meminta mahasiswa untuk mereview kembali materi yang sudah diajarkan sebelum UTS, dan juga mencari fenomena apa saja yang pernah dilakukan dan dapat diaplikasikan dengan metode numerik.
Pertemuan Kedua
Pertemuan Ketiga
Pada hari Senin, 23 November 2020 kelas Metnum diawali dengan membaca buku mengenai spring-mass systems
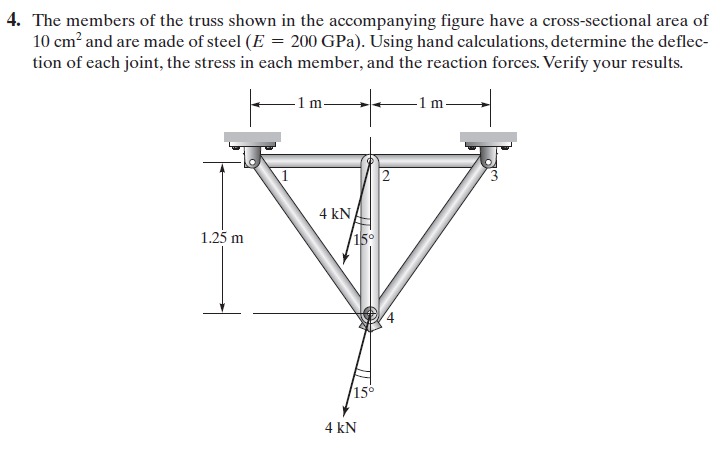
Menghitung defleksi yang terjadi di setiap elemen dan gaya reaksinya!
Quiz 1
Soal
Pertemuan Keempat
Pertemuan Kelima
Pada pertemuan kali ini, melanjutkan bahasan mengenai tugas yang diberikan minggu lalu. Tugas tersebut membahas mengenai gaya reaksi pada elemen beam penyusun yang sudah pernah dipelajari saat mata kuliah statika struktur. Kemudian dilanjutkan dengan pembahasan tugas dari beberapa rekan saya. Pertemuan ini menjelaskan hasil dari tugas rekan kami, Ahmad Mohammad Fahmi, mensenai coding yang ia buat pada tugas minggu lalu tentang Plane Truss dan Space Truss.
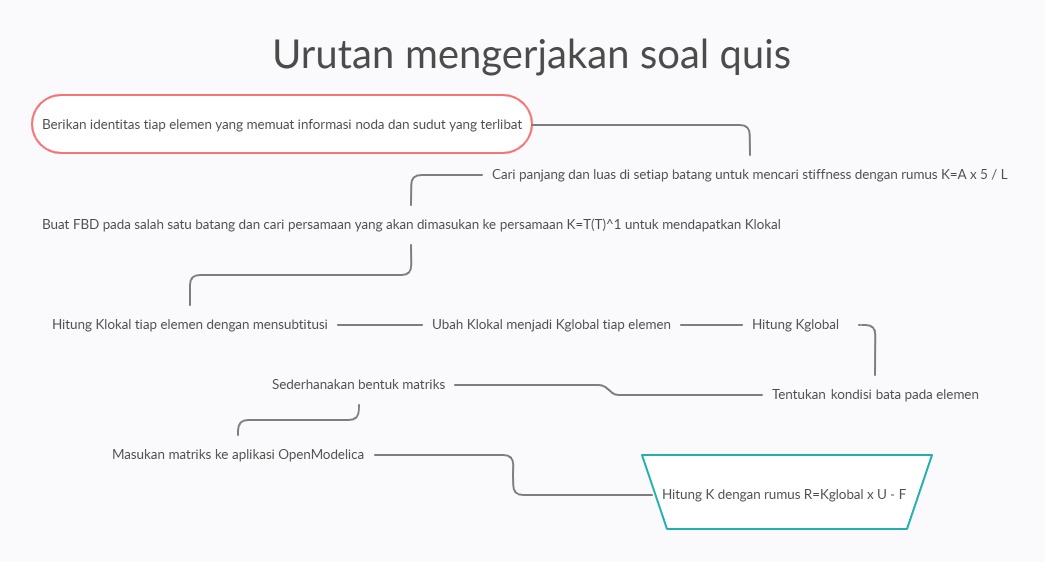
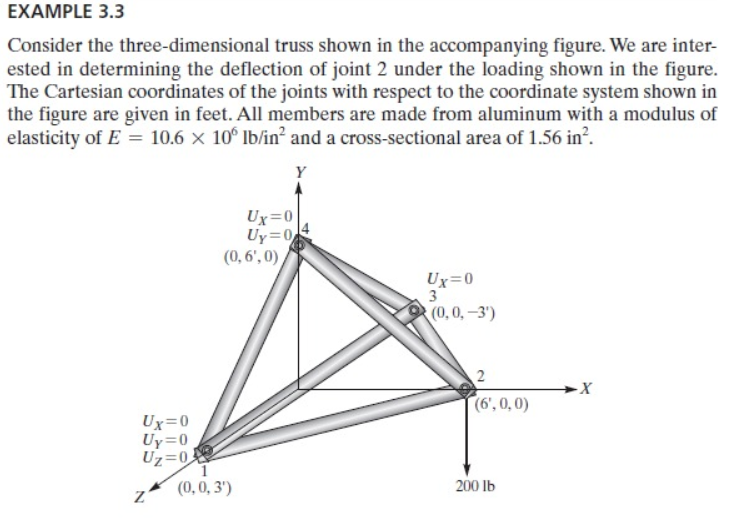
Diskusi berlangsung cutup interaktif dengan penjelasan dari Fahmi sendiri mengenai hasil tugas ia. Namun, masih banyak hal yang belum saya sepenuhnya mengerti, walau begitu tetap meneruskan progress diskusi pada platform ini. Soal baru diberikan kepada kami dari Pak Dai sebagai berikut
Pada algoritma Ahmad Muhammad Fahmi, metode yang digunakan untuk penyelesaian sama dengan flowchart yang sudah saya buat untuk Quiz. Penyelesaian kedua soal ini memiliki parameter input:
A (Luas Permukaan), E (Modulus Elastisitas), node, load
Pada algoritma ini dibuat terlebih dahulu beberapa function untuk mempermudah pemanggilan pada class. Disini terdapat function yaitu Stiffness Matrix Global, Sum Stiffness Matrix Global, Boundary Stiffness Matrix Global, Gauss Jordan, Reaction Force, dan Check Force.
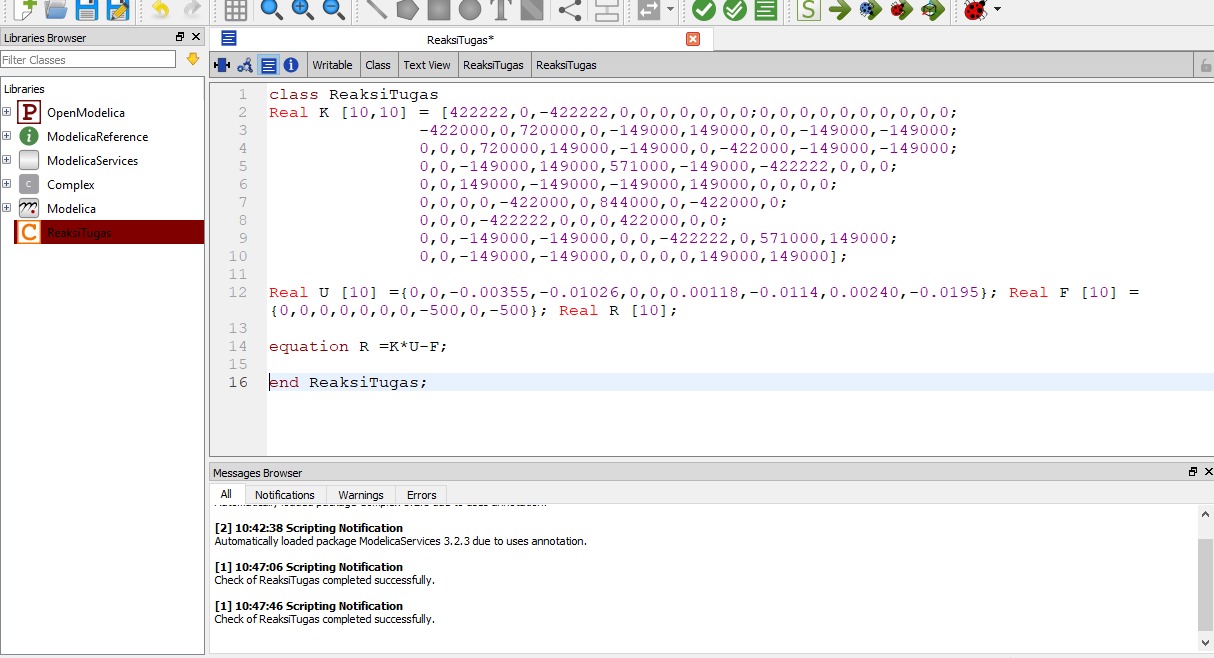
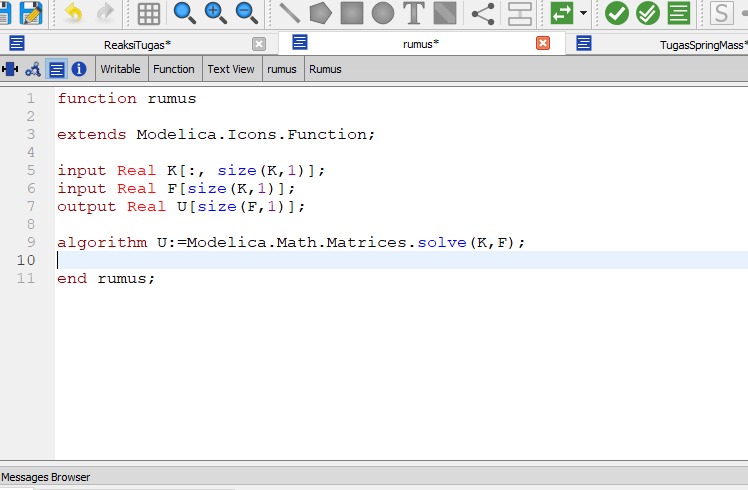
Pengaplikasian Coding Terhadap Soal
Berikut
|
Stiffness Matrix Element Function function StiffnessMatrixElement
input Real [:,6] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] L;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,2]/L[i];
cos_y := inisiasi_mat[i,3]/L[i];
cos_z := inisiasi_mat[i,4]/L[i];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
|
|
Stiffness Matrix Global Function function StiffnessMatrixGlobal input Integer x; input Integer [:,2] n; input Real [:,6,6] Ke_mat; output Real [size(Ke_mat,1),3*x,3*x] Kg_mat; algorithm Kg_mat := zeros(size(Ke_mat,1),3*x,3*x); for i in 1:size(Ke_mat,1) loop Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal; |
|
Sum Stiffness Matrix Element Function function SumStiffnessMatrixGlobal
input Real [:,:,:] Kg_mat;
output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
|
|
Boundary Stiffness Matrix Global Function function BoundaryStiffnessMatrixGlobal
input Real [:,:] KgTot_met;
input Integer[:] Boundary_xyz;
input Integer[:] Boundary_xy;
input Integer[:] Boundary_xz;
input Integer[:] Boundary_yz;
input Integer[:] Boundary_x;
input Integer[:] Boundary_y;
input Integer[:] Boundary_z;
output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
if Boundary_xyz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xyz,1) loop
for b in 0:2 loop
KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xy[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xy,1) loop
for b in 1:2 loop
KgB_met[3*(Boundary_xy[a])-b,i]:=0;
KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xz,1) loop
for b in 0:2:2 loop
KgB_met[3*(Boundary_xz[a])-b,i]:=0;
KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_yz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_yz,1) loop
for b in 0:1 loop
KgB_met[3*(Boundary_yz[a])-b,i]:=0;
KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_x[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_x,1) loop
KgB_met[3*(Boundary_x[a])-2,i]:=0;
KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
end for;
end for;
end if;
if Boundary_y[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_y,1) loop
KgB_met[3*(Boundary_y[a])-1,i]:=0;
KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
end for;
end for;
end if;
if Boundary_z[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_z,1) loop
KgB_met[3*Boundary_z[a],i]:=0;
KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
end for;
end for;
end if;
end BoundaryStiffnessMatrixGlobal;
|
|
Gauss Jordan Function function GaussJordan input Real [:,:] KgB_met; input Real [size(KgB_met,1)] load_met; output Real [size(KgB_met,1)] U_met; protected Real float_error = 10e-10; algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan; |
|
Reaction Force Function function ReactionForce input Real [:,:] KgTot_met; input Real [size(KgTot_met,1)] U_met; input Real [size(KgTot_met,1)] load_met; output Real [size(KgTot_met,1)] R_met; protected Real float_error = 10e-10; algorithm
R_met := KgTot_met*U_met-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end ReactionForce;
|
|
Check Force Function function CheckForce
input Real [:] load;
input Real [size(load,1)] R;
output Real [3] F;
protected Real float_error = 10e-10;
protected
Real load_x;
Real load_y;
Real load_z;
Real R_x;
Real R_y;
Real R_z;
algorithm
load_x := sum({load[i] for i in 1:3:(size(load,1)-2)});
load_y := sum({load[i] for i in 2:3:(size(load,1)-1)});
load_z := sum({load[i] for i in 3:3:size(load,1)});
R_x := sum({R[i] for i in 1:3:(size(load,1)-2)});
R_y := sum({R[i] for i in 2:3:(size(load,1)-1)});
R_z := sum({R[i] for i in 3:3:size(load,1)});
F[1] := load_x + R_x;
F[2] := load_y + R_y;
F[3] := load_z + R_z;
for i in 1:3 loop
if abs(F[i]) <= float_error then
F[i] := 0;
end if;
end for;
end CheckForce; |
Berikut merupakan class yang digunakan untuk memanggil function diatas dan menyelesaikan Example 3.3
|
Class class QuizSoal1
//inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data //titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
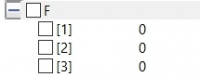
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R; //check force Real [3] F; equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(n, node, Ke); KgTot = SumStiffnessMatrixGlobal(Kg); KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); U = GaussJordan(KgB, load); R = ReactionForce(KgTot, U, load); F = CheckForce(load,R); end QuizSoal1; |
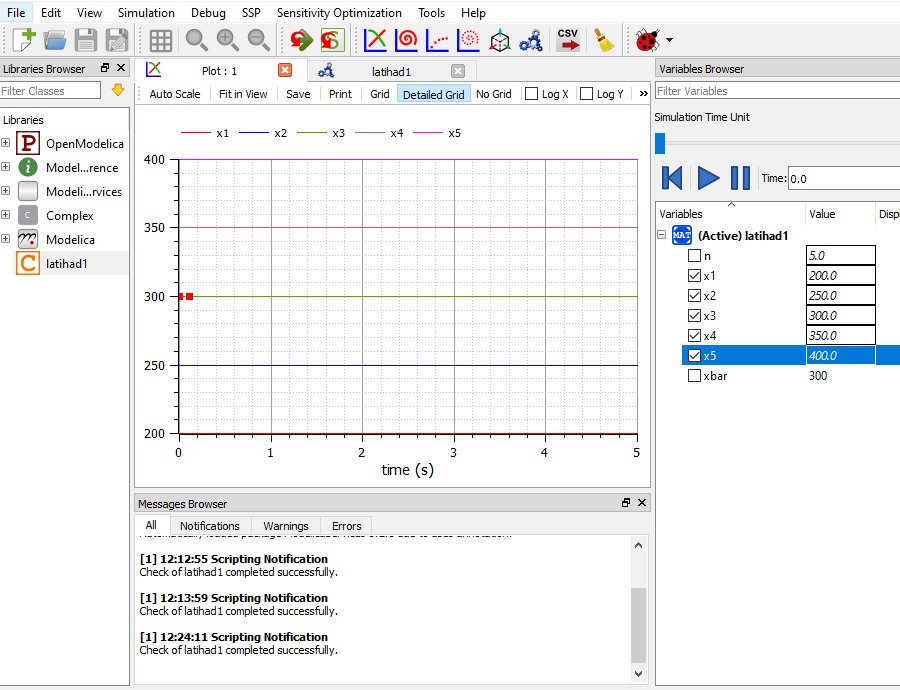
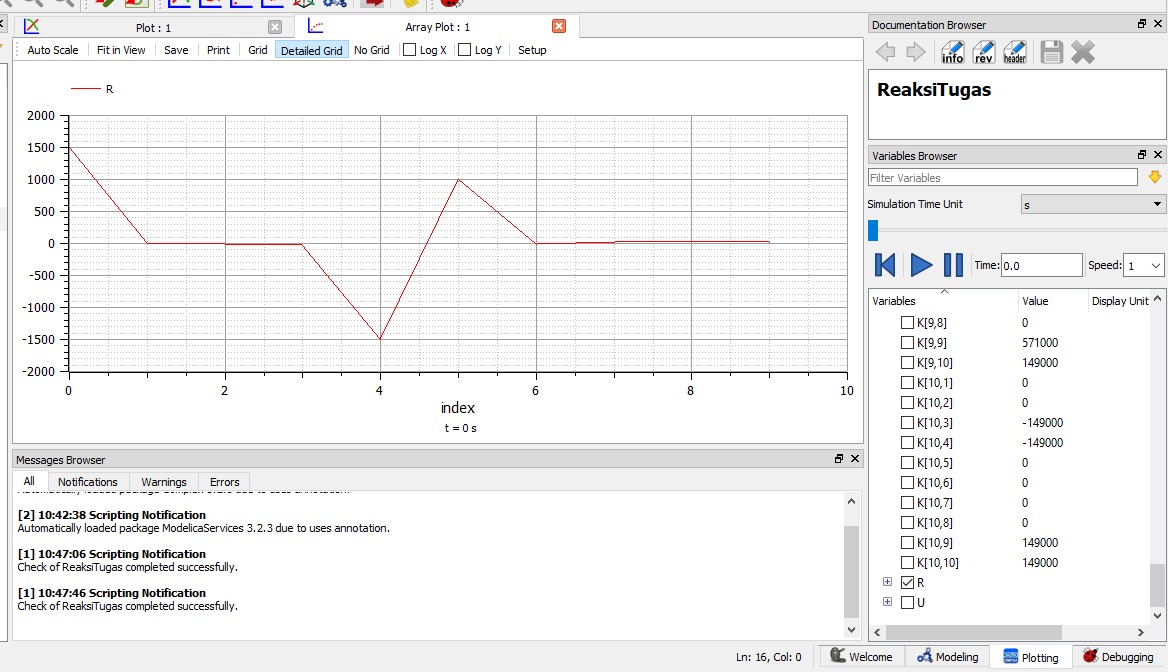
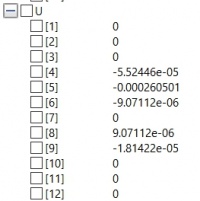
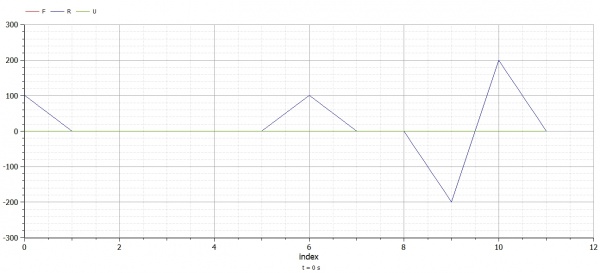
Berikut merupakan hasil dan grafik yang didapat
Pertemuan Keenam
Kelas pada hari Senin 21 Desember2020 diisi oleh Ibu Chandra. Beliau memaparkan materi pengaplikasian metode numerik pada OpenModelica.
Pada pembelajaran metode numerik ini, saya selalu berusaha mengikuti pembelajaran di kelas pada setiap pertemuan. Tentang konsep statika struktur saya sudah cukup paham, karena saya juga sudah pernah mempelajari statika struktur pada semester semester sebelumnya.
Untuk pembelajaran programming menggunakan OpenModelica, saya merasa memang cukup sulit, karena saya belum pernah mempelajari basic programming, saya mengalami kendala dalam pemahaman programmingnya(syntax). Saya selalu mengikuti tutorial dari teman sekelas ataupun platform Youtube tapi hasilnya sering kali "syntax error"
Tugas Besar Metode Numerik
Tujuan :
Mencari harga pembuatan rangka truss sederhana dengan memvariasi dimensi dan elastisitas material secara optimal!
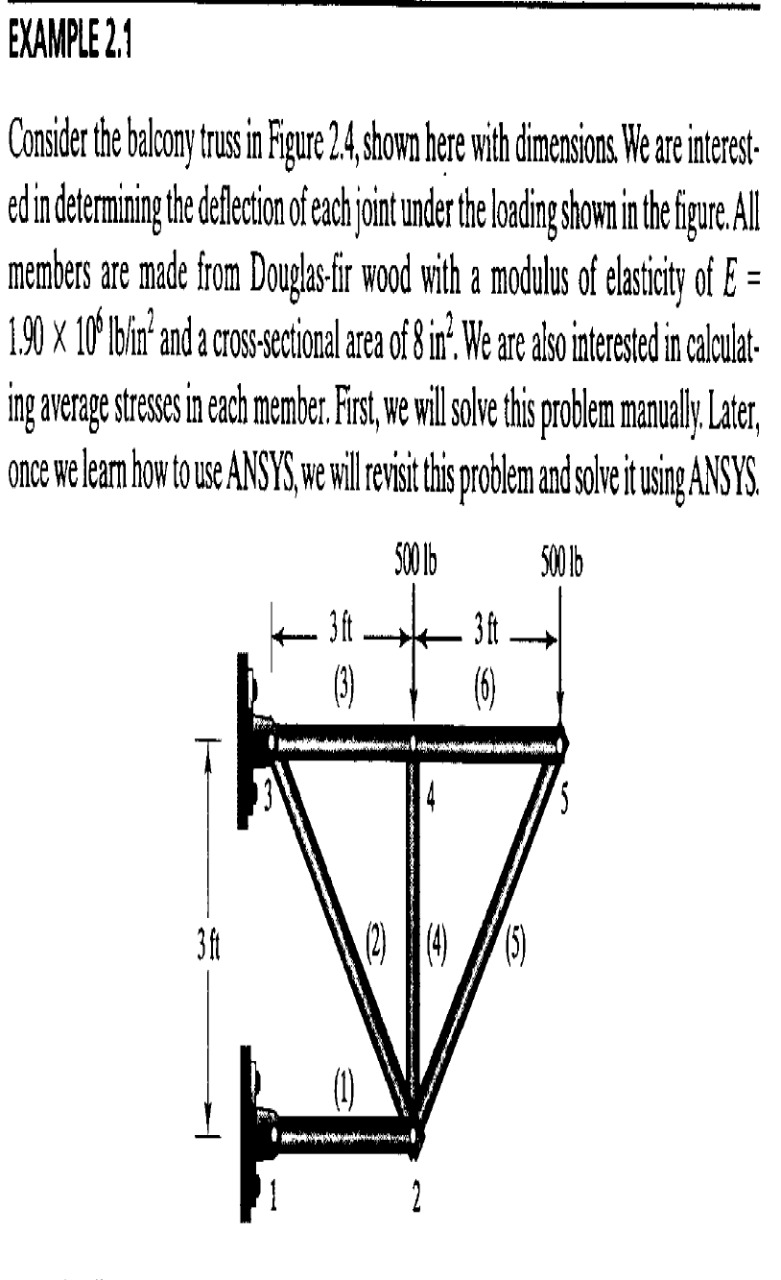
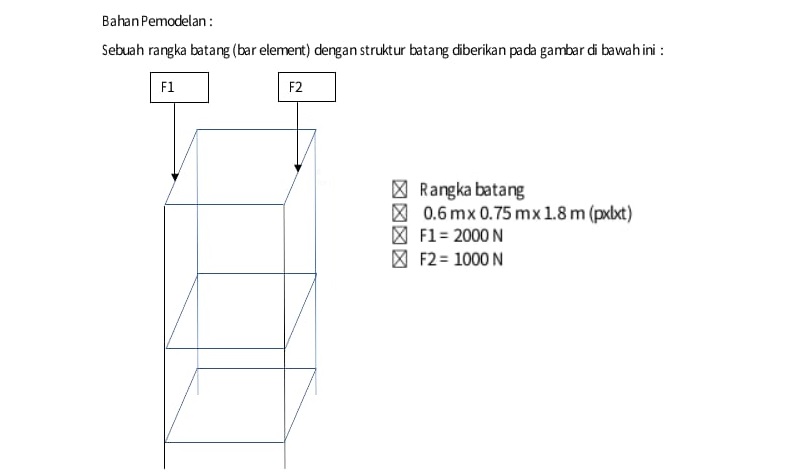
Berikut kasus yang diberikan :
Urutan penyelesaian :
1. Mendefinisikan karakteristik dari Truss
Dari soal diminta untuk mencari material pada struktur tersebut yang paling optimal. Besi siku(angle bar akan menjadi strukturnya. Membandingkan optimasi material dan optimasi luas penampang. Struktur pada kasus ini memiliki dimensi 0.75m x 0.6m x 1.8m. Pada bagian atas diberikan dua gaya yang memengaruhi struktur
F1 : 2000 N
F2 : 1000 N
2. Menentukan asusmsi dan node-node pada pengoperasian sistem
Gaya F1 dan F2 akan terdistribusi di point penghubung pada struktur. Struktur pada kasus ini memiliki sifat truss
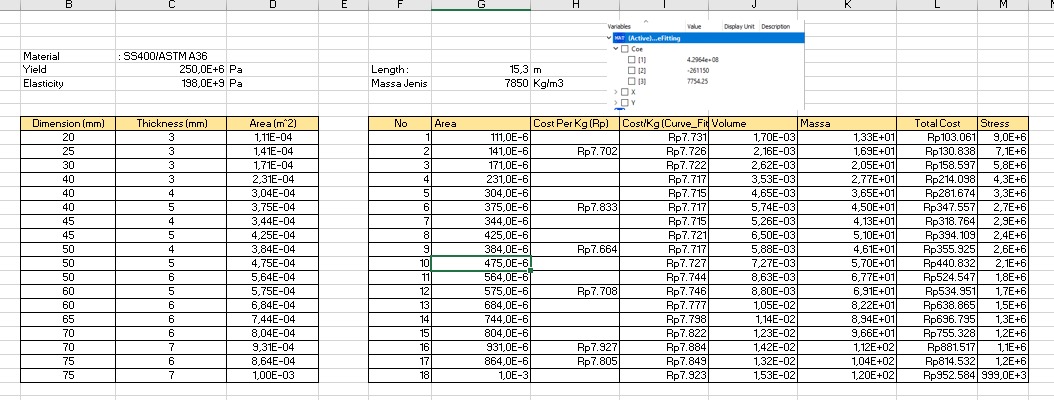
3. Mencari data profil besi siku yang digunakan
4. Melakukan simulasi pada OpenModelica
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
5. Optimasi 1 dan Optimasi 2
6. Mendapatkan kurva hasil optimasi yang telah dilakukan dan menganalisanya