Difference between revisions of "Reza Adyanto"
Reza Adyanto (talk | contribs) (→Belajar mandiri (16-12-2020)) |
Reza Adyanto (talk | contribs) (→Biodata) |
||
| (20 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
NPM : 1806201485 | NPM : 1806201485 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Assalamualaikum Wr.Wb. Nama saya adalah Reza Adyanto, Saya adalah Mahasiswa Teknik Mesin Universitas Indonesia angkatan 2018. Pada tahun ini (2020) Saya sedang menganmbil mata Kuliah Metode Numerik. | Assalamualaikum Wr.Wb. Nama saya adalah Reza Adyanto, Saya adalah Mahasiswa Teknik Mesin Universitas Indonesia angkatan 2018. Pada tahun ini (2020) Saya sedang menganmbil mata Kuliah Metode Numerik. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Minggu 1 (11 November 2020)== | ==Minggu 1 (11 November 2020)== | ||
| Line 242: | Line 224: | ||
- Mahasiswa diminta untuk Mengoptimasi harga pembuatan rangka truss dengan memvariasi dimensi dan elastisitas material. | - Mahasiswa diminta untuk Mengoptimasi harga pembuatan rangka truss dengan memvariasi dimensi dan elastisitas material. | ||
| − | + | Geometry dan Load | |
[[File:Screenshot_(762).png|600px|center]] | [[File:Screenshot_(762).png|600px|center]] | ||
| + | Diketahui: | ||
| + | panjang= 0,6 m | ||
| + | lebar= 0,75 m | ||
| + | tinggi= 1,6 m | ||
| + | F1= 2000 N | ||
| + | F2= 1000 N | ||
| + | |||
| + | kemudian diasumsikan | ||
| + | #Beban akan terdistribusi hanya pada node (karena bersifat trusses). | ||
| + | #Safety factor minimal bernilai 2. | ||
| + | #Batas displacement 0,001 m sebelum buckling (pada truss paling atas). | ||
| + | #Ketinggian trusses pada tiap lantai sama yaitu 0,6 m. | ||
| + | |||
| + | berikutnya: | ||
| + | Untuk jenis material yang sama: | ||
| + | #Mencari harga untuk 5 ukuran batang dengan material yang sama yaitu SS304. | ||
| + | #Mengitung nilai safety factor pada 5 ukuran batang dengan coding awal. | ||
| + | #Membuat rasio antara safety factor dengan harga total. | ||
| + | #Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. | ||
| + | #Melakukan optimasi menggunakan metode golden section. | ||
| + | Untuk area penampang yang sama: | ||
| + | #Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2. | ||
| + | #Mengitung nilai safety factor pada 3 jenis batang dengan coding awal. | ||
| + | #Membuat rasio antara safety factor dengan harga total. | ||
| + | #Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. | ||
| + | #Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | '''Data Material, dengan elasticity tetap''' | ||
| + | berdasarkan referensi di web https://wijayamakmur.com/siku, didapati data: | ||
| + | [[File:Screenshot_(778).png|center]] | ||
| + | |||
| + | '''Script Coding yang Digunakan''' | ||
| + | ---- | ||
| + | *Untuk menghitungan displacement, reaction force, stress, dan safety factor: | ||
| + | model TugasBesar_Trusses_3d_Safety | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end TugasBesar_Trusses_3d_Safety; | ||
| + | |||
| + | dan didapati hasil berikut dari simulasi tersebut: | ||
| + | [[File:Screenshot_(789).png|center]] | ||
| + | [[File:Screenshot_(790).png|center]] | ||
| + | [[File:Screenshot_(791).png|center]] | ||
| + | [[File:Screenshot_(792).png|center]] | ||
| + | |||
| + | *Untuk menghitung Curve fitting: | ||
| + | |||
| + | function TugasBesar_Curve_Fitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | end TugasBesar_Curve_Fitting; | ||
| + | |||
| + | *Untuk Mencari Optimasi Luas Penampang | ||
| + | |||
| + | model TugasBesar_Golden_section | ||
| + | parameter Real xd[:]={0.001216,0.000864,0.000304,0.000231,0.000171}; | ||
| + | parameter Real yd[:]={3.79387E-05,3.76909E-05,4.01305E-05,4.20011E-05,4.52247E-05}; | ||
| + | parameter Real xlo=171e-6; | ||
| + | parameter Real x hi=121e-5; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := TugasBesar_Curve_Fitting(xd,yd); | ||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end TugasBesar_Golden_section; | ||
| + | |||
| + | *Untuk Mencari Optimasi material (dengan mencari elastisitas Elastisitas) | ||
| + | |||
| + | model TugasBesar_Golden_section | ||
| + | |||
| + | parameter Real xd[:]={193000000000,197000000000,195000000000}; | ||
| + | parameter Real yd[:]={5.31939E-05,0.000120965,2.96556E-05}; | ||
| + | parameter Real xlo=1.93E+11; | ||
| + | parameter Real xhi=197000000000; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := TugasBesar_Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end TugasBesar_Golden_section; | ||
| + | |||
| + | Dan didapati list harga | ||
| + | berdasarkan referensi pada: | ||
| + | *https://www.tokopedia.com/kingsteelid/plat-stainless-steel-304-mr-3-0mm-x-4-x-8 | ||
| + | *https://www.tokopedia.com/kingsteelid/plat-stainless-steel-201-hl-3-0mm-x-4-x-8 | ||
| + | *https://www.tokopedia.com/kunigan/plat-bulat-ss316-tebal-3-mm-diamter-26-cm?whid=0 | ||
| + | didapati dta sebagai berikut | ||
| + | [[File:Screenshot_(779).png|center]] | ||
| + | [[File:Screenshot_(781).png|400px|center]] | ||
| + | Dan pada akhirnya setelah di simulasi, didapati hasil perhitungan optimasi berikut: | ||
| + | |||
| + | Nilai luas area penampang optimum untuk material SS304 adalah 176mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 30mm dan tebal 3mm | ||
| + | [[File:Screenshot_(783).png|center]] | ||
| + | *xopt=nilai optimum | ||
| + | *y[1]=koefisien x^2 | ||
| + | *y[2]=koefisien x | ||
| + | *y[3]= koefisien x^0 | ||
| + | |||
| + | Material yang dianggap paling optimum oleh simulasi openmodelica, yang dapat digunakan untuk luas penampang 171mm^2 adalah material dengan nilai elastisitas 19690000000000~19700000000000 N/m^2 yang berarti material yang paling mendekati adalah SS201. | ||
| + | [[File:Screenshot_(798).png|center]] | ||
| + | *xopt=nilai optimum | ||
| + | *y[1]=koefisien x^2 | ||
| + | *y[2]=koefisien x | ||
| + | *y[3]= koefisien x^0 | ||
| + | |||
| + | ==UAS== | ||
| + | Uas Hari ini tanggal 13 Januari 2021 | ||
| + | |||
| + | untuk nomor 1 | ||
| + | [[File:Uas_no1_Ady.jpeg|600px|center]] | ||
| + | |||
| + | nomor 2 | ||
| + | [[File:Uas_no2_Ady.jpeg|600px|center]] | ||
| + | |||
| + | nomor 3 | ||
| + | [[File:Uas_no3_Ady.jpeg|600px|center]] | ||
| + | |||
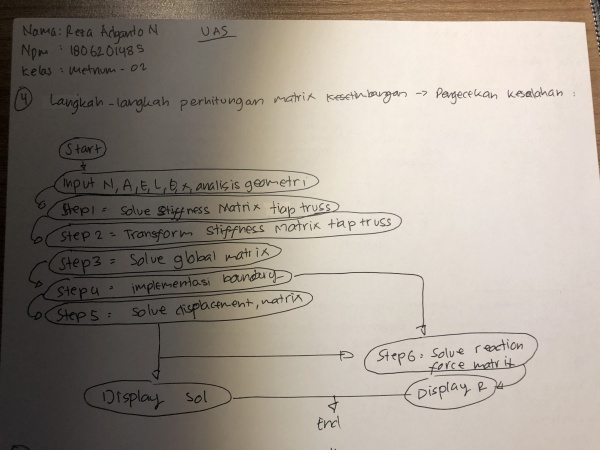
| + | nomor 4 | ||
| + | [[File:Uas_no4_Ady.jpeg|600px|center]] | ||
| + | |||
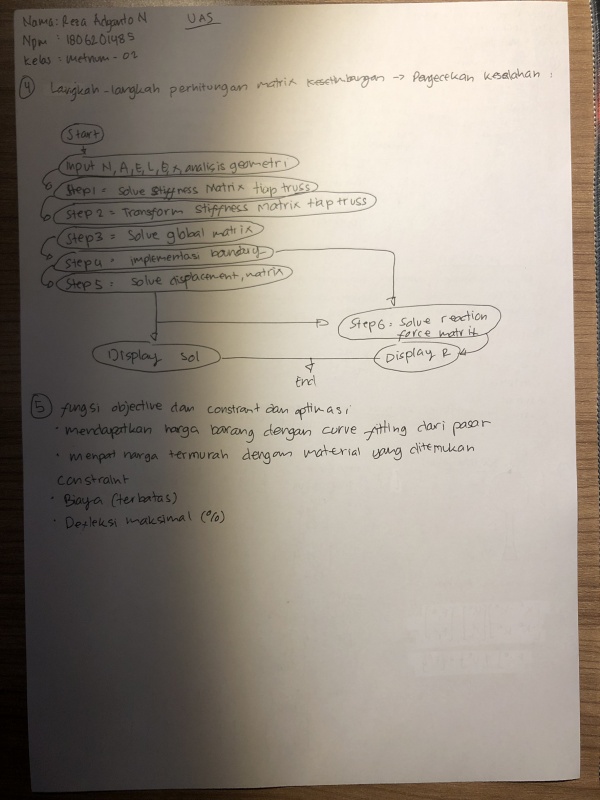
| + | nomor 5 | ||
| + | [[File:Uas_no5_Ady.jpeg|600px|center]] | ||
| + | |||
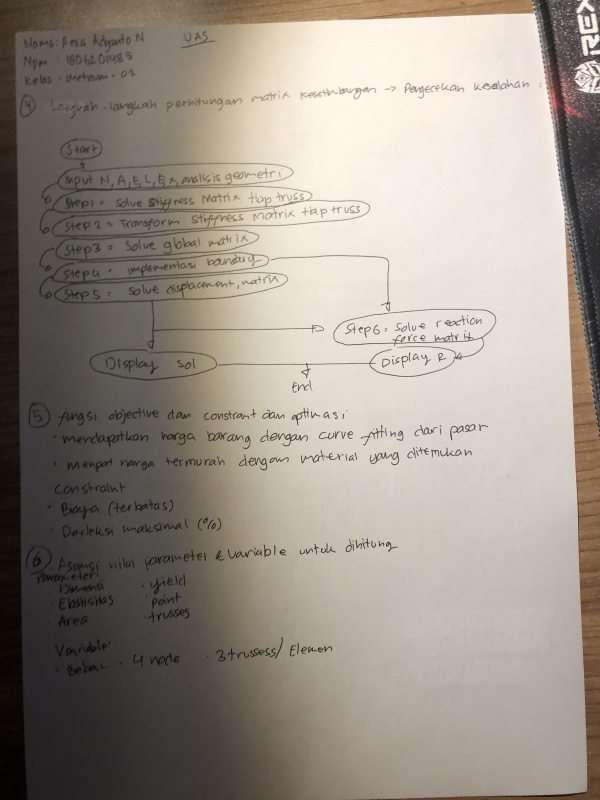
| + | nomor 6 | ||
| + | [[File:Uas_no6_Ady.jpeg|600px|center]] | ||
| + | |||
| + | |||
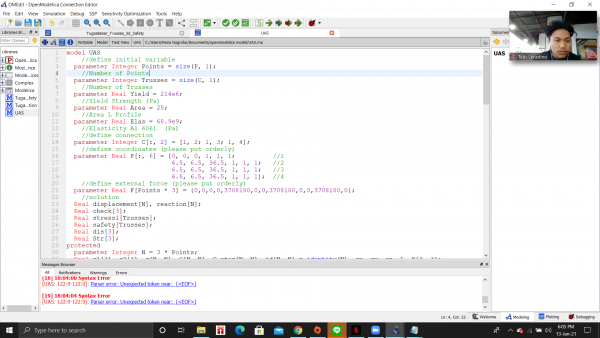
| + | nomor 7 | ||
| + | |||
| + | [[File:Uas no7 Ady 1.png|600px|center]] | ||
| + | [[File:Uas no7 Ady 2.png|600px|center]] | ||
| + | [[File:Uas no7 Ady 3.png|600px|center]] | ||
| + | [[File:Uas no7 Ady 4.png|600px|center]] | ||
| + | [[File:Uas no7 Ady 5.png|600px|center]] | ||
| + | [[File:Uas no7 Ady 6.png|600px|center]] | ||
Latest revision as of 16:54, 25 May 2022
Contents
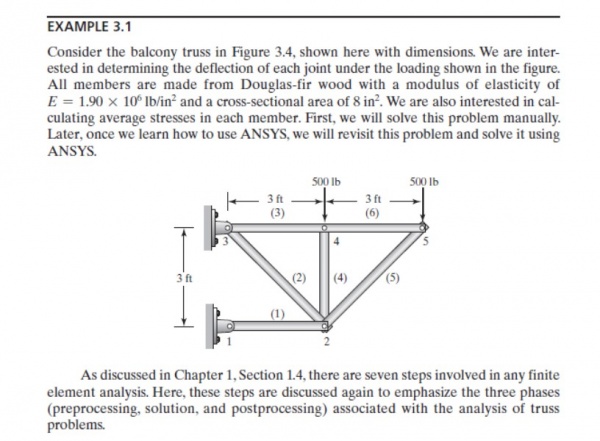
Biodata
Nama : Reza Adyanto Nugroho
NPM : 1806201485
Assalamualaikum Wr.Wb. Nama saya adalah Reza Adyanto, Saya adalah Mahasiswa Teknik Mesin Universitas Indonesia angkatan 2018. Pada tahun ini (2020) Saya sedang menganmbil mata Kuliah Metode Numerik.
Minggu 1 (11 November 2020)
Pada pertemuan minggu Pertama ini, dijelaskan tujuan-tujuan pembelajaran metode numerik, yaitu: Tujuan:
- 1.Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik, Contoh:Persamaan aljabar, algorithma, dll.
- 2.Mengerti aplikasi metode numerik.
- 3.Mampu menerapkan metode numerik dalam persoalan teknik.
- 4.Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab.
Tugas Minggu 1
Untuk tugas pertama, kami diminta mempelajari Open Modelica, yaitu sebuah aplikasi untuk membuat modelling dan simulasi. Aplikasi ini biasa digunakan di bidang industri maupun akademis.
Kemudian Saya mencoba membuat model sederhana yaitu sistem katrol Video pembelajaran dapat diakses di link:
- OpenModelica-Sistem Katrol Majemuk Gabungan https://youtu.be/c_Zb_TRQ68Y
Minggu 2 (18 November 2020)
Pada pertemuan kali ini, Pak Dai membuka pertemuan dengan memberi pembelajaran berupa sebagai manusia, kita harus memiliki perubahan setiap harinya, hari ini harus lebih baik dari hari kemarin. Sebelum memasuki materi pembelajaran metode numerik, Mahasiswa diminta mereview fungsi pembelajaran aljabar linear dan hubungannya dengan metode numerik. Kemudian, menceritakan pengalaman mempelajari aplikasi Open Modelica. Dan dari yang saya pelajari, aplikasi ini dibuat dengan tujuan bahasa pemodelan, bukan coding. Namun, ketika melakukan perhitungan, code yang ditulis harus dalam bahsa C++. Salah satu alasan pemilihan penggunaan aplikasi ini adalah karena Open Modelica dibuat open dan free, yang dimana semua orang boleh menggunakannya. Open Modelica mempunyai beberapa fitur, seperti membuat model, class, connector, expanable connector, record, function, dan lain-lain. Aplikasi ini object oriented, kita bisa membuat beberapa class fungsi dan class eksekusi, kemudian menggabungkannya ke dalam satu model, dengan pembelajaran hari dapat disebut sebagai sistem panggil.
Tugas Minggu 2
Untuk Tugas minggu 2, kami diminta untuk mempeljari kembali openmodelica dan melakukan sistem panggil dengan class dan function. Dan berikut adalah tugas saya, saya menggunakan contoh soal matriks ordo 3x3, dan berikut videonya:
Minggu 3 (25 November 2020)
pertemuan kali ini diawali dengan Pak Dai menanyakan progres belajar mandiri dari mahasiswa yang hadir. Kemudian menlanjutkan dengan dibahas aplikasi metode numerik pada suatu permasalahan. Dengan beberapa metode yang dapat digunakan yaitu Stokastik, CFD, dan FEA. Dalam proses menyelesaikan masalah teknik, angkah yang harus dilakukan adalah melakukan analisis, kemudian membuat model matematis, dengan menggunakan metode numerik untuk melakukan penyelesaian (menggunakan computer), dan mendapatkan solusi dari permasalahan.
melakukan globe code
Tugas 3
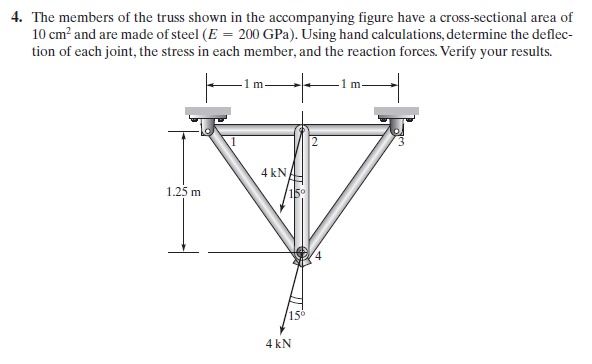
dan kami diminta untuk mengerjakan soal
kemudian setelah didapatkan hasil-hasilnya, untuk mencari displacement, perlu diberikan boundary dan external load (beban tambahan) yang dibuatkan dalam bentuk matriks A.
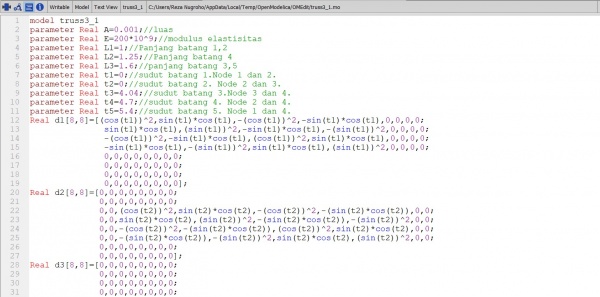
Mencari data KG
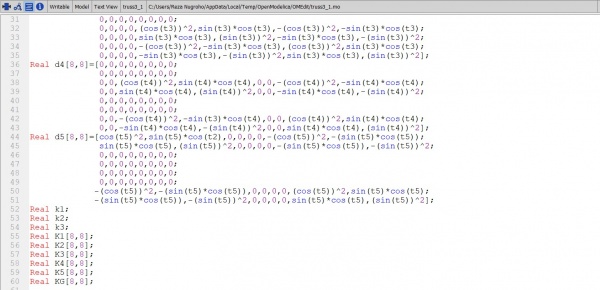
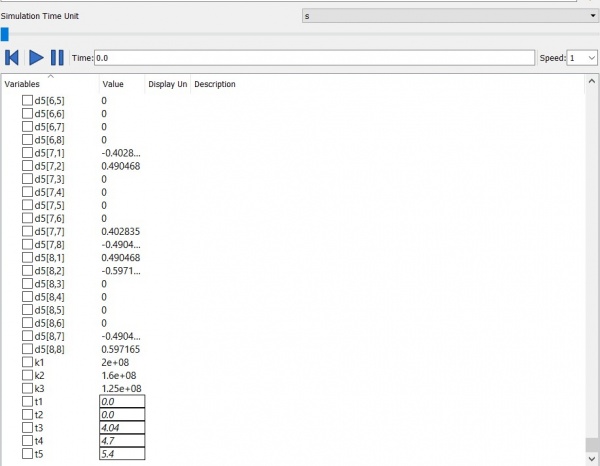
model truss3_1 parameter Real A=0.001;//luas parameter Real E=200*10^9;//modulus elastisitas parameter Real L1=1;//Panjang batang 1,2 parameter Real L2=1.25;//Panjang batang 4 parameter Real L3=1.6;//panjang batang 3,5 parameter Real t1=0;//sudut batang 1.Node 1 dan 2. parameter Real t2=0;//sudut batang 2. Node 2 dan 3. parameter Real t3=4.04;//sudut batang 3.Node 3 dan 4. parameter Real t4=4.7;//sudut batang 4. Node 2 dan 4. parameter Real t5=5.4;//sudut batang 5. Node 1 dan 4. Real d1[8,8]=[(cos(t1))^2,sin(t1)*cos(t1),-(cos(t1))^2,-sin(t1)*cos(t1),0,0,0,0;
sin(t1)*cos(t1),(sin(t1))^2,-sin(t1)*cos(t1),-(sin(t1))^2,0,0,0,0;
-(cos(t1))^2,-sin(t1)*cos(t1),(cos(t1))^2,sin(t1)*cos(t1),0,0,0,0;
-sin(t1)*cos(t1),-(sin(t1))^2,sin(t1)*cos(t1),(sin(t1))^2,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0];
Real d2[8,8]=[0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,(cos(t2))^2,sin(t2)*cos(t2),-(cos(t2))^2,-(sin(t2)*cos(t2)),0,0;
0,0,sin(t2)*cos(t2),(sin(t2))^2,-(sin(t2)*cos(t2)),-(sin(t2))^2,0,0;
0,0,-(cos(t2))^2,-(sin(t2)*cos(t2)),(cos(t2))^2,sin(t2)*cos(t2),0,0;
0,0,-(sin(t2)*cos(t2)),-(sin(t2))^2,sin(t2)*cos(t2),(sin(t2))^2,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0];
Real d3[8,8]=[0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,(cos(t3))^2,sin(t3)*cos(t3),-(cos(t3))^2,-sin(t3)*cos(t3);
0,0,0,0,sin(t3)*cos(t3),(sin(t3))^2,-sin(t3)*cos(t3),-(sin(t3))^2;
0,0,0,0,-(cos(t3))^2,-sin(t3)*cos(t3),(cos(t3))^2,sin(t3)*cos(t3);
0,0,0,0,-sin(t3)*cos(t3),-(sin(t3))^2,sin(t3)*cos(t3),(sin(t3))^2];
Real d4[8,8]=[0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,(cos(t4))^2,sin(t4)*cos(t4),0,0,-(cos(t4))^2,-sin(t4)*cos(t4);
0,0,sin(t4)*cos(t4),(sin(t4))^2,0,0,-sin(t4)*cos(t4),-(sin(t4))^2;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,-(cos(t4))^2,-sin(t3)*cos(t4),0,0,(cos(t4))^2,sin(t4)*cos(t4);
0,0,-sin(t4)*cos(t4),-(sin(t4))^2,0,0,sin(t4)*cos(t4),(sin(t4))^2];
Real d5[8,8]=[cos(t5)^2,sin(t5)*cos(t2),0,0,0,0,-(cos(t5))^2,-(sin(t5)*cos(t5));
sin(t5)*cos(t5),(sin(t5))^2,0,0,0,0,-(sin(t5)*cos(t5)),-(sin(t5))^2;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
-(cos(t5))^2,-(sin(t5)*cos(t5)),0,0,0,0,(cos(t5))^2,sin(t5)*cos(t5);
-(sin(t5)*cos(t5)),-(sin(t5))^2,0,0,0,0,sin(t5)*cos(t5),(sin(t5))^2];
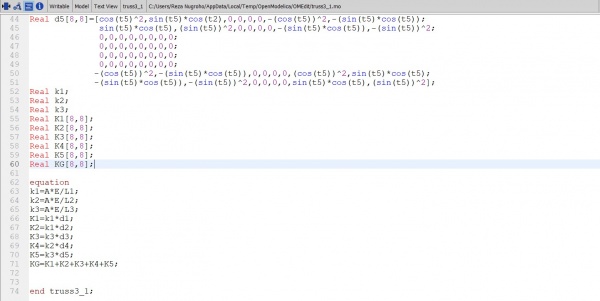
Real k1; Real k2; Real k3; Real K1[8,8]; Real K2[8,8]; Real K3[8,8]; Real K4[8,8]; Real K5[8,8]; Real KG[8,8];
equation k1=A*E/L1; k2=A*E/L2; k3=A*E/L3; K1=k1*d1; K2=k1*d2; K3=k3*d3; K4=k2*d4; K5=k3*d5; KG=K1+K2+K3+K4+K5;
end truss3_1;
Mencari data U dan R
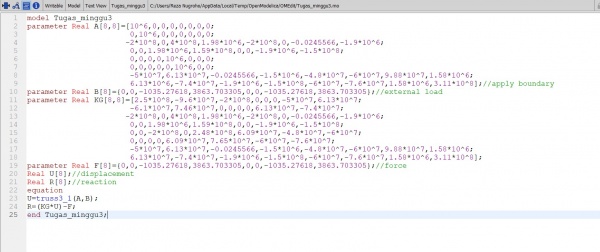
model Tugas_minggu3
parameter Real A[8,8]=[10^6,0,0,0,0,0,0,0;
0,10^6,0,0,0,0,0,0;
-2*10^8,0,4*10^8,1.98*10^6,-2*10^8,0,-0.0245566,-1.9*10^6;
0,0,1.98*10^6,1.59*10^8,0,0,-1.9*10^6,-1.5*10^8;
0,0,0,0,10^6,0,0,0;
0,0,0,0,0,10^6,0,0;
-5*10^7,6.13*10^7,-0.0245566,-1.5*10^6,-4.8*10^7,-6*10^7,9.88*10^7,1.58*10^6;
6.13*10^6,-7.4*10^7,-1.9*10^6,-1.5*10^8,-6*10^7,-7.6*10^7,1.58*10^6,3.11*10^8];//apply boundary
parameter Real B[8]={0,0,-1035.27618,3863.703305,0,0,-1035.27618,3863.703305};//external load parameter Real KG[8,8]=[2.5*10^8,-9.6*10^7,-2*10^8,0,0,0,-5*10^7,6.13*10^7;
-6.1*10^7,7.46*10^7,0,0,0,0,6.13*10^7,-7.4*10^7;
-2*10^8,0,4*10^8,1.98*10^6,-2*10^8,0,-0.0245566,-1.9*10^6;
0,0,1.98*10^6,1.59*10^8,0,0,-1.9*10^6,-1.5*10^8;
0,0,-2*10^8,0,2.48*10^8,6.09*10^7,-4.8*10^7,-6*10^7;
0,0,0,0,6.09*10^7,7.65*10^7,-6*10^7,-7.6*10^7;
-5*10^7,6.13*10^7,-0.0245566,-1.5*10^6,-4.8*10^7,-6*10^7,9.88*10^7,1.58*10^6;
6.13*10^7,-7.4*10^7,-1.9*10^6,-1.5*10^8,-6*10^7,-7.6*10^7,1.58*10^6,3.11*10^8];
parameter Real F[8]={0,0,-1035.27618,3863.703305,0,0,-1035.27618,3863.703305};//force Real U[8];//displacement Real R[8];//reaction equation U=truss3_1(A,B); R=(KG*U)-F; end Tugas_minggu3;
Minggu 4 (2 Desember 2020)
Pada pertemuan Kali ini, kami satu kelas mem-review pr yang pada minggu ke-3 sudah diberikan, =masing-masing dari kami ditanyakan mengenai PR masing-masing. Untuk PR yang saya kerjakan, saya rasa masinh banyak kekurangan dikarenakan masih banyak hal yang harus dimasukkan secara manual.
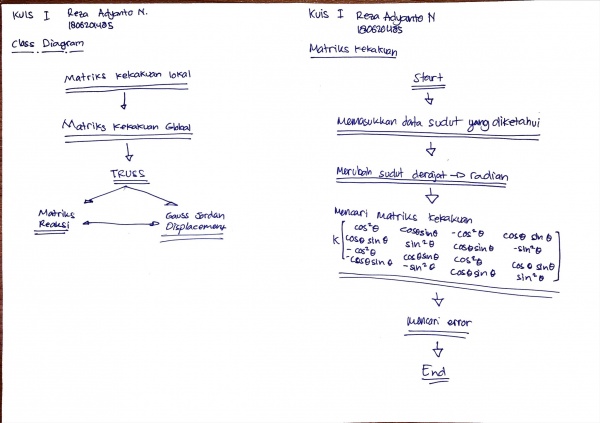
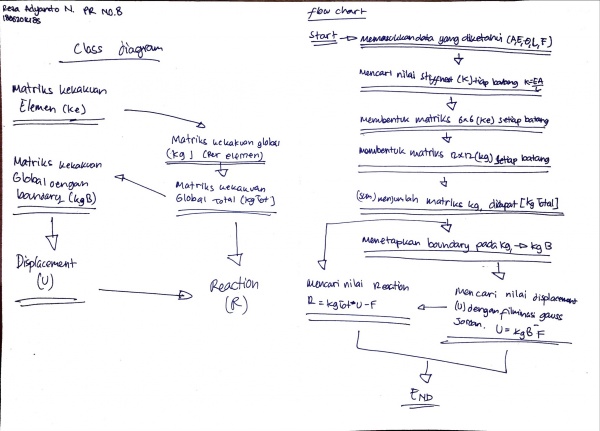
Kuis Class Diagram & Flow Chart
Dan pada minggu ini, kami kuis membuat flowchart dan class diagram dari coding penyelesaian truss milik Josiah. Terdapat 5 coding yaitu penyelesaian truss, matriks kekakuan lokal, matriks kekakuan global, matriks reaksi truss, dan Gauss Jordan untuk mendapat nilai displacement.
Tugas 4
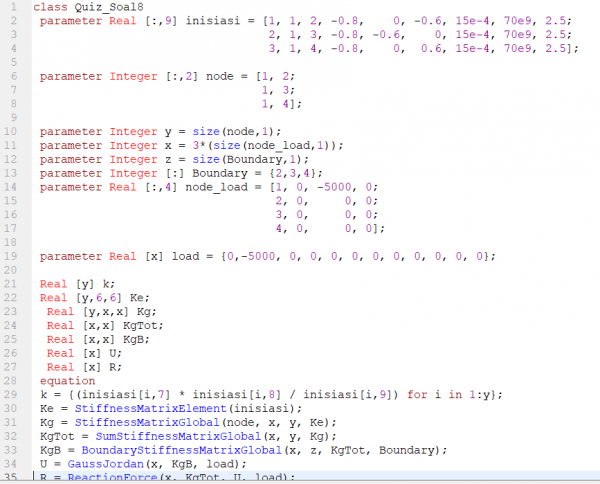
PR No. 8
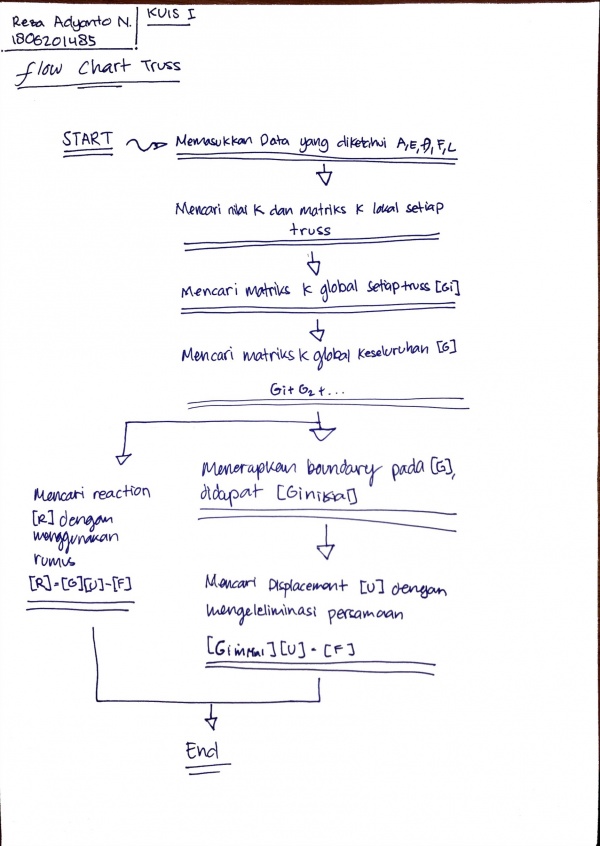
Pr minggu ini adalah 3D Truss, dimulai dengan membuat class diagram dan flow chat seperti pada tugas sebelumnya
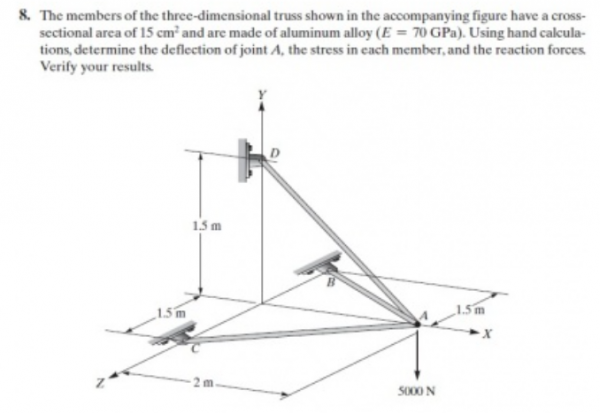
kemudian langkah berikutnya adalah membuat free body diagram untuk menentukan komponen-komponen data yang tersedia dalam soal. dari data-data yang tersdedia, berikut adalah data yang diperlukan untuk mengerjakan soal ini, node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z. Rumus untuk mencari sudut dan panjang batang saya dapatkan dari buku. Untuk gaya eksternal sendiri dapat dilihat dari gambar, hanya ada pada node 1 di sumbu y. Kemudian data-data yang sudah didapat dibuat ke dalam matriks untuk mempermudah penyelesaiannya menggunakan Open Modellica.
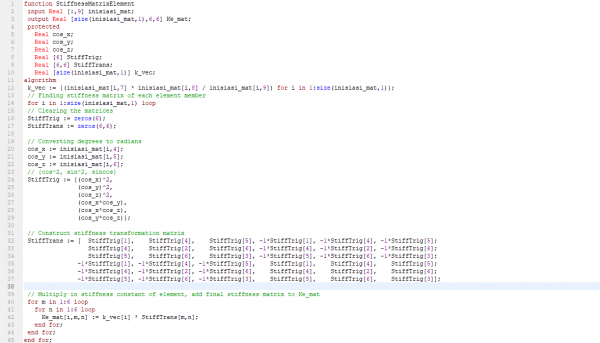
berikutnya setelah membuat matriks, mencari nilai k dapat menggunakan rumus k=AE/L. Setelah mendapa nilai k setiap batang, nilai tersebut akan digunakan untuk membuat matriks K elemental (Ke) setiap batang.
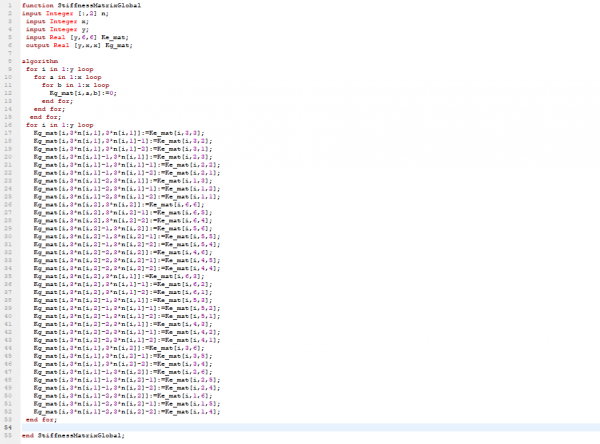
Kemudian dari matriks 6x6 tersebut dibuat menjadi matriks 12x12 sesuai dengan jumlah batang (3) * jumlah node (4) (3 x 4 = 12).Yang disebut matriks kekakuan global (Kg).
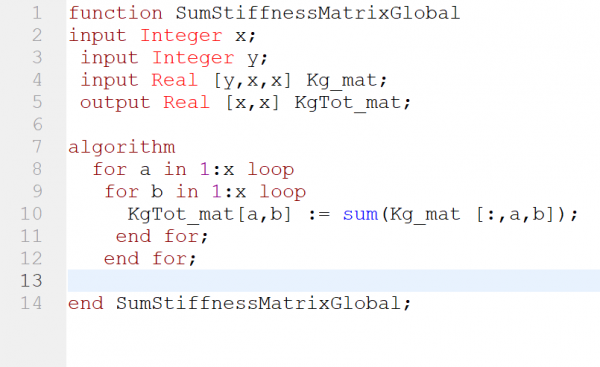
Berikutnya, matriks kekakuan global setiap batang dijumlahkan untuk mendapat matriks kekakuan global total(KgTot)
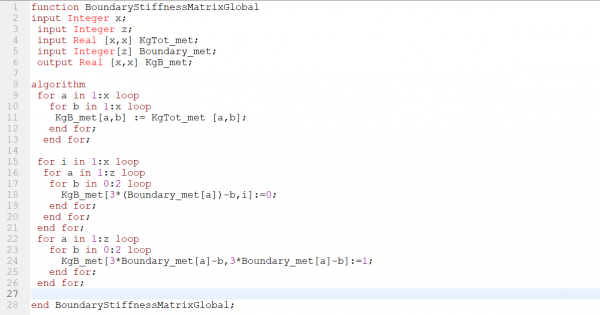
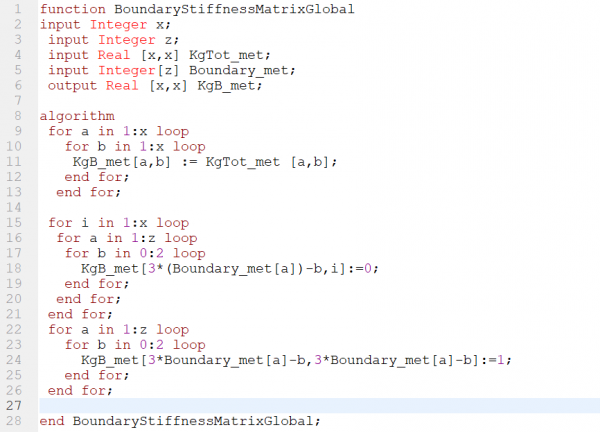
Dan kemudian, boundary diterapkan pada matriks kekakuan global total. Pada kasus ini, node 2,3, dan 4 merupakan pinned. Sehingga didapati U2X=U2Y=U2Z=U3X=U3Y=U3Z=U4X=U4Y=U4Z=0.
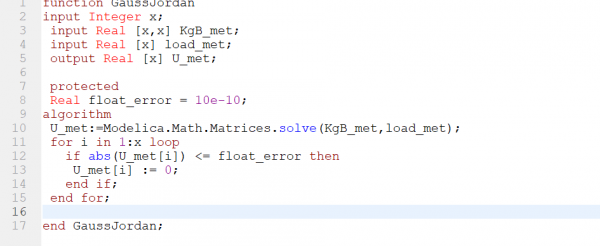
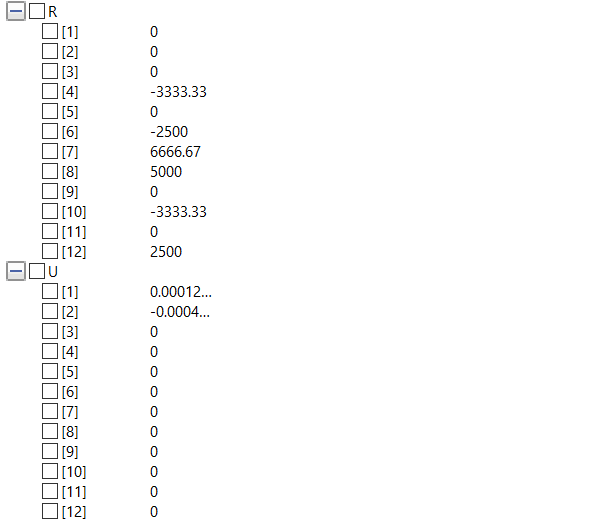
mencari nilai displacement(U) lainnya menggunakan eliminasi Gauss Jordan
Dan mencari reaction menggunakan persamaan R=Kg*U - F.
kemudian dengan materi yang sudah dipelajari pada pertemuan sebelumnya (sistem kelas panggil) Pada class akan diinput data-data yang telah docari pada langkah pertama.
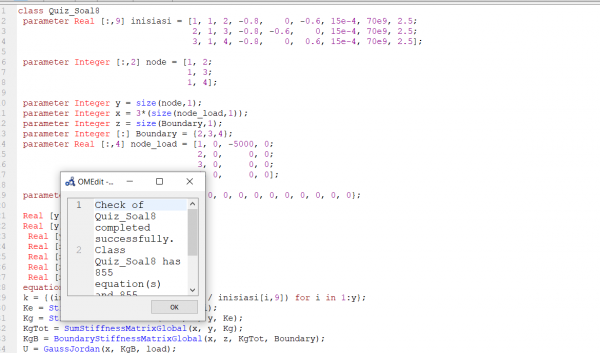
berikut, pengecekan modelica sudah successfull, dan siap di simulasi
Belajar mandiri (16-12-2020)
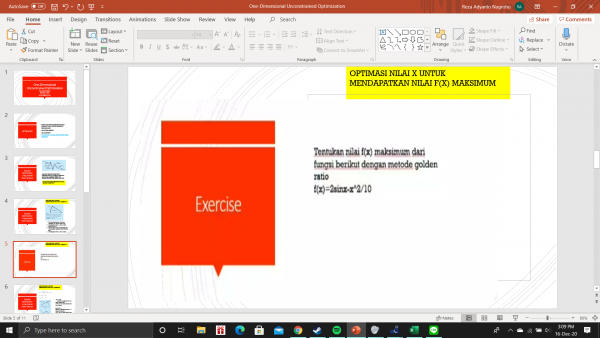
Pada kesempatan kali ini saya mencoba untuk mempelajari One-Dimensional Unconstrained Optimization, saya mempelajarinya dari video tutorial program optimasi dengan modelica, yang diupload oleh Asisten pada group WA Metnum 02.
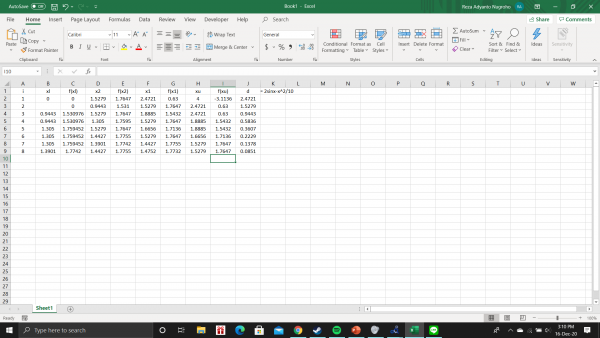
diawal saya mencari contoh soal yang diberikan f(x)= 2sinx-x^2/10
Kemudian saya memplotnya kedalam Excel sesuai dengan yang dicontohkan pada ppt yang sudah di share di group WA Metnum 02
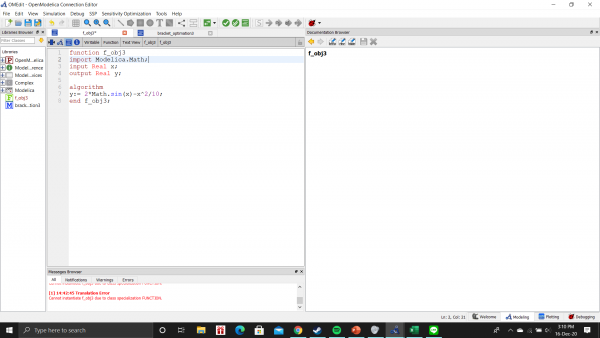
Berikutnya membuat function f_obj3
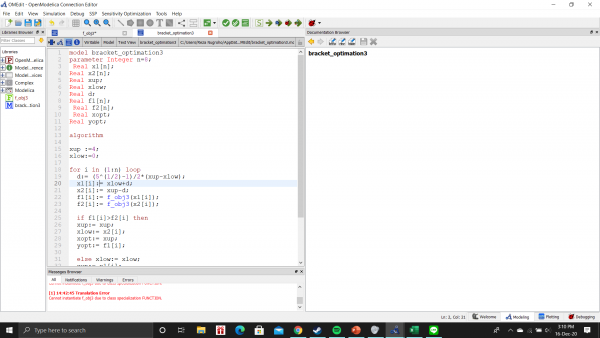
dan juga Model bracket_optimation3
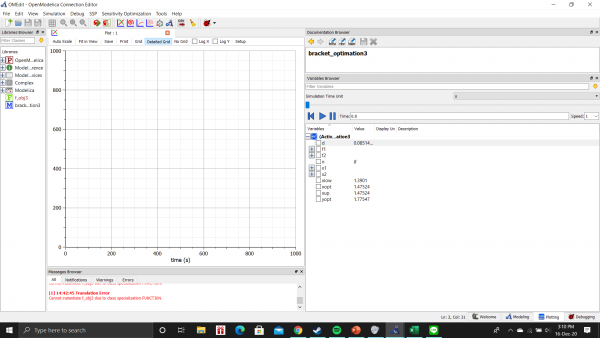
pada akhirnya memulai simulation, yang mendapatkan hasil seperti berikut.
Tugas Besar
Objektif dari Tugas ini:
- Mahasiswa diminta untuk Mengoptimasi harga pembuatan rangka truss dengan memvariasi dimensi dan elastisitas material.
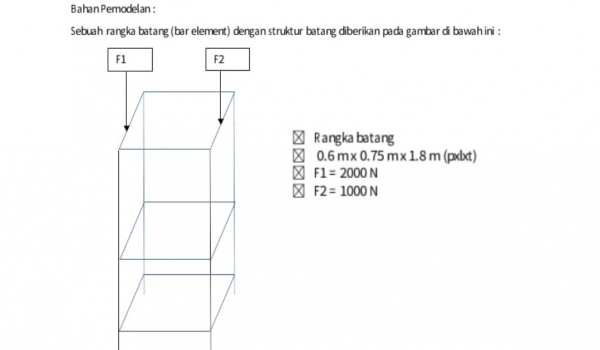
Geometry dan Load
Diketahui: panjang= 0,6 m lebar= 0,75 m tinggi= 1,6 m F1= 2000 N F2= 1000 N
kemudian diasumsikan
- Beban akan terdistribusi hanya pada node (karena bersifat trusses).
- Safety factor minimal bernilai 2.
- Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
- Ketinggian trusses pada tiap lantai sama yaitu 0,6 m.
berikutnya: Untuk jenis material yang sama:
- Mencari harga untuk 5 ukuran batang dengan material yang sama yaitu SS304.
- Mengitung nilai safety factor pada 5 ukuran batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
Untuk area penampang yang sama:
- Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2.
- Mengitung nilai safety factor pada 3 jenis batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
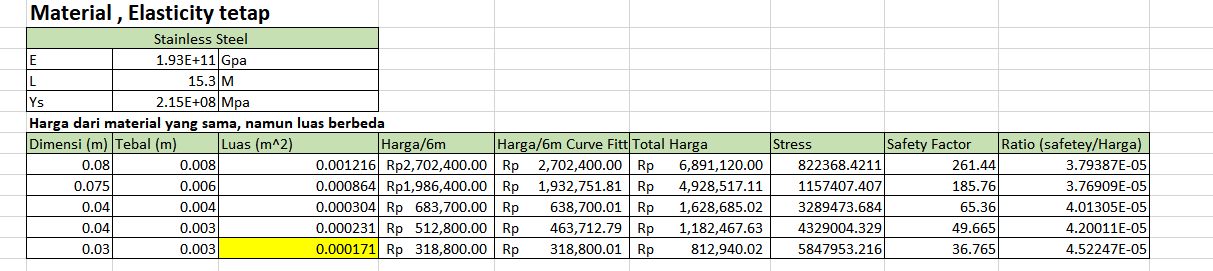
Data Material, dengan elasticity tetap berdasarkan referensi di web https://wijayamakmur.com/siku, didapati data:
Script Coding yang Digunakan
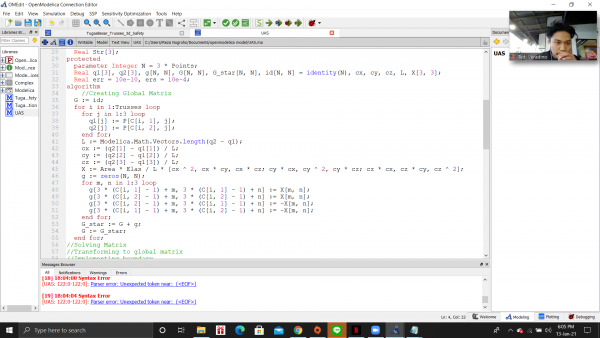
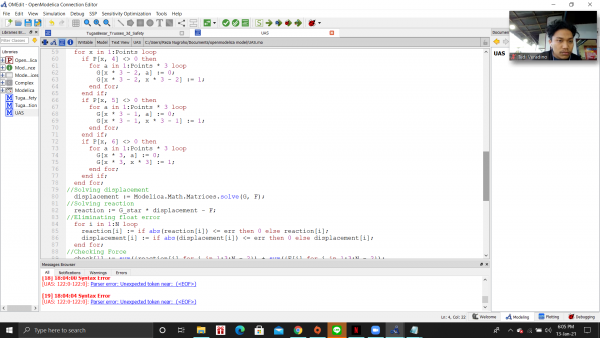
- Untuk menghitungan displacement, reaction force, stress, dan safety factor:
model TugasBesar_Trusses_3d_Safety
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
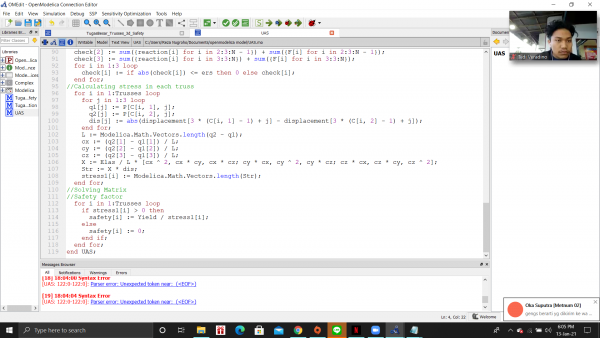
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end TugasBesar_Trusses_3d_Safety;
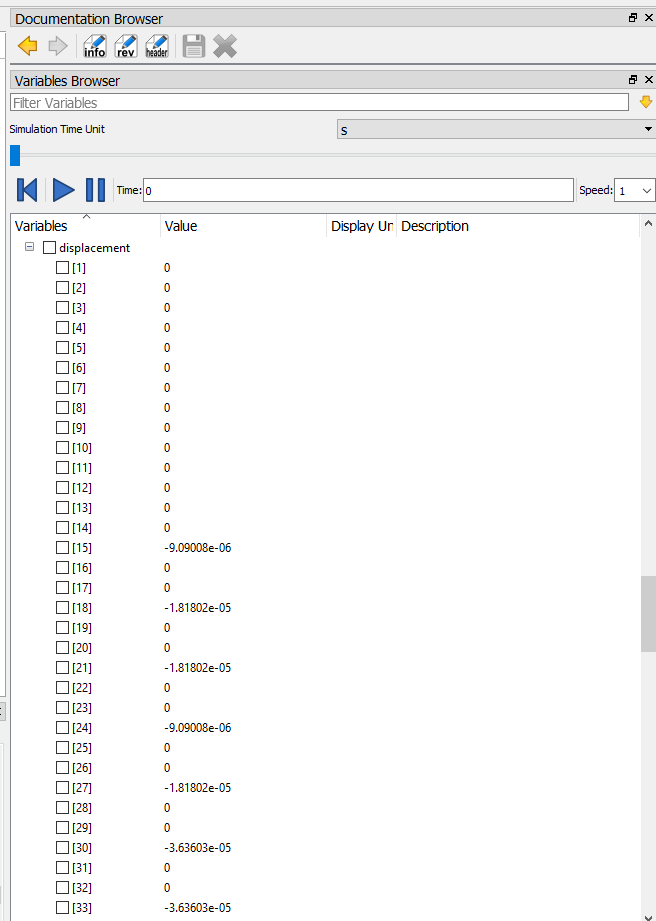
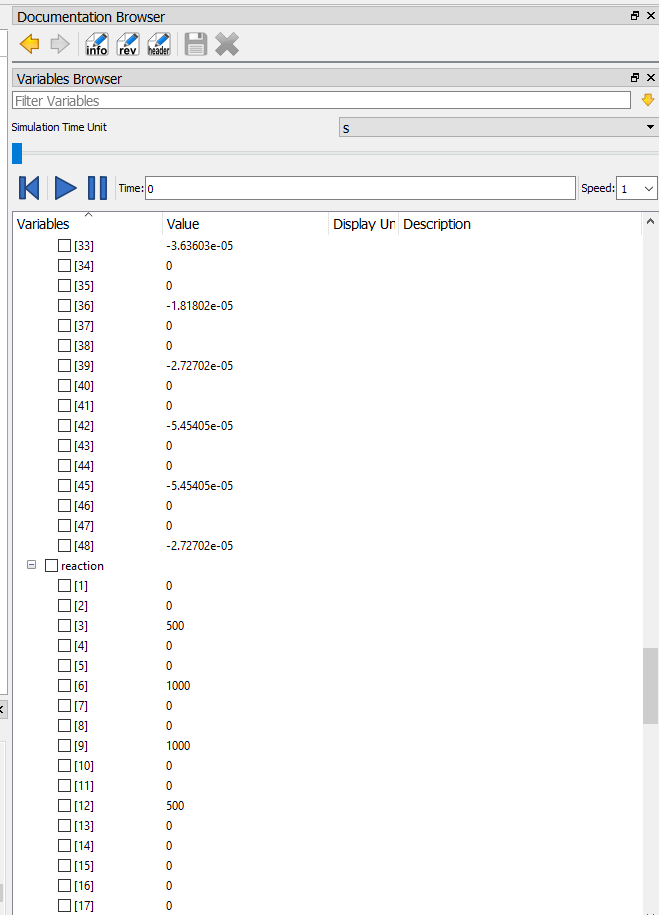
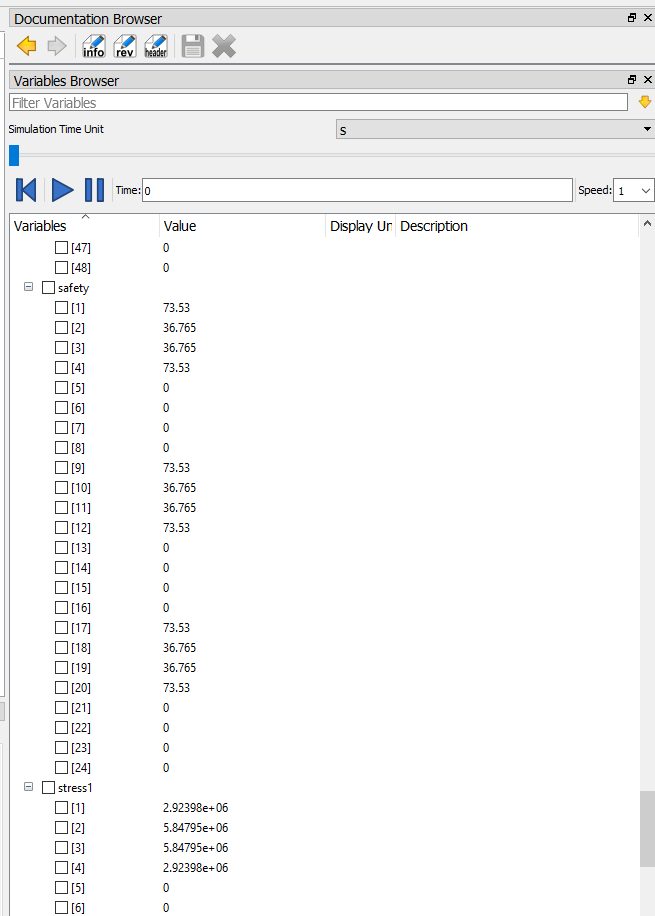
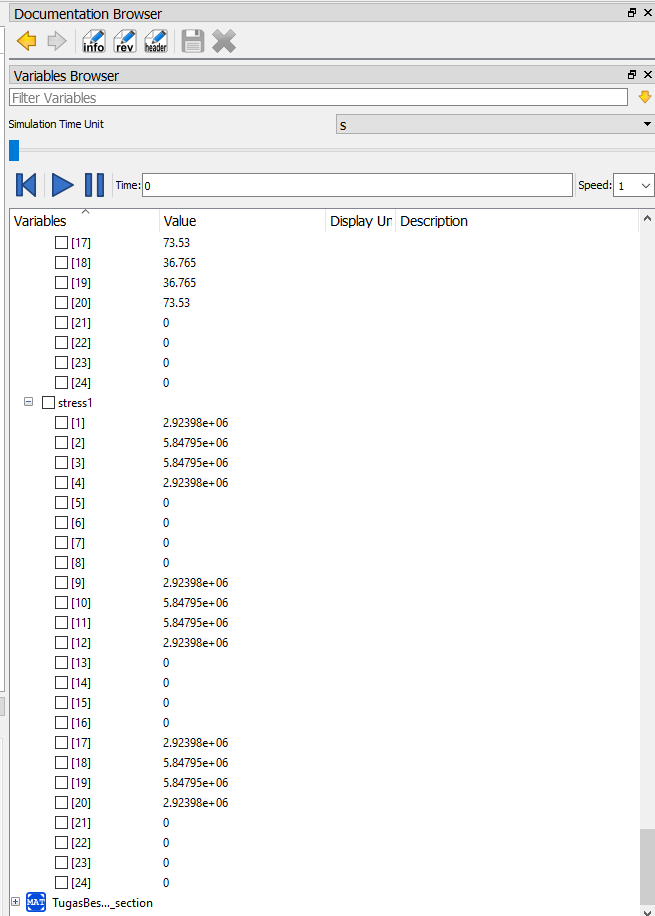
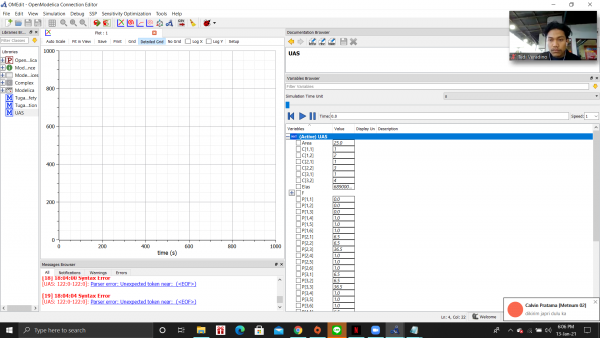
dan didapati hasil berikut dari simulasi tersebut:
- Untuk menghitung Curve fitting:
function TugasBesar_Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end TugasBesar_Curve_Fitting;
- Untuk Mencari Optimasi Luas Penampang
model TugasBesar_Golden_section
parameter Real xd[:]={0.001216,0.000864,0.000304,0.000231,0.000171};
parameter Real yd[:]={3.79387E-05,3.76909E-05,4.01305E-05,4.20011E-05,4.52247E-05};
parameter Real xlo=171e-6;
parameter Real x hi=121e-5;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := TugasBesar_Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end TugasBesar_Golden_section;
- Untuk Mencari Optimasi material (dengan mencari elastisitas Elastisitas)
model TugasBesar_Golden_section
parameter Real xd[:]={193000000000,197000000000,195000000000};
parameter Real yd[:]={5.31939E-05,0.000120965,2.96556E-05};
parameter Real xlo=1.93E+11;
parameter Real xhi=197000000000;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := TugasBesar_Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end TugasBesar_Golden_section;
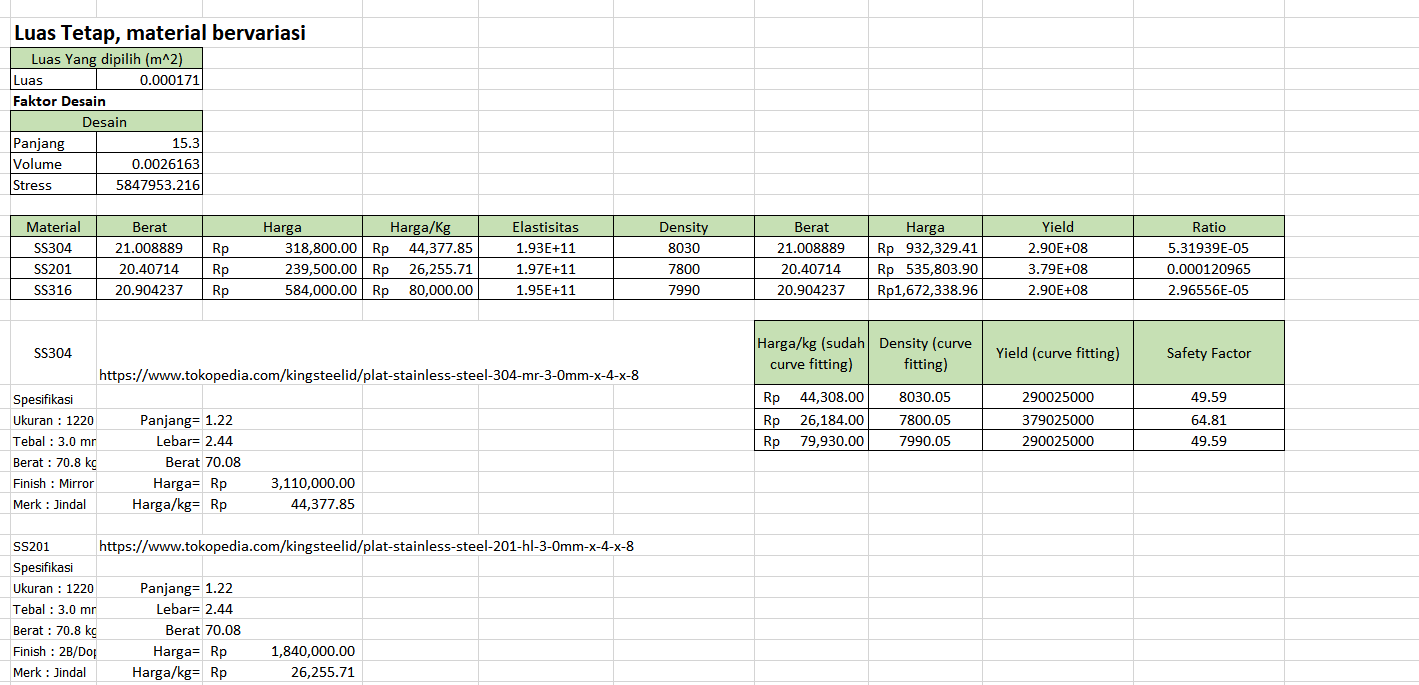
Dan didapati list harga berdasarkan referensi pada:
- https://www.tokopedia.com/kingsteelid/plat-stainless-steel-304-mr-3-0mm-x-4-x-8
- https://www.tokopedia.com/kingsteelid/plat-stainless-steel-201-hl-3-0mm-x-4-x-8
- https://www.tokopedia.com/kunigan/plat-bulat-ss316-tebal-3-mm-diamter-26-cm?whid=0
didapati dta sebagai berikut
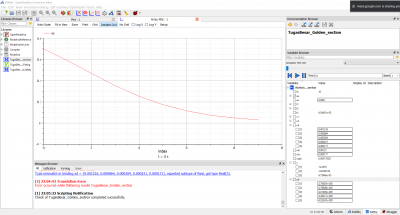
Dan pada akhirnya setelah di simulasi, didapati hasil perhitungan optimasi berikut:
Nilai luas area penampang optimum untuk material SS304 adalah 176mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 30mm dan tebal 3mm
- xopt=nilai optimum
- y[1]=koefisien x^2
- y[2]=koefisien x
- y[3]= koefisien x^0
Material yang dianggap paling optimum oleh simulasi openmodelica, yang dapat digunakan untuk luas penampang 171mm^2 adalah material dengan nilai elastisitas 19690000000000~19700000000000 N/m^2 yang berarti material yang paling mendekati adalah SS201.
- xopt=nilai optimum
- y[1]=koefisien x^2
- y[2]=koefisien x
- y[3]= koefisien x^0
UAS
Uas Hari ini tanggal 13 Januari 2021
untuk nomor 1
nomor 2
nomor 3
nomor 4
nomor 5
nomor 6
nomor 7