Difference between revisions of "Antoni"
| (2 intermediate revisions by the same user not shown) | |||
| Line 145: | Line 145: | ||
print("Maka nilai F1(reaction force) adalah : ", f1) | print("Maka nilai F1(reaction force) adalah : ", f1) | ||
| − | + | [[File:Flow chart2.jpg]] | |
TUGAS 5 | TUGAS 5 | ||
| Line 243: | Line 243: | ||
else: | else: | ||
print("Defleksi senilai : ",U[n-1]) | print("Defleksi senilai : ",U[n-1]) | ||
| + | |||
| + | |||
| + | |||
| + | UAS METODE NUMERIK TAKE HOME | ||
| + | |||
| + | optimasi L stiffener dengan metode golden range ratio | ||
| + | |||
| + | berikut kodingan yang saya gunakan untuk melakukan optimasi : | ||
| + | |||
| + | import math | ||
| + | def bracket(f,x1,h): | ||
| + | c = 1.618033989 | ||
| + | f1 = f(x1) | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | h = -h | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | return x2,x1 - h | ||
| + | for i in range (100): | ||
| + | h = c*h | ||
| + | x3 = x2 + h | ||
| + | f3 = f(x3) | ||
| + | if f3 > f2: | ||
| + | return x1,x3 | ||
| + | x1 = x2 | ||
| + | x2 = x3 | ||
| + | f1 = f2 | ||
| + | f2 = f3 | ||
| + | |||
| + | def search(f,a,b,tol=1.0e-9): | ||
| + | nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a)))) | ||
| + | R = 0.618033989 | ||
| + | C = 1.0 - R | ||
| + | x1 = R*a + C*b | ||
| + | x2 = C*a + R*b | ||
| + | f1 = f(x1) | ||
| + | f2 = f(x2) | ||
| + | for i in range(nIter): | ||
| + | if f1 > f2: | ||
| + | a = x1 | ||
| + | x1 = x2 | ||
| + | f1 = f2 | ||
| + | x2 = C*a + R*b | ||
| + | f2 = f(x2) | ||
| + | else: | ||
| + | b = x2 | ||
| + | x2 = x1 | ||
| + | f2 = f1 | ||
| + | x1 = R*a + C*b | ||
| + | f1 = f(x1) | ||
| + | if f1 < f2: | ||
| + | return x1,f1 | ||
| + | else: | ||
| + | return x2,f2 | ||
| + | print("Aplikasi Optimasi Section Modulus L Stiffner") | ||
| + | print("Kondisi Terikat : lebar alas > lebar atas > lebar tengah") | ||
| + | b1 = eval(input("Nilai lebar bangun alas :")) | ||
| + | b3 = eval(input("Nilai lebar bangun atas :")) | ||
| + | b2 = eval(input("Nilai lebar bangun tengah :")) | ||
| + | H = eval(input("Nilai tinggi L stiffner :")) | ||
| + | def f(x): | ||
| + | A1 = b1*(H-x)/2 | ||
| + | A2 = b2*x | ||
| + | A3 = b3*(H-x)/2 | ||
| + | d1 = 1/2*(H-x)/2 | ||
| + | d2 = 1/2*x+(H-x)/2 | ||
| + | d3 = 3/4*(H-x)+x | ||
| + | I1 = 1/12*b1*((H-x)/2)**3 | ||
| + | I2 = 1/12*b2*x**3 | ||
| + | I3 = 1/12*b3*((H-x)/2)**3 | ||
| + | dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) | ||
| + | I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 | ||
| + | Z = I/dc | ||
| + | return Z | ||
| + | xStart = 0.0 | ||
| + | h = 1.0 | ||
| + | x1,x2 = bracket(f,xStart,h) | ||
| + | y,fMin = search(f,x1,x2) | ||
| + | print("optimal sectional area =",-fMin) | ||
| + | print("sectional area awal" , f(H)) | ||
| + | A = -fMin/f(H)*100 | ||
| + | print ("efisiensi",A,"%") | ||
| + | input ("\nPress return to exit") | ||
| + | |||
| + | berikut link video youtube saya : | ||
| + | https://youtu.be/pDco3iFLkiY | ||
| + | |||
| + | Berikut link PPT saya di G-drive: | ||
| + | https://drive.google.com/folderview?id=1-qWXJuIkt_fYuTwWy5kYQ0NxKUXYURdu | ||
Latest revision as of 21:12, 30 May 2019
Nama : ANTONI NPM : 1706042251 Major: Naval architect and marine engineering
TUGAS 1
Tujuan dari pembelajaran metode numerik - memahami konsep/prinsip dan mampu menerapkannya - menjadi orang yang lenih mengenal dirinuya .
penerapan-penerapannya juga beberapa macam yaitu: 1.algoritma , flowchart , pemograman, metode iterative 2.menyelesaikan persamaan aljabar simultan 3.diferensial & integral 4.optimasi 5.studikasus
pada metode numerik ini kita akan banyak menjumpai angka-angka yang nilainya desimal karena dasarnya metode numerik ini ialah pedekatan sebuah nilai sebagai contoh kita punya software yang terdiri dari 34 bit dan 64 bit hal ini adalah menunjukkan koreksi pendekatan ke sebuah nilai semakin besar jumlah bit nya maka semakin banyak angka desimal yang bisa terlihat atau dapat di tampilkan.
maka perlu penalaran yang logis untuk menyelesaikan / menemukan solusi dengan metode numerik ini , bukan hafalan namun konsep berfikir kita , cara membentuk suatu konsep berfikir kita perlu banyak menganalisis dengan selalu mencari tau asal usul kenapa hal tersebut ada dan kenapa hal tersebut dapat terjadi, dengan menggunakan logika berfikir yang finite (ada batas)
salah satu logika berfikir yang kita pernah pelajari ialah kalkulus , kalkulus ialah notasi logic untuk menginterpretasikan sebuah pernyataan, kemudian dulu juga mempelajari matematika , nah kata dosen Pak Ahmad Indra (PAI) atau aki dia menyebutkan matematika bisa membantu dan juga menyesatkan , jika manusia mempunyai konsep pemikiran infinite maka matematika bisa menyesatkan. suatu saat kita akan mengerti ujar Pak Ahmad Indra
Untuk ujiannya kita menggunakan sistem muhasabah ( self reflection ) seperti yang sudah di dapatkan apa saja,dengan meliputi 3 komponen penting yaitu : 1. knowladge : yaitu pengetahuan kita, tentang yang sudah di pelajari 2. skill : keterampilan kita dalam menerapkan pengetahuan kita 3. Value : perubahan diri kita dari sebelumnya seperti; menjadi lebih rajin , menjadi lebih logis dalam berfikir.
Tugas 2
import numpy as np print("Hello this is linear algebra solution program :)") print("ix + jy = k") print("ax + by = c") print("Please input the value") i = int(input("input value of i :")) j = int(input("input value of j :")) k = int(input("input value of k :")) a = int(input("input value of a :")) b = int(input("input value of b :")) c = int(input("input value of c :")) x = np.array([[i,j],[a,b]]) y = np.array([k,c]) z = np.linalg.solve(x,y)
xval = int(z[0]) yval = int(z[1]) print("x = ",xval) print("y = ", yval)
TUGAS 3
Link video pembahasan break even point menggunakan matriks dengan metode eliminasi gauss jordan: https://youtu.be/YYITjvrmGIU
TUGAS 4
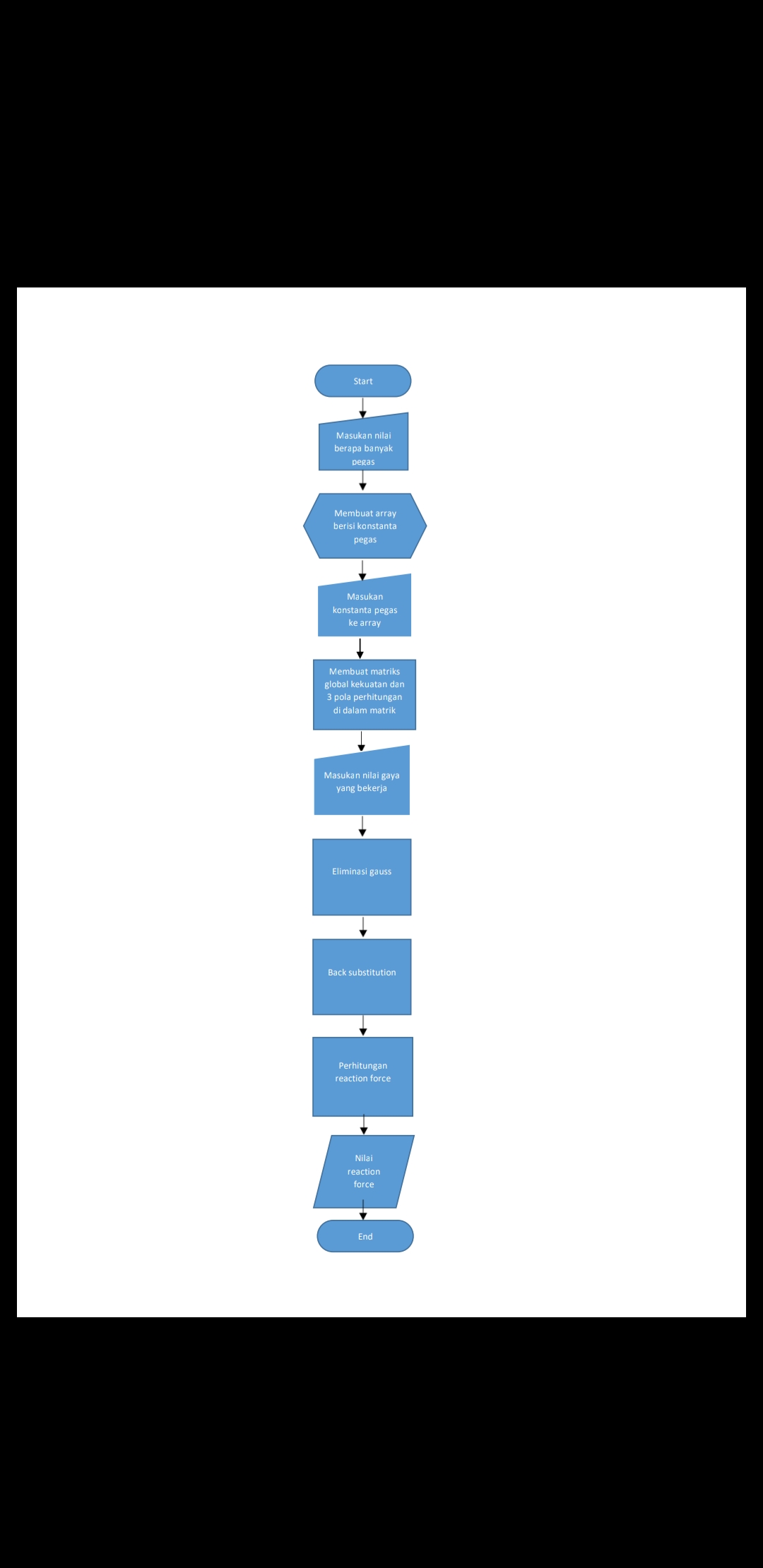
Membahas mengenai peralihan dan peregangan displacement menggunakan FEM dengan pengaplikasian pegas
import numpy as np
- menentukan jumlah pegas yang diinginkan
N = eval(input("masukan jumlah pegas yang diinginkan ? "))
y = N+1
K = np.zeros((y,y),float)
- mendefinisikan array yang berisi konstanta pegas
k_peg = np.zeros(N)
for i in range (0,N):
print("masukan nilai konstanta pegas yang ke ", i+1 , "?")
k_peg[i] = eval(input())
- membuat matriks global kekuatan
K[0,0] = k_peg[0]
K[N,N] = k_peg[N-1]
- pola1
j_1 = 0 for i_1 in range (0,N):
j_1 += 1 K[i_1,j_1] =- (k_peg[i_1])
- pola2
i_2 = 0 for j_2 in range (0,N):
i_2 += 1 K[i_2,j_2] =- (k_peg[j_2])
- pola3
j_3 = 0 for i_3 in range(1,N):
j_3 += 1 K[i_3,j_3]= k_peg[i_3]+k_peg[i_3 - 1]
print("Matriks kekakuan global sisem pegas adalah : ") print("") print (K)
- menentukan gaya yang bekerja
gaya = eval(input("masukan gaya yang bekerja atau yang diketahui ? "))
A = K[1:y , 1:y]
n = len(A)
B = np.zeros(n,float) B[n-1] = gaya
- eliminasi gauss
for k in range (0,n-1):
for i in range (k+1,n):
if A[i,k] != 0.0 :
lam = A[i,k]/A[k,k]
A[i, k:n] = A[i, k:n] - lam*A[k, k:n]
B[i]=B[i] - lam*B[k]
print("Matriks A : ") print("") print(A)
- back substitution
U = np.zeros(n,float) for m in range (n-1,-1,-1):
U[m]=(B[m]-np.dot(A[m,m+1:n], U[m+1:n]))/A[m,m]
print("Nilai U", m+2," =",U[m])
- reaction force
f1 = k_peg[0] * U[0]
print("Maka nilai F1(reaction force) adalah : ", f1)
TUGAS 5 Menentukan nilai defleksi menggunakan metode numerik di bantu dengan persamaan pegas melalui persamaan matematisnya
import numpy as np
- menentukan jumlah pegas yang diinginkan
N = 2
y = N+1
K = np.zeros((y,y),float)
- mendefinisikan bahwa array berisi konstanta pegas
k_peg = np.zeros(N) D=np.zeros(N) E=np.zeros(N) L=np.zeros(N) A_1=np.zeros(N) A=np.zeros(N) E_L=np.zeros(N) for i in range (0,N):
print("masukan nilai diameter material ", i+1," ?")
D[i]=eval(input())
print("masukan nilai Modulus Young material ", i+1," ?")
E[i]=eval(input())
print("masukan nilai panjang material ", i+1," ?")
L[i]=eval(input())
A_1[i] = float(D[i] * D[i])
A[i] = float(A_1[i] * 0.785)
E_L[i] = float(E[i] / L[i])
k_peg[i] = float(A[i] * E_L[i])
print("Nilai konstanta pegas ke - ", i+1, "adalah ",k_peg[i])
print("berapa besar jarak antara Titik B dan Material?") De=eval(input())
- membuat matriks global kekuatan
K[0,0] = k_peg[0]
K[N,N] = k_peg[N-1]
- pola1
j_1 = 0 for i_1 in range (0,N):
j_1 += 1 K[i_1,j_1] =- (k_peg[i_1])
- pola2
i_2 = 0 for j_2 in range (0,N):
i_2 += 1 K[i_2,j_2] =- (k_peg[j_2])
- pola3
j_3 = 0 for i_3 in range(1,N):
j_3 += 1 K[i_3,j_3]= k_peg[i_3]+k_peg[i_3 - 1]
print("Matriks kekakuan global sisem pegas adalah : ") print("") print (K)
gaya = eval(input("masukkan gaya yang bekerja ? "))
A = K[1:y , 1:y]
n = len(A)
B = np.zeros((n,1),float) B[0] = gaya B[1] = 0
- eliminasi gauss
for k in range (0,n-1):
for i in range (k+1,n):
if A[i,k] != 0.0 :
lam = A[i,k]/A[k,k]
A[i, k:n] = A[i, k:n] - lam*A[k, k:n]
B[i]=B[i] - lam*B[k]
- back substitution
U = np.zeros(n,float) for m in range (n-1,-1,-1):
U[m]=(B[m]-np.dot(A[m,m+1:n], U[m+1:n]))/A[m,m]
print("Nilai U", m+2," =",U[m])
if (U[n-1]>De):
print("Defleksi melebihi batas maksimum!")
else:
print("Defleksi senilai : ",U[n-1])
UAS METODE NUMERIK TAKE HOME
optimasi L stiffener dengan metode golden range ratio
berikut kodingan yang saya gunakan untuk melakukan optimasi :
import math def bracket(f,x1,h):
c = 1.618033989
f1 = f(x1)
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
h = -h
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
return x2,x1 - h
for i in range (100):
h = c*h
x3 = x2 + h
f3 = f(x3)
if f3 > f2:
return x1,x3
x1 = x2
x2 = x3
f1 = f2
f2 = f3
def search(f,a,b,tol=1.0e-9):
nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
R = 0.618033989
C = 1.0 - R
x1 = R*a + C*b
x2 = C*a + R*b
f1 = f(x1)
f2 = f(x2)
for i in range(nIter):
if f1 > f2:
a = x1
x1 = x2
f1 = f2
x2 = C*a + R*b
f2 = f(x2)
else:
b = x2
x2 = x1
f2 = f1
x1 = R*a + C*b
f1 = f(x1)
if f1 < f2:
return x1,f1
else:
return x2,f2
print("Aplikasi Optimasi Section Modulus L Stiffner") print("Kondisi Terikat : lebar alas > lebar atas > lebar tengah") b1 = eval(input("Nilai lebar bangun alas :")) b3 = eval(input("Nilai lebar bangun atas :")) b2 = eval(input("Nilai lebar bangun tengah :")) H = eval(input("Nilai tinggi L stiffner :")) def f(x):
A1 = b1*(H-x)/2 A2 = b2*x A3 = b3*(H-x)/2 d1 = 1/2*(H-x)/2 d2 = 1/2*x+(H-x)/2 d3 = 3/4*(H-x)+x I1 = 1/12*b1*((H-x)/2)**3 I2 = 1/12*b2*x**3 I3 = 1/12*b3*((H-x)/2)**3 dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 Z = I/dc return Z
xStart = 0.0 h = 1.0 x1,x2 = bracket(f,xStart,h) y,fMin = search(f,x1,x2) print("optimal sectional area =",-fMin) print("sectional area awal" , f(H)) A = -fMin/f(H)*100 print ("efisiensi",A,"%") input ("\nPress return to exit")
berikut link video youtube saya : https://youtu.be/pDco3iFLkiY
Berikut link PPT saya di G-drive: https://drive.google.com/folderview?id=1-qWXJuIkt_fYuTwWy5kYQ0NxKUXYURdu