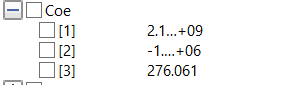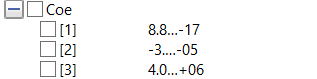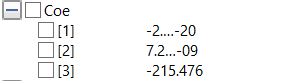Difference between revisions of "Metnum03 Rasyid Indy Nur Sasongko"
Rasyid.indy (talk | contribs) |
Rasyid.indy (talk | contribs) |
||
| (31 intermediate revisions by the same user not shown) | |||
| Line 244: | Line 244: | ||
== '''Pertemuan 6 : Senin, 14 Desember 2020''' == | == '''Pertemuan 6 : Senin, 14 Desember 2020''' == | ||
| + | |||
| + | Assalamualaikum Wr. Wb. pada pertemuan kali ini Pak Dai memberikan tugas pada setiap mahasiswa untuk melakukan muhasabah diri tentang materi pembelajaran mata kuliah metode numerik. Pak Dai berharap bahwa mahasiswa dapat menilai diri sendiri yang sesuai dengan pemahaman dan konsep yang telah dipahami. Dari muhasabah diri tersebut, Pak Dai kemudian memberikan kesempatan pada mahsiswa untuk menerangkan beberapa materi yang sudah dipahami untuk bukti bahwa mahasiswa tersebut telah sesuai dengan nilai yang diberikan pada dirinya sendiri. Parameternya adalah seberapa paham mahasiswa itu terhadap konsep dan pemahaman yang sudah diberikan selama mata kuliah metode numerik. Kemudian pembelajaran berikutnya dilanjutkan dengan materi yang diberikan oleh Christo mengenai pemahaman dari alur berfikir tentang soal-soal yang telah diberikan. Christo juga menjelaskannya ke dalam software OpenModelica mengenai bagaimana mengidentifikasi parameter apa saja yang digunakan pada soal, membentuk model, dan melakukan perhitungan dari model soal yang diberikan. Pemaparan tersebut juga dibantu oleh Josiah Enrico dan Ahmad Mohammad Fahmi untuk membandingan alur-alur pengerjaan soal-soal yang telah diberikan. | ||
| + | |||
| + | == '''Pertemuan 7 : Senin, 21 Desember 2020''' == | ||
| + | |||
| + | Assalamualaikum Wr. Wb. pada pertemuan kali ini dimulai dengan Pak Dai memberikan arahan untuk penyelesaian tugas besar. Kemudian dilanjutkan dengan menjelaskan optimasi dari truss, yang dimana pada truss tersebut terdapat 3 displacement yaitu sumbu yz, tetta dan r. Truss berbeda dengan beam dimana truss tiap titiknya mempunyai 3 derajat kebebasan dengan variabelnya displacement dalam x,y,z untuk asumsi pada suatu batang. Sedangkan pada beam, rangkanya mempunyai 6 derajat kebebasan dengan variabel x,y,z dan kearah momen atau puntirannya. Pada asumsi yang sudah dijelaskan kami sebagai mahasiswa diharapkan untuk menyusun persamaan-persamaannya. Dengan menyusun persamaannya diharapkan kami mahasiswa dapat mengerti dan memahami bagaimana menyelesaikan permasalahan tersebut dengan matriks dan variabel-variabel sudah kami susun dan dapat diaplikasikan pada aplikasi OpenModelica. Kemudian kami juga harus mengerti dan paham bagaimana menyusun persamaannya, boundary condition dan lain-lain. | ||
| + | |||
| + | Selanjutnya kami mahasiswa juga diharapkan menghitung kondisi optimal pada rangka dengan parameter seperti pada tujuan dan fungsi objektif pada optimasi. Pada perhitungan tersebut harus ada fungsi-fungsi pada batasan atau constraintsnya contohnya seperti berapa panjang siku dan harga per berapa ukuran. Optimasi ini juga mempunyai tujuan yaitu untuk meminimalisir biaya. Constraints yang diberikan harus mampu untuk menahan beban yang dimana gaya-gaya bekerja mampu didukung pada rangka tersebut. Langkah awal yang dilakukan adalah mencari displacement, memeriksa gayanya dan mengoptimasi gaya tersebut dan menghitung stress. Selanjutnya membandingkan stress dari kekuatan material yang digunakan. Tegangan yang telah dihitung tersebut tidak boleh melebihi dari allowable stress agar membentuk rangka yang sesuai dengan standar. Dari data-data yang sudah dikumpulkan, kita akan mendapatkan jenis material dan ukuran dari batang dan kita juga dapat mengetahui berapa spesifikasi siku. Lalu, kita dapat melakukan optimasi untuk mengetahui yang mana bahan yang paling optimal. | ||
| + | |||
| + | ''' k= A.E/L ''' | ||
| + | |||
| + | A= merupakan luas penampang siku | ||
| + | |||
| + | E= modulus elastisitas tiap bahan | ||
| + | |||
| + | L= panjang batang rangka | ||
| + | |||
| + | Dapat digaris bawahi bahan atau profil siku yang digunakan adalah galvanis, stainlessm dan lain-lain | ||
| + | |||
| + | '''Aplikasi Metode Numerik dalam Kasus Optimasi''' | ||
| + | |||
| + | Pembahasan tentang materi ini diberikan oleh Bu Chandra, dengan menyampaikan penjelasan-penjelasan melalui powerpoint dimana optimasi yang digunakan adalah metode bracket optimization using golden ratio. Diharapkan kita mahasiswa dapat mengikuti simulasi dengan menggunakan OpenModelica untuk menyelesaikan permasalahn dengan fungsi exercise yang telah diberikan dan tercantum pada powerpoint. Optimasi juga adalah cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi fungsi non linear, dan objektifnya adalah mencari nilai f(x) maksimum dan minimum. Kemudian dalam penerapannya dapat menggunakan persamaan sebagai berikut | ||
| + | |||
| + | d= akar5 - 1/2 x (xu-xl) | ||
| + | |||
| + | x1= x1 + d | ||
| + | |||
| + | x2= xu - d | ||
| + | |||
| + | dengan syarat sebagai berikut, | ||
| + | |||
| + | - f(x1)>f(x2), domain sebalah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama. | ||
| + | |||
| + | - f(x2)>f(x1), domain x disebelah kanan x1 daat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama. | ||
| + | |||
| + | [[File:Metn rsyd.PNG|500px|centre]] | ||
| + | |||
| + | =='''Tugas Besar Metode Numerik : Optimasi Desain Struktur Rangka (Truss) Sederhana dengan Open Modelica'''== | ||
| + | |||
| + | Pada tugas besar ini kami mahasiswa diminta untuk melakukan optimasi pemilihan material dan luas penampang trusses untuk rangka seperti gambar dibawah ini | ||
| + | |||
| + | [[File:Truss rsyd.PNG|400px]] [[File:Parameter truss.PNG|500px]] | ||
| + | |||
| + | Asumsi yang digunakan untuk melakukan perhitungan ini antara lain: | ||
| + | |||
| + | 1. Variasi Stiffness terikat dengan variabel area pada material yang akan digunakan. Karean akan sulit apabila memvariasikan elastisitas, dimana setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya | ||
| + | |||
| + | 2. Dimensi material mengikuti standar ukuran material yang dipilih | ||
| + | |||
| + | 3. Beban akan terdistribusi hanya pada node/point penghubung (karena bersifat trusses) | ||
| + | |||
| + | 4. Terdapat 2 perhitungan yaitu dengan material lock dan area lock. | ||
| + | |||
| + | '''Latar Belakang''' | ||
| + | |||
| + | Memperoleh desain dengan harga paling terjangkau dan spesifikasi atau kemampuan mumpuni untuk target penggunaan (material, luas, dan harga yang optimal) | ||
| + | |||
| + | '''Ketentuan''' | ||
| + | |||
| + | :* Optimasi dilakukan dengan mencari harga termurah dengan faktor berubah kekuatan dan area | ||
| + | |||
| + | :* Tujuan optimasi : Displacement U minimum, Cross-Area minimum, dan nilai E dan A (murah) | ||
| + | |||
| + | '''Perhitungan dan Coding''' | ||
| + | |||
| + | '''1.Elasticity Lock''' | ||
| + | |||
| + | Material lock merupakan pengambilan data dengan material yang sama dan untuk memvariasikan luas areanya. Pada material lock ini, saya menggunakan material SS400 yang berprofil siku. Dimana data yang saya ambil sebagai berikut : | ||
| + | |||
| + | [[File:SS LOCKES.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Ss harga.PNG|500px|centre]] | ||
| + | |||
| + | source : http://infoindosteel.blogspot.com/2017/02/harga-besi-baja-siku.html | ||
| + | |||
| + | '''Coding''' | ||
| + | |||
| + | '''Coding Trusses''' | ||
| + | |||
| + | model Trusses_3D_Tugas_Besar_Safety //by Rasyid Indy Nur S. 1806181874 | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=400000000; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000531; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2) | ||
| + | parameter Real Elas=79000000000; //Elasticity SS 400 A36 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Coding Curve Fitting''' | ||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | //Coe:=fill(2,size(Coe,1)); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | /* | ||
| + | for i in 1:3 loop | ||
| + | for j in 1:Points loop | ||
| + | R[j]:=reaction[3*(j-1)+i]; | ||
| + | end for; | ||
| + | Sur[i]:=sum(R); | ||
| + | end for; | ||
| + | */ | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Kemudian langkah selanjutnya adalah mencari hasil harga tiap area yang telah ditentukan melalui koding curve fitting. Sehingga kita mendapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut : | ||
| + | |||
| + | '''function''' | ||
| + | |||
| + | '''Model Tugas Besar 3D Trusses''' | ||
| + | |||
| + | [[File:Trussrsyd.PNG|500px|centre]] | ||
| + | |||
| + | '''Function Curve Fitting''' | ||
| + | |||
| + | [[File:Ss func.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Func.PNG|500px|centre]] | ||
| + | |||
| + | '''Class Curve Fitting untuk Harga Per 6M''' | ||
| + | |||
| + | [[File:Curve fit.PNG|500px|centre]] | ||
| + | |||
| + | Lalu, didapatkan hasil dari simulasi dengan nilai Coe yang akan kita ambil untuk salah satu variabel perhitungan adalah sebagai berikut: | ||
| + | |||
| + | [[File:Plotting curve.PNG|350px|centre]] | ||
| + | |||
| + | '''Hasil Excel dan Grafik''' | ||
| + | |||
| + | Setelah dilakukan perhitungan maka secara otomatis didapatkan harga di excel dengan menginput data hasil koding curve fitting. Berikut hasil dari perhitungan dan grafiknya: | ||
| + | |||
| + | [[File:Ss hasil.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Graf cost ratio.PNG|500px|centre]] | ||
| + | |||
| + | '''2. Area Locked''' | ||
| + | |||
| + | Area Locked adalah pengambilan data menggunakan luas area yang sama dan memvariasikan materialnya. Untuk area locked ini, saya menggunakan material SS400, SS304, SS403, dan SS316 yang mempunyai profil siku dengan memberikan sample yang mempunyai ariasi berupa material dan harga. Berikut data yang saya gunakan: | ||
| + | |||
| + | [[File:Area lockedrsyd.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Harga material.PNG|350px|centre]] | ||
| + | |||
| + | source : | ||
| + | |||
| + | https://www.indiamart.com/proddetail/ms-sheet-10121470997.html | ||
| + | |||
| + | https://www.tokopedia.com/kingsteelid | ||
| + | |||
| + | Setelah itu melakukan pencarian harga, density, serta yield dengan menggunakan coding curve fitting seperti yang dilakukan pada elasticity lock dengan jumlah variabel yang sesuai dengan kategorinya. Berikut adalah codingan dan masing-masing class yang saya gunakan: | ||
| + | |||
| + | '''Coding''' | ||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | //Coe:=fill(2,size(Coe,1)); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | /* | ||
| + | for i in 1:3 loop | ||
| + | for j in 1:Points loop | ||
| + | R[j]:=reaction[3*(j-1)+i]; | ||
| + | end for; | ||
| + | Sur[i]:=sum(R); | ||
| + | end for; | ||
| + | */ | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Class''' | ||
| + | |||
| + | '''class cost''' | ||
| + | |||
| + | [[File:Class cost.PNG|500px|centre]] | ||
| + | |||
| + | '''coe cost''' | ||
| + | |||
| + | [[File:Coe cost per kg.PNG|350px|centre]] | ||
| + | |||
| + | '''class density''' | ||
| + | |||
| + | [[File:Class density.PNG|500px|centre]] | ||
| + | |||
| + | '''coe density''' | ||
| + | |||
| + | [[File:Coe density.PNG|350px|centre]] | ||
| + | |||
| + | '''class yield''' | ||
| + | |||
| + | [[File:Yield rsyd.PNG|500px|centre]] | ||
| + | |||
| + | '''coe yield''' | ||
| + | |||
| + | [[File:Coe yield.PNG|350px|centre]] | ||
| + | |||
| + | '''Hasil Excel dan Grafik''' | ||
| + | |||
| + | Setelah dilakukan perhitungan maka secara otomatis didapatkan harga di excel dengan menginput data hasil koding curve fitting. Berikut hasil dari perhitungan dan grafiknya: | ||
| + | |||
| + | [[File:Hitungan area locked.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Graf cost area.PNG|500px|centre]] | ||
| + | |||
| + | == ''' Ujian Akhir Semester Metode Numerik (13 Januari 2020) ''' == | ||
| + | |||
| + | '''No. 1''' | ||
| + | |||
| + | [[File:Uas no 1rsyd.jpg|500px|centre]] | ||
| + | |||
| + | Penjelasan no. 1 : | ||
| + | |||
| + | Pada soal no. 1 ini, diberikan soal mengenai water tower dengan resevoir berbentuk bola yang diberikan oleh Pak Dai. Kemudian Pak Dai meminta untuk mahasiswa untuk membuat permodelan numerik untuk mengoptimalkan struktur water tower tersebut. No. 1 ini diberikan perintah untuk membuat prosedur permodelan numerik untuk optimasi struktur tersebut. | ||
| + | |||
| + | - 1. Mendefinisikan masalah | ||
| + | |||
| + | Pertama-tama hal yang dilakukan adalah mengidentifikasi untuk jumlah batang yang akan digunakan, kemudian dari jumlah dari batang-batang yang digunakan didapatkan node-node. Mendefinisikan masalah juga berguna untuk mengidentifikasi profil yang akan digunakan untuk struktur dari water tower tersebut. | ||
| + | |||
| + | - 2. Menentukan asumsi kondisi | ||
| + | |||
| + | Menentukan asumsi yang akan digunakan agar mudah untuk dicari data yang akan digunakan. Kemudian pada step ini, langkah yang dilakukan adalah memberikan parameter-parameter. | ||
| + | |||
| + | - 3. Research data | ||
| + | |||
| + | Research data disini digunakan untuk mencari data-data yang akan digunakan untuk membuat permodelan numerik untuk mengoptimalkan struktur water tower tersebut. | ||
| + | |||
| + | - 4. Permodelan numerik | ||
| + | |||
| + | Mempersiapkan atau membuat codingan yang sesuai dengan variabel-variabel sehingga cocok digunakan untuk mengoptimalkan struktur water tower tersebut. | ||
| + | |||
| + | - 5. Komputasi | ||
| + | |||
| + | Memasukan codingan yang sudah dipersiapkan ke software atau aplikasi OpenModelica | ||
| + | |||
| + | - 6. Penentuan akhir struktur atau material | ||
| + | |||
| + | Mendapatkan struktur yang paling optimal dan yang paling sesuai dengan kaidah hukum fisika atau sesuai dengan codingan yang telah dibuat. | ||
| + | |||
| + | '''No. 2''' | ||
| + | |||
| + | [[File:Uas no 2rsyd.jpg|500px|centre]] | ||
| + | |||
| + | Penjelasan no. 2 : | ||
| + | |||
| + | Tujuan Permodelan Numerik adalah : | ||
| + | |||
| + | - Mempermudah untuk menganalisis displacement dan gaya reaksi | ||
| + | |||
| + | - Mempermudah untuk mengidentifikasi nilai minimum atau maksimum dari struktur dan material yang akan digunakan | ||
| + | |||
| + | - Memperoleh desain dengan harga yang minimum dan spesifikasi yang optimal. | ||
| + | |||
| + | Asumsi | ||
| + | |||
| + | - Beban terdistribusi pada titik sambung | ||
| + | |||
| + | - Safety factor yang digunakan minimal 2 atau setengah dari modulus elastisitas material | ||
| + | |||
| + | - Batas displacement pada truss yang digunakan memiliki nilai yang relatif | ||
| + | |||
| + | - Ketinggian trusses pada water tower konstan | ||
| + | |||
| + | Hukum Fisika | ||
| + | |||
| + | - Stiffness (kekakuan) | ||
| + | |||
| + | - Gaya Reaksi | ||
| + | |||
| + | - Hukum Newton III | ||
| + | |||
| + | - Hukum Hooke | ||
| + | |||
| + | - Hukum Konservasi Energi | ||
| + | |||
| + | '''No. 3''' | ||
| + | |||
| + | [[File:Uas no 3rsyd.jpg|500px|centre]] | ||
| + | |||
| + | Penjelasan no. 3 : | ||
| + | |||
| + | Pada no. 3 ini dibuat variabel atau persamaan untuk membuat matriks global, yaitu untuk matriks lokal yang digunakan berdasarkan turunan dari U1x, U1y, U2x, U2y. Pada permodelan truss 1D tersebut menggunakan dua axis yaitu axis x dan axis y. Matriks lokal yang telah dihitung tersebut untuk dx dan dy kemudian dicari sudutnya untuk diinput ke matriks lokal. setelah mendapatkan matriks lokal tadi, hasilnya dijumlahkan dari masing-masing hasil matriks lokal untuk digunakan membentuk matriks global. | ||
| + | |||
| + | '''No. 4''' | ||
| + | |||
| + | [[File:Uas no 4rsyd.jpg|500px|centre]] | ||
| + | |||
| + | Penjelasan no. 4 : | ||
| + | |||
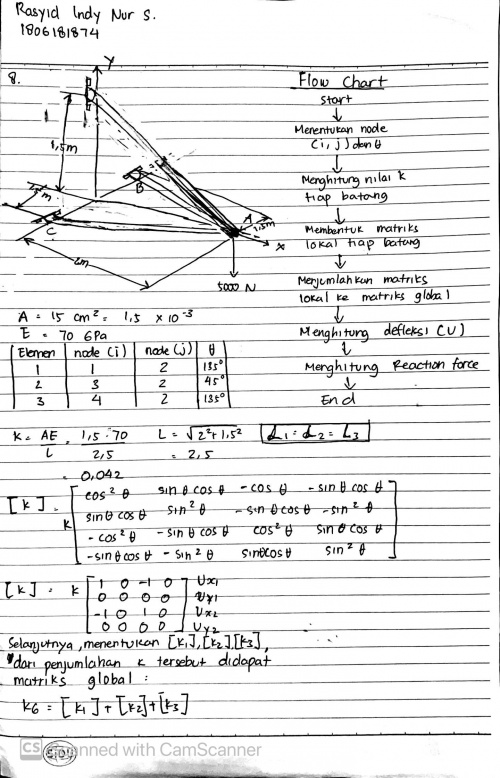
| + | Membuat flowchart untuk pseudocode dari optimasi permodelan. Dengan tahapan yaitu : | ||
| + | |||
| + | - Menuliskan class dan mendefinisikan parameter-parameter yang ada | ||
| + | |||
| + | - Menuliskan matriks element | ||
| + | |||
| + | - Menuliskan matriks global | ||
| + | |||
| + | - Menjumlahkan atau menuliskan penjumlahan matriks global | ||
| + | |||
| + | - Mengimplementasikan kondisi batas sistem | ||
| + | |||
| + | - Gauss-Jordan matriks | ||
| + | |||
| + | - Menuliskan gaya reaksi | ||
| + | |||
| + | '''No. 5''' | ||
| + | |||
| + | [[File:Uas no 5rsyd.jpg|500px|centre]] | ||
| + | |||
| + | Penjelasan no. 5 : | ||
| + | |||
| + | Fungsi Objektif : Menemukan material yang optimal | ||
| + | |||
| + | Constraint : Constraint yang digunakan yaitu luas area penampang dan elastisitas material. | ||
| + | |||
| + | '''No. 6''' | ||
| + | |||
| + | Penjelasan no. 6 : | ||
| + | |||
| + | Memberikan asumsi nilai-nilai parameter dan variable untuk mendapatkan displacement, restraint, dan stress | ||
| + | |||
| + | Parameter yang saya gunakan adalah : | ||
| + | |||
| + | - Tinggi : 120 ft = 1440 in | ||
| + | |||
| + | - L : 40 ft = 480 in | ||
| + | |||
| + | - E : 27 x 10^6 lb/in^2 | ||
| + | |||
| + | - A : 30 | ||
| + | |||
| + | - load : 30.000 | ||
| + | |||
| + | [[File:Uas no 6rsyd.jpg|500px|centre]] | ||
| + | |||
| + | '''No. 7''' | ||
| + | |||
| + | [[File:Uas no 7rsyd.jpg|500px|centre]] | ||
| + | |||
| + | Penjelasan no. 7 : | ||
| + | |||
| + | Berikut adalah codingan yang digunakan untuk menjawab nomor 7 yang saya gunakan untuk menyelesaikan permasalahan truss 1D sesuai dengan asumsi pada nomor 6: | ||
| + | |||
| + | model uasrsyd | ||
| + | /*Nama = Rasyid Indy Nur Sasongko | ||
| + | NPM = 1806181874 */ | ||
| + | |||
| + | parameter Real P[3]={30000,0,-30000};//beban dan gaya reaksinya (beban berada pada node 3 yang negatif dan gaya yang negatif dan gaya reaksi pada node 1 | ||
| + | dengan nilai positif) | ||
| + | |||
| + | /*asumsi semua elemen sejenis*/ | ||
| + | parameter Real a=30e-6;//luas penampang | ||
| + | parameter Real e=27e6;//elastisitas | ||
| + | parameter Real l=40;//panjang | ||
| + | |||
| + | /*parameter yang akan dicari*/ | ||
| + | Real k;//kekakuan elemen | ||
| + | Real kg[3,3];//matriks global | ||
| + | Real u[3];//displacement | ||
| + | Real stress[3];//stress yang dialami | ||
| + | |||
| + | |||
| + | algorithm | ||
| + | /*mencari nilai kekakuan*/ | ||
| + | k := a*e/1; | ||
| + | |||
| + | /*menuliskan persamaan matriks global*/ | ||
| + | kg := [k, 2*k, 0; | ||
| + | -k, 2*k, -k; | ||
| + | 0, -k, 2*k]; | ||
| + | |||
| + | /*mencari displacement dengan metode gauss-jordan*/ | ||
| + | u := Modelica.Math.Matrices.solve(kg,P); | ||
| + | |||
| + | /*mencari stress pada tiap elemen*/ | ||
| + | stress[1] := u[1]*k/a; | ||
| + | stress[2] := u[2]*k/a; | ||
| + | stress[3] := u[3]*k/a; | ||
| + | |||
| + | end uasrsyd; | ||
| + | |||
| + | ---- | ||
| + | |||
| + | [[File:Uas rsyd.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Rsyd uas.PNG|500px|centre]] | ||
| + | |||
| + | [[File:Hasil rasyid.PNG|500px|centre]] | ||
| + | |||
| + | Hasil yang didapatkan adalah '''displacement''' sebesar '''[26.455 , 5.291, -15.873]''' dan '''stress''' sebesar '''[7.14286e+08, 1.42857e+08, -4.28571e+08]''' | ||
Latest revision as of 23:09, 14 January 2021
Contents
- 1 Pendahuluan
- 2 Pertemuan 1 : Senin, 9 November 2020
- 3 Tugas 1 Membuat Video
- 4 Pertemuan 2 : Senin, 16 November 2020
- 5 Tugas 2 : Tugas memecahkan suatu persamaan aljabar simultan
- 6 Pertemuan 3 : Senin, 23 November 2020
- 7 Tugas 3
- 8 Pertemuan 4: Senin, 30 November 2020
- 9 Quiz Pertemuan 4 dan Tugas 4
- 10 Pertemuan 5 : Senin, 7 Desember 2020
- 11 Tugas 5
- 12 Pertemuan 6 : Senin, 14 Desember 2020
- 13 Pertemuan 7 : Senin, 21 Desember 2020
- 14 Tugas Besar Metode Numerik : Optimasi Desain Struktur Rangka (Truss) Sederhana dengan Open Modelica
- 15 Ujian Akhir Semester Metode Numerik (13 Januari 2020)
Pendahuluan
سْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Nama : Rasyid Indy Nur Sasongko
NPM : 1806181874
Perkenalkan, nama saya Rasyid Indy Nur Sasongko, saya merupakan mahasiswa S1 paralel Teknik Mesin Universitas Indonesia. Berikut ini merupakan beberapa catatan-catatan yang telah saya tulis selama Perkuliahan Jarak Jauh (PJJ) mata kuliah Metode Numerik. Catatan ini berisi tugas yang diberikan kemudian juga progress pembelajaran saya diadakan pertemuan.
Pertemuan 1 : Senin, 9 November 2020
Assalamualaikum Wr.Wb. pada pertemuan awal kali ini Pak Dai mengawali pertemuan dengan memberikan arahan dalam sistem pembelajaran menggunakan Air.eng.ui.ac.id sebagai tools untuk belajar dan bahan rangkuman setiap pertemuannya. Dalam pertemuan kali ini Pak Dai juga memberikan beberapa poin penting dalam berlangsungnya kegiatan belajar khususnya untuk mata kuliah metode numerik. Berikut beberapa poin yang disampaikan oleh Pak Dai :
- Mengenal atau mengetahui proses pengetahuannya
- Mengerti konsep
- Bisa membantu memecahkan masalah dari pemahaman tersebut
- Mendapatkan nilai tambah bagi diri sendiri
Dari keempat poin tersebut, konsep-konsep metode numerik yang telah dipelajari dari awal dan sebelum uts harus dipahami dan dimengerti agar dapat mengenal dan mengetahui proses belajarnya. Kemudian dari konsep-konsep yang kita sudah pelajari selanjutnya kita bisa mulai bisa memecahkan masalah-masalah yang berkaitan dengan teknik mesin sebagai outputnya. Dan yang terakhir kita dapat menilai diri kita sendiri dimana kita sudah bisa sejauh apa menguasai materi numerik dan peningkatan ilmu yang sudah didapat. Hal itu didapat dari nilai tambah bagi diri sendiri sebagai nilai tolak ukur. Kemudian pada akhir kelas kami diminta untuk mempelajari software Openmodelica dan mencoba aplikasi tersebut.
Materi Metode Numerik : Sebelum UTS
Pada mata kuliah metode numerik, di chapter-chapter awal kami mempelajari metode numerik secara garis besar. Namun pada chapter 5 ini, mulai diberikan beberapa metode-metode yang digunakan untuk menyelesaikan persamaan. Metode yang pertama adalah bracketing method yang berisi Graphical method, False position method, dan Bisection method. Lalu, metode selanjutnya yaitu open method yang berisikan Fixed-point iteration, Secant method, Newton Raphson method dan Brent's method.
Kemudian pada chapter selanjutnya, kami diberikan materi tentang regresi linear. Kegunaan regresi linear tersebut biasanya digunakan untuk membuktikan teori-teori yang sudah ada dengan eksperimen. Kami mengujinya dengan mengambil sampel yang bervariasi, kemudian kami dapat menghitung beberapa variabel seperti error dan lain-lain. Metode ini sering dijumpai ketika melakukan praktikum atau pada saat menganalisa suatu data.
Pada chapter terakhir sebelum uts yang diberikan kepada kami adalah materi tentang interpolasi. Interpolasi linier adalah salah satu metode yang digunakan untuk mengetahui nilai dari interval dua buah titik yang terletak dalam satu garis lurus. Interpolasi ini juga mempunyai beberapa jenis yaitu Newton Divided difference, Langrange, Spline, dan multidimesional.
Tutorial mempelajari software Open Modelica
Dalam mempelajari dan memahami modelica, saya mencoba melihat tutorialnya di youtube dengan link : https://www.youtube.com/watch?v=SW5Eclf1tRs&t=5s
Didalam video tersebut membahas pengenalan modelica untuk para pemula atau beginners. Video tersebut juga menjelaskan tentang simbol-simbol, tools, interface, dan lain-lain. Pada bagian libraries, terdapat tools yang dapat membantu kita dalam menggunakan modelica. Ada berbagai macam tools yang mempunyai berbagai fungsi yang sesuai dengan fungsinya. Berikut contoh gambarnya :
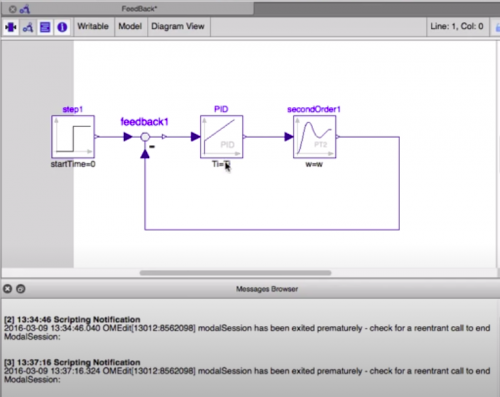
Kemudian tutorial dalam membuat sebuah simulasi menggunakan software open modelica saya menggunakan referensi : https://www.youtube.com/watch?v=Dw66ODbMS2A&t=3s dalam referensi tersebut, video tersebut menjelaskan simulasi sebuah feedback control system.
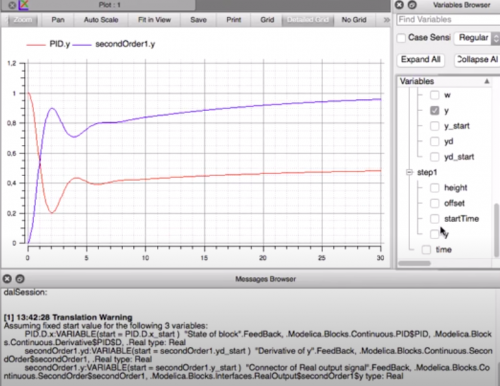
Diawal simulasi, dimulai dengan melakukan pembuatan model untuk disimulasikan. Dalam melakukan simulasi tersebut sistem yang digunakan adalah sistem linear dimana simple second order system sebagai target untuk kontrol. PID control pada Open Modelica menggunakan tool continous. Kemudian area simulasi dimasukkan dengan blok untuk PID control dan simple second order system. Lalu menu math digunakan tool feedback ke area simulasi, dan menu source yang berupa tool step, dikoneksikan ke seluruh sistem. Drag keseluruhan blok dan tools yang ada untuk membuat sistem menjadi closed loop.
Selanjutnya tahap yang dilakukan adalah tahap memasukan nilai parameter. Sistem menggunakan underdamped, nilai damping <1. Sistem kemudian dicek melalui perhitungan dan didapatkan 22 persamaan dan 22 variabel. Simulasi juga dilakukan dengan 30 interval. Hasil output data dari grafik kita mendapat variabel seperti U dan y. Diakhir simulasi kita juga dapat merubah parameter untuk mendapatkan variasi yang ditentukan dan proses simulasi hanya tinggal dilakukan kembali.
Tugas 1 Membuat Video
https://www.youtube.com/watch?v=bvXGA_v8s-k
Pertemuan 2 : Senin, 16 November 2020
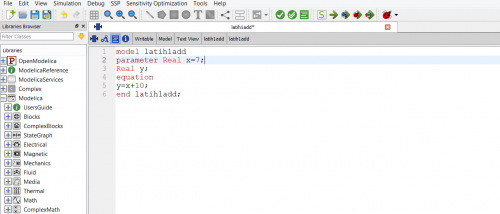
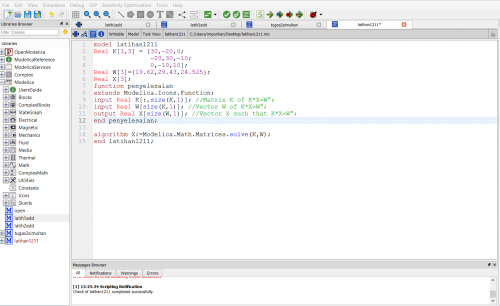
Assalamualaikum Wr. Wb. Pada pertemuan kali ini Pak Dai memulai pertemuan dengan dengan diskusi pembelajaran OpenModelica yang sudah dilakukan. Kemudian Pak Dai juga memeriksa satu persatu tugas yang telah diberikan minggu lalu yaitu melakukan simulasi OpenModelica. Setelah itu, dilanjutkan dengan memberikan latihan membuat perhitungan sederhana menjumlahkan angka 10 terhadap suatu variabel dengan software OpenModelica. Berikut adalah lampiran dari tutorial yang diberikan oleh Pak Dai. Dibuat dengan menggunakan pemrograman untuk perhitungan yang akan digunakan. Pada percobaan pertama menghitung nilai X untuk persamaan y=x+10, kemudian mendapat nilai y
Setelah itu, dapat dilihat grafik input dan hasi sebagai berikut, dengan nilai input x=7 didapatkan hasil y=17. Kita juga dapat melakukan simulasi kembali apabila ingin merubah nilai x.
Berikutnya adalah mencoba perhitungan untuk menentukan rata-rata dari kelompok data yang sudah disediakan. Yaitu a1=7,a2=14,a=3=21,a4=35,a5=42.
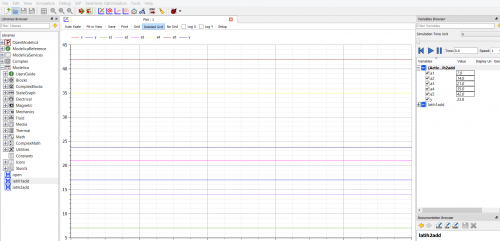
Kemudian terdapat hasil simulasi dari perhitungan untuk nilai masing-masing data dan hasil mean dari data tersebut adalah 23,8 berikut grafik yang dihasilkan dari simulasi tersebut.
Tugas 2 : Tugas memecahkan suatu persamaan aljabar simultan
Definisi dari aljabar simultan adalah suatu metode yang digunakan untuk menyelesaikan persoalan matematik yang bersangkutan dengan hal matematik yang kompleks sehingga membutuhkan bantuan softare seperti OpenModelica. Ada beberapa jenis-jenis metode yang dapat digunakan dengan cara aljabar simultan :
1. Eliminasi Gauss
2. Cramer
3. Gauss Seidel
4. Gauss Jordan
Berikut persamaan yang saya gunakan untuk aljabar simultan :
X1 + 3X2 + 2X3 = 5
2X1+ 4X2 + X3 = 4
3X1+ X2 + 3X3 = 3
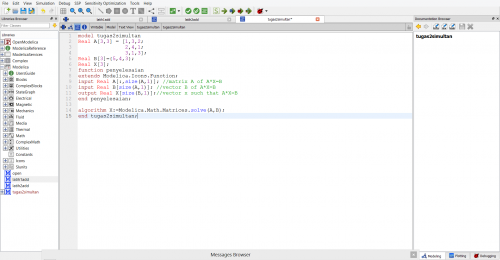
Langkah pertama yang dilakukan adalah membuat modelica class baru tipe class dan membuat fungsi-fungsi dan variabel seperti Real A[3,3] yang berarti bahwa 3,3 adalah matriks yang digunakan adalah matriks orde 3x3 dan parameter Real B[3] adalah 3 yang menunjukan matriks dengan orde 3x1 serta terakhir adalah parameter X dimana X yang akan dicari 3 akar-akarnya setelah dilakukan simulasi. Class yang saya gunakan untuk menyelesaikan persamaan adalah tipe function. Berikut hasil rangkaian bahasa modelica :
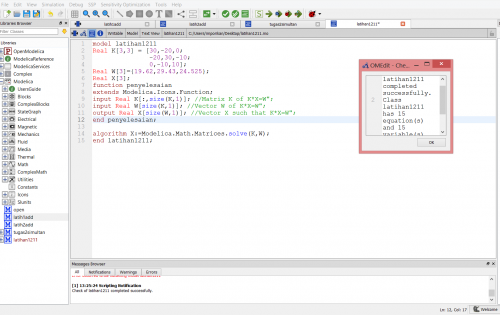
Berikut hasil rangkaian bahasa modelica yang sudah dicek dengan berisikan 15 persamaan dan 15 variabel yang sudah benar.
Selanjutnya, berikut adalah setting simulasi yang saya lakukan.
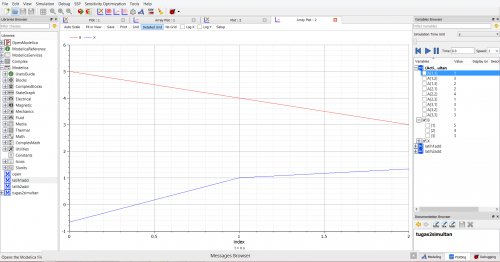
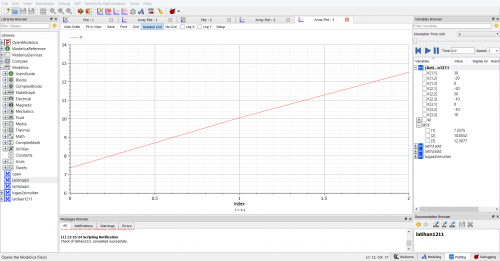
Setelah dilakukan simulasi, didapatkan akar-akar dari persamaan eliminasi gauss yaitu X1=-0.666667, X2=1, X3=1.33333. Berikut adalah hasil simulasi yang dilakukan.
Pertemuan 3 : Senin, 23 November 2020
Assalamualaikum Wr. Wb. pada pertemuan kali ini Pak Dai memberikan alur pemecahan masalah teknik menggunakan metode numerik. Cara pemecahan masalah tersebut adalah sebagai berikut :
1. Masalah teknik
2. Analisis masalah
3. Model Matematis
4. Model Numerik
5. Komputer
6. Mendapatkan Solusi
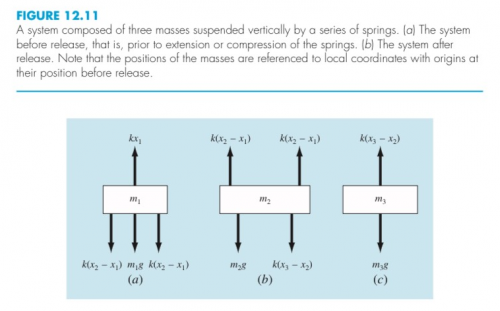
Kemudian Pak Dai juga memberikan tugas yaitu studi kasus di gambar 12.11 yaitu dengan membuktikan persamaan aljabar dan selesaikan dengan OpenModelica. Berikut gambar soal yang diberikan.
Berikut saya menggunakan function yang sudah saya buat dan membuat class baru untuk latihan 12.11
Setelah itu dapat kita lakukan pengecekan dan didapatkan 15 persamaan dan 15 variabel yang sudah benar.
Lalu kita dapat melakukan simulasi untuk mendapatkan hasil dan grafik seperti pada gambar di bawah ini. Dan didapatkan hasil yaitu :
X1 = 7.3575
X2 = 10.0552
X3 = 12.5077
Dapat disimpulkan bahwa jawaban yang sudah tertera di buku sudah sesuai dengan penyelesaian yang dilakukan melalui software OpenModelica.
Tugas 3
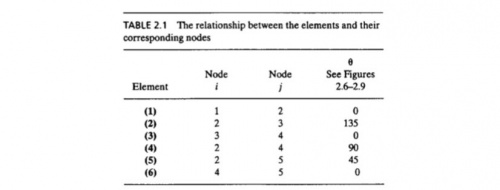
Setelah pertemuan hari ini, Pak Dai memberikan tugas untuk mengerjakan soal berikut:
Penyelesaian :
Merubah problem menjadi node dan elemen
Menentukan nilai konstanta kekakuan stifness constant dari elemen
Untuk elemen 1,2,3,4,5
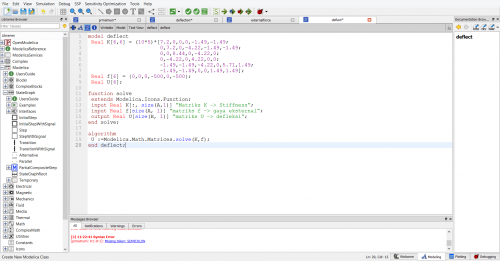
Berikut parameter yang saya digunakan untuk di OpenModelica :
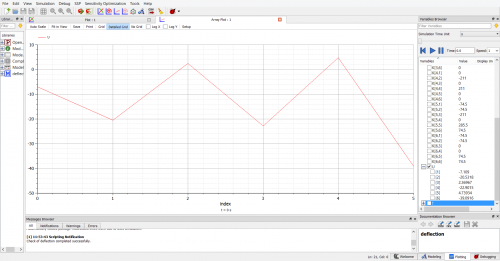
Berikut merupakan hasil simulasi dari class matriks yang saya buat :
Selanjutnya, saya lampirkan perhitungan untuk mencari R :
Berikut parameter yang digunakan :
Pertemuan 4: Senin, 30 November 2020
Assalamualaikum Wr.Wb. Pada awal pertemuan Pak Dai memberikan pertanyaan tentang perbedaan antara pembebanan statis dan pembebanan dinamik, kemudian saya menyimpulkan bahwa perbedaannya adalah pembebanan statik bebannya tidak berubah terhadap waktu sedangkan pembebanan dinamik bebannya berubah terhadap waktu. Lalu, Pak Dai juga menjelaskan manfaat metode numerik untuk persoalan-persoalan teknik.
Quiz Pertemuan 4 dan Tugas 4
Pada hari ini, Pak Dai memberikan quiz 2 soal yaitu :
Kemudian Pak Dai juga memberikan instruksi untuk menjawab soalnya dengan memberikan flow chartnya terlebih dahulu di air.eng.ui.ac.id. Berikut jawaban yang telah saya kerjakan.
Pertemuan 5 : Senin, 7 Desember 2020
Assalamualaikum Wr. Wb. pada pertemuan kali ini membahas dan berdiskusi tentang tahapan dalam menyelesaikan soal-soal pada kuis yang diberikan pada minggu sebelumnya. Kemudian pertemuan ini diberikan dan dilanjutkan oleh Ahmad Mohammad Fahmi dengan menjelaskan flowchart yang ia buat. Lalu, Ahmad menjelaskan bahasa modelica yang ia gunakan untuk menyelesaikan permasalahan atau soal yang diberikan sebelumnya. Dari penjelasan yang diberikan oleh Ahmad Mohammad Fahmi, saya mendapatkan pembelajaran baru dimana contohnya itu seperti cara looping pada aplikasi OpenModelica. Ahmada mengerjakan soal ini secara baik dan runtut sehingga yang memerhatikan bisa dengan mudah membaca dan dapat diaplikasikan.
Dari pembahasan yang dijelaskan oleh Ahmad, saya dapat menjelaskan beberapa langkah untuk mengerjakan soal-soal yang diberikan. Berikut beberapa langkah-langkah untuk mengerjakan soal-soal tersebut.
- Menentukan matriks global yang akan digunakan pada persoalan pada soal dengan cara menurunkan matriks lokal pada setiap joint di persoalan yang diberikan. Pada setiap persoalan juga perlu untuk memasukan function boundary untuk menambahkan looping.
- Matriks global total yang sudah ditemukan, dilakukan simulasi dengan menggunakan aplikasi OpenModelica
- Variabel-variabel yang ada, kita dapat menemukan variabel yang dibutuhkan contoh pada persoalan yang diberikan kita dapat menemukan variabel defleksi (U) serta variabel konstanta kekakuan (K) pada setiap elemen.
- Dengan didapatkannya variabel defleksi dan konstanta kekakuan pada batang, maka dapat ditemukan juga persamaan gaya reaksi yang terjadi pada batang tersebut.
- Simulasikan dengan menggunakan aplikasi OpenModelica untuk mendapatkan hasil reaction force atau gaya reaksi pada setiap elemen.
Tugas 5
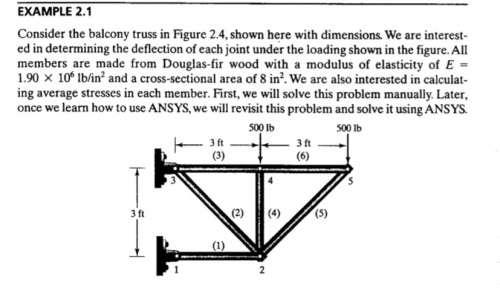
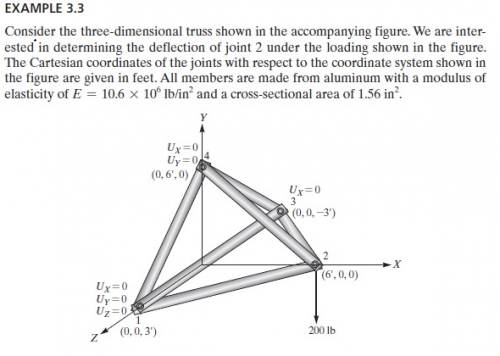
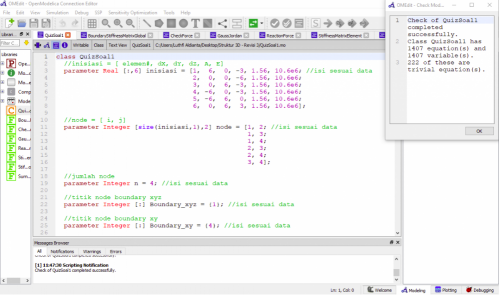
Berikut adalah contoh soal 3.3
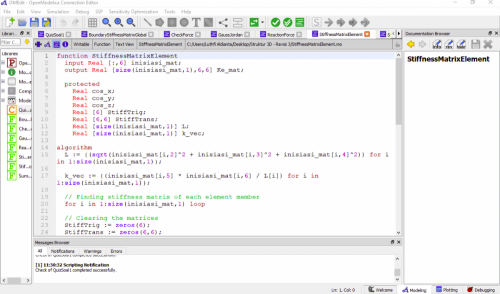
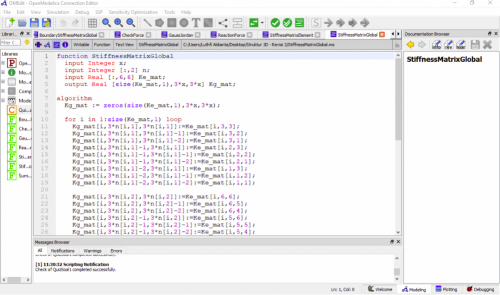
Berikut pembahasan contoh soal 3.3
Dari syntax yang digunakan, parameter dan equation yang dimasukan. Dapat dilihat bahwa variabel dan equation yang didapatkan telah setimbang.
Masukan atas codingan Ahmad Mohammad Fahmi
Hasil codingan yang dibuat oleh Ahmad Mohammad Fahmi sudah baik, karena dalam latihan soal mengenai tugas truss sudah memasukan data pada matriks dan dilakukan perhitungan secara manual pada software OpenModelica. Namun untuk contoh soal selanjutnya, Ahmad Mohammad Fahmi sudah menggunakan loop, sehingga data perhitungannya juga sudah banyak dan dapat dilakukan secara otomatis. Perhitungannya pun juga sudah ada batasan-batasan. Contohnya seperti pada batas kolom pada matriks inisiasi yang dihitung. Kemudian Ahmad Mohammad Fahmi juga menggunakan class dan funtion. Dimana bentuk perhitungan terlihat rapi. Sistem class dan function yang dibuat oleh Ahmad Mohammad Fahmi juga memberikan kemudahan dalam variasi soal yang ada contohnya seperti soal 2D atau 3D. Kemudahannya adalah yang perlu dirubah dari class dan function tidak perlu keseluruhan hanya terbatas pada variabel apa yang diketahui. Boundary condition yang terdapat pada node-node ikut dirubah pula. Untuk hasil coding dari soal 3.3, disini juga diterapkan sistem yang sama. Tetapi terdapat beberapa perubahan pada beberapa bagian di class dan function.Dalam cara pengerjaan yang sama, terdapat beberapa bentuk boundary, parameter real yang menggunakan persamaan yang berbda jika dibandingkan dengan soal sebelumnya. Mungkin untuk masukannya adalah menjelaskan istilah-istilah yang digunakan pada parameter ataupun equation dan algorithm. Untuk keseluruhan sudah baik dan perhitungan juga sudah benar untuk output yang diberikan yaitu defleksi, reaction force, dan penjumlahan gaya-gaya.
Pertemuan 6 : Senin, 14 Desember 2020
Assalamualaikum Wr. Wb. pada pertemuan kali ini Pak Dai memberikan tugas pada setiap mahasiswa untuk melakukan muhasabah diri tentang materi pembelajaran mata kuliah metode numerik. Pak Dai berharap bahwa mahasiswa dapat menilai diri sendiri yang sesuai dengan pemahaman dan konsep yang telah dipahami. Dari muhasabah diri tersebut, Pak Dai kemudian memberikan kesempatan pada mahsiswa untuk menerangkan beberapa materi yang sudah dipahami untuk bukti bahwa mahasiswa tersebut telah sesuai dengan nilai yang diberikan pada dirinya sendiri. Parameternya adalah seberapa paham mahasiswa itu terhadap konsep dan pemahaman yang sudah diberikan selama mata kuliah metode numerik. Kemudian pembelajaran berikutnya dilanjutkan dengan materi yang diberikan oleh Christo mengenai pemahaman dari alur berfikir tentang soal-soal yang telah diberikan. Christo juga menjelaskannya ke dalam software OpenModelica mengenai bagaimana mengidentifikasi parameter apa saja yang digunakan pada soal, membentuk model, dan melakukan perhitungan dari model soal yang diberikan. Pemaparan tersebut juga dibantu oleh Josiah Enrico dan Ahmad Mohammad Fahmi untuk membandingan alur-alur pengerjaan soal-soal yang telah diberikan.
Pertemuan 7 : Senin, 21 Desember 2020
Assalamualaikum Wr. Wb. pada pertemuan kali ini dimulai dengan Pak Dai memberikan arahan untuk penyelesaian tugas besar. Kemudian dilanjutkan dengan menjelaskan optimasi dari truss, yang dimana pada truss tersebut terdapat 3 displacement yaitu sumbu yz, tetta dan r. Truss berbeda dengan beam dimana truss tiap titiknya mempunyai 3 derajat kebebasan dengan variabelnya displacement dalam x,y,z untuk asumsi pada suatu batang. Sedangkan pada beam, rangkanya mempunyai 6 derajat kebebasan dengan variabel x,y,z dan kearah momen atau puntirannya. Pada asumsi yang sudah dijelaskan kami sebagai mahasiswa diharapkan untuk menyusun persamaan-persamaannya. Dengan menyusun persamaannya diharapkan kami mahasiswa dapat mengerti dan memahami bagaimana menyelesaikan permasalahan tersebut dengan matriks dan variabel-variabel sudah kami susun dan dapat diaplikasikan pada aplikasi OpenModelica. Kemudian kami juga harus mengerti dan paham bagaimana menyusun persamaannya, boundary condition dan lain-lain.
Selanjutnya kami mahasiswa juga diharapkan menghitung kondisi optimal pada rangka dengan parameter seperti pada tujuan dan fungsi objektif pada optimasi. Pada perhitungan tersebut harus ada fungsi-fungsi pada batasan atau constraintsnya contohnya seperti berapa panjang siku dan harga per berapa ukuran. Optimasi ini juga mempunyai tujuan yaitu untuk meminimalisir biaya. Constraints yang diberikan harus mampu untuk menahan beban yang dimana gaya-gaya bekerja mampu didukung pada rangka tersebut. Langkah awal yang dilakukan adalah mencari displacement, memeriksa gayanya dan mengoptimasi gaya tersebut dan menghitung stress. Selanjutnya membandingkan stress dari kekuatan material yang digunakan. Tegangan yang telah dihitung tersebut tidak boleh melebihi dari allowable stress agar membentuk rangka yang sesuai dengan standar. Dari data-data yang sudah dikumpulkan, kita akan mendapatkan jenis material dan ukuran dari batang dan kita juga dapat mengetahui berapa spesifikasi siku. Lalu, kita dapat melakukan optimasi untuk mengetahui yang mana bahan yang paling optimal.
k= A.E/L
A= merupakan luas penampang siku
E= modulus elastisitas tiap bahan
L= panjang batang rangka
Dapat digaris bawahi bahan atau profil siku yang digunakan adalah galvanis, stainlessm dan lain-lain
Aplikasi Metode Numerik dalam Kasus Optimasi
Pembahasan tentang materi ini diberikan oleh Bu Chandra, dengan menyampaikan penjelasan-penjelasan melalui powerpoint dimana optimasi yang digunakan adalah metode bracket optimization using golden ratio. Diharapkan kita mahasiswa dapat mengikuti simulasi dengan menggunakan OpenModelica untuk menyelesaikan permasalahn dengan fungsi exercise yang telah diberikan dan tercantum pada powerpoint. Optimasi juga adalah cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi fungsi non linear, dan objektifnya adalah mencari nilai f(x) maksimum dan minimum. Kemudian dalam penerapannya dapat menggunakan persamaan sebagai berikut
d= akar5 - 1/2 x (xu-xl)
x1= x1 + d
x2= xu - d
dengan syarat sebagai berikut,
- f(x1)>f(x2), domain sebalah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama.
- f(x2)>f(x1), domain x disebelah kanan x1 daat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama.
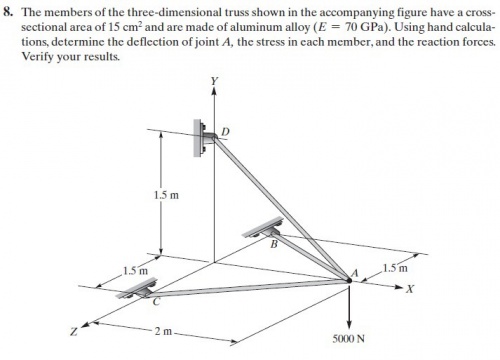
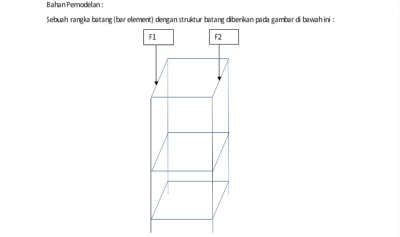
Tugas Besar Metode Numerik : Optimasi Desain Struktur Rangka (Truss) Sederhana dengan Open Modelica
Pada tugas besar ini kami mahasiswa diminta untuk melakukan optimasi pemilihan material dan luas penampang trusses untuk rangka seperti gambar dibawah ini
Asumsi yang digunakan untuk melakukan perhitungan ini antara lain:
1. Variasi Stiffness terikat dengan variabel area pada material yang akan digunakan. Karean akan sulit apabila memvariasikan elastisitas, dimana setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya
2. Dimensi material mengikuti standar ukuran material yang dipilih
3. Beban akan terdistribusi hanya pada node/point penghubung (karena bersifat trusses)
4. Terdapat 2 perhitungan yaitu dengan material lock dan area lock.
Latar Belakang
Memperoleh desain dengan harga paling terjangkau dan spesifikasi atau kemampuan mumpuni untuk target penggunaan (material, luas, dan harga yang optimal)
Ketentuan
- Optimasi dilakukan dengan mencari harga termurah dengan faktor berubah kekuatan dan area
- Tujuan optimasi : Displacement U minimum, Cross-Area minimum, dan nilai E dan A (murah)
Perhitungan dan Coding
1.Elasticity Lock
Material lock merupakan pengambilan data dengan material yang sama dan untuk memvariasikan luas areanya. Pada material lock ini, saya menggunakan material SS400 yang berprofil siku. Dimana data yang saya ambil sebagai berikut :
source : http://infoindosteel.blogspot.com/2017/02/harga-besi-baja-siku.html
Coding
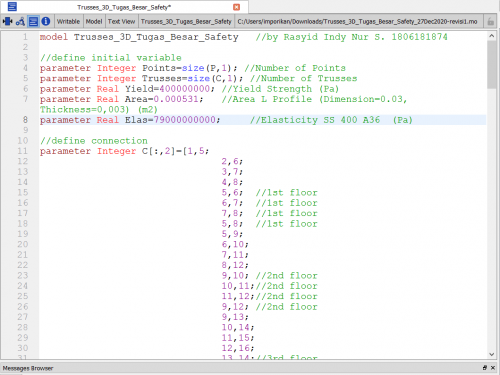
Coding Trusses
model Trusses_3D_Tugas_Besar_Safety //by Rasyid Indy Nur S. 1806181874
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=400000000; //Yield Strength (Pa) parameter Real Area=0.000531; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2) parameter Real Elas=79000000000; //Elasticity SS 400 A36 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if; end for;
end Trusses_3D_Tugas_Besar_Safety;
Coding Curve Fitting
function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting; /* for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for; */
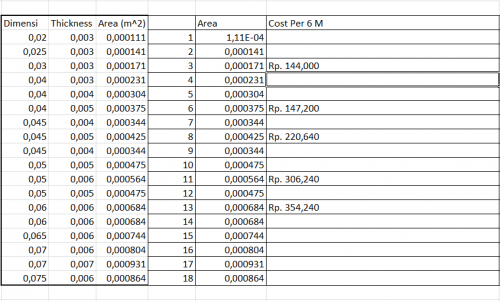
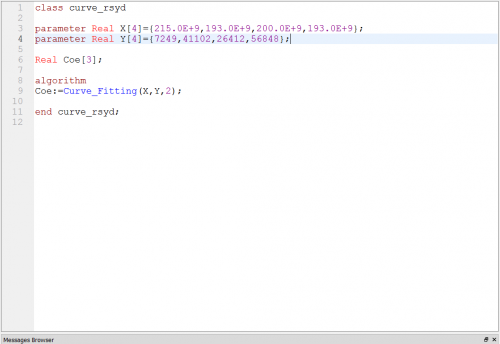
Kemudian langkah selanjutnya adalah mencari hasil harga tiap area yang telah ditentukan melalui koding curve fitting. Sehingga kita mendapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :
function
Model Tugas Besar 3D Trusses
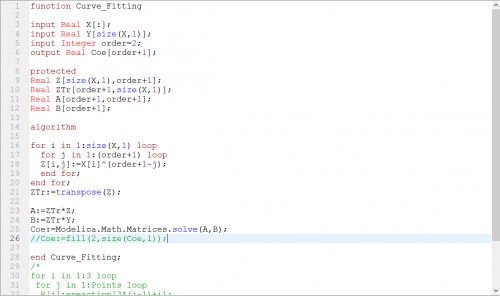
Function Curve Fitting
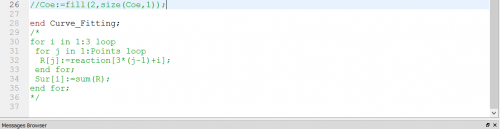
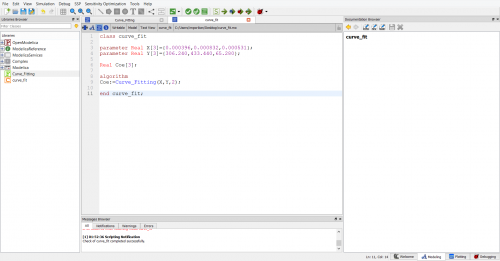
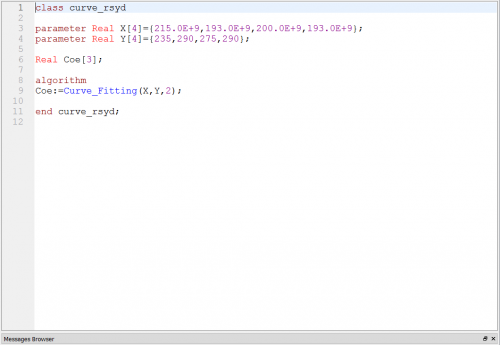
Class Curve Fitting untuk Harga Per 6M
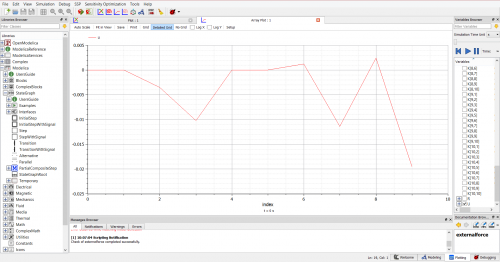
Lalu, didapatkan hasil dari simulasi dengan nilai Coe yang akan kita ambil untuk salah satu variabel perhitungan adalah sebagai berikut:
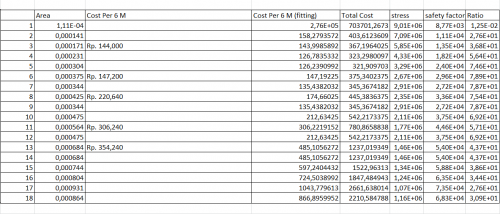
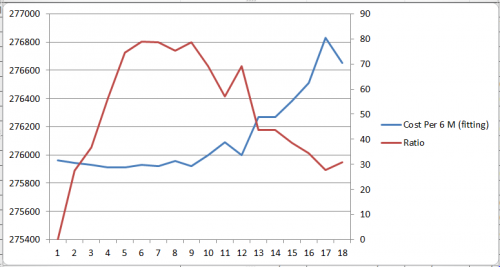
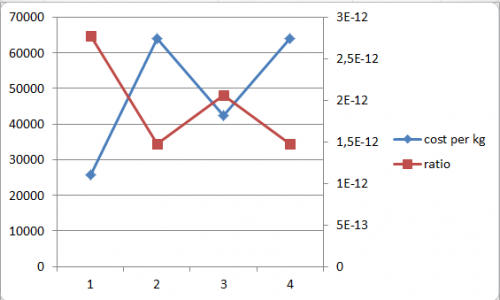
Hasil Excel dan Grafik
Setelah dilakukan perhitungan maka secara otomatis didapatkan harga di excel dengan menginput data hasil koding curve fitting. Berikut hasil dari perhitungan dan grafiknya:
2. Area Locked
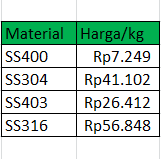
Area Locked adalah pengambilan data menggunakan luas area yang sama dan memvariasikan materialnya. Untuk area locked ini, saya menggunakan material SS400, SS304, SS403, dan SS316 yang mempunyai profil siku dengan memberikan sample yang mempunyai ariasi berupa material dan harga. Berikut data yang saya gunakan:
source :
https://www.indiamart.com/proddetail/ms-sheet-10121470997.html
https://www.tokopedia.com/kingsteelid
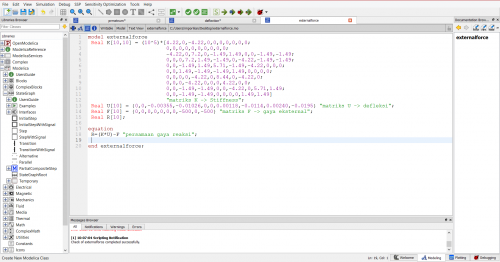
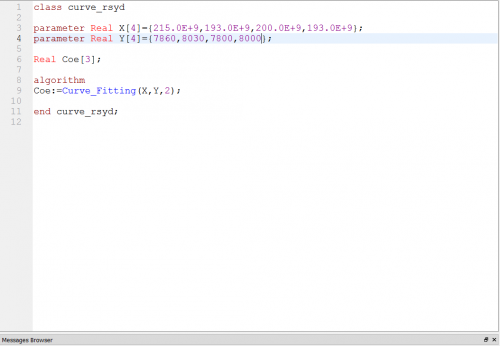
Setelah itu melakukan pencarian harga, density, serta yield dengan menggunakan coding curve fitting seperti yang dilakukan pada elasticity lock dengan jumlah variabel yang sesuai dengan kategorinya. Berikut adalah codingan dan masing-masing class yang saya gunakan:
Coding
function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting; /* for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for; */
Class
class cost
coe cost
class density
coe density
class yield
coe yield
Hasil Excel dan Grafik
Setelah dilakukan perhitungan maka secara otomatis didapatkan harga di excel dengan menginput data hasil koding curve fitting. Berikut hasil dari perhitungan dan grafiknya:
Ujian Akhir Semester Metode Numerik (13 Januari 2020)
No. 1
Penjelasan no. 1 :
Pada soal no. 1 ini, diberikan soal mengenai water tower dengan resevoir berbentuk bola yang diberikan oleh Pak Dai. Kemudian Pak Dai meminta untuk mahasiswa untuk membuat permodelan numerik untuk mengoptimalkan struktur water tower tersebut. No. 1 ini diberikan perintah untuk membuat prosedur permodelan numerik untuk optimasi struktur tersebut.
- 1. Mendefinisikan masalah
Pertama-tama hal yang dilakukan adalah mengidentifikasi untuk jumlah batang yang akan digunakan, kemudian dari jumlah dari batang-batang yang digunakan didapatkan node-node. Mendefinisikan masalah juga berguna untuk mengidentifikasi profil yang akan digunakan untuk struktur dari water tower tersebut.
- 2. Menentukan asumsi kondisi
Menentukan asumsi yang akan digunakan agar mudah untuk dicari data yang akan digunakan. Kemudian pada step ini, langkah yang dilakukan adalah memberikan parameter-parameter.
- 3. Research data
Research data disini digunakan untuk mencari data-data yang akan digunakan untuk membuat permodelan numerik untuk mengoptimalkan struktur water tower tersebut.
- 4. Permodelan numerik
Mempersiapkan atau membuat codingan yang sesuai dengan variabel-variabel sehingga cocok digunakan untuk mengoptimalkan struktur water tower tersebut.
- 5. Komputasi
Memasukan codingan yang sudah dipersiapkan ke software atau aplikasi OpenModelica
- 6. Penentuan akhir struktur atau material
Mendapatkan struktur yang paling optimal dan yang paling sesuai dengan kaidah hukum fisika atau sesuai dengan codingan yang telah dibuat.
No. 2
Penjelasan no. 2 :
Tujuan Permodelan Numerik adalah :
- Mempermudah untuk menganalisis displacement dan gaya reaksi
- Mempermudah untuk mengidentifikasi nilai minimum atau maksimum dari struktur dan material yang akan digunakan
- Memperoleh desain dengan harga yang minimum dan spesifikasi yang optimal.
Asumsi
- Beban terdistribusi pada titik sambung
- Safety factor yang digunakan minimal 2 atau setengah dari modulus elastisitas material
- Batas displacement pada truss yang digunakan memiliki nilai yang relatif
- Ketinggian trusses pada water tower konstan
Hukum Fisika
- Stiffness (kekakuan)
- Gaya Reaksi
- Hukum Newton III
- Hukum Hooke
- Hukum Konservasi Energi
No. 3
Penjelasan no. 3 :
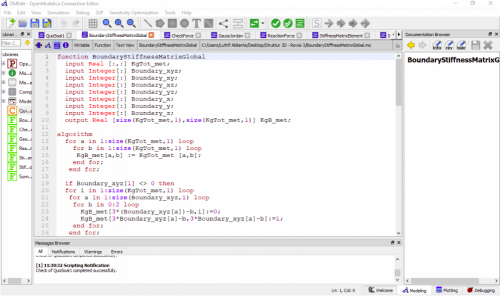
Pada no. 3 ini dibuat variabel atau persamaan untuk membuat matriks global, yaitu untuk matriks lokal yang digunakan berdasarkan turunan dari U1x, U1y, U2x, U2y. Pada permodelan truss 1D tersebut menggunakan dua axis yaitu axis x dan axis y. Matriks lokal yang telah dihitung tersebut untuk dx dan dy kemudian dicari sudutnya untuk diinput ke matriks lokal. setelah mendapatkan matriks lokal tadi, hasilnya dijumlahkan dari masing-masing hasil matriks lokal untuk digunakan membentuk matriks global.
No. 4
Penjelasan no. 4 :
Membuat flowchart untuk pseudocode dari optimasi permodelan. Dengan tahapan yaitu :
- Menuliskan class dan mendefinisikan parameter-parameter yang ada
- Menuliskan matriks element
- Menuliskan matriks global
- Menjumlahkan atau menuliskan penjumlahan matriks global
- Mengimplementasikan kondisi batas sistem
- Gauss-Jordan matriks
- Menuliskan gaya reaksi
No. 5
Penjelasan no. 5 :
Fungsi Objektif : Menemukan material yang optimal
Constraint : Constraint yang digunakan yaitu luas area penampang dan elastisitas material.
No. 6
Penjelasan no. 6 :
Memberikan asumsi nilai-nilai parameter dan variable untuk mendapatkan displacement, restraint, dan stress
Parameter yang saya gunakan adalah :
- Tinggi : 120 ft = 1440 in
- L : 40 ft = 480 in
- E : 27 x 10^6 lb/in^2
- A : 30
- load : 30.000
No. 7
Penjelasan no. 7 :
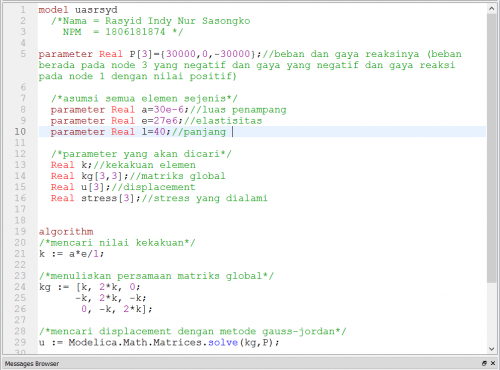
Berikut adalah codingan yang digunakan untuk menjawab nomor 7 yang saya gunakan untuk menyelesaikan permasalahan truss 1D sesuai dengan asumsi pada nomor 6:
model uasrsyd
/*Nama = Rasyid Indy Nur Sasongko
NPM = 1806181874 */
parameter Real P[3]={30000,0,-30000};//beban dan gaya reaksinya (beban berada pada node 3 yang negatif dan gaya yang negatif dan gaya reaksi pada node 1
dengan nilai positif)
/*asumsi semua elemen sejenis*/ parameter Real a=30e-6;//luas penampang parameter Real e=27e6;//elastisitas parameter Real l=40;//panjang /*parameter yang akan dicari*/ Real k;//kekakuan elemen Real kg[3,3];//matriks global Real u[3];//displacement Real stress[3];//stress yang dialami algorithm /*mencari nilai kekakuan*/ k := a*e/1;
/*menuliskan persamaan matriks global*/
kg := [k, 2*k, 0;
-k, 2*k, -k;
0, -k, 2*k];
/*mencari displacement dengan metode gauss-jordan*/ u := Modelica.Math.Matrices.solve(kg,P);
/*mencari stress pada tiap elemen*/ stress[1] := u[1]*k/a; stress[2] := u[2]*k/a; stress[3] := u[3]*k/a;
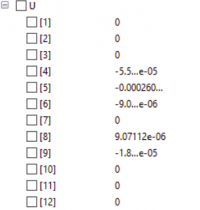
end uasrsyd;
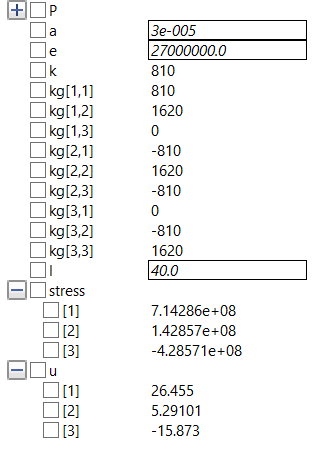
Hasil yang didapatkan adalah displacement sebesar [26.455 , 5.291, -15.873] dan stress sebesar [7.14286e+08, 1.42857e+08, -4.28571e+08]