Difference between revisions of "Iman Herlana"
Iman herlana (talk | contribs) (→Tugas Minggu 4) |
Iman herlana (talk | contribs) (→UAS) |
||
| (25 intermediate revisions by the same user not shown) | |||
| Line 187: | Line 187: | ||
berikut video pengerjaan code pada OpenModelica | berikut video pengerjaan code pada OpenModelica | ||
[[File:Tugas4 Iman Herlana.mp4|720px|center|]] | [[File:Tugas4 Iman Herlana.mp4|720px|center|]] | ||
| + | |||
| + | ===Minggu 6 (16 Desember 2020)=== | ||
| + | pada pertemuan kali ini, kita semua diberikan pengetahuan lebih, bahwa sejatinya ilmu tidak hanya berasal dari buku saja, tetapi juga dari alam sekitar. banyak fenomena yang bisa kita cari tau penyebab dan dampaknya terhadap kehidupan sehari-hari yang apabila dipelajari akan memberikan pengetahuan lebih. pengetahuan berupa teori yang sudah kita dapatkan pun, baik melalui pembelajaran di kelas maupun melalui belajar mandiri, harus dapat diaplikasikan dalam kehidupan sehari-hari. barulah ilmu tersebut menjadi bermanfaat bagi banyak orang | ||
| + | |||
| + | ====Optimasi==== | ||
| + | pada pertemuan kali ini, kita diajarkan mengenai Optimasi dengan menggunakan metode bracket oleh bu Chandra. masing masing dari kita dipersilahkan mencoba langsung dalam OpenModelica sambil dituntun oleh bu Chandra apabila ada kesulitan. berikut hasil dari yang saya coba. | ||
| + | pertama, kita harus membuat model bracket terlebih dahuli | ||
| + | [[File:Bracket 1.PNG|800px|center|]] | ||
| + | [[File:Bracket 2.PNG|800px|center|]] | ||
| + | selanjutnya, kita harus menyiapkan fungsi objektif yang nantinya akan dipanggil pada model bracket | ||
| + | [[File:Fungsi objek.PNG|800px|center|]] | ||
| + | kemudian kita melakukan cek untuk memastikan bahwa code sudah benar dan tidak ada error. apabila sudah tidak ada error, maka dapat langsung melakukan simulasi. berikut adalah hasil setelah disimulasikan | ||
| + | [[File:Hasil.PNG|800px|center|]] | ||
| + | |||
| + | ===TUGAS BESAR=== | ||
| + | Setelah sekian minggu mempelajari aplikasi OpenModelica dalam penerapan metode numerik, kami diminta untuk membuat code untuk aplikasi metode numerik dalam optimasi desain struktur rangka sederhana | ||
| + | |||
| + | ====Mengenal Lebih Jauh Tentang Apa itu Optimasi==== | ||
| + | optimasi adalah suatu cara untuk menyelesaikan masalah secara optimal. biasanya permasalah yang diselesaikan adalah masalah yang menuntut penyelesaian yang memperhatikan beberapa indikator atau capaian tertentu. misalnya, dalam membangun jembatan, diperlukan bahan yang kuat, akan tetapi tetap ekonomis (memiliki harga yang terjangkau). dengan demikian, maka diperlukan optimasi untuk mencari jalan tengah dari permasalahan tersebut. sehingga penyelesaian yang didapat adalah bahan yang cukup untuk menahan beban sebagai jembatan, dengan harga yang masih terjangkau. penyelesaian tersebut pada akhirnya akan memenuhi kedua indikator yang diinginkan yaitu kuat menahan beban sebagai jembatan, dan memiliki harga yang terjangkau. apabila ingin salah satu indikator saja yang tercapai, bisa saja menggunakan bahan yang paling kuat, akan tetapi tentu saja harganya mahal. pun sebaliknya bisa menggunakan bahan yang paling murah, akan tetapi mudah rapuh. itulah manfaat dari optimasi. optimasi sendiri terbagi menjadi 2 tujuan besar yaitu maksimasi dan minimasi. maksimasi dalam contoh yang disebutkan diatas adalah "Bahan yang kuat" sedangkan minimasi nya adalah "harga yang terjangkau". dalam optimasi, perlu memperhatikan: | ||
| + | *Objective Function | ||
| + | *Decision Variable | ||
| + | *Constraints | ||
| + | |||
| + | ====Soal yang Harus Diselesaikan==== | ||
| + | pada tugas besar ini, kami diharuskan menyelesaikan sebuah permasalahan pada rangka batang menggunakan metode optimasi. berikut adalah soalnya | ||
| + | [[File:TUBES Metnum.jpg|800px|center|]] | ||
| + | untuk dapat menyelesaikan permasalahan tersebut, diperlukan adanya asumsi yang mendukung proses perhitungan dan pertimbangan nantinya. berikut asumsi yang dibuat: | ||
| + | *beban hanya terdistribusi pada noda karena sistem bersifat trusses | ||
| + | *ketinggian trusses tiap lantai dianggap sama yaitu 0,6 meter | ||
| + | *displacement yang diizinkan pada trusses horizontal paling atas adalah sebesar 0,001 meter sebelum terjadinya buckling | ||
| + | *safety factor yang ingin didapatkan harus lebih dari 2 untuk menjamin keselamatan | ||
| + | |||
| + | ====Sistematika Pengerjaan==== | ||
| + | proses optimasi menggunakan 2 kali perhitungan dengan pertimbangan yang berbeda yaitu kesamaan jenis material dan kesamaan area dari penampang. | ||
| + | |||
| + | untuk jenis material yang sama: | ||
| + | #mencari harga untuk 6 ukuran standar batang dengan material yang sama yaitu SS201. | ||
| + | #mengitung nilai safety factor pada 6 ukuran batang dengan coding yang dikerjakan saat kuis sebelumnya. | ||
| + | #membuat rasio antara safety factor dengan harga total. | ||
| + | #membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. | ||
| + | #melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | Untuk area penampang yang sama: | ||
| + | #mencari harga untuk 4 jenis material dengan area penampang yang sama yaitu 171 mm^2. | ||
| + | #mengitung nilai safety factor pada 4 jenis batang dengan coding awal. | ||
| + | #membuat rasio antara safety factor dengan harga total. | ||
| + | #membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. | ||
| + | #melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | ====Perhitungan Displacement, Reaction Force, Stress, dan Safety Factor==== | ||
| + | model Trusses3DTugasBesar | ||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=292e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=197e9; //Elasticity SS 201 (Pa) | ||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses3DTugasBesar; | ||
| + | |||
| + | ====Perhitungan Rasio Perbandingan Safety Factor dan Biaya==== | ||
| + | selanjutnya diperlukan pendataan guna mendapatkan banyak data yang diperlukan dalam proses curve fitting, yang nantinya akan digunakan untuk optimasi. data saya kumpulkan dengan melihat beberapa website referensi berikut: | ||
| + | *https://wijayamakmur.com/siku | ||
| + | *https://ptgaja.com/stainless-steel-201/ | ||
| + | *https://www.tokopedia.com/kairosmetal/product | ||
| + | *https://www.tokopedia.com/kingsteelid | ||
| + | dengan data yang didapatkan pada 4 website tersebut, saya berhasil mengumpulkan data sementara menjadi sebagai berikut | ||
| + | [[File:ElasLock.PNG|800px|center|]] | ||
| + | [[File:AreaLock.PNG|800px|center|]] | ||
| + | terlihat dari gambar bahwa masih banyak sekali data yang kosong (tidak memiliki input. oleh karena itu, dibutuhkan curve fitting untuk mengisi kekosongan tersebut. fungsi dari dilakukannya curve fitting adalah untuk mengetahui nilai sebuah input yang tidak diketahui sebelumnya. berikut fungsi yang akan dipanggil untuk proses curve fitting | ||
| + | |||
| + | function FuncCurveFitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coef[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coef:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end FuncCurveFitting; | ||
| + | |||
| + | untuk menjalankan fungsi tersebut, tentunya kita memerlukan model untuk memanggil fungsi tersebut. berikut adalah model nya | ||
| + | |||
| + | model CurveFitting | ||
| + | parameter Real X[6]={0.000111, 0.000171, 0.000304, 0.000684, 0.000744, 0.000864}; | ||
| + | parameter Real Y[6]={179200, 239500, 429600, 963600, 1044800, 1428000}; | ||
| + | Real coef[3]; | ||
| + | |||
| + | equation | ||
| + | coef=FuncCurveFitting(X,Y,2); | ||
| + | end CurveFitting; | ||
| + | |||
| + | model tersebut dapat digunakan untuk curve fitting berkali-kali. hanya perlu menyesuaikan nilai X dan Y yang diketahui saja. sebagai contoh, code diatas merupakan code curve fitting untuk mencari besar cost per 6 meter. setelah mendapatkan nilai dari hasil curve fitting, data yang kita miliki menjadi sebagai berikut: | ||
| + | [[File:ElasLockFix.PNG|800px|center|]] | ||
| + | [[File:AreaLockFix.PNG|800px|center|]] | ||
| + | dengan demikian kita telah memiliki sejumlah data yang dapat diolah dalam proses optimasi | ||
| + | |||
| + | ====Optimasi Dengan Metode Golden Section==== | ||
| + | setelah kita mendapatkan cukup data, kita dapat melakukan optimasi dengan metode Golden Section. golden section bertujuan untuk menemukan nilai yang optimum dengan mengacu pada suatu nilai minimum dari variabel. berikut adalah code untuk metode golden section | ||
| + | |||
| + | model GoldenSection | ||
| + | parameter Real xd[:]={0.000111, 0.000141, 0.000171, 0.000231, 0.000291, 0.000304, 0.000384, 0.000684, 0.000575, 0.000744, 0.000864, 0.000725, 0.001216}; | ||
| + | parameter Real yd[size(xd,1)]={6.29E-05, 7.24E-05, 7.96E-05, 8.86E-05, 9.26E-05, 9.30E-05, 9.32E-05, 8.02E-05, 8.58E-05, 7.72E-05, 7.15E-05, 7.82E-05, 5.79E-05}; | ||
| + | parameter Real xlo=0.000111; | ||
| + | parameter Real xhi=0.001216; | ||
| + | parameter Integer N=100; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := FuncCurveFitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end GoldenSection; | ||
| + | |||
| + | setelah disimulasikan, maka akan didapatkan hasil berupa Xopt yang merupakan nilai optimum. metode golden section harus dijalankan sebanyak 2 kali, yang pertama untuk material tetap, yang kedua untuk area tetap. code diatas merupakan golden section untuk material tetap. berikut hasil simulasi dari material tetap (gambar atas) dan area tetap (gambar bawah): | ||
| + | [[File:GoldenElas.PNG|800px|center|]] | ||
| + | [[File:GoldenArea.PNG|800px|center|]] | ||
| + | |||
| + | ====Hasil dan Analisis==== | ||
| + | *Material Tetap (Elasticity Locked) | ||
| + | pada kondisi ini, material yang saya pilih adalah SS 201. terlihat dari hasil simulasi Golden Section bahwa nilai Area yang optimum adalah 0,000493439. belum terlihat adanya dimensi dan ketebalan yang cukup mendekati Area tersebut. akan tetapi, yang paling mendekati adalah nilai area 0,000575, yang disusun dari dimensi 6cm x 6cm dengan ketebalan 5mm | ||
| + | *Area Tetap (Area Locked) | ||
| + | pada kondisi ini, Area yang saya tetapkan adalah 0,000171. terlihat dari hasil simulasi Golden Section bahwa nilai Elastisitas yang iptimum adalah 194,5E+9. nilai tersebut mendekati nilai elastisitas 194E+9 yang dimiliki oleh SS201. | ||
| + | *Analisis Hasil | ||
| + | melihat hasil dari kedua simulasi di atas, didapatkan bahwa material yang paling sesuai adalah SS201. oleh karena itu, material yang paling optimal untuk desain rangka persoalan ini adalah SS 201 dengan dimensi kira kira 6cmx6cm dan ketebalan 5 mm | ||
| + | |||
| + | ===UAS=== | ||
| + | Berikut adalah jawaban UAS milik saya | ||
| + | [[File:98643.jpg|800px|center|]] | ||
| + | [[File:98644.jpg|800px|center|]] | ||
| + | [[File:98645.jpg|800px|center|]] | ||
| + | [[File:98646.jpg|800px|center|]] | ||
| + | berikut adalah code pada open modelica untuk menyelesaikan persoalan yang diberikan | ||
| + | |||
| + | model UAS_Iman | ||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=292e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=197e9; //Elasticity SS 201 (Pa) | ||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,2; | ||
| + | 1,3; | ||
| + | 1,4]; | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0,0,0,1,1,1;//1 | ||
| + | 10,10,45,1,1,1;//2 | ||
| + | 10,10,80,1,1,1;//3 | ||
| + | 10,10,115,1,1,1];//4 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0,0,2000,0,0,2000,0,0,2000,0}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end UAS_Iman; | ||
| + | |||
| + | sampai saat ini saya belum bisa mendapatkan hasil simulasi dari OpenModelica karena aplikasi saya sedang mengalami error | ||
Latest revision as of 21:20, 17 January 2021
Biodata
Nama : Iman Herlana
NPM : 1906356134
TTL : Jakarta, 2 Juni 2000
Domisili : Jakarta
Saya merupakan mahasiswa Fakultas Teknik Universitas Indonesia dengan Program Studi S1 Reguler Teknik Mesin. Saya tinggal di daerah Manggarai, Tebet, Jakarta Selatan. Banyak hal yang pada akhirnya membuat saya bisa sampai ke FTUI yang sekarang ini. Mulai dari rasa penasaran dengan fisika, hingga adanya teman seperjuangan yang berhasil mempersuasi saya untuk lebih giat belajar. Saya bersyukur menjadi salah satu dari sekian orang yang beruntung dapat diterima di FTUI.
Contents
- 1 Biodata
- 2 Metode Numerik
- 2.1 Minggu 1 (11 November 2020)
- 2.2 Minggu 2 (18 November 2020)
- 2.3 Minggu 3 (25 November 2020)
- 2.4 Minggu 4 (2 Desember 2020)
- 2.5 Minggu 6 (16 Desember 2020)
- 2.6 TUGAS BESAR
- 2.6.1 Mengenal Lebih Jauh Tentang Apa itu Optimasi
- 2.6.2 Soal yang Harus Diselesaikan
- 2.6.3 Sistematika Pengerjaan
- 2.6.4 Perhitungan Displacement, Reaction Force, Stress, dan Safety Factor
- 2.6.5 Perhitungan Rasio Perbandingan Safety Factor dan Biaya
- 2.6.6 Optimasi Dengan Metode Golden Section
- 2.6.7 Hasil dan Analisis
- 2.7 UAS
Metode Numerik
Di semester ini, saya berhadapan dengan sebuah mata kuliah yang cukup menantang yaitu metode numerik. Sebelum UTS, saya sudah mempelajari beberapa metode pencarian akar persamaan, regresi, interpolasi, dan turunan numerik. Saya berharap dapat lebih memahami lagi terkait metode numerik, dan dapat menggunakannya pada kehidupan nyata baik dalam akademik maupun karier nantinya.
Minggu 1 (11 November 2020)
Tujuan belajar Metode Numerik:
- 1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik
- 2. Menerapkan pemahaman yang didapat ke dalam model numerik
- 3. Mampu menerapkan pemahaman yang didapat ke dalam persoalan teknik
- 4. Mendapat nilai tambah sehingga menjadi orang yang beradab
Penggunaan tujuan diibaratkan dalam sebuah perjalanan. Sehingga setiap hal yang kita lakukan adalah untuk mencapai tujuan tersebut. Untuk itulah tujuan dibuat agar arah perjalanan dapat lebih terstruktur, begitu pula dalam belajar.
Bit merupakan singkatan dari Binary Digit, adalah kemampuan operating system dalam memproses jumlah data dalam satu hitungan waktu.
Tugas Minggu 1
di tugas pertama ini, kami diminta untuk menggunakan aplikasi OpenModelica untuk menyelesaikan permasalahan tertentu, kemudian membuat videonya. dalam hal ini, saya mencoba mencari properties pada keadaan tekanan tertentu dari Saturated Water (Liquid - Vapor) menggunakan metode interpolasi dengan melihat nilai-nilai yang dapat ditemukan pada tabel di buku "Fundamental of Engineering Thermodynamics"
Berikut video pembuatan tugas saya
Minggu 2 (18 November 2020)
di pertemuan ini, masing-masing dari kita dipersilahkan bertanya sambil menjelaskan hasil pekerjaannya. kemudian ada sebuah pertanyaan menarik dari seorang mahasiswa, yaitu "Kenapa kita memilih menggunakan OpenModelica dibandingkan aplikasi/platform lainnya?". jawaban dari Pak Dai cukup membuat saya semakin yakin untuk menggunakan OpenModelica. Pak Dai menjawab bahwa open modelica merupakan bahasa pemodelan, bukan sekedar bahasa coding seperti C++ dll. hal itu lebih sesuai untung engineering karena engineer bekerja dengan pemodelan. kemudian pak Dai mengarahkan kami untuk mempelajari fitur lain dari OpenModelica. salah satu fitur nya adalah fitur panggil dimana kita memanggil fungsi yang ada pada file lain untuk digunakan pada sebuah file class. hal yang kita pelajari itulah yang kemudian menjadi tugas bagi mahasiswa untuk mencoba mempelajari fitur tersebut lebih lanjut
Tugas Minggu 2
pada tugas kali ini, kami diinstruksikan untuk mencoba fitur panggil pada aplikasi OpenModelica. saya menggunakan contoh soal dari latihan pada buku "Elementary Linear Algebra" oleh Howard, dan memanfaatkan aplikasi OpenModelica untuk mengetahui jawabannya. Ada sedikit keanehan yang saya temui di hasil pengerjaan saya, yang kemungkinan besar akan saya tanyakan kepada pak Dai dan teman-teman di kelas Berikut video pembuatan tugas saya
Minggu 3 (25 November 2020)
Rumus Metode Gauss Jordan
Di pertemuan ini, kita kembali dipersilahkan untuk mempresentasikan hasil kerja kita masing masing. Ternyata apa yang diharapkan pak Dai adalah kita mencoba membuat rumus sendiri. mayoritas mahasiswa kelas Metode Numerik 02 mengerjakan tugasnya dengan menggunakan rumus yang sudah ada pada Open Modellica. ada salah satu mahasiswa yang membuat rumus sendiri yaitu bang Cristo. Berikut code yang digunakan oleh bang Cristo (disalin langsung dari milik bang Cristo sehingga hak milik adalah milik bang Cristo)
function GaussJordan
input Real [:,:] A;//matriks awal
output Real [:,:] B;//matriks tereduksi
protected
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //jumlah baris
Integer n = size(A,2); //jumlah kolom
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Baris terbawah yang mempunyai dengan pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//pindah ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
Naive Gauss Elimination
selanjutnya kami diminta untuk mengubah pseudocode yang terdapat pada buku Numerical Methods for Engineer di Figure 9.4. Berikut adalah pseudocode nya
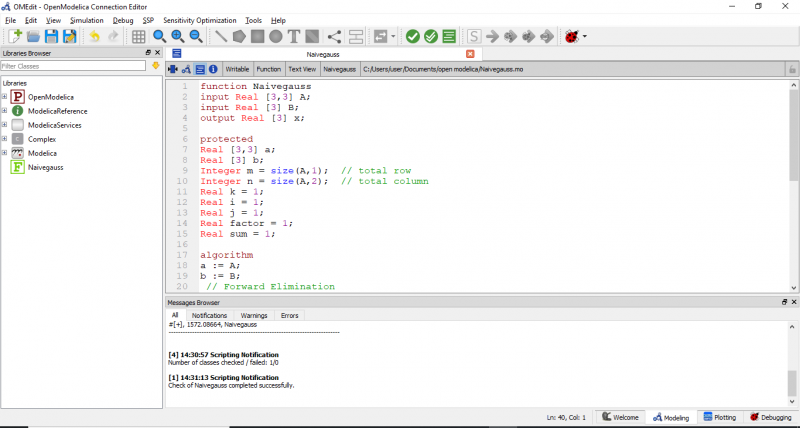
kemudian pseudocode tersebut harus kita ubah ke dalam bahasa pemograman OpenModelica manjadi
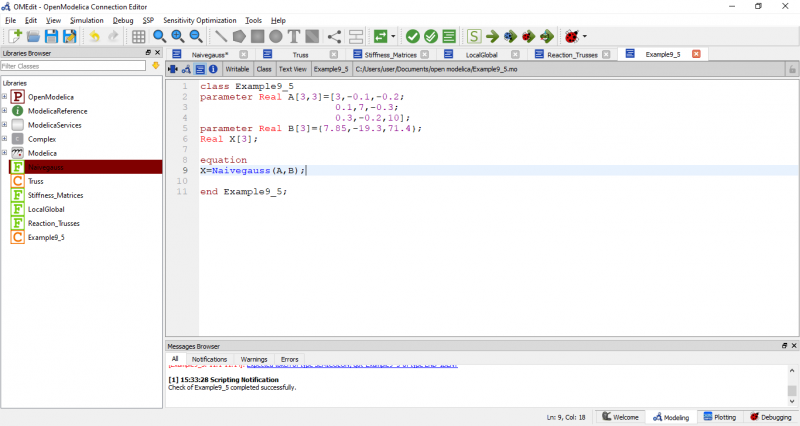
kami juga diminta untuk menyelesaikan Example 9.5 menggunakan code tersebut. berikut adalah soal nya
Dengan demikian, kita membuat class baru yang akan memanggil fungsi diatas
kita siap untuk melakukan simulate dan menemukan hasil dari soal
Tugas Minggu 3
kami juga diberikan tugas untuk menyelesaikan permasalahan pada gambar berikut
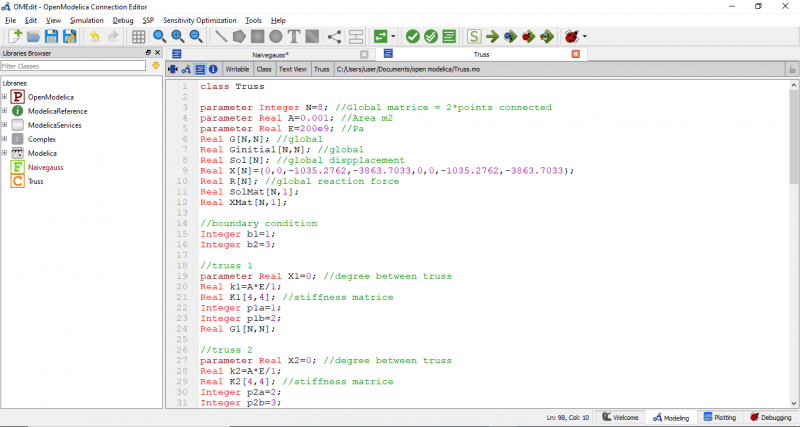
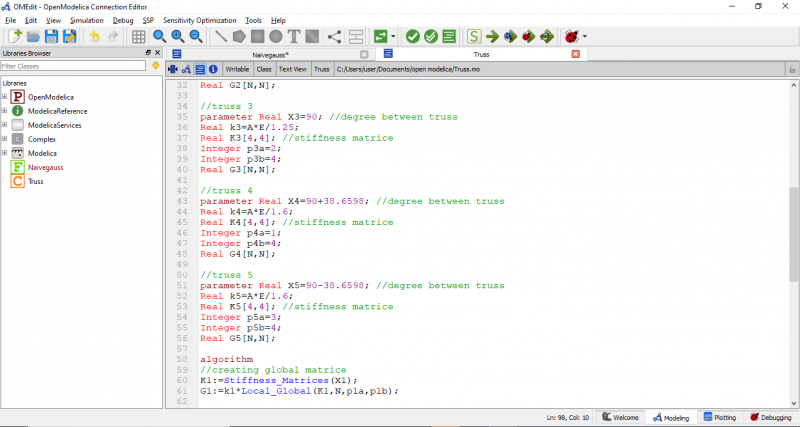
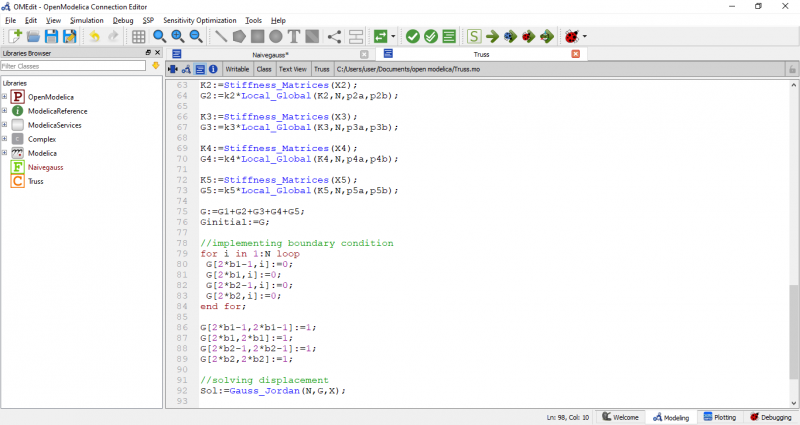
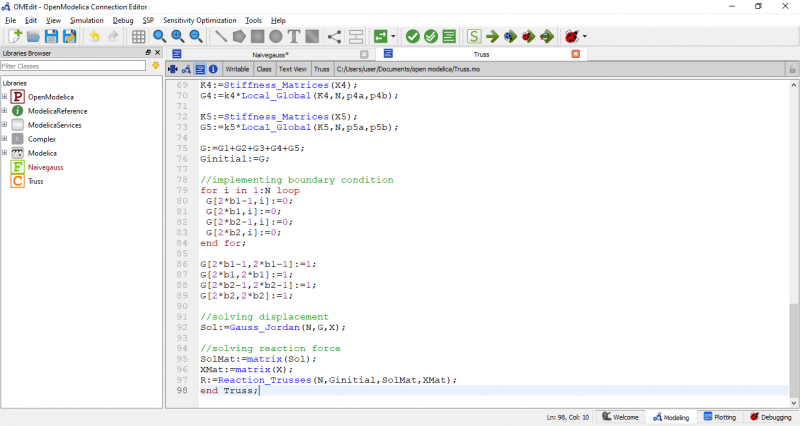
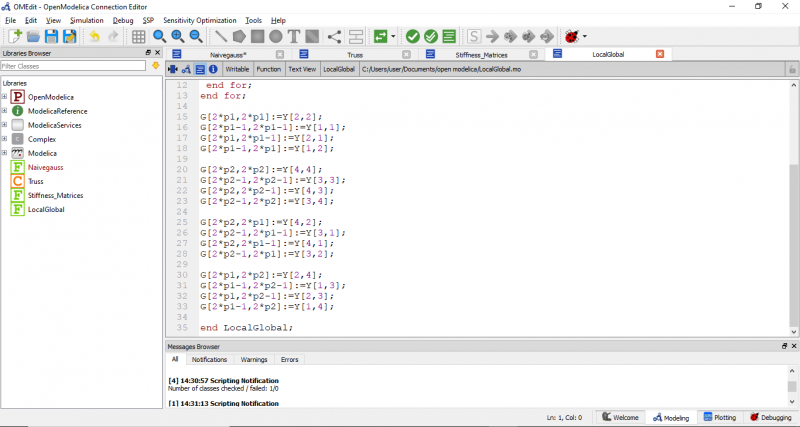
berikut adalah code pada OpenModelica yang sesuai dengan soal
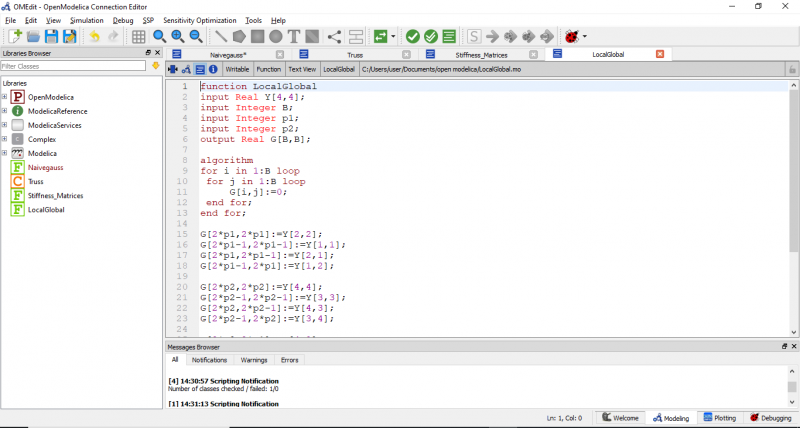
Class tersebut membutuhkan fungsi yang akan dipanggil untuk menjalankan simulasi pada class tersebut. code fungsi nya adalah
kita memerlukan fungsi lain untuk membuat fungsi diatas dapat berjalan
sebelum dapat benar benar berjalan, kita memerlukan fungsi terakhir
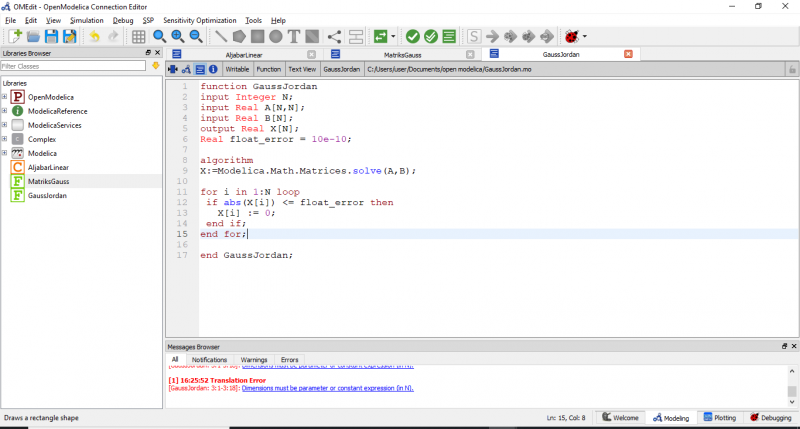
terakhir kita juga memerlukan fungsi berisi metode gauss jordan
dengan demikian code telah lengkap dan dapat langsung dijalankan (disimulate)
Minggu 4 (2 Desember 2020)
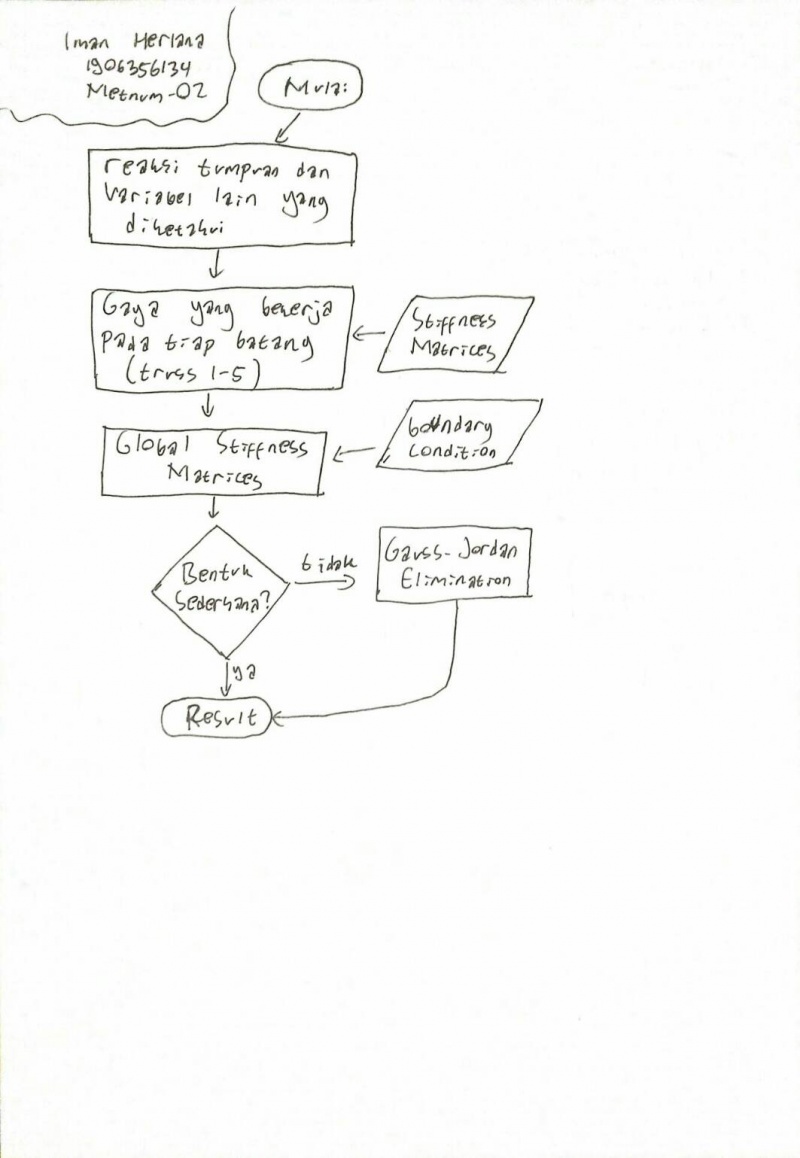
Quiz Diagram Class dan Flowchart
Kita diminta untuk membuat Class Diagram dalam bentuk Flowchart dari code milik Josiah pada tugas pekan 3. Berikut hasil kerja saya
Tugas Minggu 4
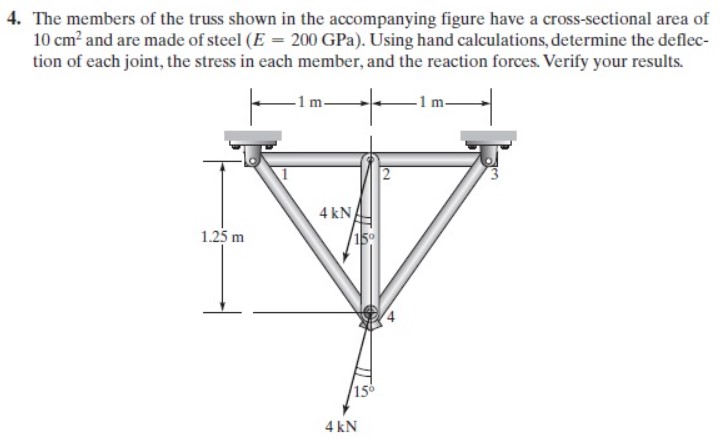
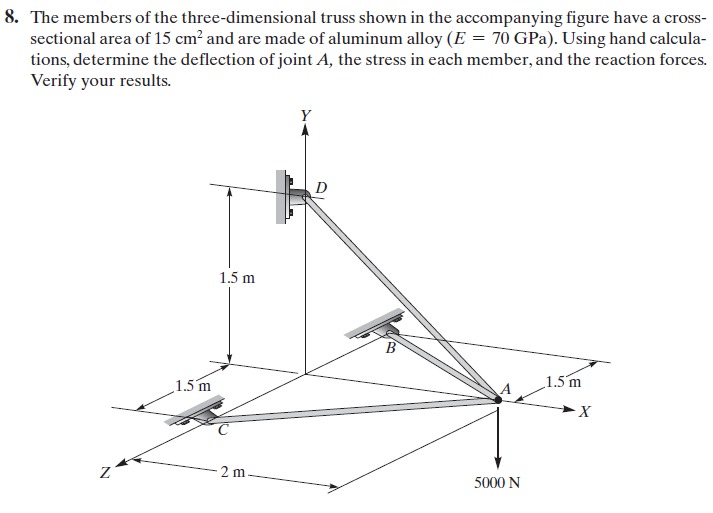
Kami diminta untuk mengerjakan soal nomor 8 tentang Space Trusses. berikut soalnya
untuk mengerjakannya, pertama-tama saya melakukan perhitungan secara manual terlebih dahulu untuk mendata panjang truss serta Cx, Cy, dan Cz
berikut video pengerjaan code pada OpenModelica
Minggu 6 (16 Desember 2020)
pada pertemuan kali ini, kita semua diberikan pengetahuan lebih, bahwa sejatinya ilmu tidak hanya berasal dari buku saja, tetapi juga dari alam sekitar. banyak fenomena yang bisa kita cari tau penyebab dan dampaknya terhadap kehidupan sehari-hari yang apabila dipelajari akan memberikan pengetahuan lebih. pengetahuan berupa teori yang sudah kita dapatkan pun, baik melalui pembelajaran di kelas maupun melalui belajar mandiri, harus dapat diaplikasikan dalam kehidupan sehari-hari. barulah ilmu tersebut menjadi bermanfaat bagi banyak orang
Optimasi
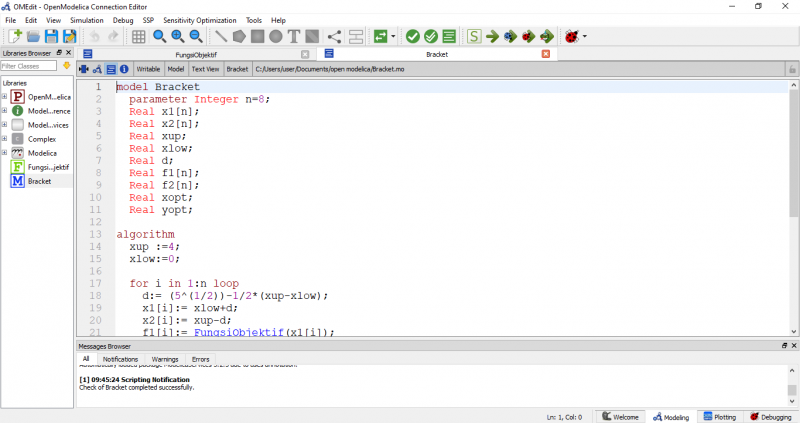
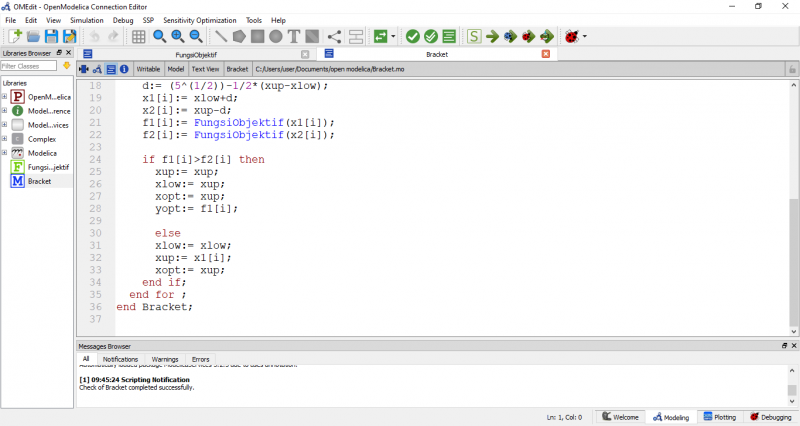
pada pertemuan kali ini, kita diajarkan mengenai Optimasi dengan menggunakan metode bracket oleh bu Chandra. masing masing dari kita dipersilahkan mencoba langsung dalam OpenModelica sambil dituntun oleh bu Chandra apabila ada kesulitan. berikut hasil dari yang saya coba. pertama, kita harus membuat model bracket terlebih dahuli
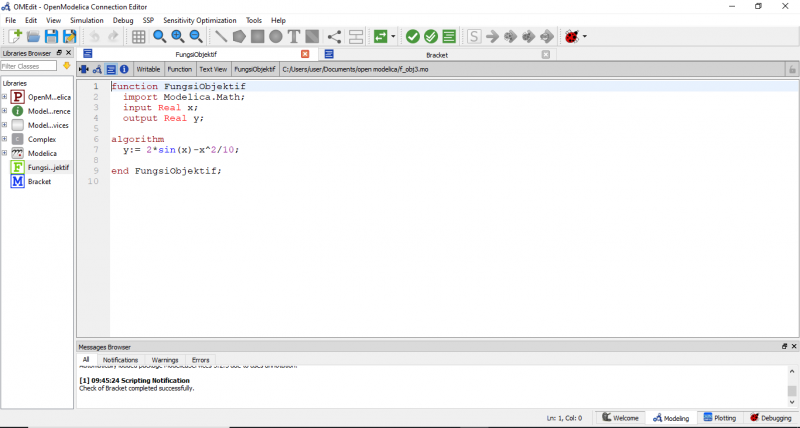
selanjutnya, kita harus menyiapkan fungsi objektif yang nantinya akan dipanggil pada model bracket
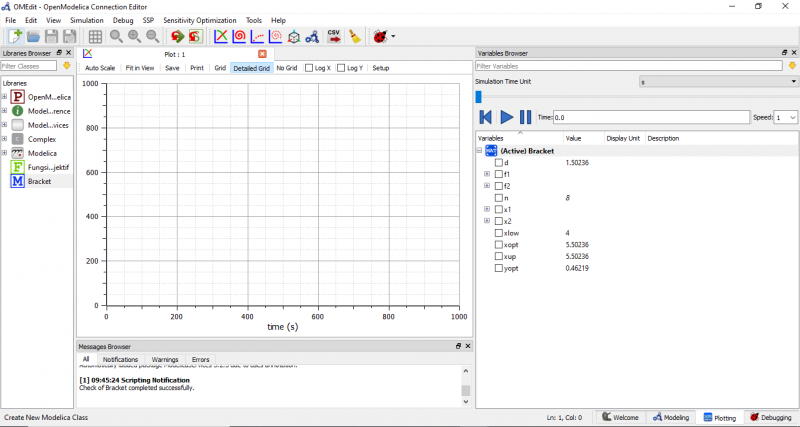
kemudian kita melakukan cek untuk memastikan bahwa code sudah benar dan tidak ada error. apabila sudah tidak ada error, maka dapat langsung melakukan simulasi. berikut adalah hasil setelah disimulasikan
TUGAS BESAR
Setelah sekian minggu mempelajari aplikasi OpenModelica dalam penerapan metode numerik, kami diminta untuk membuat code untuk aplikasi metode numerik dalam optimasi desain struktur rangka sederhana
Mengenal Lebih Jauh Tentang Apa itu Optimasi
optimasi adalah suatu cara untuk menyelesaikan masalah secara optimal. biasanya permasalah yang diselesaikan adalah masalah yang menuntut penyelesaian yang memperhatikan beberapa indikator atau capaian tertentu. misalnya, dalam membangun jembatan, diperlukan bahan yang kuat, akan tetapi tetap ekonomis (memiliki harga yang terjangkau). dengan demikian, maka diperlukan optimasi untuk mencari jalan tengah dari permasalahan tersebut. sehingga penyelesaian yang didapat adalah bahan yang cukup untuk menahan beban sebagai jembatan, dengan harga yang masih terjangkau. penyelesaian tersebut pada akhirnya akan memenuhi kedua indikator yang diinginkan yaitu kuat menahan beban sebagai jembatan, dan memiliki harga yang terjangkau. apabila ingin salah satu indikator saja yang tercapai, bisa saja menggunakan bahan yang paling kuat, akan tetapi tentu saja harganya mahal. pun sebaliknya bisa menggunakan bahan yang paling murah, akan tetapi mudah rapuh. itulah manfaat dari optimasi. optimasi sendiri terbagi menjadi 2 tujuan besar yaitu maksimasi dan minimasi. maksimasi dalam contoh yang disebutkan diatas adalah "Bahan yang kuat" sedangkan minimasi nya adalah "harga yang terjangkau". dalam optimasi, perlu memperhatikan:
- Objective Function
- Decision Variable
- Constraints
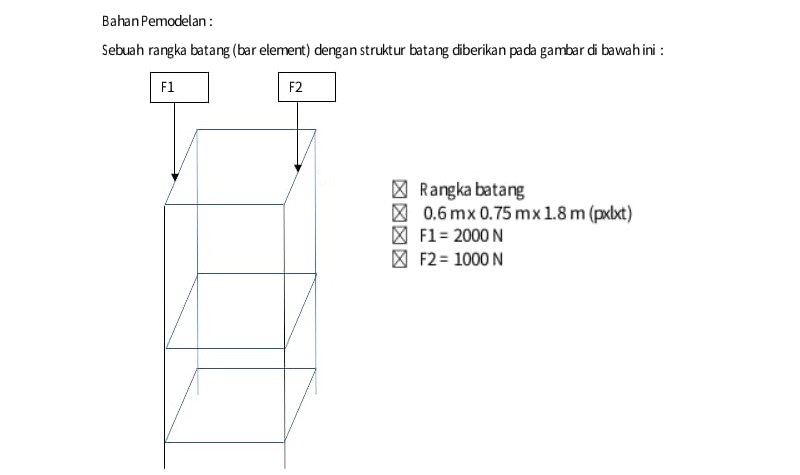
Soal yang Harus Diselesaikan
pada tugas besar ini, kami diharuskan menyelesaikan sebuah permasalahan pada rangka batang menggunakan metode optimasi. berikut adalah soalnya
untuk dapat menyelesaikan permasalahan tersebut, diperlukan adanya asumsi yang mendukung proses perhitungan dan pertimbangan nantinya. berikut asumsi yang dibuat:
- beban hanya terdistribusi pada noda karena sistem bersifat trusses
- ketinggian trusses tiap lantai dianggap sama yaitu 0,6 meter
- displacement yang diizinkan pada trusses horizontal paling atas adalah sebesar 0,001 meter sebelum terjadinya buckling
- safety factor yang ingin didapatkan harus lebih dari 2 untuk menjamin keselamatan
Sistematika Pengerjaan
proses optimasi menggunakan 2 kali perhitungan dengan pertimbangan yang berbeda yaitu kesamaan jenis material dan kesamaan area dari penampang.
untuk jenis material yang sama:
- mencari harga untuk 6 ukuran standar batang dengan material yang sama yaitu SS201.
- mengitung nilai safety factor pada 6 ukuran batang dengan coding yang dikerjakan saat kuis sebelumnya.
- membuat rasio antara safety factor dengan harga total.
- membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting.
- melakukan optimasi menggunakan metode golden section.
Untuk area penampang yang sama:
- mencari harga untuk 4 jenis material dengan area penampang yang sama yaitu 171 mm^2.
- mengitung nilai safety factor pada 4 jenis batang dengan coding awal.
- membuat rasio antara safety factor dengan harga total.
- membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting.
- melakukan optimasi menggunakan metode golden section.
Perhitungan Displacement, Reaction Force, Stress, dan Safety Factor
model Trusses3DTugasBesar
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=292e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=197e9; //Elasticity SS 201 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star; end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses3DTugasBesar;
Perhitungan Rasio Perbandingan Safety Factor dan Biaya
selanjutnya diperlukan pendataan guna mendapatkan banyak data yang diperlukan dalam proses curve fitting, yang nantinya akan digunakan untuk optimasi. data saya kumpulkan dengan melihat beberapa website referensi berikut:
- https://wijayamakmur.com/siku
- https://ptgaja.com/stainless-steel-201/
- https://www.tokopedia.com/kairosmetal/product
- https://www.tokopedia.com/kingsteelid
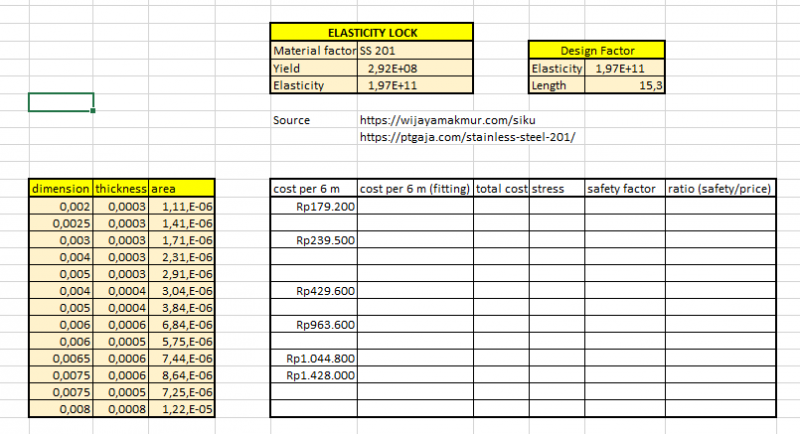
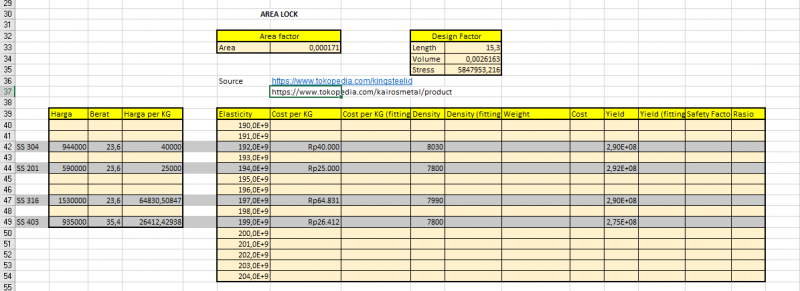
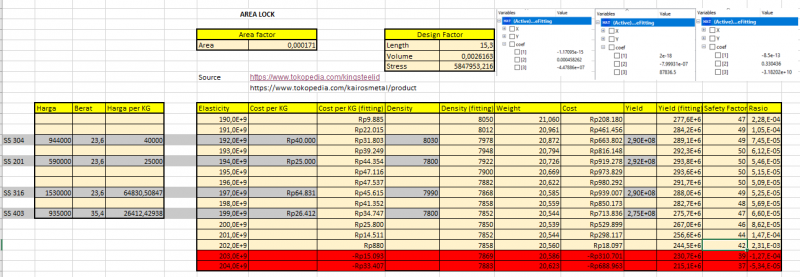
dengan data yang didapatkan pada 4 website tersebut, saya berhasil mengumpulkan data sementara menjadi sebagai berikut
terlihat dari gambar bahwa masih banyak sekali data yang kosong (tidak memiliki input. oleh karena itu, dibutuhkan curve fitting untuk mengisi kekosongan tersebut. fungsi dari dilakukannya curve fitting adalah untuk mengetahui nilai sebuah input yang tidak diketahui sebelumnya. berikut fungsi yang akan dipanggil untuk proses curve fitting
function FuncCurveFitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coef[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coef:=Modelica.Math.Matrices.solve(A,B);
end FuncCurveFitting;
untuk menjalankan fungsi tersebut, tentunya kita memerlukan model untuk memanggil fungsi tersebut. berikut adalah model nya
model CurveFitting
parameter Real X[6]={0.000111, 0.000171, 0.000304, 0.000684, 0.000744, 0.000864};
parameter Real Y[6]={179200, 239500, 429600, 963600, 1044800, 1428000};
Real coef[3];
equation
coef=FuncCurveFitting(X,Y,2);
end CurveFitting;
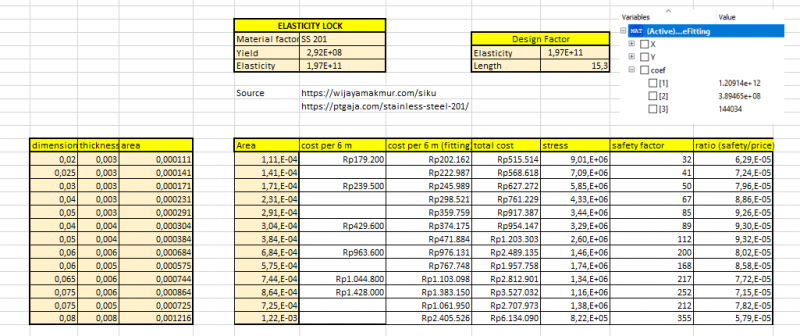
model tersebut dapat digunakan untuk curve fitting berkali-kali. hanya perlu menyesuaikan nilai X dan Y yang diketahui saja. sebagai contoh, code diatas merupakan code curve fitting untuk mencari besar cost per 6 meter. setelah mendapatkan nilai dari hasil curve fitting, data yang kita miliki menjadi sebagai berikut:
dengan demikian kita telah memiliki sejumlah data yang dapat diolah dalam proses optimasi
Optimasi Dengan Metode Golden Section
setelah kita mendapatkan cukup data, kita dapat melakukan optimasi dengan metode Golden Section. golden section bertujuan untuk menemukan nilai yang optimum dengan mengacu pada suatu nilai minimum dari variabel. berikut adalah code untuk metode golden section
model GoldenSection
parameter Real xd[:]={0.000111, 0.000141, 0.000171, 0.000231, 0.000291, 0.000304, 0.000384, 0.000684, 0.000575, 0.000744, 0.000864, 0.000725, 0.001216};
parameter Real yd[size(xd,1)]={6.29E-05, 7.24E-05, 7.96E-05, 8.86E-05, 9.26E-05, 9.30E-05, 9.32E-05, 8.02E-05, 8.58E-05, 7.72E-05, 7.15E-05, 7.82E-05, 5.79E-05};
parameter Real xlo=0.000111;
parameter Real xhi=0.001216;
parameter Integer N=100; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := FuncCurveFitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end GoldenSection;
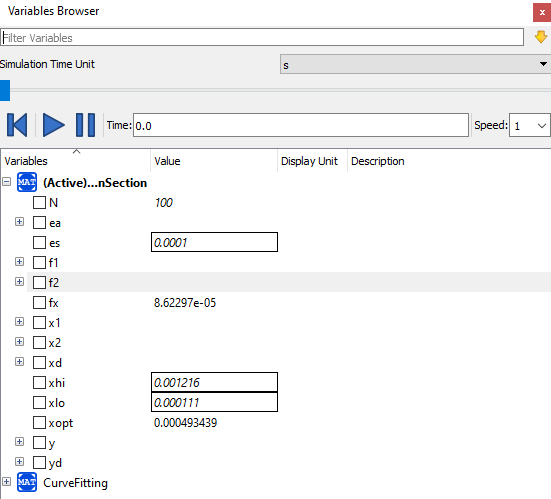
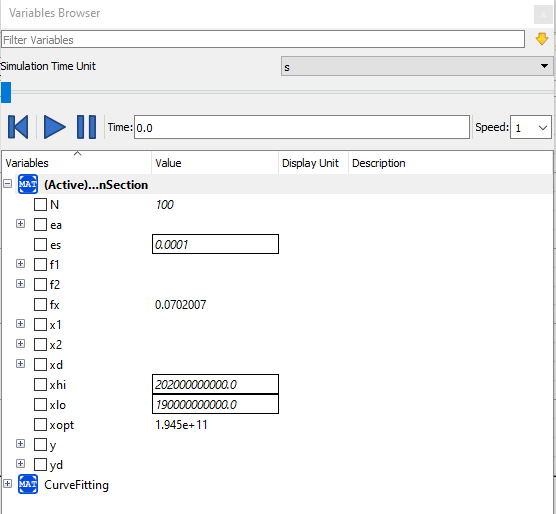
setelah disimulasikan, maka akan didapatkan hasil berupa Xopt yang merupakan nilai optimum. metode golden section harus dijalankan sebanyak 2 kali, yang pertama untuk material tetap, yang kedua untuk area tetap. code diatas merupakan golden section untuk material tetap. berikut hasil simulasi dari material tetap (gambar atas) dan area tetap (gambar bawah):
Hasil dan Analisis
- Material Tetap (Elasticity Locked)
pada kondisi ini, material yang saya pilih adalah SS 201. terlihat dari hasil simulasi Golden Section bahwa nilai Area yang optimum adalah 0,000493439. belum terlihat adanya dimensi dan ketebalan yang cukup mendekati Area tersebut. akan tetapi, yang paling mendekati adalah nilai area 0,000575, yang disusun dari dimensi 6cm x 6cm dengan ketebalan 5mm
- Area Tetap (Area Locked)
pada kondisi ini, Area yang saya tetapkan adalah 0,000171. terlihat dari hasil simulasi Golden Section bahwa nilai Elastisitas yang iptimum adalah 194,5E+9. nilai tersebut mendekati nilai elastisitas 194E+9 yang dimiliki oleh SS201.
- Analisis Hasil
melihat hasil dari kedua simulasi di atas, didapatkan bahwa material yang paling sesuai adalah SS201. oleh karena itu, material yang paling optimal untuk desain rangka persoalan ini adalah SS 201 dengan dimensi kira kira 6cmx6cm dan ketebalan 5 mm
UAS
Berikut adalah jawaban UAS milik saya
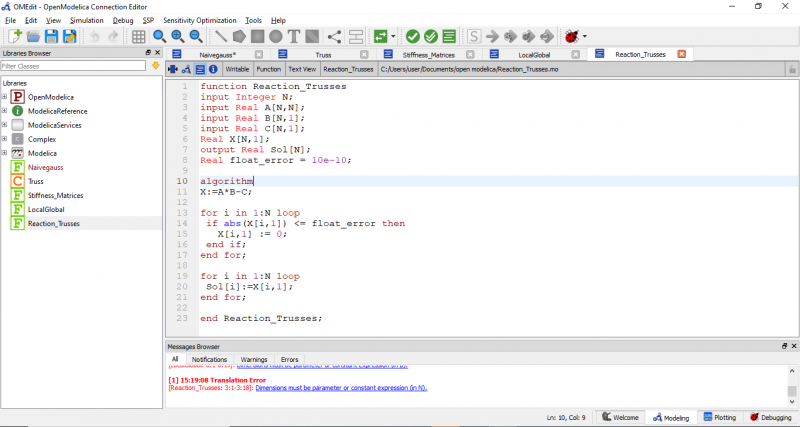
berikut adalah code pada open modelica untuk menyelesaikan persoalan yang diberikan
model UAS_Iman
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=292e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=197e9; //Elasticity SS 201 (Pa)
//define connection
parameter Integer C[:,2]=[1,2;
1,3;
1,4];
//define coordinates (please put orderly)
parameter Real P[:,6]=[0,0,0,1,1,1;//1
10,10,45,1,1,1;//2
10,10,80,1,1,1;//3
10,10,115,1,1,1];//4
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,0,2000,0,0,2000,0,0,2000,0};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star; end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end UAS_Iman;
sampai saat ini saya belum bisa mendapatkan hasil simulasi dari OpenModelica karena aplikasi saya sedang mengalami error