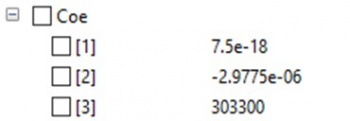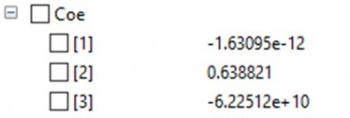Difference between revisions of "Metnum03 Muhammad Ridhwan Sunandar"
| (36 intermediate revisions by the same user not shown) | |||
| Line 171: | Line 171: | ||
[[File:Jawabanquizridhwanexample8.jpeg|600px|center]] | [[File:Jawabanquizridhwanexample8.jpeg|600px|center]] | ||
| − | ='''Metode Numerik: 7 Desember 2020 (PJJ Pertemuan ke-5)'''== | + | =='''Metode Numerik: 7 Desember 2020 (PJJ Pertemuan ke-5)'''== |
| − | Assalamu'alaikum wr.wb. Pertemuan hari ini membahas tentang soal quiz yang telah diberikan pada pertemuan ke 4. Mahasiswa dihimbau untuk diskusi dan Ahmad Mohammad Fahmi telah berhasil mengerjakan soal tersebut dan menjelaskan kepada kami bagaimana menyelesaikan soal tersebut menggunakan software OpenModelica. Dari penjelasan yang diberikan, dapat hasil belajar dari penjelasan tersebut adalah sebagai berikut : | + | Assalamu'alaikum wr.wb. Pertemuan hari ini membahas tentang soal quiz yang telah diberikan pada pertemuan ke 4. Mahasiswa dihimbau untuk diskusi dan Ahmad Mohammad Fahmi telah berhasil mengerjakan soal tersebut dan menjelaskan kepada kami bagaimana menyelesaikan soal no 4 dan 8 tersebut menggunakan software OpenModelica. Penjelasan diawali dengan flowchart yang dibuat sendiri sebelum aplikasi pada hitungannya. Alur pertama nya adalah solve stiffness, lalu matrix global dari setiap elemen, dan melanjutkan dengan menyelesaikan matriks global dan boundary condition, yang akan mendapatkan variabel U. |
| + | |||
| + | Pada function stiffness matrix elemen, terdapat float error karena adanya perhitungan dalam radian. Lalu, melakukan eliminasi menggunakan gauss jordan matrix global dan harus juga menghilangkan floating error. Selanjutnya, memasukkan rumus R=(K*U)-F. Setelah penjelasan oleh Ahmad, Pak Dai menghimbau kami untuk mengerjakan tugas mengenai kodingan yang berkaitan dengan soal kuis No.4 dan No. 8. Ahmad memberikan tutorial untuk kami dengan diskusi yang direkam pada file berikut : | ||
| + | |||
| + | https://drive.google.com/file/d/1n0zvwmn-3G4DWYCSPD48-Xfrp9_kT3R0/view | ||
| + | |||
| + | Dari penjelasan yang diberikan, dapat hasil belajar dari penjelasan tersebut adalah sebagai berikut : | ||
| + | |||
| + | Pertama, memasukkan parameter yang akan digunakan. Pada kasus ini, terdapat node-node, cross section area, modulus elastisitas, serta panjang untuk sumbu x, y, dan z. Lalu, dari elemen tersebut dibuat matriks untuk memasukkan variabel-variabel. Dari referensi Ahmad, digunakan kolom yang menggunakan (:) dan 5 baris untuk soal no.4, serta 7 baris untuk soal no. 8. Lalu, digunakan parameter integer untuk memasukkan node-node dari elemen. Pada soal no.4 dimasukkan jumlah i, j pada node adalah 5. Serta no 8 jumlah node i,j adalah 3. Setelah itu, memasukkan boundary dan load yang terdapat pada node. Load yang dimasukkan terdapat pada axis yang searah pada gaya batang yang ada di soal. Selanjutnya, memasukkan parameter real yang digunakan untuk function dan looping. | ||
| + | |||
| + | Lalu, memasukkan persamaan untuk menghitung K dan persamaan tersebut menggunakan loop untuk setiap batang. Pada function stiffness matrix element, menggunakan parameter yang ada di class untuk dipanggil dan membuat matrix lokal berdasarkan truss yang digunakan. | ||
| + | |||
| + | Soal no. 4 menggunakan matriks dengan stifftrig cos^theta, sin^2theta, dan sin theta * cos theta. Lalu, pada soal no. 8 menggunakan (cos_x)^2, (cos_y)^2, (cos_z)^2, (cos_x*cos_y), (cos_x*cos_z), dan (cos_y*cos_z). | ||
| + | |||
| + | Lalu setelah memasukkan matriks element, dikerjakan matriks global yang mencakup semua nilai pada matriks lokal. Setelah itu, function GaussJordan digunakan untuk mendapat variabel U, R, dan check force. Lalu, fuction dimasukkan ke dalam class kembali. Setelah check model, dapat dilakukan simulasi yang didapatkan nilai U dan R pada masing-masing simulasi. | ||
| + | |||
| + | Setelah memahami penjelasan dari Ahmad, kami diberikan tugas untuk mengerjakan example 3.3. Soal yang diberikan adalah sebagai berikut : | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Soalexamplecodingr1.jpg|600px|center]] | ||
| + | |||
| + | Menurut saya, pengerjaan soal diatas serupa dengan pengerjaan no.8 pada kuis sebelumnya. Tetapi, ada beberapa perubahan karena batang pada soal example 3.3 ini batang-batangnya tidak merupakan tumpuan fixed nya. Parameter yang diubah adalah pada parameter sudut batang Ux, Uy, Uz yang disesuaikan pada soal dan dimensi load nya menjadi berdimensi 3 berupa Fx, Fy, Fz. | ||
| + | |||
| + | Setelah melakukan penyesuaian tersebut, saya melakukan Check Model yang mendapatkan 1407 equation dan 1407 variable serta 216 trivial equation seperti berikut : | ||
| + | |||
| + | [[File:Example33r1.jpg|600px|center]] | ||
| + | |||
| + | Lalu, hasil yang didapat untuk nilai R, U, dan F adalah sebagai berikut : | ||
| + | |||
| + | [[File:RUexample33r1.jpg|200px|center]] | ||
| + | |||
| + | [[File:Fexample33r1.jpg|200px|center]] | ||
| + | |||
| + | =='''Metode Numerik: 14 Desember 2020 (PJJ Pertemuan ke-6)'''== | ||
| + | |||
| + | Assalamu'alaikum wr.wb. Hari ini Pak Dai menghimbau mahasiswa untuk melakukan muhasabah.Muhasabah yang dilakukan adalah terkait dengan pembelajaran mata kuliah metode numerik ini. Mahasiswa dihimbau untuk menilai diri sendiri sesuai apa yang telah didapat serta konsep yang telah dipahami masing-masing individu. | ||
| + | |||
| + | Selanjutnya, pembelajaran dilanjutkan dengan penjelasan materi oleh Christo terkait dengan alur berfikir mengenai soal-soal yang telah diberikan dan menjelaskannya ke teman-teman yang ada di kelas menggunakan software OpenModelica. Penjelasannya adalah terkait bagaimana mengidentifikasi parameter, membentuk model, serta melakukan perhitungan dari model soal yang digunakan. Selain itu, Ahmad Mohammad dan Josiah Enrigo menjelaskan sebagai perbandingan dari soal-soal yang telah dikerjakan. Terima kasih, Wassalamu'alaikum wr.wb. | ||
| + | |||
| + | =='''Metode Numerik: 21 Desember 2020 (PJJ Pertemuan ke-7)'''== | ||
| + | |||
| + | Assalamu'alaikum wr.wb. | ||
| + | |||
| + | Aplikasi Metode Numerik dalam Kasus Optimasi. Hari ini dijelaskan terkait optimasi dan truss yang terdapat 3 displacement, yaitu pada sumbu yz, tetta, dan r. Dijelaskan juga pembuatan pemodelan dari persamaan, boundary condition, serta codingan terkait. Penerapan dari tugas besar adalah untuk menekan biaya dari desain yang akan digunakan. Lalu, dari optimasi tersebut berguna untuk mencari gaya dan kesetimbangan gaya (cek stress, perhitungan, serta kekuatan material). Untuk hal tersebut, kekuatan material harus lebih kuat dari stress dari beban yaitu stress dari beban tersebut tidak boleh lebih besar 1/2 kali nya dari kekuatan material. | ||
| + | |||
| + | Terkait dengan truss, hal tersebut berbeda dengan beam yaitu truss tiap titik mempunyai 3 derajat kebebasan dengan variabel displacement dalam x,y,z untuk asumsi pada sebuah batang. Lalu, untuk beam pada sebuah rangka mempunyai 6 derajat dengan variabel x,y,z kearah momen atau puntirannya. Pada asumsi yang dijelaskan, mahasiswa dihimbau untuk mengerti dan paham bagaimana menyelesaikan permasalahan terkait dengan matriks dan variabel yang sudah disusun dan mengaplikasikannya pada software OpenModelica. | ||
| + | |||
| + | Lalu, mahasiswa dihimbau untuk menghitung kondisi optimal pada rangka dengan parameter seperti pada tujuan dan objektif optimasi. Pada perhitungan, terdapat fungsi-fungsi batasan atau constraint seperti panjang siku ataupun harga per ukurannya. Optimasi mempunyai tujuan untuk meminimalisir biaya. Constrains yang diberikan adalah mampu menahan beban dimana gaya tersebut bekerja yang mampu didukung pada rangka tersebut. Langkah pertama adalah mencari displacement, memeriksa gaya, dan mengoptimasi gaya tersebut lalu menghitung stressnya. Setelah itu, membandingkan stress untuk kekuatan material yang akan digunakan. Tegangan yang dihitung tidak boleh melebihi allowable stress agar rangka sesuai standard nya. Dari data yang dikumpulkan, akan didapatkan jenis material serta ukuran batang dan spesifikasi siku. Setelah hal tersebut, dapat dilakukan optimasi untuk mendapatkan bahan yang paling optimal. | ||
| + | |||
| + | k = A.E/L | ||
| + | |||
| + | dimana : | ||
| + | |||
| + | A = Luas penampang siku | ||
| + | |||
| + | E = Modulus elastisitas tiap bahan | ||
| + | |||
| + | L = Panjang batang rangka | ||
| + | |||
| + | Bahan / profil siku yang akan digunakan merupakan galvanis, stainless, dan sebagainya. | ||
| + | |||
| + | Untuk pembahasan Aplikasi Metode Numerik dalam Kasus Optimasi, hal ini disampaikan oleh Bu Chandra dengan penjelasan optimasi yang digunakan merupakan metode bracket optimization using golden ratio. Bahan pembelajaran tersebut terdapat di PPT yang di share pada WA Group. Mahasiswa dihimbau untuk mengikuti simulasi menggunakan software OpenModelica untuk dapat menyelesaikan permasalahan terkait fungsi exercise yang diberikan. | ||
| + | |||
| + | Optimasi merupakan cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi fungsi non linear dan objektifnya merupakan cara untuk mencari nilai f(x) maksimum dan f(x) minimum. Berikut adalah persamaannya : | ||
| + | |||
| + | d = akar5 - 1/2 x (xu-xl) | ||
| + | |||
| + | x1 = x1 + d | ||
| + | |||
| + | x2 = xu . d | ||
| + | |||
| + | dengan syarat : | ||
| + | |||
| + | - f(x1) > f(x2), domain sebelah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama | ||
| + | |||
| + | - f(x2) > f(x1), domain x sebelah kanan x1 dapat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama | ||
| + | |||
| + | [[File:Pertemuan7sisfluridhwan.jpg|600px|center]] | ||
| + | |||
| + | Kesimpulannya adalah dari penyampaian tugas besar, secara garis besar merupakaan persamaan truss. Fungsi optimasi diharuskan memiliki fungsi objektif seperti mendapatkan stress yang maksimum dan biaya yang minimum. Lalu, variabel yang dapat diubah merupakan dimensi dari truss siku dan juga raw materialnya. Cara menyelesaikan tugas besar yaitu pada awal dibuat alur proses/flowchart cara penyelesaian optimasi, lalu cari 3 material yang berbeda untuk mensimulasikannya dengan tugas besar masing-masing. Lalu, menentukan fungsi objektif, menentukan fungsi constraint yaitu stress yang tidak kurang dari setengah allowable stress dari kekuatan materialnya. Lalu, membandingkan dengan tabel yang ada di buku untuk menyesuaikannya. | ||
| + | |||
| + | =='''Tugas Besar: Optimasi Desain Struktur Rangka (Truss) Sederhana dengan Open Modelica'''== | ||
| + | |||
| + | Assalamu'alaikum wr.wb. Berikut adalah Tugas Besar Metode Numerik untuk melakukan optimasi pemilihan material serta luas penampang trusses untuk rangka beserta parameter yang diketahui seperti berikut : | ||
| + | |||
| + | [[File:Soaltubesmetnumr1.jpg|400px|center]] | ||
| + | |||
| + | [[File:Soaltubesmetnumr2.jpg|200px|center]] | ||
| + | |||
| + | Dengan pemodelan yang sudah diberikan, variasi yang dapat dilakukan adalah dalam parameter material & luas permukaan truss. Lalu, dapat dilakukan asumsi untuk perhitungan adalah sebagai berikut : | ||
| + | |||
| + | 1. Variasi Stiffness terikat dengan variabel area terkait material yang digunakan. Jika variasi elastisitas berbeda akan sulit karena setiap material memiliki range yang tidak teratur dalam satu material sejenis. | ||
| + | |||
| + | 2. Beban akan terdistribusi hanya pada node penghubung (bersifat trusses) | ||
| + | |||
| + | 3. Dimensi material mengikuti standar ukuran material | ||
| + | |||
| + | 4. Melakukan 2 perhitungan dengan Elasticity Locked dan Area Locked | ||
| + | |||
| + | '''Ketentuan :''' | ||
| + | |||
| + | - Tujuan Optimasi : Displacement U minimum, Cross Area minimum, dan nilai E dan A (murah) | ||
| + | |||
| + | - Optimasi untuk mencari harga termurah dengan faktor berubah kekuatan serta area | ||
| + | |||
| + | '''Perhitungan :''' | ||
| + | |||
| + | '''1. Elasticity Locked''' | ||
| + | |||
| + | Merupakan pengambilan data dengan material yang sama untuk memvariasikan luas area. Material yang saya gunakan adalah SS201 berprofil siku. Data yang didapatkan adalah sebagai berikut : | ||
| + | |||
| + | [[File:Elasticitylockedr1.jpg|600px|center]] | ||
| + | |||
| + | source: https://wijayamakmur.com/siku/ | ||
| + | |||
| + | Lalu, melakukan curve fitting untuk mendapatkan hasil harga tiap area yang telah ditentukan, stress, safety factor, serta ratio. Berikut adalah koding terkait dengan hal tersebut : | ||
| + | |||
| + | '''Model Tugas Besar 3D Trusses''' | ||
| + | |||
| + | [[File:Trusses3Dr1.jpg|600px|center]] | ||
| + | |||
| + | '''Function Curve Fitting''' | ||
| + | |||
| + | [[File:Curvefittingr1.jpg|600px|center]] | ||
| + | |||
| + | '''Class Curve Fit untuk Harga Per 6M''' | ||
| + | |||
| + | [[File:Classcurvefitr1.jpg|600px|center]] | ||
| + | |||
| + | Lalu, didapatkan hasil dari simulationnya dengan nilai Coe yang akan kita ambil sebagai salah satu variabel dalam perhitungan adalah sebagai berikut : | ||
| + | |||
| + | [[File:CoeTubesRidhwan.jpg|200px|center]] | ||
| + | |||
| + | Setelah dilakukan perhitungan, didapat hasil cost yang telah dilakukan fitting, total cost, stress, safety factor, ratio dengan hasil sebagai berikut : | ||
| + | |||
| + | [[File:Hasiltotalcostr1.jpg|600px|center]] | ||
| + | |||
| + | Lalu, didapatkan grafik dengan Area sebagai kordinat X nya, lalu ada 2 variabel Y yaitu Cost per 6M (Fitting) dan Ratio sebagai perbandingan. Berikut adalah grafik yang didapat : | ||
| + | |||
| + | [[File:Grafikelasticitylockedr1.jpg|500px|center]] | ||
| + | |||
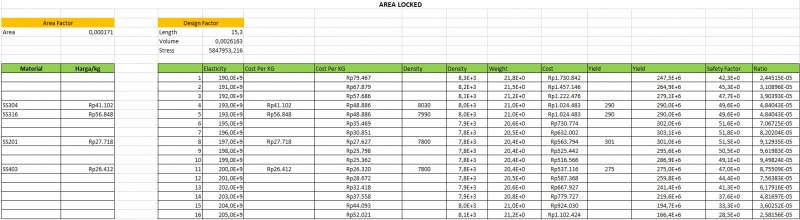
| + | '''2. Area Locked''' | ||
| + | |||
| + | Merupakan pengambilan data menggunakan luas area yang sama dan menggunakan material yang berbeda-beda. Pada perhitungan ini, saya menggunakan 4 material yaitu SS304, SS316, SS201, dan SS403 dengan masing-masing sample variasi material serta harga. Data yang didapat adalah sebagai berikut : | ||
| + | |||
| + | [[File:Arealockedr2.jpg|500px|center]] | ||
| + | |||
| + | Source : | ||
| + | |||
| + | https://www.tokopedia.com/kingsteelid | ||
| + | |||
| + | https://www.stindia.com/316-stainless-steel-supplier.html | ||
| + | |||
| + | Lalu, melakukan pencarian harga, density, serta yield menggunakan curve fitting seperti yang dilakukan pada Elasticity Lock dengan jumlah variabel yang menyesuaikan pada setiap kategorinya. Berikut adalah masing-masing kodingan setiap kategori : | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Curve Fit untuk Cost Per KG''' | ||
| + | |||
| + | class curve_fit | ||
| + | |||
| + | parameter Real X[4]={190.0E+9, 193.0E+9, 193.0E+9, 200.0E+9}; | ||
| + | |||
| + | parameter Real Y[4]={48886, 56848, 27718, 26412}; | ||
| + | |||
| + | Real Coe[3]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Coe:=Curve_Fitting(X,Y,2); | ||
| + | |||
| + | end curve_fit; | ||
| + | |||
| + | Lalu, didapatkan hasil Coe untuk mendapatkan perhitungan Cost per Kg nya adalah sebagai berikut : | ||
| + | |||
| + | [[File:Çoe1r1.jpg|400px|center]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Curve Fit untuk Density''' | ||
| + | |||
| + | class curve_fit | ||
| + | |||
| + | parameter Real X[4]={190.0E+9, 193.0E+9, 193.0E+9, 200.0E+9}; | ||
| + | |||
| + | parameter Real Y[4]={8030, 7990, 7800, 7800}; | ||
| + | |||
| + | Real Coe[3]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Coe:=Curve_Fitting(X,Y,2); | ||
| + | |||
| + | end curve_fit; | ||
| + | |||
| + | Lalu, didapatkan hasil Coe untuk mendapatkan perhitungan Density nya adalah sebagai berikut : | ||
| + | |||
| + | [[File:Coe2r1.jpg|350px|center]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Curve Fit untuk Yield''' | ||
| + | |||
| + | class curve_fit | ||
| + | |||
| + | parameter Real X[4]={190.0E+9, 193.0E+9, 193.0E+9, 200.0E+9}; | ||
| + | |||
| + | parameter Real Y[4]={290, 290, 301, 275}; | ||
| + | |||
| + | Real Coe[3]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Coe:=Curve_Fitting(X,Y,2); | ||
| + | |||
| + | end curve_fit; | ||
| + | |||
| + | Lalu, didapatkan hasil Coe untuk mendapatkan perhitungan Density nya adalah sebagai berikut : | ||
| + | |||
| + | [[File:Coe3r1.jpg|350px|center]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Setelah mendapatkan semua nilai Coe untuk mendapatkan hasil Cost per KG, Density, dan Yield didapatkan hasil lengkap untuk beberapa material tersebut dengan Elasticity yang berbeda-beda sebagai berikut : | ||
| + | |||
| + | [[File:Arealockedr1.jpg|800px|center]] | ||
| + | |||
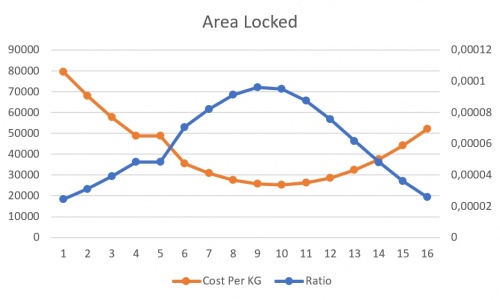
| + | Lalu, didapatkan grafik dengan kordinat X nya Elasticity serta untuk kordinat Y nya adalah Cost per Kg & Ratio. Didapatkan hasil grafik sebagai berikut : | ||
| + | |||
| + | [[File:Grafikarealockedr1.jpg|500px|center]] | ||
| + | |||
| + | Sekian Tugas Besar ini yang sampaikan, terima kasih atas perhatiannya. Mohon maaf apabila ada kesalahan ataupun kekurangan dari penulis. Wassalamu'alaikum wr.wb. | ||
| + | |||
| + | =='''UAS'''== | ||
| + | |||
| + | Assalamu'alaikum wr.wb. Berikut saya lampirkan jawaban saya terkait Ujian Akhir Semester Metode Numerik : | ||
| + | |||
| + | '''No.1''' | ||
| + | |||
| + | [[File:No1uasridhwan.jpg|600px|center]] | ||
| + | |||
| + | Penjelasan No. 1 : | ||
| + | |||
| + | Pada soal ini, saya menjelaskan terkait pemodelan struktur optimum untuk diaplikasikan pada sebuah struktur berupa water tank dengan ketinggian 120 feet dari permukaan serta 300.000 galon. Berikut adalah langkah-langkah pemodelan numerik untuk optimasi striktur tersebut diawali dengan menentukan node-node dari struktur variabel dan sudut dan dilanjutkan dengan penentuan parameter dari struktur. Setelah itu, dapat dibuat asumsi dengan pendekatan sifat elemen dan variabel yang diperlukan yang setelahnya dapat ditentukan matriks lokal sehingga didapatkan K global. Lalu, dapat dihitung U (defleksi) dari struktur tersebut. Selain itu, dapat juga dihitung gaya reaksi, gaya internal, dan stress dari struktur terkait. Untuk optimasi bahan material, dapat digunakan metode Elasticity Locked yang menggunakan elasticity sama namun dengan variasi yang berbeda & Area Locked yang menggunakan area sama dengan variasi material yang berbeda. Setelah hal tersebut, dapat dilakukan optimasi untuk mendapatkan ukuran serta material yang paling optimal untuk struktur tersebut. | ||
| + | |||
| + | '''No.2''' | ||
| + | |||
| + | [[File:No2uasridhwan.jpg|600px|center]] | ||
| + | |||
| + | Penjelasan No. 2 : | ||
| + | |||
| + | Tujuan pemodelan nomerik pada soal no.1 adalah untuk menganalisa optimasi paling optimal serta untuk menentukan material ataupun ukuran yang paling optimal untuk struktur tersebut. | ||
| + | |||
| + | Hukum / dalil fisika yang dipakai adalah Hukum Hooke, Hukum Newton (ΣF = m.a ; ΣF = 0), serta Hukum Kekakuan ( K = A.E / L). | ||
| + | |||
| + | Lalu, untuk asumsi yang dipakai dalam perhitungan adalah beban yang terjadi terdistribusi pada titik sambung, variasi stiffness terkait dengan variabel area tersebut, serta bisa menggunakan asumsi elasticity locked dan area locked untuk melakukan optimasi selanjutnya. | ||
| + | |||
| + | '''No.3''' | ||
| + | |||
| + | [[File:No3uasridhwan.jpg|600px|center]] | ||
| + | |||
| + | Penjelasan No. 3 : | ||
| + | |||
| + | Pada nomor ini dilakukan pembuatan variabel serta persamaan yang digunakan pada matriks lokal dan matriks global. Matriks lokal digunakan berdasarkan turunan dari U1x, U1y, U2x, dan U2y yang didapatkan dari batang pada struktur water tank pada soal. Matriks lokal yang didapat dimasukkan ke matriks lokal berserta sudutnya. Lalu, matriks global didapatkan melalui matriks lokal yang ditambahkan dari seluruh batang pada struktur tersebut. | ||
| + | |||
| + | '''No. 4 & 5 :''' | ||
| + | |||
| + | [[File:No45uasridhwan.jpg|600px|center]] | ||
| + | |||
| + | Penjelasan No. 4 : | ||
| + | |||
| + | Urutan langkah-langkah (pseucode) perhitungan matriks kesetimbangan global no.3 termasuk pengecekan kesalahan (verifikasi) perhitungannya dapat dilakuan dengan tahapan yang diawali dengan Penulisan class serta mendefinisikan parameter terkait dengan memasukkan variabel-variabel, lalu menuliskan matriks lokal dan matriks global, dan melakukan penjumlahan matriks global tersebut. Setelah itu, dapat diimplementasi boundary condition dan melakukan solve displacement matrix. Dari langkah tersebut dapat dilanjutkan dengan menjumlahkan gaya reaksi untuk dibandingkan dengan gaya beban untuk penentuan error dari perhitungannya. | ||
| + | |||
| + | Penjelasan No. 5 : | ||
| + | |||
| + | Fungsi Objektif : Berguna untuk mendapatkan jenis material yang paling optimal untuk digunakan | ||
| + | |||
| + | Constraint : Digunakan untuk optimasi struktur terkait adalah luas area penampang serta Elastisitas material | ||
| + | |||
| + | '''No.6''' | ||
| + | |||
| + | [[File:No6uasridhwan.jpg|600px|center]] | ||
| + | |||
| + | Penjelasan No. 6 : | ||
| + | |||
| + | Pada nomor ini berisi asumsi yang digunakan untuk menghitung pemodelan di software OpenModelica. Asumsi yang digunakan setelah dilakukan pengecekan adalah sebagai berikut : | ||
| + | |||
| + | - L = 50 ft = 600 in | ||
| + | |||
| + | - E = 28 x 10^6 lg/in^2 | ||
| + | |||
| + | - A = 16 m^2 | ||
| + | |||
| + | - Load = 30.000 | ||
| + | |||
| + | '''No.7''' | ||
| + | |||
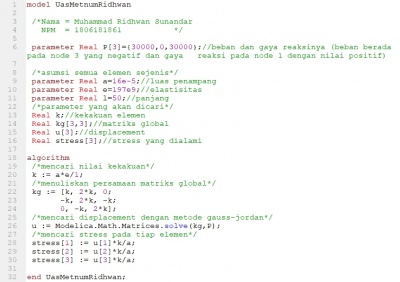
| + | Berikut adalah codingan untuk mendapatkan hasil penyelesaian masalah perhitungan pada no.7 : | ||
| + | |||
| + | model UasMetnumRidhwan | ||
| + | /*Nama = Muhammad Ridhwan Sunandar | ||
| + | NPM = 1806181861 */ | ||
| + | |||
| + | parameter Real P[3]={30000,0,30000};//beban dan gaya reaksinya (beban berada pada node 3 yang negatif dan gaya reaksi pada node 1 dengan nilai positif) | ||
| + | |||
| + | /*asumsi semua elemen sejenis*/ | ||
| + | parameter Real a=16e-5;//luas penampang | ||
| + | parameter Real e=197e9;//elastisitas | ||
| + | parameter Real l=50;//panjang | ||
| + | |||
| + | /*parameter yang akan dicari*/ | ||
| + | Real k;//kekakuan elemen | ||
| + | Real kg[3,3];//matriks global | ||
| + | Real u[3];//displacement | ||
| + | Real stress[3];//stress yang dialami | ||
| + | |||
| + | algorithm | ||
| + | /*mencari nilai kekakuan*/ | ||
| + | k := a*e/1; | ||
| + | |||
| + | /*menuliskan persamaan matriks global*/ | ||
| + | kg := [k, 2*k, 0; | ||
| + | -k, 2*k, -k; | ||
| + | 0, -k, 2*k]; | ||
| + | |||
| + | /*mencari displacement dengan metode gauss-jordan*/ | ||
| + | u := Modelica.Math.Matrices.solve(kg,P); | ||
| + | /*mencari stress pada tiap elemen*/ | ||
| + | stress[1] := u[1]*k/a; | ||
| + | stress[2] := u[2]*k/a; | ||
| + | stress[3] := u[3]*k/a; | ||
| + | |||
| + | end UasMetnumRidhwan; | ||
| + | |||
| + | [[File:KodingUasMetnumRidhwan.jpg|400px|center]] | ||
| + | |||
| + | Dan didapatkan hasil dari simulasi kodingan tersebut sebagai berikut : | ||
| + | |||
| + | [[File:Coe1metnumr1.jpg|200px|center]] | ||
| + | |||
| + | [[File:Coe2metnumr1.jpg|200px|center]] | ||
| + | |||
| + | [[File:Coe3metnumr1.jpg|200px|center]] | ||
| + | |||
| + | Dari hasil simulasi tersebut didapatkan data sebagai berikut : | ||
| + | |||
| + | - Displacement : [0.000135968, 0.000407904, 0.00067984] | ||
| + | |||
| + | - Stress : [2.67857e+07, 8.03571e+07, 1.33929e+08] | ||
Latest revision as of 23:58, 14 January 2021
Contents
- 1 PENDAHULUAN
- 2 BIODATA DIRI
- 3 Metode Numerik: 9 November 2020 (PJJ Pertemuan ke-1)
- 4 Metode Numerik: 16 November 2020 (PJJ Pertemuan ke-2)
- 5 Metode Numerik: 23 November 2020 (PJJ Pertemuan ke-3)
- 6 Metode Numerik: 30 November 2020 (PJJ Pertemuan ke-4)
- 7 Metode Numerik: 7 Desember 2020 (PJJ Pertemuan ke-5)
- 8 Metode Numerik: 14 Desember 2020 (PJJ Pertemuan ke-6)
- 9 Metode Numerik: 21 Desember 2020 (PJJ Pertemuan ke-7)
- 10 Tugas Besar: Optimasi Desain Struktur Rangka (Truss) Sederhana dengan Open Modelica
- 11 UAS
PENDAHULUAN
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Perkenalkan, saya Muhammad Ridhwan Sunandar dengan NPM 1806181861. Merupakan salah satu mahasiswa S1 Paralel Teknik Mesin Universitas Indonesia angkatan 2018. Di halaman ini saya cantumkan biodata saya beserta tugas ataupun ringkasan sesuai dengan dosen dari mata kuliah yang dicantumkan. Semoga apa yang saya tulis disini bisa berkah dan bermanfaat bagi kita semua.
BIODATA DIRI
NAMA : Muhammad Ridhwan Sunandar
NPM : 1806181861
JURUSAN : Teknik Mesin
ANGKATAN : 2018
Metode Numerik: 9 November 2020 (PJJ Pertemuan ke-1)
Assalamu'alaikum wr.wb. Pada pertemuan pertama ini, Pak Dai menerangkan keberlangsungan pembelajaran yang berkaitan dengan air.eng.ui.ac.id. Mahasiswa dianjurkan untuk menggunakan website tersebut untuk menjadi salah satu platform pengembangan diri untuk selalu belajar dan mengaplikasikan apa yang dipelajari. Hal ini berkaitan dengan apa yang disampaikan Pak Dai, yaitu tentang 4 poin penting dalam kegiatan belajar yang diterapkan pada kelas Metode Numerik ini. Poin pertama adalah mengenal atau mengetahui proses pengetahuannya. Hal ini berkaitan dengan pembelajaran di website ini, dimana mahasiswa dapat mengetahui proses pengetahuannya dengan menulis kembali apa yang telah dipelajari. Lalu, poin kedua adalah mengerti konsep. Konsep yang telah diajarkan diharapkan dapat diserap oleh masing-masing mahasiswa semaksimal mungkin. Poin ketiga adalah bisa membantu memecahkan masalah dari pemahaman tersebut. Hal ini dapat dilihat dari pengaplikasian dari pembelajaran yang akan dilakukan pada suatu software bernama Open Modelica yang Inshaa Allah dapat diaplikasikan dalam kasus di kehidupan sehari-hari. Serta poin keempat adalah mendapatkan nilai tambah di dalam usaha mengenal diri sendiri. Di poin ini setiap individu diharapkan dapat mengenal diri sendiri dengan tujuan untuk mengetahui sampai mana ilmu yang sudah di dapat, sehingga bisa mendapatkan nilai tambah seiringan dengan mengembangkan apa yang sudah dipelajari. Selain itu, Pak Dai memberi arahan kepada mahasiswa untuk diskusi mengenai pengaplikasian materi yang telah dipelajari sebelum UTS dan pengaplikasiannya pada kehidupan sehari hari. Setelah itu, mahasiswa dianjurkan untuk mempelajari software Open Modelica dan mencoba menggunakannya. Setelah itu dituliskan apa yang telah di dapat mengenai software tersebut di website ini beserta di upload ke youtube masing-masing mahasiswa sebagai proses pembelajaran. Kami juga dianjurkan untuk mengingat kembali materi sebelum UTS. Pertama-tama, kami mempelajari bagaimana metode numerik secara garis besar. kemudian pada bab 5, kami belajar mengenai metode-metode yang dapat digunakan untuk menyelesaikan beberapa persamaan. Beberapa metode tersebut ada bracketing method yang berisi graphical method, bisection method, dan False position method. Lalu, kemudian ada beberapa metode berikutnya yaitu open method yang berisi Fixed-point iteration, Newton Raphson method, Secant method, dan Brent's method. Pada Bab selanjutnya, kami belajar mengenai regresi linear. Disini, regresi linear dapat digunakan untuk membuktikan teori yang sudah ada dengan beberapa eksperimen. Dengan mengambil sampel yang bervariasi, kami bisa menghitung variabel yang ada serta error dan lain-lain. Metode ini sering dilakukan pada saat praktikum atau pada saat analisa setelah pengambilan data. Materi terakhir sebelum uts yang kami pelajari adalah interpolasi, yang merupakan salah satu metode yang digunakan untuk mengetahui nilai dari suatu interval dua buah titik yang terletak dalam satu garis lurus. ada beberapa jenis yaitu newton Divided difference, Langrange, Spline, dan multidimensional. Setelah membahas materi ini, kami dianjurkan untuk menggunakan software OpenModelica dan diberikan tugas.
Pembelajaran OpenModelica (Tugas 1)
Pada proses pembelajaran OpenModelica ini, saya menggunakan referensi berikut untuk dipelajari : https://www.youtube.com/watch?v=esGAcZ_ViRU
Di video tersebut dijelaskan bagaimana cara membuat model grafik dari sirkuit listrik menggunakan OpenModelica. Tahap awal dilakukan dengan pembuatan class baru dengan nama "FirstSteps" dengan specialization > package dan extends icon berupa example package. Di tahap ini ada info jika belum di save, hal ini cukup penting agar menjaga file tersebut jika terjadi kendala yang tidak diinginkan dan beresiko menghilangkan file jika belum di save. Dapat dilihat pada gambar di bawah maka di bagian tulisan "FirstSteps" di sebelah kiri tersebut akan berwarna merah jika belum di save seperti gambar di sebelah kiri, sementara jika sudah di save maka akan berwarna biru seperti gambar sebelah kanan berikut :
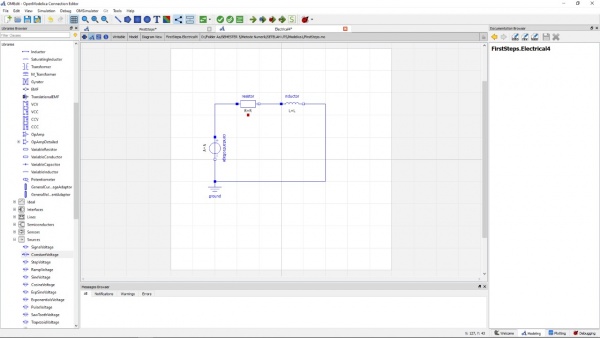
Setelah itu, dilanjutkan dengan pembuatan Model Electric4 pada FirstSteps. Kemudian klik modelica pada kolom libraries sebelah kiri pada menu electrical untuk memasukkan beberapa unsur yang diinginkan. Setelah memasukkan beberapa unsur tersebut dan disambungkan didapatkan model seperti berikut :
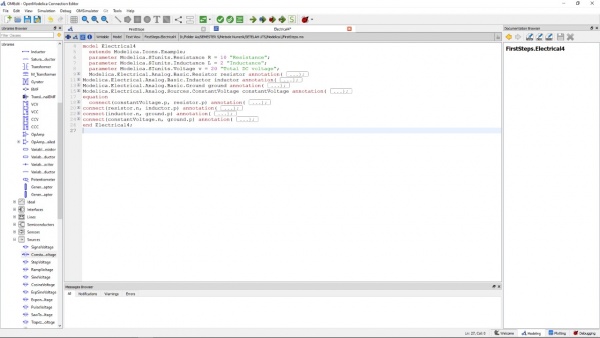
Selanjutnya, dilakukan proses penentuan parameter di kolom Text View. Parameter ditulis sesuai dengan yang diinginkan pada model agar sesuai dengan apa yang diinginkan, sehingga akan seperti berikut :
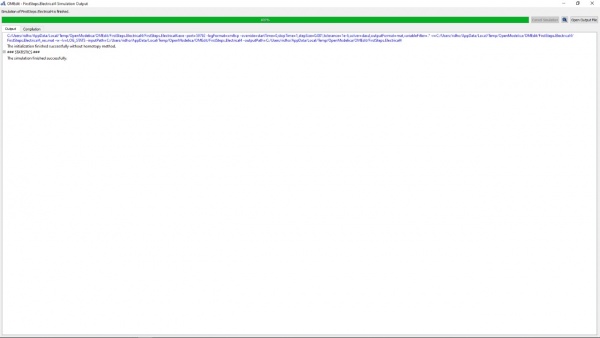
Proses dilanjutkan kembali pada Diagram View untuk menentukan parameter pada setiap unsur yang ada pada model tersebut. Jika sudah selesai, langsung klik Simulation Setup yang ada di bagian atas dan masukkan sesuai dengan bentuk model yang diinginkan dan tekan OK. Maka akan muncul proses simulasi dan tunggu hingga selesai sehingga tampilan dari Simulation Output tersebut seperti berikut :
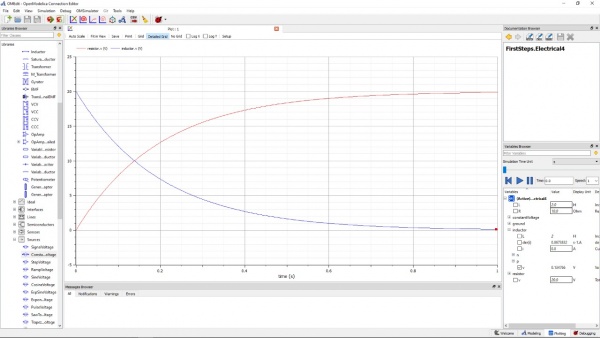
Setelah selesai proses simulasi maka akan muncul grafik dengan variabel yang dapat kita pilih pada Variabel Browser yang terletak pada bagian kanan bawah, seperti contohnya pada grafik berikut dengan variabel v pada resistor dan v pada induktor :
Berikut adalah video tutorial untuk percobaan simulasi yang saya lakukan :
Metode Numerik: 16 November 2020 (PJJ Pertemuan ke-2)
Assalamu'alaikum wr.wb. Hari ini Pak Dai memulai dengan diskusi pembelajaran OpenModelica yang sudah dilakukan. Masing-masing mahasiswa diberi kesempatan untuk mempresentasikan apa yang sudah dilakukan dalam hal mencoba software OpenModelica seperti Tugas1 yang sudah saya tulis dibagian atas. Lalu, dilanjutkan dengan latihan membuat perhitungan sederhana menjumlahkan angka 10 terhadap suatu variabel dan menghitung rata-rata dengan menggunakan Software OpenModelica.
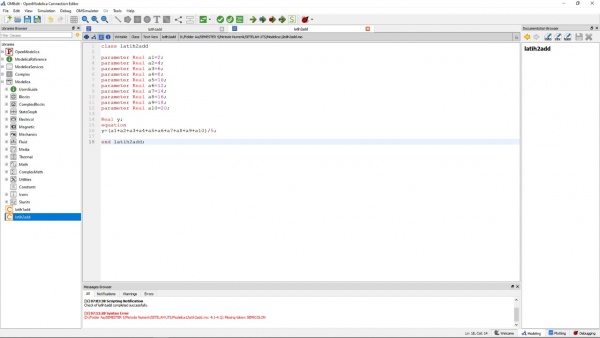
Pada langkah pertama, dilakukan perhitungan nilai x untuk persamaan y=x+10 dengan x=2. Berikut adalah tampilan nya :
Lalu, dilanjutkan dengan memproses nya sehingga didapatkan grafik seperti berikut dan juga didapatkan hasil y yang diinginkan :
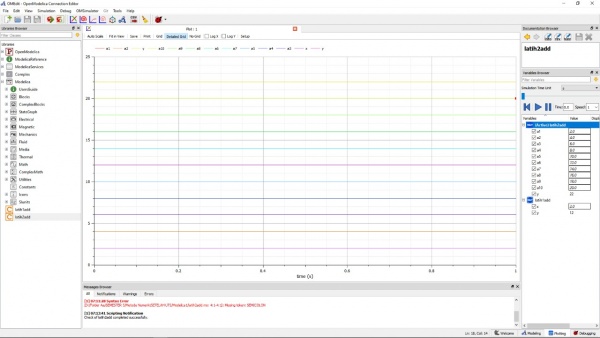
Langkah selanjutnya adalah menghitung rata-rata dari data yang sudah ada. Berikut adalah tampilan nya :
Pada langkah keempat ini didapatkan hasil dari rata-rata yang sudah dimasukkan data nya tadi. Terlihat angka dan grafik yang didapat adalah sebagai berikut :
Type Function untuk menyelesaikan persamaan-persamaan Aljabar Simultan (Tugas 2)
Selain simulasi yang dilakukan diatas, Pak Dai juga memberikan tugas untuk menyelesaikan persamaan Aljabar Simultan. Pengertian dari Aljabar Simultan adalah suatu penyelesaian matematik yang cukup rumit dimana membutuhkan suatu penyelesaian yang lebih sederhana menggunakan suatu software yang telah disediakan, seperti OpenModelica. Berikut adalah beberapa jenis metode yang bisa diterapkan pada aljabar simultan :
1. Metode Eliminasi Gauss
2. Metode Crammer
3. Metode Gauss Seidel
4. Metode Gauss-Jordan
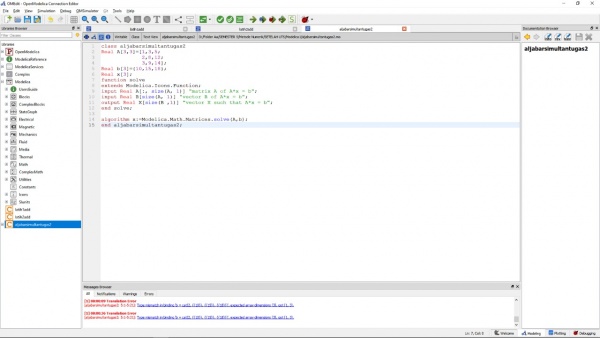
Persamaan yang akan saya terapkan untuk penyelesaian Aljabar Simultan adalah sebagai berikut :
X1 + 3X2 + 5X3 = 10
2X1 + 8X2 + 12X3 = 15
3X1 + 9X2 + 14X3 = 18
Berikut adalah simulasi yang saya lakukan untuk menyelesaikan persamaan diatas :
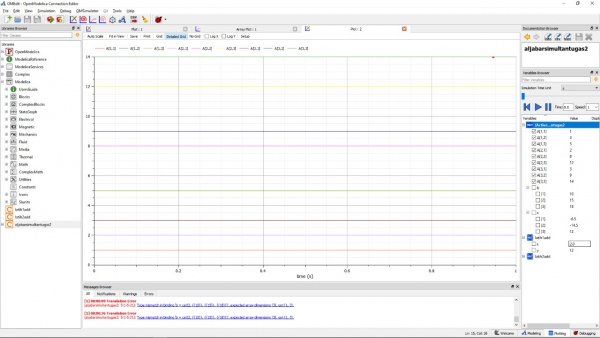
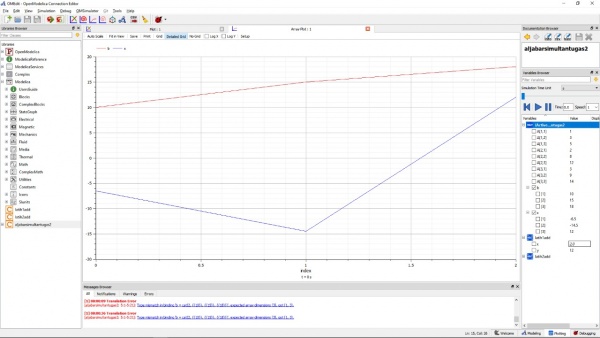
Dan didapatkan hasil untuk x berserta grafik nya adalah sebagai berikut :
Metode Numerik: 23 November 2020 (PJJ Pertemuan ke-3)
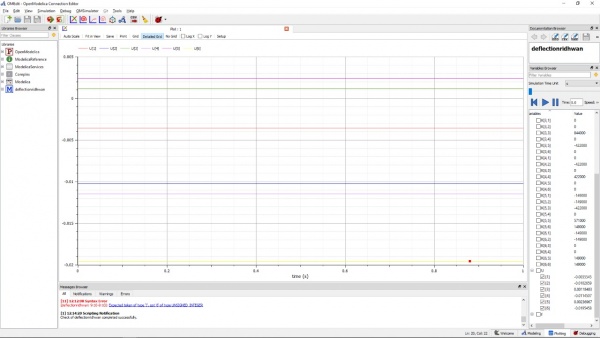
Assalamu'alaikum wr.wb. Hari ini diawali dengan Pak Dai dengan diskusi Tugas 2 bersama mahasiswa di kelas. Lalu, dilanjutkan dengan pembahasan simulasi yang diberikan Pak Dai untuk pengaplikasiannya. Setelah itu, ada tugas untuk dikerjakan dan dikumpulkan minggu depan. Tugas tersebut adalah mencari defleksi menggunakan matriks. Berikut adalah soal yang diberikan Pak Dai :
Tugas 3
Kemudian berikut adalah asumsi yang ada untuk soal tersebut :
Berikut adalah hasil untuk simulasi yang pertama :
Dari kodingan tersebut, didapatkan data sebagai berikut :
Lalu, untuk mendapatkan gaya reaksi, dilakukan koding seperti tampilan berikut :
Didapat data untuk gaya reaksi adalah seperti berikut :
Lalu, untuk mendapatkan defleksi total dilakukan koding dan didapatkan hasil data sebagai berikut :
Terima kasih, Wassalamu'alaikum wr.wb.
Metode Numerik: 30 November 2020 (PJJ Pertemuan ke-4)
Assalamu'alaikum wr.wb. Hari ini Pak Dai membuka pertemuan ke 3 dengan pembahasan mengenai Metode Numerik. Selanjutnya, dibahas mengenai pembebanan statik dan dinamik serta hubungannya dengan pemahaman Metode Numerik. Kemudian Pak Dai memberikan soal untuk dijadikan Quiz.
Quiz
Pada quiz kali ini, diberikan soal seperti berikut :
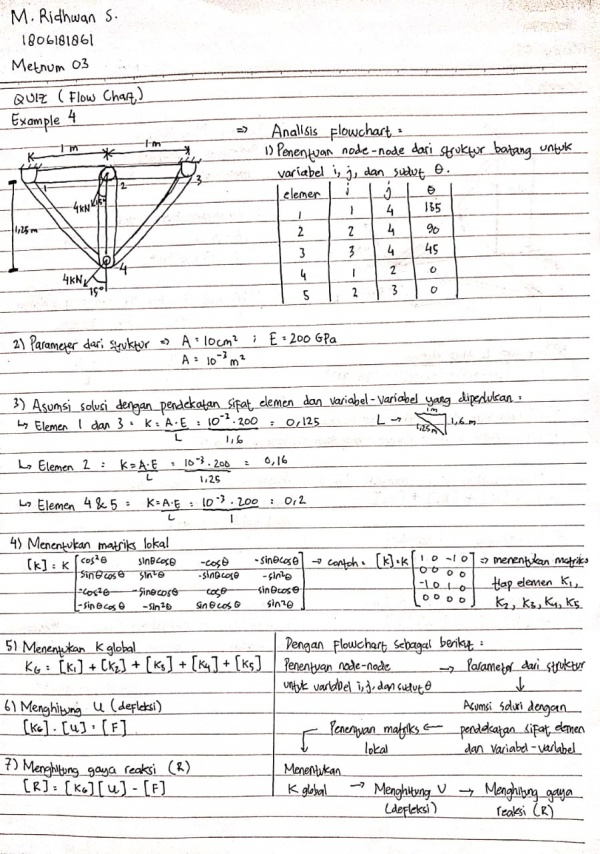
Lalu untuk pengumpulan pertama mahasiswa diminta untuk membuat flowchart, berikut adalah file terkait :
Metode Numerik: 7 Desember 2020 (PJJ Pertemuan ke-5)
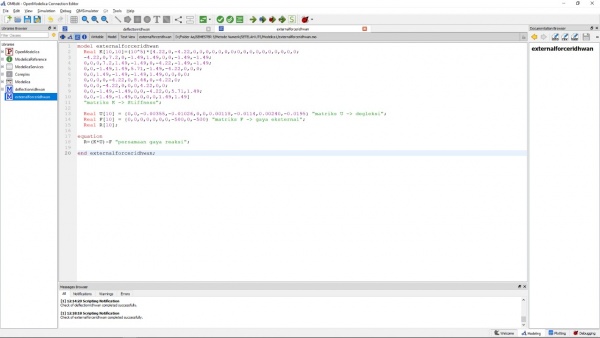
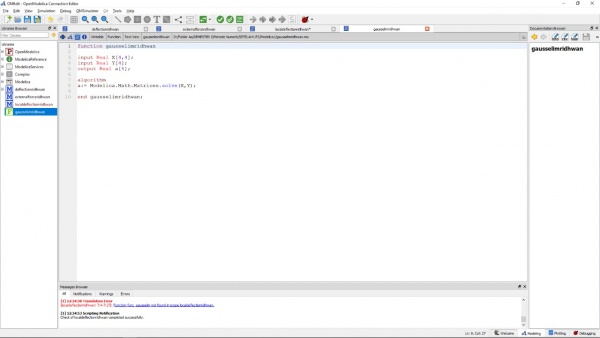
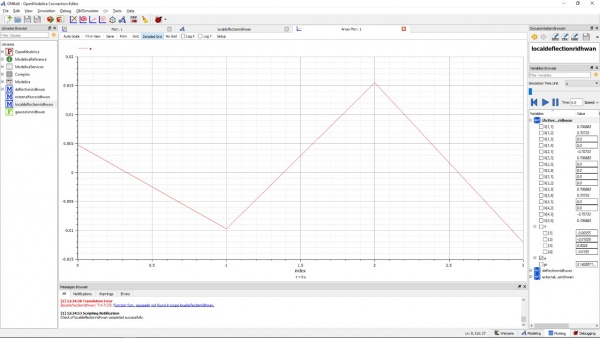
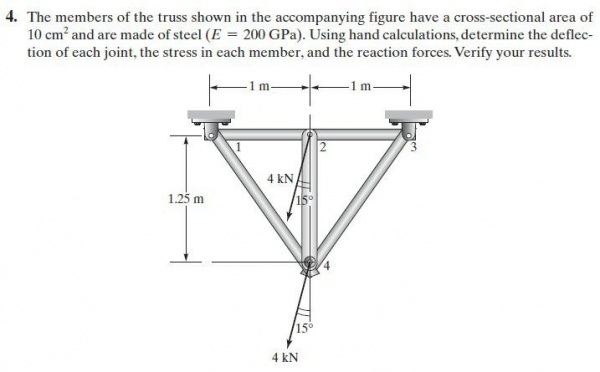
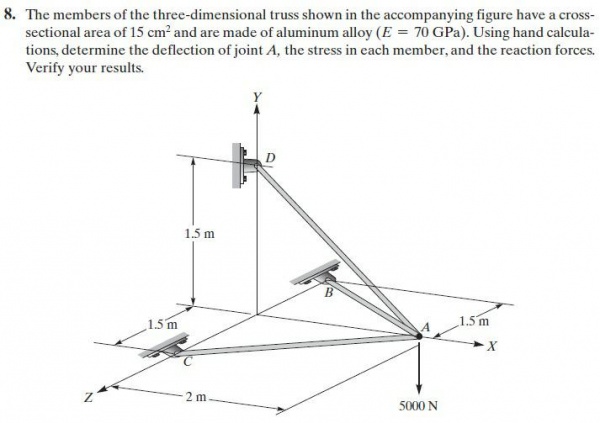
Assalamu'alaikum wr.wb. Pertemuan hari ini membahas tentang soal quiz yang telah diberikan pada pertemuan ke 4. Mahasiswa dihimbau untuk diskusi dan Ahmad Mohammad Fahmi telah berhasil mengerjakan soal tersebut dan menjelaskan kepada kami bagaimana menyelesaikan soal no 4 dan 8 tersebut menggunakan software OpenModelica. Penjelasan diawali dengan flowchart yang dibuat sendiri sebelum aplikasi pada hitungannya. Alur pertama nya adalah solve stiffness, lalu matrix global dari setiap elemen, dan melanjutkan dengan menyelesaikan matriks global dan boundary condition, yang akan mendapatkan variabel U.
Pada function stiffness matrix elemen, terdapat float error karena adanya perhitungan dalam radian. Lalu, melakukan eliminasi menggunakan gauss jordan matrix global dan harus juga menghilangkan floating error. Selanjutnya, memasukkan rumus R=(K*U)-F. Setelah penjelasan oleh Ahmad, Pak Dai menghimbau kami untuk mengerjakan tugas mengenai kodingan yang berkaitan dengan soal kuis No.4 dan No. 8. Ahmad memberikan tutorial untuk kami dengan diskusi yang direkam pada file berikut :
https://drive.google.com/file/d/1n0zvwmn-3G4DWYCSPD48-Xfrp9_kT3R0/view
Dari penjelasan yang diberikan, dapat hasil belajar dari penjelasan tersebut adalah sebagai berikut :
Pertama, memasukkan parameter yang akan digunakan. Pada kasus ini, terdapat node-node, cross section area, modulus elastisitas, serta panjang untuk sumbu x, y, dan z. Lalu, dari elemen tersebut dibuat matriks untuk memasukkan variabel-variabel. Dari referensi Ahmad, digunakan kolom yang menggunakan (:) dan 5 baris untuk soal no.4, serta 7 baris untuk soal no. 8. Lalu, digunakan parameter integer untuk memasukkan node-node dari elemen. Pada soal no.4 dimasukkan jumlah i, j pada node adalah 5. Serta no 8 jumlah node i,j adalah 3. Setelah itu, memasukkan boundary dan load yang terdapat pada node. Load yang dimasukkan terdapat pada axis yang searah pada gaya batang yang ada di soal. Selanjutnya, memasukkan parameter real yang digunakan untuk function dan looping.
Lalu, memasukkan persamaan untuk menghitung K dan persamaan tersebut menggunakan loop untuk setiap batang. Pada function stiffness matrix element, menggunakan parameter yang ada di class untuk dipanggil dan membuat matrix lokal berdasarkan truss yang digunakan.
Soal no. 4 menggunakan matriks dengan stifftrig cos^theta, sin^2theta, dan sin theta * cos theta. Lalu, pada soal no. 8 menggunakan (cos_x)^2, (cos_y)^2, (cos_z)^2, (cos_x*cos_y), (cos_x*cos_z), dan (cos_y*cos_z).
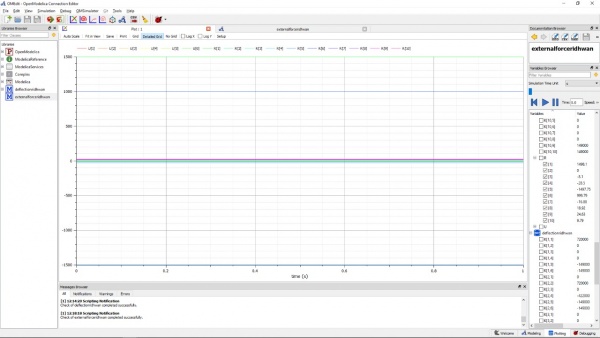
Lalu setelah memasukkan matriks element, dikerjakan matriks global yang mencakup semua nilai pada matriks lokal. Setelah itu, function GaussJordan digunakan untuk mendapat variabel U, R, dan check force. Lalu, fuction dimasukkan ke dalam class kembali. Setelah check model, dapat dilakukan simulasi yang didapatkan nilai U dan R pada masing-masing simulasi.
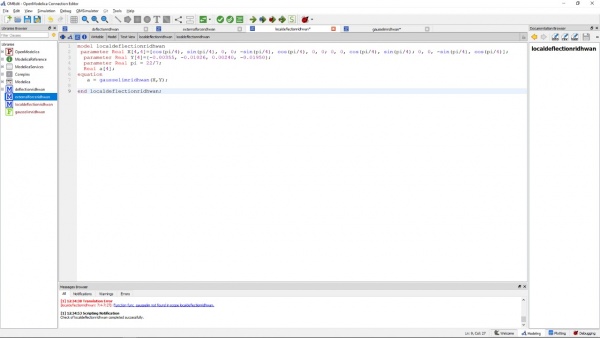
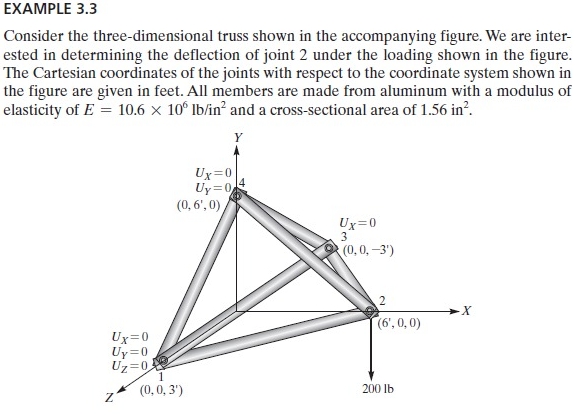
Setelah memahami penjelasan dari Ahmad, kami diberikan tugas untuk mengerjakan example 3.3. Soal yang diberikan adalah sebagai berikut :
Menurut saya, pengerjaan soal diatas serupa dengan pengerjaan no.8 pada kuis sebelumnya. Tetapi, ada beberapa perubahan karena batang pada soal example 3.3 ini batang-batangnya tidak merupakan tumpuan fixed nya. Parameter yang diubah adalah pada parameter sudut batang Ux, Uy, Uz yang disesuaikan pada soal dan dimensi load nya menjadi berdimensi 3 berupa Fx, Fy, Fz.
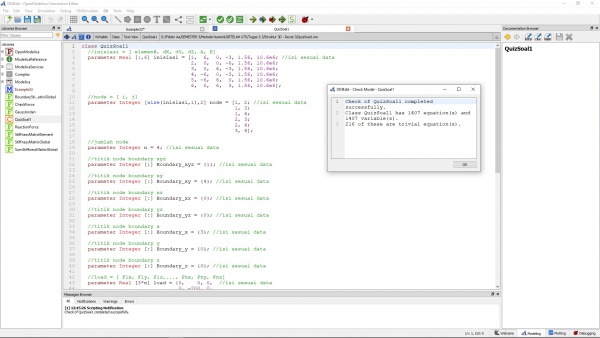
Setelah melakukan penyesuaian tersebut, saya melakukan Check Model yang mendapatkan 1407 equation dan 1407 variable serta 216 trivial equation seperti berikut :
Lalu, hasil yang didapat untuk nilai R, U, dan F adalah sebagai berikut :
Metode Numerik: 14 Desember 2020 (PJJ Pertemuan ke-6)
Assalamu'alaikum wr.wb. Hari ini Pak Dai menghimbau mahasiswa untuk melakukan muhasabah.Muhasabah yang dilakukan adalah terkait dengan pembelajaran mata kuliah metode numerik ini. Mahasiswa dihimbau untuk menilai diri sendiri sesuai apa yang telah didapat serta konsep yang telah dipahami masing-masing individu.
Selanjutnya, pembelajaran dilanjutkan dengan penjelasan materi oleh Christo terkait dengan alur berfikir mengenai soal-soal yang telah diberikan dan menjelaskannya ke teman-teman yang ada di kelas menggunakan software OpenModelica. Penjelasannya adalah terkait bagaimana mengidentifikasi parameter, membentuk model, serta melakukan perhitungan dari model soal yang digunakan. Selain itu, Ahmad Mohammad dan Josiah Enrigo menjelaskan sebagai perbandingan dari soal-soal yang telah dikerjakan. Terima kasih, Wassalamu'alaikum wr.wb.
Metode Numerik: 21 Desember 2020 (PJJ Pertemuan ke-7)
Assalamu'alaikum wr.wb.
Aplikasi Metode Numerik dalam Kasus Optimasi. Hari ini dijelaskan terkait optimasi dan truss yang terdapat 3 displacement, yaitu pada sumbu yz, tetta, dan r. Dijelaskan juga pembuatan pemodelan dari persamaan, boundary condition, serta codingan terkait. Penerapan dari tugas besar adalah untuk menekan biaya dari desain yang akan digunakan. Lalu, dari optimasi tersebut berguna untuk mencari gaya dan kesetimbangan gaya (cek stress, perhitungan, serta kekuatan material). Untuk hal tersebut, kekuatan material harus lebih kuat dari stress dari beban yaitu stress dari beban tersebut tidak boleh lebih besar 1/2 kali nya dari kekuatan material.
Terkait dengan truss, hal tersebut berbeda dengan beam yaitu truss tiap titik mempunyai 3 derajat kebebasan dengan variabel displacement dalam x,y,z untuk asumsi pada sebuah batang. Lalu, untuk beam pada sebuah rangka mempunyai 6 derajat dengan variabel x,y,z kearah momen atau puntirannya. Pada asumsi yang dijelaskan, mahasiswa dihimbau untuk mengerti dan paham bagaimana menyelesaikan permasalahan terkait dengan matriks dan variabel yang sudah disusun dan mengaplikasikannya pada software OpenModelica.
Lalu, mahasiswa dihimbau untuk menghitung kondisi optimal pada rangka dengan parameter seperti pada tujuan dan objektif optimasi. Pada perhitungan, terdapat fungsi-fungsi batasan atau constraint seperti panjang siku ataupun harga per ukurannya. Optimasi mempunyai tujuan untuk meminimalisir biaya. Constrains yang diberikan adalah mampu menahan beban dimana gaya tersebut bekerja yang mampu didukung pada rangka tersebut. Langkah pertama adalah mencari displacement, memeriksa gaya, dan mengoptimasi gaya tersebut lalu menghitung stressnya. Setelah itu, membandingkan stress untuk kekuatan material yang akan digunakan. Tegangan yang dihitung tidak boleh melebihi allowable stress agar rangka sesuai standard nya. Dari data yang dikumpulkan, akan didapatkan jenis material serta ukuran batang dan spesifikasi siku. Setelah hal tersebut, dapat dilakukan optimasi untuk mendapatkan bahan yang paling optimal.
k = A.E/L
dimana :
A = Luas penampang siku
E = Modulus elastisitas tiap bahan
L = Panjang batang rangka
Bahan / profil siku yang akan digunakan merupakan galvanis, stainless, dan sebagainya.
Untuk pembahasan Aplikasi Metode Numerik dalam Kasus Optimasi, hal ini disampaikan oleh Bu Chandra dengan penjelasan optimasi yang digunakan merupakan metode bracket optimization using golden ratio. Bahan pembelajaran tersebut terdapat di PPT yang di share pada WA Group. Mahasiswa dihimbau untuk mengikuti simulasi menggunakan software OpenModelica untuk dapat menyelesaikan permasalahan terkait fungsi exercise yang diberikan.
Optimasi merupakan cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi fungsi non linear dan objektifnya merupakan cara untuk mencari nilai f(x) maksimum dan f(x) minimum. Berikut adalah persamaannya :
d = akar5 - 1/2 x (xu-xl)
x1 = x1 + d
x2 = xu . d
dengan syarat :
- f(x1) > f(x2), domain sebelah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama
- f(x2) > f(x1), domain x sebelah kanan x1 dapat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama
Kesimpulannya adalah dari penyampaian tugas besar, secara garis besar merupakaan persamaan truss. Fungsi optimasi diharuskan memiliki fungsi objektif seperti mendapatkan stress yang maksimum dan biaya yang minimum. Lalu, variabel yang dapat diubah merupakan dimensi dari truss siku dan juga raw materialnya. Cara menyelesaikan tugas besar yaitu pada awal dibuat alur proses/flowchart cara penyelesaian optimasi, lalu cari 3 material yang berbeda untuk mensimulasikannya dengan tugas besar masing-masing. Lalu, menentukan fungsi objektif, menentukan fungsi constraint yaitu stress yang tidak kurang dari setengah allowable stress dari kekuatan materialnya. Lalu, membandingkan dengan tabel yang ada di buku untuk menyesuaikannya.
Tugas Besar: Optimasi Desain Struktur Rangka (Truss) Sederhana dengan Open Modelica
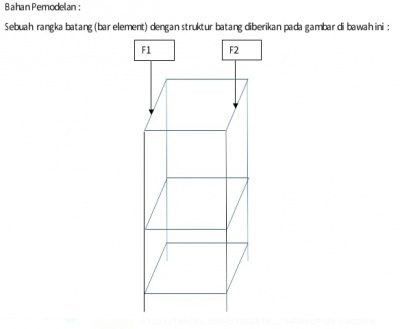
Assalamu'alaikum wr.wb. Berikut adalah Tugas Besar Metode Numerik untuk melakukan optimasi pemilihan material serta luas penampang trusses untuk rangka beserta parameter yang diketahui seperti berikut :
Dengan pemodelan yang sudah diberikan, variasi yang dapat dilakukan adalah dalam parameter material & luas permukaan truss. Lalu, dapat dilakukan asumsi untuk perhitungan adalah sebagai berikut :
1. Variasi Stiffness terikat dengan variabel area terkait material yang digunakan. Jika variasi elastisitas berbeda akan sulit karena setiap material memiliki range yang tidak teratur dalam satu material sejenis.
2. Beban akan terdistribusi hanya pada node penghubung (bersifat trusses)
3. Dimensi material mengikuti standar ukuran material
4. Melakukan 2 perhitungan dengan Elasticity Locked dan Area Locked
Ketentuan :
- Tujuan Optimasi : Displacement U minimum, Cross Area minimum, dan nilai E dan A (murah)
- Optimasi untuk mencari harga termurah dengan faktor berubah kekuatan serta area
Perhitungan :
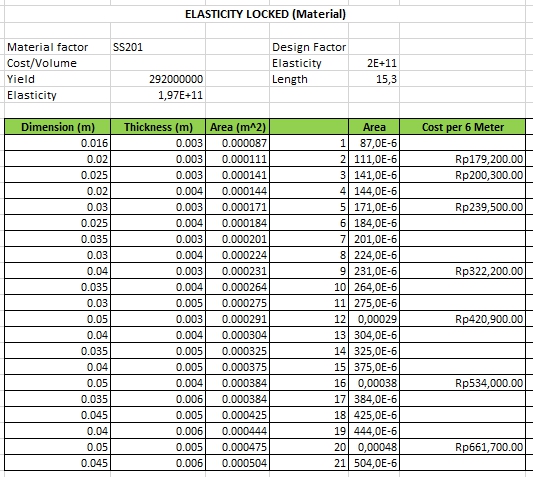
1. Elasticity Locked
Merupakan pengambilan data dengan material yang sama untuk memvariasikan luas area. Material yang saya gunakan adalah SS201 berprofil siku. Data yang didapatkan adalah sebagai berikut :
source: https://wijayamakmur.com/siku/
Lalu, melakukan curve fitting untuk mendapatkan hasil harga tiap area yang telah ditentukan, stress, safety factor, serta ratio. Berikut adalah koding terkait dengan hal tersebut :
Model Tugas Besar 3D Trusses
Function Curve Fitting
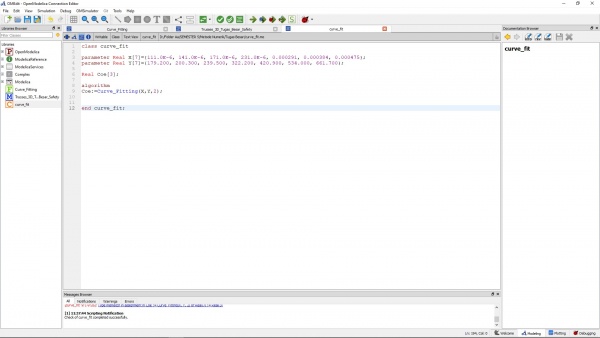
Class Curve Fit untuk Harga Per 6M
Lalu, didapatkan hasil dari simulationnya dengan nilai Coe yang akan kita ambil sebagai salah satu variabel dalam perhitungan adalah sebagai berikut :
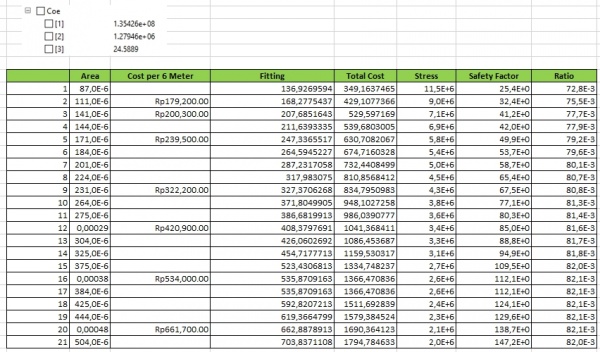
Setelah dilakukan perhitungan, didapat hasil cost yang telah dilakukan fitting, total cost, stress, safety factor, ratio dengan hasil sebagai berikut :
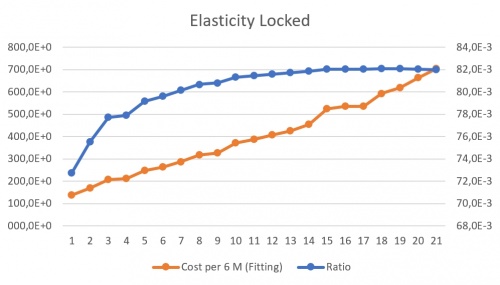
Lalu, didapatkan grafik dengan Area sebagai kordinat X nya, lalu ada 2 variabel Y yaitu Cost per 6M (Fitting) dan Ratio sebagai perbandingan. Berikut adalah grafik yang didapat :
2. Area Locked
Merupakan pengambilan data menggunakan luas area yang sama dan menggunakan material yang berbeda-beda. Pada perhitungan ini, saya menggunakan 4 material yaitu SS304, SS316, SS201, dan SS403 dengan masing-masing sample variasi material serta harga. Data yang didapat adalah sebagai berikut :
Source :
https://www.tokopedia.com/kingsteelid
https://www.stindia.com/316-stainless-steel-supplier.html
Lalu, melakukan pencarian harga, density, serta yield menggunakan curve fitting seperti yang dilakukan pada Elasticity Lock dengan jumlah variabel yang menyesuaikan pada setiap kategorinya. Berikut adalah masing-masing kodingan setiap kategori :
Curve Fit untuk Cost Per KG
class curve_fit
parameter Real X[4]={190.0E+9, 193.0E+9, 193.0E+9, 200.0E+9};
parameter Real Y[4]={48886, 56848, 27718, 26412};
Real Coe[3];
algorithm
Coe:=Curve_Fitting(X,Y,2);
end curve_fit;
Lalu, didapatkan hasil Coe untuk mendapatkan perhitungan Cost per Kg nya adalah sebagai berikut :
Curve Fit untuk Density
class curve_fit
parameter Real X[4]={190.0E+9, 193.0E+9, 193.0E+9, 200.0E+9};
parameter Real Y[4]={8030, 7990, 7800, 7800};
Real Coe[3];
algorithm
Coe:=Curve_Fitting(X,Y,2);
end curve_fit;
Lalu, didapatkan hasil Coe untuk mendapatkan perhitungan Density nya adalah sebagai berikut :
Curve Fit untuk Yield
class curve_fit
parameter Real X[4]={190.0E+9, 193.0E+9, 193.0E+9, 200.0E+9};
parameter Real Y[4]={290, 290, 301, 275};
Real Coe[3];
algorithm
Coe:=Curve_Fitting(X,Y,2);
end curve_fit;
Lalu, didapatkan hasil Coe untuk mendapatkan perhitungan Density nya adalah sebagai berikut :
Setelah mendapatkan semua nilai Coe untuk mendapatkan hasil Cost per KG, Density, dan Yield didapatkan hasil lengkap untuk beberapa material tersebut dengan Elasticity yang berbeda-beda sebagai berikut :
Lalu, didapatkan grafik dengan kordinat X nya Elasticity serta untuk kordinat Y nya adalah Cost per Kg & Ratio. Didapatkan hasil grafik sebagai berikut :
Sekian Tugas Besar ini yang sampaikan, terima kasih atas perhatiannya. Mohon maaf apabila ada kesalahan ataupun kekurangan dari penulis. Wassalamu'alaikum wr.wb.
UAS
Assalamu'alaikum wr.wb. Berikut saya lampirkan jawaban saya terkait Ujian Akhir Semester Metode Numerik :
No.1
Penjelasan No. 1 :
Pada soal ini, saya menjelaskan terkait pemodelan struktur optimum untuk diaplikasikan pada sebuah struktur berupa water tank dengan ketinggian 120 feet dari permukaan serta 300.000 galon. Berikut adalah langkah-langkah pemodelan numerik untuk optimasi striktur tersebut diawali dengan menentukan node-node dari struktur variabel dan sudut dan dilanjutkan dengan penentuan parameter dari struktur. Setelah itu, dapat dibuat asumsi dengan pendekatan sifat elemen dan variabel yang diperlukan yang setelahnya dapat ditentukan matriks lokal sehingga didapatkan K global. Lalu, dapat dihitung U (defleksi) dari struktur tersebut. Selain itu, dapat juga dihitung gaya reaksi, gaya internal, dan stress dari struktur terkait. Untuk optimasi bahan material, dapat digunakan metode Elasticity Locked yang menggunakan elasticity sama namun dengan variasi yang berbeda & Area Locked yang menggunakan area sama dengan variasi material yang berbeda. Setelah hal tersebut, dapat dilakukan optimasi untuk mendapatkan ukuran serta material yang paling optimal untuk struktur tersebut.
No.2
Penjelasan No. 2 :
Tujuan pemodelan nomerik pada soal no.1 adalah untuk menganalisa optimasi paling optimal serta untuk menentukan material ataupun ukuran yang paling optimal untuk struktur tersebut.
Hukum / dalil fisika yang dipakai adalah Hukum Hooke, Hukum Newton (ΣF = m.a ; ΣF = 0), serta Hukum Kekakuan ( K = A.E / L).
Lalu, untuk asumsi yang dipakai dalam perhitungan adalah beban yang terjadi terdistribusi pada titik sambung, variasi stiffness terkait dengan variabel area tersebut, serta bisa menggunakan asumsi elasticity locked dan area locked untuk melakukan optimasi selanjutnya.
No.3
Penjelasan No. 3 :
Pada nomor ini dilakukan pembuatan variabel serta persamaan yang digunakan pada matriks lokal dan matriks global. Matriks lokal digunakan berdasarkan turunan dari U1x, U1y, U2x, dan U2y yang didapatkan dari batang pada struktur water tank pada soal. Matriks lokal yang didapat dimasukkan ke matriks lokal berserta sudutnya. Lalu, matriks global didapatkan melalui matriks lokal yang ditambahkan dari seluruh batang pada struktur tersebut.
No. 4 & 5 :
Penjelasan No. 4 :
Urutan langkah-langkah (pseucode) perhitungan matriks kesetimbangan global no.3 termasuk pengecekan kesalahan (verifikasi) perhitungannya dapat dilakuan dengan tahapan yang diawali dengan Penulisan class serta mendefinisikan parameter terkait dengan memasukkan variabel-variabel, lalu menuliskan matriks lokal dan matriks global, dan melakukan penjumlahan matriks global tersebut. Setelah itu, dapat diimplementasi boundary condition dan melakukan solve displacement matrix. Dari langkah tersebut dapat dilanjutkan dengan menjumlahkan gaya reaksi untuk dibandingkan dengan gaya beban untuk penentuan error dari perhitungannya.
Penjelasan No. 5 :
Fungsi Objektif : Berguna untuk mendapatkan jenis material yang paling optimal untuk digunakan
Constraint : Digunakan untuk optimasi struktur terkait adalah luas area penampang serta Elastisitas material
No.6
Penjelasan No. 6 :
Pada nomor ini berisi asumsi yang digunakan untuk menghitung pemodelan di software OpenModelica. Asumsi yang digunakan setelah dilakukan pengecekan adalah sebagai berikut :
- L = 50 ft = 600 in
- E = 28 x 10^6 lg/in^2
- A = 16 m^2
- Load = 30.000
No.7
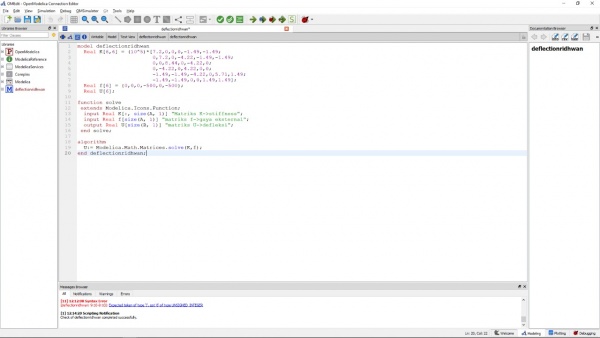
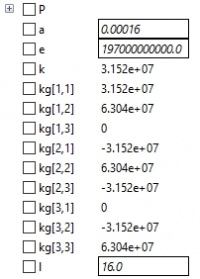
Berikut adalah codingan untuk mendapatkan hasil penyelesaian masalah perhitungan pada no.7 :
model UasMetnumRidhwan
/*Nama = Muhammad Ridhwan Sunandar
NPM = 1806181861 */
parameter Real P[3]={30000,0,30000};//beban dan gaya reaksinya (beban berada pada node 3 yang negatif dan gaya reaksi pada node 1 dengan nilai positif)
/*asumsi semua elemen sejenis*/
parameter Real a=16e-5;//luas penampang
parameter Real e=197e9;//elastisitas
parameter Real l=50;//panjang
/*parameter yang akan dicari*/ Real k;//kekakuan elemen Real kg[3,3];//matriks global Real u[3];//displacement Real stress[3];//stress yang dialami
algorithm /*mencari nilai kekakuan*/ k := a*e/1;
/*menuliskan persamaan matriks global*/ kg := [k, 2*k, 0; -k, 2*k, -k; 0, -k, 2*k];
/*mencari displacement dengan metode gauss-jordan*/ u := Modelica.Math.Matrices.solve(kg,P); /*mencari stress pada tiap elemen*/ stress[1] := u[1]*k/a; stress[2] := u[2]*k/a; stress[3] := u[3]*k/a;
end UasMetnumRidhwan;
Dan didapatkan hasil dari simulasi kodingan tersebut sebagai berikut :
Dari hasil simulasi tersebut didapatkan data sebagai berikut :
- Displacement : [0.000135968, 0.000407904, 0.00067984]
- Stress : [2.67857e+07, 8.03571e+07, 1.33929e+08]