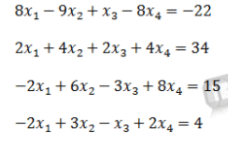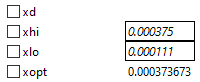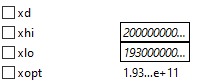Difference between revisions of "Muhammad Faja Taufiqurrahman"
| (30 intermediate revisions by the same user not shown) | |||
| Line 459: | Line 459: | ||
[[File:Flowchart_Faja.jpeg|600px]][[File:Class Diagram.jpeg|600px]] | [[File:Flowchart_Faja.jpeg|600px]][[File:Class Diagram.jpeg|600px]] | ||
| + | |||
| + | </div> | ||
| + | |||
| + | ==== Tugas Minggu Keempat ==== | ||
| + | Soal No. 8 | ||
| + | [[File:Prno8.png|600px|center]] | ||
| + | Soal tersebut menggunakan 3D Truss, ditugaskan untuk membuat flowchart, class diagram, dan codingan untuk menyelesaikan persoalan tersebut. | ||
| + | Flowchart dan Class Diagram | ||
| + | [[File:Flowchart_&_Class_Diagram.jpeg|600px|center]] | ||
| + | Kemudian langkah berikutnya adalah membuat free body diagram untuk menentukan komponen-komponen data yang tersedia dalam soal. Dari data-data yang tersdedia, berikut adalah data yang diperlukan untuk mengerjakan soal ini, node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z. Rumus untuk mencari sudut dan panjang batang saya dapatkan dari buku. Untuk gaya eksternal sendiri dapat dilihat dari gambar. Kemudian data-data yang sudah didapat, dibuat ke dalam matriks untuk mempermudah penyelesaiannya menggunakan Open Modellica. | ||
| + | [[File:Jawaban_No.8.jpeg|600px|center]] | ||
| + | Setelah mendapatkan matriks yang diperlukan, selanjutnya menghitung nilai k = AE/L. Setelah mendapatkan nilai k pada setiap batang, selanjutnya membuat matriks K elemental (Ke) setiap batang dari nilai k tersebut pada OpenModelica. | ||
| + | [[File:StiffnessMatrixElement.png|600px|center]] | ||
| + | Kemudian dari matriks 6x6 tersebut dibuat menjadi matriks 12x12 sesuai dengan jumlah batang (3) * jumlah node (4) (3 x 4 = 12).Yang disebut matriks kekakuan global (Kg). | ||
| + | [[File:StiffnessMatrixGlobal.png|600px|center]] | ||
| + | Berikutnya, matriks kekakuan global setiap batang dijumlahkan untuk mendapat matriks kekakuan global total(KgTot) | ||
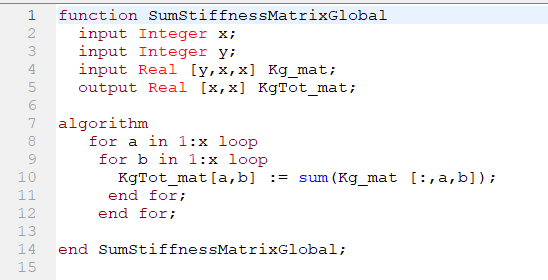
| + | [[File:SumStiffnessMatrixGlobal.png|600px|center]] | ||
| + | Kemudian menghitung Boundary dari matriks kekakuan global total. Pada kasus ini, node 2,3, dan 4 merupakan pinned. Sehingga didapati U2X=U2Y=U2Z=U3X=U3Y=U3Z=U4X=U4Y=U4Z=0. | ||
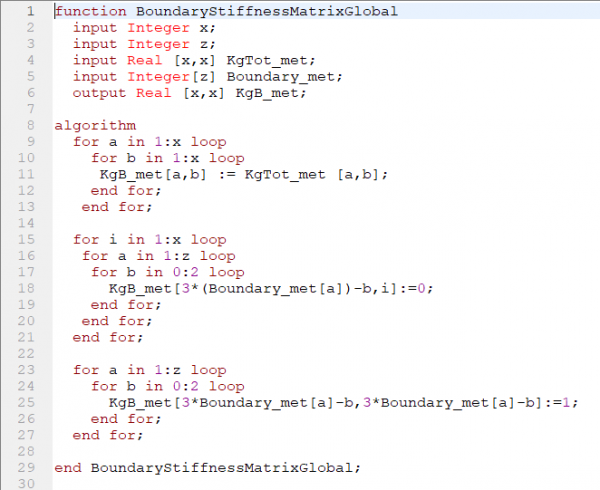
| + | [[File:BoundaryStiffnessMatrixGlobal.png|600px|center]] | ||
| + | Kemudian mencari nilai Displacement (U) menggunakan eliminasi Gauss Jordan. | ||
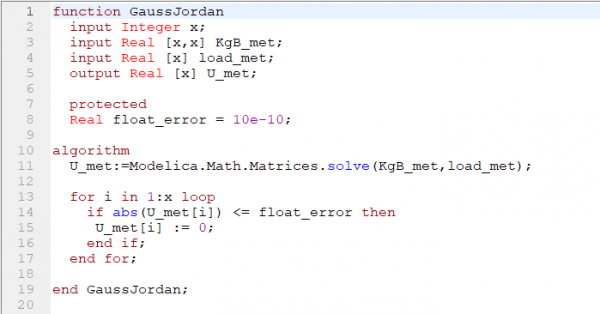
| + | [[File:GaussJordan.png|600px|center]] | ||
| + | Kemudian dengan menerapkan materi yang sudah dipelajari pada pertemuan sebelumnya (sistem kelas panggil) Pada class akan diinput data-data yang telah dicari pada langkah pertama. | ||
| + | [[File:Class3DTrusses.png|600px|center]] | ||
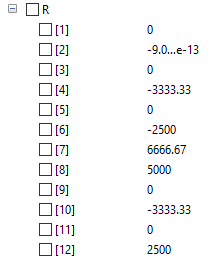
| + | Setelah disimulasikan didapatkan nilai U (displacement) dan R (Reaction) | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
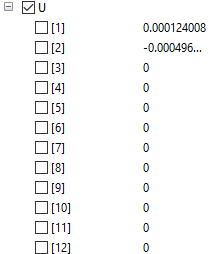
| + | [[File:Hasil_Displacement.png|300px]][[File:Hasil_ReactionForce.png|300px]] | ||
| + | |||
| + | </div> | ||
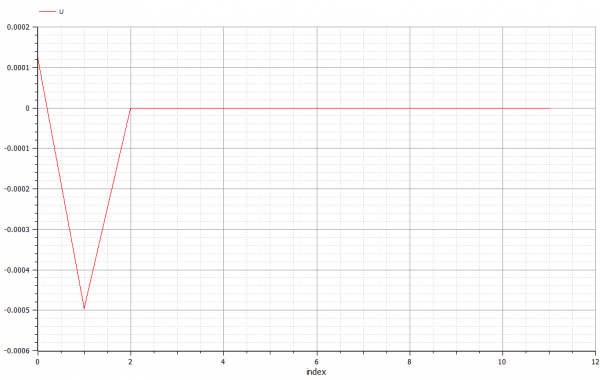
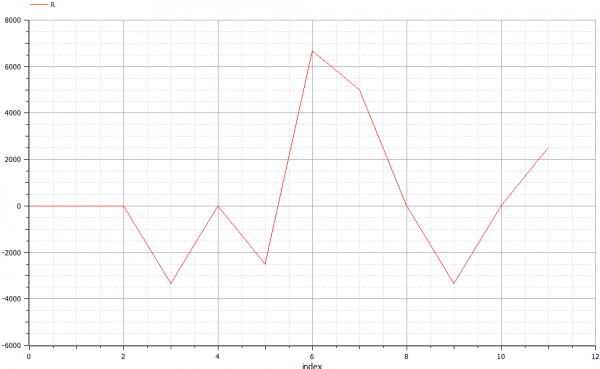
| + | dan setelah di plotting didapatkan diagram U (discplacement) dan R (Reaction). | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | [[File:Plotting_Displacement.png|600px]][[File:Plotting_ReactionForce.png|600px]] | ||
| + | |||
| + | </div> | ||
| + | |||
| + | |||
| + | === Pertemuan Kelima (Rabu, 16 Desember 2020) === | ||
| + | Aplikasi Metode Numerik dalam Kasus Optimasi | ||
| + | |||
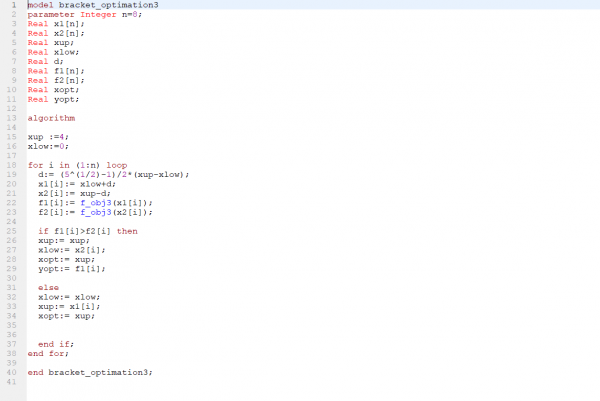
| + | Pada awal pertemuan minggu ini, kami diberi wawasan jika ilmu tidak hanya didapat dari buku namun juga dari alam nyata. Oleh sebab itu, kita harus aware terhadap lingkungan sekitar. Ilmu yang sudah kita dapatkan di perkuliahan pun baiknya diaplikasikan dalam kehidupan. Topik metode numerik kali ini adalah mengenai optimasi. Sebelum perkuliahan dimulai, Bu Chandra memberikan kami sebuah video pembelajaran mengenai optimasi menggunakan metode Bracket dan di kelas kami berdiskusi jika ada kesulitan. Saya mencoba perhitungan optimasi berdasarkan video tutorial oleh Bu Candra. | ||
| + | |||
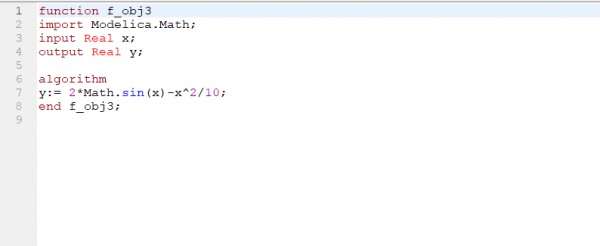
| + | Fungsi yang dipanggil: | ||
| + | [[File:F_obj3_faja.png|600px|center]] | ||
| + | Model Optimasi untuk memanggil fungsi: | ||
| + | [[File:Optimasi_faja.png|600px|center]] | ||
| + | Hasil Optimasi yang didapat: | ||
| + | [[File:Hasil_optimasi_faja.png|600px|center]] | ||
| + | |||
| + | === Progress Tugas Besar Metode Numerik === | ||
| + | Sebagai akhir pembelajaran Metode Numerik, dua kelas yang diajar oleh Pak Dai diberikan satu tugas besar. Tugas ini adalah aplikasi Openmodelica dalam kasus optimasi trusses. | ||
| + | [[File:SoalTugasBesarFaja.png|400px|center]] | ||
| + | dengan spesifikasi rangka batang: | ||
| + | [[File:SpesifikasiRangkaBatangFaja.png|300px|center]] | ||
| + | Dalam kasus tersebut dapat dilihat berupa rangka berbentuk tray dengan 3 lantai. Dalam rangka tersebut lalu diaplikasikan beban sebesar 1000 N pada salah satu sisi dan 2000 N pada sisi lainya, dengan dimensi yang diberikan adalah Panjang = 0.6 m, Lebar = 0.75 m, dan Tinggi = 1.8 m. Beban diaplikasikan pada lebar rangka dengan panjang 0.75m. | ||
| + | |||
| + | Tugas kita adalah mengoptimasikan desain tersebut dengan mempertimbangkan sisi efisiensi ekonomi dengan tetap mempertimbangkan safety factor yang wajar. Untuk optimasi sendiri, nantinya akan dilakukan dengan metode curve-fitting seperti least square polynomial. Pada tugas ini, kami juga harus menentukan jenis material dan luas penampang yang akan diaplikasikan. Material dan jenis penampang akan berpengaruh nantinya terhadap harga produk. | ||
| + | |||
| + | Pada proses pengerjaan Tugas Besar, kelas Metode Numerik 02 dan 03 melakukan dua kali diskusi menggunakan platform meeting. Diskusi dilakukan pada tanggal 29 Desember 2020 dan 3 Januari 2021. Hasil dari diskusi pertama yaitu saya dapat mulai memahami tentang bagaimana input yang dapat disesuaikan dengan analisis yang akan dipakai yaitu: 1. Parameter Elastisitas, berhubungan dengan pemilihan jenis material yang akan digunakan 2. Parameter Luas Penampang, berhubungan dengan bentuk rangka yang akan diubah menjadi parameter no point, trusses, dan definisi koordinat dan connection Pada saat mendeklarasikan, kita mendefinisikan point sambungan dan jumlah trusses karena point dan trusses akan seiring dengan bentuk design yang akan dibuat. Saya membuat model menggunakan aplikasi Autodesk Inventor terlebih dahulu untuk mempermudah pengerjaan karena bisa melihat bentuk aslinya secara 3D. Kemudian diberikan element area yang satuan luas. Setelah itu diberikan parameter elastisitas sesuai dengan material yang akan digunakan. Bentuk permodelan dalam aplikasi OpenModelica saat melakukan deklarasi adalah sebagai berikut: | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000375; //Area (Dimension = 0,04m, Thickness = 0,005m) | ||
| + | parameter Real Elas=193e9; //Elasticity of SS 309 | ||
| + | |||
| + | |||
| + | Setelah deklarasi komponen dasar pemodelan, kemudian melakukan pendefinisian terhadap connection & koordinat trusses. Kemudian melakukan pendefinisian terhadap connection & koordinat trusses. Pada saat mendefinisikan connection, dibuat kumpulan matriks 1x2 yang berisi 2 nama truss yang dihubungkan, untuk mempermudah pemahaman, susunan koneksi rangka dibangun berdasarkan tingkatan rankga pada desain. | ||
| + | Berikut contoh pemodelan Connection yang ada pada program: | ||
| + | |||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | Setelah memdefinisikan connection, diperlukan untuk menuliskan koordinat dari point connection diatas. Karena model yang dibuat dalam 3D, pada saat pendefisian ditulis dalam bentuk matrix 1x3 yang tiap nilainya menunjukkan jarak terhadap titik referensi (0,0,0). Pemograman OpenModelica sebagai berikut: | ||
| + | |||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | |||
| + | Langkah selanjutnya adalah menuliskan definisi terhadap beban yang diberikan. Saya memasukkan beban sesuai dengan soal yaitu 1000N dan 2000N ada tepat di tengah kedua rangka paling atas seperti pada gambar soal. Namun karena analisa yang dibuat menggunakan point connection, maka tiap beban dibagi dua karena beban yang ditulis adalah beban yang diterima oleh point sehingga masing-masing beban menjadi 500, 1000, 1000, dan 500. Beban dituliskan dalam bentuk matrix 1x3 untuk tiap truss dari lantai 1 ke lantai 3. Pemograman Open Modelica sebagai berikut: | ||
| + | |||
| + | |||
| + | //define external force | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | |||
| + | Untuk pendeklarasian terakhir yaitu memasukkan hal-hal yang ingin diketahui (dicari) dengan memasukkan komponen-komponen displacement, reaction, stress, safety, dan lainnya, dengan dilakukan pemrogaraman sebagai berikut: | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | |||
| + | Saat masuk tahap perhitungan, diperlukan pendeklarasian pula untuk notasi-notasi yang dipakai. Dalam pembuatan global matriks diperlukan notasi notasi baru, yaitu matriks X (matriks 3x3 hasil kali A*Elastisitas/L dikali dengan matriks), lalu ada notasi cx,cy,cz, untuk membantu perhitungan matriks global. Juga matriks q1 dan q2 [1x3] yang akan menjadi variable yang mempermudah proses perhitungan matriks global. Tidak lupa juga error untuk validasi nya. Berikut pemodelannya: | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | Kemudian memulai algoritma tentang pembentukkan Global Matrix dengan notasi G sehingga terjadi proses looping notasi i dan j yang akan mengisi variable q1 dan q2. Perbedaan loop i dan j adalah loop i akan memanggil matriks trusses (connection) pada kolom 1, sedangkan loop j akan melakukan looping untuk angka 1-3 hingga q berada dalam fungsi j, q[j] | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | L dicari dengan menentukan jarak vector. Notasi cx, cy, dan cz dibuat untuk memudahkan saat membuat matriks u. Notasi cx seperti menjadi shortcut untuk dibentuknya matriks stiffness. Perhitungan selanjutnya menggunakan pemograman di bawah ini: | ||
| + | |||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| + | |||
| + | |||
| + | |||
| + | Sehingga dari hasil simulasi didapatkan nilai Displacement, Reaction Force, Stress, dan Safety Factor (yield/stress) sebagai berikut: | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | [[File:DisplacementFaja1.png|300px]][[File:DisplacementFaja2.png|300px]][[File:ReactionFaja1.png|300px]][[File:ReactionFaja2.png|300px]] | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | [[File:SafetyFaja.png|300px]][[File:StressFaja.png|300px]] | ||
| + | |||
| + | </div> | ||
| + | |||
| + | Berikut ini adalah variasi data untuk material yang sama, yaitu SS304 dan menggunakan area factor yang sama, yaitu 0.000171. Setelah melakukan simulate, maka kita akan mendapatkan nilai dari safety factor, kemudian kita mencari Rasio dengan melakukan perbandingan Safety factor dengan total harga, maka akan didapatkan : | ||
| + | [[File:SafetyFactorRatioFaja.png|1000px|center]] | ||
| + | |||
| + | Kemudian, berdasarkan hasil data yang telah didapat, kita bisa mendapatkan Luas area dan material yang baik digunakan pada rangka yang akan dibuat dengan menggunakan optimasi dengan curve fitting dan golden bracket. Fungsi untuk Curve Fittingnya adalah sebagai berikut: | ||
| + | |||
| + | function CurveFitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | end CurveFitting; | ||
| + | |||
| + | Kemudian melakukan optimasi golden ratio pada material tetap: | ||
| + | |||
| + | model Opt_Gold | ||
| + | parameter Real xd[:]={0.000111,0.000144,0.000184,0.000224,0.000325,0.000375}; | ||
| + | parameter Real yd[size(xd,1)]={678148,845155,1053955,1269736,1845642,2147211}; | ||
| + | parameter Real xlo=111e-6; | ||
| + | parameter Real xhi=375e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Opt_Gold; | ||
| + | |||
| + | Setelah dilakukan stimulate akan didapatkan hasil optimum pada material yang tetap, sebagai berikut: | ||
| + | [[File:OptimasiMaterialTetapFaja.png|400px|center]] | ||
| + | |||
| + | Maka dapat disimpulkan bahwa area yang paling optimum untuk material yang tetap adalah 0.000373673 mm^2 | ||
| + | |||
| + | Pada area yang tetap, saya juga melakukan optimasi golden ratio | ||
| + | |||
| + | model Opt_Gold | ||
| + | parameter Real xd[:]={193000000000,197000000000,200000000000}; | ||
| + | parameter Real yd[size(xd,1)]={1109361,531151,538340}; | ||
| + | parameter Real xlo=193000000000; | ||
| + | parameter Real xhi=200000000000; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Opt_Gold; | ||
| + | |||
| + | Kemudian untuk Hasil pada Area tetap, didapatkan hasil optimum material: | ||
| + | [[File:OptimasiAreaTetapFaja.png|400px|center]] | ||
| + | |||
| + | Untuk area tetap, saya mendapatkan material dengan elastisitas 1.93e11 N/m^2, yang mana itu merupakan material SS304. | ||
| + | |||
| + | === Jawaban UAS (13 Januari 2021) === | ||
| + | Berikut nomor 1 dan 2 | ||
| + | [[File:JawabanUAS4Faja.jpg|600px|center]] | ||
| + | Kemudian nomor 3 dan 4 | ||
| + | [[File:JawabanUAS5Faja.jpg|600px|center]] | ||
| + | dan terakhir 5, 6 dan 7 | ||
| + | [[File:JawabanUAS6Faja.jpg|600px|center]] | ||
| + | Coding yang saya gunakan pada open modelica adalah sebagai berikut, dimana menggunakan coding untuk Trusses karena hasil yang dicari berupa displacement, dan reaction pada batang | ||
| + | [[File:JawabanUAS1Faja.png|600px|center]] | ||
| + | [[File:JawabanUAS2Faja.png|600px|center]] | ||
| + | [[File:JawabanUAS3Faja.png|600px|center]] | ||
Latest revision as of 19:02, 14 January 2021
Contents
- 1 Biodata
- 2 Metode Numerik
- 3 Pertemuan Perkuliahan
- 3.1 Pertemuan Pertama (Rabu, 11 November 2020)
- 3.2 Pertemuan Kedua (Rabu, 18 November 2020)
- 3.3 Pertemuan Ketiga (Rabu, 25 November 2020)
- 3.4 Pertemuan Keempat (Rabu, 2 Desember 2020)
- 3.5 Pertemuan Kelima (Rabu, 16 Desember 2020)
- 3.6 Progress Tugas Besar Metode Numerik
- 3.7 Jawaban UAS (13 Januari 2021)
Biodata
Nama : Muhammad Faja Taufiqurrahman
NPM : 1906301223
Angkatan : 2019
Program Studi : Teknik Mesin, S1 Reguler
Tempat, Tanggal lahir : Jakarta, 09 Juni 2001
Domisili : Jakarta Selatan
Alamat Surel : muhammadfaja87@gmail.com / muhammad.faja@ui.ac.id
Metode Numerik
Metode numerik merupapakan teknik dalam penyelesaian permsalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik.
Pada kelas Metode Numerik-02 semester gasal 2020/2021, perkuliahan pekan pertama sampai UTS diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. telah membahas beberapa topik, antara lain:
- Pseudocode
- Sistem Persamaan
- Turunan Numerik
- Metode Newton Rhapson, Secant, dan Bisection
- Regresi Linear
- Interpolasi
Setelah UTS proses pembelajaran diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Pertemuan Perkuliahan
Pertemuan Pertama (Rabu, 11 November 2020)
Pada pertemuan pertama setelah UTS ini, Bapak Dr. Ir. Ahmad Indra Siswantara mengenalkan mengenai situs Wiki AIR. Dalam Wiki AIR tersebut, kami dijelaskan mengenai cara pembuatan akun dan membuat page sendiri. Dalam page tersebut lah nantinya akan digunakan sebagai review pembelajaran serta tempat pengumpulan tugas. Selain itu juga dijelaskan terkait esensi atau tujuan pembelajaran metode numerik, yaitu:
1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik seperti : Persamaan algoritma, aljabar, pencocokan kurva, persamaan diferensial parsial, dll.
2. Mengerti dan mampu menerapkan pemahaman atau aplikasi terhadap konsep metode numerik.
3. Mampu menerapkan metode numerik dalam hal terkait persoalan keteknikan.
4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab.
Selain empat poin tersebut, kami juga mendapat pelajaran terkait awalan memakai OpenModelica. Dimana kami diperlihatkan praktek sederhana penggunaan OpenModelica ini. Hingga kami tahu bila komputer selain dapat membantu dalam menyelesaikan permasalahan namun juga memiliki batasan atau limit tertentu dan kita sebagai manusia lah yang dapat mengoperasikannya.
Tugas Minggu Pertama
- Mempelajari aplikasi OpenModelica melalui video Youtube serta menyertakan link hasil pembelajaran.
Saya mempelajari bagaimana mengoperasikan OpenModelica melalui video berikut :
Saya mencoba untuk membuat interpolasi menggunakan OpenModelica
Video hasil pembelajaran yang telah saya buat :
Pertemuan Kedua (Rabu, 18 November 2020)
Di awal pertemuan disampaikan oleh Pak Dai, jika kita sebagai manusia harus memiliki perubahan setiap harinya, hari ini harus lebih baik dari hari kemarin, jangan sampai hari ini lebih buruk dari hari kemarin. Sebelum memasuki materi, kami diminta mereview fungsi pembelajaran aljabar linear dan hubungannya dengan metode numerik. Kemudian, kami diminta menceritakan pengalaman mempelajari aplikasi Open Modelica. Aplikasi ini dibuat dengan tujuan bahasa pemodelan, bukan coding. Akan tetapi, ketika melakukan perhitungan, code yang ditulis harus dalam bahasa C++. Salah satu alasan pemilihan penggunaan aplikasi ini adalah karena Open Modelica dibuat free, sehingga bisa digunakan oleh siapa saja. Open Modelica mempunyai beberapa fitur, seperti membuat model, class, function, dan lain-lain. Aplikasi ini object oriented, kita bisa membuat beberapa class fungsi dan class eksekusi, kemudian menggabungkannya menjadi satu model.
Sebagai contoh pembelajaran, kami dipandu oleh Pak Dai untuk membuat sebuah function dan class yang akan dihubungkan. Function yang dibuat adalah "Fungsi Tambah X1" dengan X sebagai input, Y sebagai output, dan fungsi yang dibuat adalah Y=10+x. Dibuat dalam Open Modelica sebagai berikut:
Selanjutnya dibuat class "Panggil" yang berfungsi "memanggil" FungsitambahX1 tersebut. Pada class ini, kita dapat mengubah-ubah nilai input X1.
Dengan gabungan class dan function ini, kita dapat mencari nilai output Y dengan memasukkan nilai input X1. Sebagai contoh, dimasukkan nilai X1 sebesar 5 maka sesuai fungsi Y=10+X, akan didapatkan nilai Hasil tambah X1=10+X1=10+5=15.
Nilai X1 dapat diubah-ubah kemudian dilakukan re-simulate untuk mendapatkan nilai outputnya.
Tugas Minggu Kedua
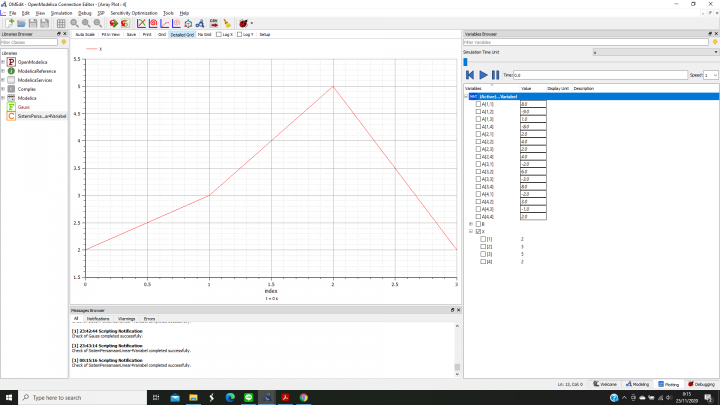
Untuk tugas minggu ini kami diminta membuat sebuah fungsi berupa persamaan aljabar simultan dengan variabel array kemudian membuat class untuk memanggil fungsi tersebut. Persamaan aljabar simultan adalah sebuah persoalan matematika yang kompleks sehingga dengan menggunakan tools, penyelesaiannya dapat dibuat lebih sederhana. Metode yang dapat digunakan untuk menyelesaikan persamaan aljabar simultan adalah metode Gauss, Gauss-Jordan, Crammer, dan Gauss-Seidel. Sedangkan variabel array adalah sebuah variabel yang di dalamnya terdapat banyak data. Sebagai contoh, jika kita memiliki data X1, X2, dan X3, dengan menggunakan variabel array cukup dituliskan X[3] saja. Pada tugas kali ini, saya mencoba menyelesaikan persoalan yang saya ambil dari persoalan sistem persamaan linear 4 variabel untuk menentukan nilai X1, X2, X3, dan X4 menggunakan variabel array.
Dengan menggunakan OpenModelica dan metode Gauss, didapatkan hasil X1, X2, X3, dan X4 yang sebagai berikut:
Video penyelesaian SPL4V menggunakan OpenModelica yang telah saya buat :
Pertemuan Ketiga (Rabu, 25 November 2020)
Pada pertemuan ketiga, Pak Dai menjelaskan mengenai tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik
- 1. Computation Fluid Dynamics (CFD)
- 2. Finite Element Analysis
- 3. Metode Stokastik.
Dalam menyelesaikan masalah teknik, langkah yang harus dilakukan adalah melakukan analisis, membuat model matematis, menggunakan metode numerik untuk penyelesain (menggunakan computer), dan didapatkan solusi dari permasalahan. Salah satu permasalahan teknik yang kami pelajari adalah Truss.
Pak Dai kemudian menugaskan untuk membuat fungsi mengenai gauss jordan, kemudian dijelaskan oleh christofer dengan fungsi sebagai berikut :
// Gauss-Jordan Algorithm
// Transforms input matrix A into reduced row echelon form matrix B
// Christopher S.E. November 2020
input Real [:,:] A; // An augmented matrix of m*n
output Real [:,:] B; // Output matrix in reduced row echelon form
// Local variables
protected
Integer h = 1; // Initialize pivot row
Integer k = 1; // Initialize pivot column
Integer m = size(A,1); // Number of rows in matrix
Integer n = size(A,2); // Number of columns in matrix
Integer c = 0; // Index counter
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column; // Vector containing pivot column data
Real [:] pivot_row; // Vector containing backwards pivot row data
Real [:,:] temp_array; // Stores matrix data when switching rows
Real r; // Ratio value used for row operations
// Limit to handle floating point errors
Real float_error = 10e-10;
algorithm
// Transfer input matrix A into variable B
B := A;
while h <= m and k <= n loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_column := {B[i,h] for i in h:m};
// Get position index of lowest row with greatest pivot number
c:= h-1;
for element in pivot_column loop
c := c+1;
if abs(element) == max(abs(pivot_column)) then
max_row := c;
end if;
end for;
// No pivot in this column, move on to next column
if B[max_row, k] == 0 then
k := k+1;
else
// Swap Rows h <-> max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
// Divide pivot row by pivot number
B[h] := B[h]/B[h,k];
// For all rows below the pivot
for i in (h+1):m loop
// Store the ratio of the row to the pivot
r := B[i,k] / B[h,k];
// Set lower part of pivot column to zero
B[i,k] := 0;
// Operations on the remaining row elements
for j in (k+1):n loop
B[i,j] := B[i,j] - B[h,j] * r;
end for;
end for;
// Move on to next pivot row and column
h := h+1;
k := k+1;
end if;
end while;
// The matrix is now in row echelon form
// Set values of (h,k) to (m,n)
h := m;
k := n;
while h >= 1 and k >=1 loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_row := {B[h,i] for i in 1:k};
// Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k := c;
// No pivot in this row, move on to next row
if B[h, k] == 0 then
h := h-1;
else
// Perform row operations
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] * r;
end for;
// Move on to next pivot row and column
h := h-1;
k := k-1;
end if;
end while;
// The matrix is now in reduced row echelon form
end GaussJordan;
Tugas Minggu Ketiga
Mencari Truss Analysis menggunakan OpenModelica
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation
function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
|
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
|
Reaction Matrices Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
|
Gauss Jordan function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;
|
Pertemuan Keempat (Rabu, 2 Desember 2020)
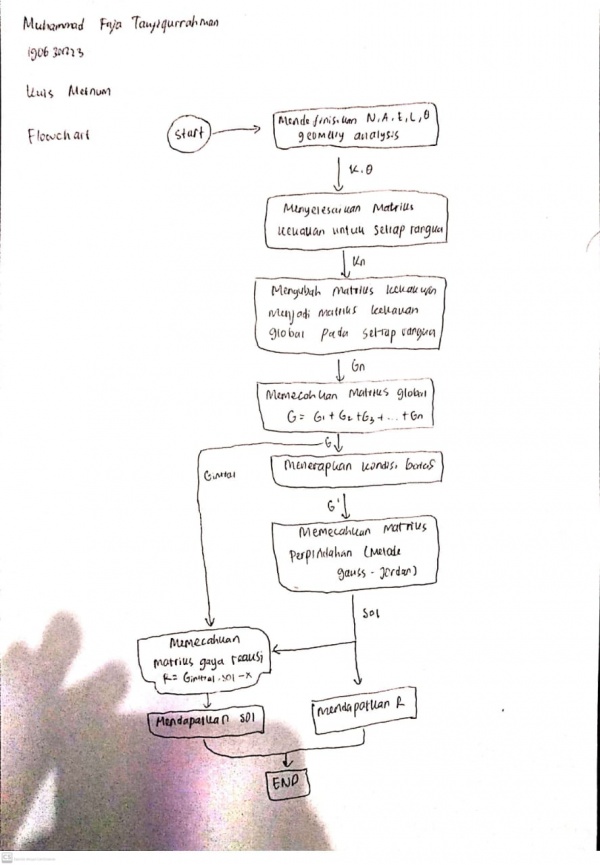
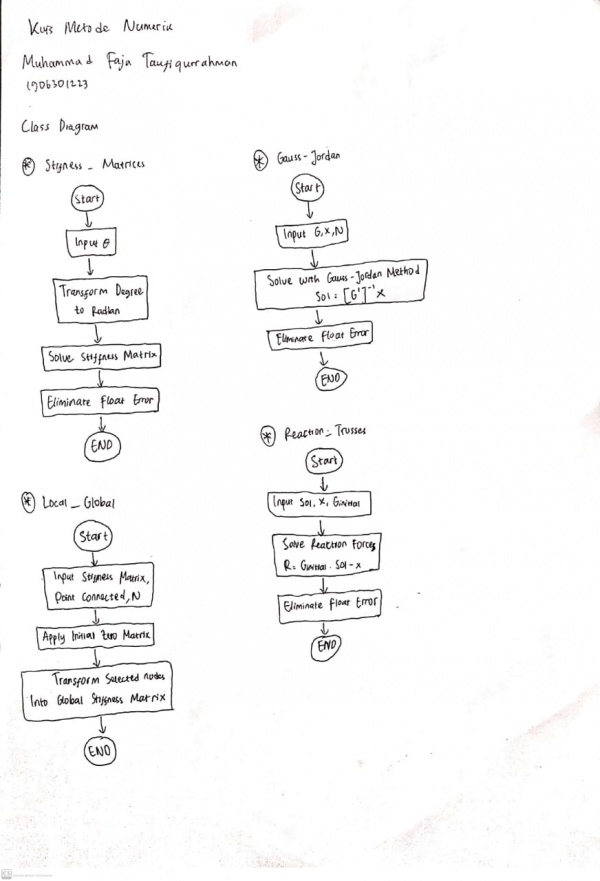
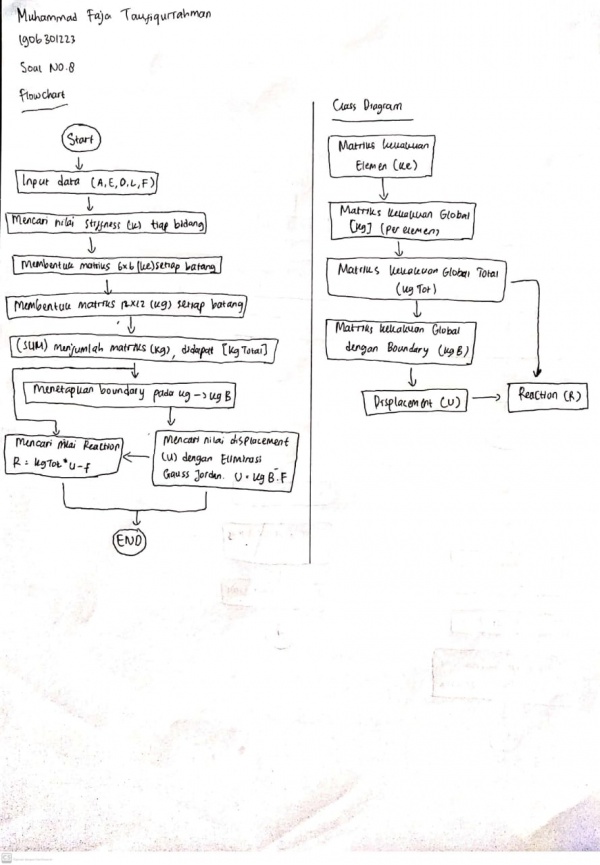
Kuis Flowchart & Diagram Class
Tugas Minggu Keempat
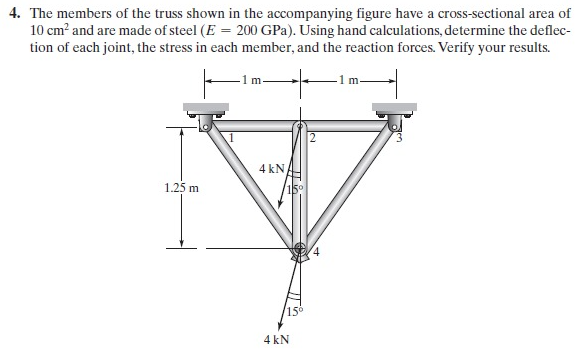
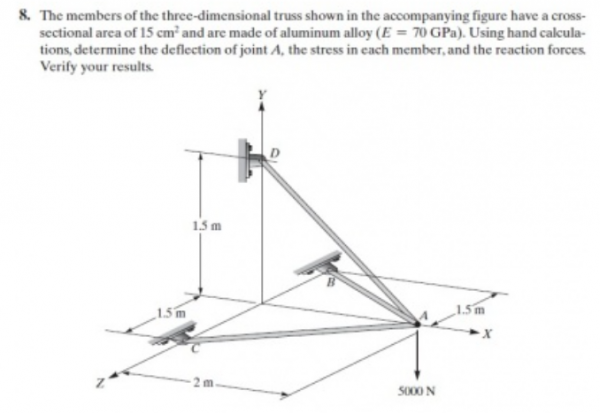
Soal No. 8
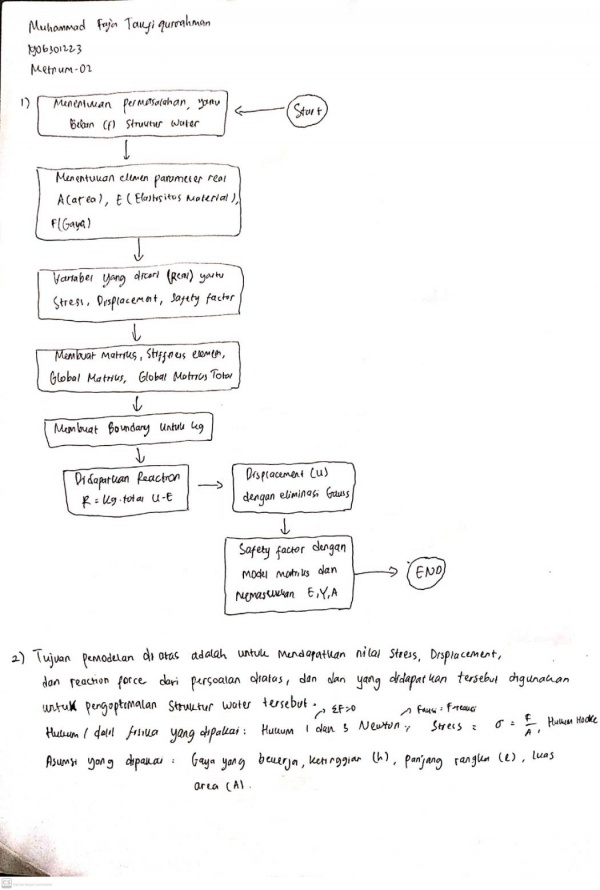
Soal tersebut menggunakan 3D Truss, ditugaskan untuk membuat flowchart, class diagram, dan codingan untuk menyelesaikan persoalan tersebut. Flowchart dan Class Diagram
Kemudian langkah berikutnya adalah membuat free body diagram untuk menentukan komponen-komponen data yang tersedia dalam soal. Dari data-data yang tersdedia, berikut adalah data yang diperlukan untuk mengerjakan soal ini, node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z. Rumus untuk mencari sudut dan panjang batang saya dapatkan dari buku. Untuk gaya eksternal sendiri dapat dilihat dari gambar. Kemudian data-data yang sudah didapat, dibuat ke dalam matriks untuk mempermudah penyelesaiannya menggunakan Open Modellica.
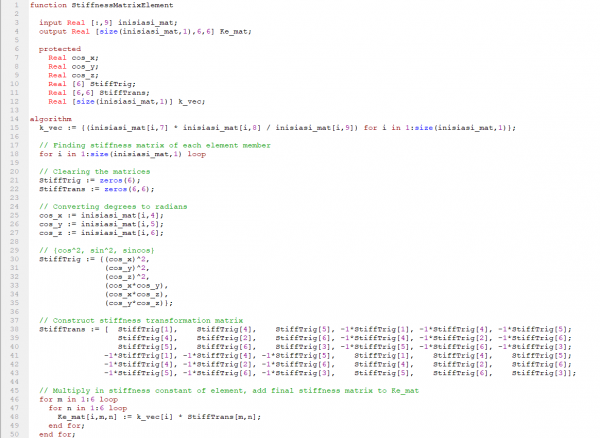
Setelah mendapatkan matriks yang diperlukan, selanjutnya menghitung nilai k = AE/L. Setelah mendapatkan nilai k pada setiap batang, selanjutnya membuat matriks K elemental (Ke) setiap batang dari nilai k tersebut pada OpenModelica.
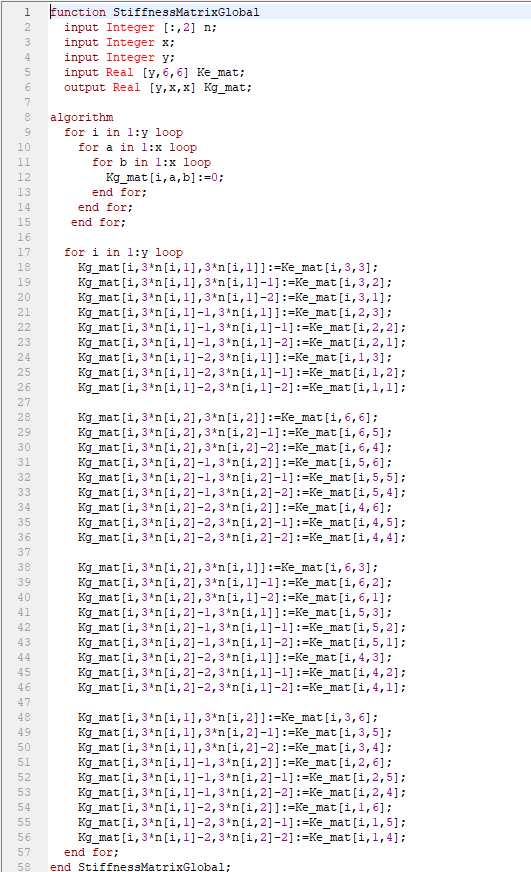
Kemudian dari matriks 6x6 tersebut dibuat menjadi matriks 12x12 sesuai dengan jumlah batang (3) * jumlah node (4) (3 x 4 = 12).Yang disebut matriks kekakuan global (Kg).
Berikutnya, matriks kekakuan global setiap batang dijumlahkan untuk mendapat matriks kekakuan global total(KgTot)
Kemudian menghitung Boundary dari matriks kekakuan global total. Pada kasus ini, node 2,3, dan 4 merupakan pinned. Sehingga didapati U2X=U2Y=U2Z=U3X=U3Y=U3Z=U4X=U4Y=U4Z=0.
Kemudian mencari nilai Displacement (U) menggunakan eliminasi Gauss Jordan.
Kemudian dengan menerapkan materi yang sudah dipelajari pada pertemuan sebelumnya (sistem kelas panggil) Pada class akan diinput data-data yang telah dicari pada langkah pertama.
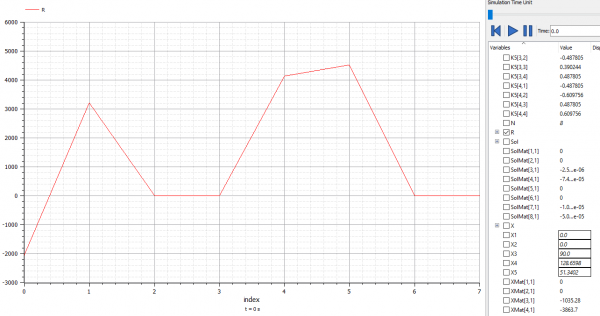
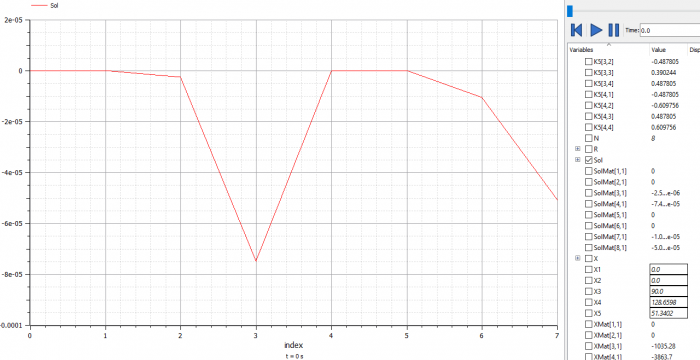
Setelah disimulasikan didapatkan nilai U (displacement) dan R (Reaction)
dan setelah di plotting didapatkan diagram U (discplacement) dan R (Reaction).
Pertemuan Kelima (Rabu, 16 Desember 2020)
Aplikasi Metode Numerik dalam Kasus Optimasi
Pada awal pertemuan minggu ini, kami diberi wawasan jika ilmu tidak hanya didapat dari buku namun juga dari alam nyata. Oleh sebab itu, kita harus aware terhadap lingkungan sekitar. Ilmu yang sudah kita dapatkan di perkuliahan pun baiknya diaplikasikan dalam kehidupan. Topik metode numerik kali ini adalah mengenai optimasi. Sebelum perkuliahan dimulai, Bu Chandra memberikan kami sebuah video pembelajaran mengenai optimasi menggunakan metode Bracket dan di kelas kami berdiskusi jika ada kesulitan. Saya mencoba perhitungan optimasi berdasarkan video tutorial oleh Bu Candra.
Fungsi yang dipanggil:
Model Optimasi untuk memanggil fungsi:
Hasil Optimasi yang didapat:
Progress Tugas Besar Metode Numerik
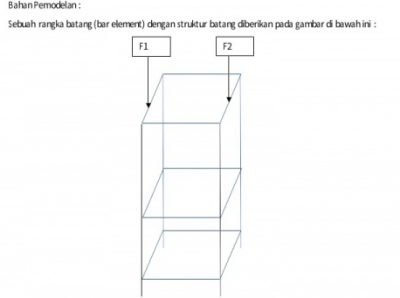
Sebagai akhir pembelajaran Metode Numerik, dua kelas yang diajar oleh Pak Dai diberikan satu tugas besar. Tugas ini adalah aplikasi Openmodelica dalam kasus optimasi trusses.
dengan spesifikasi rangka batang:
Dalam kasus tersebut dapat dilihat berupa rangka berbentuk tray dengan 3 lantai. Dalam rangka tersebut lalu diaplikasikan beban sebesar 1000 N pada salah satu sisi dan 2000 N pada sisi lainya, dengan dimensi yang diberikan adalah Panjang = 0.6 m, Lebar = 0.75 m, dan Tinggi = 1.8 m. Beban diaplikasikan pada lebar rangka dengan panjang 0.75m.
Tugas kita adalah mengoptimasikan desain tersebut dengan mempertimbangkan sisi efisiensi ekonomi dengan tetap mempertimbangkan safety factor yang wajar. Untuk optimasi sendiri, nantinya akan dilakukan dengan metode curve-fitting seperti least square polynomial. Pada tugas ini, kami juga harus menentukan jenis material dan luas penampang yang akan diaplikasikan. Material dan jenis penampang akan berpengaruh nantinya terhadap harga produk.
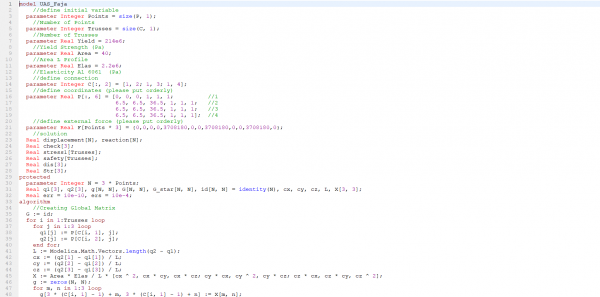
Pada proses pengerjaan Tugas Besar, kelas Metode Numerik 02 dan 03 melakukan dua kali diskusi menggunakan platform meeting. Diskusi dilakukan pada tanggal 29 Desember 2020 dan 3 Januari 2021. Hasil dari diskusi pertama yaitu saya dapat mulai memahami tentang bagaimana input yang dapat disesuaikan dengan analisis yang akan dipakai yaitu: 1. Parameter Elastisitas, berhubungan dengan pemilihan jenis material yang akan digunakan 2. Parameter Luas Penampang, berhubungan dengan bentuk rangka yang akan diubah menjadi parameter no point, trusses, dan definisi koordinat dan connection Pada saat mendeklarasikan, kita mendefinisikan point sambungan dan jumlah trusses karena point dan trusses akan seiring dengan bentuk design yang akan dibuat. Saya membuat model menggunakan aplikasi Autodesk Inventor terlebih dahulu untuk mempermudah pengerjaan karena bisa melihat bentuk aslinya secara 3D. Kemudian diberikan element area yang satuan luas. Setelah itu diberikan parameter elastisitas sesuai dengan material yang akan digunakan. Bentuk permodelan dalam aplikasi OpenModelica saat melakukan deklarasi adalah sebagai berikut:
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000375; //Area (Dimension = 0,04m, Thickness = 0,005m) parameter Real Elas=193e9; //Elasticity of SS 309
Setelah deklarasi komponen dasar pemodelan, kemudian melakukan pendefinisian terhadap connection & koordinat trusses. Kemudian melakukan pendefinisian terhadap connection & koordinat trusses. Pada saat mendefinisikan connection, dibuat kumpulan matriks 1x2 yang berisi 2 nama truss yang dihubungkan, untuk mempermudah pemahaman, susunan koneksi rangka dibangun berdasarkan tingkatan rankga pada desain.
Berikut contoh pemodelan Connection yang ada pada program:
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
Setelah memdefinisikan connection, diperlukan untuk menuliskan koordinat dari point connection diatas. Karena model yang dibuat dalam 3D, pada saat pendefisian ditulis dalam bentuk matrix 1x3 yang tiap nilainya menunjukkan jarak terhadap titik referensi (0,0,0). Pemograman OpenModelica sebagai berikut:
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
Langkah selanjutnya adalah menuliskan definisi terhadap beban yang diberikan. Saya memasukkan beban sesuai dengan soal yaitu 1000N dan 2000N ada tepat di tengah kedua rangka paling atas seperti pada gambar soal. Namun karena analisa yang dibuat menggunakan point connection, maka tiap beban dibagi dua karena beban yang ditulis adalah beban yang diterima oleh point sehingga masing-masing beban menjadi 500, 1000, 1000, dan 500. Beban dituliskan dalam bentuk matrix 1x3 untuk tiap truss dari lantai 1 ke lantai 3. Pemograman Open Modelica sebagai berikut:
//define external force
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
Untuk pendeklarasian terakhir yaitu memasukkan hal-hal yang ingin diketahui (dicari) dengan memasukkan komponen-komponen displacement, reaction, stress, safety, dan lainnya, dengan dilakukan pemrogaraman sebagai berikut:
//solution Real displacement[N], reaction[N]; Real check[3]; Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
Saat masuk tahap perhitungan, diperlukan pendeklarasian pula untuk notasi-notasi yang dipakai. Dalam pembuatan global matriks diperlukan notasi notasi baru, yaitu matriks X (matriks 3x3 hasil kali A*Elastisitas/L dikali dengan matriks), lalu ada notasi cx,cy,cz, untuk membantu perhitungan matriks global. Juga matriks q1 dan q2 [1x3] yang akan menjadi variable yang mempermudah proses perhitungan matriks global. Tidak lupa juga error untuk validasi nya. Berikut pemodelannya:
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
Kemudian memulai algoritma tentang pembentukkan Global Matrix dengan notasi G sehingga terjadi proses looping notasi i dan j yang akan mengisi variable q1 dan q2. Perbedaan loop i dan j adalah loop i akan memanggil matriks trusses (connection) pada kolom 1, sedangkan loop j akan melakukan looping untuk angka 1-3 hingga q berada dalam fungsi j, q[j]
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
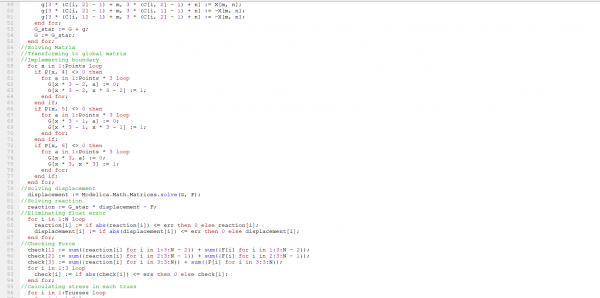
L dicari dengan menentukan jarak vector. Notasi cx, cy, dan cz dibuat untuk memudahkan saat membuat matriks u. Notasi cx seperti menjadi shortcut untuk dibentuknya matriks stiffness. Perhitungan selanjutnya menggunakan pemograman di bawah ini:
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
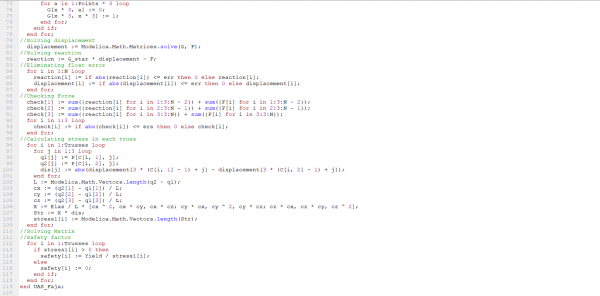
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
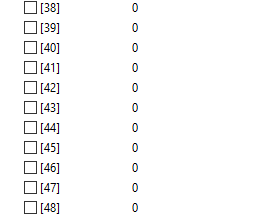
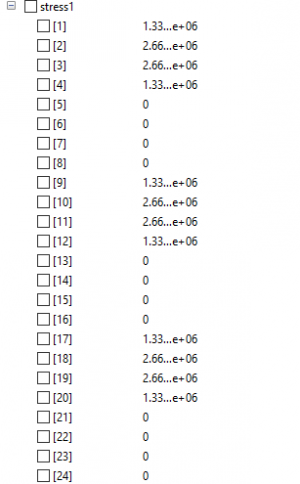
Sehingga dari hasil simulasi didapatkan nilai Displacement, Reaction Force, Stress, dan Safety Factor (yield/stress) sebagai berikut:
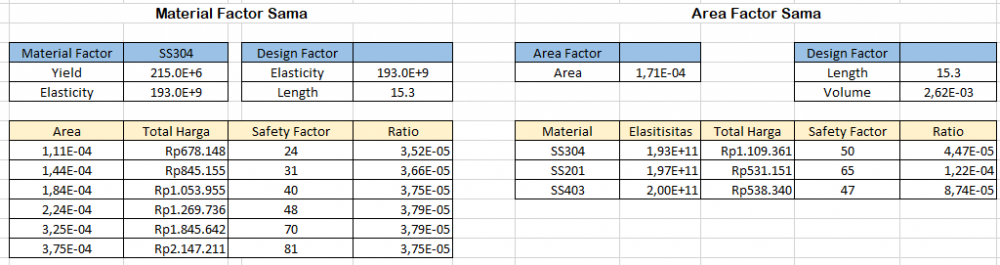
Berikut ini adalah variasi data untuk material yang sama, yaitu SS304 dan menggunakan area factor yang sama, yaitu 0.000171. Setelah melakukan simulate, maka kita akan mendapatkan nilai dari safety factor, kemudian kita mencari Rasio dengan melakukan perbandingan Safety factor dengan total harga, maka akan didapatkan :
Kemudian, berdasarkan hasil data yang telah didapat, kita bisa mendapatkan Luas area dan material yang baik digunakan pada rangka yang akan dibuat dengan menggunakan optimasi dengan curve fitting dan golden bracket. Fungsi untuk Curve Fittingnya adalah sebagai berikut:
function CurveFitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end CurveFitting;
Kemudian melakukan optimasi golden ratio pada material tetap:
model Opt_Gold
parameter Real xd[:]={0.000111,0.000144,0.000184,0.000224,0.000325,0.000375};
parameter Real yd[size(xd,1)]={678148,845155,1053955,1269736,1845642,2147211};
parameter Real xlo=111e-6;
parameter Real xhi=375e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Setelah dilakukan stimulate akan didapatkan hasil optimum pada material yang tetap, sebagai berikut:
Maka dapat disimpulkan bahwa area yang paling optimum untuk material yang tetap adalah 0.000373673 mm^2
Pada area yang tetap, saya juga melakukan optimasi golden ratio
model Opt_Gold
parameter Real xd[:]={193000000000,197000000000,200000000000};
parameter Real yd[size(xd,1)]={1109361,531151,538340};
parameter Real xlo=193000000000;
parameter Real xhi=200000000000;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Kemudian untuk Hasil pada Area tetap, didapatkan hasil optimum material:
Untuk area tetap, saya mendapatkan material dengan elastisitas 1.93e11 N/m^2, yang mana itu merupakan material SS304.
Jawaban UAS (13 Januari 2021)
Berikut nomor 1 dan 2
Kemudian nomor 3 dan 4
dan terakhir 5, 6 dan 7
Coding yang saya gunakan pada open modelica adalah sebagai berikut, dimana menggunakan coding untuk Trusses karena hasil yang dicari berupa displacement, dan reaction pada batang