Difference between revisions of "Cornelius"
| (8 intermediate revisions by the same user not shown) | |||
| Line 204: | Line 204: | ||
== FEM == | == FEM == | ||
| − | Penerapan metode elimination gauss dalam python juga dilakukan dalam dunia professional. Salah satunya adalah penggunaan metode ini dalam Finite Element Method(FEM). | + | Penerapan metode elimination gauss dalam python juga dilakukan dalam dunia professional. Salah satunya adalah penggunaan metode ini dalam Finite Element Method(FEM). Metode ini digunakan untuk bisa menghitung gaya dan reaksi-reaksi yang terjadi pada suatu model. Prinsip dasar dari metode ini adalah penetapan node-node pada suatu model sehingga membaginya dalam bentuk yang lebih kecil. Hubungan antara node-node itu akan membentuk sebuah elemen. Elemen ini pun berhubungan satu sama lain dan akan bereaksi saat sesuatu terjadi pada model tersebut, seperti tertekan atau tertarik. Hubungan antara elemen kita bayangkan seperti ada pegas yg menghubungkannya. Dengan kita membayangkan pegas, kita dapat menggunakan matrix dalam perhitungan untuk menentukan gaya reaksi pada setiap hubungan elemen tersebut. Kita akan coba membuat sebuah model FEM dengan asumsi satu gaya yang menariknya ,gaya-gaya yang di antaranya dianggap nol, dan dengan ujung yang sudah fixed. Dengan model ini, kita diminta untuk menentukan gaya yang terjadi pada ujung fixed saat ditarik dengan gaya tertentu. Berikut adalah coding untuk FEM model ini: |
| + | |||
| + | import numpy as np | ||
| + | P=eval(input("Berapa jumlah pegas yang ingin diterapkan pada sistem?" )) | ||
| + | |||
| + | Ini digunakan untuk menentukan jumlah pegas dan yang akan memengaruhi jumlah dari n x n matrix yang akan dihitung | ||
| + | |||
| + | Pk=P+1 | ||
| + | S=np.zeros((Pk,Pk),float) | ||
| + | |||
| + | Jumlah pegas yang digunakan selalu 1 angka di bawah jumlah elemen yang digunakan sehingga nilainya harus ditambah dengan 1 untuk matrixnya | ||
| + | |||
| + | K=np.zeros(P) | ||
| + | for i in range(0,P): | ||
| + | print("Berapa nilai konstanta pegas yang ke-", i+1," ?") | ||
| + | K[i]=eval(input()) | ||
| + | |||
| + | Ini untuk menentukan konstanta pada setiap pegas yang ada di antara setiap elemen | ||
| + | |||
| + | S[0,0]=K[0] | ||
| + | S[P,P]=K[P-1] | ||
| + | |||
| + | Karena nilai dari baris ke 1 kolom ke 1 selalu konstanta pegas pertama dan nilai dari baris terakhir kolom terakhir selalu konstanta pegas yang terakhir juga | ||
| + | |||
| + | j_1=0 | ||
| + | for i_1 in range(0,P): | ||
| + | j_1+=1 | ||
| + | S[i_1,j_1]=-(K[i_1]) | ||
| + | i_2=0 | ||
| + | for j_2 in range(0,P): | ||
| + | i_2+=1 | ||
| + | S[i_2,j_2]=-(K[j_2]) | ||
| + | j_3=0 | ||
| + | for i_3 in range(1,P): | ||
| + | j_3+=1 | ||
| + | S[i_3,j_3]=K[i_3]+K[i_3-1] | ||
| + | print ("Matrix Kekakuan Global Sistem Pegas adalah","\n",S) | ||
| + | |||
| + | definisi dari penempatan setiap konstanta pegas yang ingin diletakan dalam matrix. Hasil dari penempatan ini adalah matrix kekakuan global dari sistem pegas dari elemen-element tersebut | ||
| + | |||
| + | A=S[1:Pk, 1:Pk] | ||
| + | n=len(A) | ||
| + | |||
| + | definisi dari matrix 1 nilai di bawah dari matrix utama | ||
| + | |||
| + | B=np.zeros((n,1), float) | ||
| + | for c in range (0,n): | ||
| + | for v in range (0,1): #(0,1) karena per barisnya hanya memiliki 1 data | ||
| + | print ('masukan besar pada pegas ke', c+1) | ||
| + | B[c,v]= eval(input('masukan:')) | ||
| + | |||
| + | menentukan nilai gaya pada setiap pegas yang diasumsikan berada di antara elemen | ||
| + | |||
| + | for k in range (0,n-1): | ||
| + | for i in range (k+1,n): | ||
| + | if A[i,k] != 0.0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i, k:n] = A[i, k:n] - lam*A[k, k:n] | ||
| + | B[i]=B[i]-B[k]*lam | ||
| + | U=np.zeros(n,float) | ||
| + | for q in range (n-1,-1,-1): | ||
| + | U[q]=(B[q]-np.dot(A[q,q+1:n], U[q+1:n]))/A[q,q] | ||
| + | print (U[q]) | ||
| + | |||
| + | elimination gauss dan back substition | ||
| + | |||
| + | F1=-K[0]*U[0] | ||
| + | print("Nilai dari gaya reaksinya adalah ", F1) | ||
| + | |||
| + | Hasilnya adalah nilai dari gaya reaksi dari ujung fixed. | ||
| + | |||
| + | |||
| + | == Simple FEM pada Python untuk kasus 2 material == | ||
| + | |||
| + | Kasus ini hamper mirip dengan kasus sebelumnya. Hal yang membedakannya adalah ditentukannya jumlah dari material, sehingga tidak diperlukan jumlah dari pegas, dan nilai K (konstanta pegas) harus dipecah lagi menjadi (A x E)/L. Setelah defleksi sudah ditentukan, kita juga perlu untuk mengetahui apakah defleksi yang terjadi akan melewati batas titik B. Berikut adalah coding untuk kasus ini: | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | N = 2 | ||
| + | y = N+1 | ||
| + | |||
| + | K = np.zeros((y,y),float) | ||
| + | |||
| + | #mendefinisikan array berisi konstanta pegas | ||
| + | P = np.zeros(N) | ||
| + | D=np.zeros(N) | ||
| + | E=np.zeros(N) | ||
| + | L=np.zeros(N) | ||
| + | A_1=np.zeros(N) | ||
| + | A=np.zeros(N) | ||
| + | E_L=np.zeros(N) | ||
| + | for i in range (0,N): | ||
| + | print("Berapa nilai diameter material ", i+1," ?") | ||
| + | D[i]=eval(input()) | ||
| + | print("Berapa nilai Modulus Young material ", i+1," ?") | ||
| + | E[i]=eval(input()) | ||
| + | print("Berapa nilai panjang material ", i+1," ?") | ||
| + | L[i]=eval(input()) | ||
| + | A_1[i] = float(D[i] * D[i]) | ||
| + | A[i] = float(A_1[i] * 0.785) | ||
| + | E_L[i] = float(E[i] / L[i]) | ||
| + | P[i] = float(A[i] * E_L[i]) | ||
| + | print("Nilai konstanta pegas ke - ", i+1, "adalah ",P[i]) | ||
| + | |||
| + | print("Berapa jarak antara Titik B dan Material?") | ||
| + | D_B=eval(input()) | ||
| + | |||
| + | K[0,0] = P[0] | ||
| + | K[N,N] = P[N-1] | ||
| + | |||
| + | j_1 = 0 | ||
| + | for i_1 in range (0,N): | ||
| + | j_1 += 1 | ||
| + | K[i_1,j_1] =- (P[i_1]) | ||
| + | i_2 = 0 | ||
| + | for j_2 in range (0,N): | ||
| + | i_2 += 1 | ||
| + | K[i_2,j_2] =- (P[j_2]) | ||
| + | j_3 = 0 | ||
| + | for i_3 in range(1,N): | ||
| + | j_3 += 1 | ||
| + | K[i_3,j_3]= P[i_3]+P[i_3 - 1] | ||
| + | |||
| + | print("Matriks kekakuan global sisem pegas adalah : ") | ||
| + | print("") | ||
| + | print (K) | ||
| + | |||
| + | F = eval(input("berapa gaya yang bekerja ? ")) | ||
| + | |||
| + | A = K[1:y , 1:y] | ||
| + | |||
| + | n = len(A) | ||
| + | |||
| + | B = np.zeros((n,1),float) | ||
| + | B[0] = F | ||
| + | B[1] = 0 | ||
| + | |||
| + | #eliminasi gauss | ||
| + | for k in range (0,n-1): | ||
| + | for i in range (k+1,n): | ||
| + | if A[i,k] != 0.0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i, k:n] = A[i, k:n] - lam*A[k, k:n] | ||
| + | B[i]=B[i] - lam*B[k] | ||
| + | |||
| + | #back substitution | ||
| + | U = np.zeros(n,float) | ||
| + | for t in range (n-1,-1,-1): | ||
| + | U[t]=(B[t]-np.dot(A[t,t+1:n], U[t+1:n]))/A[t,t] | ||
| + | print("Nilai U", t+2," =",U[t]) | ||
| + | |||
| + | print ("\n", "Material berpindah sebesar ",U[1]) | ||
| + | |||
| + | if (U[n-1]>De): | ||
| + | print("Defleksi melebihi batas maksimum!") | ||
| + | else: | ||
| + | print("Defleksi masih dalam batas aman") | ||
| + | |||
| + | Untuk penjelasan lebih mendalam dapat dilihat dari video yang sudah saya buat tentang kasus ini. Berikut adalah link video : https://youtu.be/O8BHCAAxovk | ||
| + | |||
| + | |||
| + | == Golden Search Ratio == | ||
| + | |||
| + | Berikut ini adalah coding untuk penerapan golden search ratio pada stiffner L: | ||
| + | |||
| + | import math | ||
| + | def bracket(f,x1,h): | ||
| + | c = 1.618033989 | ||
| + | f1 = f(x1) | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | h = -h | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | return x2,x1 - h | ||
| + | for i in range (100): | ||
| + | h = c*h | ||
| + | x3 = x2 + h | ||
| + | f3 = f(x3) | ||
| + | if f3 > f2: | ||
| + | return x1,x3 | ||
| + | x1 = x2 | ||
| + | x2 = x3 | ||
| + | f1 = f2 | ||
| + | f2 = f3 | ||
| + | print ("Bracket did not find a minimum") | ||
| + | def search(f,a,b,tol=1.0e-9): | ||
| + | nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a)))) | ||
| + | R = 0.618033989 | ||
| + | C = 1.0 - R | ||
| + | x1 = R*a + C*b | ||
| + | x2 = C*a + R*b | ||
| + | f1 = f(x1) | ||
| + | f2 = f(x2) | ||
| + | for i in range(nIter): | ||
| + | if f1 > f2: | ||
| + | a = x1 | ||
| + | x1 = x2 | ||
| + | f1 = f2 | ||
| + | x2 = C*a + R*b | ||
| + | f2 = f(x2) | ||
| + | else: | ||
| + | b = x2 | ||
| + | x2 = x1 | ||
| + | f2 = f1 | ||
| + | x1 = R*a + C*b | ||
| + | f1 = f(x1) | ||
| + | if f1 < f2: | ||
| + | return x1,f1 | ||
| + | else: | ||
| + | return x2,f2 | ||
| + | print("Aplikasi Optimasi Section Modulus L Stiffner") | ||
| + | print("Kondisi Terikat : lebar alas > lebar atas > lebar tengah") | ||
| + | b1 = eval(input("Nilai lebar bangun alas :")) | ||
| + | b3 = eval(input("Nilai lebar bangun atas :")) | ||
| + | b2 = eval(input("Nilai lebar bangun tengah :")) | ||
| + | H = eval(input("Nilai tinggi T stiffner :")) | ||
| + | def f(x): | ||
| + | A1 = b1*(H-x)/2 | ||
| + | A2 = b2*x | ||
| + | A3 = b3*(H-x)/2 | ||
| + | d1 = 1/2*(H-x)/2 | ||
| + | d2 = 1/2*x+(H-x)/2 | ||
| + | d3 = 3/4*(H-x)+x | ||
| + | I1 = 1/12*b1*((H-x)/2)**3 | ||
| + | I2 = 1/12*b2*x**3 | ||
| + | I3 = 1/12*b3*((H-x)/2)**3 | ||
| + | dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) | ||
| + | I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 | ||
| + | Z = I/dc | ||
| + | return Z | ||
| + | xStart = 0.0 | ||
| + | h = 1.0 | ||
| + | x1,x2 = bracket(f,xStart,h) | ||
| + | y,fMin = search(f,x1,x2) | ||
| + | print("optimal sectional area =",-fMin) | ||
| + | print("sectional area awal" , f(H)) | ||
| + | A = -fMin/f(H)*100 | ||
| + | print ("efisiensi",A,"%") | ||
| + | |||
| + | Penjelasan saya mengenai coding ini bisa dilihat dari link ini : https://www.youtube.com/watch?v=Eilqr3DwL8Q | ||
| + | File coding dan ppt penjelasan singkat dapat diunduh dari link ini : https://drive.google.com/drive/folders/1EVYZW4e5QlVVAhiQqhHSbXAmqIE7Ddlq?usp=sharing | ||
Latest revision as of 22:48, 29 May 2019
Contents
Metode Numerik
METODE NUMERIK adalah teknik yang digunakan untuk memformulasikan persoalan matematik sehingga dapat dipecahkan dengan operasi perhitungan/aritmetika biasa (tambah, kurang, kali, dan bagi). Itulah pengertian yang tentunya saya dapatkan dari google. Sebuah pengertian yang singkat, jelas, dan padat. Saya pun cukup tertarik mendengar apa yang akan saya pelajari pada mata kuliah kali ini. Saya tahu bawah logika saya akan terus diuji dan dipicu selama pelajaran ini, tetapi bagaimana prosesnya tentu masih belum jelas. Bagaimana prosesnya akan dimulai bergantung pada dosen saya pada mata kuliah kali ini, yaitu Dr. Ahmad Indra atau yang kerap ingin disapa Aki Dai. Sebuah introduksi yang unik dilontarkan oleh Aki Dai waktu itu. Sebuah perkenalan yang mungkin kurang berbau "metode numerik, tetapi seperti sebuah peta untuk melihat arah dari ilmu yang akan diberikan oleh Aki Dai.
Akal
Kata yang kerap ditekankan oleh Aki Dai dalam diskusi hari itu. Apa yang membedakan manusia dari semua mahkluk hidup lainnya? Akal budi. Jawaban yang sudah sering dilontarkan ini menjadi topik bahasan kali ini. Topik ini pun bukan sekadar sebuah intermezzo untuk introduksi hari itu saja. Ini dibuktikan dari tujuan perkuliahan yang ingin dicapai oleh Aki Dai. Berikut adalah Kalimat dari tujuan perkuliahan metode numerik ini :
1. Memahami konsep/prinsip dan mampu menerapkannya
2. Menjadi orang yang lebih mengenal siapa dirinya
Tujuan kedua merupakan poin yang menarik. Kenapa harus mengenal diri? Apa yang membuat kita menjadi lebih mengenal diri? Bagaimana Metode Numerik dapat memberikan kita sebuah pandangan mengenai diri kita? Menurut saya, hal yang dimaksud oleh Aki Dai adalah cara kita berpikir. Dalam diskusi hari itu, Aki Dai juga menyebutkan tujuan dan kegunaan dari kita belajar matematika dari kecil. Matematika membantu kita berpikir lebih logis dan sistematis. Pola pikir itu lah yang sebenarnya ingin ditanamkan sejak kecil. Belajar metode numerik tidak jauh berbeda tujuannya dengan matematika. Kita diharapkan bias lebih baik lagi sebagai manusia yang berakal.
Masalah Teknik
Kita kerap mencari solusi dari masalah-masalah yang ada di sekitar kita. Kita menggunakan berbagai metode untuk bisa menerapkan solusi yang paling efektif dan efisien agar masalah yang ada dapat diselesaikan secepatnya. Dari berbagai metode yang ada, beberapa orang mulai mencari cara yang universal yang dapat merepresentasikan metode penyelesaian masalah yang tepat guna. Salah satu metode yang dikembangkan adalah metode numerik.
Ini merupakan contoh dari metode penyelesaian masalah dengan menggunakan bantuan komputasi. Kita bisa membuat model matematis dari masalah yang ada. Model ini seperti bayangan yang merepresentasikan masalah yang benar-benar terjadi. Contohnya, kita bisa menghitung efisiensi dari pemakaian energi kapal dalam satu kali perjalanan. Kita sudah tidak perlu melakukan uji coba berulang-ulang untuk menemukan data yang diperlukan agar dapat mengetahui efisiensinya. Kita bisa menggunakan bantuan komputasi dengan membuat model dari permasalahn tersebut. Dengan data-data yang tepat, keakuratan model ini bisa menjamin solusi yang tepat atas masalah tersebut.
Nonlinear Equation in Python
Tugas kali ini adalah mencoba membahasakan pertidaksamaan linear dengan menggunakan Bahasa python. Pertidaksamaan yang ingin diselesaikan adalah sebagai berikut:
ax + by = c
px + qy = r
Nilai a, b, p, q adalah konstanta dengan nilai tertentu. x dan y adalah variabel yang merupakan solusi dari pertidaksamaan tersebut. Dengan menggunakan python kita harus bisa menyelesaikan masalah itu. Berikut adalah program untuk menyelesaikan pertidaksamaan linear dengan menggunakan python:
import numpy as np
print("Please input the value")
a = int(input("input value of a :"))
b = int(input("input value of b :"))
c = int(input("input value of c :"))
p = int(input("input value of p :"))
q = int(input("input value of q :"))
r = int(input("input value of r :"))
x = np.array([[a,b],[p,q]])
y = np.array([c,r])
z = np.linalg.solve(x,y)
xval = int(z[0])
yval = int(z[1])
print("x = ",xval)
print("y = ",yval)
Program python ini menggunakan numpy untuk membantu dalam membahasakan apa itu x dan y sebagai variable. Modul numpy yang digunakan adalah array untuk matriks, linalg untuk menyelesaikan permasalahan aljabar linear ini. Dengan memasukkan berbagai nilai untuk konstanta, dengan catatan nilainya adalah angka, kita akan mendapatkan nilai x dan y dari program ini.
Python
Dari contoh sebelumnya, kita dapat melihat penyelesaian masalah dengan menggunakan python. Metode-metode ini merupakan penyelesaian dari aljabar linear. Kita hanya menerjemahkannya dengan menggunakan bahasa python. Python hanya bisa mengerti tambah, kurang, kali, dan bagi. Kita harus bisa menemukan pola dalam metode penyelesaian pertidaksamaan linear. Tentu saja python tidak hanya bisa menyelesaikan permasalahan pertidaksamaan linear. Python bisa menyelesaikan berbagai permasalahan matematik, dengan catatan kita bisa menuliskannya dalam bahasa yang dimengerti oleh python. Pertidaksamaan yang sebelumnya pun bisa diselesaikan dengan berbagai metode. Metode lainnya untuk menyelesaikannya adalah dengan menggunakan elimination gauss. Contoh lainnya dalam penyelesaian masalah matematik dengan menggunakan python adalah limit. Dua contoh ini bisa dilihat dalam penjelasan selanjutnya.
Elimination Gauss
Ini adalah metode lain dalam penyelesaian pertidaksamaan linear. Berikut adalah hasil coding untuk penyelesaian menggunakan elimination gauss:
line 1 :import numpy as np line 2 :from numpy import array
line 3 : # define the matrix [A] line 4 : A=array([[5, -4, 5], [-3, 3, -5], [6, -7, 1]], float)
line 5 : # define matrix b line 6 : b = array ([[9], [-1], [ 13]], float)
line 7 : #matrix nya menjadi line 8 : c=array([[5, -4, 5, 9], [-3, 3, -5, -1], [6, -7, 1, 13]], float)
line 9 : print ('Matrix dari persamaan adalah : ')
line 10 : print (c)
line 11 : #define rows column
line 12 : n=len(b) #number of rows and colomn, due too the matrix that is square matrix
line 13 : print ('n adalah ' + str(n))
line 14 : x=np.zeros((3), float)
line 15 : for k in range (0,n-1):
line 16 : for i in range (k+1,n):
line 17 : if A[i,k] != 0.0 : #perintah jika sebuah baris yang akan di eliminasi, ada bagiannya yang tidak 0, maka akan di substract dengan pivot
line 18 : lam = A[i,k]/A[k,k]
line 19 : A[i, k+1:n] = A[i, k+1:n] - lam*A[k, k+1:n]
line 20 : b[i]=b[i] - lam*b[k]
line 21 : for k in range (n-1,-1,-1): line 22 : x[k]=(b[k]-np.dot(A[k,k+1:n], x[k+1:n]))/A[k,k] line 23 : print (x[k])
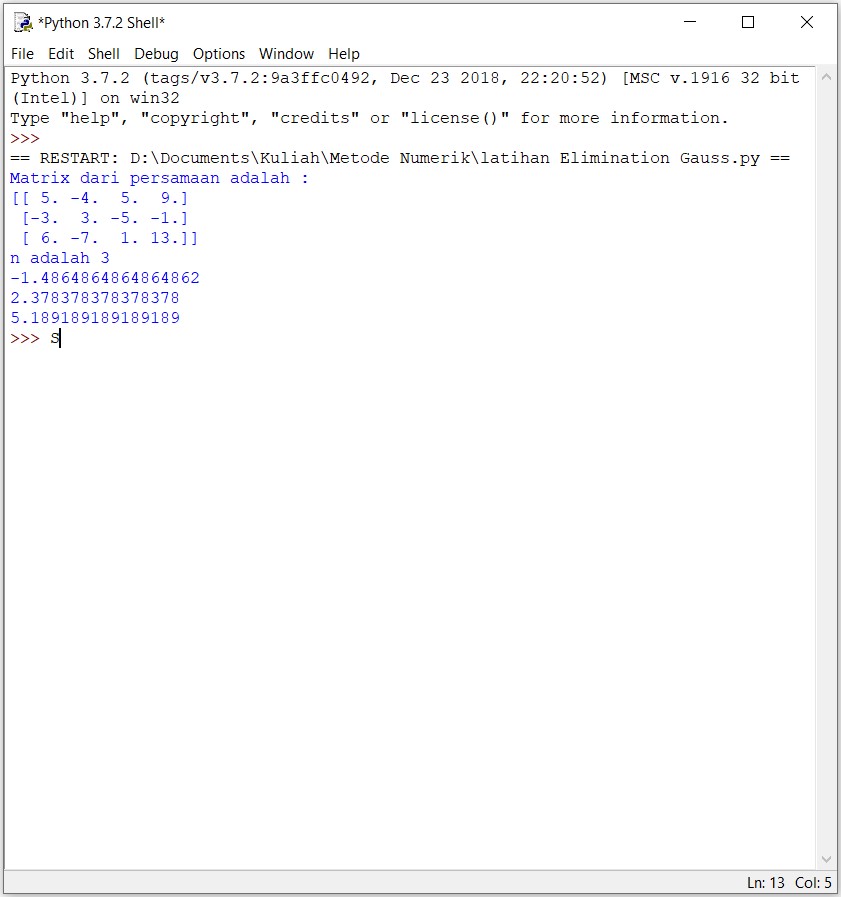
Ini adalah hasil dari Modul tersebut:
Ini adalah model dari metode elimination Gauss. Sekarang saya akan mencoba menjabarkan arti beberapa line dari metode ini. Line 1 dan 2 adalah perintah untuk menerapkan numpy dalam coding ini agar mempermudah berbagai bentuk matematik digunakan dalam coding ini. Array berguna untuk membuat data yang dinginkan dituliskan dalam format matrix. Semua kalimat yang diawali dengan tanda # hanya merupakan angka yang tidak ada hubungan dengan coding secara keseluruhan. Bagian itu bisa dihiraukan dalam coding ini. Line 4 sama line 10 adalah perintah untuk memunculkan matrix. Namun, dari coding tersebut, matrix a, b, dan c tidak berhubungan. Matrix yang muncul hanya lah matrix c dari line 8 karena perintah print hanya ditujukan pada c, sedangkan nilai c tidak dipengaruhi oleh a maupun b. Line 11 hanya perintah menuliskan apa yang ada di dalamnya. Line 12 berguna untuk mengetahui jumlah data dari b. Dalam kasus ini, nilai tersebut adalah 3 karena b memiliki 3 jenis data yang berbeda. Float dalam b tidak termasuk jenis data lain karena itu berguna untuk mendefinisikan nilai angka di dalamnya memiliki nilai 0 tambahan di belakangnya. Line 11 untuk memunculkan kalimat dan string dari n. String adalah Bahasa lain dari kalimat di dalam python. Line 14 adalah perintah untuk memunculkan zero matrix. Dengan nilai 3, berarti yang muncul adalah matrix 3 x 3. Ini digunakan untuk mendefinisikan bentuk matrix yang akan dibaca oleh perintah selanjutnya dalam line 15 sampai line 23. Line 15 sampai line 23 adalah proses eliminasi bagian dari baris yang harusnya 0. Karena kita memerlukan matrix segitiga atas untuk menyelesaikan dengan metode elimination gauss. For digunakan untuk menjalankan perintah hanya ketika argumen yang ada bersifat true. Proses yang berjalan adalah pengecekan setiap angka pada segitiga bawah dalam matrix tersebut agar nilainya menjadi 0. Line 21 juga menggunakan perintah for yang berarti hanya berjalan kalua argumennya bersifat true. Range disini memiliki 3 argumen. Argumen yang ketiga adalah interval dari setiap data yang ada dalam range tersebut. Line 22 juga merupakan pembagian nilai di koordinat data yang diberikan, tetapi ada penggunaan np.dot disana. Perintah np.dot sama seperti dot product dalam aljabar linear. Kemudian diakhiri pada line 23 dengan print (x[k]).
Input yang digunakan disini sudah ditentukan sebelum run module dilakukan. Kita bisa membuat sebuah coding yang memperbolehkan kita menentukan nilai dari matrix awal sebelum program dijalankan. Berikut adalah coding tersebut:
import numpy as np #memasukkan galeri numpy untuk python bisa mengerti perhitungan matematis lainnya selain tambah, kurang, kali, bagi
n= eval(input ('berapa ukuran matrixnya?')) #mendefinisikan jumlah matrix yang diinginkan
a=np.zeros((n,n), float) #pendefinisian matrix 0
print (a) #mengecek bentuk matrixnya
for i in range (0,n): #loop untuk mengecek baris
for j in range (0,n): #look untuk mengecek data ke - n pada baris yg ditentukan
print ('masukan elemen matrix baris ke', i+1, 'kolom ke', j+1)
a[i,j]=eval(input('masukan:')) # nilai yang diinginkan di dalam matrix
print (a) #mengecek matrix a
b=np.zeros((n,1), float) #menggunakan (n,1) untuk membuat hanya matrix n x 1 print (b)
for i in range (0,n):
for j in range (0,1): #(0,1) karena per barisnya hanya memiliki 1 data
print ('masukan elemen matrix baris ke', i+1, 'kolom ke', j+1)
b[i,j]= eval(input('masukan:'))
print (b)
n=len(a) #jumlah elemen pada argumen a
print ('n adalah ' + str(n))
x=np.zeros(n)
for k in range (0,n-1): #menentukan baris yang ingin dijadikan pivot
for i in range (k+1,n): #baris - baris yang ada di bawah pivot
if a[i,k] != 0.0 : #artinya jika pada matrix a baris ke - i pada data yang ke - k nilainya tidak sama dengan 0, berarti perintah yang selanjutnya akan dijalankan
lam = a[i,k]/a[k,k] #lamda untuk mengalikan pivot
a[i, k:n] = a[i, k:n] - lam*a[k, k:n] #baris di bawah pivot akan dikurangi dengan pivot yang sudah dikali dengan lamda
b[i]=b[i]-(b[k]*lam) #pengurangan baris di bawah pivot juga dilakukan pada matrix b
for k in range (n-1,-1,-1): #nilai k dalam range n-1 sampai -1 dengan interval -1, berarti mencari nilai x dari baris yang paling bawah
x[k]=(b[k]-np.dot(a[k,k+1:n], x[k+1:n]))/a[k,k] #data ke - k pada matrix b dikurang dengan hasil perkalian dot matrix a baris ke - k dengan matrix x dan semuanya akan dibagi dengan matrix
a baris ke - k data ke - k
print (x[k]) #memunculkan hasil dari x untuk k yang masuk dalam range
Penjelasan mengenai kegunaan dari perintah-perintah yang ada di dalam coding tersebut dijelaskan dengan kalimat yang diawali dengan tanda pagar(#).
Bisnis kos-kosan
Sebelumnya, kita sudah bisa mengetahui bagaimana cara menerapkan elimination gauss pada python. Kita bisa menggunakan berbagai jumlah n x n matrix elimination gauss dalam python. Dengan pengetahuan ini, kita juga bisa menerapkannya dalam kehidupan kita sehari-hari. Contoh yang akan digunakan kali ini adalah penerapannya dalam menghitung break even point untuk sebuah bisnis kos-kosan. Berikut adalah hasil coding untuk menentukan break even point bisnis kos-kosan:
#Bapak Budi memiliki bisnis kos-kosan di daerah sekitar kutek. Bapak Budi ingin tahu berapa lama beliau akan mendapatkan keuntungan dari aset yang ia milikki. Aset yang ia miliki #berupa kos-kosan 3 lantai dengan lantai 1 memiliki 6 kamar, lantai 2 memiliki 4 kamar, dan lantai 3 memiliki 2 kamar. Bapak Budi memberikan menyewakannya dengan harga #per 1 bulan. Dia mengeluarkan biaya untuk biaya listrik, air, dan lain-lainnya kurang lebih setengah dari biaya sewanya. Bantu Bapak Budi Menghitung BEP Bisnisnya!
import numpy as np from numpy import array
a = array([[1, -10, 5], [1, -6, 2], [1, -4, 2]], float) b = array ([[2.5], [3.6], [4.6]]) print(b)
n=len(a)
print ('n adalah ' + str(n))
x=np.zeros(3)
for k in range (0,n-1):
for i in range (k+1,n):
if a[i,k] != 0.0 :
lam = a[i,k]/a[k,k]
a[i, k:n+1] = a[i, k:n+1] - lam*a[k, k:n+1]
print(a) #mengecek matrix
print(b[i])
b[i]=b[i]-(b[k]*lam)
print (a[k,k+1:n])
for k in range (n-1,-1,-1):
print (b[k])
print (a[k])
x[k]=(b[k]-np.dot(a[k,k+1:n], x[k+1:n]))/a[k,k] #biaya yang dibutuhkan dalam BEP, nilai dalam ribu rupiah
BTT = (str(x[0]))
print ("Biaya Tetap Per Tahun adalah " + BTT + " Juta Rupiah")
BPU = (str(x[1]))
print ("Biaya Per Unit adalah " + BPU + " Juta Rupiah")
VC = (str(x[2]))
print ("Variabel Cost adalah " + VC + " Juta Rupiah")
#Rumus BEP adalah "BTT / (BPU - VC)"
#Rumus ini memberitahukan jumlah unit yang harus dijual untuk mendapatkan keuntungan
print ("\n")
BEP = str(x[0] / (x[1] - x[2]))
print ("Jumlah Unit yang harus dijual untuk Bapak Budi mulai mendapat keuntungan adalah " + BEP + " Unit")
FEM
Penerapan metode elimination gauss dalam python juga dilakukan dalam dunia professional. Salah satunya adalah penggunaan metode ini dalam Finite Element Method(FEM). Metode ini digunakan untuk bisa menghitung gaya dan reaksi-reaksi yang terjadi pada suatu model. Prinsip dasar dari metode ini adalah penetapan node-node pada suatu model sehingga membaginya dalam bentuk yang lebih kecil. Hubungan antara node-node itu akan membentuk sebuah elemen. Elemen ini pun berhubungan satu sama lain dan akan bereaksi saat sesuatu terjadi pada model tersebut, seperti tertekan atau tertarik. Hubungan antara elemen kita bayangkan seperti ada pegas yg menghubungkannya. Dengan kita membayangkan pegas, kita dapat menggunakan matrix dalam perhitungan untuk menentukan gaya reaksi pada setiap hubungan elemen tersebut. Kita akan coba membuat sebuah model FEM dengan asumsi satu gaya yang menariknya ,gaya-gaya yang di antaranya dianggap nol, dan dengan ujung yang sudah fixed. Dengan model ini, kita diminta untuk menentukan gaya yang terjadi pada ujung fixed saat ditarik dengan gaya tertentu. Berikut adalah coding untuk FEM model ini:
import numpy as np
P=eval(input("Berapa jumlah pegas yang ingin diterapkan pada sistem?" ))
Ini digunakan untuk menentukan jumlah pegas dan yang akan memengaruhi jumlah dari n x n matrix yang akan dihitung
Pk=P+1 S=np.zeros((Pk,Pk),float)
Jumlah pegas yang digunakan selalu 1 angka di bawah jumlah elemen yang digunakan sehingga nilainya harus ditambah dengan 1 untuk matrixnya
K=np.zeros(P)
for i in range(0,P):
print("Berapa nilai konstanta pegas yang ke-", i+1," ?")
K[i]=eval(input())
Ini untuk menentukan konstanta pada setiap pegas yang ada di antara setiap elemen
S[0,0]=K[0] S[P,P]=K[P-1]
Karena nilai dari baris ke 1 kolom ke 1 selalu konstanta pegas pertama dan nilai dari baris terakhir kolom terakhir selalu konstanta pegas yang terakhir juga
j_1=0
for i_1 in range(0,P):
j_1+=1
S[i_1,j_1]=-(K[i_1])
i_2=0
for j_2 in range(0,P):
i_2+=1
S[i_2,j_2]=-(K[j_2])
j_3=0
for i_3 in range(1,P):
j_3+=1
S[i_3,j_3]=K[i_3]+K[i_3-1]
print ("Matrix Kekakuan Global Sistem Pegas adalah","\n",S)
definisi dari penempatan setiap konstanta pegas yang ingin diletakan dalam matrix. Hasil dari penempatan ini adalah matrix kekakuan global dari sistem pegas dari elemen-element tersebut
A=S[1:Pk, 1:Pk] n=len(A)
definisi dari matrix 1 nilai di bawah dari matrix utama
B=np.zeros((n,1), float)
for c in range (0,n):
for v in range (0,1): #(0,1) karena per barisnya hanya memiliki 1 data
print ('masukan besar pada pegas ke', c+1)
B[c,v]= eval(input('masukan:'))
menentukan nilai gaya pada setiap pegas yang diasumsikan berada di antara elemen
for k in range (0,n-1):
for i in range (k+1,n):
if A[i,k] != 0.0 :
lam = A[i,k]/A[k,k]
A[i, k:n] = A[i, k:n] - lam*A[k, k:n]
B[i]=B[i]-B[k]*lam
U=np.zeros(n,float)
for q in range (n-1,-1,-1):
U[q]=(B[q]-np.dot(A[q,q+1:n], U[q+1:n]))/A[q,q]
print (U[q])
elimination gauss dan back substition
F1=-K[0]*U[0]
print("Nilai dari gaya reaksinya adalah ", F1)
Hasilnya adalah nilai dari gaya reaksi dari ujung fixed.
Simple FEM pada Python untuk kasus 2 material
Kasus ini hamper mirip dengan kasus sebelumnya. Hal yang membedakannya adalah ditentukannya jumlah dari material, sehingga tidak diperlukan jumlah dari pegas, dan nilai K (konstanta pegas) harus dipecah lagi menjadi (A x E)/L. Setelah defleksi sudah ditentukan, kita juga perlu untuk mengetahui apakah defleksi yang terjadi akan melewati batas titik B. Berikut adalah coding untuk kasus ini:
import numpy as np
N = 2 y = N+1
K = np.zeros((y,y),float)
#mendefinisikan array berisi konstanta pegas
P = np.zeros(N)
D=np.zeros(N)
E=np.zeros(N)
L=np.zeros(N)
A_1=np.zeros(N)
A=np.zeros(N)
E_L=np.zeros(N)
for i in range (0,N):
print("Berapa nilai diameter material ", i+1," ?")
D[i]=eval(input())
print("Berapa nilai Modulus Young material ", i+1," ?")
E[i]=eval(input())
print("Berapa nilai panjang material ", i+1," ?")
L[i]=eval(input())
A_1[i] = float(D[i] * D[i])
A[i] = float(A_1[i] * 0.785)
E_L[i] = float(E[i] / L[i])
P[i] = float(A[i] * E_L[i])
print("Nilai konstanta pegas ke - ", i+1, "adalah ",P[i])
print("Berapa jarak antara Titik B dan Material?")
D_B=eval(input())
K[0,0] = P[0] K[N,N] = P[N-1]
j_1 = 0 for i_1 in range (0,N): j_1 += 1 K[i_1,j_1] =- (P[i_1]) i_2 = 0 for j_2 in range (0,N): i_2 += 1 K[i_2,j_2] =- (P[j_2]) j_3 = 0 for i_3 in range(1,N): j_3 += 1 K[i_3,j_3]= P[i_3]+P[i_3 - 1]
print("Matriks kekakuan global sisem pegas adalah : ")
print("")
print (K)
F = eval(input("berapa gaya yang bekerja ? "))
A = K[1:y , 1:y]
n = len(A)
B = np.zeros((n,1),float) B[0] = F B[1] = 0
#eliminasi gauss
for k in range (0,n-1):
for i in range (k+1,n):
if A[i,k] != 0.0 :
lam = A[i,k]/A[k,k]
A[i, k:n] = A[i, k:n] - lam*A[k, k:n]
B[i]=B[i] - lam*B[k]
#back substitution
U = np.zeros(n,float)
for t in range (n-1,-1,-1):
U[t]=(B[t]-np.dot(A[t,t+1:n], U[t+1:n]))/A[t,t]
print("Nilai U", t+2," =",U[t])
print ("\n", "Material berpindah sebesar ",U[1])
if (U[n-1]>De):
print("Defleksi melebihi batas maksimum!")
else:
print("Defleksi masih dalam batas aman")
Untuk penjelasan lebih mendalam dapat dilihat dari video yang sudah saya buat tentang kasus ini. Berikut adalah link video : https://youtu.be/O8BHCAAxovk
Golden Search Ratio
Berikut ini adalah coding untuk penerapan golden search ratio pada stiffner L:
import math
def bracket(f,x1,h):
c = 1.618033989
f1 = f(x1)
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
h = -h
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
return x2,x1 - h
for i in range (100):
h = c*h
x3 = x2 + h
f3 = f(x3)
if f3 > f2:
return x1,x3
x1 = x2
x2 = x3
f1 = f2
f2 = f3
print ("Bracket did not find a minimum")
def search(f,a,b,tol=1.0e-9):
nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
R = 0.618033989
C = 1.0 - R
x1 = R*a + C*b
x2 = C*a + R*b
f1 = f(x1)
f2 = f(x2)
for i in range(nIter):
if f1 > f2:
a = x1
x1 = x2
f1 = f2
x2 = C*a + R*b
f2 = f(x2)
else:
b = x2
x2 = x1
f2 = f1
x1 = R*a + C*b
f1 = f(x1)
if f1 < f2:
return x1,f1
else:
return x2,f2
print("Aplikasi Optimasi Section Modulus L Stiffner")
print("Kondisi Terikat : lebar alas > lebar atas > lebar tengah")
b1 = eval(input("Nilai lebar bangun alas :"))
b3 = eval(input("Nilai lebar bangun atas :"))
b2 = eval(input("Nilai lebar bangun tengah :"))
H = eval(input("Nilai tinggi T stiffner :"))
def f(x):
A1 = b1*(H-x)/2
A2 = b2*x
A3 = b3*(H-x)/2
d1 = 1/2*(H-x)/2
d2 = 1/2*x+(H-x)/2
d3 = 3/4*(H-x)+x
I1 = 1/12*b1*((H-x)/2)**3
I2 = 1/12*b2*x**3
I3 = 1/12*b3*((H-x)/2)**3
dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3)
I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2
Z = I/dc
return Z
xStart = 0.0
h = 1.0
x1,x2 = bracket(f,xStart,h)
y,fMin = search(f,x1,x2)
print("optimal sectional area =",-fMin)
print("sectional area awal" , f(H))
A = -fMin/f(H)*100
print ("efisiensi",A,"%")
Penjelasan saya mengenai coding ini bisa dilihat dari link ini : https://www.youtube.com/watch?v=Eilqr3DwL8Q File coding dan ppt penjelasan singkat dapat diunduh dari link ini : https://drive.google.com/drive/folders/1EVYZW4e5QlVVAhiQqhHSbXAmqIE7Ddlq?usp=sharing