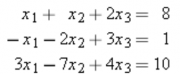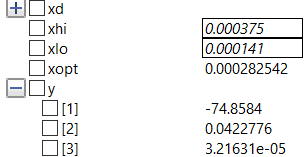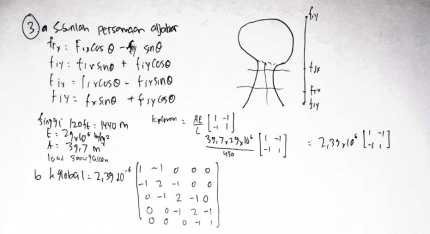Difference between revisions of "Muhammad Helmy Yusuf"
| (53 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | '''السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ | + | '''بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ''' |
| + | '''السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ''' | ||
{| class="wikitable" style="float:right; margin-left: 10px;" | {| class="wikitable" style="float:right; margin-left: 10px;" | ||
!colspan="2"|Muhammad Helmy Yusuf | !colspan="2"|Muhammad Helmy Yusuf | ||
| Line 21: | Line 22: | ||
| − | '''Muhammad Helmy Yusuf''' (lahir di Kebumen, 13 Juni 2001 | + | '''Muhammad Helmy Yusuf''' (lahir di Kebumen, 13 Juni 2001) adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. Selain menjalankan tugas utama menjadi mahasiswa, '''Helmy''' dikenal aktif dalam berorganisasi dan aktif melakukan kegiatan sosial yang dapat bermanfaat dan berdampak untuk orang lain. |
__TOC__ | __TOC__ | ||
| − | == | + | == Biografi == |
Helmy lahir di Kebumen, Jawa Tengah. Saat sebelum dilahirkan, orang tuanya mengubah namanya hingga 5 kali. Mereka akhirnya memberi nama Helmy, yang Yusuf diberi oleh ibunya dengan harapan menjadi pribadi penyabar dan tumbuh menjadi laki - laki pemaaf dan setampan Nabi Yusuf AS serta memiliki kepribadian luhur seperti Nabi Muhammad SAW. | Helmy lahir di Kebumen, Jawa Tengah. Saat sebelum dilahirkan, orang tuanya mengubah namanya hingga 5 kali. Mereka akhirnya memberi nama Helmy, yang Yusuf diberi oleh ibunya dengan harapan menjadi pribadi penyabar dan tumbuh menjadi laki - laki pemaaf dan setampan Nabi Yusuf AS serta memiliki kepribadian luhur seperti Nabi Muhammad SAW. | ||
| Line 35: | Line 36: | ||
Selama berkuliah, Helmy juga mengikuti beberapa organisasi, kepanitiaan, bahkan kegiatan sosial pun pernah diikuti. Saat ini ia menjabat sebagai Badan Pengurus Penelitian dan Pengembangan (LITBANG) di IMM FTUI dan TIS FTUI. Tak hanya di lingkup kampus, ia juga mengikuti organisasi kepemudaan di Indonesia bernama Young On Top dan pernah menjadi ''Project Officer'' dalam acara organisasi tersebut. Di TIS FTUI, ia juga menjadi kesatria pengajar dimana mengajar anak-anak di lapak pemulung daerah karang pola, Pasar Minggu, Jakarta Selatan. Melalui hal-hal yang diikutinya membuat Helmy memiliki skill dalam mengolah data, menganalis, mengevaluasi suatu hal berdasarkan data yang diperoleh, dan skill manajemen personal yang baik. Selain itu juga tumbuh kepedulian terhadap sesama dalam dirinya. | Selama berkuliah, Helmy juga mengikuti beberapa organisasi, kepanitiaan, bahkan kegiatan sosial pun pernah diikuti. Saat ini ia menjabat sebagai Badan Pengurus Penelitian dan Pengembangan (LITBANG) di IMM FTUI dan TIS FTUI. Tak hanya di lingkup kampus, ia juga mengikuti organisasi kepemudaan di Indonesia bernama Young On Top dan pernah menjadi ''Project Officer'' dalam acara organisasi tersebut. Di TIS FTUI, ia juga menjadi kesatria pengajar dimana mengajar anak-anak di lapak pemulung daerah karang pola, Pasar Minggu, Jakarta Selatan. Melalui hal-hal yang diikutinya membuat Helmy memiliki skill dalam mengolah data, menganalis, mengevaluasi suatu hal berdasarkan data yang diperoleh, dan skill manajemen personal yang baik. Selain itu juga tumbuh kepedulian terhadap sesama dalam dirinya. | ||
| + | |||
| + | Saat ini, Helmy menjabat sebagai Program Director di Young on Top Depok periode kepengurusan 2021 yang membawahi divisi energy, entrepreneur, catalyst, dan green. Young on Top sendiri bukan hanya perusahaan, namun juga youth community-organization di Indonesia yang berdiri sejak 2009 dengan ratusan ribu member. Berikut website resmi Young on Top dapat akses '''https://www.youngontop.com/''' | ||
| + | |||
| + | Linkedin '''https://www.linkedin.com/in/muhammadhelmyyusuf/''' | ||
== Metode Numerik == | == Metode Numerik == | ||
| Line 99: | Line 104: | ||
*(+) Open teknologi dan free. beda dengan mathlab dan lainnya yg berbayar | *(+) Open teknologi dan free. beda dengan mathlab dan lainnya yg berbayar | ||
| − | + | ====Latihan Membuat Function dan Class==== | |
Selanjutnya, Pak Dai juga memerintahkan kami untuk ikut mencoba membuat sebuah function dan class yang nantinya akan dihubungkan. Lewat Share screen yang dipandu oleh Pak Dai, saya mulai mencoba dan mendapatkan hasil yang sama. Ilustrasinya sebagai berikut: | Selanjutnya, Pak Dai juga memerintahkan kami untuk ikut mencoba membuat sebuah function dan class yang nantinya akan dihubungkan. Lewat Share screen yang dipandu oleh Pak Dai, saya mulai mencoba dan mendapatkan hasil yang sama. Ilustrasinya sebagai berikut: | ||
[[File:344476.jpg|720px|center]] | [[File:344476.jpg|720px|center]] | ||
| Line 160: | Line 165: | ||
*3. Menerjemahkan pemodelan matematis yang sudah dibuat menjadi metode numerik agar bisa dhitung oleh komputer | *3. Menerjemahkan pemodelan matematis yang sudah dibuat menjadi metode numerik agar bisa dhitung oleh komputer | ||
*4. Melakukan perhitungan metode numerik menggunakan software dan dihasilkanlah solusi dari masalah engineering tersebut | *4. Melakukan perhitungan metode numerik menggunakan software dan dihasilkanlah solusi dari masalah engineering tersebut | ||
| + | |||
| + | ====Code Modelica untuk Gauss Jordan==== | ||
| + | Ketika kelas kami juga mendapat penjabaran menarik mengenai aljabar simultan, variable array, dan metode Gauss. Kemudian ketika sedang membahas hal ini, saudara Christo yang diminta menjelaskan hasil tugasnya pun menjelaskan terkait apa yang sudah ia buat dan kami turut mendengarkan pemaparannya sembari mencatat hal-hal tersebut. Berikut adalah code modelica untuk Gauss Jordan : | ||
| + | |||
| + | function GaussJordan | ||
| + | input Real [:,:] A;//matriks awal | ||
| + | output Real [:,:] B;//matriks tereduksi | ||
| + | protected | ||
| + | Integer h = 1; //pivot row | ||
| + | Integer k = 1; //pivot coloumn | ||
| + | Integer m = size(A,1); //jumlah baris | ||
| + | Integer n = size(A,2); //jumlah kolom | ||
| + | Integer c = 0; | ||
| + | Integer max_row; // Row index of max number in pivot column | ||
| + | Real [:] pivot_column; | ||
| + | Real [:] pivot_row; | ||
| + | Real [:,:] temp_array; | ||
| + | Real r; | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | B := A; | ||
| + | while h <= m and k <= n loop | ||
| + | for i in 1 : m loop | ||
| + | for j in 1 : n loop | ||
| + | if abs(B[i,j]) <= float_error then | ||
| + | B[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | //Finding pivot | ||
| + | pivot_column:= {B[i,h] for i in h:m}; | ||
| + | //Baris terbawah yang mempunyai dengan pivot tertinggi | ||
| + | c:=h-1; | ||
| + | for element in pivot_column loop | ||
| + | c:= c+1; | ||
| + | if abs(element)== max(abs(pivot_column)) then | ||
| + | max_row :=c; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya | ||
| + | if B[max_row,k] == 0 then | ||
| + | k:=k+1; | ||
| + | else | ||
| + | // tukar row h - max_row | ||
| + | temp_array := B; | ||
| + | temp_array[h] := B[max_row]; | ||
| + | temp_array[max_row] := B[h]; | ||
| + | B:= temp_array; | ||
| + | //devide pivot row by pivot number | ||
| + | B[h] := B[h]/B[h,k]; | ||
| + | for i in (h+1) :m loop | ||
| + | r := B[i,k]/B[h,k]; | ||
| + | B[i,k]:=0; | ||
| + | for j in (k+1) : n loop | ||
| + | B[i,j] := B[i,j]-B[h,j] * r; | ||
| + | end for; | ||
| + | end for; | ||
| + | //pindah ke pivot kolom dan row selanjutnya | ||
| + | h := h+1; | ||
| + | k := k+1; | ||
| + | end if; | ||
| + | end while; | ||
| + | // proses dari kanan atas | ||
| + | h :=m; | ||
| + | k :=n; | ||
| + | while h >=1 and k>=1 loop | ||
| + | //dealing with error | ||
| + | for i in 1:m loop | ||
| + | for j in 1:n loop | ||
| + | if abs(B[i,j]) <=float_error then | ||
| + | B[i,j]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | //finding pivot | ||
| + | pivot_row := {B[h,i] for i in 1:k}; | ||
| + | //Get position index k of pivot | ||
| + | c := 0; | ||
| + | for element in pivot_row loop | ||
| + | c := c+1; | ||
| + | if element <> 0 then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | k:= c; | ||
| + | // no pivot in this row, move to next row | ||
| + | if B[h,k] == 0 then | ||
| + | h:= h-1; | ||
| + | else | ||
| + | //perform row operatation | ||
| + | for i in 1:(h-1) loop | ||
| + | r := B[i,k]; | ||
| + | B[i] := B[i] - B[h] *r; | ||
| + | end for; | ||
| + | //move to next pivot row dan column | ||
| + | h:=h+1; | ||
| + | k:=k+1; | ||
| + | end if; | ||
| + | end while; | ||
| + | end GaussJordan; | ||
| + | |||
====Tugas 3==== | ====Tugas 3==== | ||
| Line 271: | Line 377: | ||
end TrussesTugas; | end TrussesTugas; | ||
| + | |||
| + | ''Transformasi Matriks'' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function Stiffness_Matrices | ||
| + | input Real A; | ||
| + | Real Y; | ||
| + | output Real X[4,4]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | final constant Real pi=2*Modelica.Math.asin(1.0); | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Y:=A/180*pi; | ||
| + | |||
| + | X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; | ||
| + | |||
| + | -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2]; | ||
| + | |||
| + | for i in 1:4 loop | ||
| + | for j in 1:4 loop | ||
| + | if abs(X[i,j]) <= float_error then | ||
| + | X[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | |||
| + | end Stiffness_Matrices; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | ''Global Element Matrice'' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function Local_Global | ||
| + | input Real Y[4,4]; | ||
| + | input Integer B; | ||
| + | input Integer p1; | ||
| + | input Integer p2; | ||
| + | output Real G[B,B]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:B loop | ||
| + | for j in 1:B loop | ||
| + | G[i,j]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | G[2*p1,2*p1]:=Y[2,2]; | ||
| + | G[2*p1-1,2*p1-1]:=Y[1,1]; | ||
| + | G[2*p1,2*p1-1]:=Y[2,1]; | ||
| + | G[2*p1-1,2*p1]:=Y[1,2]; | ||
| + | |||
| + | G[2*p2,2*p2]:=Y[4,4]; | ||
| + | G[2*p2-1,2*p2-1]:=Y[3,3]; | ||
| + | G[2*p2,2*p2-1]:=Y[4,3]; | ||
| + | G[2*p2-1,2*p2]:=Y[3,4]; | ||
| + | |||
| + | G[2*p2,2*p1]:=Y[4,2]; | ||
| + | G[2*p2-1,2*p1-1]:=Y[3,1]; | ||
| + | G[2*p2,2*p1-1]:=Y[4,1]; | ||
| + | G[2*p2-1,2*p1]:=Y[3,2]; | ||
| + | |||
| + | G[2*p1,2*p2]:=Y[2,4]; | ||
| + | G[2*p1-1,2*p2-1]:=Y[1,3]; | ||
| + | G[2*p1,2*p2-1]:=Y[2,3]; | ||
| + | G[2*p1-1,2*p2]:=Y[1,4]; | ||
| + | |||
| + | end Local_Global; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | ''Reaction Matrice Equation'' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function Reaction_Trusses | ||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N,1]; | ||
| + | input Real C[N,1]; | ||
| + | Real X[N,1]; | ||
| + | output Real Sol[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=A*B-C; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i,1]) <= float_error then | ||
| + | X[i,1] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | Sol[i]:=X[i,1]; | ||
| + | end for; | ||
| + | |||
| + | end Reaction_Trusses; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | ''Gauss Jordan'' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function Gauss_Jordan | ||
| + | |||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N]; | ||
| + | output Real X[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i]) <= float_error then | ||
| + | X[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Gauss_Jordan; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
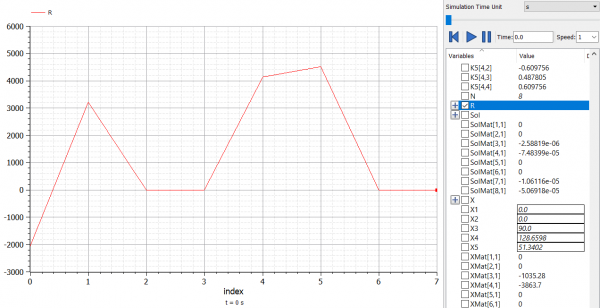
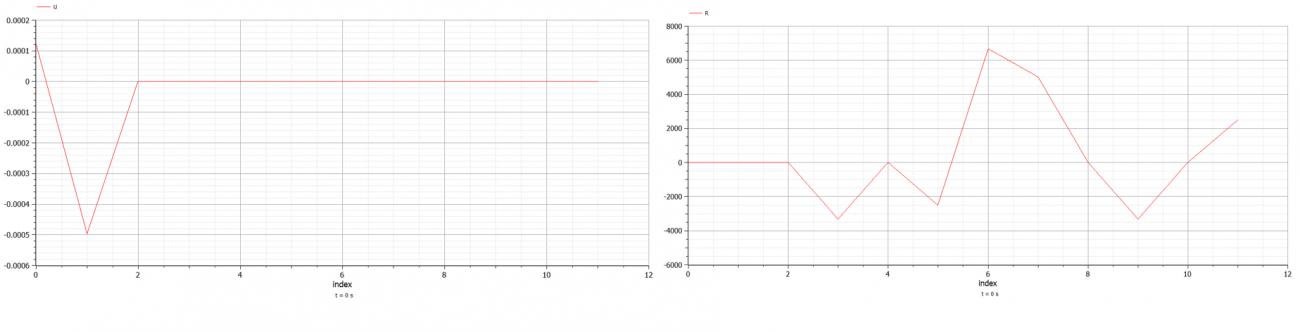
| + | [[File:Screenshot 2020-12-02 151917.png|600px|thumb|center|Grafik Displacement]] | ||
| + | [[File:Screenshot 2020-12-02 151745.png|600px|thumb|center|Grafik Reaction Forces]] | ||
| + | |||
| + | === Pertemuan Keempat (Rabu, 02 Desember 2020) === | ||
| + | |||
| + | Pada pertemuan keempat pada tanggal 2 Desember diawali dengan mendiskusikan terkait tugas yang diberikan pada pekan sebelumnya. Disaat teman-teman memaparkan tugas yang dibuatnya ternyata terdapat perbedaan dalam penyelesaiannya, sehingga setelah itu dibahas lebih lanjut agar dapat menemukan penyelesaian yang lebih efektif | ||
| + | |||
| + | ====Kuis Class Diagram dan Flowchart==== | ||
| + | Pada pekan ke 4 kami juga diberikan kuis untuk membuat class diagram dan flowchart. kedua hal tersebut berasal dari coding penyelesaian trusses milik josiah enrico. Disini terdapat 5 coding seperti : class tusses, stiffness matrices, local global, gauss-jordan, dan reaction trusses berdasarkan yang josiah buat. | ||
| + | |||
| + | Terlebih dahulu kami diberi instruksi oleh pak dai untuk mendahulukan membuat class diagram dan dilanjutkan membuat flowchartnya. | ||
| + | |||
| + | [[File:ClassDiagram.helmy.png|415px]] [[File:Flowcharthelmy.png|415px]] [[File:Supportflowcharthelmy.png|415px]] | ||
| + | |||
| + | |||
| + | ====Tugas 4==== | ||
| + | |||
| + | Pada PR keempat, kami diperintahkan untuk membuat class diagram, flowchart, dan coding OpenModelica | ||
| + | [[File:Nomer8pr4.png|600px|center]] | ||
| + | Pertama, saya membuat terlebih dahulu class diagram dan Flowchartnya sebagai berikut : | ||
| + | [[File:T4.png|600px|center]] | ||
| + | |||
| + | Dalam pengerjaan soal ini, saya membuat FBD terlebih dahulu untuk mencari data-data yang diperlukan, yaitu node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z. | ||
| + | [[File:Tugas4truss.png|700px|center]] | ||
| + | |||
| + | '''StiffnessMatrixElement''' | ||
| + | function StiffnessMatrixElement | ||
| + | |||
| + | input Real [:,9] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | |||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real cos_z; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | |||
| + | algorithm | ||
| + | k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | |||
| + | // Finding stiffness matrix of each element member | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | |||
| + | // Clearing the matrices | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | |||
| + | // Converting degrees to radians | ||
| + | cos_x := inisiasi_mat[i,4]; | ||
| + | cos_y := inisiasi_mat[i,5]; | ||
| + | cos_z := inisiasi_mat[i,6]; | ||
| + | |||
| + | // {cos^2, sin^2, sincos} | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | |||
| + | // Construct stiffness transformation matrix | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | |||
| + | // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end for; | ||
| + | end StiffnessMatrixElement; | ||
| + | |||
| + | Setelah itu dibuat matriks K global 12x12 dari masing-masing element | ||
| + | |||
| + | '''StiffnessMatrixGlobal''' | ||
| + | function StiffnessMatrixGlobal | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,6,6] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | |||
| + | algorithm | ||
| + | for i in 1:y loop | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | Kg_mat[i,a,b]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:y loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal; | ||
| + | |||
| + | Setelah itu semua matriks global dari masing-masing element akan dijumlahkan | ||
| + | |||
| + | '''SumStiffnessMatrixGlobal''' | ||
| + | function SumStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,x,x] Kg_mat; | ||
| + | output Real [x,x] KgTot_mat; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end SumStiffnessMatrixGlobal; | ||
| + | |||
| + | Setelah itu tentukan juga boundaries yang ada | ||
| + | |||
| + | '''BoundaryStiffnessMatrixGlobal''' | ||
| + | function BoundaryStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer z; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Integer[z] Boundary_met; | ||
| + | output Real [x,x] KgB_met; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:x loop | ||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_met[a])-b,i]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end BoundaryStiffnessMatrixGlobal; | ||
| + | |||
| + | Untuk mencari displacement-nya digunakan gauss jordan untuk menyelesaikan matriks | ||
| + | |||
| + | '''GaussJordan''' | ||
| + | function GaussJordan | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgB_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] U_met; | ||
| + | |||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | |||
| + | for i in 1:x loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end GaussJordan; | ||
| + | |||
| + | Dan untuk melihat reaction nya digunakan code sebagai berikut : | ||
| + | |||
| + | '''ReactionForce.mo''' | ||
| + | function ReactionForce | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Real [x] U_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] R_met; | ||
| + | |||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | end ReactionForce; | ||
| + | |||
| + | Terakhir dibuat Class untuk memproses data yang sudah dibuat dan melihat hasil U dan R | ||
| + | |||
| + | '''Tugas4TrussNomor8''' | ||
| + | class Tugas4TrussNomor8 | ||
| + | |||
| + | parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5; | ||
| + | 2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5; | ||
| + | 3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5]; | ||
| + | |||
| + | parameter Integer [:,2] node = [1, 2; | ||
| + | 1, 3; | ||
| + | 1, 4]; | ||
| + | |||
| + | parameter Integer y = size(node,1); | ||
| + | |||
| + | parameter Integer x = 3*(size(node_load,1)); | ||
| + | |||
| + | parameter Integer z = size(Boundary,1); | ||
| + | |||
| + | parameter Integer [:] Boundary = {2,3,4}; | ||
| + | |||
| + | parameter Real [:,4] node_load = [1, 0, -5000, 0; | ||
| + | 2, 0, 0, 0; | ||
| + | 3, 0, 0, 0; | ||
| + | 4, 0, 0, 0]; | ||
| + | |||
| + | parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; | ||
| + | |||
| + | Real [y] k; | ||
| + | |||
| + | Real [y,6,6] Ke; | ||
| + | |||
| + | Real [y,x,x] Kg; | ||
| + | |||
| + | Real [x,x] KgTot; | ||
| + | |||
| + | Real [x,x] KgB; | ||
| + | |||
| + | Real [x] U; | ||
| + | |||
| + | Real [x] R; | ||
| + | |||
| + | equation | ||
| + | k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y}; | ||
| + | |||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | |||
| + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | ||
| + | |||
| + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | ||
| + | |||
| + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | ||
| + | |||
| + | U = GaussJordan(x, KgB, load); | ||
| + | |||
| + | R = ReactionForce(x, KgTot, U, load); | ||
| + | end Tugas4TrussNomor8; | ||
| + | |||
| + | Sehingga dalam persoalan tersebut didapatkan hasil dari displacement (U) dan Reaction force (R) sebagai berikut : | ||
| + | |||
| + | [[File:Simulate.png|1300px|thumb|center|Hasil ''Displacement''(U) dan ''reaction force''(R)]] | ||
| + | [[File:Screenshot 2020-12-09 215708.png|1300px|thumb|center|Grafik ''Displacement''(U) dan ''reaction force''(R)]] | ||
| + | berikut adalah video terkait penyelesaian 3D Truss menggunakan OpenModelica : | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <youtube width="200" height="100">https://youtu.be/DwET3xY7a48</youtube> | ||
| + | </div> | ||
| + | |||
| + | === Pertemuan Kelima/Kelas Pengganti (Senin, 14 Desember 2020) === | ||
| + | Pada kelas pengganti ini, kami berdiskusi bersama terkait apa yang sudah dipelajari di dalam OpenModelica, lalu kami juga membahas mengenai sistem truss berupa diskusi juga dengan kelas MetNum-03. Kemudian kami diminta pak pak Dai untuk muhasabah diri dan juga memberi penilaian terhadap diri sendiri terkait seberapa jauh pemahaman mengenai mata kuliah Metode Numerik. | ||
| + | |||
| + | === Pertemuan Keenam (Senin, 16 Desember 2020) === | ||
| + | Pada pertemuan keenam kelas Metnum-02 sebagian besar diisi oleh Bu Chandra yang mempresentasikan dan melakukan pembahasan terkait ''"One-Dimensional Unconstrained Optimization Using OpenModelica"''. | ||
| + | |||
| + | Optimasi ialah : | ||
| + | -Suatu cara mendapatkan nilai maksimum atau minimum dari suatu | ||
| + | permasalahan | ||
| + | -Ada fungsi objektif | ||
| + | -Ada konstrain | ||
| + | |||
| + | Namun dalam topik yang dibahas pada pertemuan saat ini ialah optimasi fungsi grafik tanpa konstrain. Kami juga di jelaskan mengenai Bracket Optimization Using Golden Ratio Method, yang mana ada satu grafik yang memiliki nilai f(x) global maksimu dan lokal maksimum serta f(x) global minimum dan lokal minimum. | ||
| + | |||
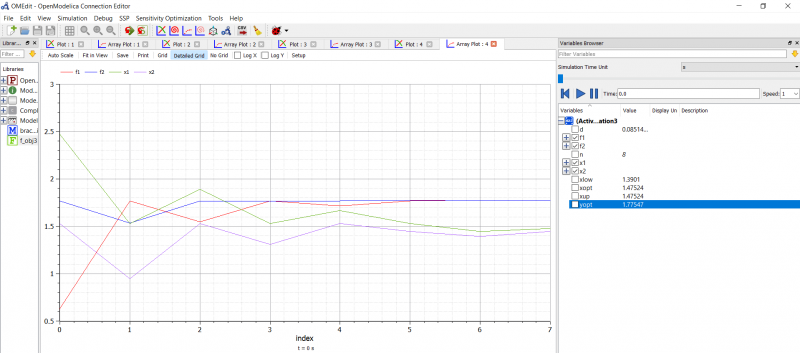
| + | ====Latihan pengaplikasian optimasi menggunakan OpenModelica==== | ||
| + | kemudian contoh pengaplikasian optimasi di dalam OpenModelica juga disampaikan di dalam kelas. Kemudian saya turut memncoba menggunakan OpenModelica sebagai berikut : | ||
| + | |||
| + | membuat fungsi yang akan dipanggil | ||
| + | function f_obj3 | ||
| + | import Modelica.Math; | ||
| + | input Real x; | ||
| + | output Real y; | ||
| + | algorithm | ||
| + | y:= 2*Math.sin(x)-x^2/10; | ||
| + | end f_obj3; | ||
| + | |||
| + | kemudian membuat model yang memanggi fungsi dan merupakan alur proses dari penyelesaian metode optimasi yang sudah dibahas | ||
| + | model bracket_optimation3 | ||
| + | parameter Integer n=8; | ||
| + | Real x1[n]; | ||
| + | Real x2[n]; | ||
| + | Real xup; | ||
| + | Real xlow; | ||
| + | Real d; | ||
| + | Real f1[n]; | ||
| + | Real f2[n]; | ||
| + | Real xopt; | ||
| + | Real yopt; | ||
| + | algorithm | ||
| + | xup :=4; | ||
| + | xlow:=0; | ||
| + | for i in (1:n) loop | ||
| + | d:= (5^(1/2)-1)/2*(xup-xlow); | ||
| + | x1[i]:= xlow+d; | ||
| + | x2[i]:= xup-d; | ||
| + | f1[i]:= f_obj3(x1[i]); | ||
| + | f2[i]:= f_obj3(x2[i]); | ||
| + | if f1[i]>f2[i] then | ||
| + | xup:= xup; | ||
| + | xlow:= x2[i]; | ||
| + | xopt:= xup; | ||
| + | yopt:= f1[i]; | ||
| + | else | ||
| + | xlow:= xlow; | ||
| + | xup:= x1[i]; | ||
| + | xopt:= xup; | ||
| + | end if; | ||
| + | end for; | ||
| + | end bracket_optimation3; | ||
| + | |||
| + | Hasil yag diperoleh : | ||
| + | |||
| + | [[File:HasilOM.png|800px|center]] | ||
| + | |||
| + | ==Tugas Besar Metode Numerik== | ||
| + | ===Pendahuluan=== | ||
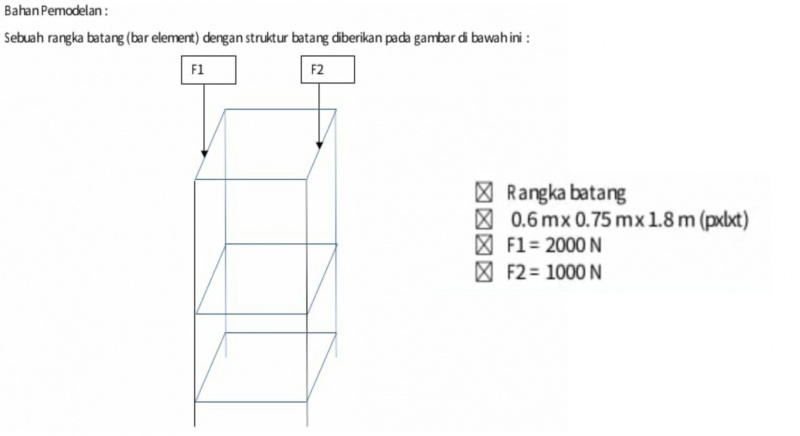
| + | Tugas besar yang diberikan untuk kelas metnum 02 dan 03 adalah optimasi desain struktur rangka batang. Kami diminta untuk mendesain rangka yang baik dan mengoptimalkan pemilihan material, penentuan luas serta cost yang dibutuhkan sehingga menjadi efisien. | ||
| + | |||
| + | Diberikan struktur rangka seperti pada gambar, dengan data yang diberikan seperti berikut: | ||
| + | [[File:390386.jpg|800px|center]] | ||
| + | |||
| + | Diharapkan dari soal tersebut dapat mendesain rangka batang dengan harga terjangkau dan optimal untuk fungsinya. | ||
| + | |||
| + | Faktor atau variabel bebasnya meliputi : Harga, Material yang digunakan, cross section | ||
| + | Dilakukan dengan metode optimasi dan membentuk curve fitting pada variabel harga | ||
| + | |||
| + | ===Mendefinisikan Asumsi Dalam Perhitungan=== | ||
| + | ---- | ||
| + | ====Asumsi yang digunakan untuk melakukan perhitungan==== | ||
| + | *Beban akan terdistribusi hanya pada node (karena bersifat trusses). | ||
| + | *Safety factor minimal bernilai 2. | ||
| + | *Batas displacement 0,001 m sebelum buckling (pada truss paling atas). | ||
| + | *Ketinggian trusses pada tiap lantai sama yaitu 0,6 m. | ||
| + | *Beban terdistribusi pada node | ||
| + | *Tidak ada bending karena bersifat truss | ||
| + | |||
| + | ====Metodologi==== | ||
| + | |||
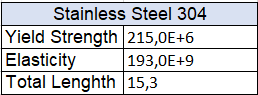
| + | Untuk jenis material yang sama: | ||
| + | *Mencari data terkait material yang dipilih (''Stainless Steel 304'') mulai dari elasticity, yield strength, dsb. | ||
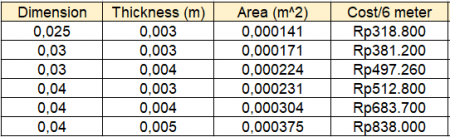
| + | *Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304. | ||
| + | *Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal. | ||
| + | *Membuat rasio antara safety factor dengan harga total. | ||
| + | *Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. | ||
| + | *Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | Untuk area penampang yang sama: | ||
| + | *Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2. | ||
| + | *Mengitung nilai safety factor pada 3 jenis batang dengan coding awal. | ||
| + | *Membuat rasio antara safety factor dengan harga total. | ||
| + | *Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. | ||
| + | *Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | Membuat Codingan untuk Mencari nilai displacement, reaction force, dan melakukan optima | ||
| + | |||
| + | ===Perhitungan displacement, reaction force, safety dan strees=== | ||
| + | ---- | ||
| + | *Untuk perhitungan displacement, reaction force, stress, dan safety factor: | ||
| + | Diasumsikan material SS304 dengan luas truss 171mm^2 (L profile 30x30mm thickness 3mm). | ||
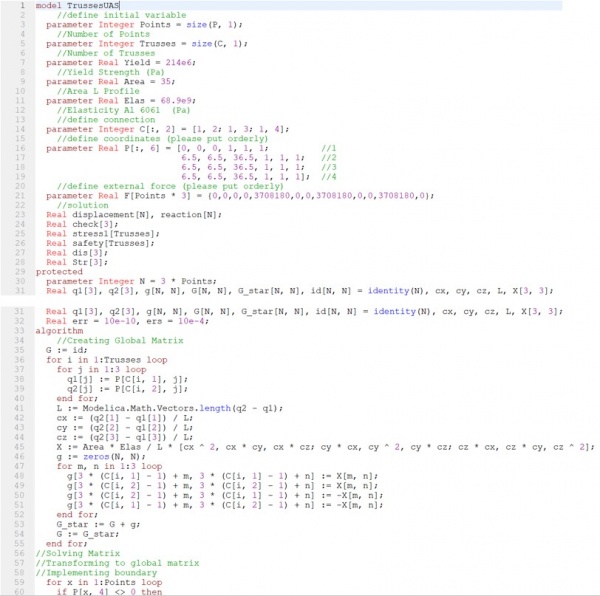
| + | model Trusses_3D_Tugas_Besar | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses_3D_Tugas_Besar; | ||
| + | |||
| + | |||
| + | ====Hasil Perhitungan==== | ||
| + | ---- | ||
| + | |||
| + | Displacement | ||
| + | |||
| + | [[File:Displacementtubes.png|350px]] | ||
| + | |||
| + | Reaction Force | ||
| + | |||
| + | [[File:Reactiontubes.png|350px]] | ||
| + | |||
| + | |||
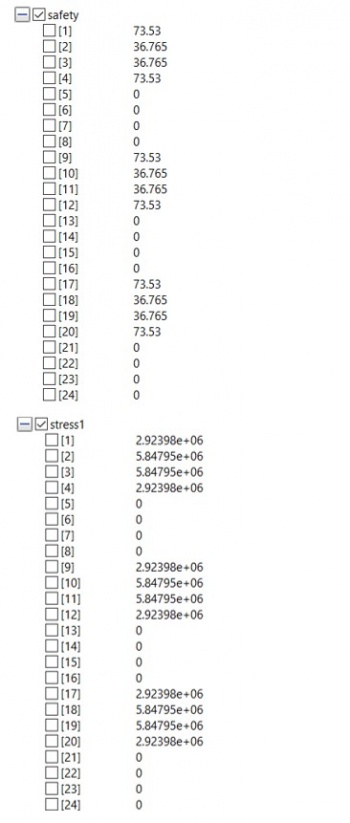
| + | Safety dan Stress | ||
| + | |||
| + | [[File:Safetystresstubes.jpg|350px]] | ||
| + | |||
| + | Kemudian dilakukan optimasi dengan menggunakan 2 metode, yaitu elastisitas tetap (material) - area berbeda dan area tetap - elastisitas (material) berbeda | ||
| + | |||
| + | ===Perhitungan untuk Elasticity Locked (Material)=== | ||
| + | ---- | ||
| + | Material yang saya gunakan adalah SS304 dengan 6 variasi area. Berikut ialah data dari material SS304: | ||
| + | |||
| + | [[File:SS304Helmy.png|300px|thumb|center|SS304 dengan Yield(MPa), Elasticity(GPa), dan Length]][[File:SS304MHY.png|450px|thumb|center|SS304]] | ||
| + | |||
| + | Selanjutnya dalam hal mencari fitting cost/6m perlu menggunakan OpenModelica untuk mencari koefisien persamaanya dengan metode curve fitting. | ||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | |||
| + | Setelah itu saya membuat fungsi panggil yang digunakan untuk mencari koefisien persamaannya sebagai berikut: | ||
| + | |||
| + | model Panggil_CurveFittingCost | ||
| + | parameter Real X[6]={0.000141, 0.000171, 0.000224, 0.000231, 0.000304, 0.000375}; | ||
| + | parameter Real Y[6]={318800, 381200, 497260,512800,683700,838000}; | ||
| + | |||
| + | Real Coe[3]; | ||
| + | |||
| + | equation | ||
| + | Coe=Curve_Fitting(X,Y,2); | ||
| + | end Panggil_CurveFittingCost; | ||
| + | |||
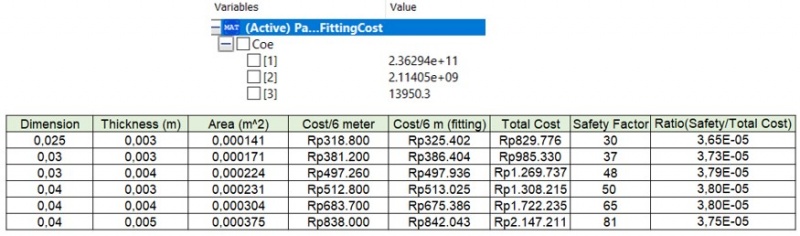
| + | maka didapatkan koefisien yang terlihat pada gambar dan saya gunakan untuk menghitung harga dan variabel lainya. Hasil perhitungan saya ilustrasikan melalui gambar di bawah. | ||
| + | |||
| + | [[File:TubesHelmy'.jpg|800px|thumb|center]] | ||
| + | |||
| + | Lalu. saya melakukan optimasi Golden Section terhadap area dan rasio yang sudah dihitung dengan excel. Di bawah merupakan coding menggunakan OpenModelica: | ||
| + | |||
| + | model Optimasi_Tubes | ||
| + | parameter Real xd[:]={141e-6,171e-6,224e-6,231e-6,304e-6,375e-6}; | ||
| + | parameter Real yd[size(xd,1)]={3.6534e-5,3.73124e-5,3.79292e-5,3.79639e-5,3.79507e-5,3.75487e-5}; | ||
| + | parameter Real xlo=141e-6; | ||
| + | parameter Real xhi=375e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Optimasi_Tubes; | ||
| + | |||
| + | Sehingga didapatkan hasil sebagai berikut : | ||
| + | |||
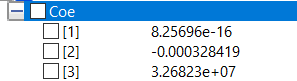
| + | [[File:Optimasitubes.png|400px|thumb|center|xopt=nilai optimum, y[1]=koefisien x^2, y[2]=koefisien x, y[3]=koefisien x^0]] | ||
| + | |||
| + | '''Kesimpulannya''', dihasilkan nilai luas area penampang yang optimum untuk material SS304 adalah 283mm^2. Dalam ukuran yag terdapat pada umumnya di pasaran, maka sesuai dengan nilai optimum yang saya dapatkan ialah batang L 30x30x4mm | ||
| + | |||
| + | ===Perhitungan untuk Area Locked=== | ||
| + | ---- | ||
| + | Pada perhitungan kali ini ialah area yang tetap namun terdapat variasi material. Diantaranya material : | ||
| + | *SS304 | ||
| + | *SS201 | ||
| + | *SS316 | ||
| + | *SS403 | ||
| + | |||
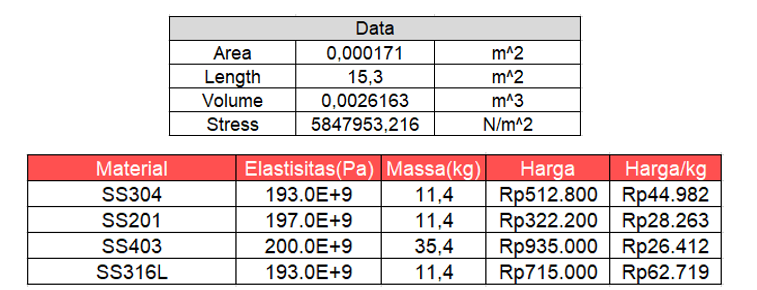
| + | Di bawah ini merupakan data dari masing-masing material yang telah saya rangkum berdasar sumber pencarian saya di Internet. (''sumber di referensi'') | ||
| + | |||
| + | [[File:Areatubes.png|800px|thumb|center]] | ||
| + | |||
| + | Saya kembali menggunakan metode curve fitting untuk mencari fitting harga/kg menggunakan OpenModelica.. X disini ialah elastisitas material dan Y adalah harga dari material yang terdapat di data. | ||
| + | |||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | |||
| + | Setelah itu saya membuat fungsi panggil yang digunakan untuk mencari koefisien persamaannya sebagai berikut: | ||
| + | |||
| + | model Panggil_CurveFittingAreaLocked | ||
| + | |||
| + | parameter Real X[4]={193.0E+9,197.0E+9,200.0E+9,193.0E+9}; | ||
| + | parameter Real Y[4]={44982,28263,26412,62719}; | ||
| + | |||
| + | Real Coe[3]; | ||
| + | |||
| + | equation | ||
| + | |||
| + | Coe=Curve_Fitting(X,Y,2); | ||
| + | end Panggil_CurveFittingAreaLocked; | ||
| + | |||
| + | maka didapatkan koefisien yang terlihat pada gambar dan saya gunakan untuk menghitung harga/kg dan variabel lainya. Hasil perhitungan saya ilustrasikan melalui gambar di bawah. | ||
| + | |||
| + | [[File:Coetubes.png|700px|thumb|center]] | ||
| + | [[File:Tubes area.png|800px|thumb|center]] | ||
| + | |||
| + | |||
| + | Lalu. saya melakukan optimasi Golden Section | ||
| + | |||
| + | model Optimasi_Tubes | ||
| + | //menginput variabel yang dibutuhkan | ||
| + | //xd adalah data elastisitas material | ||
| + | //yd adalah rasio(safety factor/harga) | ||
| + | //xlo merupakan nilai elastisitas(x) terendah | ||
| + | //xhi merupakan nilai elastisitas(x) tertinggi | ||
| + | //N=10 merupakan iterasi maksimum | ||
| + | //es=0.0001 merupakan maximum error | ||
| + | |||
| + | parameter Real xd[:]={193.0E+9,197.0E+9,200.0E+9,193.0E+9}; | ||
| + | parameter Real yd[size(xd,1)]={4.39E-05,0.00011239,8.73E-05,8.07E-05}; | ||
| + | parameter Real xlo=193.0E+9; | ||
| + | parameter Real xhi=200.0E+9; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Optimasi_Tubes; | ||
| + | |||
| + | Sehingga didapatkan hasil sebagai berikut : | ||
| + | |||
| + | [[File:Hasilopt.png|800px|thumb|center|xopt=nilai optimum, y[1]=koefisien x^2, y[2]=koefisien x, y[3]=koefisien x^0]] | ||
| + | |||
| + | |||
| + | '''Kesimpulannya''',Material optimum untuk luas penampang 171mm^2 yang dapat digunakan ialah material dengan elastisitas 1.97085e+11 N/m^2. Pada data yang saya cari dan tabel yang saya buat, maka material yang paling mendekati adalah SS201. | ||
| + | |||
| + | |||
| + | ===Referensi=== | ||
| + | ---- | ||
| + | *https://wijayamakmur.com/ | ||
| + | *http://www.wermac.org/steel/dim_angle_eq.html | ||
| + | *http://www.matweb.com/index.aspx | ||
| + | *https://www.jayastainless.co.id/2018/07/19/mengenal-jenis-jenis-logam-stainless-steel-ss201-ss304-ss316-dan-ss430/ | ||
| + | |||
| + | ==UAS Metetode Numerik (Rabu, 13 Januari 2021)== | ||
| + | ---- | ||
| + | |||
| + | ===Soal=== | ||
| + | [[File:Uasmetnum2.jpg|400px|thumb|center|UAS Metnum-02]] | ||
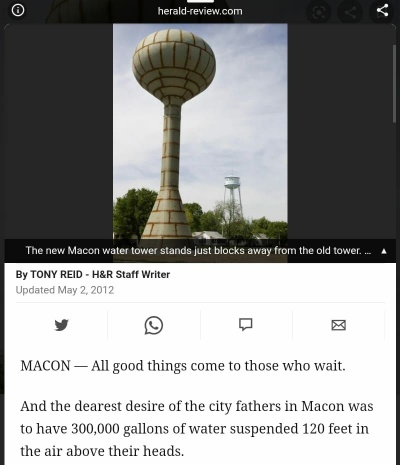
| + | Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas. Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut. | ||
| + | |||
| + | ===Jawaban Pembahasan=== | ||
| + | '''Nomor 1''' | ||
| + | |||
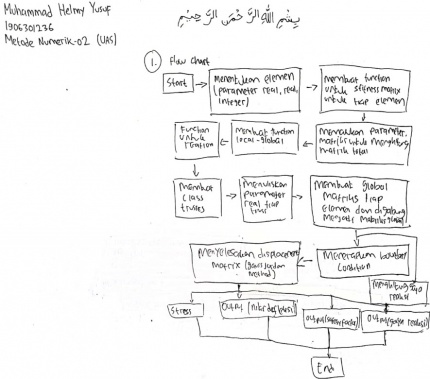
| + | Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut! | ||
| + | [[File:Helmy1.jpg|430px|thumb|center|Nomor 1]] | ||
| + | Secara sederhana, diawali dengan mendefinisikan elemen/parameter-parameter yang ada, kemudian mulai menentukan boundary atau constraint pada struktur, selanjutnya membuat asumsi terkait pemodelan struktur yang digunakan, melakukan perhitungan komputasi pada analisa struktur. Variasi dapat dilakukan seperti material dll, setelah itu melakukan metode optimasi yang sesuai dan melakukan simulasi dan mendapat fungsi untuk melakukan optimasi serta melakukan optimasi untukmendapat nilai optimum. | ||
| + | |||
| + | '''Nomor 2''' | ||
| + | |||
| + | Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan! | ||
| + | [[File:Helmy2.jpg|430px|thumb|center|Nomor 2]] | ||
| + | Pada pemodelan kali ini memiliki tujuan utama yaitu mengoptimasi kekuatan material struktur dan dinding water tank, selain itu juga untuk mengoptimalkan struktur water tower mulai dari pemilihan material, luas penampang, hingga dapat memperkirakan atau meminimalkan cost yang dikeluarkan namun struktur tetap aman. | ||
| + | Hukum/dalil fisika yang digunakan ialah mulai dari stress, strain, hukum hooke, elastisity, gaya hidrostatis, gaya, beban, gravitasi. Asumsinya ialah bangunan/struktur statis tidak bergerak sehingga dapat menggunakan hukum 1 newton. | ||
| + | |||
| + | '''Nomor 3''' | ||
| + | |||
| + | Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D) | ||
| + | |||
| + | a). Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal) | ||
| + | |||
| + | b) Matriks kesetimbangan global | ||
| + | |||
| + | [[File:Helmy3.jpg|430px|thumb|center|Nomor 3]] | ||
| + | |||
| + | '''Nomor 4''' | ||
| + | |||
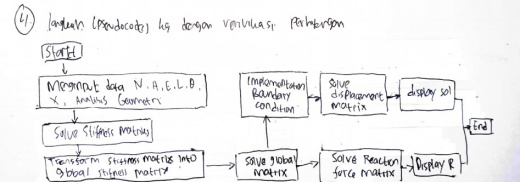
| + | Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya! | ||
| + | |||
| + | [[File:Helmy4.jpg|520px|thumb|center|Nomor 4]] | ||
| + | Pada bagian nomor 4, yang dapat dilakukan ialah dengan menginput terlebih dahulu data yang diketahui. Selanjutnya, mulai membuat coding stiffnes matriksnya. Setelah itu, stiffness matriks dapat diinput kedalam global matriks dan lalu melakukan solve global matriks. Dalam hal ini juga harus mengimplementasikan boundary condition, dan solve discplacement matriks, kemudian dari displacement matrix akan didapatkan display solutionnya. | ||
| + | |||
| + | '''Nomor 5''' | ||
| + | |||
| + | Tulis dan jelaskan fungsi objektif dan constraint untuk optimasi struktur water tower tersebut! | ||
| + | |||
| + | [[File:Helmy5.jpg|550px|thumb|center|Nomor 5]] | ||
| + | Fungsi objektif yaitu memperoleh data tentang struktur tersebut seperti gaya reaksi kesetimbangan statis dan usaha optimasi struktur. sementara itu constraint ialah batas-batas dari simulasi atau boundary pada node | ||
| + | '''Nomor 6''' | ||
| + | |||
| + | Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas | ||
| + | |||
| + | [[File:6fiks.jpg|430px|thumb|center|Nomor 6]] | ||
| + | |||
| + | '''Nomor 7''' | ||
| + | |||
| + | Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6! | ||
| + | |||
| + | [[File:OME1.jpg|600px|center]] | ||
| + | |||
| + | [[File:OME2.jpg|600px|center]] | ||
| + | [[File:HasilUAS.jpg|600px|center]] | ||
| + | [[File:7fiks.jpg|280px|center]] | ||
| + | |||
| + | ==Kutipan Pelajaran Hidup== | ||
| + | ---- | ||
| + | |||
| + | |||
| + | ''Orang yang hari ini '''lebih baik''' dari hari kemarin adalah orang yang '''beruntung''''' | ||
| + | |||
| + | ''Orang yang hari ini '''sama''' dengan hari kemarin adalah orang yang '''rugi''''' | ||
| + | |||
| + | ''Orang yang hari ini '''lebih buruk''' dari hari kemarin adalah orang yang '''celaka''' | ||
| + | |||
| + | '''- (Pak Ahmad Indra Siswantara)''' | ||
Latest revision as of 10:08, 28 March 2021
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
| Muhammad Helmy Yusuf | |
|---|---|

| |
| Nama Lengkap | Muhammad Helmy Yusuf |
| NPM | 1906301236 |
| Jurusan | Teknik Mesin |
| Alamat Surel | muhammad.helmy@ui.ac.id |
Muhammad Helmy Yusuf (lahir di Kebumen, 13 Juni 2001) adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. Selain menjalankan tugas utama menjadi mahasiswa, Helmy dikenal aktif dalam berorganisasi dan aktif melakukan kegiatan sosial yang dapat bermanfaat dan berdampak untuk orang lain.
Contents
- 1 Biografi
- 2 Metode Numerik
- 3 Pertemuan Perkuliahan
- 4 Tugas Besar Metode Numerik
- 5 UAS Metetode Numerik (Rabu, 13 Januari 2021)
- 6 Kutipan Pelajaran Hidup
Biografi
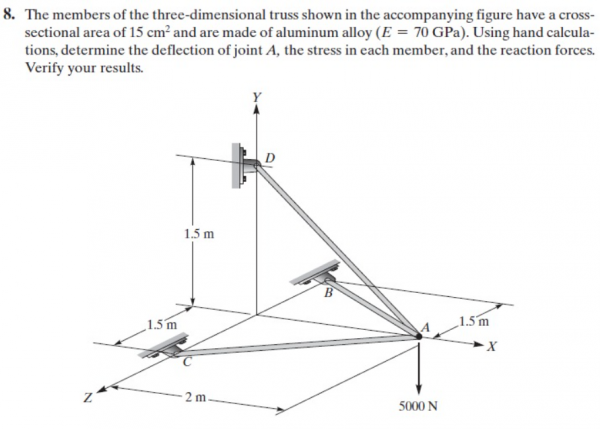
Helmy lahir di Kebumen, Jawa Tengah. Saat sebelum dilahirkan, orang tuanya mengubah namanya hingga 5 kali. Mereka akhirnya memberi nama Helmy, yang Yusuf diberi oleh ibunya dengan harapan menjadi pribadi penyabar dan tumbuh menjadi laki - laki pemaaf dan setampan Nabi Yusuf AS serta memiliki kepribadian luhur seperti Nabi Muhammad SAW.
Helmy menjalani proses pendidikan dasar hingga SMA di Kota Depok. Semasa pendidikannya, Helmy juga aktif dalam berbagai kegiatan ekstrakulikuler sekolah seperti mengikuti Futsal maupun rohani Islam di sekolahnya dan berhasil menjuarai berbagai macam turnamen olahraga maupun akademis. Sehabis menyelesaikan pendidikan SMA-nya di SMAN 2 Depok, pada tahun 2019 ia mengambil jurusan Teknik Mesin di Universitas Indonesia.
Selama berkuliah, Helmy juga mengikuti beberapa organisasi, kepanitiaan, bahkan kegiatan sosial pun pernah diikuti. Saat ini ia menjabat sebagai Badan Pengurus Penelitian dan Pengembangan (LITBANG) di IMM FTUI dan TIS FTUI. Tak hanya di lingkup kampus, ia juga mengikuti organisasi kepemudaan di Indonesia bernama Young On Top dan pernah menjadi Project Officer dalam acara organisasi tersebut. Di TIS FTUI, ia juga menjadi kesatria pengajar dimana mengajar anak-anak di lapak pemulung daerah karang pola, Pasar Minggu, Jakarta Selatan. Melalui hal-hal yang diikutinya membuat Helmy memiliki skill dalam mengolah data, menganalis, mengevaluasi suatu hal berdasarkan data yang diperoleh, dan skill manajemen personal yang baik. Selain itu juga tumbuh kepedulian terhadap sesama dalam dirinya.
Saat ini, Helmy menjabat sebagai Program Director di Young on Top Depok periode kepengurusan 2021 yang membawahi divisi energy, entrepreneur, catalyst, dan green. Young on Top sendiri bukan hanya perusahaan, namun juga youth community-organization di Indonesia yang berdiri sejak 2009 dengan ratusan ribu member. Berikut website resmi Young on Top dapat akses https://www.youngontop.com/
Linkedin https://www.linkedin.com/in/muhammadhelmyyusuf/
Metode Numerik
Metode numerik merupapakan teknik dalam penyelesaian permsalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik.
Pada kelas Metode Numerik-02 semester gasal 20120/2021, perkuliahan pekan pertama sampai UTS diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Dimana telah membahas materi seperti:
- Pseudocode
- Sistem Persamaan
- Turunan Numerik
- Metode Newton Rhapson, Secant, dan Bisection
- Regresi Linear
- Interpolasi
Barulah sehabis UTS proses pembelajaran diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Pertemuan Perkuliahan
Pertemuan Pertama (Rabu, 11 November 2020)
Pada pertemuan pertama setelah UTS diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara. Dimana dijelaskan terkait esensi atau tujuan pembelajaran metode numerik, yaitu:
1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik seperti:Persamaan algoritma, aljabar, pencocokan kurva, persamaan diferensial parsial, dan lainnya
2. Mengerti dan mampu menerapkan pemahaman atau aplikasi terhadap konsep metode numerik
3. Mampu menerapkan metode numerik dalam hal terkait persoalan keteknikan
4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab
Selain empat poin tersebut, kami juga mendapat pelajaran terkait awalan memakai OpenModelica. Dimana kami diperlihatkan praktek sederhana penggunaan OpenModelica ini. Hingga kami tahu bila komputer selain dapat membantu dalam menyelesaikan permasalahan namun juga memiliki batasan atau limit tertentu seperti tidak mampu menentukan nilai 1/0 yang hanya Tuhan yang tahu nilainya. Pelajaran yang dapat dipetik dari kejadian ini ialah kita sebagai manusia haruslah beriman dan jangan pernah melupakan Tuhan yang mengetahui segalanya.
Tugas 1
Pada pertemuan pertama setelah UTS pada tanggal 11 November 2020, kami diminta untuk mempelajari dan memahami penggunaan OpenModelica. Dimana OpenModelica ini merupakan suatu software yang menggunakan bahasa program modelica untuk melakukan simulasi dan perhitungan lainnya. Untuk mempelejarinya saya belajar dari beberapa sumber di YouTube, saya menonton beberapa video dari youtube dalam proses pembelajarannya. Berikut adalah yang telah saya tonton:
Selain itu kami diminta membuat video hasil pembelajaran dan pada video kali ini, saya akan menjelaskan terkait apa yang sudah saya pelajari tentang open modelica dan juga penerapan atau simulasi sederhananya. Berikut rekaman videonya:
pengalaman perdana saya setelah mencobanya, saya merasakan disini menyediakan beberapa fitur yang ramah pengguna untuk membuat, menjelajah, mengedit, dan mensimulasikan model.
Pertemuan Kedua (Rabu, 18 November 2020)
Pada pertemuan kedua ini diawali dengan penjelasan pak Dai tentang orang yang beruntung itu adalah orang yang menjalani hari ini lebih baik dari hari kemarin, dimana memiliki gradien hidup positif. sedangkan apabila masih sama saja berarti gradiennya 0. Bila lebih buruk dari hari kemarin gradiennya negatif. Jadi usahakan untuk lebih baik dari hari sebelumnya dan terus bersikap positif. Kami juga dijelaskan bahwa setiap bahasa ada compilernya, compiler biasa digunakan untuk program komputer yang menerjemahkan program yang ditulis dalam bahasa pemograman tingkat tinggi seperti fortran, pascal, basic, c++ itu diterjemahkan kedalam bahasa mesinnya. Compiler juga berpengaruh ke kecepatan pemrosesannya karena kodingnya akan berbeda beda yang dihasilkan meskipun prinsipnya sama. Compiler biasanya untuk mahasiswa engineering diantaranya fortran dan c karena engineering sangat penting untuk kecepatan perhitungan itu.
Modelica ,singkatnya adalah sebuah bahasa, namun bukan bahasa pemograman/koding. sebenernya koding hanya saja lebih ke bahasa pemodelan. Modelica dibuat dan di desain untuk bahasa pemodelan, dan bukan semata mata untuk bahasa koding seperti python, c, c++ dsb. klo modelica itu bahasa pemodelan. Namun dalam melakukan perhitungannya, sebelom melakukan perhitungan, kode kita yg dituliskan di modelica itu diterjemahkan dulu dalam bahasa c. setelah itu baru dikompilasi ke dalam bahasa mesin baru dapat executable file nya. Kemudian ketika klik simulate lama karena butuh waktu menerjemahkan bahasa modelica ke bahasa c kemudian juga mencompile ke bahasa mesinnya/komputer. sehingga dapat file yg dapat dieksekusi. kalau mau cepat menggunakan parameter-parameter yang dirubah itu dalam bentuk syntaxnya itu parameter, sehingga kita bisa merubah nilainya kemudian tanpa mensimulate ulang.
Di dalam OpenModelica juga memiliki nilai plus. yaitu : *(+) Bukan semata - mata bahasa koding, namun dia bahasa pemodelan. Dimana kita seorang engineering yang memang bukan khusus membuat koding, tapi kita membuat model dan cocok untuk insiyur, juga perhitungannya lumayan cepat juga banyak penggunanya. dan banyak aplikasi2 yg dikembangkan disini *(+) Memudahkan kita untuk cross function atau mempelajari berbagai dasar ilmu dalam 1 software *(+) Open teknologi dan free. beda dengan mathlab dan lainnya yg berbayar
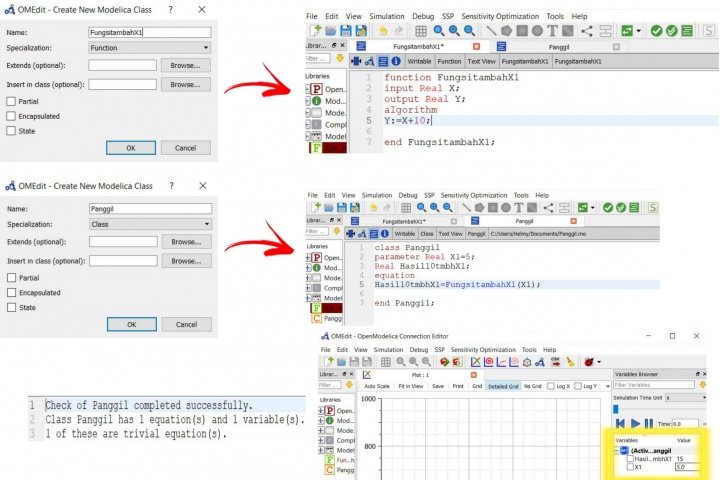
Latihan Membuat Function dan Class
Selanjutnya, Pak Dai juga memerintahkan kami untuk ikut mencoba membuat sebuah function dan class yang nantinya akan dihubungkan. Lewat Share screen yang dipandu oleh Pak Dai, saya mulai mencoba dan mendapatkan hasil yang sama. Ilustrasinya sebagai berikut:
Fungsi yang dibuat yaitu "Fungsi Tambah X1" dengan X sebagai input, Y sebagai output, dan Fungsi yang dibuat adalah Y=10+X. Setelah itu membuat class "Panggil" dimana berfungsi untuk memanggil fungsi tambah X1 yang tadi dibuat. Untuk mendapatkan nilai output Y maka dimasukkanlah nilai input X1. Contohnya saat dibimbing oleh Pak Dai, kami memasukkan X1 sebesar 5. Sehingga didapatkan Hasil yang sesuai yaitu 15. serta dapat diubah-ubah X1 nya dengan re-simulate untuk mendapatkan nilai outputnya.
Tugas 2
Kami diminta untuk mengerjakan aljabar simultan dengan menggunakan variabel array di open modelica. Aljabar simultan adalah metode penyelesaian persoalan matematik yang melibatkan kekompleksan yang sangat rumit sehingga memerlukan cara penyelesaian yang membuatnya simple dengan menggunakan tools yang ada, seperti komputer dengan program visual basic, matlab atau lainnya.
beberapa metode yang terdapat pada aljabar simultan ialah :
1. metode Eliminasi Gauss
2. Metode Cramer
3. Gauss seidel
4. Gauss – jordan.
Sementara itu, variable array adalah variabel yang didalamnya memiliki beberapa data nilai. Contohnya, bila ada data X1, X2, X3 ,dan X4, makadengan menggunakan variabel array cukup dituliskan X[4] saja. Pada tugas 2 ini saya mencoba membuatnya menggunakan 3 persamaan yang sederhana dan memiliki 3 variabel yang harus dicari sebagai berikut :
function
function Gauss_Jordan input Real P[3,3]; input Real Q[3]; output Real X[3]; algorithm X:=Modelica.Math.Matrices.solve(P,Q); end Gauss_Jordan;
class
class SPL
parameter Real P[3,3]=[1,1,2;
-1,-2,3;
3,-7,4];
parameter Real
Q[3]={8,1,10};
Real X[3];
equation
X=Gauss_Jordan(P,Q);
end SPL;
Berikut adalah rekaman Video dari tugas 2:
Pertemuan Ketiga (Rabu, 25 November 2020)
Pada pertemuan ketiga kali ini diawali dengan menanyakan kabar dan juga kami diperintahkan untuk membagi/melakukan share screen terkait progress belajar metode numerik dan pemahaman tentang penggunaan OpenModelica. Kemudian dilakukan juga pembahasan tentang penggunaan OpenModelica pada permasalahan engineering. Pada permasalahan engineering, metode numerik dapat membantu menyelesaikan persoalan agar lebih cepat. Beberapa contoh metode numerik yang dapat membantu menyelesaikan permasalaha engineering diantaranya CFD(Computation fluid dynamics, Metode Stokastik, dan FEA ( FInite Element Analaysis). Tahapan untuk menyelesaikan masalah engineering menggunakan metode numerik:
- 1. Melakukan analisis terhadap masalah engineering
- 2. Melakukan pemodelan matematis dari masalah yang sudah dianalisis
- 3. Menerjemahkan pemodelan matematis yang sudah dibuat menjadi metode numerik agar bisa dhitung oleh komputer
- 4. Melakukan perhitungan metode numerik menggunakan software dan dihasilkanlah solusi dari masalah engineering tersebut
Code Modelica untuk Gauss Jordan
Ketika kelas kami juga mendapat penjabaran menarik mengenai aljabar simultan, variable array, dan metode Gauss. Kemudian ketika sedang membahas hal ini, saudara Christo yang diminta menjelaskan hasil tugasnya pun menjelaskan terkait apa yang sudah ia buat dan kami turut mendengarkan pemaparannya sembari mencatat hal-hal tersebut. Berikut adalah code modelica untuk Gauss Jordan :
function GaussJordan
input Real [:,:] A;//matriks awal
output Real [:,:] B;//matriks tereduksi
protected
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //jumlah baris
Integer n = size(A,2); //jumlah kolom
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Baris terbawah yang mempunyai dengan pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//pindah ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
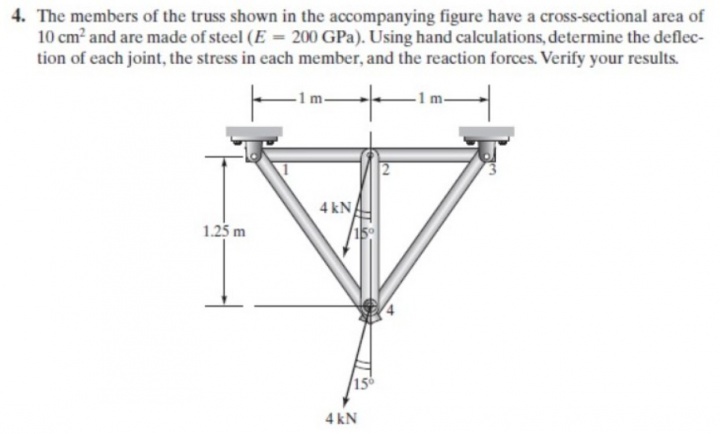
Tugas 3
Persamaan
class TrussesTugas
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end TrussesTugas;
Transformasi Matriks
function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;Global Element Matrice
function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Reaction Matrice Equation
function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;
algorithm
X:=A*B-C;
for i in 1:N loop
if abs(X[i,1]) <= float_error then
X[i,1] := 0;
end if;
end for;
for i in 1:N loop
Sol[i]:=X[i,1];
end for;
end Reaction_Trusses;Gauss Jordan
function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;Pertemuan Keempat (Rabu, 02 Desember 2020)
Pada pertemuan keempat pada tanggal 2 Desember diawali dengan mendiskusikan terkait tugas yang diberikan pada pekan sebelumnya. Disaat teman-teman memaparkan tugas yang dibuatnya ternyata terdapat perbedaan dalam penyelesaiannya, sehingga setelah itu dibahas lebih lanjut agar dapat menemukan penyelesaian yang lebih efektif
Kuis Class Diagram dan Flowchart
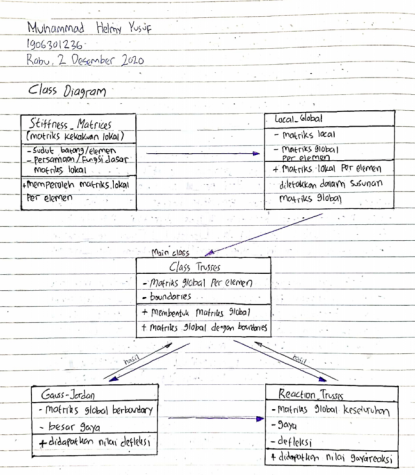
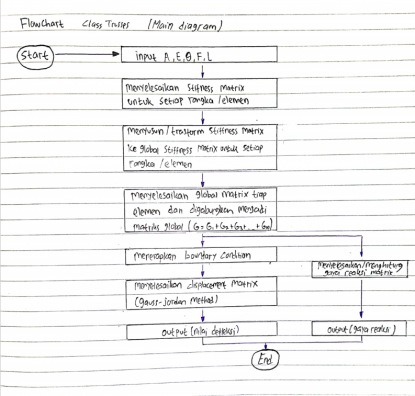
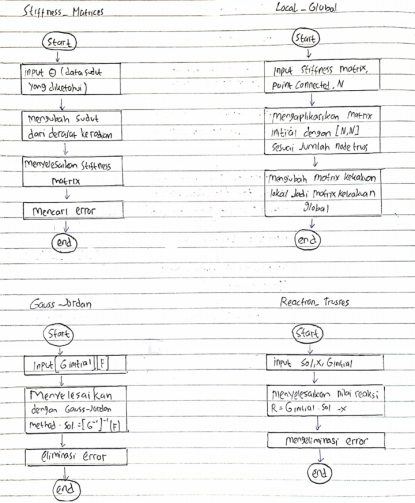
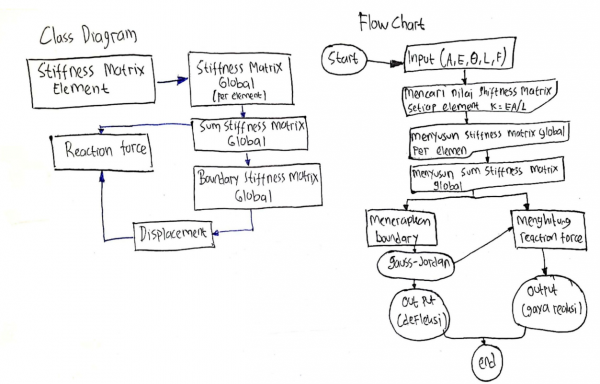
Pada pekan ke 4 kami juga diberikan kuis untuk membuat class diagram dan flowchart. kedua hal tersebut berasal dari coding penyelesaian trusses milik josiah enrico. Disini terdapat 5 coding seperti : class tusses, stiffness matrices, local global, gauss-jordan, dan reaction trusses berdasarkan yang josiah buat.
Terlebih dahulu kami diberi instruksi oleh pak dai untuk mendahulukan membuat class diagram dan dilanjutkan membuat flowchartnya.
Tugas 4
Pada PR keempat, kami diperintahkan untuk membuat class diagram, flowchart, dan coding OpenModelica
Pertama, saya membuat terlebih dahulu class diagram dan Flowchartnya sebagai berikut :
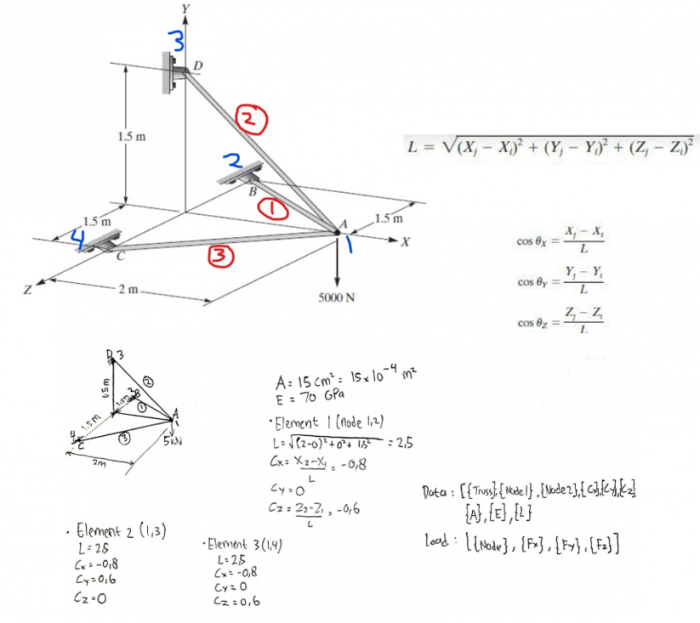
Dalam pengerjaan soal ini, saya membuat FBD terlebih dahulu untuk mencari data-data yang diperlukan, yaitu node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z.
StiffnessMatrixElement
function StiffnessMatrixElement
input Real [:,9] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,4];
cos_y := inisiasi_mat[i,5];
cos_z := inisiasi_mat[i,6];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
Setelah itu dibuat matriks K global 12x12 dari masing-masing element
StiffnessMatrixGlobal
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;
Setelah itu semua matriks global dari masing-masing element akan dijumlahkan
SumStiffnessMatrixGlobal
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
Setelah itu tentukan juga boundaries yang ada
BoundaryStiffnessMatrixGlobal
function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
Untuk mencari displacement-nya digunakan gauss jordan untuk menyelesaikan matriks
GaussJordan
function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
Dan untuk melihat reaction nya digunakan code sebagai berikut :
ReactionForce.mo function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce;
Terakhir dibuat Class untuk memproses data yang sudah dibuat dan melihat hasil U dan R
Tugas4TrussNomor8
class Tugas4TrussNomor8
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end Tugas4TrussNomor8;
Sehingga dalam persoalan tersebut didapatkan hasil dari displacement (U) dan Reaction force (R) sebagai berikut :
berikut adalah video terkait penyelesaian 3D Truss menggunakan OpenModelica :
Pertemuan Kelima/Kelas Pengganti (Senin, 14 Desember 2020)
Pada kelas pengganti ini, kami berdiskusi bersama terkait apa yang sudah dipelajari di dalam OpenModelica, lalu kami juga membahas mengenai sistem truss berupa diskusi juga dengan kelas MetNum-03. Kemudian kami diminta pak pak Dai untuk muhasabah diri dan juga memberi penilaian terhadap diri sendiri terkait seberapa jauh pemahaman mengenai mata kuliah Metode Numerik.
Pertemuan Keenam (Senin, 16 Desember 2020)
Pada pertemuan keenam kelas Metnum-02 sebagian besar diisi oleh Bu Chandra yang mempresentasikan dan melakukan pembahasan terkait "One-Dimensional Unconstrained Optimization Using OpenModelica".
Optimasi ialah : -Suatu cara mendapatkan nilai maksimum atau minimum dari suatu permasalahan -Ada fungsi objektif -Ada konstrain
Namun dalam topik yang dibahas pada pertemuan saat ini ialah optimasi fungsi grafik tanpa konstrain. Kami juga di jelaskan mengenai Bracket Optimization Using Golden Ratio Method, yang mana ada satu grafik yang memiliki nilai f(x) global maksimu dan lokal maksimum serta f(x) global minimum dan lokal minimum.
Latihan pengaplikasian optimasi menggunakan OpenModelica
kemudian contoh pengaplikasian optimasi di dalam OpenModelica juga disampaikan di dalam kelas. Kemudian saya turut memncoba menggunakan OpenModelica sebagai berikut :
membuat fungsi yang akan dipanggil
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end f_obj3;
kemudian membuat model yang memanggi fungsi dan merupakan alur proses dari penyelesaian metode optimasi yang sudah dibahas
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket_optimation3;
Hasil yag diperoleh :
Tugas Besar Metode Numerik
Pendahuluan
Tugas besar yang diberikan untuk kelas metnum 02 dan 03 adalah optimasi desain struktur rangka batang. Kami diminta untuk mendesain rangka yang baik dan mengoptimalkan pemilihan material, penentuan luas serta cost yang dibutuhkan sehingga menjadi efisien.
Diberikan struktur rangka seperti pada gambar, dengan data yang diberikan seperti berikut:
Diharapkan dari soal tersebut dapat mendesain rangka batang dengan harga terjangkau dan optimal untuk fungsinya.
Faktor atau variabel bebasnya meliputi : Harga, Material yang digunakan, cross section Dilakukan dengan metode optimasi dan membentuk curve fitting pada variabel harga
Mendefinisikan Asumsi Dalam Perhitungan
Asumsi yang digunakan untuk melakukan perhitungan
- Beban akan terdistribusi hanya pada node (karena bersifat trusses).
- Safety factor minimal bernilai 2.
- Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
- Ketinggian trusses pada tiap lantai sama yaitu 0,6 m.
- Beban terdistribusi pada node
- Tidak ada bending karena bersifat truss
Metodologi
Untuk jenis material yang sama:
- Mencari data terkait material yang dipilih (Stainless Steel 304) mulai dari elasticity, yield strength, dsb.
- Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304.
- Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
Untuk area penampang yang sama:
- Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2.
- Mengitung nilai safety factor pada 3 jenis batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
Membuat Codingan untuk Mencari nilai displacement, reaction force, dan melakukan optima
Perhitungan displacement, reaction force, safety dan strees
- Untuk perhitungan displacement, reaction force, stress, dan safety factor:
Diasumsikan material SS304 dengan luas truss 171mm^2 (L profile 30x30mm thickness 3mm).
model Trusses_3D_Tugas_Besar
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar;
Hasil Perhitungan
Displacement
Reaction Force
Safety dan Stress
Kemudian dilakukan optimasi dengan menggunakan 2 metode, yaitu elastisitas tetap (material) - area berbeda dan area tetap - elastisitas (material) berbeda
Perhitungan untuk Elasticity Locked (Material)
Material yang saya gunakan adalah SS304 dengan 6 variasi area. Berikut ialah data dari material SS304:
Selanjutnya dalam hal mencari fitting cost/6m perlu menggunakan OpenModelica untuk mencari koefisien persamaanya dengan metode curve fitting.
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
Setelah itu saya membuat fungsi panggil yang digunakan untuk mencari koefisien persamaannya sebagai berikut:
model Panggil_CurveFittingCost
parameter Real X[6]={0.000141, 0.000171, 0.000224, 0.000231, 0.000304, 0.000375};
parameter Real Y[6]={318800, 381200, 497260,512800,683700,838000};
Real Coe[3];
equation
Coe=Curve_Fitting(X,Y,2);
end Panggil_CurveFittingCost;
maka didapatkan koefisien yang terlihat pada gambar dan saya gunakan untuk menghitung harga dan variabel lainya. Hasil perhitungan saya ilustrasikan melalui gambar di bawah.
Lalu. saya melakukan optimasi Golden Section terhadap area dan rasio yang sudah dihitung dengan excel. Di bawah merupakan coding menggunakan OpenModelica:
model Optimasi_Tubes
parameter Real xd[:]={141e-6,171e-6,224e-6,231e-6,304e-6,375e-6};
parameter Real yd[size(xd,1)]={3.6534e-5,3.73124e-5,3.79292e-5,3.79639e-5,3.79507e-5,3.75487e-5};
parameter Real xlo=141e-6;
parameter Real xhi=375e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Optimasi_Tubes;
Sehingga didapatkan hasil sebagai berikut :
Kesimpulannya, dihasilkan nilai luas area penampang yang optimum untuk material SS304 adalah 283mm^2. Dalam ukuran yag terdapat pada umumnya di pasaran, maka sesuai dengan nilai optimum yang saya dapatkan ialah batang L 30x30x4mm
Perhitungan untuk Area Locked
Pada perhitungan kali ini ialah area yang tetap namun terdapat variasi material. Diantaranya material :
- SS304
- SS201
- SS316
- SS403
Di bawah ini merupakan data dari masing-masing material yang telah saya rangkum berdasar sumber pencarian saya di Internet. (sumber di referensi)
Saya kembali menggunakan metode curve fitting untuk mencari fitting harga/kg menggunakan OpenModelica.. X disini ialah elastisitas material dan Y adalah harga dari material yang terdapat di data.
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
Setelah itu saya membuat fungsi panggil yang digunakan untuk mencari koefisien persamaannya sebagai berikut:
model Panggil_CurveFittingAreaLocked
parameter Real X[4]={193.0E+9,197.0E+9,200.0E+9,193.0E+9};
parameter Real Y[4]={44982,28263,26412,62719};
Real Coe[3];
equation
Coe=Curve_Fitting(X,Y,2);
end Panggil_CurveFittingAreaLocked;
maka didapatkan koefisien yang terlihat pada gambar dan saya gunakan untuk menghitung harga/kg dan variabel lainya. Hasil perhitungan saya ilustrasikan melalui gambar di bawah.
Lalu. saya melakukan optimasi Golden Section
model Optimasi_Tubes
//menginput variabel yang dibutuhkan
//xd adalah data elastisitas material
//yd adalah rasio(safety factor/harga)
//xlo merupakan nilai elastisitas(x) terendah
//xhi merupakan nilai elastisitas(x) tertinggi
//N=10 merupakan iterasi maksimum
//es=0.0001 merupakan maximum error
parameter Real xd[:]={193.0E+9,197.0E+9,200.0E+9,193.0E+9};
parameter Real yd[size(xd,1)]={4.39E-05,0.00011239,8.73E-05,8.07E-05};
parameter Real xlo=193.0E+9;
parameter Real xhi=200.0E+9;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Optimasi_Tubes;
Sehingga didapatkan hasil sebagai berikut :
Kesimpulannya,Material optimum untuk luas penampang 171mm^2 yang dapat digunakan ialah material dengan elastisitas 1.97085e+11 N/m^2. Pada data yang saya cari dan tabel yang saya buat, maka material yang paling mendekati adalah SS201.
Referensi
- https://wijayamakmur.com/
- http://www.wermac.org/steel/dim_angle_eq.html
- http://www.matweb.com/index.aspx
- https://www.jayastainless.co.id/2018/07/19/mengenal-jenis-jenis-logam-stainless-steel-ss201-ss304-ss316-dan-ss430/
UAS Metetode Numerik (Rabu, 13 Januari 2021)
Soal
Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas. Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut.
Jawaban Pembahasan
Nomor 1
Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut!
Secara sederhana, diawali dengan mendefinisikan elemen/parameter-parameter yang ada, kemudian mulai menentukan boundary atau constraint pada struktur, selanjutnya membuat asumsi terkait pemodelan struktur yang digunakan, melakukan perhitungan komputasi pada analisa struktur. Variasi dapat dilakukan seperti material dll, setelah itu melakukan metode optimasi yang sesuai dan melakukan simulasi dan mendapat fungsi untuk melakukan optimasi serta melakukan optimasi untukmendapat nilai optimum.
Nomor 2
Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan!
Pada pemodelan kali ini memiliki tujuan utama yaitu mengoptimasi kekuatan material struktur dan dinding water tank, selain itu juga untuk mengoptimalkan struktur water tower mulai dari pemilihan material, luas penampang, hingga dapat memperkirakan atau meminimalkan cost yang dikeluarkan namun struktur tetap aman. Hukum/dalil fisika yang digunakan ialah mulai dari stress, strain, hukum hooke, elastisity, gaya hidrostatis, gaya, beban, gravitasi. Asumsinya ialah bangunan/struktur statis tidak bergerak sehingga dapat menggunakan hukum 1 newton.
Nomor 3
Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D)
a). Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal)
b) Matriks kesetimbangan global
Nomor 4
Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya!
Pada bagian nomor 4, yang dapat dilakukan ialah dengan menginput terlebih dahulu data yang diketahui. Selanjutnya, mulai membuat coding stiffnes matriksnya. Setelah itu, stiffness matriks dapat diinput kedalam global matriks dan lalu melakukan solve global matriks. Dalam hal ini juga harus mengimplementasikan boundary condition, dan solve discplacement matriks, kemudian dari displacement matrix akan didapatkan display solutionnya.
Nomor 5
Tulis dan jelaskan fungsi objektif dan constraint untuk optimasi struktur water tower tersebut!
Fungsi objektif yaitu memperoleh data tentang struktur tersebut seperti gaya reaksi kesetimbangan statis dan usaha optimasi struktur. sementara itu constraint ialah batas-batas dari simulasi atau boundary pada node
Nomor 6
Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas
Nomor 7
Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6!
Kutipan Pelajaran Hidup
Orang yang hari ini lebih baik dari hari kemarin adalah orang yang beruntung
Orang yang hari ini sama dengan hari kemarin adalah orang yang rugi
Orang yang hari ini lebih buruk dari hari kemarin adalah orang yang celaka
- (Pak Ahmad Indra Siswantara)