Difference between revisions of "Metnum03-Muhammad Bagir Alaydrus"
(→Pertemuan 4) |
(→UAS) |
||
| (18 intermediate revisions by the same user not shown) | |||
| Line 257: | Line 257: | ||
[[File:Quizbagir1.jpg|500px]] | [[File:Quizbagir1.jpg|500px]] | ||
| + | |||
[[File:Quizbagir2.jpg|500px]] | [[File:Quizbagir2.jpg|500px]] | ||
| + | |||
| + | == Tugas 4 == | ||
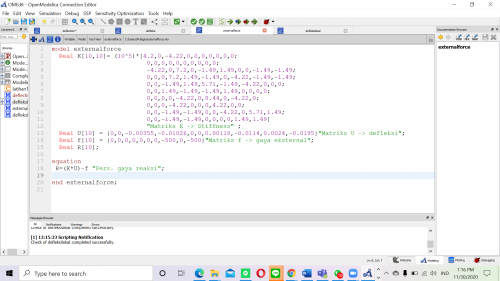
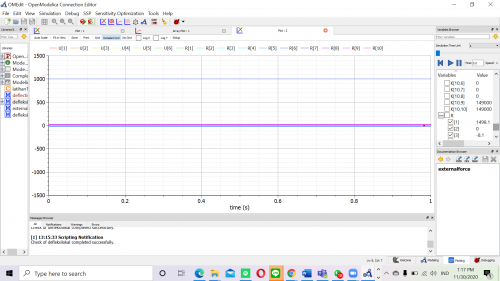
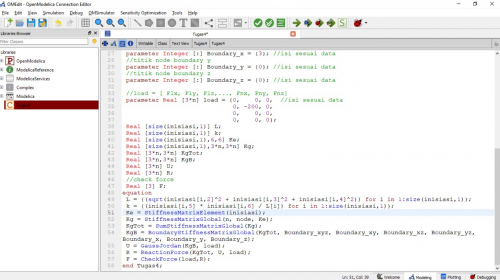
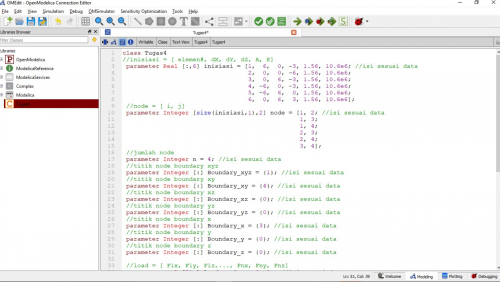
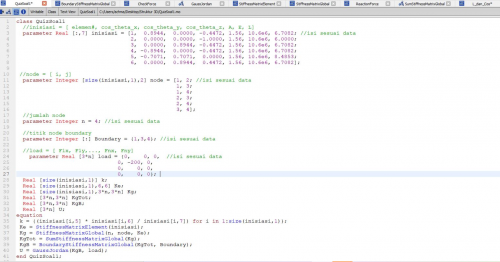
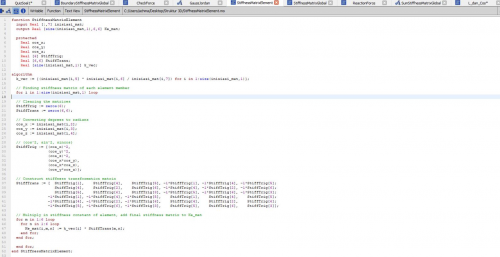
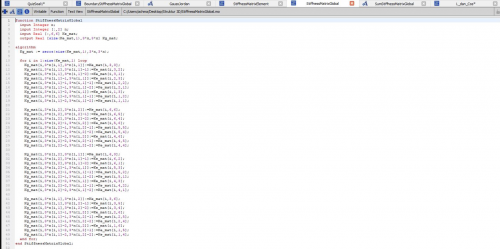
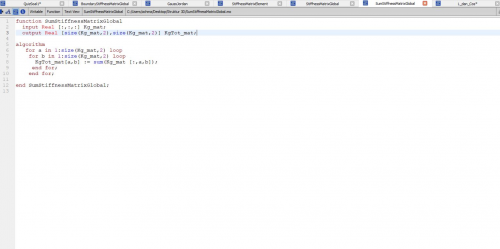
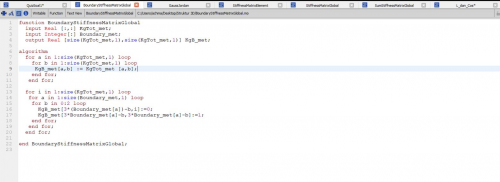
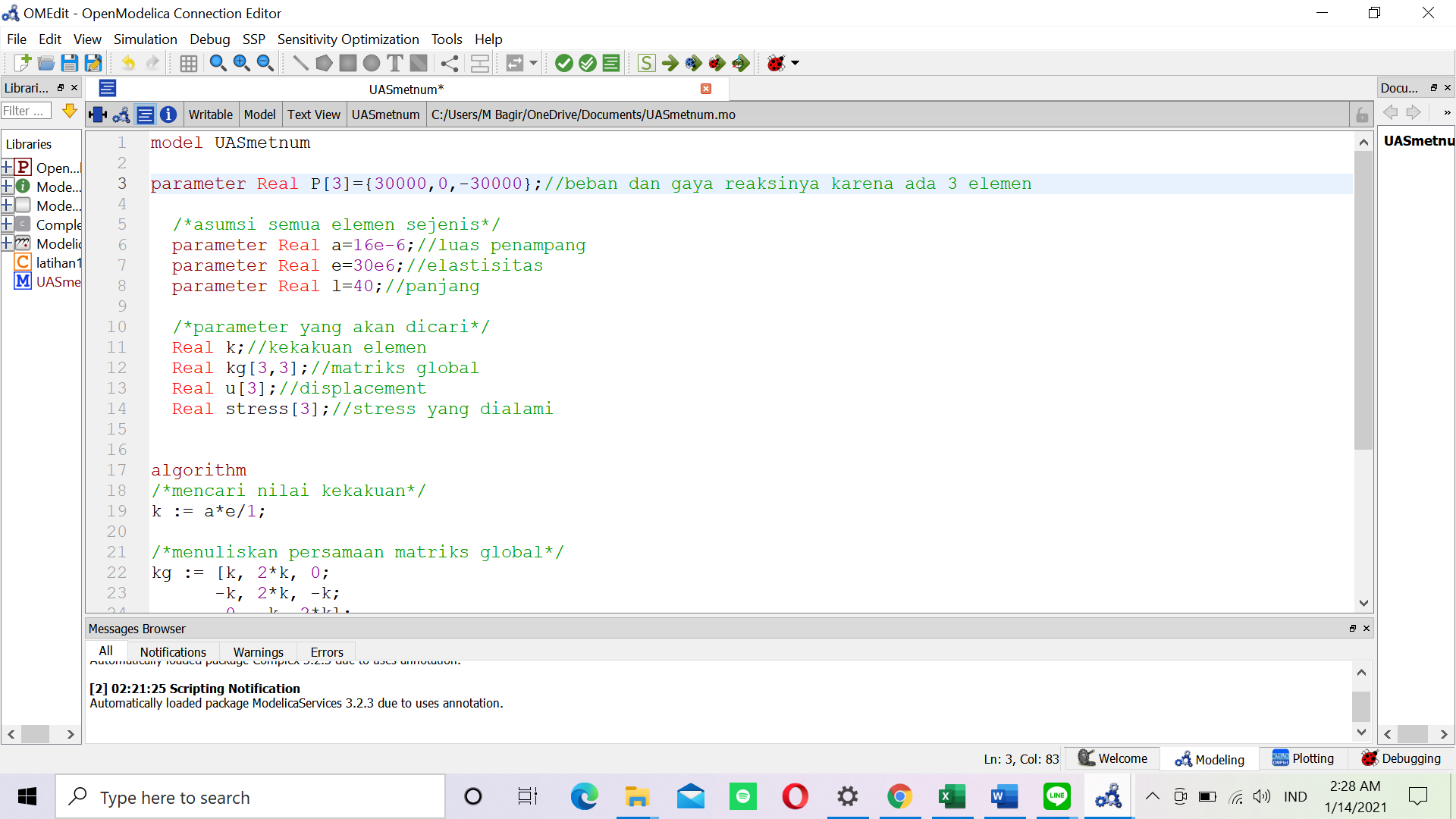
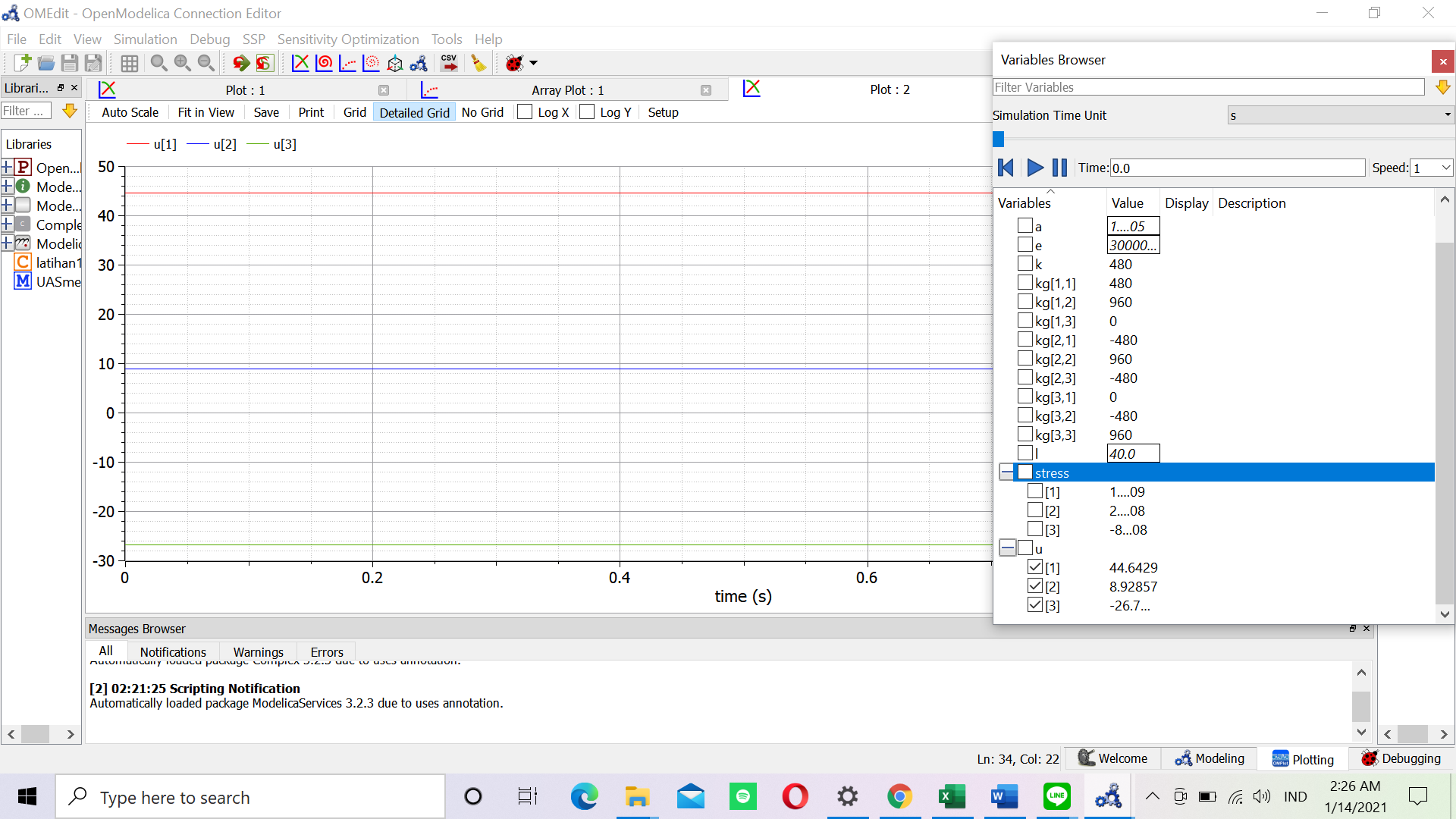
| + | Dalam tugas ini, saya diminta untuk mencari matrix displacement dimana U = {U1x, U1y, U1z,..., Unx, Uny, Unz} ; matrix gaya reaksi dimana R = {R1x, R1y, R1z,...,Rnx, Rny, Rnz}; dan matrix gaya total pada sumbu x, y, dan z dan berikut merupakan coding yang saya lakukan didalam OpenModelica | ||
| + | |||
| + | [[File:metnumbagir1.png|500px]] | ||
| + | |||
| + | [[File:metnumbagir2.png|500px]] | ||
| + | |||
| + | == Pertemuan 5 == | ||
| + | |||
| + | Pada pertemuan 5 ini beberapa teman saya menjelaskan mengenai cara mereka menyelesaikan soal quiz yang lalu menggunakan OpenModelica, edo menyelesaikan persamaan di Open Modelica setelah mendapat Konstata kekakuan baru memsukkan matriksnya, namun kata pak Dai kita akan kesusahan jika variabel nya semakin banyak sehingga diperlukan codingan yang lebih dasar lagii. kemudian edo menjelaskan wiki punya josiah tentang tugas minggu lalu, Memet menjelasakan flow chart yang dia buat dimana pertama dia mencari K lokal kmudian mencari K global kemudian mencari matriks global yang bisa mendapatkan U atau defleksi dan kemudian kita dapat mencari reaction forcenya. Step 2 input matriks lokal yang sudah ada kemudian input node dan elemen dan akan mendapatkan matriks glogabl, pada step ke 5 kita mengeliminasi KGB untuk mencari displacement disini juga harus menggunakan floating error, perbedaan 2 dan 3 dimensi hanya berbeda di persamaan matriks lokal dan global dan boundary global. DI openmodelica nya dia membuat 6 funtion/class agar tidak perlu banyak input di satu kelas,Lalu ahmad menjelaskan mengenai flowchart yang dia telah buat ahmad juga menjelaskan mengenai tahapan untuk menyelesaikan soal. Berikut tahapan yang Ahmad jelaskan : | ||
| + | |||
| + | 1.Solve stiffness | ||
| + | |||
| + | 2.Membuat dan menyelesaikan Matrix global dari setiap elemen | ||
| + | |||
| + | 3.Mengimplementasikan boundary condition, kemudian didapatkan U. | ||
| + | |||
| + | Kemudian pak Dai memberikan kami tugas mengenai pembahasan oleh saudara Ahmad Mohammad Fahmi tentang kodingan yang dibuat olehnya mengenai kuis nomer 4 dan 8. Untuk membantu pembelajaran kami, Ahmad memberikan video rekaman tutorial yang berisi diskusi pada link dibawah ini : | ||
| + | |||
| + | https://drive.google.com/file/d/1n0zvwmn-3G4DWYCSPD48-Xfrp9_kT3R0/view?usp=sharing | ||
| + | |||
| + | Dalam video tersebut Ahmad menjelaskan tenting kodingan yang dia buat. | ||
| + | |||
| + | 1.Untuk mengerjakan nomer 4, Ahmad membuat beberapa function yang nanti akan digunakan dan 1 class untuk membuat penyelesaian atas soal yang diberikan. Pada class, Saudara ahmad memasukkan parameter REAL (inisiasi) yang berisi element, theta, A, E, L. | ||
| + | |||
| + | 2.Kemudian kita menginput node - node yang ada dengan memasukkan matriks dengan parameter integer. Pada parameter integer kita memanggil matriks inisiasi pada kolom satu untuk di sesuaikan dengan node-node yang bersangkutan. | ||
| + | |||
| + | 3.Lalu kita masukan jumlah node yaitu n=4 dan Boundaries pada node. Boundaries pada node ini yaitu pada titik 1 dan 3 karena mereka merupakan tumpuan. Setelah itu, kita memasukkan load dengan menginput parameter real (2*n). Kita mengalikan n dengan 2 karena disini gaya ada 2 arah yaitu x dan y. | ||
| + | |||
| + | 4.Sesudah mengisi load, kita menginput equation dengan fungsi-fungsi yang sudah dibuat juga pada function oleh Ahmad. | ||
| + | |||
| + | Pembahasan dari function : | ||
| + | |||
| + | 1.Lihat terlebih dahulu dari function stiffnessmatrixelement. | ||
| + | |||
| + | 2.Input matriks inisiasi (:,5) dan outputnya adalah matriks dari Ke yang tadi ada pada equation pada class | ||
| + | |||
| + | 3.Gunakan protected maka parameter dapat dipanggil. Fungsinya adalah agar kita bisa memasuki parameter tanpa harus menulis ulang pada function dengan memanggil parameter pada Class | ||
| + | |||
| + | 4.Parameter yang kita ambil untuk Ke adalah Theta, StiffTrig, Stifftrans, k_vec, dan Floating error\ | ||
| + | |||
| + | == Tugas 5 == | ||
| + | Berikut adalah soal yang diberikan moleh pak Dai | ||
| + | |||
| + | [[File:metnumbagir3.png|500px]] | ||
| + | |||
| + | Diketahui pada soal diatas,tahapan pertama kita harus mencari sudut cos x ,cos y ,cos z dan L pada gambar tersebut.Disini saya membuat class khusus untuk mendapatkan nilai - nilai yang dicari diatas di dalam OpenModelica | ||
| + | |||
| + | [[File:metnumbagir4.png|500px]] | ||
| + | |||
| + | Setelah kita mendapatkan sudut cos x ,cos y ,cos z dan L melalui class diatas kita masukkan hasilnya ke dalam class dan function yang diajarkan oleh ahmad muhammad fahmi yaitu 1 class dengan 6 fungsi pembantunya | ||
| + | |||
| + | [[File:metnumbagir5.png|500px]] | ||
| + | |||
| + | Pada soal ini boundarynya sangat berbeda dikarenakan setiap batangnya ada yang dapat menjadi fix di sumbu xyz,xy,dan x setelah itu tahap kedua ialah kita mencari K lokal di setiap elmentnya dengan fungsi berikut | ||
| + | |||
| + | [[File:metnumbagir6.png|500px]] | ||
| + | |||
| + | Setelah mendapatkan K lokal sebagai variabel baru kita harus menempatkan K lokal ke K global agar nantinya bisa di satukan menjadi K global total dengan fungsi | ||
| + | |||
| + | [[File:metnumbagir7.png|500px]] | ||
| + | |||
| + | pada fungsi diatas menghasilkan KG1,KG2,KG3,KG4,KG5 dan KG6 dapat dilihat pada hasil ditandai oleh kg yang dimana (melambangkan elment berapa,baris keberapa,kolom keberapa) Setelah itu kita menjumlahkan KG1 sampai KG6 | ||
| + | |||
| + | [[File:metnumbagir8.png|500px]] | ||
| + | |||
| + | Setelah itu kita mendapatkan KG total yang digunakan untuk mencari displacement dan Reaction force dari gambar diatas,tetapi sebelum memasukkan kesana kita harus memberi batasan yang dimana pada soal ini pada node 1 sumbu XYZ = 0,pada node 4 XY = 0 dan pada node 3 X = 0 tetapi saya menggunakan fungsi yang diberikan oleh fahmi untuk mengerjakan soal nomor 8 yang dimana dianggap pada node 1,3,4 ialah 0 | ||
| + | |||
| + | [[File:metnumbagir9.png|500px]] | ||
| + | |||
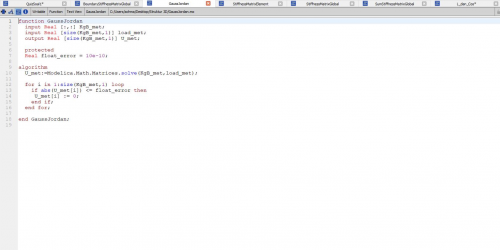
| + | Lalu hasil dari KG total yang diberi boundary dimasukkan ke persamaan gauss jordan yang dimana function dari gauss jordan menggunakan function bawaan dari open modelica | ||
| + | |||
| + | [[File:metnumbagir10.png|500px]] | ||
| + | |||
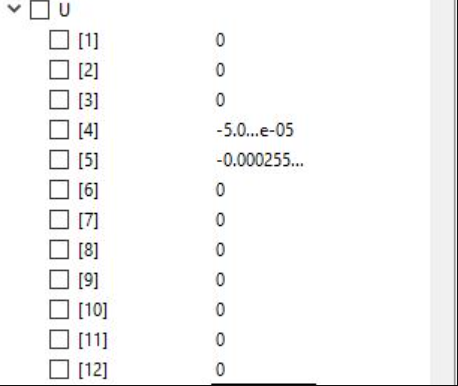
| + | Dan berikut adalah hasil displacement nya | ||
| + | |||
| + | [[File:metnumbagir11.png|500px]] | ||
| + | |||
| + | == Pertemuan 6 == | ||
| + | Pada pertemuan ini pak Dai meminta kami untuk melakukan muhasabah terhadap hasil pembelajaran kami selama kelas Metode Numerik bersama Pak Dai. | ||
| + | |||
| + | Menurut saya sendiri selama belajar metode numerik setelah uts saya merasa masih belum baik, pada pertemuan -pertemuan awal saya merasa masih dapat memahami arahan dan pelajaran yang diberikan oleh pak Dai terkait dengan penggunaan aplikasi-aplikasi yang dapat membantu kita dalam menyelesaikan metode numerik. Dalam hal ini aplikasi yang sering dipakai yaitu Open Modelica dan juga pernah memekai CFDSOF untuk menyelesaikan masalah seperti menghitung defleksi pada batang dengan cara melakukan coding sederhana, dimana saya mengikuit petunjuk sesuai buku pedoman yang diberikan oleh pak Dai, disitu diberikan contoh memakai aplikasi Open Modelica ketika kita sudah tahu kekauan dari batang itu sendiri,tetapi pada saat diberikan soal quiz untuk dapat menghitung defleksi dan gaya reaksi batang dengan cara peng codingan yang lebih advance saya merasa belum terlalu memahami, karena bagi saya apa yang dicontohkan teman saya Ahmad dan Christo masih menjadi hal yang baru bagi saya, saya belum pernah tahu atau belajar mengenai symbol fungsi-fungsi terkait codingan di dalam aplikasi khususnya Open Modelica, sehingga saya masih harus lebih belajar dan mengetahui apa-apa fungsi yang harus di ketahui dan kegunaan dari masing-masing fungsi itu sendiri. | ||
| + | |||
| + | |||
| + | == Tugas Besar == | ||
| + | Dalam Tugas besar ini kami diminta untuk melakukan optimasi dalam pemilihan material dan mencari area yang optimum dalam pembuatan rangka truss dengan memvariasikan dimensi dan elastisitas material. | ||
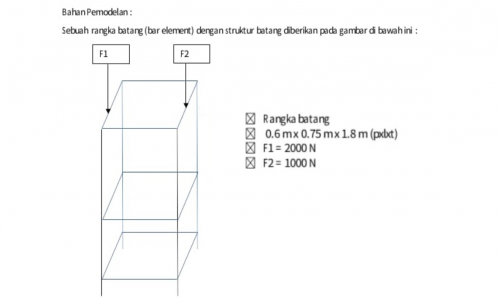
| + | Beriku adalh soalnya: | ||
| + | |||
| + | [[File:Tubesbagir1.png|500px]] | ||
| + | |||
| + | '''Asumsi''' | ||
| + | |||
| + | Dalam menyelesaikan permaslahan ini kita dapat menentukan terlebih dahulu sumsi di awal agar memudahkan kita menyelesaikan permasalahan. | ||
| + | Adapun Asumsi nya yaitu : | ||
| + | Tidak ada bending pada truss | ||
| + | Beban terdistribusi pada node | ||
| + | Safety Factor | ||
| + | Variabel bebas | ||
| + | |||
| + | '''Metodologi''' | ||
| + | |||
| + | Kita dapat memvariasikan variabel bebas yaitu dengan, mengasumsikan elastisitas konstan dengan memvariasikan ukuran dari material yang kita asumsikan. dan kita dapat mengasumsikan area yang konstan dan memvariasikan elastisitas dari beberapa material. | ||
| + | |||
| + | |||
| + | '''Elasticity Locked''' | ||
| + | |||
| + | Kita mengasumsikan elastisitas yang konstan dan memvariasikan ukuran dari material yang datanya kita dapat dari internet dan kita masukkan ke excel. | ||
| + | |||
| + | [[File:Tubesbagir2.png|500px]] | ||
| + | |||
| + | Kemudian setelah itu kita dapat mencari nilai stress,safety factor dan membantu dalam curve fitting untuk mendapatkan coefisien dengan melakukan komputasi di Open modelica dengan function yang diajarkan oleh josiah dan Fahmi. Dimana X adalah area dan Y adalah harga. | ||
| + | Adapun Komputasi nya yaitu: | ||
| + | model tugasbesar | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=250e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=200e9; //Elasticity ASTM A 36 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | |||
| + | end tugasbesar; | ||
| + | |||
| + | Untuk Function Curve Fitting nya yaitu | ||
| + | function Curve_Fitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); | ||
| + | end Curve_Fitting; | ||
| + | |||
| + | Kemudian untuk kelas curve fitting nya yaitu | ||
| + | |||
| + | [[File:Tubesbagir4.png|500px]] | ||
| + | |||
| + | dan akan didapati Koefisiennya yaitu: | ||
| + | |||
| + | [[File:Tubesbagir5.png|500px]] | ||
| + | |||
| + | dan kemudian kita masukkan ke excel untuk mencari nilai total cost setelah fitting,stress, safety factor, ratio dan berikut hasilnya: | ||
| + | |||
| + | [[File:Tubesbagir6.png|500px]] | ||
| + | |||
| + | Setelah kita dapat semua variabel kemudian kita bandingkan cost per fitting dengan ratio dan berikut chart yang saya dapatkan | ||
| + | |||
| + | [[File:chartbagir.png|500px]] | ||
| + | |||
| + | |||
| + | '''Area Locked''' | ||
| + | |||
| + | Pada Area locked kita memvariasikan elastisitas dari beberapa material dalam area yang sama, yang data nya kita dapat dari internet kemudian kita masukkan ke dalam excel. | ||
| + | |||
| + | [[File:Tubesbagir2.png|500px]] | ||
| + | |||
| + | == UAS == | ||
| + | NO.1 | ||
| + | |||
| + | [[File:UASbagir1.jpg]] | ||
| + | |||
| + | NO.2 | ||
| + | |||
| + | [[File:UASbagir2.jpg]] | ||
| + | |||
| + | No.3 | ||
| + | |||
| + | [[File:UASbagir3.jpg]] | ||
| + | |||
| + | |||
| + | No.4 | ||
| + | |||
| + | [[File:UASbagir4.jpg]] | ||
| + | |||
| + | |||
| + | No.5&6 | ||
| + | |||
| + | [[File:UASbagir5&6.jpg]] | ||
| + | |||
| + | No.7 | ||
| + | |||
| + | [[File:UASbagir7.png]] | ||
| + | |||
| + | [[File:UASbagir8.png]] | ||
Latest revision as of 02:36, 14 January 2021
Assalamualiakum Wr. Wb. Berikut adalah Page saya untuk kelas Metnum 03
Contents
BIODATA
Nama : Muhammad Bagir Alaydrus
NPM : 1806233373
TTL : Jakarta, 8 Oktober 2000
Jurusan : Teknik Mesin
Pertemuan 1
Assalamualaikum Wr. Wb, Metode numerik merupakan teknik penyelesaian permsalahn yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik. Jikapun terdapat penyelesaiannya secara analitik, proses penyelesaiaannya sering kali cukup rumit dan memakan banyak waktu sehingga tidak efisien.
Terdapat keuntungan dan kerugian terkait penggunaan metode numerik. Keuntungan dari metode ini antara lain:
. Solusi persoalan selalu dapat diperoleh.
. Dengan bantuan komputer, perhitungan dapat dilakukan dengan cepat serta hasil yang diperoleh dapat dibuat sedekat mungkin dengan nilai sesungguhnya.
. Tampilan hasil perhitungan dapat disimulasikan.
Adapun kelemahan metode ini antara lain:
. Nilai yang diperoleh berupa pendekatan atau hampiran.
. Tanpa bantuan komputer, proses perhitungan akan berlangsung lama dan berulang-ulang.
Menentukan Akar-Akar
Ada beberapa metode yang dapat digunakan untuk menyelesaikan suatu persamaan. Metode ini merupakan penyelesaian perkiraan, tetapi lebih sistematis untuk menghitung akar-akar persamaan. Dalam metode numerik, pencarian akar f(x)=0 dilakukan secara lelaran (iteratif). Secara umum, semua metode pencarian akar dapat dikelompokkan menjadi 2 golongan besar :
• Metode Tertutup
Metode yang termasuk ke dalam golongan ini mencari akar di dalam selang [a,b]. Selang [a,b] sudah dipastikan berisi minimal satu buah akar, karena itu metode jenis ini selalu berhasil menemukan akar. Dengan kata lain, lelarannya selalu konvergen (menuju) ke akar, karena itu metode tertutup kadang-kadang dinamakan juga metode konvergen.
Metode yang termasuk dalam golongan ini antara lain :
a. Metode Biseksi atau Metode Setengah Interval ini merupakan Metode dengan bentuk paling sederhana diantara beberapa metode yang akan dipelajari.
b. Metode Regula Falsi atau Metode Interpolasi Linier adalah metode mudah tapi tidak efisien. Untuk mendapatkan hasil yang mendekati nilai eksak diperlukan langkah iterasi yang cukup panjang. Metode Regula Falsi dapat menutup kekurangan itu. Metode Regula Falsi didasarkan pada interpolasi antara dua nilai dari fungsi yang mempunyai tanda berlawanan
• Metode Terbuka
Yang diperlukan pada metode ini, adalah tebakan awal akar, lalu dengan prosedur lelaran, kita menggunakannya untuk menghitung hampiran akar yang baru. Pada setiap lelaran, hampiran akar lama yang dipakai untuk menghitung hampiran akar yang baru. Mungkin saja hampiran akar yang baru mendekati akar sejati (konvergen), atau mungkin menjauhinya (divergen). Karena itu, metode terbuka tidak selalu berhasil menemukan akar, kadang-kadang konvergen, kadangkala ia divergen.
Metode yang termasuk dalam golongan ini antara lain :
a. Metode Newton Raphson,Metode ini paling banyak digunakan dalam mencari akar-akar dari suatu persamaan.Metode ini menggunakan metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.
b. Metode Secant,Kekurangan Metode Newton Raphson adalah diperlukannya turunan pertama (differensial) dari f(x) dalam hitungan. Kadang-kadang sulit untuk mendiferensialkan persamaan yang diselesaikan. Untuk itu maka bentuk diferensial didekati dengan nilai perkiraan berdasarkan diferensial beda hingga.
c. Metode Iterasi,Dalam metode iterasi ini digunakan suatu persamaan untuk memperkirakan nilai akar persamaan. Persamaan tersebut dikembangkan dari fungsi f(x) = 0 sehingga parameter x berada disisi kiri dari persamaan, yaitu :
X= g(x)
Persamaan ini menunjukkan bahwa nilai x merupakan fungsi dari x, sehingga dengan memberi nilai perkiraan awal dari akar dapat dihitung perkiraan baru dengan rumus iteratif berikut :
Xi+1 = g ( xi )
Besar kesalahan dihitung dengan rumus berikut :
∈a = | (Xi+1 – Xi )/(Xi+1 ) | X 100%
Regresi Linier
Regresi merupakan alat ukur yg digunakan untuk mengetahui ada tidaknya korelasi antarvariabel. Analisis regresi lebih akurat dlm analisis korelasi karena tingkat perubahan suatu variabel terhdp variabel lainnya dpt ditentukan). Jadi pada regresi, peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula.
Regresi linier adalah regresi yang variabel bebasnya (variabel X) berpangkat paling tinggi satu. Utk regresi sederhana, yaitu regresi linier yg hanya melibatkan dua variabel (variabel X dan Y).
Y = a + bX
Keterangan :
Y = variabel terikat
X = variabel bebas
a = intersep / konstanta
b = koefisien regresi / slop
Persamaan regresi linear di atas dpt pula dituliskan dlm bentuk :
Turunan Numerik
Ini digunakan untuk menentukan nilai turunan fungsi f yang diberikan dalam bentik tabel. Ada 3 pendekatan zalm menghitung Turunan Numerik :
1. Hampiran selisih-maju (forward difference approximation)
2. Hampiran selisih-mundur (backward difference approximation)
3. Hampiran selisih-pusat (central difference approximation)
Video contoh openmodelica
Sebelumnya saya memohon maaf atas keterlambatan membuat video dikarenakan kesalahan saya, pada contoh pengaplikasian modelica ini saya mengambil referensi dari youtube
link: https://www.youtube.com/watch?v=Dw66ODbMS2A
Mengenai Feedback PID control system dimana video penjelasan saya lampirkan dibawah
link: https://youtu.be/x5l8KyqMPqQ
Pertemuan 2
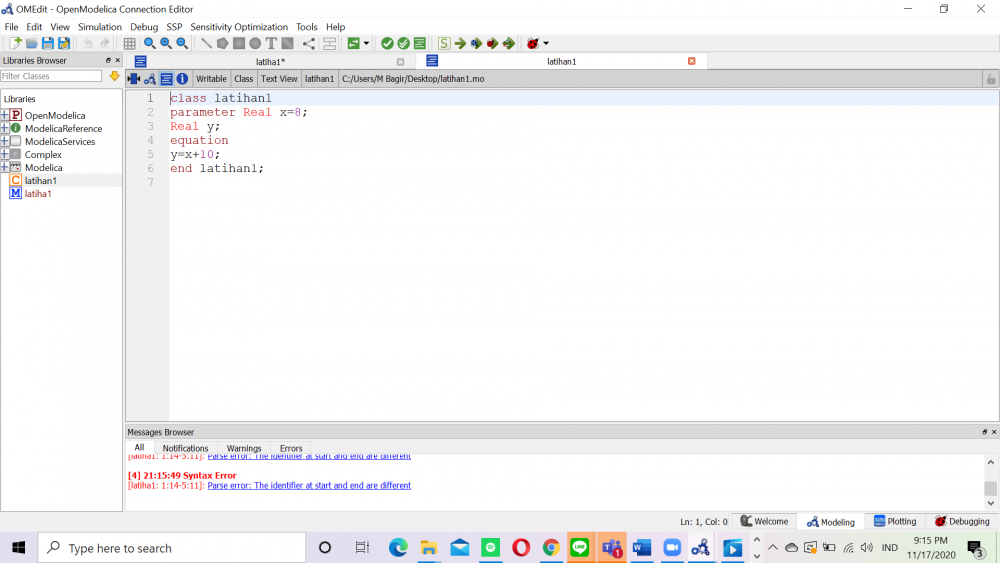
Pada pertemuan 2 kali ini saya tidak masuk kelas dikarenakan ada suatu keperluan diluar,namun saya tetap mencoba untuk melakukan simulasi di modelica seperti yang disuruh oleh Pak Dai, saya mencoba melakukan persamaan sederhana yaitu menjumlahkan 10 dengan suatu variabel x yang saya beri nilai 8, langkah pertama yaitu kita menulis nama class kemudian kita menulis parameter, karena kita hanya mencoba persamaan sederhana sehingga parameter yang saya tulis yaitu "x=8" dan parameter lain yaitu "y", kemudian setelah itu saya menuliskan equation nya yaitu y= x + 10
kemudian setelah itu kita dapatkan hasil dari simulasi di bagian plotting dengan variabel x dan y yang kita dapat plot ke diagram, sehingga ini memudahkan kita dalam melihat hasilnya jika kita menggunakan persamaan yang lebih sulit
Kemudian teman-teman juga melakukan persamaan sederhan dengan mencari mean.
dan di akhir pak Dai juga memberikan PR untuk melakukan Buat class dengan type function untuk menyelesaikan persamaa2n aljabar simultan (metoda gauss elim, gauss seidel ataupun metoda lain) ... Dan sebuah class untuk menjalankan fungsi tersebut.
Pr 2
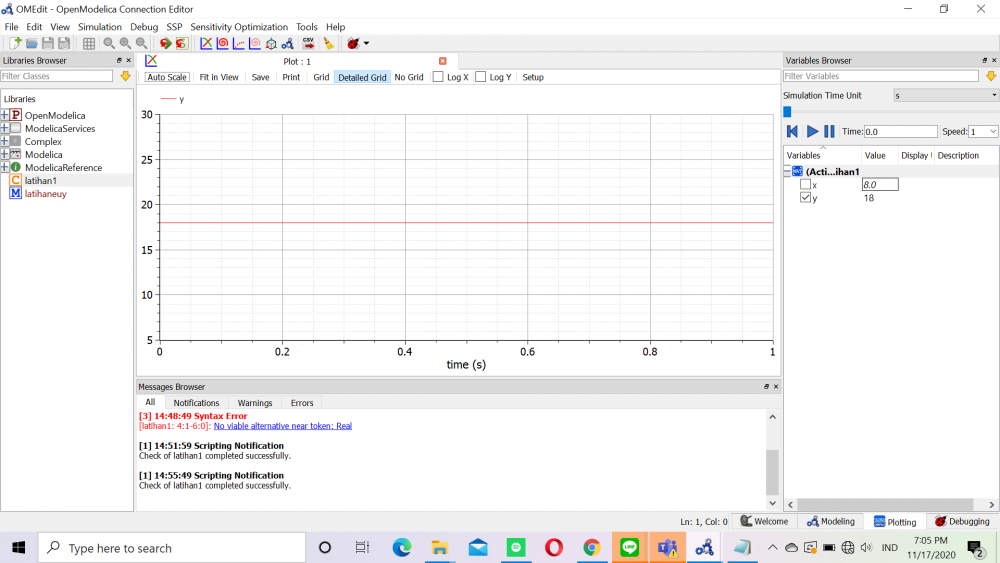
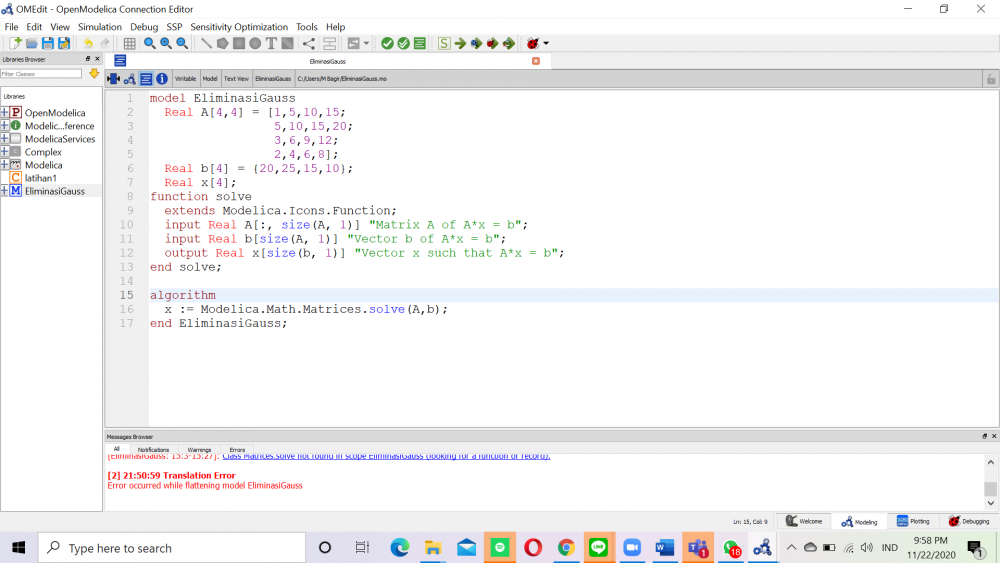
Pada Pr kali inii saya mencoba openmodelica dengan mensimulasikan persamaan aljabar simultan, saya mengambil contoh dengan mensimulasikan persamaan aljabar 4 Variabel dengan 4 persamaan. aljabar simultan adalah metode penyelesaian persoalan matematik yang melibatkan kekompleksan yang sangat rumit sehingga memerlukan cara penyelesaian yang membuatnya simple dengan menggunakan tools yang ada, seperti komputer dengan program visual basic, matlab atau lainnya.
beberapa metode yang terdapat pada aljabar simultan ialah :
1. metode Eliminasi Gauss
2. metode Cramer
3. Gauss seidel
4. Gauss – jordan
Yang mana saya mencoba salah satu metode diatas yaitu dengan menggunakan eliminasi Gauss di OpenModelica.Saya mengambil refernsi dari https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html
Adapun persamaan yang saya buat adalah:
x1+ 5x2 + 10x3 +15x4 = 20
5x1+ 10x2 + 15x3 + 20x4 = 25
3x1+ 6x2+ 9x3+ 12x4 = 15
2x1+ 4x2 + 6x3 + 8x4 = 10
Kemudian setelah saya tulis di OpenModelica menjadi:
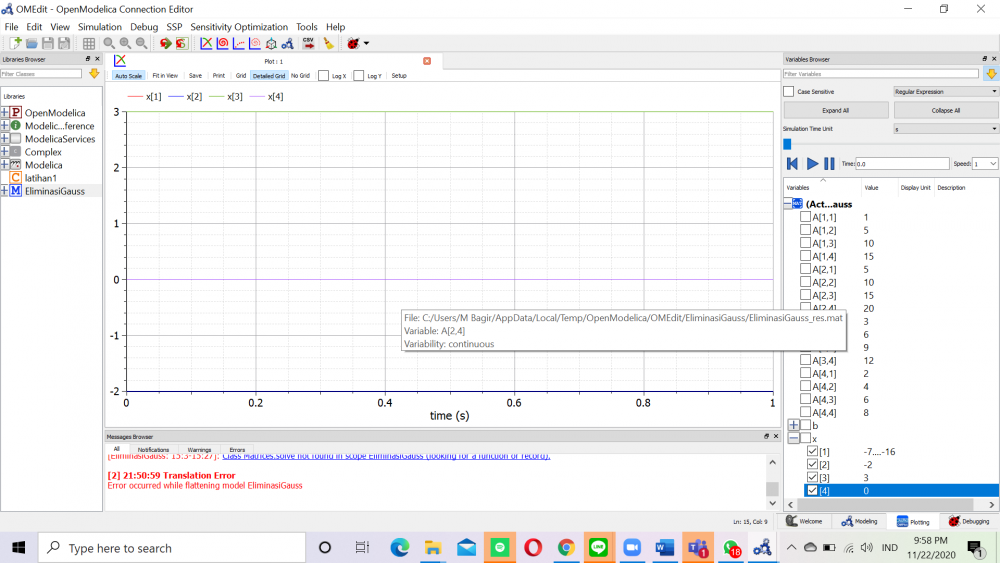
Dan setelah itu saya mensimulasikannya dan didaptkan plot seperti:
Dimana didapatkan hasil yaitu
x1 = -7e-16
x2 = -2
x3 = 3
x4 = 0
Pertemuan 3
Pak Dai menjelaskan alur pemecahan masalah teknik menggunakan metode numerik.
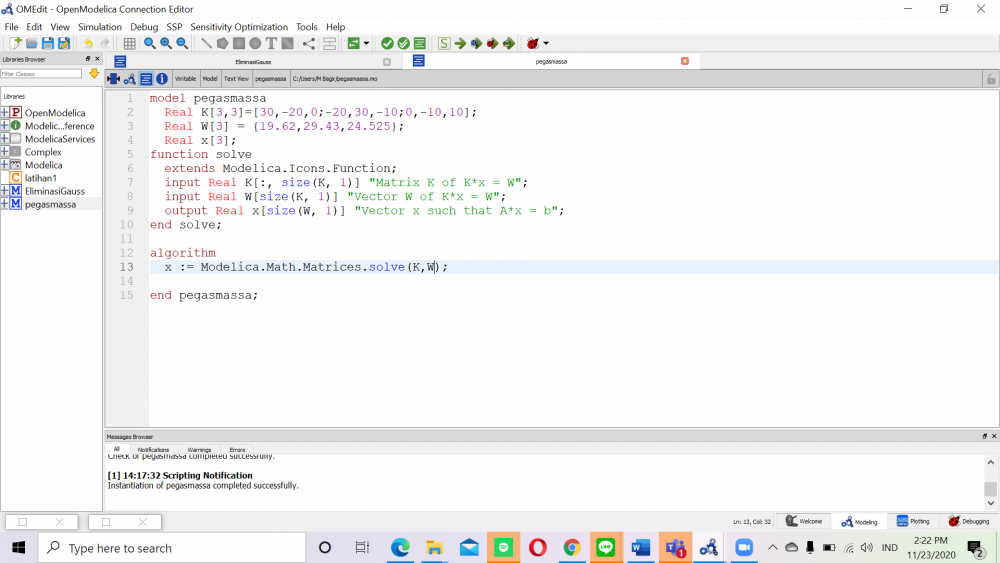
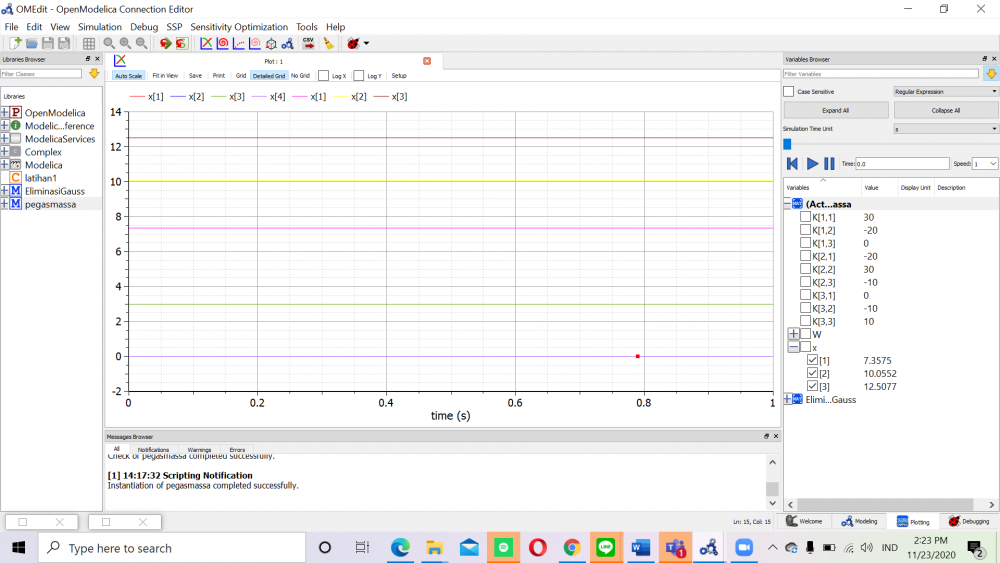
Yaitu yang pertama yaitu masalah teknik - kemudian analasis masalah - model matematis - model numerik - komputer - kemudian mendapatkan Solusi. Dimana dibahas kali ini permasalahan tekniknya berupa sistem pegas massa yang ada di chapter 12.4. dimana persamaanya dapat dilihat dibuku dan berikut ketika saya memasukan ke OpenModelica.
Setelah itu saya melakukan simulasi dan didapatkann x yang sama seperti dibuku yaitu x1 = 7,36 , x2 = 10,06 , x3 = 12,51
Tugas 3
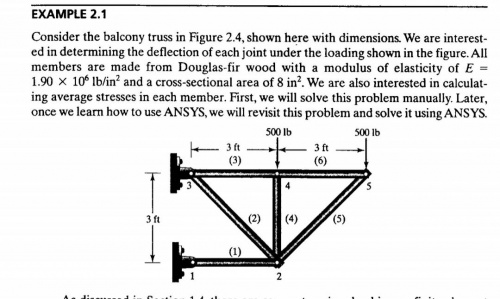
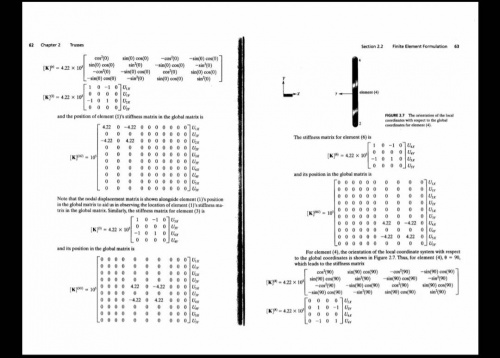
Pada tugas 3 ini kami diminta mengerjakan soal di contoh 2.1 pada buku yang pak Dai berikan. adapun soalnya yaitu
Kemudian untuk menyelesaikan soal ini kita dapat mengerjakanannya dengan beberapa langakh penyelesaiaan.
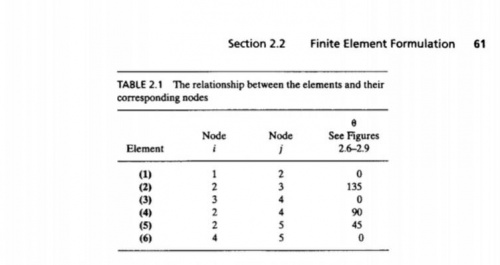
Yang Pertama yaitu mengubah soal ke bentuk node dan elemen
Kemudian menentukan nilai konstata stiffness constannya dari elemen
Kemudian membuat persamaan elemen ke bentuk matriks untuk kekakuan batang yaitu seperti:
Kemudian menggabungkan matriks elemen-elemennya
sehingga dengan menerapkan kondisi batas dan beban dapat diketahui:
-Kondisi batas untuk node 1 dann 3 adalah fixed
-external force pada node 4 dan 5
Dengan menerapkan hk. Hooke didapatkan:
Kemudian untuk mencari solusi dari persamaan matriks nya kita menggunakan OpenModelica
Kemudian didapatkan plotting yaitu:
Kemudian kita dapat menentukan gaya reaksi dapat ditemukan dengan persamaan:
berikut ketika di OpenModelica:
dan ini hasil plottingnya:
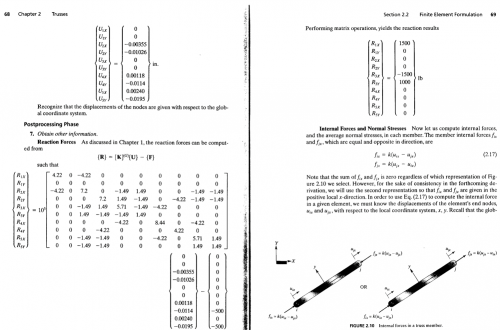
Kemudian setelah itu kita dapat menghitung gaya internal dan normal stress
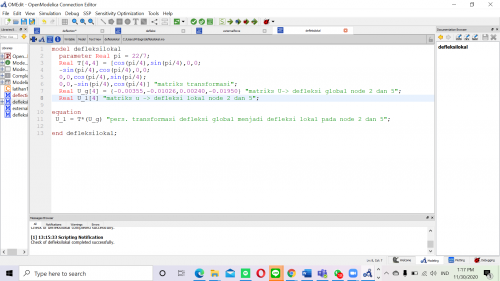
Untuk menghitung normal stress, perlu dilakukan transformasi dari hasil defleksi ditinjau dari koordinat global menjadi transformasi lokal, berikut adalah persamaan yang dapat digunakan
Misalkan kita menganalisis stress pada elemen 5, maka node yang dianalisis adalah node 2 dan 5 Sehingga persamaan matriks defleksi pada koordinat lokal menjadi
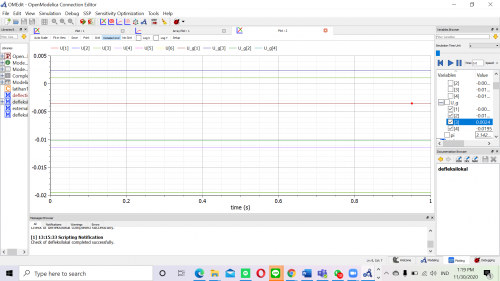
dan ini kertika di OpenModelica
dan berikut hasil plottingnya
dimana didapatkan U2x=-0.00976 inchi dan U6x=-0.01209 inchi
sehingga didapat internal force pada elemen 5 sebesar 696lb.
sehingga didapat normal stress pada elemen 5 sebesar 87lb/in^2
Pertemuan 4
Pada pertemuan ini pak Dai menjelaskan tentang perbedaan pembebanan statik dan dinamik, dari yang saya tangkap perbedaannya yaitu pada pembebanan statik bebannya tidak berubah terhadap waktu namun kalau pembebanan dinamik berubah terhdapa waktu.
kemudian pak Dai juga emnjelaskan manfaat metode numerik untuk persoalan2 teknik, yaitu untuk membantu kita menyelesaikan masalah-masalah dari pemodelan matematis yang rumit diselesaikan dengan pemodelan numerik, namun kita juga harus mengetahui dari mana model matematisnya berasal karena itu adalah dasar untuk kita dapat memahami metode numerik, dan saya sendiri merasa belum terlalu memahami terutama pada pemodelan untuk kasus defleksi pada batang.
dan di akhir kelas pak Dai memberikan soal untuk diselesaikan flow chartnya,adapun jawabannya yaituu
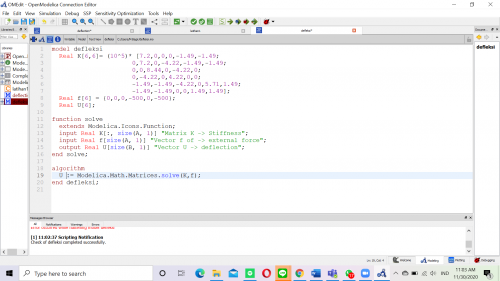
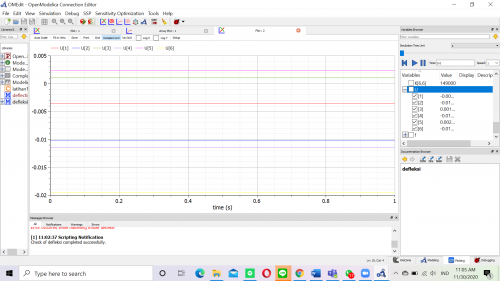
Tugas 4
Dalam tugas ini, saya diminta untuk mencari matrix displacement dimana U = {U1x, U1y, U1z,..., Unx, Uny, Unz} ; matrix gaya reaksi dimana R = {R1x, R1y, R1z,...,Rnx, Rny, Rnz}; dan matrix gaya total pada sumbu x, y, dan z dan berikut merupakan coding yang saya lakukan didalam OpenModelica
Pertemuan 5
Pada pertemuan 5 ini beberapa teman saya menjelaskan mengenai cara mereka menyelesaikan soal quiz yang lalu menggunakan OpenModelica, edo menyelesaikan persamaan di Open Modelica setelah mendapat Konstata kekakuan baru memsukkan matriksnya, namun kata pak Dai kita akan kesusahan jika variabel nya semakin banyak sehingga diperlukan codingan yang lebih dasar lagii. kemudian edo menjelaskan wiki punya josiah tentang tugas minggu lalu, Memet menjelasakan flow chart yang dia buat dimana pertama dia mencari K lokal kmudian mencari K global kemudian mencari matriks global yang bisa mendapatkan U atau defleksi dan kemudian kita dapat mencari reaction forcenya. Step 2 input matriks lokal yang sudah ada kemudian input node dan elemen dan akan mendapatkan matriks glogabl, pada step ke 5 kita mengeliminasi KGB untuk mencari displacement disini juga harus menggunakan floating error, perbedaan 2 dan 3 dimensi hanya berbeda di persamaan matriks lokal dan global dan boundary global. DI openmodelica nya dia membuat 6 funtion/class agar tidak perlu banyak input di satu kelas,Lalu ahmad menjelaskan mengenai flowchart yang dia telah buat ahmad juga menjelaskan mengenai tahapan untuk menyelesaikan soal. Berikut tahapan yang Ahmad jelaskan :
1.Solve stiffness
2.Membuat dan menyelesaikan Matrix global dari setiap elemen
3.Mengimplementasikan boundary condition, kemudian didapatkan U.
Kemudian pak Dai memberikan kami tugas mengenai pembahasan oleh saudara Ahmad Mohammad Fahmi tentang kodingan yang dibuat olehnya mengenai kuis nomer 4 dan 8. Untuk membantu pembelajaran kami, Ahmad memberikan video rekaman tutorial yang berisi diskusi pada link dibawah ini :
https://drive.google.com/file/d/1n0zvwmn-3G4DWYCSPD48-Xfrp9_kT3R0/view?usp=sharing
Dalam video tersebut Ahmad menjelaskan tenting kodingan yang dia buat.
1.Untuk mengerjakan nomer 4, Ahmad membuat beberapa function yang nanti akan digunakan dan 1 class untuk membuat penyelesaian atas soal yang diberikan. Pada class, Saudara ahmad memasukkan parameter REAL (inisiasi) yang berisi element, theta, A, E, L.
2.Kemudian kita menginput node - node yang ada dengan memasukkan matriks dengan parameter integer. Pada parameter integer kita memanggil matriks inisiasi pada kolom satu untuk di sesuaikan dengan node-node yang bersangkutan.
3.Lalu kita masukan jumlah node yaitu n=4 dan Boundaries pada node. Boundaries pada node ini yaitu pada titik 1 dan 3 karena mereka merupakan tumpuan. Setelah itu, kita memasukkan load dengan menginput parameter real (2*n). Kita mengalikan n dengan 2 karena disini gaya ada 2 arah yaitu x dan y.
4.Sesudah mengisi load, kita menginput equation dengan fungsi-fungsi yang sudah dibuat juga pada function oleh Ahmad.
Pembahasan dari function :
1.Lihat terlebih dahulu dari function stiffnessmatrixelement.
2.Input matriks inisiasi (:,5) dan outputnya adalah matriks dari Ke yang tadi ada pada equation pada class
3.Gunakan protected maka parameter dapat dipanggil. Fungsinya adalah agar kita bisa memasuki parameter tanpa harus menulis ulang pada function dengan memanggil parameter pada Class
4.Parameter yang kita ambil untuk Ke adalah Theta, StiffTrig, Stifftrans, k_vec, dan Floating error\
Tugas 5
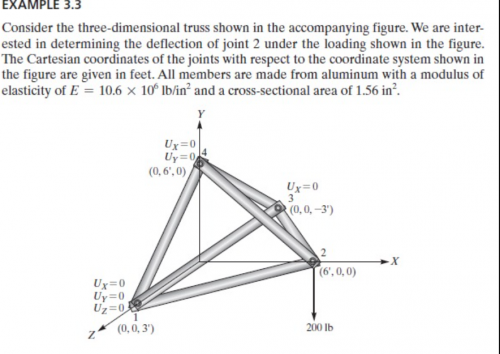
Berikut adalah soal yang diberikan moleh pak Dai
Diketahui pada soal diatas,tahapan pertama kita harus mencari sudut cos x ,cos y ,cos z dan L pada gambar tersebut.Disini saya membuat class khusus untuk mendapatkan nilai - nilai yang dicari diatas di dalam OpenModelica
Setelah kita mendapatkan sudut cos x ,cos y ,cos z dan L melalui class diatas kita masukkan hasilnya ke dalam class dan function yang diajarkan oleh ahmad muhammad fahmi yaitu 1 class dengan 6 fungsi pembantunya
Pada soal ini boundarynya sangat berbeda dikarenakan setiap batangnya ada yang dapat menjadi fix di sumbu xyz,xy,dan x setelah itu tahap kedua ialah kita mencari K lokal di setiap elmentnya dengan fungsi berikut
Setelah mendapatkan K lokal sebagai variabel baru kita harus menempatkan K lokal ke K global agar nantinya bisa di satukan menjadi K global total dengan fungsi
pada fungsi diatas menghasilkan KG1,KG2,KG3,KG4,KG5 dan KG6 dapat dilihat pada hasil ditandai oleh kg yang dimana (melambangkan elment berapa,baris keberapa,kolom keberapa) Setelah itu kita menjumlahkan KG1 sampai KG6
Setelah itu kita mendapatkan KG total yang digunakan untuk mencari displacement dan Reaction force dari gambar diatas,tetapi sebelum memasukkan kesana kita harus memberi batasan yang dimana pada soal ini pada node 1 sumbu XYZ = 0,pada node 4 XY = 0 dan pada node 3 X = 0 tetapi saya menggunakan fungsi yang diberikan oleh fahmi untuk mengerjakan soal nomor 8 yang dimana dianggap pada node 1,3,4 ialah 0
Lalu hasil dari KG total yang diberi boundary dimasukkan ke persamaan gauss jordan yang dimana function dari gauss jordan menggunakan function bawaan dari open modelica
Dan berikut adalah hasil displacement nya
Pertemuan 6
Pada pertemuan ini pak Dai meminta kami untuk melakukan muhasabah terhadap hasil pembelajaran kami selama kelas Metode Numerik bersama Pak Dai.
Menurut saya sendiri selama belajar metode numerik setelah uts saya merasa masih belum baik, pada pertemuan -pertemuan awal saya merasa masih dapat memahami arahan dan pelajaran yang diberikan oleh pak Dai terkait dengan penggunaan aplikasi-aplikasi yang dapat membantu kita dalam menyelesaikan metode numerik. Dalam hal ini aplikasi yang sering dipakai yaitu Open Modelica dan juga pernah memekai CFDSOF untuk menyelesaikan masalah seperti menghitung defleksi pada batang dengan cara melakukan coding sederhana, dimana saya mengikuit petunjuk sesuai buku pedoman yang diberikan oleh pak Dai, disitu diberikan contoh memakai aplikasi Open Modelica ketika kita sudah tahu kekauan dari batang itu sendiri,tetapi pada saat diberikan soal quiz untuk dapat menghitung defleksi dan gaya reaksi batang dengan cara peng codingan yang lebih advance saya merasa belum terlalu memahami, karena bagi saya apa yang dicontohkan teman saya Ahmad dan Christo masih menjadi hal yang baru bagi saya, saya belum pernah tahu atau belajar mengenai symbol fungsi-fungsi terkait codingan di dalam aplikasi khususnya Open Modelica, sehingga saya masih harus lebih belajar dan mengetahui apa-apa fungsi yang harus di ketahui dan kegunaan dari masing-masing fungsi itu sendiri.
Tugas Besar
Dalam Tugas besar ini kami diminta untuk melakukan optimasi dalam pemilihan material dan mencari area yang optimum dalam pembuatan rangka truss dengan memvariasikan dimensi dan elastisitas material. Beriku adalh soalnya:
Asumsi
Dalam menyelesaikan permaslahan ini kita dapat menentukan terlebih dahulu sumsi di awal agar memudahkan kita menyelesaikan permasalahan. Adapun Asumsi nya yaitu : Tidak ada bending pada truss Beban terdistribusi pada node Safety Factor Variabel bebas
Metodologi
Kita dapat memvariasikan variabel bebas yaitu dengan, mengasumsikan elastisitas konstan dengan memvariasikan ukuran dari material yang kita asumsikan. dan kita dapat mengasumsikan area yang konstan dan memvariasikan elastisitas dari beberapa material.
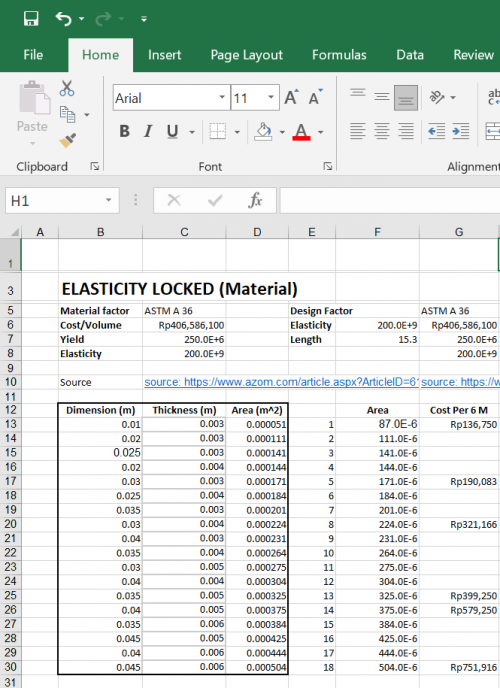
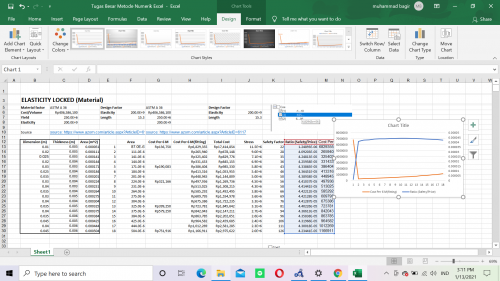
Elasticity Locked
Kita mengasumsikan elastisitas yang konstan dan memvariasikan ukuran dari material yang datanya kita dapat dari internet dan kita masukkan ke excel.
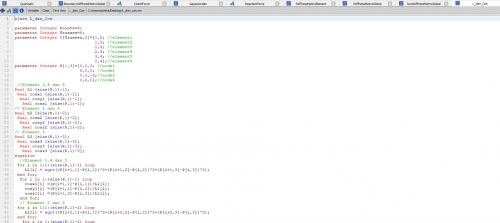
Kemudian setelah itu kita dapat mencari nilai stress,safety factor dan membantu dalam curve fitting untuk mendapatkan coefisien dengan melakukan komputasi di Open modelica dengan function yang diajarkan oleh josiah dan Fahmi. Dimana X adalah area dan Y adalah harga. Adapun Komputasi nya yaitu: model tugasbesar
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=250e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=200e9; //Elasticity ASTM A 36 (Pa)
//define connection parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for;
end tugasbesar;
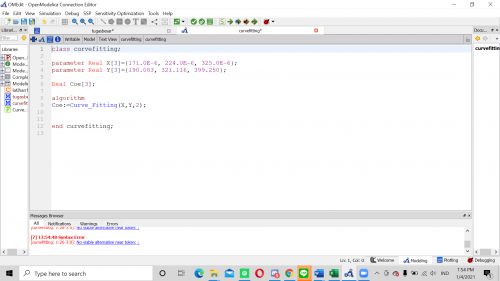
Untuk Function Curve Fitting nya yaitu function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected
Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for;
ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting;
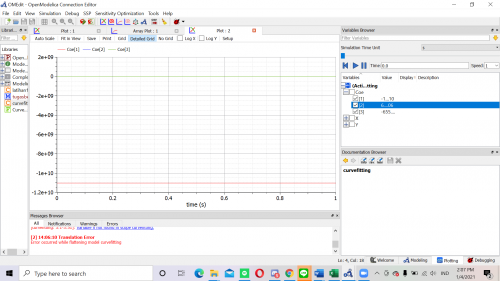
Kemudian untuk kelas curve fitting nya yaitu
dan akan didapati Koefisiennya yaitu:
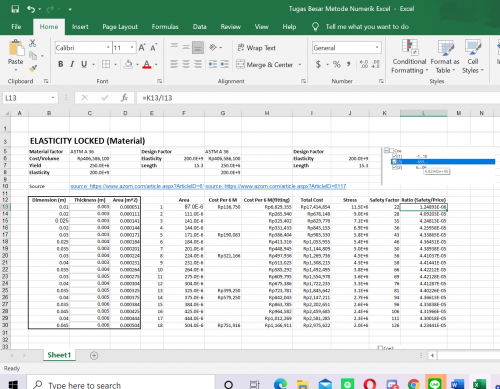
dan kemudian kita masukkan ke excel untuk mencari nilai total cost setelah fitting,stress, safety factor, ratio dan berikut hasilnya:
Setelah kita dapat semua variabel kemudian kita bandingkan cost per fitting dengan ratio dan berikut chart yang saya dapatkan
Area Locked
Pada Area locked kita memvariasikan elastisitas dari beberapa material dalam area yang sama, yang data nya kita dapat dari internet kemudian kita masukkan ke dalam excel.
UAS
NO.1
NO.2
No.3
No.4
No.5&6
No.7