Difference between revisions of "Metnum03-Yudho Wicaksono"

From ccitonlinewiki
Jump to: navigation, search
 
(16 intermediate revisions by the same user not shown)
Line 4: Line 4:
 
NPM  : 1706070690
 
NPM  : 1706070690
  
−
Tugas 3
+
----
 +
 
 +
'''Pertemuan ke-1'''
 +
 
 +
Pertemuan pertama pada kelas metode numerik dengan Pak Dai saya diminta untuk menginstall aplikasi OpenModelica. Fungsi dari aplikasi ini untuk mensimulaikan suatu sistem yang didistribusikan dalam bentuk kode dan biner untuk penelitian. Pada pertemuan tersebut Pak Dai belum menjelaskan menggunakan aplikasi tersebut secara dalam, melainkan Pak Dai meminta mahasiswa untuk mereview kembali materi yang sudah diajarkan sebelum UTS, dan juga mencari fenomena apa saja yang pernah dilakukan dan dapat diaplikasikan dengan metode numerik.
 +
 
 +
----
 +
 
 +
'''Pertemuan Ke-2'''
 +
 
 +
[[File:Om1bm.jpg]]
 +
 
 +
[[File:Om2bm.jpg]]
 +
 
 +
[[File:Om3bm.jpg]]
 +
 
 +
----
 +
 
 +
'''Pertemuan ke-3'''
 +
 
 +
Pertemuan kali ini membahas tentang aplikasi metnum dalam permasalahan teknik.Contoh yang kita ambil yaitu bagaimana penyelesaian masalah teknik dalam Pegas-massa menggunakan Openmodelica
 +
 
 +
[[File:Metnumnaufal9.png]]
 +
 
 +
Pertama kita buat matriksnya dari persamaan yang ada kemudian kita masukan juga Fuction nya;
 +
 
 +
input Real K[:, size(K, 1)];
 +
input Real W[size(K, 1)] ;
 +
output Real x[size(W, 1)] ;
 +
 
 +
Setelah itu kita masukan juga algoritma x:=Modelica.Math.Matrices.solve(K,W) dan simulate untuk mecari X
 +
 
 +
[[File:Metnumnaufal10.png]]
 +
 
 +
[[File:Metnumnaufal11.png]]
 +
 
 +
----
 +
 
 +
'''Tugas 3'''
 +
 
 
Menyelesaikan yang diberikan oleh Pak Dai menggunakan OpenModelica
 
Menyelesaikan yang diberikan oleh Pak Dai menggunakan OpenModelica
−
[[File:Soal.jpg]]
+
 
 +
[[File:Soal Tugas 3.jpg]]
  
 
[[File:REAKSI.jpg]]
 
[[File:REAKSI.jpg]]
Line 15: Line 55:
  
 
[[File:DEFLEKSI.jpg]]
 
[[File:DEFLEKSI.jpg]]
 +
 +
----
 +
 +
 +
----
 +
'''Quiz 1'''
 +
 +
[[File:soal quiz.jpg]]
 +
 +
Dapat diselesaikan dengan langkah-langkah berikut
 +
 +
[[File:Langkah.jpg]]
 +
 +
----
 +
 +
'''Pertemuan ke-5'''
 +
 +
----
 +
 +
'''Pertemuan ke-6'''
 +
 +
----
 +
 +
'''Tugas Besar'''
 +
 +
Tugas besar kami diminta untuk mencari optimasi pemilihan material untuk rangka berikut. Optimasi pemilihan material bergantung kepada 2 hal yaitu optimasi elastisitas dan luas penampang.
 +
 +
[[File:Tugas Besar Metnum Geometri Jos.jpg]]
 +
 +
Dari soal diminta untuk mencari 1.)Material pada struktur tersebut yang paling optimal yang terbuat dari besi siku; dan 2.)Membandingkan optimasi material dan optimasi luas penampang. Struktur pada kasus ini memiliki dimensi 0.6m x 0.75m x 1.8m. Pada bagian atas diberikan gaya F1 : 2000 N dan F2 : 1000 N yang memengaruhi struktur.
 +
 +
F1 dan F2 terdistribusi pada point penghubung pada struktur dan struktur memiliki sifat truss.
 +
 +
 +
 +
model Trusses_3D_Tugas_Besar_Safety
 +
 +
//define initial variable
 +
parameter Integer Points=size(P,1); //Number of Points
 +
parameter Integer Trusses=size(C,1); //Number of Trusses
 +
parameter Real Yield=215e6; //Yield Strength (Pa)
 +
parameter Real Area=0.000224;  //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
 +
parameter Real Elas=193e9;    //Elasticity SS 304  (Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=[1,5;
 +
                          2,6;
 +
                          3,7;
 +
                          4,8;
 +
                          5,6;  //1st floor
 +
                          6,7;  //1st floor
 +
                          7,8;  //1st floor
 +
                          5,8;  //1st floor
 +
                          5,9;
 +
                        6,10;
 +
                        7,11;
 +
                        8,12;
 +
                        9,10; //2nd floor
 +
                        10,11;//2nd floor
 +
                        11,12;//2nd floor
 +
                          9,12; //2nd floor
 +
                          9,13;
 +
                        10,14;
 +
                        11,15;
 +
                        12,16;
 +
                        13,14;//3rd floor
 +
                        14,15;//3rd floor
 +
                        15,16;//3rd floor
 +
                        13,16];//3rd floor
 +
                                                             
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1;    //1
 +
                      -0.3,-0.375,0,1,1,1;    //2
 +
                      -0.3,0.375,0,1,1,1;    //3
 +
                      0.3,0.375,0,1,1,1;      //4
 +
                         
 +
                      0.3,-0.375,0.6,0,0,0;  //5
 +
                      -0.3,-0.375,0.6,0,0,0;  //6
 +
                      -0.3,0.375,0.6,0,0,0;  //7
 +
                      0.3,0.375,0.6,0,0,0;    //8
 +
                           
 +
                      0.3,-0.375,1.2,0,0,0;  //9
 +
                      -0.3,-0.375,1.2,0,0,0;  //10 
 +
                      -0.3,0.375,1.2,0,0,0;  //11
 +
                      0.3,0.375,1.2,0,0,0;    //12
 +
                           
 +
                      0.3,-0.375,1.8,0,0,0;  //13
 +
                      -0.3,-0.375,1.8,0,0,0;  //14
 +
                      -0.3,0.375,1.8,0,0,0;  //15
 +
                      0.3,0.375,1.8,0,0,0];  //16
 +
                         
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,-500,
 +
                            0,0,-1000,
 +
                            0,0,-1000,
 +
                            0,0,-500};
 +
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
 +
Real stress1[Trusses];
 +
Real safety[Trusses];
 +
Real dis[3];
 +
Real Str[3];
 +
 +
protected
 +
parameter Integer N=3*Points;
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-4;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
end for;
 +
     
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                    cy*cx,cy^2,cy*cz;
 +
                    cz*cx,cz*cy,cz^2];
 +
 +
  //Transforming to global matrix
 +
  g:=zeros(N,N);
 +
  for m,n in 1:3 loop
 +
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
  end for; 
 +
 +
G_star:=G+g;
 +
G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
if P[x,4] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-2,a]:=0;
 +
    G[(x*3)-2,(x*3)-2]:=1;
 +
  end for;
 +
end if;
 +
if P[x,5] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-1,a]:=0;
 +
    G[(x*3)-1,(x*3)-1]:=1;
 +
  end for;
 +
end if;
 +
if P[x,6] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[x*3,a]:=0;
 +
    G[x*3,x*3]:=1;
 +
  end for;
 +
end if;
 +
end for;
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F;
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
end for;
 +
     
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
 
 +
  Str:=(X*dis);
 +
  stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for;
 +
 +
//Safety factor
 +
for i in 1:Trusses loop
 +
if stress1[i]>0 then
 +
  safety[i]:=Yield/stress1[i];
 +
else
 +
  safety[i]:=0;
 +
end if;
 +
end for;
 +
 +
end Trusses_3D_Tugas_Besar_Safety;
 +
 +
----
 +
 +
Jawaban UAS
 +
 +
[[File:UAS No 1 Yudho.jpg]]
 +
 +
[[File:UAS No 2 Yudho.jpg]]
 +
 +
[[File:UAS No 3 Yudho.jpg]]
 +
 +
[[File:UAS No 4 Yudho.jpg]]
 +
 +
[[File:UAS No 5 Yudho.jpg]]
 +
 +
[[File:UAS No 6 Yudho.jpg]]
 +
 +
[[File:UAS No 7a Yudho.jpg]]
 +
 +
[[File:UAS No 7b Yudho.jpg]]

Latest revision as of 22:12, 14 January 2021

Assalamualaikum Wr.Wb.

Nama : Yudho Wicaksono NPM  : 1706070690

Pertemuan ke-1

Pertemuan pertama pada kelas metode numerik dengan Pak Dai saya diminta untuk menginstall aplikasi OpenModelica. Fungsi dari aplikasi ini untuk mensimulaikan suatu sistem yang didistribusikan dalam bentuk kode dan biner untuk penelitian. Pada pertemuan tersebut Pak Dai belum menjelaskan menggunakan aplikasi tersebut secara dalam, melainkan Pak Dai meminta mahasiswa untuk mereview kembali materi yang sudah diajarkan sebelum UTS, dan juga mencari fenomena apa saja yang pernah dilakukan dan dapat diaplikasikan dengan metode numerik.

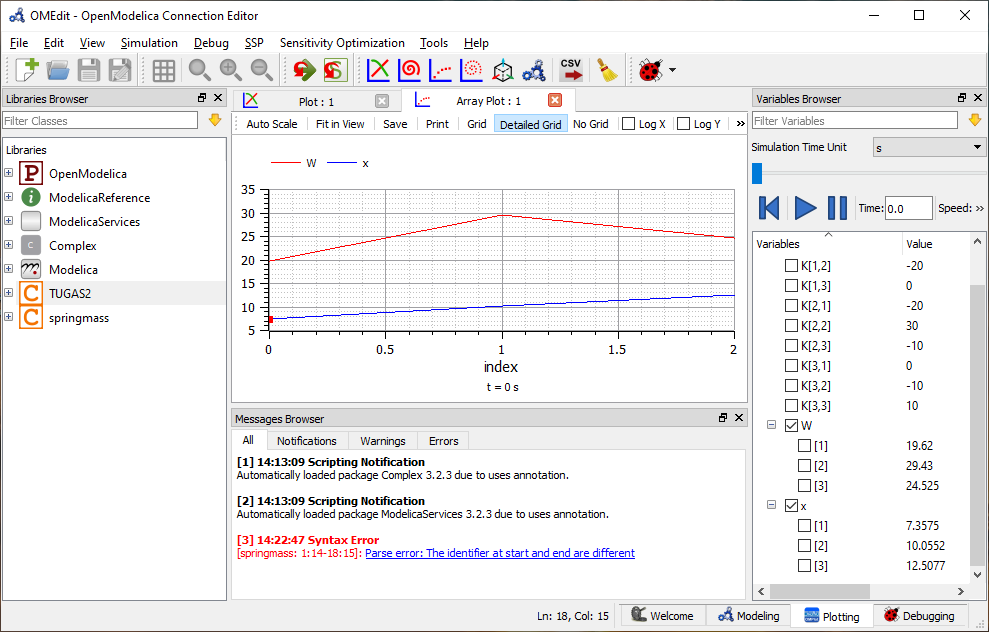
Pertemuan Ke-2

Om1bm.jpg

Om2bm.jpg

Om3bm.jpg

Pertemuan ke-3

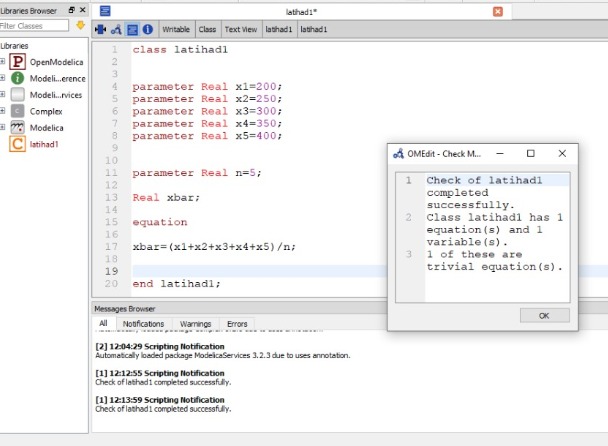
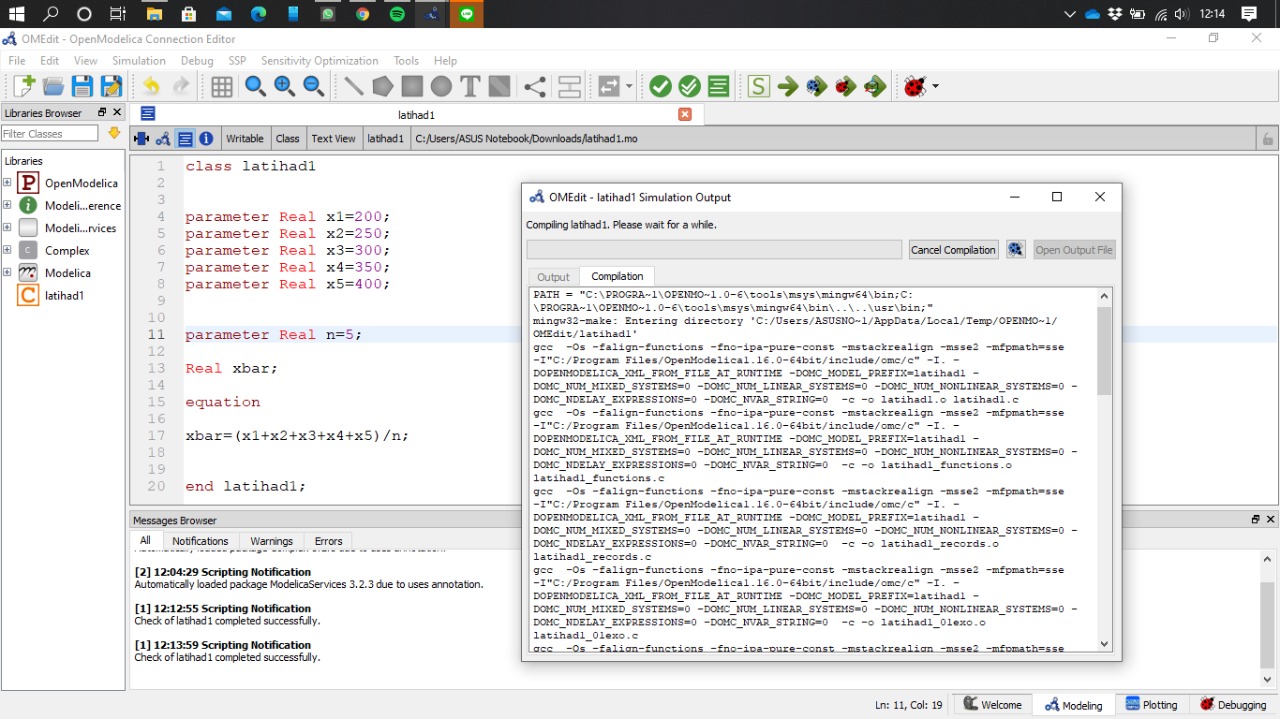
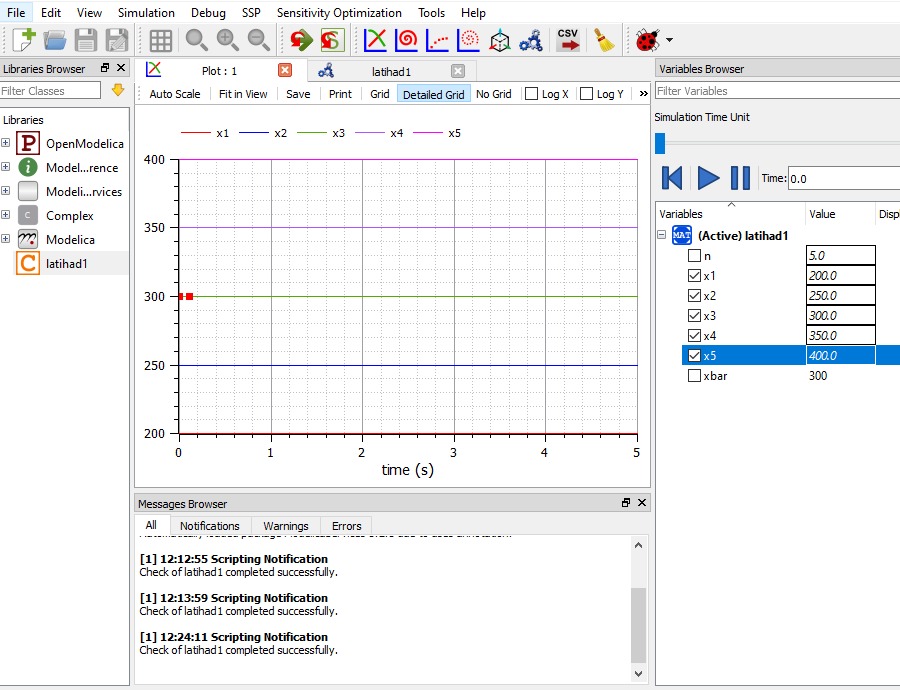
Pertemuan kali ini membahas tentang aplikasi metnum dalam permasalahan teknik.Contoh yang kita ambil yaitu bagaimana penyelesaian masalah teknik dalam Pegas-massa menggunakan Openmodelica

Metnumnaufal9.png

Pertama kita buat matriksnya dari persamaan yang ada kemudian kita masukan juga Fuction nya;

input Real K[:, size(K, 1)]; 

input Real W[size(K, 1)] ;
output Real x[size(W, 1)] ;

Setelah itu kita masukan juga algoritma x:=Modelica.Math.Matrices.solve(K,W) dan simulate untuk mecari X

Metnumnaufal10.png

Metnumnaufal11.png

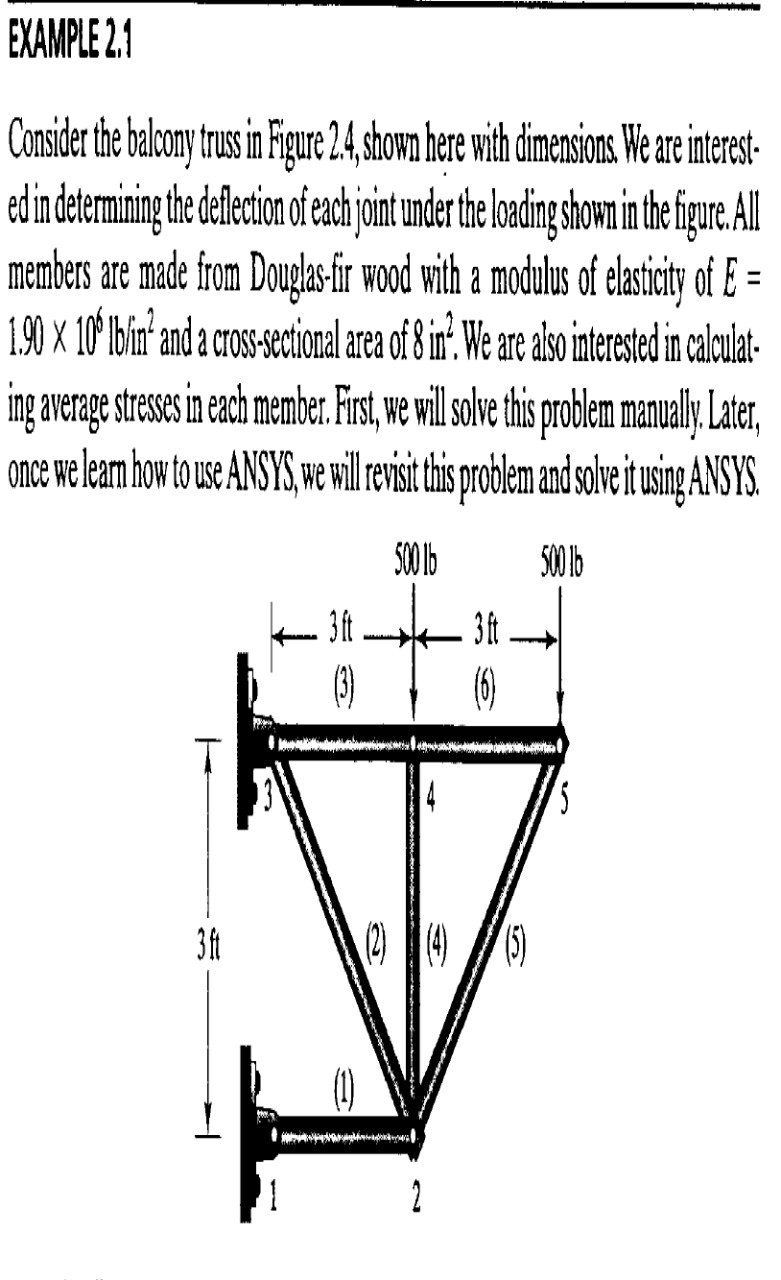
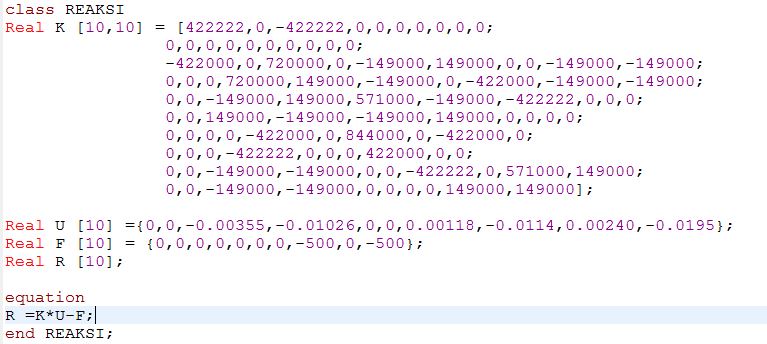
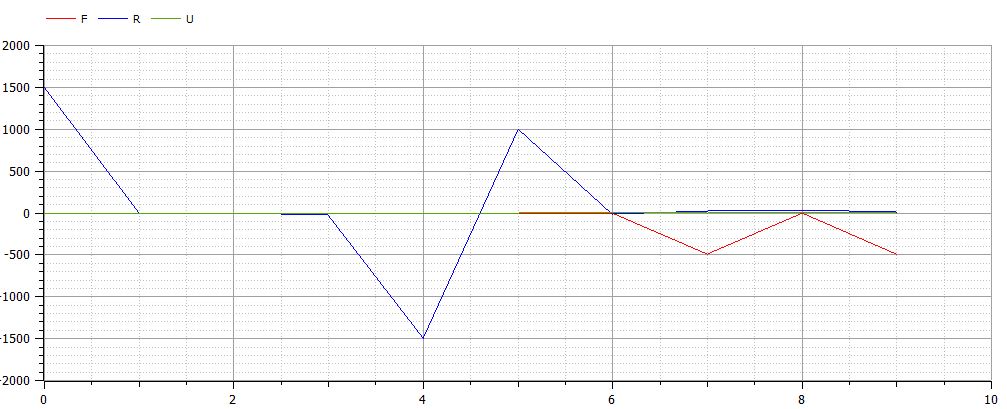
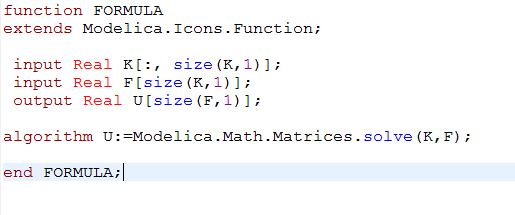
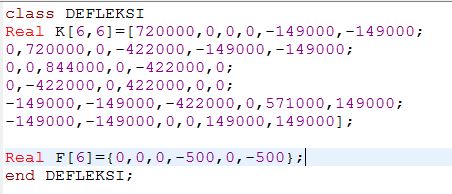
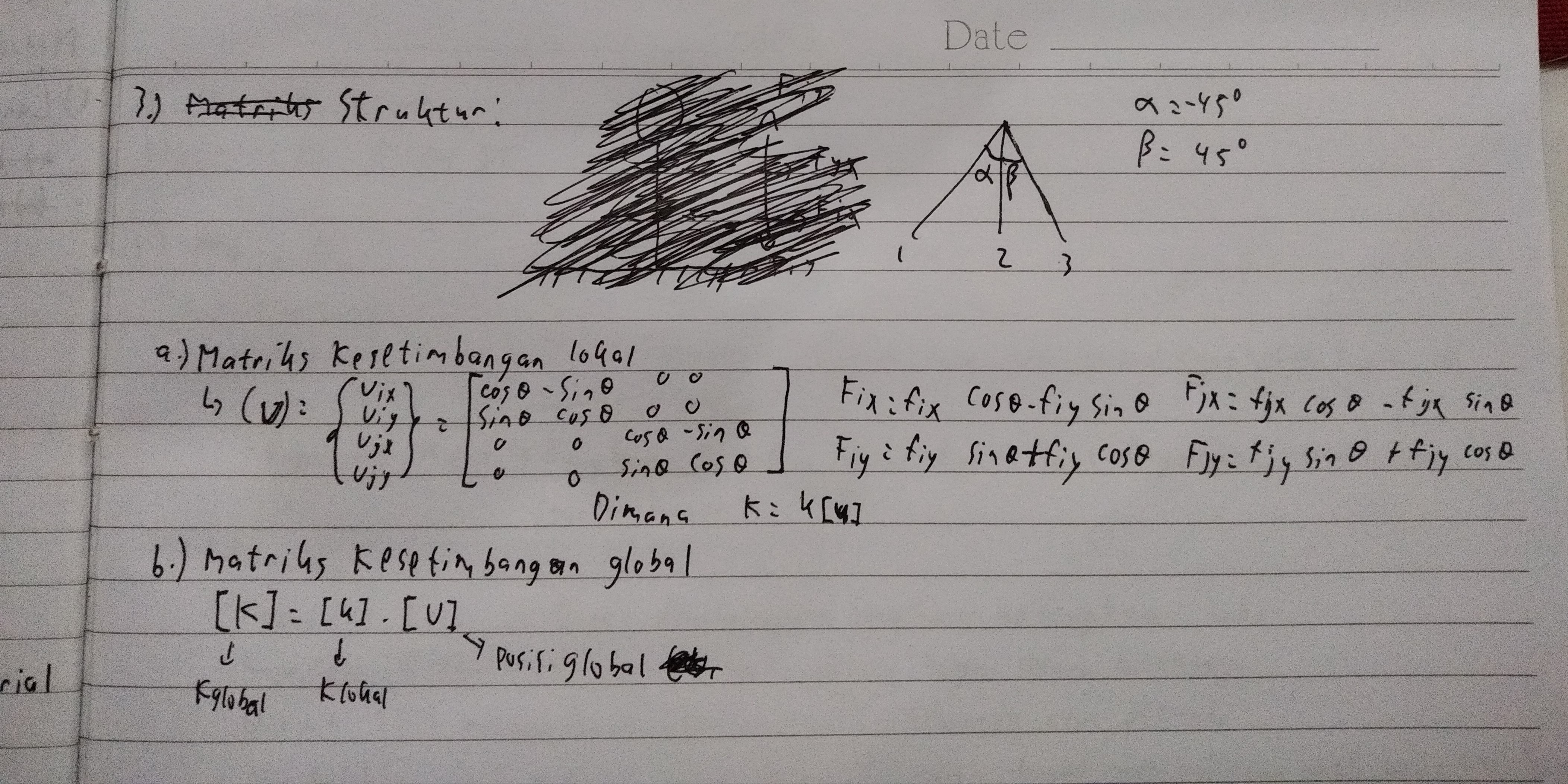
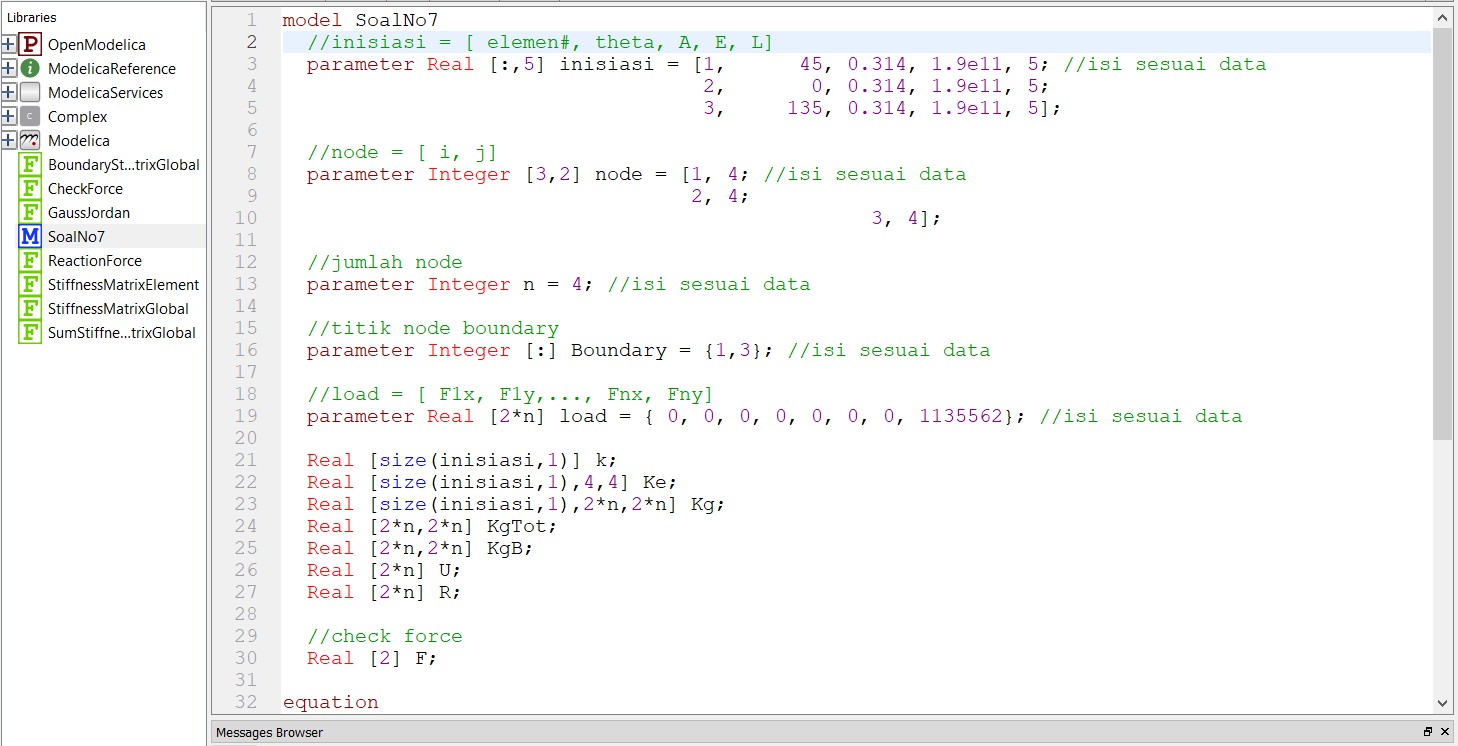
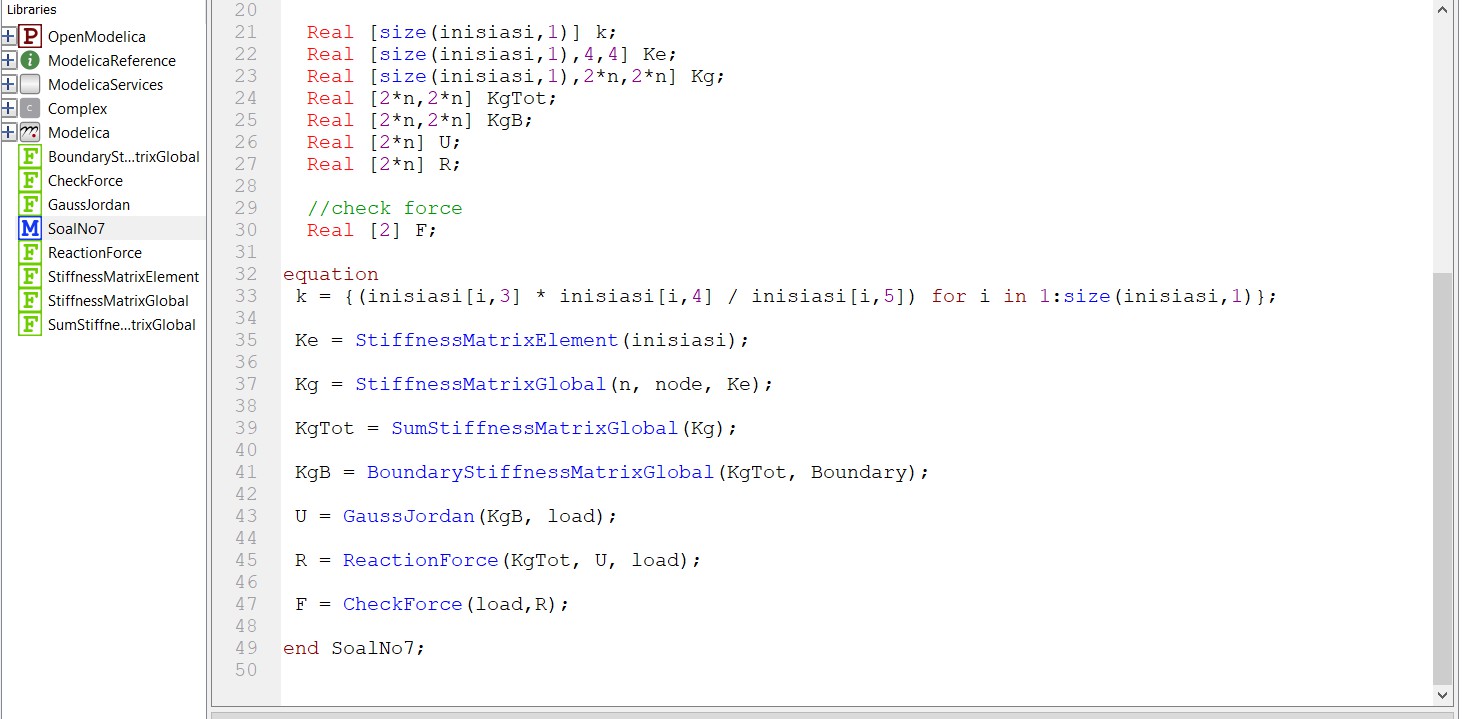
Tugas 3

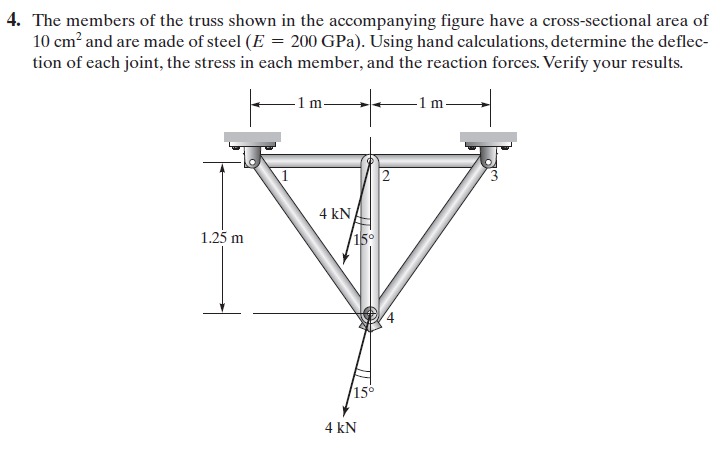
Menyelesaikan yang diberikan oleh Pak Dai menggunakan OpenModelica

Soal Tugas 3.jpg

REAKSI.jpg

REAKSI Simulation.jpg

FORMULA.jpg

DEFLEKSI.jpg


Quiz 1

Soal quiz.jpg

Dapat diselesaikan dengan langkah-langkah berikut

Langkah.jpg

Pertemuan ke-5

Pertemuan ke-6

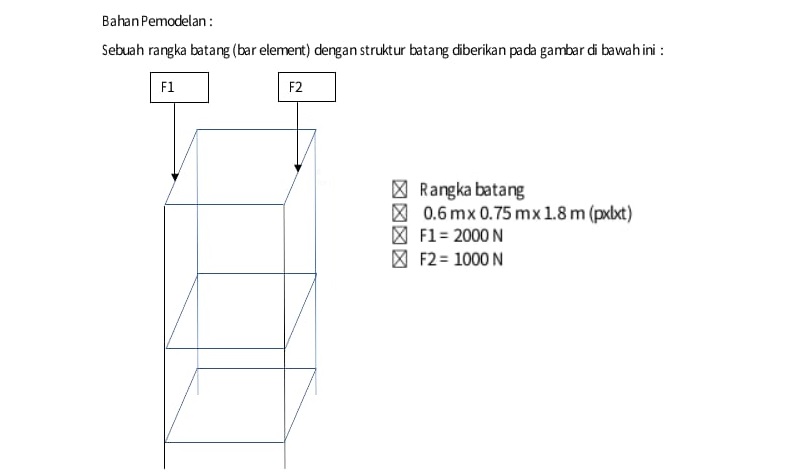
Tugas Besar

Tugas besar kami diminta untuk mencari optimasi pemilihan material untuk rangka berikut. Optimasi pemilihan material bergantung kepada 2 hal yaitu optimasi elastisitas dan luas penampang.

Tugas Besar Metnum Geometri Jos.jpg

Dari soal diminta untuk mencari 1.)Material pada struktur tersebut yang paling optimal yang terbuat dari besi siku; dan 2.)Membandingkan optimasi material dan optimasi luas penampang. Struktur pada kasus ini memiliki dimensi 0.6m x 0.75m x 1.8m. Pada bagian atas diberikan gaya F1 : 2000 N dan F2 : 1000 N yang memengaruhi struktur.

F1 dan F2 terdistribusi pada point penghubung pada struktur dan struktur memiliki sifat truss.


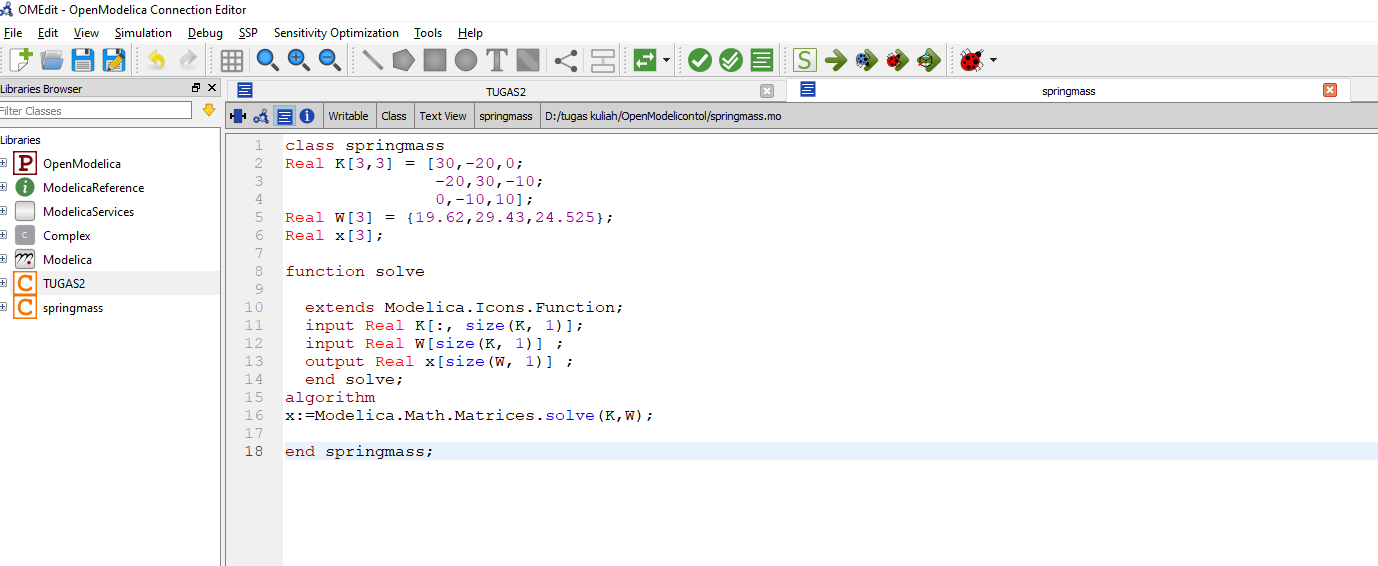
model Trusses_3D_Tugas_Besar_Safety

//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)

//define connection parameter Integer C[:,2]=[1,5; 

                         2,6;
                         3,7;
                         4,8;
                         5,6;  //1st floor
                         6,7;  //1st floor
                         7,8;  //1st floor
                         5,8;  //1st floor
                         5,9;
                        6,10;
                        7,11;
                        8,12;
                        9,10; //2nd floor
                        10,11;//2nd floor 
                        11,12;//2nd floor
                         9,12; //2nd floor
                         9,13;
                        10,14;
                        11,15;
                        12,16;
                        13,14;//3rd floor
                        14,15;//3rd floor
                        15,16;//3rd floor
                       13,16];//3rd floor

//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 

                      -0.3,-0.375,0,1,1,1;    //2
                      -0.3,0.375,0,1,1,1;     //3
                      0.3,0.375,0,1,1,1;      //4
                          
                      0.3,-0.375,0.6,0,0,0;   //5
                      -0.3,-0.375,0.6,0,0,0;  //6
                      -0.3,0.375,0.6,0,0,0;   //7
                      0.3,0.375,0.6,0,0,0;    //8
                           
                      0.3,-0.375,1.2,0,0,0;   //9
                      -0.3,-0.375,1.2,0,0,0;  //10  
                      -0.3,0.375,1.2,0,0,0;   //11
                      0.3,0.375,1.2,0,0,0;    //12
                           
                      0.3,-0.375,1.8,0,0,0;   //13
                      -0.3,-0.375,1.8,0,0,0;  //14
                      -0.3,0.375,1.8,0,0,0;   //15
                      0.3,0.375,1.8,0,0,0];   //16

//define external force (please put orderly) parameter Real F[Points*3]={0,0,0, 

                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,-500, 
                           0,0,-1000, 
                           0,0,-1000, 
                           0,0,-500};

//solution Real displacement[N], reaction[N]; Real check[3];

Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];

protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;

algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop 

for j in 1:3 loop
 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];
end for;
     
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                    cy*cx,cy^2,cy*cz;
                    cz*cx,cz*cy,cz^2];

  //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;  

G_star:=G+g;
G:=G_star;

end for;

//Implementing boundary for x in 1:Points loop 

if P[x,4] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-2,a]:=0;
    G[(x*3)-2,(x*3)-2]:=1;
  end for;
end if;
if P[x,5] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-1,a]:=0;
    G[(x*3)-1,(x*3)-1]:=1;
  end for;
end if;
if P[x,6] <> 0 then
  for a in 1:Points*3 loop
    G[x*3,a]:=0;
    G[x*3,x*3]:=1;
  end for;
end if;

end for;

//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction reaction:=(G_star*displacement)-F;

//Eliminating float error for i in 1:N loop 

reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];

end for;

//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});

for i in 1:3 loop 

check[i] := if abs(check[i])<=ers then 0 else check[i];

end for;

//Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop 

 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];
 dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);

end for; 

  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
               cy*cx,cy^2,cy*cz;
               cz*cx,cz*cy,cz^2];
  
  Str:=(X*dis);
  stress1[i]:=Modelica.Math.Vectors.length(Str);

end for;

//Safety factor for i in 1:Trusses loop 

if stress1[i]>0 then
  safety[i]:=Yield/stress1[i];
else
  safety[i]:=0;
end if;

end for;

end Trusses_3D_Tugas_Besar_Safety;

Jawaban UAS

UAS No 1 Yudho.jpg

UAS No 2 Yudho.jpg

UAS No 3 Yudho.jpg

UAS No 4 Yudho.jpg

UAS No 5 Yudho.jpg

UAS No 6 Yudho.jpg

UAS No 7a Yudho.jpg

UAS No 7b Yudho.jpg

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03-Yudho_Wicaksono&oldid=56401"