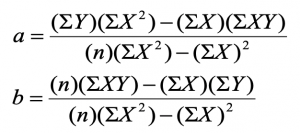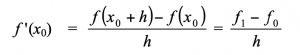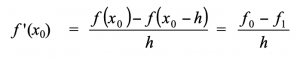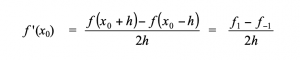Difference between revisions of "Metnum03-Muhammad Afdhal Pradisto"
(→Tugas 3: Menentukan titik reaksi displacement pada setiap joint dan gaya-gaya reaksinya) |
(→UAS) |
||
| (35 intermediate revisions by the same user not shown) | |||
| Line 261: | Line 261: | ||
| − | + | Ada 4 cara pertama Dalam menyelesaikan soal diatas : | |
| − | + | 1.Mengubah problem menjadi node dan elemen | |
| + | 2.Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen | ||
| − | + | 3.Membuat persamaan untuk elemen | |
| − | + | 4.Menyusun dan menggabungkan matriks elemen-elemen | |
| − | + | 4 cara diatas ada pada buku "Finite Element Analysis" pada halaman 60-70 : | |
| − | + | [[File:metnumafdhal31.png|600px|center]] | |
| − | [[File: | + | [[File:metnumafdhal30.png|600px|center]] |
| − | + | [[File:metnumafdhal32.png|600px|center]] | |
| − | + | [[File:metnumafdhal33.png|600px|center]] | |
| − | [[File: | + | [[File:metnumafdhal34.png|600px|center]] |
| − | [[File: | + | [[File:metnumafdhal35.png|600px|center]] |
| − | |||
| − | + | [[File:metnumafdhal36.png|600px|center]] | |
| − | |||
| − | + | [[File:metnumafdhal26.png|600px|center]] | |
| − | |||
| − | + | == Pertemuan 4: 30 November 2020 == | |
| + | Assalamualaikum wr.wb. | ||
| − | + | [[File:metnumafdhal37.png|600px|center]] | |
| − | |||
| − | + | Pada pertemuan keempat ini, Pak Dai membuka diskusi dengan membahas analisa beban static dan dynamic. Pak Dai memberi kesempatan kepada mahasiswa untuk memberi pengertian dari analisa static dan dynamic. Kesimpulan dari diskusi yang saya dapat adalah analisa beban static merupakan respon material dari beban yang diam atau bebannya tidak mengalami perubahan terhadap waktu atau kata lain sigma F sama dengan 0. Sedangkan analisa beban dynamic merupakan respon beban yang mengalami perubahan terhadap perubahan waktu atau sigma F tidak sama dengan 0. | |
| − | 7. | + | Hubungan antara metode numerik dengan statika struktur yaitu untuk memecahkan suatu permasalahan dari suatu kasus sehari-hari seperti pada Tugas 3 yaitu batang yang bisa dilakukan dengan breakdown gaya-gaya yang ada pada sistem tersebut. |
| + | |||
| + | Metode Numerik untuk permasalahan teknik seperti permasalahan fisika yang diubah menjadi lebih matematis dan menggunakan komputer sebagai perhitungan numerik sebagai tools untuk menghitung perhitungan yang rumit. | ||
| + | |||
| + | |||
| + | === Quiz === | ||
| + | |||
| + | Pak Dai memberi 2 soal untuk quiz pada pertemuan keempat ini. Pak Dai meminta untuk mengirimkan Flow Chart terlebih dahulu. Berikut Flow Chart untuk soal yang diberikan Pak Dai. | ||
| + | |||
| + | |||
| + | [[File:metnumafdhal38.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | [[File:metnumafdhal39.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Jawab No.8 : | ||
| + | |||
| + | [[File:metnumafdhal41.png|600px|center]] | ||
| + | |||
| + | [[File:metnumafdhal42.png|600px|center]] | ||
| + | |||
| + | [[File:metnumafdhal43.png|600px|center]] | ||
| + | |||
| + | [[File:metnumafdhal44.png|600px|center]] | ||
| + | |||
| + | [[File:metnumafdhal45.png|600px|center]] | ||
| + | |||
| + | == Pertemuan 5: 7 Desember 2020 == | ||
| + | |||
| + | |||
| + | Assalamualaikum wr.wb. | ||
| + | |||
| + | Pada pertemuan ke-5 ini, Pak Dai membuka kelas dengan menanyakan tentang 2 soal minggu lalu yang diberikan oleh Pak Dai. Pak Dai memberi kesempatan untuk mahasiswa yang sudah bisa dan berhasil dalam mengerjakan soal tersebut. Salah satunya adalah Ahmad Mohammad Fahmi. Fahmi menjelaskan tentang codingan yang sudah dia buat yang bisa diterapkan untuk mengerjakan soal seperti itu. Fahmi menggunakan 1 class dan beberapa function didalam OpenModelica untuk mengerjakan soal tersebut. Alur dari pengerjaannya adalah pertama membuat class untuk menaruh semua data yang ada dari soal dengan equation yaitu beberapa fungsi. Fungsi tersebut yaitu untuk matrix element, matrix global, total dari matrix global, matrix global yang sudah dipengaruhi oleh boundary, gauss jordan untuk mendapatkan nilai U, dan mencari gaya reaksi. Tiap function tersebut memiliki codingan yang berbeda dan saling terhubung. Tetapi menurut Pak Dai, masih butuh 1 function lagi yaitu untuk memastikan gaya yang ada dalam sistem tersebut apakah sudah setimbang. Hal itu menjadi sebuah revisi untuk pekerjaan minggu depan. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''Tugas 5''' | ||
| + | |||
| + | |||
| + | Soal : | ||
| + | |||
| + | |||
| + | [[File:metnumafdhal40.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Stiffness Matrix Element Function''' | ||
| + | |||
| + | function StiffnessMatrixElement | ||
| + | input Real [:,6] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real cos_z; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] L; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | algorithm | ||
| + | L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)}; | ||
| + | k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | // Finding stiffness matrix of each element member | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | // Clearing the matrices | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | // Converting degrees to radians | ||
| + | cos_x := inisiasi_mat[i,2]/L[i]; | ||
| + | cos_y := inisiasi_mat[i,3]/L[i]; | ||
| + | cos_z := inisiasi_mat[i,4]/L[i]; | ||
| + | // {cos^2, sin^2, sincos} | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | // Construct stiffness transformation matrix | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end StiffnessMatrixElement; | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Stiffness Matrix Global Function''' | ||
| + | |||
| + | function StiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer [:,2] n; | ||
| + | input Real [:,6,6] Ke_mat; | ||
| + | output Real [size(Ke_mat,1),3*x,3*x] Kg_mat; | ||
| + | algorithm | ||
| + | Kg_mat := zeros(size(Ke_mat,1),3*x,3*x); | ||
| + | for i in 1:size(Ke_mat,1) loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal; | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | ''' Sum Stiffness Matrix Element Function''' | ||
| + | |||
| + | function SumStiffnessMatrixGlobal | ||
| + | input Real [:,:,:] Kg_mat; | ||
| + | output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat; | ||
| + | algorithm | ||
| + | for a in 1:size(Kg_mat,2) loop | ||
| + | for b in 1:size(Kg_mat,2) loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | end SumStiffnessMatrixGlobal; | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | ''' Boundary Stiffness Matrix Global Function''' | ||
| + | |||
| + | function BoundaryStiffnessMatrixGlobal | ||
| + | input Real [:,:] KgTot_met; | ||
| + | input Integer[:] Boundary_xyz; | ||
| + | input Integer[:] Boundary_xy; | ||
| + | input Integer[:] Boundary_xz; | ||
| + | input Integer[:] Boundary_yz; | ||
| + | input Integer[:] Boundary_x; | ||
| + | input Integer[:] Boundary_y; | ||
| + | input Integer[:] Boundary_z; | ||
| + | output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:size(KgTot_met,1) loop | ||
| + | for b in 1:size(KgTot_met,1) loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | if Boundary_xyz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xyz,1) loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_xyz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | |||
| + | if Boundary_xy[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xy,1) loop | ||
| + | for b in 1:2 loop | ||
| + | KgB_met[3*(Boundary_xy[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | |||
| + | if Boundary_xz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xz,1) loop | ||
| + | for b in 0:2:2 loop | ||
| + | KgB_met[3*(Boundary_xz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | |||
| + | if Boundary_yz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_yz,1) loop | ||
| + | for b in 0:1 loop | ||
| + | KgB_met[3*(Boundary_yz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | |||
| + | if Boundary_x[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_x,1) loop | ||
| + | KgB_met[3*(Boundary_x[a])-2,i]:=0; | ||
| + | KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | |||
| + | if Boundary_y[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_y,1) loop | ||
| + | KgB_met[3*(Boundary_y[a])-1,i]:=0; | ||
| + | KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | |||
| + | if Boundary_z[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_z,1) loop | ||
| + | KgB_met[3*Boundary_z[a],i]:=0; | ||
| + | KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | end BoundaryStiffnessMatrixGlobal; | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Gauss Jordan Function''' | ||
| + | |||
| + | function GaussJordan | ||
| + | input Real [:,:] KgB_met; | ||
| + | input Real [size(KgB_met,1)] load_met; | ||
| + | output Real [size(KgB_met,1)] U_met; | ||
| + | |||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | |||
| + | for i in 1:size(KgB_met,1) loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end GaussJordan; | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Reaction Force Function''' | ||
| + | |||
| + | function ReactionForce | ||
| + | input Real [:,:] KgTot_met; | ||
| + | input Real [size(KgTot_met,1)] U_met; | ||
| + | input Real [size(KgTot_met,1)] load_met; | ||
| + | output Real [size(KgTot_met,1)] R_met; | ||
| + | protected Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | R_met := KgTot_met*U_met-load_met; | ||
| + | |||
| + | for t in 1:size(KgTot_met,1) loop | ||
| + | if abs(R_met[t]) <= float_error then | ||
| + | R_met[t] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end ReactionForce; | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Check Force Function''' | ||
| + | |||
| + | function CheckForce | ||
| + | input Real [:] load; | ||
| + | input Real [size(load,1)] R; | ||
| + | output Real [3] F; | ||
| + | protected Real float_error = 10e-10; | ||
| + | |||
| + | protected | ||
| + | Real load_x; | ||
| + | Real load_y; | ||
| + | Real load_z; | ||
| + | Real R_x; | ||
| + | Real R_y; | ||
| + | Real R_z; | ||
| + | |||
| + | algorithm | ||
| + | load_x := sum({load[i] for i in 1:3:(size(load,1)-2)}); | ||
| + | load_y := sum({load[i] for i in 2:3:(size(load,1)-1)}); | ||
| + | load_z := sum({load[i] for i in 3:3:size(load,1)}); | ||
| + | R_x := sum({R[i] for i in 1:3:(size(load,1)-2)}); | ||
| + | R_y := sum({R[i] for i in 2:3:(size(load,1)-1)}); | ||
| + | R_z := sum({R[i] for i in 3:3:size(load,1)}); | ||
| + | |||
| + | F[1] := load_x + R_x; | ||
| + | F[2] := load_y + R_y; | ||
| + | F[3] := load_z + R_z; | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | if abs(F[i]) <= float_error then | ||
| + | F[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end CheckForce; | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Class''' | ||
| + | |||
| + | class QuizSoal1 | ||
| + | //inisiasi = [ elemen#, dX, dY, dZ, A, E] | ||
| + | parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data | ||
| + | 2, 0, 0, -6, 1.56, 10.6e6; | ||
| + | 3, 0, 6, -3, 1.56, 10.6e6; | ||
| + | 4, -6, 0, -3, 1.56, 10.6e6; | ||
| + | 5, -6, 6, 0, 1.56, 10.6e6; | ||
| + | 6, 0, 6, 3, 1.56, 10.6e6]; | ||
| + | |||
| + | //node = [ i, j] | ||
| + | parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data | ||
| + | 1, 3; | ||
| + | 1, 4; | ||
| + | 2, 3; | ||
| + | 2, 4; | ||
| + | 3, 4]; | ||
| + | |||
| + | //jumlah node | ||
| + | parameter Integer n = 4; //isi sesuai data | ||
| + | |||
| + | //titik node boundary xyz | ||
| + | parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary xy | ||
| + | parameter Integer [:] Boundary_xy = {4}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary xz | ||
| + | parameter Integer [:] Boundary_xz = {0}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary yz | ||
| + | parameter Integer [:] Boundary_yz = {0}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary x | ||
| + | parameter Integer [:] Boundary_x = {3}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary y | ||
| + | parameter Integer [:] Boundary_y = {0}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary z | ||
| + | parameter Integer [:] Boundary_z = {0}; //isi sesuai data | ||
| + | |||
| + | //load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz] | ||
| + | parameter Real [3*n] load = {0, 0, 0, //isi sesuai data | ||
| + | 0, -200, 0, | ||
| + | 0, 0, 0, | ||
| + | 0, 0, 0}; | ||
| + | |||
| + | Real [size(inisiasi,1)] L; | ||
| + | Real [size(inisiasi,1)] k; | ||
| + | Real [size(inisiasi,1),6,6] Ke; | ||
| + | Real [size(inisiasi,1),3*n,3*n] Kg; | ||
| + | Real [3*n,3*n] KgTot; | ||
| + | Real [3*n,3*n] KgB; | ||
| + | Real [3*n] U; | ||
| + | Real [3*n] R; | ||
| + | |||
| + | //check force | ||
| + | Real [3] F; | ||
| + | |||
| + | equation | ||
| + | L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)}; | ||
| + | |||
| + | k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)}; | ||
| + | |||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | |||
| + | Kg = StiffnessMatrixGlobal(n, node, Ke); | ||
| + | |||
| + | KgTot = SumStiffnessMatrixGlobal(Kg); | ||
| + | |||
| + | KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); | ||
| + | |||
| + | U = GaussJordan(KgB, load); | ||
| + | |||
| + | R = ReactionForce(KgTot, U, load); | ||
| + | |||
| + | F = CheckForce(load,R); | ||
| + | |||
| + | end QuizSoal1; | ||
| + | |||
| + | |} | ||
| + | |||
| + | == Pertemuan 6: 14 Desember 2020 == | ||
| + | |||
| + | |||
| + | Assalamualaikum wr.wb. Pada pertemuan ini Pak Dai meminta mahasiswanya muasabah diri untuk pencapaian dalam memahami materi Metode Numerik ini. Saya sudah agak memahami bagaimana menggunakan openmodelica walaupun belum sepenuhnya. Saya sudah mengerti flow chart dalam mengerjakan persoalan fisika tetapi untuk codingannya saya belum mengerti sepenuhnya. | ||
| + | |||
| + | == Pertemuan 7: 21 Desember 2020 == | ||
| + | |||
| + | Assalamualaikum wr.wb. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Tugas Besar == | ||
| + | |||
| + | |||
| + | Assalamualaikum wr.wb. | ||
| + | |||
| + | Berikut merupakan progres dari tugas besar yang saya kerjakan. | ||
| + | |||
| + | |||
| + | [[File:metnumafdhal46.png|600px|center]] | ||
| + | |||
| + | |||
| + | '''Flow Chart''' | ||
| + | |||
| + | 1. Mendefinisikan masalah | ||
| + | |||
| + | 2. Menentukan asumsi dan constraint | ||
| + | |||
| + | 3. Researh data profil besi siku | ||
| + | |||
| + | 4. Permodelan Numerik | ||
| + | |||
| + | 5. Komputasi | ||
| + | |||
| + | 6. Optimasi 1 (Area Locked) | ||
| + | |||
| + | 7. Optimasi 2 (Elasticity Locked) | ||
| + | |||
| + | 8. Penentuan akhir material | ||
| + | |||
| + | |||
| + | '''Asumsi dan Constraint''' | ||
| + | |||
| + | Asumsi: | ||
| + | |||
| + | - Diasumsikan tidak ada bending karena bersifat truss | ||
| + | |||
| + | - Beban terdistribusi pada node | ||
| + | |||
| + | - Safety Factor = 2 | ||
| + | |||
| + | - Batas displacement 0,001m sebelum terjadi buckling | ||
| + | |||
| + | - Variabel bebas | ||
| + | |||
| + | Constraint: | ||
| + | |||
| + | - Node 1,2,3,4 (lantai dasar) fixed | ||
| + | |||
| + | - Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga: | ||
| + | |||
| + | 1. Node 13 & 16 = 1000N | ||
| + | |||
| + | 2. Node 14 & 15 = 500N | ||
| + | |||
| + | |||
| + | '''Permodelan Numerik''' | ||
| + | |||
| + | |||
| + | 3D Trusses Model | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa) | ||
| + | parameter Real Area= (nilai area) ; //Luas Besi Siku (Dimension=30x30x3mm) | ||
| + | parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa) | ||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; // (Elemen 1) | ||
| + | 2,6; // (Elemen 2) | ||
| + | 3,7; // (Elemen 3) | ||
| + | 4,8; // (Elemen 4) | ||
| + | 5,6; // (Elemen 5) | ||
| + | 6,7; // (Elemen 6) | ||
| + | 7,8; // (Elemen 7) | ||
| + | 5,8; // (Elemen 8) | ||
| + | 5,9; // (Elemen 9) | ||
| + | 6,10; // (Elemen 10) | ||
| + | 7,11; // (Elemen 11) | ||
| + | 8,12; // (Elemen 12) | ||
| + | 9,10; // (Elemen 13) | ||
| + | 10,11;// (Elemen 14) | ||
| + | 11,12;// (Elemen 15) | ||
| + | 9,12; // (Elemen 16) | ||
| + | 9,13; // (Elemen 17) | ||
| + | 10,14;// (Elemen 18) | ||
| + | 11,15;// (Elemen 19) | ||
| + | 12,16;// (Elemen 20) | ||
| + | 13,14;// (Elemen 21) | ||
| + | 14,15;// (Elemen 22) | ||
| + | 15,16;// (Elemen 23) | ||
| + | 13,16];//(Elemen 24) | ||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1 | ||
| + | 0.75,0 ,0,1,1,1; //node 2 | ||
| + | 0.75,0.6,0,1,1,1; //node 3 | ||
| + | 0 ,0.6,0,1,1,1; //node 4 | ||
| + | |||
| + | 0 ,0 ,0.3,0,0,0; //node 5 | ||
| + | 0.75,0 ,0.3,0,0,0; //node 6 | ||
| + | 0.75,0.6,0.3,0,0,0; //node 7 | ||
| + | 0 ,0.6,0.3,0,0,0; //node 8 | ||
| + | |||
| + | 0 ,0 ,1.05,0,0,0; //node 9 | ||
| + | 0.75,0 ,1.05,0,0,0; //node 10 | ||
| + | 0.75,0.6,1.05,0,0,0; //node 11 | ||
| + | 0 ,0.6,1.05,0,0,0; //node 12 | ||
| + | |||
| + | 0 ,0 ,1.8,0,0,0; //node 13 | ||
| + | 0.75,0 ,1.8,0,0,0; //node 14 | ||
| + | 0.75,0.6,1.8,0,0,0; //node 15 | ||
| + | 0 ,0.6,1.8,0,0,0]; //node 16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-15, ers=10e-8; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Trusses_3D_Tugas_Besar; | ||
| + | |||
| + | |||
| + | '''Komputasi''' | ||
| + | |||
| + | Berikut coding untuk menentukan curve fitting untung cost pada excel | ||
| + | |||
| + | function Curve_Fitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | //Coe:=fill(2,size(Coe,1)); | ||
| + | end Curve_Fitting; | ||
| + | /* | ||
| + | for i in 1:3 loop | ||
| + | for j in 1:Points loop | ||
| + | R[j]:=reaction[3*(j-1)+i]; | ||
| + | end for; | ||
| + | Sur[i]:=sum(R); | ||
| + | end for; | ||
| + | */ | ||
| + | |||
| + | model callcurve | ||
| + | parameter Real [3] X={171e-6,291e-6,924e-6}; | ||
| + | parameter Real [3] Y={239500,420900,1697700}; | ||
| + | Real [3] Coe; | ||
| + | algorithm | ||
| + | Coe:=Curve_Fitting(X,Y); | ||
| + | end callcurve; | ||
| + | |||
| + | |||
| + | |||
| + | [[File:metnumafdhal48.png|600px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | Berikut merupakan grafik yang saya dapat | ||
| + | |||
| + | |||
| + | [[File:metnumafdhal49.png|600px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | == UAS == | ||
| + | |||
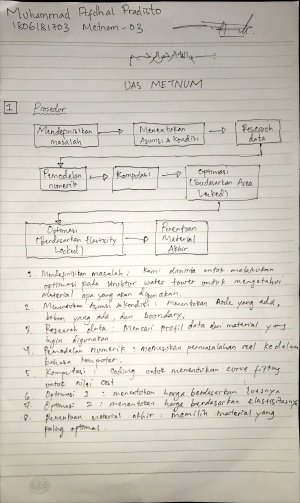
| + | No1 | ||
| + | |||
| + | [[File:UASafdhalno1.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | No2 | ||
| + | |||
| + | [[File:UASafdhalno2.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | No3 | ||
| + | |||
| + | [[File:UASafdhalno3.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | No4 | ||
| + | |||
| + | [[File:UASafdhalno4.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | No5 | ||
| + | |||
| + | [[File:UASafdhalno5.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | No6 | ||
| + | |||
| + | [[File:UASafdhalno6.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | No7 | ||
| + | |||
| + | [[File:UASafdhalno7a.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | [[File:UASafdhalno7b.jpg|300px|center]] | ||
| + | |||
| + | |||
| + | [[File:UASafdhalno7c.jpg|300px|center]] | ||
Latest revision as of 18:51, 14 January 2021
بِسْمِ اللّهِ الرَّحْمَنِ الرَّحِيْ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
BIODATA DIRI
Nama : Muhammad Afdhal Pradisto
NPM : 1806181703
Fakultas/ Jurusan : Teknik/ Teknik Mesin
Tempat dan Tanggal Lahir : Jakarta, 11 Oktober 2000
Contents
Pertemuan 1: 9 November 2020
Assalamualaikum wr. Wb. Perkenalkan nama saya Muhammad Afdhal Pradisto dari kelas Metode Numerik 03. Pada pertemuan ini saya akan menjelaskan apa yang sudah saya pelajari tentang Metode Numerik sebelum UTS. Metode Numerik ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik.
Keuntungan dari Metode Numerik:
1. Solusi persoalan selalu dapat diperoleh.
2. Dengan bantuan komputer, perhitungan dapat dilakukan dengan cepat serta hasil yang diperoleh dapat dibuat sedekat mungkin dengan nilai sesungguhnya.
3. Tampilan hasil perhitungan dapat disimulasikan.
Kelemahan dari Metode Numerik:
1. Nilai yang diperoleh berupa pendekatan atau hampiran.
2. Tanpa bantuan komputer, proses perhitungan akan berlangsung lama dan berulang-ulang.
1. Menentukan Akar-Akar
Ada beberapa metode yang dapat digunakan untuk menyelesaikan suatu persamaan. Metode ini merupakan penyelesaian perkiraan, tetapi lebih sistematis untuk menghitung akar-akar persamaan. Dalam metode numerik, pencarian akar f(x)=0 dilakukan secara lelaran (iteratif). Secara umum, semua metode pencarian akar dapat dikelompokkan menjadi 2 golongan besar :
• Metode Tertutup
Metode yang termasuk ke dalam golongan ini mencari akar di dalam selang [a,b]. Selang [a,b] sudah dipastikan berisi minimal satu buah akar, karena itu metode jenis ini selalu berhasil menemukan akar. Dengan kata lain, lelarannya selalu konvergen (menuju) ke akar, karena itu metode tertutup kadang-kadang dinamakan juga metode konvergen.
Metode yang termasuk dalam golongan ini antara lain :
a. Metode Biseksi atau Metode Setengah Interval ini merupakan Metode dengan bentuk paling sederhana diantara beberapa metode yang akan dipelajari.
b. Metode Regula Falsi atau Metode Interpolasi Linier adalah metode mudah tapi tidak efisien. Untuk mendapatkan hasil yang mendekati nilai eksak diperlukan langkah iterasi yang cukup panjang. Metode Regula Falsi dapat menutup kekurangan itu. Metode Regula Falsi didasarkan pada interpolasi antara dua nilai dari fungsi yang mempunyai tanda berlawanan
• Metode Terbuka
Yang diperlukan pada metode ini, adalah tebakan awal akar, lalu dengan prosedur lelaran, kita menggunakannya untuk menghitung hampiran akar yang baru. Pada setiap lelaran, hampiran akar lama yang dipakai untuk menghitung hampiran akar yang baru. Mungkin saja hampiran akar yang baru mendekati akar sejati (konvergen), atau mungkin menjauhinya (divergen). Karena itu, metode terbuka tidak selalu berhasil menemukan akar, kadang-kadang konvergen, kadangkala ia divergen.
Metode yang termasuk dalam golongan ini antara lain :
a. Metode Newton Raphson, Metode ini paling banyak digunakan dalam mencari akar-akar dari suatu persamaan.
b. Metode Secant, Kekurangan Metode Newton Raphson adalah diperlukannya turunan pertama (differensial) dari f(x) dalam hitungan. Kadang-kadang sulit untuk mendiferensialkan persamaan yang diselesaikan. Untuk itu maka bentuk diferensial didekati dengan nilai perkiraan berdasarkan diferensial beda hingga.
c. Metode Iterasi, Dalam metode iterasi ini digunakan suatu persamaan untuk memperkirakan nilai akar persamaan. Persamaan tersebut dikembangkan dari fungsi f(x) = 0 sehingga parameter x berada disisi kiri dari persamaan, yaitu :
X= g(x)
Persamaan ini menunjukkan bahwa nilai x merupakan fungsi dari x, sehingga dengan memberi nilai perkiraan awal dari akar dapat dihitung perkiraan baru dengan rumus iteratif berikut : Xi+1 = g ( xi )
Besar kesalahan dihitung dengan rumus berikut : ∈a = | (Xi+1 – Xi )/(Xi+1 ) | X 100%
2. Regresi Linier
Regresi merupakan alat ukur yg digunakan untuk mengetahui ada tidaknya korelasi antarvariabel. Analisis regresi lebih akurat dlm analisis korelasi karena tingkat perubahan suatu variabel terhadap variabel lainnya dpt ditentukan). Jadi pada regresi, peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula. Regresi linier adalah regresi yang variabel bebasnya (variabel X) berpangkat paling tinggi satu. Untuk regresi sederhana, yaitu regresi linier yg hanya melibatkan dua variabel (variabel X dan Y).
Y = a + bX
Keterangan :
Y = variabel terikat
X = variabel bebas
a = intersep / konstanta
b = koefisien regresi / slop
Persamaan regresi linear di atas dapat pula dituliskan dalam bentuk :
3. Turunan Numerik
Ini digunakan untuk menentukan nilai turunan fungsi f yang diberikan dalam bentik tabel. Ada 3 pendekatan zalm menghitung Turunan Numerik :
1. Hampiran selisih-maju (forward difference approximation)
2. Hampiran selisih-mundur (backward difference approximation)
3. Hampiran selisih-pusat (central difference approximation)
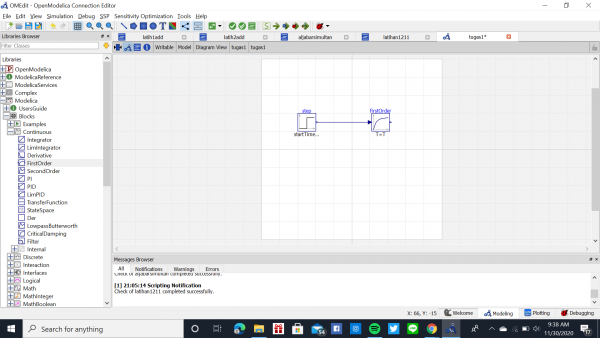
Tugas 1: Pembelajaran OpenModelica
Saya menggunakan tutorial yang ada di youtube sebagai referensi saya dalam mencoba memahami OpenModelica ini. Link video youtube yang saya gunakan : https://www.youtube.com/watch?v=GhtBMIlO70w
Video tersebut menjelaskan tentang tools yang bisa digunakan pada OpenModelica dan libraries yang sudah tersedia. Seperti yang dilakukan pada video, saya mencoba menggunakan step dan first order untuk membuat suatu sistem.
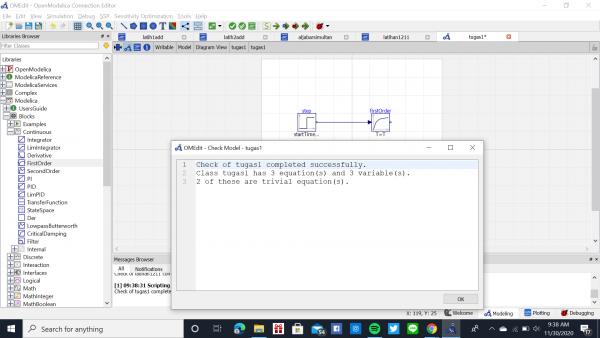
Setelah itu sistem tersebut saya cek dan memiliki 3 persamaan dan 3 variabel yang sudah benar.
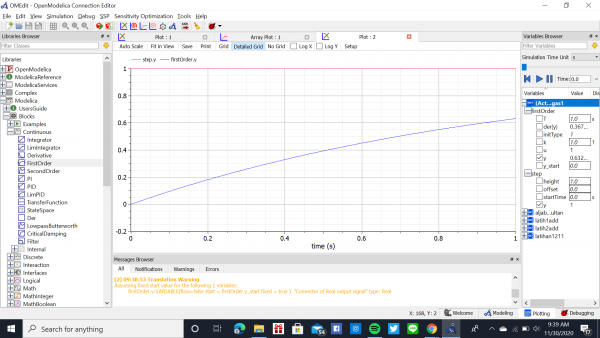
Lalu saya simulasi dan mendapatkan hasil grafiknya seperti dibawah ini.
Pertemuan 2: 16 November 2020
Assalamualaikum wr. wb.
Pada pertemuan kedua ini, Pak Dai membuka diskusi tentang pembelajaran OpenModelica. Mahasiswa diberikan kesempatan untuk menjelaskan tentang pembelajaran aplikasi OpenModelica yang sudah dilakukan masing-masing pada tugas 1. Lalu dilanjutkan dengan latihan membuat perhitungan sederhana menjumlahkan angka 10 terhadap suatu variabel dan menghitung rata-rata dengan menggunakan OpenModelica.
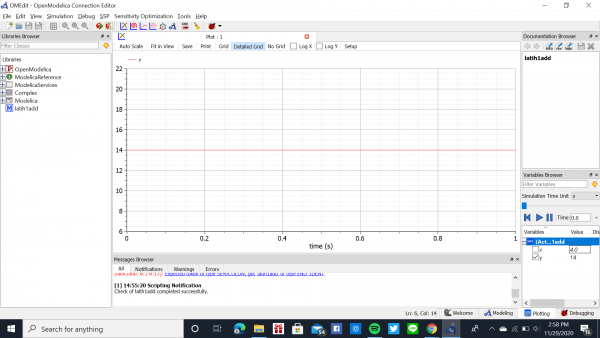
Pada percobaan pertama dilakukan perhitungan nilai x untuk persamaan y=x+10 dan saya mencoba dengan x=4
Lalu dilanjutkan dengan mensimulasikannya dan mendapat grafik seperti gambar berikut dan juga didapatkan hasil y=14
Berikutnya percobaan kedua melakukan perhitungan untuk menentukan rata-rata dari kelompok data.
Kemudian disimulasi dan mendapatkan nilai rata-rata yaitu 12. Berikut hasil grafik yang didapat dari simulasi tersebut
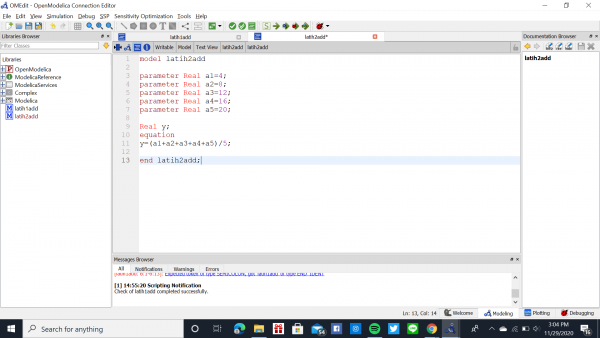
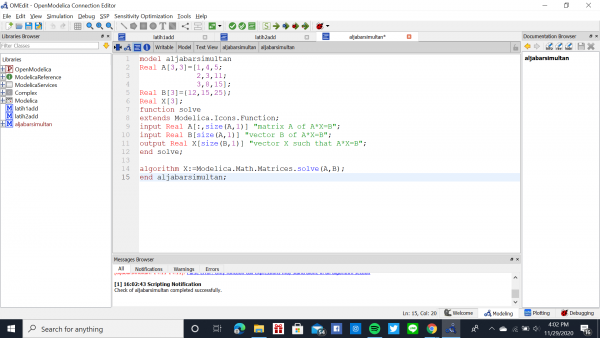
Tugas 2: Menyelesaikan persamaan Aljabar Simultan
Aljabar Simultan adalah suatu penyelesaian matematik yang kompleks sehingga membutuhkan penyederhanaan dengan menggunakan bantuan software yang sudah disediakan seperti OpenModelica. Ada beberapa metode yang bisa digunakan pada Aljabar Simultan:
1. Metode Eliminasi Gauss
2. Metode Crammer
3. Metode Gauss Seidel
4. Metode Gauss-Jordan
Berikut persamaan yang saya gunakan untuk aljabar simultan:
X1 + 4X2 + 5X3 = 12
2X1 + 3X2 + 11X3 = 15
3X1 + 8X2 + 15X3 = 25
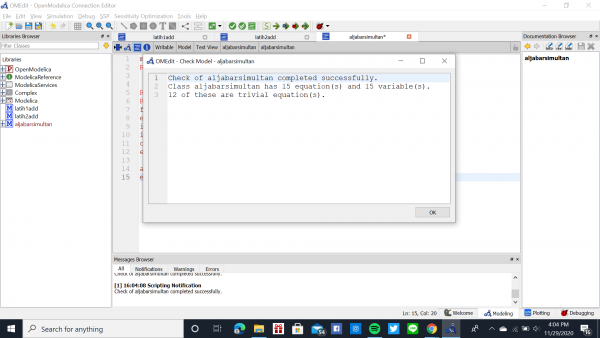
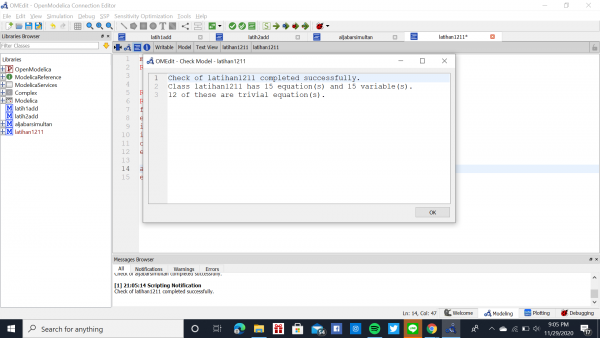
Berikut dibawah ini adalah hasil screenshot yang saya lakukan untuk menyelesaikan persamaan tersebut
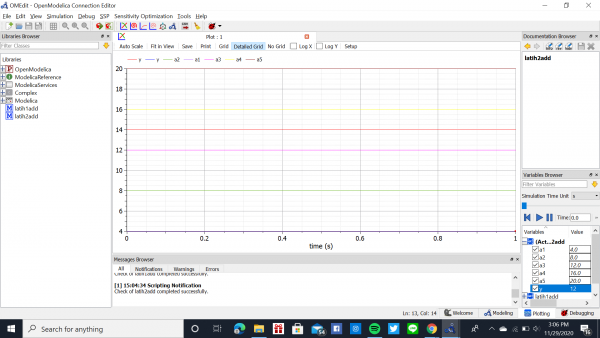
Rangkaian bahasa modelica sudah dicek dengan berisikan 15 persamaan dan 15 variabel yang sudah benar
Berikut adalah hasil grafik yang didapat setelah melakukan simulasi. Didapatkan juga akar-akarnya yaitu
X1 = -22.75
X2 = 2.75
X3 = 4.75
Pertemuan 3: 23 November 2020
Assalamualaikum wr.wb.
Pada pertemuan ketiga ini, Pak Dai membuka diskusi dengan membahas tentang Tugas 2 yang diberikan minggu sebelumnya. Lalu Pak Dai membahas tentang step by step dalam memecahkan masalah teknik menggunakan metode numerik. Step dalam pemecahan masalah tersebut adalah :
1. Masalah Teknik
2. Analisis Masalah
3. Model matematis
4. Model Numerik
5. Komputer
6. Mendapatkan Solusi
Pak Dai juga memberikan tugas yaitu studi kasus seperti yang ada di gambar bawah ini. Kami diminta untuk menyelesaikannya dalam OpenModelica.
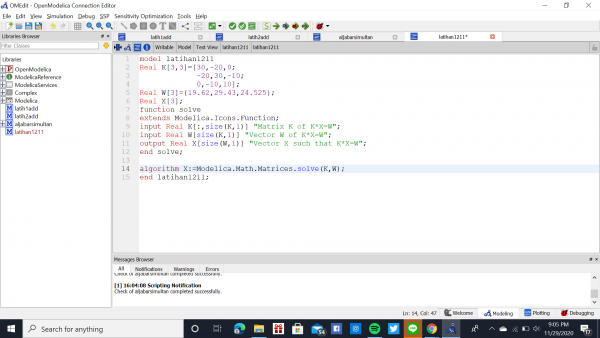
Sistem tersebut diubah menjadi bentuk matriks seperti dibawah ini.
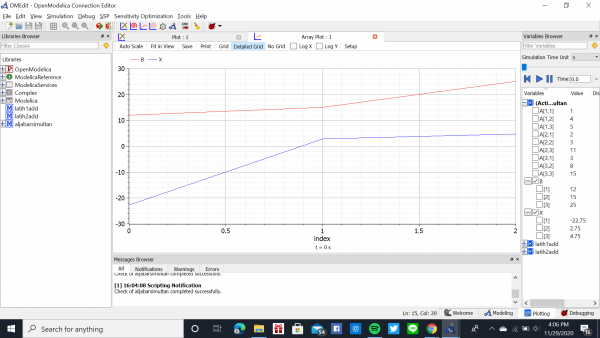
Dibawah ini adalah hasil screenshot dari percobaan function yang saya buat.
Setelah itu function tersebut di cek dan didapatkan 15 persamaan dan 15 variabel yang sudah benar.
Lalu function itu disimulasi dan mendapatkan grafik sepeti dibawah ini. Didapatkan juga nila-nilai X nya, yaitu:
X1 = 7.3575
X2 = 10.0552
X3 = 12.5077
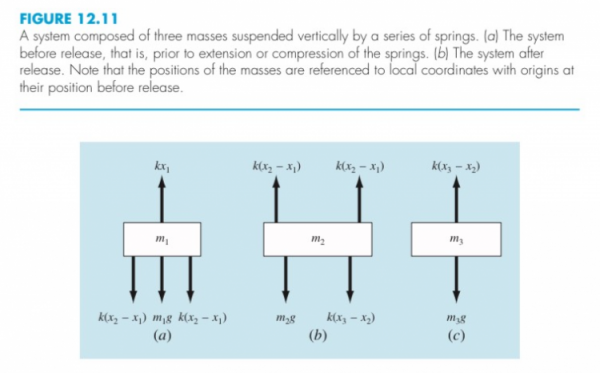
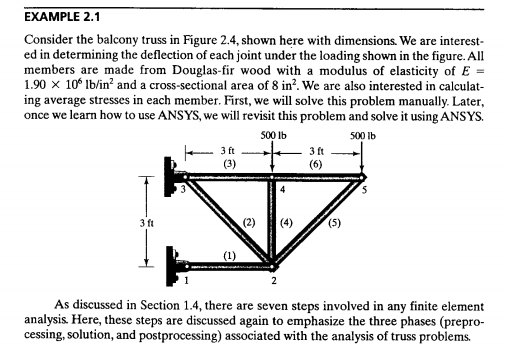
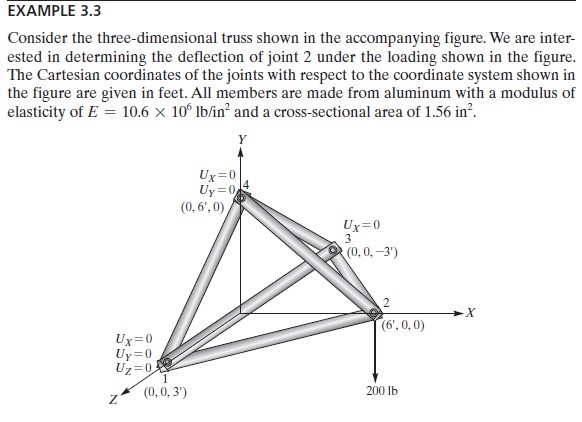
Tugas 3: Menentukan titik reaksi displacement pada setiap joint dan gaya-gaya reaksinya
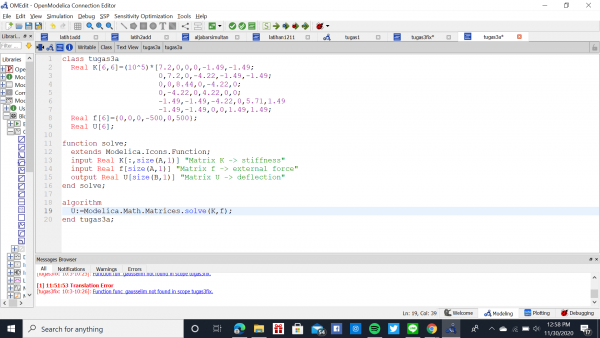
Pada tugas 3 ini Pak Dai meminta kami untuk menyelesaikan soal dibawah ini dengan menggunakan OpenModelica.
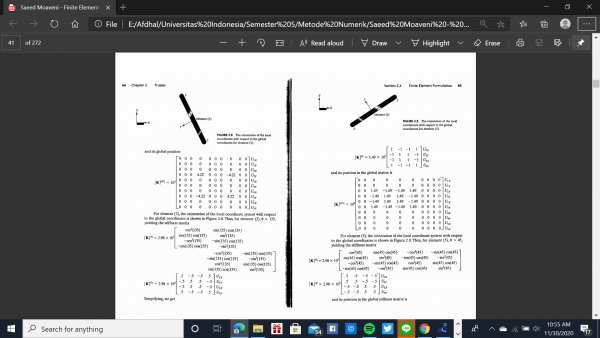
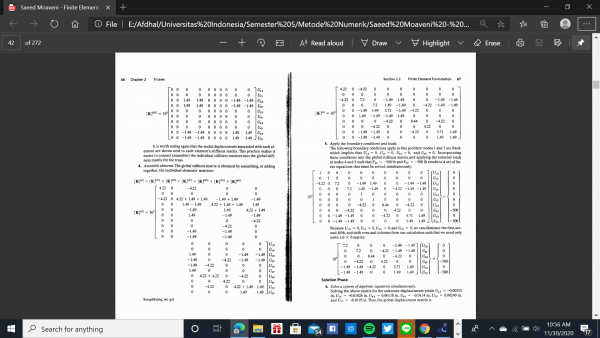
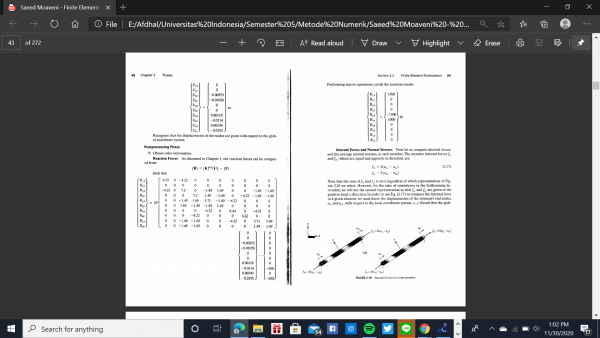
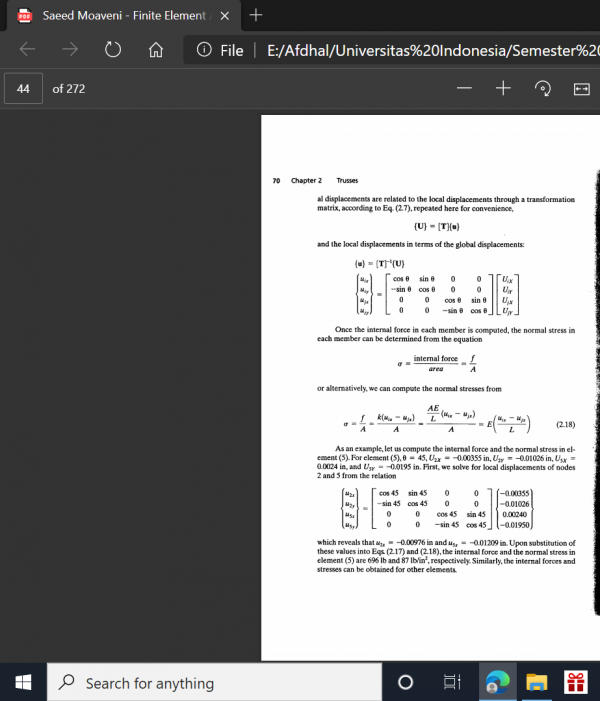
Ada 4 cara pertama Dalam menyelesaikan soal diatas :
1.Mengubah problem menjadi node dan elemen
2.Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen
3.Membuat persamaan untuk elemen
4.Menyusun dan menggabungkan matriks elemen-elemen
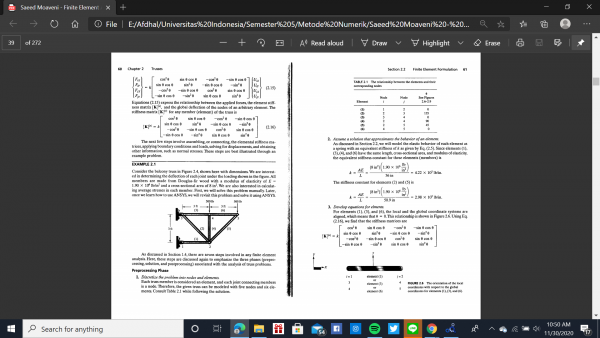
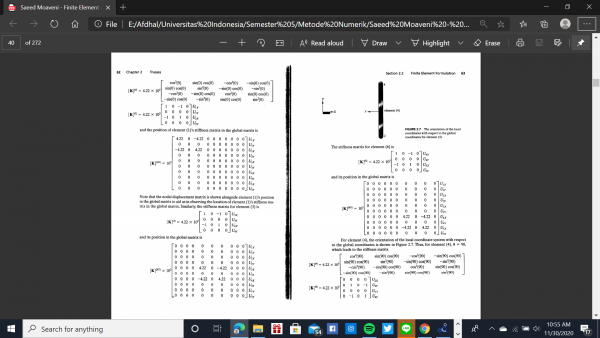
4 cara diatas ada pada buku "Finite Element Analysis" pada halaman 60-70 :
Pertemuan 4: 30 November 2020
Assalamualaikum wr.wb.
Pada pertemuan keempat ini, Pak Dai membuka diskusi dengan membahas analisa beban static dan dynamic. Pak Dai memberi kesempatan kepada mahasiswa untuk memberi pengertian dari analisa static dan dynamic. Kesimpulan dari diskusi yang saya dapat adalah analisa beban static merupakan respon material dari beban yang diam atau bebannya tidak mengalami perubahan terhadap waktu atau kata lain sigma F sama dengan 0. Sedangkan analisa beban dynamic merupakan respon beban yang mengalami perubahan terhadap perubahan waktu atau sigma F tidak sama dengan 0.
Hubungan antara metode numerik dengan statika struktur yaitu untuk memecahkan suatu permasalahan dari suatu kasus sehari-hari seperti pada Tugas 3 yaitu batang yang bisa dilakukan dengan breakdown gaya-gaya yang ada pada sistem tersebut.
Metode Numerik untuk permasalahan teknik seperti permasalahan fisika yang diubah menjadi lebih matematis dan menggunakan komputer sebagai perhitungan numerik sebagai tools untuk menghitung perhitungan yang rumit.
Quiz
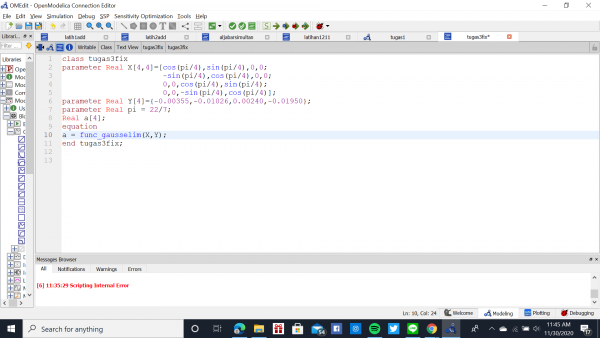
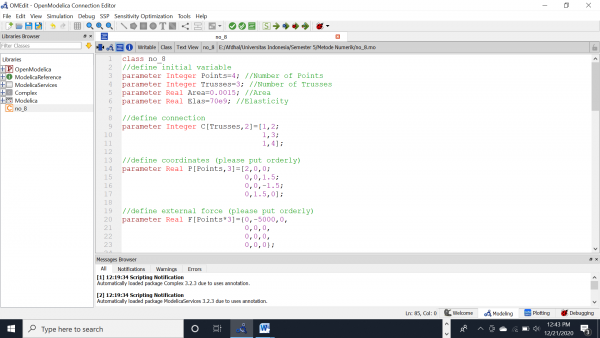
Pak Dai memberi 2 soal untuk quiz pada pertemuan keempat ini. Pak Dai meminta untuk mengirimkan Flow Chart terlebih dahulu. Berikut Flow Chart untuk soal yang diberikan Pak Dai.
Jawab No.8 :
Pertemuan 5: 7 Desember 2020
Assalamualaikum wr.wb.
Pada pertemuan ke-5 ini, Pak Dai membuka kelas dengan menanyakan tentang 2 soal minggu lalu yang diberikan oleh Pak Dai. Pak Dai memberi kesempatan untuk mahasiswa yang sudah bisa dan berhasil dalam mengerjakan soal tersebut. Salah satunya adalah Ahmad Mohammad Fahmi. Fahmi menjelaskan tentang codingan yang sudah dia buat yang bisa diterapkan untuk mengerjakan soal seperti itu. Fahmi menggunakan 1 class dan beberapa function didalam OpenModelica untuk mengerjakan soal tersebut. Alur dari pengerjaannya adalah pertama membuat class untuk menaruh semua data yang ada dari soal dengan equation yaitu beberapa fungsi. Fungsi tersebut yaitu untuk matrix element, matrix global, total dari matrix global, matrix global yang sudah dipengaruhi oleh boundary, gauss jordan untuk mendapatkan nilai U, dan mencari gaya reaksi. Tiap function tersebut memiliki codingan yang berbeda dan saling terhubung. Tetapi menurut Pak Dai, masih butuh 1 function lagi yaitu untuk memastikan gaya yang ada dalam sistem tersebut apakah sudah setimbang. Hal itu menjadi sebuah revisi untuk pekerjaan minggu depan.
Tugas 5
Soal :
|
Stiffness Matrix Element Function function StiffnessMatrixElement
input Real [:,6] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] L;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,2]/L[i];
cos_y := inisiasi_mat[i,3]/L[i];
cos_z := inisiasi_mat[i,4]/L[i];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
|
|
Stiffness Matrix Global Function function StiffnessMatrixGlobal input Integer x; input Integer [:,2] n; input Real [:,6,6] Ke_mat; output Real [size(Ke_mat,1),3*x,3*x] Kg_mat; algorithm Kg_mat := zeros(size(Ke_mat,1),3*x,3*x); for i in 1:size(Ke_mat,1) loop Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal; |
|
Sum Stiffness Matrix Element Function function SumStiffnessMatrixGlobal
input Real [:,:,:] Kg_mat;
output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
|
|
Boundary Stiffness Matrix Global Function function BoundaryStiffnessMatrixGlobal
input Real [:,:] KgTot_met;
input Integer[:] Boundary_xyz;
input Integer[:] Boundary_xy;
input Integer[:] Boundary_xz;
input Integer[:] Boundary_yz;
input Integer[:] Boundary_x;
input Integer[:] Boundary_y;
input Integer[:] Boundary_z;
output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
if Boundary_xyz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xyz,1) loop
for b in 0:2 loop
KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xy[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xy,1) loop
for b in 1:2 loop
KgB_met[3*(Boundary_xy[a])-b,i]:=0;
KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xz,1) loop
for b in 0:2:2 loop
KgB_met[3*(Boundary_xz[a])-b,i]:=0;
KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_yz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_yz,1) loop
for b in 0:1 loop
KgB_met[3*(Boundary_yz[a])-b,i]:=0;
KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_x[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_x,1) loop
KgB_met[3*(Boundary_x[a])-2,i]:=0;
KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
end for;
end for;
end if;
if Boundary_y[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_y,1) loop
KgB_met[3*(Boundary_y[a])-1,i]:=0;
KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
end for;
end for;
end if;
if Boundary_z[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_z,1) loop
KgB_met[3*Boundary_z[a],i]:=0;
KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
end for;
end for;
end if;
end BoundaryStiffnessMatrixGlobal;
|
|
Gauss Jordan Function function GaussJordan input Real [:,:] KgB_met; input Real [size(KgB_met,1)] load_met; output Real [size(KgB_met,1)] U_met; protected Real float_error = 10e-10; algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan; |
|
Reaction Force Function function ReactionForce input Real [:,:] KgTot_met; input Real [size(KgTot_met,1)] U_met; input Real [size(KgTot_met,1)] load_met; output Real [size(KgTot_met,1)] R_met; protected Real float_error = 10e-10; algorithm
R_met := KgTot_met*U_met-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end ReactionForce;
|
|
Check Force Function function CheckForce
input Real [:] load;
input Real [size(load,1)] R;
output Real [3] F;
protected Real float_error = 10e-10;
protected
Real load_x;
Real load_y;
Real load_z;
Real R_x;
Real R_y;
Real R_z;
algorithm
load_x := sum({load[i] for i in 1:3:(size(load,1)-2)});
load_y := sum({load[i] for i in 2:3:(size(load,1)-1)});
load_z := sum({load[i] for i in 3:3:size(load,1)});
R_x := sum({R[i] for i in 1:3:(size(load,1)-2)});
R_y := sum({R[i] for i in 2:3:(size(load,1)-1)});
R_z := sum({R[i] for i in 3:3:size(load,1)});
F[1] := load_x + R_x;
F[2] := load_y + R_y;
F[3] := load_z + R_z;
for i in 1:3 loop
if abs(F[i]) <= float_error then
F[i] := 0;
end if;
end for;
end CheckForce; |
|
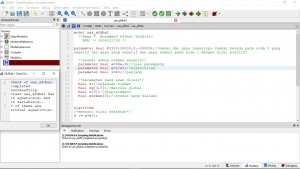
Class class QuizSoal1
//inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data //titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
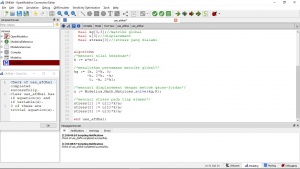
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R; //check force Real [3] F; equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
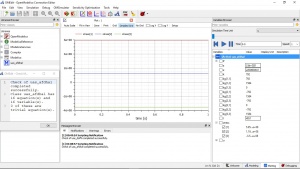
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(n, node, Ke); KgTot = SumStiffnessMatrixGlobal(Kg); KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); U = GaussJordan(KgB, load); R = ReactionForce(KgTot, U, load); F = CheckForce(load,R); end QuizSoal1; |
Pertemuan 6: 14 Desember 2020
Assalamualaikum wr.wb. Pada pertemuan ini Pak Dai meminta mahasiswanya muasabah diri untuk pencapaian dalam memahami materi Metode Numerik ini. Saya sudah agak memahami bagaimana menggunakan openmodelica walaupun belum sepenuhnya. Saya sudah mengerti flow chart dalam mengerjakan persoalan fisika tetapi untuk codingannya saya belum mengerti sepenuhnya.
Pertemuan 7: 21 Desember 2020
Assalamualaikum wr.wb.
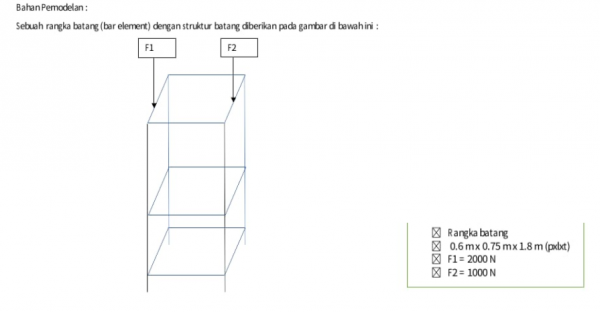
Tugas Besar
Assalamualaikum wr.wb.
Berikut merupakan progres dari tugas besar yang saya kerjakan.
Flow Chart
1. Mendefinisikan masalah
2. Menentukan asumsi dan constraint
3. Researh data profil besi siku
4. Permodelan Numerik
5. Komputasi
6. Optimasi 1 (Area Locked)
7. Optimasi 2 (Elasticity Locked)
8. Penentuan akhir material
Asumsi dan Constraint
Asumsi:
- Diasumsikan tidak ada bending karena bersifat truss
- Beban terdistribusi pada node
- Safety Factor = 2
- Batas displacement 0,001m sebelum terjadi buckling
- Variabel bebas
Constraint:
- Node 1,2,3,4 (lantai dasar) fixed
- Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga:
1. Node 13 & 16 = 1000N
2. Node 14 & 15 = 500N
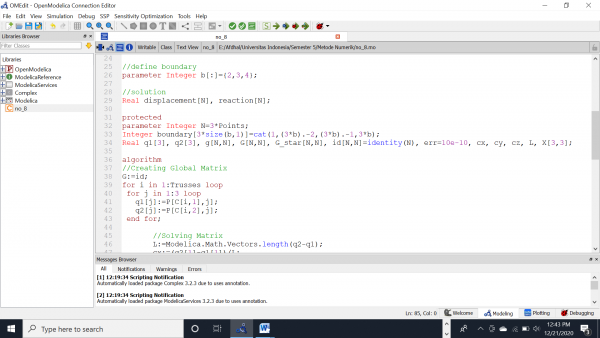
Permodelan Numerik
3D Trusses Model
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa)
parameter Real Area= (nilai area) ; //Luas Besi Siku (Dimension=30x30x3mm)
parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa)
//define connection
parameter Integer C[:,2]=[1,5; // (Elemen 1)
2,6; // (Elemen 2)
3,7; // (Elemen 3)
4,8; // (Elemen 4)
5,6; // (Elemen 5)
6,7; // (Elemen 6)
7,8; // (Elemen 7)
5,8; // (Elemen 8)
5,9; // (Elemen 9)
6,10; // (Elemen 10)
7,11; // (Elemen 11)
8,12; // (Elemen 12)
9,10; // (Elemen 13)
10,11;// (Elemen 14)
11,12;// (Elemen 15)
9,12; // (Elemen 16)
9,13; // (Elemen 17)
10,14;// (Elemen 18)
11,15;// (Elemen 19)
12,16;// (Elemen 20)
13,14;// (Elemen 21)
14,15;// (Elemen 22)
15,16;// (Elemen 23)
13,16];//(Elemen 24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
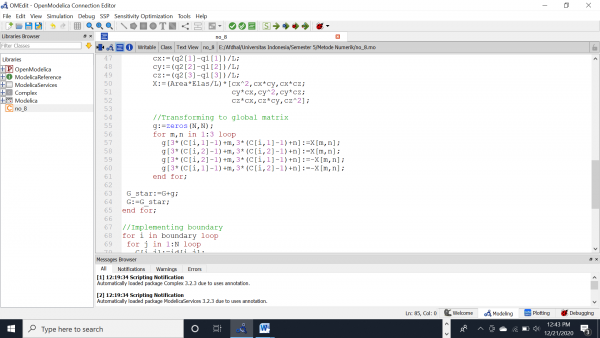
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
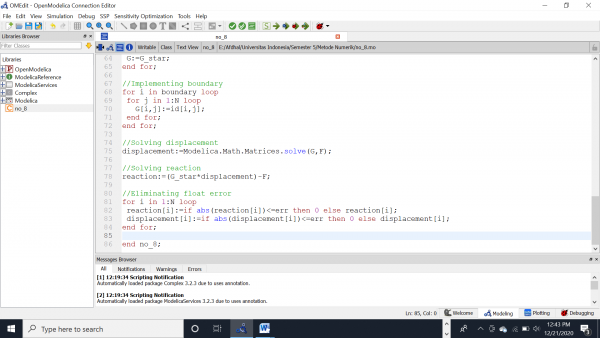
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar;
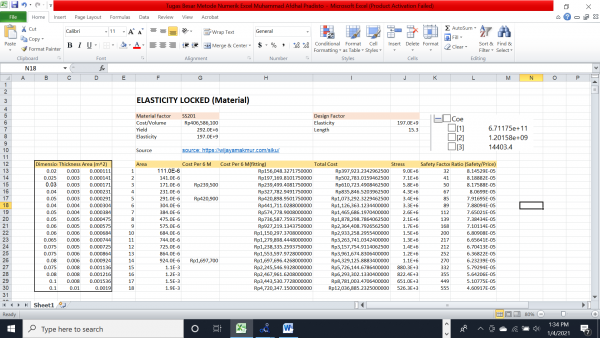
Komputasi
Berikut coding untuk menentukan curve fitting untung cost pada excel
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting; /* for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for; */
model callcurve
parameter Real [3] X={171e-6,291e-6,924e-6};
parameter Real [3] Y={239500,420900,1697700};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
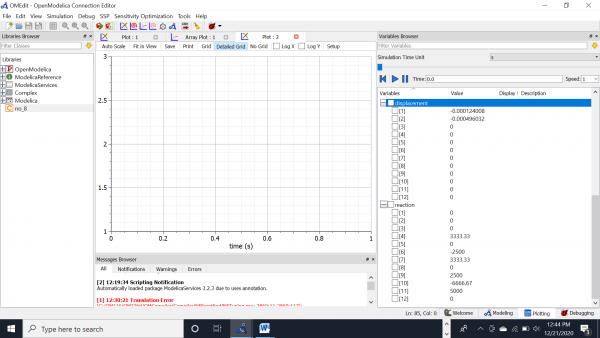
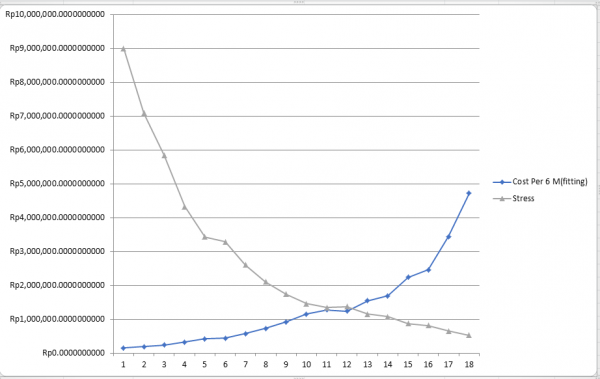
Berikut merupakan grafik yang saya dapat
UAS
No1
No2
No3
No4
No5
No6
No7