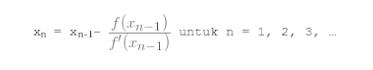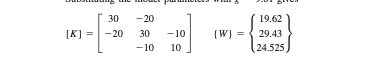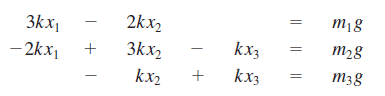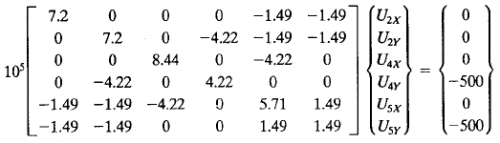Difference between revisions of "Metnum03-Anbia Maulana"

From ccitonlinewiki
Jump to: navigation, search
(→‎Pertemuan 3)
(→‎UAS)
 
(55 intermediate revisions by the same user not shown)
Line 229: Line 229:
 
X(3) = 6.06
 
X(3) = 6.06
  
−
=== Pertemuan 3 ===
+
= Pertemuan 3 =
  
 
Hari ini Pak Dai memberi tugas untuk membuktikan persamaan berikut
 
Hari ini Pak Dai memberi tugas untuk membuktikan persamaan berikut
Line 283: Line 283:
  
 
[[File:Screen Shot 2020-11-23 at 16.36.26.png]]
 
[[File:Screen Shot 2020-11-23 at 16.36.26.png]]
 +
 +
== Tugas 3 ==
 +
 +
Berikut adalah tugas yang diberikan, saya dapat menyelesaikanya
 +
 +
[[File:sistem-persamaan-aljabar-pegas-massa.png]]
 +
 +
[[File:figure12_11.jpg]]
 +
 +
Persamaan tersebut diselesaikan dengan cara eliminasi Gauss, berikut adalah yang saya modelkan
 +
 +
[[File:spring-mass-model.png]]
 +
 +
setelah melakukan melakukan pengecekan dan tidak ada masalah, saya melakukan simulasi untuk menemukan nilai x1,x2, dan x3 dari persamaan matriks tersebut. Setelah melakukan simulasi, saya melakukan plotting untuk melihat hasil yang ditemukan
 +
 +
[[File:Screen Shot 2020-11-30 at 10.23.18.png]]
 +
 +
dapat dilihat bahwa nilai x1 = 7.3575; x2 = 10.0552; x3 = 12.5077, sesuai dengan hasil yang ada di buku Metode Numerik.
 +
 +
Setelah pertemuan ini, pak Dai memberikan PR untuk mengerjakan soal berikut:
 +
 +
[[File:example2-1.png|500px|center]]
 +
 +
Penyelesaian :
 +
 +
1. Mengubah sebuah problem menjadi matrix, lalu dibuat masukan menjadi syntax yang sudah ada sebelumnya, namun kita harus memahami persoalan tersebut sehingga dapat mendapatkan kesimpulan
 +
 +
 +
'''Menerapkan kondisi batas dan beban'''
 +
Diketahui:
 +
 +
- Kondisi batas untuk node 1 dan 3 adalah fixed
 +
 +
[[File:Boundary-condition-deflection-node13.png|400px]]
 +
 +
- External force pada node 4 dan 5
 +
 +
[[File:Externalforce-node45.png|400px]]
 +
 +
Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat:
 +
 +
[[File:Deflection-matrix-simplified.png|500px|center]]
 +
 +
 +
Defleksi
 +
 +
Lalu saya memasukan ke syntax dimana dengan rumus :
 +
 +
[[File:Screen Shot 2020-11-30 at 10.43.48.png]]
 +
 +
Menghasilkan hasil sebagai berikut :
 +
 +
[[File:Screen Shot 2020-11-30 at 10.45.30.png]]
 +
 +
'''Untuk mendapatkan nilai gaya reaksi'''
 +
 +
Saya memasukan kedalam syntax :
 +
 +
[[File:Screen Shot 2020-11-30 at 10.47.54.png]]
 +
 +
Dan menghasilkan data sebagai berikut :
 +
 +
 +
[[File:Screen Shot 2020-11-30 at 10.23.18.png]]
 +
 +
'''Defleksi Total'''
 +
 +
[[File:Screen Shot 2020-11-30 at 11.01.29.png]]
 +
 +
Menghasilkan :
 +
 +
[[File:Screen Shot 2020-11-30 at 11.02.10.png]]
 +
 +
Didapatkan U2x=-0.00976 inch dan U6x=-0.01209 inch
 +
 +
= Pertemuan 4 =
 +
 +
Pertanyaan no 4
 +
 +
[[File:CamScanner 11-30-2020 16.41 1.jpg]]
 +
 +
Untuk Jawaban no 8
 +
 +
[[File:CamScanner 11-30-2020 18.29 1.jpg]]
 +
 +
Untuk Coding pertanyaan 4
 +
 +
 +
----
 +
 +
*Class
 +
 +
| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Fungsi Utama''
 +
 +
class QuizSoal1
 +
  parameter Real [:,7] inisiasi = [1, 1, 2,      0, 10e-4, 200e9, 1.00;
 +
                                  2, 2, 3,      0, 10e-4, 200e9, 1.00;
 +
                                  3, 1, 4, 308.66, 10e-4, 200e9, 1.60;
 +
                                  4, 2, 4, 270.00, 10e-4, 200e9, 1.25;
 +
                                  5, 3, 4, 231.34, 10e-4, 200e9, 1.60];
 +
                                 
 +
  parameter Integer [:,2] node = [1, 2;
 +
                                  2, 3;
 +
                                  1, 4;
 +
                                  2, 4;
 +
                                  3, 4];
 +
                                 
 +
  parameter Integer y = size(node,1);
 +
 
 +
  parameter Integer x = 2*(size(node_load,1));
 +
 
 +
  parameter Integer z = size(Boundary,1);
 +
 
 +
  parameter Integer [:] Boundary = {1,3};
 +
                             
 +
  parameter Real [:,3] node_load = [1,        0,        0;
 +
                                    2, -1035.28, -3863.70;
 +
                                    3,        0,        0;
 +
                                    4, -1035.28, -3863.70];
 +
                                   
 +
  parameter Real [2*(size(node_load,1))] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70};
 +
                                 
 +
  Real [y] k;
 +
 +
  Real [y,4,4] Ke;
 +
 
 +
  Real [y,x,x] Kg;
 +
 
 +
  Real [x,x] KgTot;
 +
 
 +
  Real [x,x] KgB;
 +
 
 +
  Real [x] U;
 +
 
 +
  Real [x] R;
 +
 
 +
equation
 +
  k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};
 +
 +
  Ke = StiffnessMatrixElement(inisiasi);
 +
 
 +
  Kg = StiffnessMatrixGlobal(node, x, y, Ke);
 +
 
 +
  KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
 +
 +
  KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
 +
 +
  U = GaussJordan(x, KgB, load);
 +
 +
  R = ReactionForce(x, KgTot, U, load);
 +
end QuizSoal1;
 +
 +
|}
 +
 +
 +
 +
Hasil yang didapat sebagai berikut:
 +
[[File:Screen Shot 2020-12-07 at 10.16.56.png|center]]
 +
 +
 +
'''Untuk menyelesaikan soal no.8 saya menggunakan coding berikut:'''
 +
 +
*Class
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Fungsi Utama''
 +
 +
class QuizSoal1
 +
  parameter Real [:,9] inisiasi = [1, 1, 2, -0.8,    0, -0.6, 15e-4, 70e9, 2.5;
 +
                                  2, 1, 3, -0.8, -0.6,    0, 15e-4, 70e9, 2.5;
 +
                                  3, 1, 4, -0.8,    0,  0.6, 15e-4, 70e9, 2.5];
 +
                                 
 +
  parameter Integer [:,2] node = [1, 2;
 +
                                  1, 3;
 +
                                  1, 4];
 +
                                 
 +
  parameter Integer y = size(node,1);
 +
 
 +
  parameter Integer x = 3*(size(node_load,1));
 +
 
 +
  parameter Integer z = size(Boundary,1);
 +
 
 +
  parameter Integer [:] Boundary = {2,3,4};
 +
                             
 +
  parameter Real [:,4] node_load = [1, 0, -5000, 0;
 +
                                    2, 0,    0, 0;
 +
                                    3, 0,    0, 0;
 +
                                    4, 0,    0, 0];
 +
                                   
 +
  parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
 +
                                 
 +
  Real [y] k;
 +
 +
  Real [y,6,6] Ke;
 +
 
 +
  Real [y,x,x] Kg;
 +
 
 +
  Real [x,x] KgTot;
 +
 
 +
  Real [x,x] KgB;
 +
 
 +
  Real [x] U;
 +
 
 +
  Real [x] R;
 +
 
 +
equation
 +
  k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
 +
 +
  Ke = StiffnessMatrixElement(inisiasi);
 +
 +
  Kg = StiffnessMatrixGlobal(node, x, y, Ke);
 +
 +
  KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
 +
 +
  KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
 +
 +
  U = GaussJordan(x, KgB, load);
 +
 +
  R = ReactionForce(x, KgTot, U, load);
 +
 +
end QuizSoal1;
 +
 +
|}
 +
 +
= Pertemuan 5 =
 +
 +
Fahmi menjelaskan mengenai codingnya dan saya mencoba untuk melakukan simulasi dan mengerjakan syntax2 tertentu
 +
 +
- looping menggunakan fungsi for.
 +
- bentuk array.
 +
- fungsi if.
 +
- floating number dan bagaimana cara menghilangkannya.
 +
- protected variable.
 +
- specialization class dan function.
 +
 +
 +
[[File:Screen Shot 2020-12-08 at 15.07.36.png]]
 +
 +
[[File:Screen Shot 2020-12-08 at 15.10.28.png]]
 +
 +
[[File:Screen Shot 2020-12-08 at 15.11.00.png]]
 +
 +
Menggunakan gauss jordan
 +
 +
[[File:Screen Shot 2020-12-08 at 15.11.55.png]]
 +
 +
[[File:Screen Shot 2020-12-08 at 15.12.26.png]]
 +
 +
[[File:Screen Shot 2020-12-08 at 15.12.49.png]]
 +
 +
Menghasilkan
 +
 +
[[File:Screen Shot 2020-12-08 at 15.16.35.png]]
 +
 +
== tugas 5 ==
 +
 +
1. Melakukan inisiasi syntax
 +
 +
[[File:Screen Shot 2020-12-14 at 11.03.55.png]]
 +
 +
2. Melakukan programing dengan Matriks stiffness Global
 +
 +
[[File:Screen Shot 2020-12-14 at 11.04.41.png]]
 +
 +
3. Didapatkan hasil sebagai berikut
 +
 +
[[File:Screen Shot 2020-12-14 at 11.05.22.png]]
 +
 +
4. [[File:Screen Shot 2020-12-14 at 11.06.10.png]]
 +
 +
[[File:Screen Shot 2020-12-14 at 11.06.40.png]]
 +
 +
[[File:Screen Shot 2020-12-14 at 11.07.04.png]]
 +
 +
== Example 3.3 ==
 +
 +
Pak dai memberikan contoh soal yang harus diselesaikan menggunakan ilmu yang diberika oleh fahmi
 +
 +
[[File:Screen Shot 2020-12-14 at 11.12.10.png]]
 +
 +
menggunakan coding sebagai berikut
 +
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Fungsi Utama''
 +
 +
class QuizSoal1
 +
  //inisiasi = [ elemen#, dX, dY, dZ, A, E]
 +
  parameter Real [:,6] inisiasi = [1,  6,  0, -3, 1.56, 10.6e6; //isi sesuai data
 +
                                  2,  0,  0, -6, 1.56, 10.6e6;
 +
                                  3,  0,  6, -3, 1.56, 10.6e6;
 +
                                  4, -6,  0, -3, 1.56, 10.6e6;
 +
                                  5, -6,  6,  0, 1.56, 10.6e6;
 +
                                  6,  0,  6,  3, 1.56, 10.6e6];
 +
 +
  //node = [ i, j]                               
 +
  parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
 +
                                                1, 3;
 +
                                                1, 4;
 +
                                                2, 3;
 +
                                                2, 4;
 +
                                                3, 4];
 +
 +
  //jumlah node
 +
  parameter Integer n = 4; //isi sesuai data
 +
 +
  //titik node boundary xyz
 +
  parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
 +
 +
  //titik node boundary xy
 +
  parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
 +
 +
  //titik node boundary xz
 +
  parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
 +
 +
  //titik node boundary yz
 +
  parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
 +
 +
  //titik node boundary x
 +
  parameter Integer [:] Boundary_x = {3}; //isi sesuai data
 +
 +
  //titik node boundary y
 +
  parameter Integer [:] Boundary_y = {0}; //isi sesuai data
 +
 +
  //titik node boundary z
 +
  parameter Integer [:] Boundary_z = {0}; //isi sesuai data
 +
                           
 +
  //load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
 +
  parameter Real [3*n] load = {0,    0, 0,  //isi sesuai data
 +
                              0, -200, 0,
 +
                              0,    0, 0,
 +
                              0,    0, 0};
 +
 +
  Real [size(inisiasi,1)] L;
 +
  Real [size(inisiasi,1)] k;
 +
  Real [size(inisiasi,1),6,6] Ke;
 +
  Real [size(inisiasi,1),3*n,3*n] Kg;
 +
  Real [3*n,3*n] KgTot;
 +
  Real [3*n,3*n] KgB;
 +
  Real [3*n] U;
 +
  Real [3*n] R;
 +
 +
  //check force
 +
  Real [3] F;
 +
 +
equation
 +
  L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
 +
 +
  k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
 +
 +
  Ke = StiffnessMatrixElement(inisiasi);
 +
 +
  Kg = StiffnessMatrixGlobal(n, node, Ke);
 +
 +
  KgTot = SumStiffnessMatrixGlobal(Kg);
 +
 +
  KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z);
 +
 +
  U = GaussJordan(KgB, load);
 +
 +
  R = ReactionForce(KgTot, U, load);
 +
 +
  F = CheckForce(load,R);
 +
 +
end QuizSoal1;
 +
 +
 +
Menghasilkan
 +
 +
[[File:Screen Shot 2020-12-14 at 11.15.34.png]]
 +
 +
Matrix Displacement dimana U = (U1x, U2x, ...)
 +
 +
[[File:Screen Shot 2020-12-14 at 11.16.34.png]]
 +
 +
Matrix gaya reaksi
 +
 +
[[File:Screen Shot 2020-12-14 at 11.17.16.png]]
 +
 +
Menghasilkan F = 0
 +
 +
Fx = 0
 +
 +
Fy = 0
 +
 +
Fz = 0
 +
 +
= Pertemuan 6 =
 +
 +
Hari ini Pak dai akan menjelaskan tentang model matematis dalam fungsi aljabar dalam metode numerik
 +
 +
menyusun model dan menyelesaikan dalam persoalan fisika ( diskrit dan continue)
 +
 +
Lalu dijelaskan oleh saudara Christo
 +
 +
1. Logical thinking membehasa tentang  soal - soal yang telah diberikan,
 +
 +
2. bagaimana mengidentifikasi parameter apa saja dari soal yang diketahui
 +
 +
3 membentuk model dari soal yang diberikan, melakukan perhitungan dari model function apa saja yang digunakan
 +
 +
= pertemuan 7 =
 +
 +
Best Efficiency point = Kecepatan sebuah fluida dimana pump beroprasi di level tertinggi atau optimum efficiency pada impeller dengan diameter tertentu
 +
 +
Pada saat 300 hp, 60% efficiency dan +- 11.000 gpm Capacity Q
 +
 +
Menentukan X upper dan X lower
 +
 +
[[File:Screen Shot 2020-12-21 at 13.10.33.png]]
 +
 +
 +
[[File:Screen Shot 2020-12-21 at 13.35.10.png]]
 +
 +
Mencari nilai
 +
 +
1. Nilai XL & XU (sudah terdapat batasan )
 +
 +
2. Memasukan persamaan d
 +
 +
3. mendapat x1 & x2
 +
 +
4. mencari F(x)
 +
 +
5. memasukan ke peraturan / rules sebelum iterasi
 +
 +
6. [[File:Screen Shot 2020-12-21 at 13.44.30.png]]
 +
 +
7. constraint : 1. menahan beban ( mencari Stress)
 +
 +
Melakukan exercise
 +
 +
[[File:Screen Shot 2020-12-21 at 13.46.29.png]]
 +
 +
[[File:91806.jpg]]
 +
 +
Internet saya drop pak, izin saya mau nunggu untuk kembali normal
 +
 +
= Pertemuan 7 =
 +
 +
One-Dimensional Unconstrained Optimization
 +
 +
Untuk menentukan fungsi global maximum
 +
 +
1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH)
 +
 +
2. Mendapatkan nilai x1 dan x2 dari golden ratio (d)
 +
 +
3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru
 +
 +
4.Mendapatkan nilai x1 dan x2 baru
 +
 +
model bracket_optimation3 parameter Integer n=8;
 +
Real x1[n];
 +
Real x2[n];
 +
Real xup;
 +
Real xlow;
 +
Real d;
 +
Real f1[n];
 +
Real f2[n];
 +
Real xopt;
 +
Real yopt; �algorithm �xup :=4; xlow:=0; �for i in (1:n) loop
 +
d:= (5^(1/2)-1)/2*(xup-xlow);
 +
x1[i]:= xlow+d;
 +
x2[i]:= xup-d;
 +
f1[i]:= f_obj3(x1[i]);
 +
f2[i]:= f_obj3(x2[i]);
 +
 +
if f1[i]>f2[i] then
 +
xup:= xup;
 +
xlow:= x2[i];
 +
xopt:= xup;
 +
yopt:= f1[i];
 +
else xlow:= xlow;
 +
xup:= x1[i];
 +
xopt:= xup;
 +
end if;
 +
end for; �end bracket_optimation3
 +
�
 +
 +
= Sinopsis Tugas Besar =
 +
 +
Pada kali ini saya akan membahas tentang tugas besar dimana menganalisa '''Optimasi design struktur sederhana'''
 +
 +
[[File:Screen Shot 2021-01-03 at 19.15.34.png]]
 +
 +
[[File:Screen Shot 2021-01-03 at 19.15.17.png]]
 +
 +
Diketahui
 +
 +
F1 = 2000 N
 +
 +
F2 = 1000 N
 +
 +
Dimensi Rangka Batang (L)
 +
 +
Bentuk Rangka
 +
 +
 +
Objective :
 +
 +
1. Membuat design seefisien mungkin dengan biaya yang rendah
 +
 +
2. Kualitas yang optimum
 +
 +
3. Menampilkan perbandingan dan menampilkan grafik terhadap
 +
 +
A) Y = '''Cost''', X = '''Area''' variabel terikat. Variabel bebas = Material
 +
 +
B)  Y = '''Cost''', X = '''Material''' variabel terikat. Variabel bebas = Areal
 +
 +
 +
Asumsi:
 +
 +
1.  Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
 +
 +
2. Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
 +
 +
3. Safety factor bernilai 2.
 +
 +
4. Batas displacement 0,001 m sebelum buckling(pada kolom paling atas)
 +
 +
Consideration :
 +
 +
1. Harga
 +
 +
2. Jenis material
 +
 +
3. Luas Cross Section
 +
 +
4. Penampang yang digunakan
 +
 +
Jenis batang yang dianalisa :
 +
 +
[[File:Screen Shot 2021-01-04 at 08.21.33.png]]
 +
 +
dengan Properties sebagai berikut :
 +
 +
[[File:Screen Shot 2021-01-04 at 08.24.09.png]]
 +
 +
Constraint :
 +
 +
1. Gaya beban terhadap struktur (1000 N dan 2000 N)
 +
 +
Metode :
 +
 +
Modeling Trusses = digunakan untuk mencari beberapa parameter seperti '''stress''' dan '''defleksi.'''
 +
 +
curve fitting =  digunakan untuk mencari '''data - data yang belum didapatkan. Sama halnya seperti sistem regresi linear.'''
 +
 +
 +
Lalu akan dilakukan simulasi optimasi dan kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.
 +
 +
----
 +
 +
Cara / Prosedur pengerjaan
 +
 +
1. Memilih bahan area, material dan harga. Terdapat 3 variasi jenis batang
 +
 +
2. Konfigurasi : Panjang L, koordinat titik node
 +
 +
3. Melakukan perhitungan
 +
 +
4. melakukan verifikasi dan chech antara '''Stress / cost'''
 +
 +
 +
----
 +
 +
Landasan Teori
 +
 +
[[File:Screen Shot 2021-01-03 at 21.17.31.png]]
 +
 +
[[File:Screen Shot 2021-01-04 at 11.52.51.png]]
 +
 +
[[File:Screen Shot 2021-01-04 at 11.53.26.png]]
 +
 +
 +
----
 +
 +
'''Syntax'''
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Trusses Modelling''
 +
 +
model Trusses_3D_Tugas_Besar_Simplified2
 +
 +
//define initial variable
 +
parameter Integer Points=16; //Number of Points
 +
parameter Integer Trusses=24; //Number of Trusses
 +
parameter Real Area=3777777.778; //Area
 +
parameter Real Elas=1; //Elasticity (equals to one in order to determine the displacement limit)
 +
 +
//define connection
 +
parameter Integer C[Trusses,2]=[1,5;
 +
                                2,6;
 +
                                3,7;
 +
                                4,8;
 +
                                5,6;  //1st floor
 +
                                6,7;  //1st floor
 +
                                7,8;  //1st floor
 +
                                5,8;  //1st floor
 +
                                5,9;
 +
                                6,10;
 +
                                7,11;
 +
                                8,12;
 +
                                9,10; //2nd floor
 +
                                10,11;//2nd floor
 +
                                11,12;//2nd floor
 +
                                9,12; //2nd floor
 +
                                9,13;
 +
                                10,14;
 +
                                11,15;
 +
                                12,16;
 +
                                13,14;//3rd floor
 +
                                14,15;//3rd floor
 +
                                15,16;//3rd floor
 +
                                13,16];//3rd floor
 +
                                                             
 +
//define coordinates (please put orderly)
 +
parameter Real P[Points,3]=[0.3,-0.375,0;    //1
 +
                            -0.3,-0.375,0;    //2
 +
                            -0.3,0.375,0;    //3
 +
                            0.3,0.375,0;      //4
 +
                            0.3,-0.375,0.6;  //5
 +
                            -0.3,-0.375,0.6;  //6
 +
                            -0.3,0.375,0.6;  //7
 +
                            0.3,0.375,0.6;    //8
 +
                            0.3,-0.375,1.2;  //9
 +
                            -0.3,-0.375,1.2;  //10 
 +
                            -0.3,0.375,1.2;  //11
 +
                            0.3,0.375,1.2;    //12
 +
                            0.3,-0.375,1.8;  //13
 +
                            -0.3,-0.375,1.8;  //14
 +
                            -0.3,0.375,1.8;  //15
 +
                            0.3,0.375,1.8];  //16
 +
                           
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,-500,
 +
                            0,0,-1000,
 +
                            0,0,-1000,
 +
                            0,0,-500};
 +
 +
//define boundary
 +
parameter Integer b[:]={1,2,3,4};
 +
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
 +
parameter Integer N=3*Points;
 +
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10;
 +
Real ers=10e-4;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
end for;
 +
     
 +
//Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                      cy*cx,cy^2,cy*cz;
 +
                      cz*cx,cz*cy,cz^2];
 +
 +
//Transforming to global matrix
 +
    g:=zeros(N,N);
 +
    for m,n in 1:3 loop
 +
      g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
      g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
    end for; 
 +
 +
G_star:=G+g;
 +
G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for i in boundary loop
 +
for j in 1:N loop
 +
  G[i,j]:=id[i,j];
 +
end for;
 +
end for;
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F;
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
  reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
  displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
  check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
end Trusses_3D_Tugas_Besar_Simplified2;
 +
 +
 
 +
Curve Fitting Function''
 +
 +
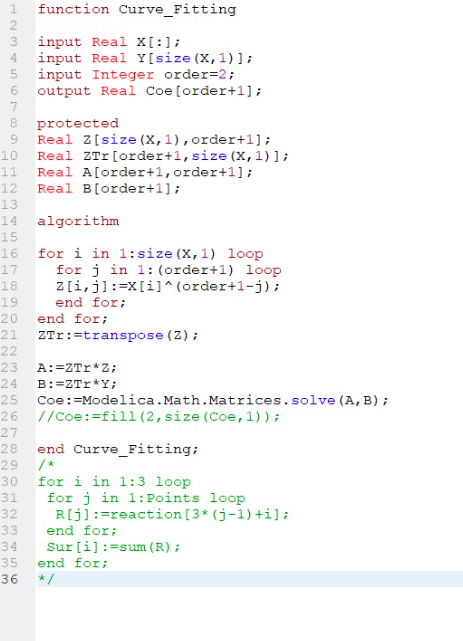
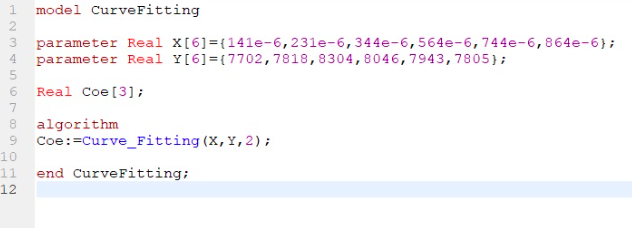
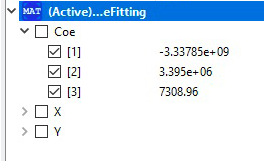
function Curve_Fitting
 +
 +
input Real X[:];
 +
input Real Y[size(X,1)];
 +
input Integer order=2;
 +
output Real Coe[order+1];
 +
 +
protected
 +
Real Z[size(X,1),order+1];
 +
Real ZTr[order+1,size(X,1)];
 +
Real A[order+1,order+1];
 +
Real B[order+1];
 +
 +
algorithm
 +
 +
for i in 1:size(X,1) loop
 +
  for j in 1:(order+1) loop
 +
  Z[i,j]:=X[i]^(order+1-j);
 +
  end for;
 +
end for;
 +
ZTr:=transpose(Z);
 +
 +
A:=ZTr*Z;
 +
B:=ZTr*Y;
 +
Coe:=Modelica.Math.Matrices.solve(A,B);
 +
 +
end Curve_Fitting;
 +
|}
 +
 +
Berikut saya lampirkan saat melakukan iterasi :
 +
 +
[[File:Screen Shot 2021-01-04 at 19.11.15.png]]
 +
 +
[[File:Screen Shot 2021-01-04 at 19.12.11.png]]
 +
 +
Dan menghasilkan
 +
 +
[[File:Screen Shot 2021-01-04 at 19.12.34.png]]
 +
 +
 +
Berikut saat dimasukan ke Excel
 +
 +
'''1. Elasticity Locked'''
 +
 +
[[File:Screen Shot 2021-01-04 at 08.30.21.png]]
 +
 +
[[File:Screen Shot 2021-01-04 at 10.48.06.png]]
 +
 +
'''2. Area locked'''
 +
 +
[[File:Screen Shot 2021-01-04 at 08.34.59.png]]
 +
 +
[[File:Screen Shot 2021-01-04 at 11.40.01.png]]
 +
 +
Disini saya membandingkan antara 3 material yaitu
 +
 +
'''SS 316 dengan SS400, SS 355, SS304'''
 +
 +
[[File:Screen Shot 2021-01-04 at 10.46.06.png]]
 +
 +
= UAS =
 +
 +
File UAS
 +
 +
no. 1
 +
 +
[[File:BED025D4-8CDB-42AF-8506-ED801D40E8A2.JPG]]
 +
 +
https://drive.google.com/file/d/1b9ZOYwH8S8XQCL5YJOA9COCq6fMluwFD/view?usp=sharing
 +
 +
 +
Syntax
 +
 +
model UasMetnumAnbia // Anbia Maulana
 +
 +
//define initial variable
 +
parameter Integer Points=size(P,1); //Number of Points
 +
parameter Integer Trusses=size(C,1); //Number of Trusses
 +
parameter Real Yield=310e6; //Yield Strength (SS403)(Pa)
 +
parameter Real Area=0.0005; //Area L Profile (m2)
 +
parameter Real Elas=1.9e11;  //Elasticity SS400 (SS403)(Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=[1,2;
 +
                          2,3;
 +
                          3,4];
 +
                                                           
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[0,0,0,1,1,1;      //1
 +
                        0,0.04,0,0,0,0;  //2
 +
                        0,0.08,0,0,0,0;  //3
 +
                        0,0.12,0,0,0,0];  //4
 +
                         
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,      //1
 +
                            0,0,0,      //2
 +
                            0,0,0,      //3
 +
                            0,200,0};  //4
 +
                         
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
Real stress1[Trusses];
 +
Real safety[Trusses];
 +
Real dis[3];
 +
Real Str[3];
 +
 +
protected
 +
parameter Integer N=3*Points;
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-4;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
    q1[j]:=P[C[i,1],j];
 +
    q2[j]:=P[C[i,2],j];
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                      cy*cx,cy^2,cy*cz;
 +
                      cz*cx,cz*cy,cz^2];
 +
 +
    //Transforming to global matrix
 +
    g:=zeros(N,N);
 +
    for m,n in 1:3 loop
 +
      g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
      g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
    end for; 
 +
 +
  G_star:=G+g;
 +
  G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
  if P[x,4] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-2,a]:=0;
 +
      G[(x*3)-2,(x*3)-2]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,5] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-1,a]:=0;
 +
      G[(x*3)-1,(x*3)-1]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,6] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[x*3,a]:=0;
 +
      G[x*3,x*3]:=1;
 +
    end for;
 +
  end if;
 +
end for; 
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F; 
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
  reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
  displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
  check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
    q1[j]:=P[C[i,1],j];
 +
    q2[j]:=P[C[i,2],j];
 +
    dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
   
 +
    Str:=(X*dis);
 +
    stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for; 
 +
 +
//Safety factor
 +
for i in 1:Trusses loop
 +
  if stress1[i]>0 then
 +
    safety[i]:=Yield/stress1[i];
 +
  else
 +
    safety[i]:=0;
 +
  end if;
 +
end for;
 +
 +
end UASMetnumMizan;
 +
model UASMetnumMizan //Mizan Eryandhika Guntorozi
 +
 +
//define initial variable
 +
parameter Integer Points=size(P,1); //Number of Points
 +
parameter Integer Trusses=size(C,1); //Number of Trusses
 +
parameter Real Yield=310e6; //Yield Strength (SS403)(Pa)
 +
parameter Real Area=0.0005; //Area L Profile (m2)
 +
parameter Real Elas=1.9e11;  //Elasticity SS400 (SS403)(Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=[1,2;
 +
                          2,3;
 +
                          3,4];
 +
                                                           
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[0,0,0,1,1,1;      //1
 +
                        0,0.04,0,0,0,0;  //2
 +
                        0,0.08,0,0,0,0;  //3
 +
                        0,0.12,0,0,0,0];  //4
 +
                         
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,      //1
 +
                            0,0,0,      //2
 +
                            0,0,0,      //3
 +
                            0,200,0};  //4
 +
                         
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
Real stress1[Trusses];
 +
Real safety[Trusses];
 +
Real dis[3];
 +
Real Str[3];
 +
 +
protected
 +
parameter Integer N=3*Points;
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-4;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
    q1[j]:=P[C[i,1],j];
 +
    q2[j]:=P[C[i,2],j];
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                      cy*cx,cy^2,cy*cz;
 +
                      cz*cx,cz*cy,cz^2];
 +
 +
    //Transforming to global matrix
 +
    g:=zeros(N,N);
 +
    for m,n in 1:3 loop
 +
      g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
      g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
    end for; 
 +
 +
  G_star:=G+g;
 +
  G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
  if P[x,4] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-2,a]:=0;
 +
      G[(x*3)-2,(x*3)-2]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,5] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-1,a]:=0;
 +
      G[(x*3)-1,(x*3)-1]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,6] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[x*3,a]:=0;
 +
      G[x*3,x*3]:=1;
 +
    end for;
 +
  end if;
 +
end for; 
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F; 
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
  reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
  displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
  check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
    q1[j]:=P[C[i,1],j];
 +
    q2[j]:=P[C[i,2],j];
 +
    dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
   
 +
    Str:=(X*dis);
 +
    stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for; 
 +
 +
//Safety factor
 +
for i in 1:Trusses loop
 +
  if stress1[i]>0 then
 +
    safety[i]:=Yield/stress1[i];
 +
  else
 +
    safety[i]:=0;
 +
  end if;
 +
end for;
 +
 +
end UASMetnumMizan;
 +
model UASMetnumMizan //Mizan Eryandhika Guntorozi
 +
 +
//define initial variable
 +
parameter Integer Points=size(P,1); //Number of Points
 +
parameter Integer Trusses=size(C,1); //Number of Trusses
 +
parameter Real Yield=310e6; //Yield Strength (SS403)(Pa)
 +
parameter Real Area=0.0005; //Area L Profile (m2)
 +
parameter Real Elas=1.9e11;  //Elasticity SS400 (SS403)(Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=[1,2;
 +
                          2,3;
 +
                          3,4];
 +
                                                           
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[0,0,0,1,1,1;      //1
 +
                        0,0.04,0,0,0,0;  //2
 +
                        0,0.08,0,0,0,0;  //3
 +
                        0,0.12,0,0,0,0];  //4
 +
                         
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,      //1
 +
                            0,0,0,      //2
 +
                            0,0,0,      //3
 +
                            0,200,0};  //4
 +
                         
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
Real stress1[Trusses];
 +
Real safety[Trusses];
 +
Real dis[3];
 +
Real Str[3];
 +
 +
protected
 +
parameter Integer N=3*Points;
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-4;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
    q1[j]:=P[C[i,1],j];
 +
    q2[j]:=P[C[i,2],j];
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                      cy*cx,cy^2,cy*cz;
 +
                      cz*cx,cz*cy,cz^2];
 +
 +
    //Transforming to global matrix
 +
    g:=zeros(N,N);
 +
    for m,n in 1:3 loop
 +
      g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
      g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
    end for; 
 +
 +
  G_star:=G+g;
 +
  G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
  if P[x,4] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-2,a]:=0;
 +
      G[(x*3)-2,(x*3)-2]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,5] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-1,a]:=0;
 +
      G[(x*3)-1,(x*3)-1]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,6] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[x*3,a]:=0;
 +
      G[x*3,x*3]:=1;
 +
    end for;
 +
  end if;
 +
end for; 
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F; 
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
  reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
  displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
  check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
    q1[j]:=P[C[i,1],j];
 +
    q2[j]:=P[C[i,2],j];
 +
    dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
   
 +
    Str:=(X*dis);
 +
    stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for; 
 +
 +
//Safety factor
 +
for i in 1:Trusses loop
 +
  if stress1[i]>0 then
 +
    safety[i]:=Yield/stress1[i];
 +
  else
 +
    safety[i]:=0;
 +
  end if;
 +
end for;
 +
 +
end UAS Metnum Anbia Maulana ;

Latest revision as of 21:26, 14 January 2021

Pertemuan Metode Numerik 03


Pendahuluan

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

Nama : Anbia Maulana Pujiantoro

NPM: 1806181842

Pertemuan 1: 9 November 2020

PR Mengenai Pemahaman Metode Numerik

Metode Numerik merupakan mata kuliah di Semester 5. Metode numerik merupakan teknik penyelesaian permsalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik. Jikapun terdapat penyelesaiannya secara analitik, proses penyelesaiaannya sering kali cukup rumit dan memakan banyak waktu sehingga tidak efisien.

Terdapat keuntungan dan kerugian terkait penggunaan metode numerik. Keuntungan dari metode ini antara lain:

1. Solusi persoalan selalu dapat diperoleh. 2. Dengan bantuan komputer, perhitungan dapat dilakukan dengan cepat serta hasil yang diperoleh dapat dibuat sedekat mungkin dengan nilai sesungguhnya. Tampilan hasil perhitungan dapat disimulasikan.


Tahapan Penyelesaian Menggunakan Metode Numerik

Terdapat beberapa tahapan dalam menyelesaikan suatu permasalahan dengan metode numerik. Tahapan-tahapan tersebut antara lain:

Pemodelan Persoalan dunia nyata dimodelkan ke dalam persamaan matematika. Persamaan matematika yang terbentuk dapat berupa persamaan linier, non-linier, dan sebagainya sesuai dengan persoalan yang dihadapi.

Penyederhanaan Model Model matematika yang dihasilkan dari tahap 1 mungkin saja terlalu kompleks. Semakin kompleks suatu model, semakin rumit penyelesaiaannya, sehingga model perlu disederhanakan.

Seberapa sederhana model yang akan kita buat? tergantung pada permasalahan apa yang hendak pembaca selesaikan. Model yang terlalu sederhana akan tidak cocok digunakan untuk digunakan sebagai pendekatan sistem nyata atau lingkungan yang begitu kompleks. Penyederhanaan dapat berupa asumsi sejumlah variabel yang terlibat tidak signifikan, atau asumsi kondisi reaktor (steady atau non-steady).

Formulasi Numerik Setelah model matematika sederhana diperoleh, tahap selanjutnya adalah memformulasikan model matematika secara numerik. Tahapan ini terdiri atas: + menentukan metode numerik yang akan dipakai bersama-sama dengan analisis galat (error) awal. + menyusun algoritma dari metode numerik yang dipilih.

Sejauh ini yang telah saya pelajari sebelum UTS mencakup 3 materi besar yaitu mencari akar-akar, regresi linier, dan turunan numerik.

1. Mencari Akar-Akar

Persamaan non-linier dapat diartikan sebagai persamaan yang tidak mengandung syarat seperti persamaan linier, sehingga persamaan non-linier dapat merupakan Beberapa metode yang saya pelajari adalah metode pencarian akar menggunakan Closed methods (Bracketing Method) dan Open Methods.


Close method

Metode tertutup disebut juga metode bracketing. Disebut sebagai metode tertutup karena dalam pencarian akar-akar persamaan non-linier dilakukan dalam suatu selang [x,y] merupakan metode untuk mencari akar-akar dengan dan tingkat error untuk mengetahui seberapa besar error saat iteration

Metode yang saya pelajari ada 3 yaitu Graphical Methods, Bisection Methods, dan False-Position Methods.

- Table / graphic method

Screen Shot 2020-11-15 at 07.41.54.png

Tabelviz.PNG


- Bisection Methods

Metode ini merupakan salah satu jenis metode incremental search method yang menggunakan batas atas dan batas bawah untuk mempersempit area pencarian akar-akar.

- False-Position Methods

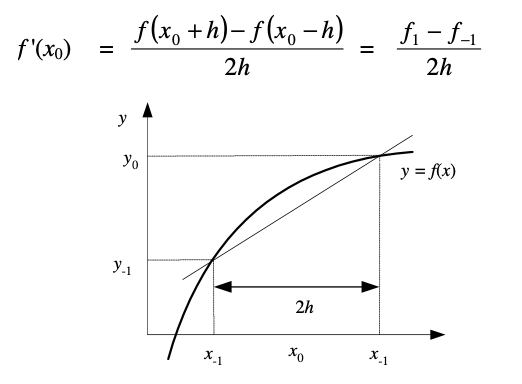
Metode ini sangat mirip dengan metode Bisection. Hal yang membedakan metode False-Position dengan Bisection adalah penentuan titik tengah dari batas-batas yang ditentukan. Penentuan titik tengah dari False-Position Method menggunakan persamaan berikut.

Open Method

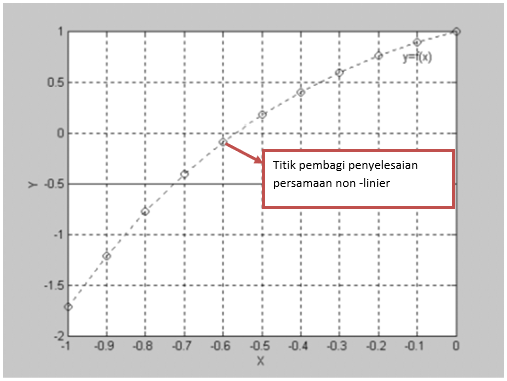
Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method

- Fixed-Point Iteration Metode ini disebut juga metode iterasi sederhana, adalah metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x)

- Newton-Raphson

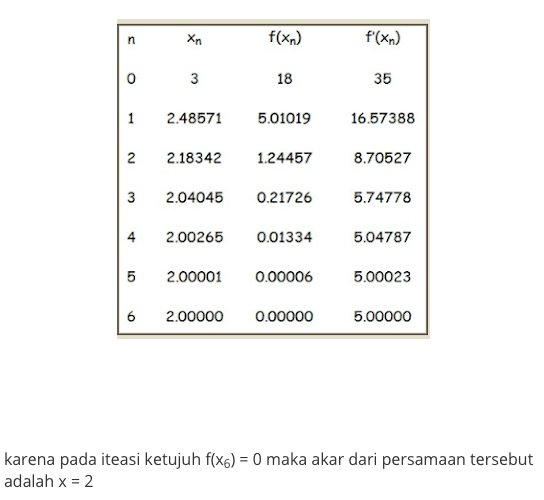
Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.


Screen Shot 2020-11-15 at 20.50.44.png

contoh soal :

Tentukan akar dari persamaan 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Newton Raphson. Penyelesaian : f(x) = 4x3 – 15x2 + 17x – 6 f’(x) = 12x2 – 30x + 17

Screen Shot 2020-11-15 at 20.51.49.png

- Secant Method

Metode ini merupakan metode modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). Persaman untuk metode Secant adalah sebagai berikut

2. Regresi Linier

regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.

Persamaan umum Regresi Linier adalah sebagai berikut:

dimana:

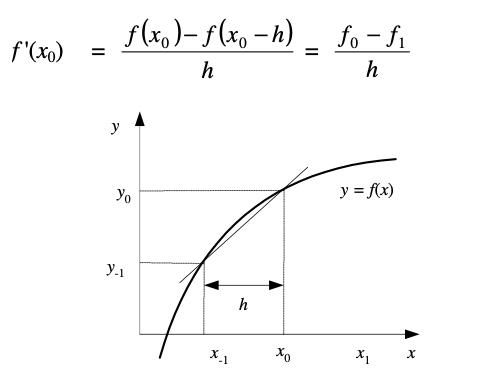
3. Turunan Numerik

Turunan Numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdiri dari 3 penyelesaian untuk permasalahan tertentu

a. Forward difference approximation


b. backward difference approximation

Screen Shot 2020-11-16 at 08.55.14.png

c. central difference approximation

Screen Shot 2020-11-16 at 08.55.53.png

Tugas 1 : 16 November 2020

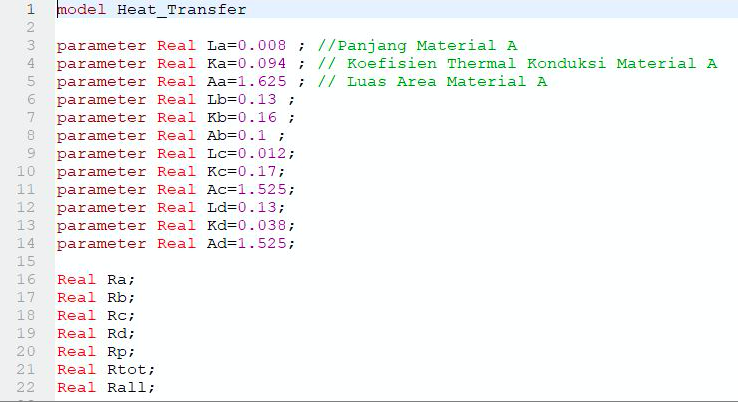
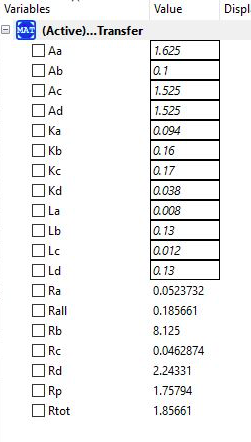
Untuk Tugas mengenai bagaimana penggunaan OpenModelica berikut saya akan menjelaskan bagaiman applikasi OpenModelica dapat menyelesaikan problem di kehidupan sehari-hari maupun berkaitan dengan mata kuliah yang lainya Pada tugas ini saya mencoba menggunakan open modelica dalam menyelesaikan soal thermal resistance. Berikut ini adalah soal dari thermal resistance beserta hasilnya.

Berikut soalnya

Screen Shot 2020-11-16 at 12.45.27.png

Screen Shot 2020-11-16 at 12.46.19.png

Dengan melakukan coding dengan openmodelica, maka hasil sebagai berikut

Screen Shot 2020-11-16 at 12.46.53.png

Screen Shot 2020-11-16 at 12.48.39.png

Lalu menghasilkan, hasil apabila di compare adalah sesuai dengan pembahasan

Screen Shot 2020-11-16 at 12.49.22.png

Untuk Video tutorial berikut file terlampir (Mohon maaf sedang uploading, file sebesar 340 MB namun upload velocity saya sangat2 lambat, segera setelah sudah diupload)


Disclaimer : Saya mempelajari & soal dari saudara Gandes, namun insyallah saya sudah paham

Pertemuan 2 : 16 November 2020

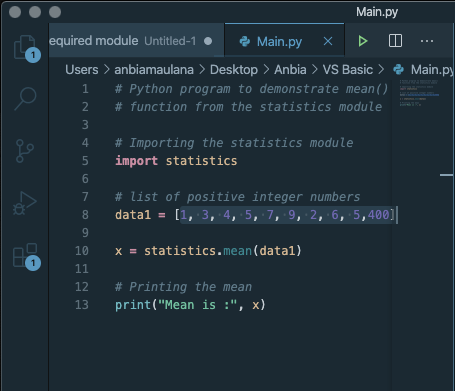
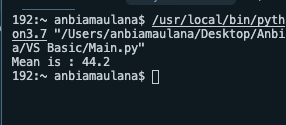
Hari ini Pak Dai menjelaskan tentang bagaimana membuat syntax sederhana untuk menghasilkan semua nilai Namun karena Openmodelica Error di MAC, maka saya mengerjakan di python

Berikut untuk hasil saya yang dikerjakan

Dimana X = 1, 3, 4, 5, 7, 9, 2, 6, 5,400

Screen Shot 2020-11-16 at 14.38.05.png

Dimana menghasilkan Screen Shot 2020-11-16 at 14.38.40.png

Mean = 44.2

Untuk grafik akan saya tambahkan karena saya harus belajar terlebih dahulu pak, besok setelah UTS akan saya input disini

Tugas 2

Assalamualaikum pak dai, mohon maaf berhubung saya menggunakan MACOS, saya melakukan iterasi menggunakan Python dan Visual Code

Dibawah ini merupakan gauss elimination yang saya akan coba eliminasi. Berikut refrensi yang saya pelajari https://www.youtube.com/watch?v=ZDxONtacA_4

Dengan soal sebagai berikut :

Screen Shot 2020-11-23 at 12.33.47.png

Lalu diubah menjadi bentuk

Screen Shot 2020-11-23 at 12.36.38.png

A -> [3, -2, 5, 2]

B ->[ 4 , 5, 8, 1, 4]

C -> [ 1, 1, 2, 1, 5]

D ->[2, 7, 6, 5, 7]

Apabila dilakukan secara manual menghasilkan

Screen Shot 2020-11-23 at 12.38.07.png


Tutorial / Step : 1. Melakukan install pada Terminal menggunakan code Import numpy as py

2. Lalu membuka python

3. Numpy sudah terinstall

Screen Shot 2020-11-23 at 12.32.31.png


Pada aplikasi Python terdapat model untuk menyelesaikan permasalahan aljabar simultan dengan menggunakan metode Gauss Elimination. Berikut ialah model yang saya buat dengan software Visual code:

1. Terlihat bahwa coding seperti ini

Screen Shot 2020-11-23 at 12.49.11.png

2. Melakukan Print (x) 3. Didapatkan hasil sebagai berikut

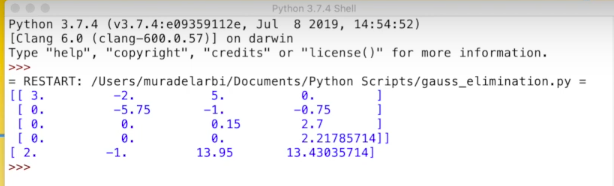
Screen Shot 2020-11-23 at 12.50.59.png

Screen Shot 2020-11-23 at 12.52.51.png


Dengan kesimpulan bahwa syntax berhasil sama dengan contoh

Screen Shot 2020-11-23 at 12.52.47.png

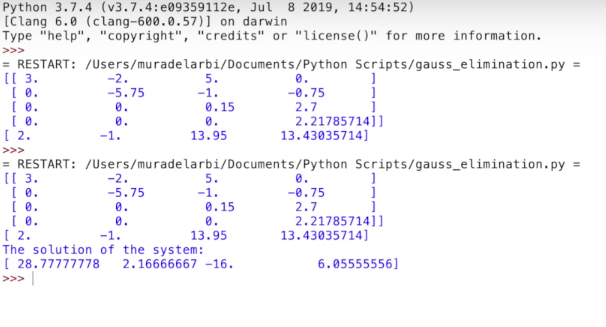
X(0) = 28,7 X(1) = 2,16 X(2) = -16 X(3) = 6.06

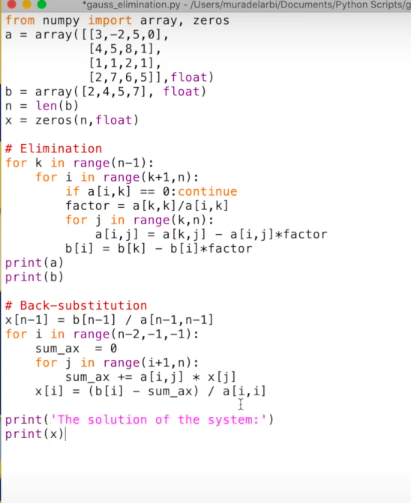
Pertemuan 3

Hari ini Pak Dai memberi tugas untuk membuktikan persamaan berikut

Screen Shot 2020-11-23 at 13.38.45.png

Dengan persamaan

K1 = [ 30, 20, 0, 19.62] ; K2 = [ -20, 30, -10, 29.42] ; k3 = [0, -10, 10, 24.525] ;

Menggunakan syntax sebagai berikut 


import numpy as array, zeros

a = array([[30, 20, 0],
           [-20, 30, -10],
           [0, -10, 10],float)

b = array ( [19.62,29.42,24.525], float)
n = len(b) 
x = zeros(n,float)

#elimination

for k in range (n-1):
   for i in range(k+1,n) :
       if a[i,k] == 0: continue
       factor = a[k,k] / a[i/k]
       for j in range(k,n) : 
           a[i,j] = a[k,j] - a[i,j]*factor
       b [i] = b [k] - b[i]*factor

print[a]
 print[b]

#back subtitution

x[n-1] = b[n-1] / a[n-1, n-1]
for i in range (n-2,-1,-1) : 
   sum_ax = 0 
   for j in range (i+1,n) : 
       sum_ax += a[i,j] * x[j]
   x[i] = (b[i] - sum_ax) / a[i,i]

print ['The solution of system : ']
print [x]

Berikut hasil syntax saya pak, namun seperti komputer saya masih kurang package Python Numpy

Screen Shot 2020-11-23 at 16.36.26.png

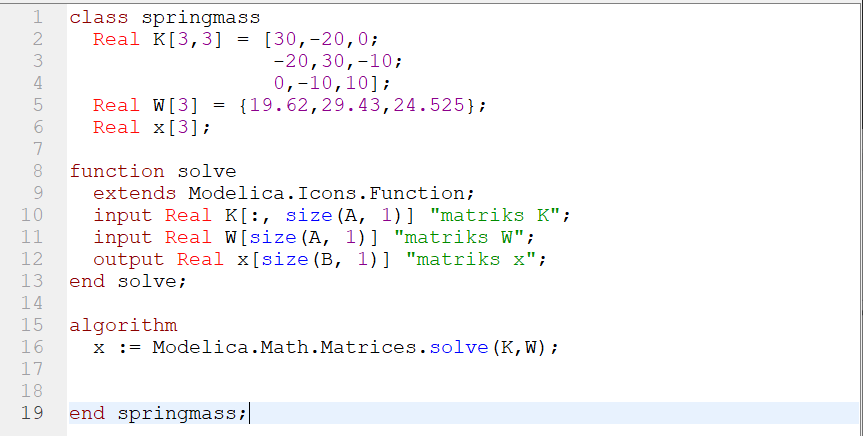
Tugas 3

Berikut adalah tugas yang diberikan, saya dapat menyelesaikanya

Sistem-persamaan-aljabar-pegas-massa.png

Figure12 11.jpg

Persamaan tersebut diselesaikan dengan cara eliminasi Gauss, berikut adalah yang saya modelkan

Spring-mass-model.png

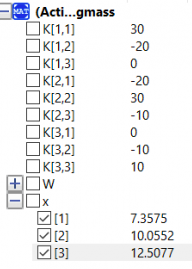
setelah melakukan melakukan pengecekan dan tidak ada masalah, saya melakukan simulasi untuk menemukan nilai x1,x2, dan x3 dari persamaan matriks tersebut. Setelah melakukan simulasi, saya melakukan plotting untuk melihat hasil yang ditemukan

Screen Shot 2020-11-30 at 10.23.18.png

dapat dilihat bahwa nilai x1 = 7.3575; x2 = 10.0552; x3 = 12.5077, sesuai dengan hasil yang ada di buku Metode Numerik.

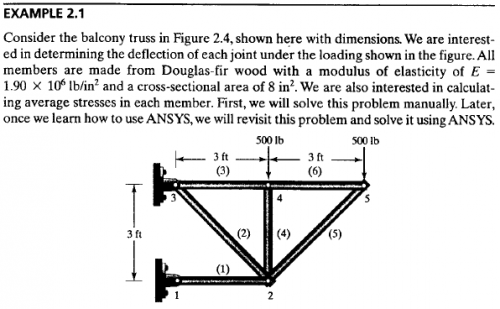
Setelah pertemuan ini, pak Dai memberikan PR untuk mengerjakan soal berikut:

Example2-1.png

Penyelesaian :

1. Mengubah sebuah problem menjadi matrix, lalu dibuat masukan menjadi syntax yang sudah ada sebelumnya, namun kita harus memahami persoalan tersebut sehingga dapat mendapatkan kesimpulan


Menerapkan kondisi batas dan beban Diketahui:

- Kondisi batas untuk node 1 dan 3 adalah fixed

Boundary-condition-deflection-node13.png

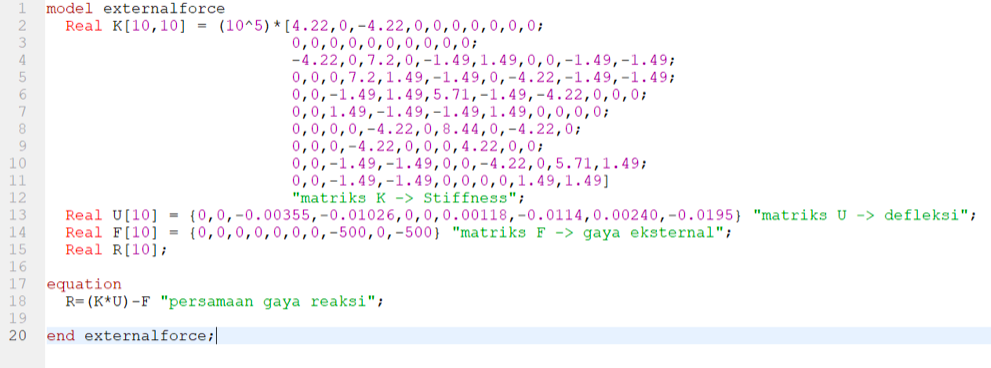
- External force pada node 4 dan 5

Externalforce-node45.png

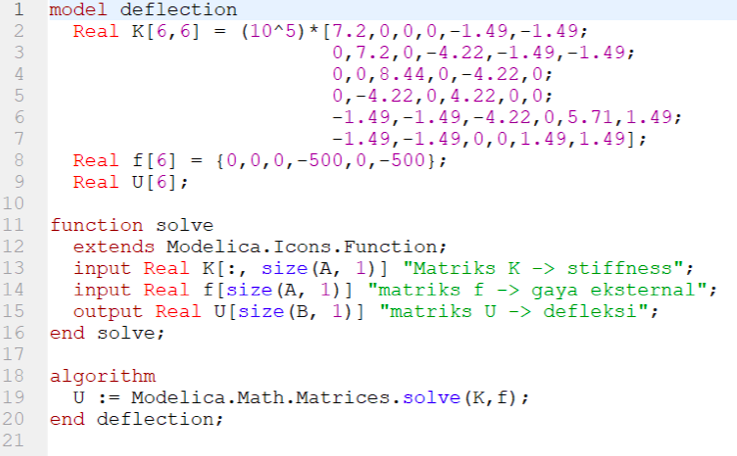
Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat:

Deflection-matrix-simplified.png


Defleksi

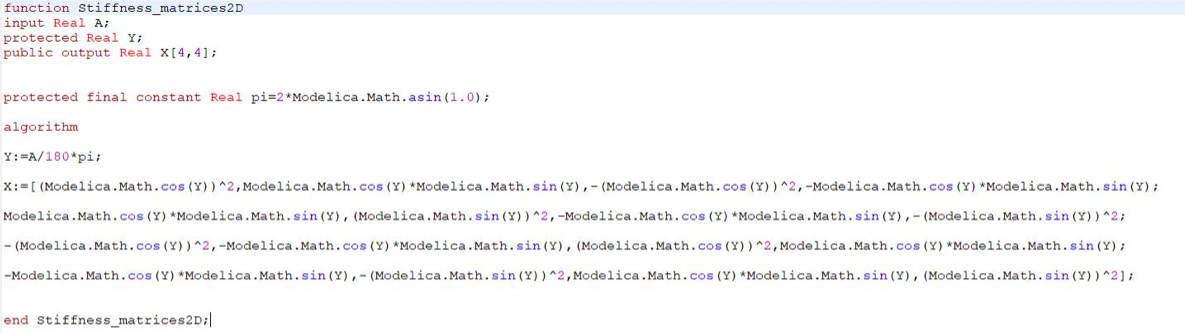
Lalu saya memasukan ke syntax dimana dengan rumus :

Screen Shot 2020-11-30 at 10.43.48.png

Menghasilkan hasil sebagai berikut :

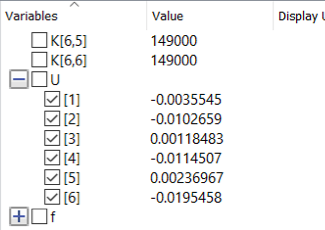
Screen Shot 2020-11-30 at 10.45.30.png

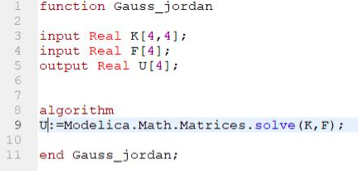
Untuk mendapatkan nilai gaya reaksi

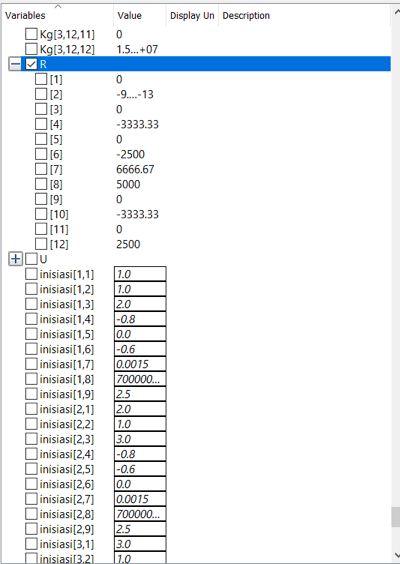
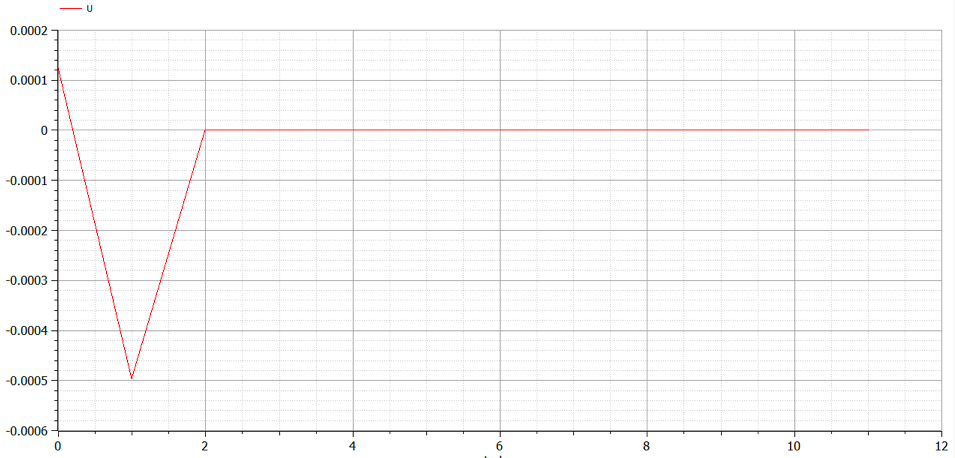
Saya memasukan kedalam syntax :

Screen Shot 2020-11-30 at 10.47.54.png

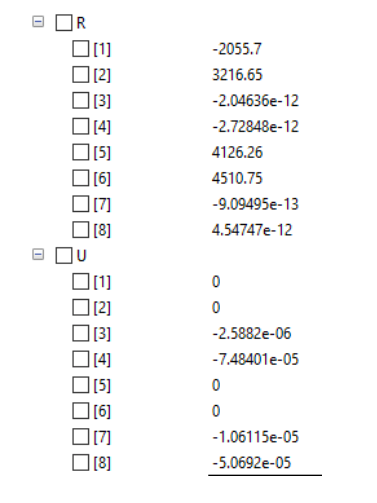
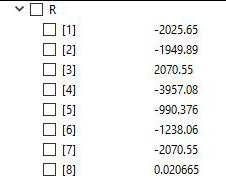
Dan menghasilkan data sebagai berikut :


Screen Shot 2020-11-30 at 10.23.18.png

Defleksi Total

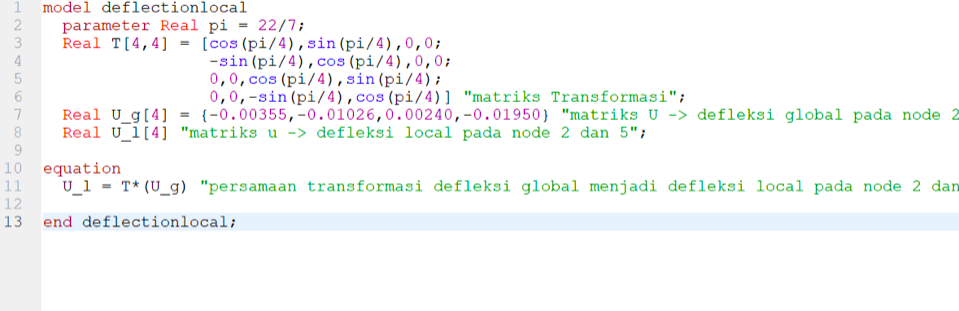
Screen Shot 2020-11-30 at 11.01.29.png

Menghasilkan :

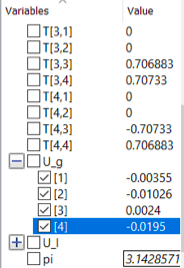
Screen Shot 2020-11-30 at 11.02.10.png

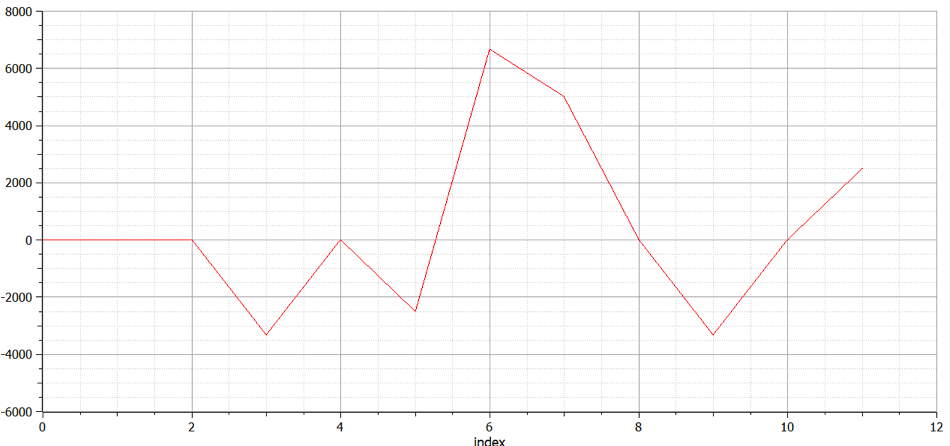
Didapatkan U2x=-0.00976 inch dan U6x=-0.01209 inch

Pertemuan 4

Pertanyaan no 4

CamScanner 11-30-2020 16.41 1.jpg

Untuk Jawaban no 8

CamScanner 11-30-2020 18.29 1.jpg

Untuk Coding pertanyaan 4


  • Class

| class="wikitable" |- | style='border-style: none none solid solid;' | Fungsi Utama 

class QuizSoal1
 parameter Real [:,7] inisiasi = [1, 1, 2,      0, 10e-4, 200e9, 1.00;
                                  2, 2, 3,      0, 10e-4, 200e9, 1.00;
                                  3, 1, 4, 308.66, 10e-4, 200e9, 1.60;
                                  4, 2, 4, 270.00, 10e-4, 200e9, 1.25; 
                                  5, 3, 4, 231.34, 10e-4, 200e9, 1.60];
                                  
 parameter Integer [:,2] node = [1, 2;
                                 2, 3;
                                 1, 4;
                                 2, 4;
                                 3, 4];
                                 
 parameter Integer y = size(node,1);
 
 parameter Integer x = 2*(size(node_load,1));
 
 parameter Integer z = size(Boundary,1);
 
 parameter Integer [:] Boundary = {1,3};
                              
 parameter Real [:,3] node_load = [1,        0,        0;
                                   2, -1035.28, -3863.70;
                                   3,        0,        0;
                                   4, -1035.28, -3863.70];
                                   
 parameter Real [2*(size(node_load,1))] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70};
                                  
 Real [y] k;

 Real [y,4,4] Ke;
 
 Real [y,x,x] Kg;
 
 Real [x,x] KgTot;
 
 Real [x,x] KgB;
 
 Real [x] U;
 
 Real [x] R;
 
equation
 k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};

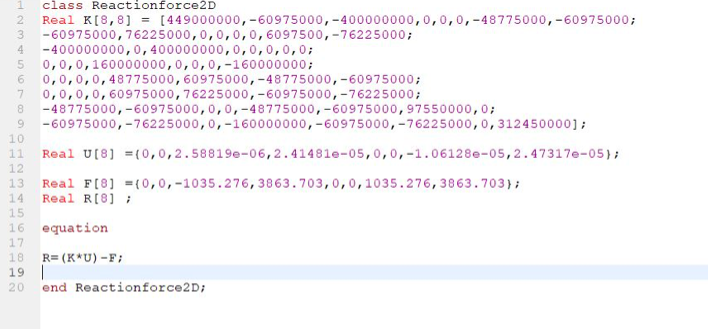
 Ke = StiffnessMatrixElement(inisiasi);
 
 Kg = StiffnessMatrixGlobal(node, x, y, Ke);
 
 KgTot = SumStiffnessMatrixGlobal(x, y, Kg);

 KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);

 U = GaussJordan(x, KgB, load);

 R = ReactionForce(x, KgTot, U, load);
end QuizSoal1;

|}


Hasil yang didapat sebagai berikut:

Screen Shot 2020-12-07 at 10.16.56.png


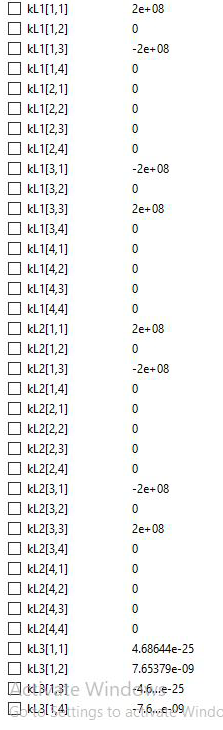
Untuk menyelesaikan soal no.8 saya menggunakan coding berikut:

  • Class

Fungsi Utama 

class QuizSoal1
 parameter Real [:,9] inisiasi = [1, 1, 2, -0.8,    0, -0.6, 15e-4, 70e9, 2.5;
                                  2, 1, 3, -0.8, -0.6,    0, 15e-4, 70e9, 2.5;
                                  3, 1, 4, -0.8,    0,  0.6, 15e-4, 70e9, 2.5];
                                  
 parameter Integer [:,2] node = [1, 2;
                                 1, 3;
                                 1, 4];
                                 
 parameter Integer y = size(node,1);
 
 parameter Integer x = 3*(size(node_load,1));
 
 parameter Integer z = size(Boundary,1);
 
 parameter Integer [:] Boundary = {2,3,4};
                              
 parameter Real [:,4] node_load = [1, 0, -5000, 0;
                                   2, 0,     0, 0;
                                   3, 0,     0, 0;
                                   4, 0,     0, 0];
                                   
 parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
                                  
 Real [y] k;

 Real [y,6,6] Ke;
 
 Real [y,x,x] Kg;
 
 Real [x,x] KgTot;
 
 Real [x,x] KgB;
 
 Real [x] U;
 
 Real [x] R;
 
equation
 k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};

 Ke = StiffnessMatrixElement(inisiasi);

 Kg = StiffnessMatrixGlobal(node, x, y, Ke);

 KgTot = SumStiffnessMatrixGlobal(x, y, Kg);

 KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);

 U = GaussJordan(x, KgB, load);

 R = ReactionForce(x, KgTot, U, load);

end QuizSoal1;

Pertemuan 5

Fahmi menjelaskan mengenai codingnya dan saya mencoba untuk melakukan simulasi dan mengerjakan syntax2 tertentu

- looping menggunakan fungsi for. - bentuk array. - fungsi if. - floating number dan bagaimana cara menghilangkannya. - protected variable. - specialization class dan function.


Screen Shot 2020-12-08 at 15.07.36.png

Screen Shot 2020-12-08 at 15.10.28.png

Screen Shot 2020-12-08 at 15.11.00.png

Menggunakan gauss jordan

Screen Shot 2020-12-08 at 15.11.55.png

Screen Shot 2020-12-08 at 15.12.26.png

Screen Shot 2020-12-08 at 15.12.49.png

Menghasilkan

Screen Shot 2020-12-08 at 15.16.35.png

tugas 5

1. Melakukan inisiasi syntax

Screen Shot 2020-12-14 at 11.03.55.png

2. Melakukan programing dengan Matriks stiffness Global

Screen Shot 2020-12-14 at 11.04.41.png

3. Didapatkan hasil sebagai berikut

Screen Shot 2020-12-14 at 11.05.22.png

4. Screen Shot 2020-12-14 at 11.06.10.png

Screen Shot 2020-12-14 at 11.06.40.png

Screen Shot 2020-12-14 at 11.07.04.png

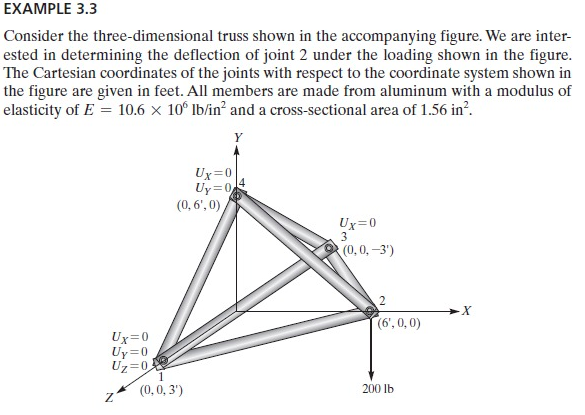
Example 3.3

Pak dai memberikan contoh soal yang harus diselesaikan menggunakan ilmu yang diberika oleh fahmi

Screen Shot 2020-12-14 at 11.12.10.png

menggunakan coding sebagai berikut

|- | style='border-style: none none solid solid;' | Fungsi Utama 

class QuizSoal1
 //inisiasi = [ elemen#, dX, dY, dZ, A, E]
 parameter Real [:,6] inisiasi = [1,  6,  0, -3, 1.56, 10.6e6; //isi sesuai data
                                  2,  0,  0, -6, 1.56, 10.6e6;
                                  3,  0,  6, -3, 1.56, 10.6e6;
                                  4, -6,  0, -3, 1.56, 10.6e6;
                                  5, -6,  6,  0, 1.56, 10.6e6;
                                  6,  0,  6,  3, 1.56, 10.6e6];

 //node = [ i, j]                                 
 parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
                                                1, 3;
                                                1, 4;
                                                2, 3;
                                                2, 4;
                                                3, 4];

 //jumlah node
 parameter Integer n = 4; //isi sesuai data

 //titik node boundary xyz
 parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data

 //titik node boundary xy
 parameter Integer [:] Boundary_xy = {4}; //isi sesuai data

 //titik node boundary xz
 parameter Integer [:] Boundary_xz = {0}; //isi sesuai data

 //titik node boundary yz
 parameter Integer [:] Boundary_yz = {0}; //isi sesuai data

 //titik node boundary x
 parameter Integer [:] Boundary_x = {3}; //isi sesuai data

 //titik node boundary y
 parameter Integer [:] Boundary_y = {0}; //isi sesuai data

 //titik node boundary z
 parameter Integer [:] Boundary_z = {0}; //isi sesuai data
                            
 //load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
 parameter Real [3*n] load = {0,    0, 0,  //isi sesuai data
                              0, -200, 0, 
                              0,    0, 0, 
                              0,    0, 0}; 

 Real [size(inisiasi,1)] L;
 Real [size(inisiasi,1)] k;
 Real [size(inisiasi,1),6,6] Ke;
 Real [size(inisiasi,1),3*n,3*n] Kg;
 Real [3*n,3*n] KgTot;
 Real [3*n,3*n] KgB;
 Real [3*n] U;
 Real [3*n] R;

 //check force
 Real [3] F;

equation
 L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)}; 

 k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};

 Ke = StiffnessMatrixElement(inisiasi);

 Kg = StiffnessMatrixGlobal(n, node, Ke);

 KgTot = SumStiffnessMatrixGlobal(Kg);

 KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z);

 U = GaussJordan(KgB, load);

 R = ReactionForce(KgTot, U, load);

 F = CheckForce(load,R);

end QuizSoal1;


Menghasilkan

Screen Shot 2020-12-14 at 11.15.34.png

Matrix Displacement dimana U = (U1x, U2x, ...)

Screen Shot 2020-12-14 at 11.16.34.png

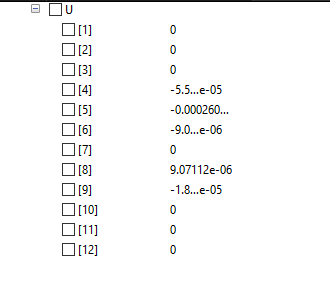
Matrix gaya reaksi

Screen Shot 2020-12-14 at 11.17.16.png

Menghasilkan F = 0

Fx = 0

Fy = 0

Fz = 0

Pertemuan 6

Hari ini Pak dai akan menjelaskan tentang model matematis dalam fungsi aljabar dalam metode numerik

menyusun model dan menyelesaikan dalam persoalan fisika ( diskrit dan continue)

Lalu dijelaskan oleh saudara Christo

1. Logical thinking membehasa tentang soal - soal yang telah diberikan,

2. bagaimana mengidentifikasi parameter apa saja dari soal yang diketahui

3 membentuk model dari soal yang diberikan, melakukan perhitungan dari model function apa saja yang digunakan

pertemuan 7

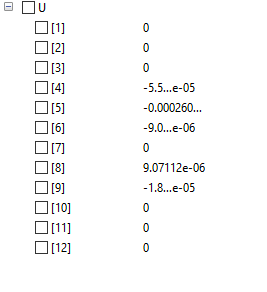
Best Efficiency point = Kecepatan sebuah fluida dimana pump beroprasi di level tertinggi atau optimum efficiency pada impeller dengan diameter tertentu

Pada saat 300 hp, 60% efficiency dan +- 11.000 gpm Capacity Q

Menentukan X upper dan X lower

Screen Shot 2020-12-21 at 13.10.33.png


Screen Shot 2020-12-21 at 13.35.10.png

Mencari nilai

1. Nilai XL & XU (sudah terdapat batasan )

2. Memasukan persamaan d

3. mendapat x1 & x2

4. mencari F(x)

5. memasukan ke peraturan / rules sebelum iterasi

6. Screen Shot 2020-12-21 at 13.44.30.png

7. constraint : 1. menahan beban ( mencari Stress)

Melakukan exercise

Screen Shot 2020-12-21 at 13.46.29.png

91806.jpg

Internet saya drop pak, izin saya mau nunggu untuk kembali normal

Pertemuan 7

One-Dimensional Unconstrained Optimization

Untuk menentukan fungsi global maximum

1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH)

2. Mendapatkan nilai x1 dan x2 dari golden ratio (d)

3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru

4.Mendapatkan nilai x1 dan x2 baru 

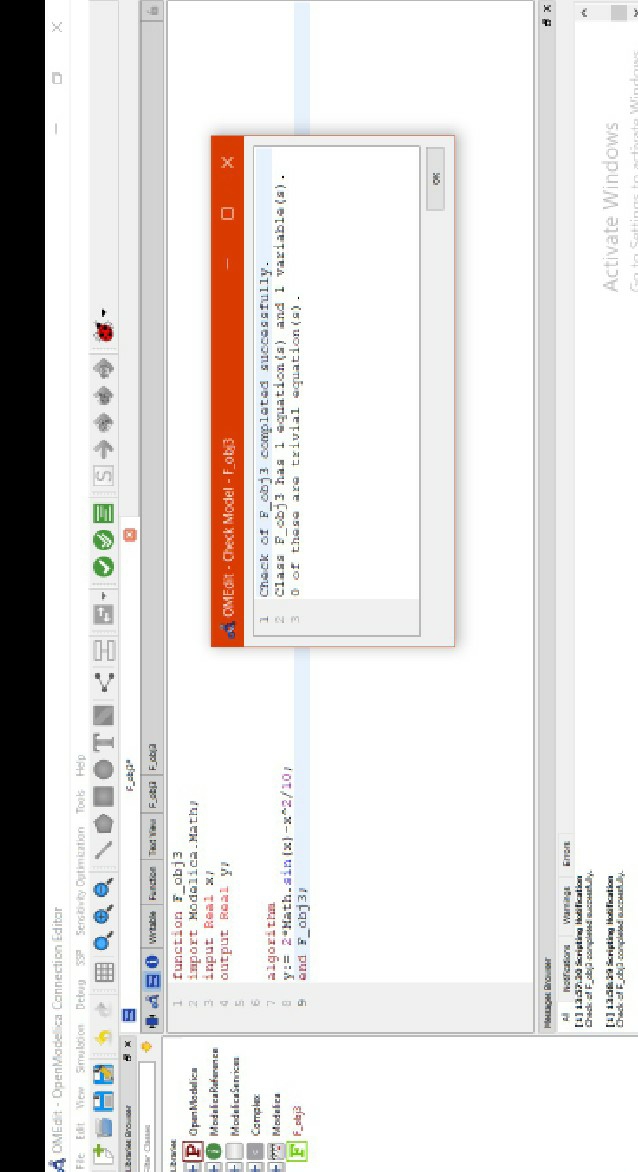
model bracket_optimation3 parameter Integer n=8;
Real x1[n]; 
Real x2[n]; 
Real xup; 
Real xlow; 
Real d; 
Real f1[n];
Real f2[n];
Real xopt; 
Real yopt; �algorithm �xup :=4; xlow:=0; �for i in (1:n) loop 
d:= (5^(1/2)-1)/2*(xup-xlow); 
x1[i]:= xlow+d; 
x2[i]:= xup-d; 
f1[i]:= f_obj3(x1[i]);
f2[i]:= f_obj3(x2[i]);

if f1[i]>f2[i] then 
xup:= xup;
xlow:= x2[i];
xopt:= xup; 
yopt:= f1[i];
else xlow:= xlow; 
xup:= x1[i];
xopt:= xup;
end if;
end for; �end bracket_optimation3

�

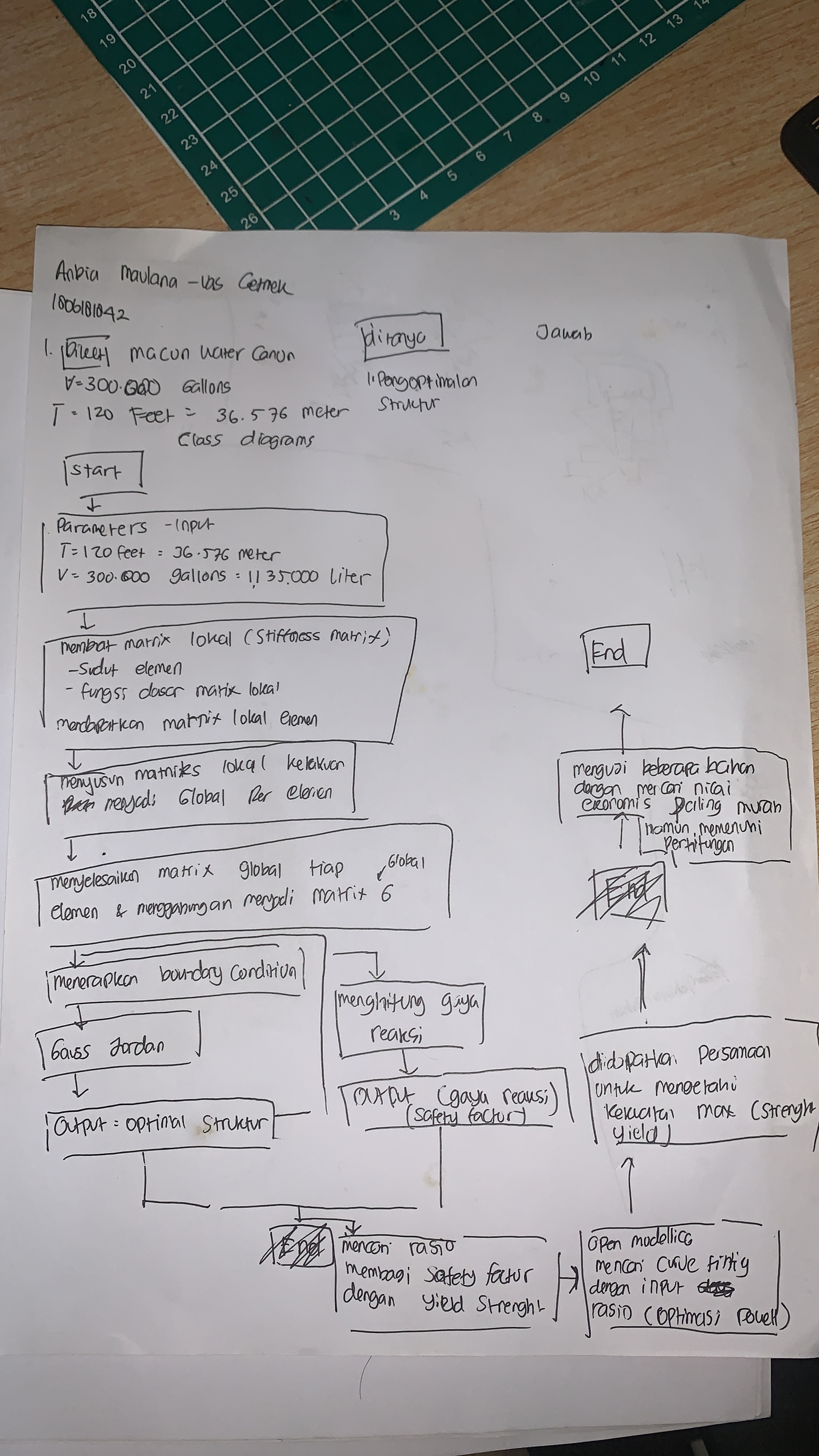
Sinopsis Tugas Besar

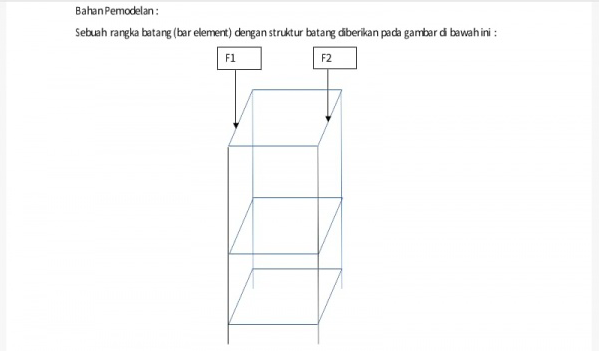
Pada kali ini saya akan membahas tentang tugas besar dimana menganalisa Optimasi design struktur sederhana

Screen Shot 2021-01-03 at 19.15.34.png

Screen Shot 2021-01-03 at 19.15.17.png

Diketahui

F1 = 2000 N

F2 = 1000 N

Dimensi Rangka Batang (L)

Bentuk Rangka


Objective :

1. Membuat design seefisien mungkin dengan biaya yang rendah

2. Kualitas yang optimum

3. Menampilkan perbandingan dan menampilkan grafik terhadap

A) Y = Cost, X = Area variabel terikat. Variabel bebas = Material

B) Y = Cost, X = Material variabel terikat. Variabel bebas = Areal


Asumsi:

1. Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.

2. Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)

3. Safety factor bernilai 2.

4. Batas displacement 0,001 m sebelum buckling(pada kolom paling atas)

Consideration :

1. Harga

2. Jenis material

3. Luas Cross Section

4. Penampang yang digunakan

Jenis batang yang dianalisa :

Screen Shot 2021-01-04 at 08.21.33.png

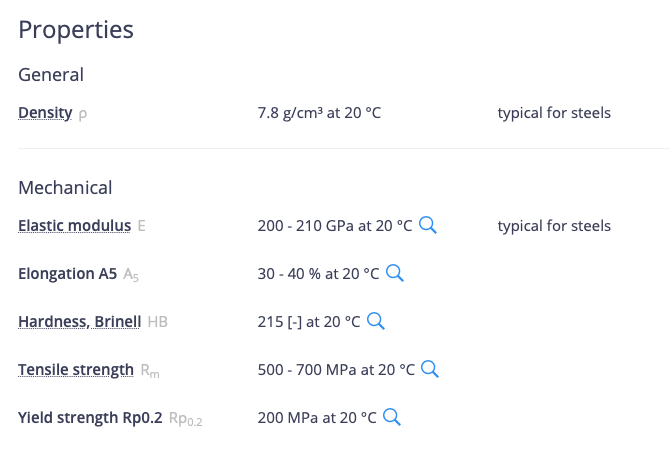
dengan Properties sebagai berikut :

Screen Shot 2021-01-04 at 08.24.09.png

Constraint :

1. Gaya beban terhadap struktur (1000 N dan 2000 N)

Metode :

Modeling Trusses = digunakan untuk mencari beberapa parameter seperti stress dan defleksi.

curve fitting = digunakan untuk mencari data - data yang belum didapatkan. Sama halnya seperti sistem regresi linear.


Lalu akan dilakukan simulasi optimasi dan kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.

Cara / Prosedur pengerjaan

1. Memilih bahan area, material dan harga. Terdapat 3 variasi jenis batang

2. Konfigurasi : Panjang L, koordinat titik node

3. Melakukan perhitungan

4. melakukan verifikasi dan chech antara Stress / cost


Landasan Teori

Screen Shot 2021-01-03 at 21.17.31.png

Screen Shot 2021-01-04 at 11.52.51.png

Screen Shot 2021-01-04 at 11.53.26.png


Syntax

Trusses Modelling 

model Trusses_3D_Tugas_Besar_Simplified2

//define initial variable
parameter Integer Points=16; //Number of Points
parameter Integer Trusses=24; //Number of Trusses
parameter Real Area=3777777.778; //Area
parameter Real Elas=1; //Elasticity (equals to one in order to determine the displacement limit)

//define connection
parameter Integer C[Trusses,2]=[1,5; 
                                2,6;
                                3,7;
                                4,8;
                                5,6;  //1st floor
                                6,7;  //1st floor
                                7,8;  //1st floor
                                5,8;  //1st floor
                                5,9;
                                6,10;
                                7,11;
                                8,12;
                                9,10; //2nd floor
                                10,11;//2nd floor 
                                11,12;//2nd floor
                                9,12; //2nd floor
                                9,13;
                                10,14;
                                11,15;
                                12,16;
                                13,14;//3rd floor
                                14,15;//3rd floor
                                15,16;//3rd floor
                                13,16];//3rd floor
                                                             
//define coordinates (please put orderly)
parameter Real P[Points,3]=[0.3,-0.375,0;     //1
                            -0.3,-0.375,0;    //2
                            -0.3,0.375,0;     //3
                            0.3,0.375,0;      //4
                            0.3,-0.375,0.6;   //5
                            -0.3,-0.375,0.6;  //6
                            -0.3,0.375,0.6;   //7
                            0.3,0.375,0.6;    //8
                            0.3,-0.375,1.2;   //9
                            -0.3,-0.375,1.2;  //10  
                            -0.3,0.375,1.2;   //11
                            0.3,0.375,1.2;    //12
                            0.3,-0.375,1.8;   //13
                            -0.3,-0.375,1.8;  //14
                            -0.3,0.375,1.8;   //15
                            0.3,0.375,1.8];   //16
                            
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,-500, 
                            0,0,-1000, 
                            0,0,-1000, 
                            0,0,-500};

//define boundary
parameter Integer b[:]={1,2,3,4};

//solution
Real displacement[N], reaction[N];
Real check[3];

parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10;
Real ers=10e-4;

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
end for;
      
//Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2];

//Transforming to global matrix
   g:=zeros(N,N); 
   for m,n in 1:3 loop
     g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
     g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
   end for;  

G_star:=G+g;
G:=G_star;
end for;

//Implementing boundary
for i in boundary loop
for j in 1:N loop
  G[i,j]:=id[i,j];
end for;
end for;

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction
reaction:=(G_star*displacement)-F;

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for; 

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
  
for i in 1:3 loop
 check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;

end Trusses_3D_Tugas_Besar_Simplified2;



Curve Fitting Function

function Curve_Fitting

input Real X[:];
input Real Y[size(X,1)];
input Integer order=2;
output Real Coe[order+1];

protected
Real Z[size(X,1),order+1];
Real ZTr[order+1,size(X,1)];
Real A[order+1,order+1];
Real B[order+1];

algorithm

for i in 1:size(X,1) loop
 for j in 1:(order+1) loop
 Z[i,j]:=X[i]^(order+1-j);
 end for;
end for;
ZTr:=transpose(Z);

A:=ZTr*Z;
B:=ZTr*Y;
Coe:=Modelica.Math.Matrices.solve(A,B);

end Curve_Fitting;

Berikut saya lampirkan saat melakukan iterasi :

Screen Shot 2021-01-04 at 19.11.15.png

Screen Shot 2021-01-04 at 19.12.11.png

Dan menghasilkan

Screen Shot 2021-01-04 at 19.12.34.png


Berikut saat dimasukan ke Excel

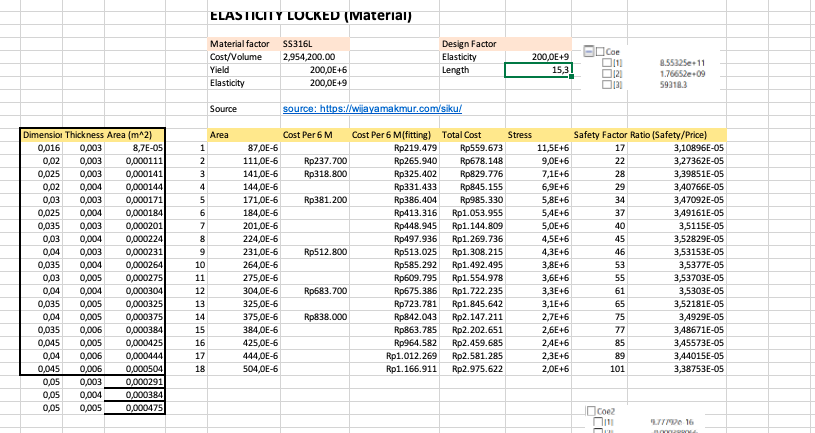
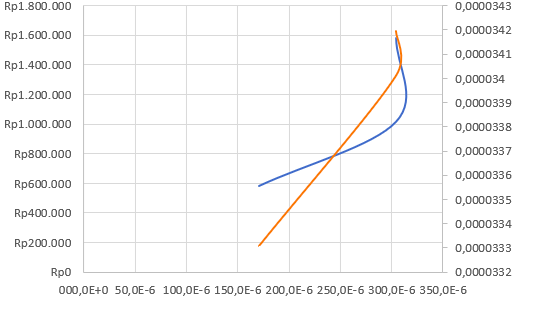
1. Elasticity Locked

Screen Shot 2021-01-04 at 08.30.21.png

Screen Shot 2021-01-04 at 10.48.06.png

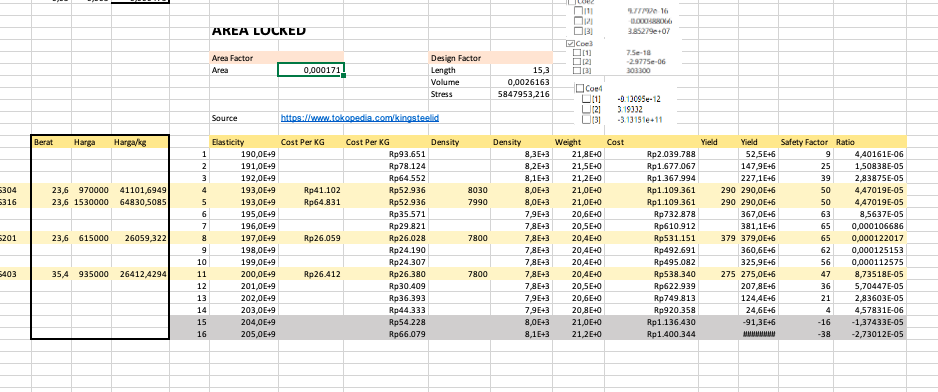
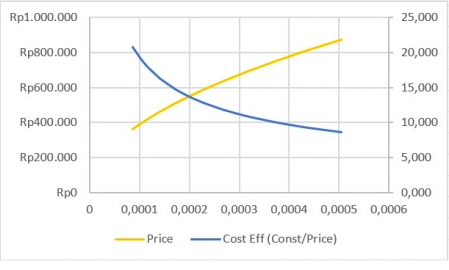
2. Area locked

Screen Shot 2021-01-04 at 08.34.59.png

Screen Shot 2021-01-04 at 11.40.01.png

Disini saya membandingkan antara 3 material yaitu

SS 316 dengan SS400, SS 355, SS304

Screen Shot 2021-01-04 at 10.46.06.png

UAS

File UAS

no. 1

BED025D4-8CDB-42AF-8506-ED801D40E8A2.JPG

https://drive.google.com/file/d/1b9ZOYwH8S8XQCL5YJOA9COCq6fMluwFD/view?usp=sharing


Syntax 

model UasMetnumAnbia // Anbia Maulana

//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=310e6; //Yield Strength (SS403)(Pa)
parameter Real Area=0.0005; //Area L Profile (m2)
parameter Real Elas=1.9e11;  //Elasticity SS400 (SS403)(Pa)

//define connection
parameter Integer C[:,2]=[1,2; 
                          2,3;
                          3,4];
                                                            
//define coordinates (please put orderly)
parameter Real P[:,6]=[0,0,0,1,1,1;      //1
                       0,0.04,0,0,0,0;   //2
                       0,0.08,0,0,0,0;   //3
                       0,0.12,0,0,0,0];  //4
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,      //1
                            0,0,0,      //2
                            0,0,0,      //3
                            0,200,0};   //4
                          
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];

protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
 end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2];

   //Transforming to global matrix
   g:=zeros(N,N); 
   for m,n in 1:3 loop
     g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
     g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
   end for;  

 G_star:=G+g;
 G:=G_star;
end for;

//Implementing boundary
for x in 1:Points loop
  if P[x,4] <> 0 then
    for a in 1:Points*3 loop
      G[(x*3)-2,a]:=0;
      G[(x*3)-2,(x*3)-2]:=1;
    end for;
  end if;
  if P[x,5] <> 0 then
    for a in 1:Points*3 loop
      G[(x*3)-1,a]:=0;
      G[(x*3)-1,(x*3)-1]:=1;
    end for;
  end if;
  if P[x,6] <> 0 then
    for a in 1:Points*3 loop
      G[x*3,a]:=0;
      G[x*3,x*3]:=1;
    end for;
  end if;
end for;  

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F); 

//Solving reaction
reaction:=(G_star*displacement)-F;  

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 
for i in 1:3 loop
  check[i] := if abs(check[i])<=ers then 0 else check[i];
end for; 

//Calculating stress in each truss 
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
   dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 end for;
      
    //Solving Matrix
    L:=Modelica.Math.Vectors.length(q2-q1);
    cx:=(q2[1]-q1[1])/L;
    cy:=(q2[2]-q1[2])/L;
    cz:=(q2[3]-q1[3])/L; 
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
                cy*cx,cy^2,cy*cz;
                cz*cx,cz*cy,cz^2];
   
    Str:=(X*dis);
    stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;  

//Safety factor
for i in 1:Trusses loop
  if stress1[i]>0 then
    safety[i]:=Yield/stress1[i];
  else
    safety[i]:=0;
  end if; 
end for; 

end UASMetnumMizan;

model UASMetnumMizan //Mizan Eryandhika Guntorozi 

//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=310e6; //Yield Strength (SS403)(Pa)
parameter Real Area=0.0005; //Area L Profile (m2)
parameter Real Elas=1.9e11;  //Elasticity SS400 (SS403)(Pa)

//define connection
parameter Integer C[:,2]=[1,2; 
                          2,3;
                          3,4];
                                                            
//define coordinates (please put orderly)
parameter Real P[:,6]=[0,0,0,1,1,1;      //1
                       0,0.04,0,0,0,0;   //2
                       0,0.08,0,0,0,0;   //3
                       0,0.12,0,0,0,0];  //4
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,      //1
                            0,0,0,      //2
                            0,0,0,      //3
                            0,200,0};   //4
                          
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];

protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
 end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2];

   //Transforming to global matrix
   g:=zeros(N,N); 
   for m,n in 1:3 loop
     g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
     g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
   end for;  

 G_star:=G+g;
 G:=G_star;
end for;

//Implementing boundary
for x in 1:Points loop
  if P[x,4] <> 0 then
    for a in 1:Points*3 loop
      G[(x*3)-2,a]:=0;
      G[(x*3)-2,(x*3)-2]:=1;
    end for;
  end if;
  if P[x,5] <> 0 then
    for a in 1:Points*3 loop
      G[(x*3)-1,a]:=0;
      G[(x*3)-1,(x*3)-1]:=1;
    end for;
  end if;
  if P[x,6] <> 0 then
    for a in 1:Points*3 loop
      G[x*3,a]:=0;
      G[x*3,x*3]:=1;
    end for;
  end if;
end for;  

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F); 

//Solving reaction
reaction:=(G_star*displacement)-F;  

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 
for i in 1:3 loop
  check[i] := if abs(check[i])<=ers then 0 else check[i];
end for; 

//Calculating stress in each truss 
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
   dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 end for;
      
    //Solving Matrix
    L:=Modelica.Math.Vectors.length(q2-q1);
    cx:=(q2[1]-q1[1])/L;
    cy:=(q2[2]-q1[2])/L;
    cz:=(q2[3]-q1[3])/L; 
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
                cy*cx,cy^2,cy*cz;
                cz*cx,cz*cy,cz^2];
   
    Str:=(X*dis);
    stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;  

//Safety factor
for i in 1:Trusses loop
  if stress1[i]>0 then
    safety[i]:=Yield/stress1[i];
  else
    safety[i]:=0;
  end if; 
end for; 

end UASMetnumMizan;

model UASMetnumMizan //Mizan Eryandhika Guntorozi 

//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=310e6; //Yield Strength (SS403)(Pa)
parameter Real Area=0.0005; //Area L Profile (m2)
parameter Real Elas=1.9e11;  //Elasticity SS400 (SS403)(Pa)

//define connection
parameter Integer C[:,2]=[1,2; 
                          2,3;
                          3,4];
                                                            
//define coordinates (please put orderly)
parameter Real P[:,6]=[0,0,0,1,1,1;      //1
                       0,0.04,0,0,0,0;   //2
                       0,0.08,0,0,0,0;   //3
                       0,0.12,0,0,0,0];  //4
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,      //1
                            0,0,0,      //2
                            0,0,0,      //3
                            0,200,0};   //4
                          
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];

protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
 end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2];

   //Transforming to global matrix
   g:=zeros(N,N); 
   for m,n in 1:3 loop
     g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
     g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
   end for;  

 G_star:=G+g;
 G:=G_star;
end for;

//Implementing boundary
for x in 1:Points loop
  if P[x,4] <> 0 then
    for a in 1:Points*3 loop
      G[(x*3)-2,a]:=0;
      G[(x*3)-2,(x*3)-2]:=1;
    end for;
  end if;
  if P[x,5] <> 0 then
    for a in 1:Points*3 loop
      G[(x*3)-1,a]:=0;
      G[(x*3)-1,(x*3)-1]:=1;
    end for;
  end if;
  if P[x,6] <> 0 then
    for a in 1:Points*3 loop
      G[x*3,a]:=0;
      G[x*3,x*3]:=1;
    end for;
  end if;
end for;  

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F); 

//Solving reaction
reaction:=(G_star*displacement)-F;  

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 
for i in 1:3 loop
  check[i] := if abs(check[i])<=ers then 0 else check[i];
end for; 

//Calculating stress in each truss 
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
   dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 end for;
      
    //Solving Matrix
    L:=Modelica.Math.Vectors.length(q2-q1);
    cx:=(q2[1]-q1[1])/L;
    cy:=(q2[2]-q1[2])/L;
    cz:=(q2[3]-q1[3])/L; 
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
                cy*cx,cy^2,cy*cz;
                cz*cx,cz*cy,cz^2];
   
    Str:=(X*dis);
    stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;  

//Safety factor
for i in 1:Trusses loop
  if stress1[i]>0 then
    safety[i]:=Yield/stress1[i];
  else
    safety[i]:=0;
  end if; 
end for; 

end UAS Metnum Anbia Maulana ;
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03-Anbia_Maulana&oldid=56351"