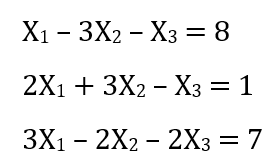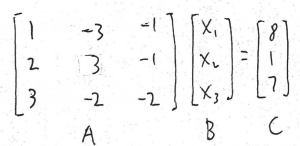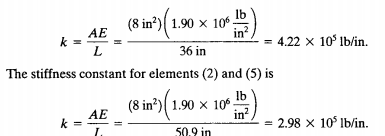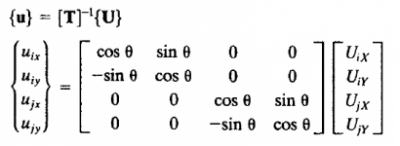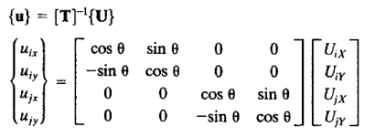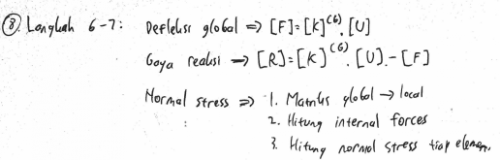Difference between revisions of "Metnum03 Favian Adyatma"
(→Pertemuan 2: 16 November 2020) |
(→Ujian Akhir Semester Metnum 03) |
||
| (44 intermediate revisions by the same user not shown) | |||
| Line 251: | Line 251: | ||
[[File:Codingvian4.PNG|thumb|center|400px]] | [[File:Codingvian4.PNG|thumb|center|400px]] | ||
| + | |||
== '''Pertemuan 3: 23 November 2020''' == | == '''Pertemuan 3: 23 November 2020''' == | ||
| − | + | Kelas ketiga, tanggal 23 November 2020, kegiatan diawali dengan diskusi buku bab 12 (hal. 328) mengenai ''displacement'' pegas massa. Di bawah ini saya unggah foto dari buku ''textbook'' MK. Metoda Numerik tersebut. | |
| + | |||
| + | [[File:Pegasmassa.PNG|275px]] | ||
| + | |||
| + | Berangkat dari gambar tersebut, kami dipersilakan untuk membaca terlebih dahulu sebelum diskusi dimulai. Diskusi diawali dengan penjelasan peristiwa yang terjadi jika sebuah benda diberikan ''displacement''. Melalui itu juga kami meneruskan pembahasan mengenai persamaannya. | ||
| + | |||
| + | Sesi kelas dilanjutkan dengan sesi tanya jawab satu per satu mahasiswa oleh dosen Pak Dai. Kami menjelaskan mengenai progres pembelajaran kami di ''website'' air.eng.ui.ac.id. Namun, saya belum dapat kesempatan untuk menjelaskan progres pembelajaran saya. Sembari melakukan tanya jawab satu per satu, kami juga melakukan simulasi mengenai ''displacement'' dari suatu persoalan pegas massa yang terdapat pada ''textbook'' Metode Numerik halaman 330. Berikut gambaran dan penyelesaian simulasinya pada aplikasi OpenModelica. | ||
| + | |||
| + | [[File:Classpegasmassa.PNG|400px]] | ||
| + | |||
| + | Tidak berbeda jauh dari PR yang sudah diberikan sebelumnya, tahap awal simulasi dilakukan dengan meng-''input'' data yang tersedia dan dikemas dalam bentuk matriks. Hal tersebut tercermin pada gambar di atas, dimana matriks K adalah matriks 3x3 dan matriks W (3x1) dengan nilainya yang sudah tertulis, serta matriks X (3x1) yang kita cari. | ||
| + | |||
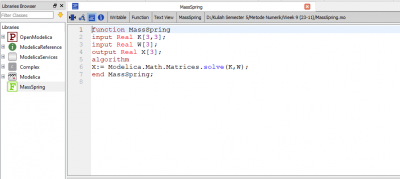
| + | [[File:Functionpegasmassa.PNG|400px]] | ||
| + | |||
| + | Melalui fitur Function, seperti yang digambar di atas, maka matriks yang dicari dapat ditentukan. Gambar di bawah ini adalah jawaban dari matriks yang ingin dicari. | ||
| + | |||
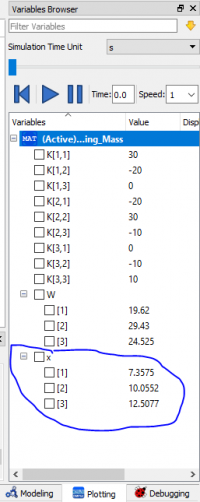
| + | [[File:Mass_Springhasil2.png|200px]] | ||
| + | |||
| + | Sesaat sebelum kelas selesai, seperti biasa, kami diberikan tugas untuk mengerjakan soal tentang statika struktur dan disimulasikan pada OpenModelica. Berikut adalah gambar dari soal yang diberikan sebagai tugas kepada peserta didik kelas Metode Numerik 03. | ||
| + | |||
| + | [[File:PR_Metnum.png|425px]] | ||
| + | |||
| + | '''Tugas 3''' | ||
| + | |||
| + | Melalui referensi yang saya gunakan, yaitu solusi dari buku terkait, soal tersebut dijawab dengan beberapa tahapan. Tahapan-tahapannya adalah sebagai berikut: | ||
| + | |||
| + | 1. Mengubah permasalahan menjadi noda dan elemen | ||
| + | |||
| + | Mengubah soal statika struktur di atas menjadi noda dan elemen digambarkan dengan tabel berikut ini. | ||
| + | |||
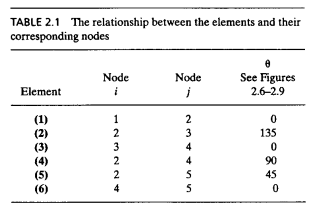
| + | [[File:Tabel1vian.PNG|350px]] | ||
| + | |||
| + | 2. Tahap berikutnya adalah membuat asumsi solusi yang mendekati sifat elemen | ||
| + | |||
| + | [[File:Asumsi1.PNG]] | ||
| + | |||
| + | Pada tahap ini kami menentukan asumsi untuk mendapatkan properties dari beam, yaitu k dengan rumus (AE)/L. L pada beam 1, 3, 4, dan 6 adalah 3 ft atau 36 inchi dan beam 2, 5 adalah 50.9 inchi (3 akar 2 ft) | ||
| + | |||
| + | 3. Mengembangkan persamaan untuk menyelesaikan persamaan tiap elemen | ||
| + | |||
| + | Setiap elemen akan dianalisis berdasarkan posisi dan gaya reaksi yang terjadi pada elemennya. Analisis akan dimanifestasikand alam bentuk matriks. Berikut hasil analisis dari elemen ''beam''-nya | ||
| + | |||
| + | - Elemen 1, 3, dan 6 | ||
| + | |||
| + | [[File:k1global.png|275px]] [[File:k3global.png|275px]] [[File:k6global.png|275px]] | ||
| + | |||
| + | - Elemen 4 | ||
| + | |||
| + | [[File:Elemen4.PNG|275px]] | ||
| + | |||
| + | - Elemen 2 dan 5 | ||
| + | |||
| + | [[File:k2global.png|275px]] [[File:k5global.png|275px]] | ||
| + | |||
| + | 4. Penggabungan matriks | ||
| + | |||
| + | Setelah di atas kita melakukan analisis per golongan elemen, maka berikutnya adalah melakukan penggabungan matriks. Di bawah ini adalah hasil dari penggabungan tersebut. | ||
| + | |||
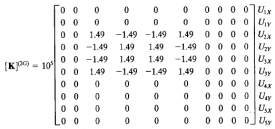
| + | [[File:Matriksmix.PNG|400px]] | ||
| + | |||
| + | 5. Menentukan ''boundary condition'' | ||
| + | |||
| + | Berdasarkan solusi dari referensi yang ada, ditentukan beberapa kondisi batas: | ||
| + | |||
| + | U1(x)=U1(y)=U3(x)=U3(y)=0 | ||
| + | |||
| + | F4(y) = -500 lb dan F5(y) = -500 lb | ||
| + | |||
| + | Dengan memasukkannya ke dalam matriks, maka menjadi: | ||
| + | |||
| + | [[File:Hitungmodelica.PNG|350px|left|thumb|Matriks gabungan ini adalah yang akan kita simulasikan ke dalam OpenModelica]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 6. Mencari solusi (OpenModelica) | ||
| + | |||
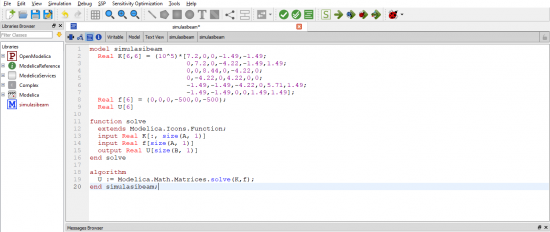
| + | Tahap pencarian solusi inilah yang akan digunakan aplikasi OpenModelica. ''Input'' yang dilakukan pada aplikasi OpenModelica adalah seperti berikut. | ||
| + | |||
| + | [[File:Simulasimodelicavian.PNG|550px]] | ||
| + | |||
| + | Ketika saya menggunakan fitur simulate, maka hasilnya akan digambarkan seperti ini. | ||
| + | |||
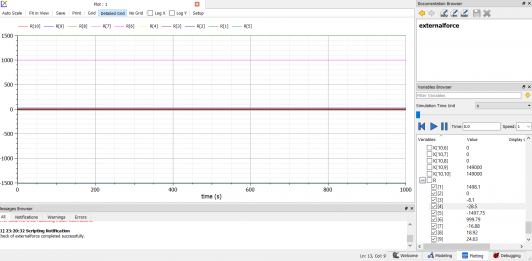
| + | [[File:Hasilvianbeam.png|550px]] | ||
| + | |||
| + | 7. Memperoleh besaran gaya-gaya | ||
| + | |||
| + | Proses pertama untuk mendapatkan besaran gaya yang ingin diukur adalah dengan ''input'' data pada matriks berikut. | ||
| + | |||
| + | [[File:Matrikscarigaya.PNG|400px]] | ||
| + | |||
| + | dengan {u} adalah koordinat lokal, [U] koordinat global, dan [T] adalah matriks transformasi. | ||
| + | |||
| + | Melalui referensi yang digunakan, kita coba menghitung ''stress'' pada elemen ''beam'' 5. Berikut adalah perwujudannya dalam bentuk matriks. | ||
| + | |||
| + | [[File:Matrikscarigaya.PNG|375px]] | ||
| + | |||
| + | Maka, saya melakukan simulasinya pada OpenModelica dan menghasilkan simulasi berikut. | ||
| + | |||
| + | [[File:Simulasimodelicavian.PNG|450px]] | ||
| + | |||
| + | Melalui formula ''coding'' yang telah dilakukan seperti diatas, saya mendapatkan hasil seperti di bawah ini. | ||
| + | |||
| + | [[File:Hasilvianbeam.png|450px]] | ||
| + | |||
| + | Beberapa proses tersebut menghasilkan hasil defleksi dengan besaran U2(x)=-0.00976 inchi dan U6(x)=-0.01209 inchi. | ||
| + | |||
| + | Demikianlah besaran-besaran yang dapat didapatkan melalui OpenModelica dengan referensi yang diberikan. | ||
| + | |||
| + | == '''Pertemuan 4: 30 November 2020''' == | ||
| + | |||
| + | Seperti kelas biasanya, sesi kelas diawali dengan berdiskusi. Diskusi kali ini diawali dengan hal yang mendasar, yaitu berdiskusi mengenai pengertian perbedaan statika struktur dan dinamika struktur. Diskusi pun berjalan dengan hangat, dimana terjadi saling lempar jawaban dan tanggapan selama beberapa belas menit. Bisa disimpulkan bahwa mempelajari struktur pada dasarnya sama, hanya saja perbedaan mendasarnya terdapat pada situasi beban yang ada. Beban pada statika struktur adalah beban yang besarannya tidak berubah seiring waktu, sedangkan dinamika struktur adalah pembahasan struktur saat beban yang ada dapat berubah seiring waktu bahkan gaya reaksi yang terjadi pun berubah. | ||
| + | |||
| + | '''Tugas 4''' | ||
| + | |||
| + | Pada tugas ini, tugas yang diberikan hampir sama seperti tugas sebelumnya, yaitu mengenai gaya reaksi dan internal pada struktur diam (struktur statis). Kali ini tugas yang berikan berjumlah dua, soal nomor 4 dan nomor 8. Berikut adalah gambar dari soal tersebut. | ||
| + | |||
| + | Soal No. 4: | ||
| + | |||
| + | [[File:soal1_iff.JPEG|centre|400px]] | ||
| + | |||
| + | Soal No. 8: | ||
| + | |||
| + | [[File:soal2_iff.JPEG|centre|400px]] | ||
| + | |||
| + | Pada hari yang sama, 30 November 2020, Pak Dai menyampaikan bahwa ''flowchart'' harus dikerjakan pada hari ini, sedangkan untuk pengerjaannya akan diserahkan dan diliput melalui air.eng.ui.ac.id pada pekan depan. | ||
| + | |||
| + | Berikut adalah ''flowchart'' yang saya buat untuk pengerjaan yang tenggat waktunya adalah pekan depan. | ||
| + | |||
| + | [[File:FlowVianNew.jpg|centre|350px]] | ||
| + | |||
| + | Sebagai tindak lanjut dari ''flow chart'' di atas, saya melakukan beberapa langkah penyelesaian di atas kertas. | ||
| + | |||
| + | ''Soal nomor 4'' | ||
| + | |||
| + | [[File:No4(1-2).PNG|500px]] | ||
| + | |||
| + | [[File:No4(3-5).PNG|500px]] | ||
| + | |||
| + | Setelah uraian di atas, maka tahap berikutnya adalah melakukan simulasi dengan aplikasi OpenModelica untuk menemuka ''values'' melalui eksekusi perhitungan matriks yang telah ditulis di kertas. | ||
| + | |||
| + | (permodelan di OpenModelica) | ||
| + | |||
| + | ''Soal nomor 8'' | ||
| + | |||
| + | Soal nomor 8 juga saya lakukan langkah-langkah sesuai dengan apa yang sudah tertera pada ''flow chart''. Berikut adalah | ||
| + | |||
| + | [[File:No8(1-2).PNG|500px]] | ||
| + | |||
| + | [[File:No8(3-5).PNG|500px]] | ||
| + | |||
| + | [[File:No8(6-7).PNG|500px]] | ||
| + | |||
| + | Sedikit berbeda dengan nomor 4, nomor 8 ini memiliki alur pengerjaan yang lebih sesuai dengan rencana di ''flow chart''. Setelah uraian di atas, maka tahap berikutnya adalah melakukan simulasi dengan aplikasi OpenModelica untuk menemukan ''values'' melalui eksekusi perhitungan matriks yang telah ditulis di kertas. | ||
| + | |||
| + | == '''Pertemuan 5: 7 Desember 2020''' == | ||
| + | |||
| + | '''Tugas Quiz 1''' | ||
| + | |||
| + | Pertemuan kelima dari kelas Metode Numerik 03 menyisakan tugas kepada kami sebagai tindaklanjut dari tugas sebelumnya. Sebagaimana kita tahu, bahwa tugas sebelumnya, kami ditugaskan untuk menghitung gaya reaksi pada elemen beam penyusun statika struktur. Dengan arahan Pak Dai, kami kembali diberikan tugas untuk mengembangkan sistem coding yang telah dirancang oleh rekan kami, Ahmad Mohammad Fahmi. | ||
| + | |||
| + | Maka dari itu, kami berdiskusi untuk mengembangkan serta menyempurnakan apa yang telah tersedia dari coding sebelumnya. Melalui platform ini, saya coba memaparkan apa yang telah saya dapat melalui diskusi yang telah kami lakukan. Kendati demikian, masih banyak yang belum saya mengerti dari apa yang saya akan tulis pada laman ini. Namun, saya tetap tuliskan karena telah dilakukan karena tetap merupakan progres dari diskusi yang dilakukan. | ||
| + | |||
| + | [[File:Soal3.jpeg|center|425px]] | ||
| + | |||
| + | Di atas merupakan soal yang diberikan. Soal tersebut diminta kepada kami untuk dijawab berdasarkan pengembangan dari jawaban yang telah ada pembahasannya. | ||
| + | |||
| + | Berikut adalah link yang terintegrasi kepada berkas hasil pengerjaan perhitungan beam di OpenModelica: | ||
| + | |||
| + | https://drive.google.com/drive/folders/14SGfwkzNHtDlkqLvbO_ZxoGc9JmKBJM1?usp=sharing | ||
| + | |||
| + | Kemudian saya akan menyertakan beberapa bagian dari hasil pekerjaan tersebut di bawah ini. | ||
| + | |||
| + | [[File:FCFC.PNG|200px]] | ||
| + | |||
| + | Pada proses perhitungan yang dilakukan kali ini menggunakan tujuh function, untuk kemudian di-''input'' pada class. Saya menggunakan fitur Class tersebut saat semua function sudah benar, sehingga dapat dilakukan panggilan pada Class. | ||
| + | |||
| + | [[File:MatriksElemenVian.PNG|600px]] | ||
| + | |||
| + | Memasukkan rumus pertama kali dilakukan untuk kalkulasi pada tiap elemen beam (Matriks Elemen). | ||
| + | |||
| + | [[File:MatriksGlobal.PNG|600px]] | ||
| + | |||
| + | Berawal dari matriks tiap elemen, tahap berikutnya adalah melakukan perhitungan dengan cara input matriks global. | ||
| + | |||
| + | Tahap terus berlanjut, dimana diteruskan dengan perhitungan matriks total, menentukan ''boundary condition'', penyelesaian dengan Gauss-Jordan, dan diakhiri dengan perhitungan gaya reaksi. Diantara proses tersebut, dilakukan juga perhitungan pemeriksaan gaya, dimana hal tersebut adalah tindaklanjut dari tugas yang diberikan Pak Dai. Tempo hari disampaikan kepada Ahmad dan teman sekelas bahwa kami harus menemukan formula untuk memastikan sigma F dari segala axis adalah 0. Maka, pemeriksaan gaya tersebut adalah ''result''-nya. | ||
| + | |||
| + | Di bawah ini adalah tampilan dari coding pemeriksaan gaya. | ||
| + | |||
| + | [[File:PeriksaGaya.PNG|600px]] | ||
| + | |||
| + | Kemudian, berikut adalah sedikit cuplikan dari hasil simulate Class yang diperoleh. | ||
| + | |||
| + | [[File:HasilVian.PNG|220px]] | ||
| + | |||
| + | Hasil dari pengerjaan dapat dilihat melalui link drive di atas. | ||
| + | |||
| + | == '''Pertemuan 6: 14 Desember 2020''' == | ||
| + | |||
| + | Kelas keenam ini dibuka oleh Pak Ahmad Indra, ditambah dengan penjelasannya tentang optimasi perhitungan ''truss'' sederhana dengan menggunakan metode numerik. Metode numerik disebut memungkinkan untuk mempermudah kita mendapatkan data objektif yang diinginkan dari suatu sistem ''truss'' sederhana. | ||
| + | |||
| + | Pada penjelasan mengenai tugas besar dari dosen disebut bahwa kita diharapkan dapat menemukan ''stress'' atau tegangan yang maksimum dengan harga minimum. Aspek-aspek yang dapat diubah (variabel bebas) antara lain dimensi dari batangan ''truss''. Untuk tahap akhir, kami diminta untuk membandingkan hasil ''stress'' dengan tabel ''properties''. | ||
| + | |||
| + | Sesi kelas pun berlanjut dengan pendampingan simulasi oleh Bu Chandra mengenai sebuah kasus. Kasus tersebut diambil dari buku teks oleh Steven Chapra mengenai perhitungan ''Bracket Optimization Using Golden Ratio Method''. Proses perhitungan tersebut diakhiri dengan membandingkan hasil simulasi OpenModelica dengan hasil riil di buku teks. | ||
| + | |||
| + | == '''Tugas Besar Metnum''' == | ||
| + | |||
| + | Tugas besar yang diberikan adalah optimasi perhitungan susunan statika struktur sederhana. Saya berprogres dengan merancang lini masa atau ''timeline'' untuk pengerjaan tugas besar ini. Saya pun masih memiliki kekurangan di sana sini dan memerlukan pembelajaran dari teman-teman yang lain. | ||
| + | |||
| + | [[File:TLTubesMetnum2.PNG|620px]] | ||
| + | |||
| + | Tabel di atas adalah lini masa yang saya buat untuk menuntaskan tugas besar yang diberikan ini. | ||
| + | |||
| + | '''Kelas 28 Desember 2020''' | ||
| + | |||
| + | Kelas ketujuh pada tanggal 28 Desember 2020 ini kami mengulas progres tugas besar dari peserta didik masing-masing didampingi oleh Pak Dai. Kami menjelaskan kendala-kendala yang dihadapi. Namun, kelas hanya dihadiri oleh beberapa peserta didik saja disebabkan adanya miskomunikasi tanggal merah. Sesi kelas tetap dilanjutkan dengan arahan untuk melanjutkan tugas besar yang telah diberikan. Sebagai tindaklanjutnya, kelas Metode Numerik 02 dan 03 akan mengadakan asistensi serta diskusi bersama demi kelancara tugas besar ini. Sementara ini, kami akan mempelajari coding dari Ahmad Fahmi yang telah dikirim ke Whatsapp ''Group'' kelas kami. | ||
| + | |||
| + | Tugas besar kali ini adalah tugas untuk mengoptimasi desain struktur sederhana. Berikut adalah model yang telah dibahas bersama oleh teman-teman sekelas beserta ''properties'' dari struktur tersebut. | ||
| + | |||
| + | [[File:FotoTuMet.PNG|370px]] | ||
| + | |||
| + | Kemudian ada beberapa tujuan dari tugas besar ini, yaitu: | ||
| + | |||
| + | 1. Membuat design optimum dengan biaya yang rendah | ||
| + | |||
| + | 2. Membandingkan grafik terhadap | ||
| + | |||
| + | A) Y = Cost, X = Area variabel terikat. Variabel bebas = Material | ||
| + | |||
| + | B) Y = Cost, X = Material variabel terikat. Variabel bebas = Areal | ||
| + | |||
| + | Untuk mencapai tujuan tersebut, akan dilakukan proses perhitungan dengan tahap sebagai berikut. | ||
| + | |||
| + | Cara / Prosedur pengerjaan | ||
| + | |||
| + | 1. Memilih bahan area dan material, dari data akan tersedia harga per satuan panjang | ||
| + | |||
| + | 2. Konfigurasi: Panjang L, koordinat titik node | ||
| + | |||
| + | 3. Melakukan perhitungan | ||
| + | |||
| + | 4. melakukan verifikasi dan check antara ''stress/cost'' | ||
| + | |||
| + | '''Data Material yang Dibutuhkan''' | ||
| + | |||
| + | [[File:DataBesi.PNG]] | ||
| + | |||
| + | '''Spesifikasi dan Harga Material''' | ||
| + | |||
| + | [[File:SpesifikasiMaterial.PNG]] | ||
| + | |||
| + | '''Permodelan Numerik''' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | ''' 3D Trusses Model''' | ||
| + | |||
| + | //define initial variable | ||
| + | |||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | |||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | |||
| + | parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa) | ||
| + | |||
| + | parameter Real Safety= (nilai yield/nilai stress) ; //Safety factor | ||
| + | |||
| + | parameter Real Area= (nilai area) ; //Luas Besi Siku (Dimension=30x30x3mm) | ||
| + | |||
| + | parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; // (Elemen 1) | ||
| + | 2,6; // (Elemen 2) | ||
| + | 3,7; // (Elemen 3) | ||
| + | 4,8; // (Elemen 4) | ||
| + | 5,6; // (Elemen 5) | ||
| + | 6,7; // (Elemen 6) | ||
| + | 7,8; // (Elemen 7) | ||
| + | 5,8; // (Elemen 8) | ||
| + | 5,9; // (Elemen 9) | ||
| + | 6,10; // (Elemen 10) | ||
| + | 7,11; // (Elemen 11) | ||
| + | 8,12; // (Elemen 12) | ||
| + | 9,10; // (Elemen 13) | ||
| + | 10,11;// (Elemen 14) | ||
| + | 11,12;// (Elemen 15) | ||
| + | 9,12; // (Elemen 16) | ||
| + | 9,13; // (Elemen 17) | ||
| + | 10,14;// (Elemen 18) | ||
| + | 11,15;// (Elemen 19) | ||
| + | 12,16;// (Elemen 20) | ||
| + | 13,14;// (Elemen 21) | ||
| + | 14,15;// (Elemen 22) | ||
| + | 15,16;// (Elemen 23) | ||
| + | 13,16];//(Elemen 24) | ||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1 | ||
| + | 0.75,0 ,0,1,1,1; //node 2 | ||
| + | 0.75,0.6,0,1,1,1; //node 3 | ||
| + | 0 ,0.6,0,1,1,1; //node 4 | ||
| + | |||
| + | 0 ,0 ,0.3,0,0,0; //node 5 | ||
| + | 0.75,0 ,0.3,0,0,0; //node 6 | ||
| + | 0.75,0.6,0.3,0,0,0; //node 7 | ||
| + | 0 ,0.6,0.3,0,0,0; //node 8 | ||
| + | |||
| + | 0 ,0 ,1.05,0,0,0; //node 9 | ||
| + | 0.75,0 ,1.05,0,0,0; //node 10 | ||
| + | 0.75,0.6,1.05,0,0,0; //node 11 | ||
| + | 0 ,0.6,1.05,0,0,0; //node 12 | ||
| + | |||
| + | 0 ,0 ,1.8,0,0,0; //node 13 | ||
| + | 0.75,0 ,1.8,0,0,0; //node 14 | ||
| + | 0.75,0.6,1.8,0,0,0; //node 15 | ||
| + | 0 ,0.6,1.8,0,0,0]; //node 16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-15, ers=10e-8; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Trusses_3D_Tugas_Besar; | ||
| + | |} | ||
| + | |||
| + | Metode numerik curve fitting | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''Curve Fitting''' | ||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | //Coe:=fill(2,size(Coe,1)); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | /* | ||
| + | for i in 1:3 loop | ||
| + | for j in 1:Points loop | ||
| + | R[j]:=reaction[3*(j-1)+i]; | ||
| + | end for; | ||
| + | Sur[i]:=sum(R); | ||
| + | end for; | ||
| + | */ | ||
| + | |} | ||
| + | |||
| + | '''Hasil dan Kesimpulan''' | ||
| + | |||
| + | Walaupun ''coding'' yang mencakup formula telah di-''input'', saya belum dapat menyertakan hasilnya disebabkan oleh kendala teknis. Perangkat yang saya gunakan masih mengalami gangguan saat ''simulate''. | ||
| + | |||
| + | [[File:NotResponding2.PNG|800px]] | ||
| + | |||
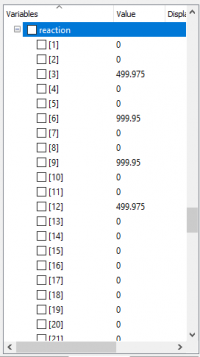
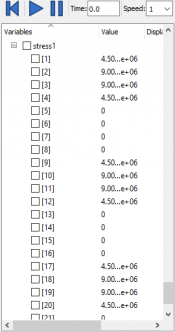
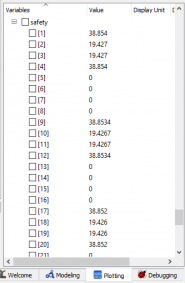
| + | Setelah beberapa saat, saya kembali mencoba untuk mendapatkan hasil yang diinginkan. Dari dua jenis material, yakni SS 304 dan SS 316L, saya mendapatkan hasil sebagai berikut. | ||
| + | |||
| + | [[File:HasilTumet.PNG|175px]] | ||
| + | |||
| + | [[File:HasilTumet2.PNG|200px]] | ||
| + | |||
| + | [[File:HasilTumet3.PNG|175px]] | ||
| + | |||
| + | Di atas adalah data-data yang didapat dari gaya reaksi, ''safety'', hingga ''stress'' yang dialami oleh ''beam'' pada material SS304. | ||
| + | |||
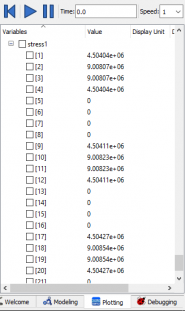
| + | Berikut ini adalah hasil data-data sama yang dihasilkan dari SS316L. | ||
| + | |||
| + | [[File:HasilTumet363.PNG|185px] | ||
| + | |||
| + | [[File:HasilTumet363(1).PNG|185px]] | ||
| + | |||
| + | [[File:HasilTumet363(2).PNG|185px]] | ||
| + | |||
| + | Sama halnya dengan material SS304, simulasi dengan material SS316L memberikan hasil yang kurang lebih sama. | ||
| + | |||
| + | == '''Ujian Akhir Semester Metnum 03''' == | ||
| + | |||
| + | Soal 1 | ||
| + | |||
| + | [[File:Nomer1vian.jpg|300px]] | ||
| + | |||
| + | Soal 2 | ||
| + | |||
| + | [[File:Nomer2vian.jpg|300px]] | ||
| + | |||
| + | Soal 3 | ||
| + | |||
| + | [[File:Nomer3vian.jpg|300px]] | ||
| + | |||
| + | Soal 4 | ||
| + | |||
| + | [[File:Nomer3vian2.jpg|310px]] | ||
| + | |||
| + | Soal 5 | ||
| + | |||
| + | [[File:Nomer4vian.jpg|310px]] | ||
| + | |||
| + | Soal 6 | ||
| + | |||
| + | [[File:Nomer5vian.jpg|310px]] | ||
| + | |||
| + | Soal 7 | ||
| + | |||
| + | [[File:Nomer7vian2.jpg|310px]] | ||
| + | |||
| + | Soal nomor 7 telah dikirim via WhatsApp Pak Dai. | ||
| + | |||
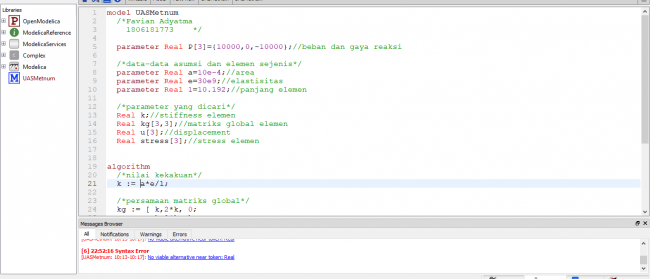
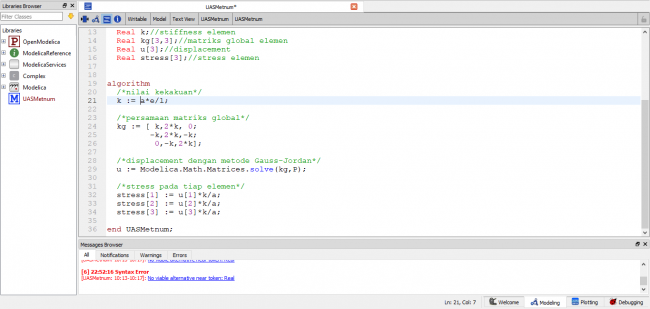
| + | Berikut adalah coding yang saya tuliskan pada Ujian AKhir Semester Metoda Numerik. | ||
| + | |||
| + | [[File:CodingUAS1.PNG|650px]] | ||
| + | |||
| + | [[File:CodingUAS2.PNG|650px]] | ||
Latest revision as of 22:57, 14 January 2021
Assalamualaikum Wr. Wb.
Salam sejahtera untuk kita semua. Semoga kita semua selalu dalam lindungan Tuhan Yang Maha Esa.
Nama: Favian AdyatmaNPM: 1806181773
Mata Kuliah: Metode Numerik 03 (TA 2020/2021 Ganjil)
Contents
Pertemuan 1: 9 November 2020
Pertemuan perdana kelas Metnum 03 merupakan pengenalan terhadap mata kuliah Metode Numerik. Kami membahas mulai dari akarnya dan kaitannya terhadap kehidupan kita sehari-hari, seperti proses berpikir dan aplikasinya terhadap device yang digunakan pada kehidupan sehari-sehari. Pada akhir kelas, kami diberikan tugas untuk memasukkan laporan mengenai hasil belajar pada akun masing-masing kita di air.eng.ui.ac.id, yaitu proses kami mempelajari software Open Modelica yang dapat diunduh melalui jejaring openmodelica.org dan menceritakan proses pembelajaran sebelum UTS.
Proses Pembelajaran Sebelum UTS
Sebelum UTS, kami mempelajari beberapa bab Metode Numerik dengan dosen Pak Engkos, yaitu sebagai berikut:
- Turunan Numerik
Turunan numerik dibagi menjadi tiga pendekatan, yaitu turunan mundur, turunan maju, dan turunan pusat. Berikut adalah prakteknya dalam Microsoft Excel.
- Pencarian Akar secara Numerik
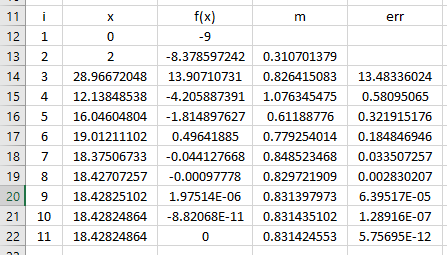
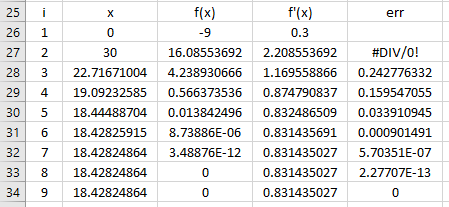
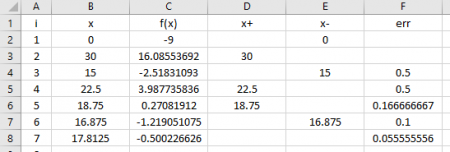
Pencarian akar ini bisa dilakukan dengan dua metode, yaitu Bracketing Method dan Open Method. Bracketing Method terdiri dari metode Bisecant, Graphical, dan False Position, sedangkan Open Method terdiri dari Newton-Raphson, Secant, dan Sample Fix Point. Di bawah ini akan saya sertakan tangkapan layar dari hasil pencarian akar di Excel dari metode Bisecat, Secant, dan Newton Raphson.
- Materi lainnya
Ada beberapa materi lainnya yang sempat dipelajari pada kelas Metode Numetik 03, antara penjabaran iterasi sin x dan cos x secara numerik dan praktik metode numerik pada alat-alat tertentu.
Open Modelica
Tugas berikutnya adalah merekap hasil pembelajaran aplikasi Open Modelica. Mengenai hal tersebut, hambatan yang ada sangat terasa karena saya tidak dapat mengunggah perangkat lunak tersebut disebabkan oleh network issue yang terjadi pada proses pengunggahannya. Akibatnya software tersebut gagal diunggah. Kedepannya saya akan menanyakan kepada teman-teman mengenai masalah tersebut. Namun, pembelajaran tetap saya lakukan dengan meriset situs openmodelica.org dan mencari tahu kegunaan dari aplikasi ini. Salah satu referensi yang saya gunakan adalah melalui YouTube dengan tautan berikut:
Open Modelica merupakan perangkat lunak yang digunakan untuk mempermudah simulasi permodelan metode numerik. Seperti CFDSOF-NG yang menjadi alat untuk simulasi aliran fluida, aplikasi ini adalah alat untuk simulasi metode numerik. Selain itu, dapat dipraktekkan pula pengendalian sistem dengan meng-input rangkaian yang biasa dilakukan saat proses pengendalian sistem baik elektronik maupun mekanik. Open Modelica juga seringkali digunakan pada industri yang membutuhkan kinerja pengendalian sistem didalamnya.
Pertemuan 2: 16 November 2020
Tugas 2
Sebelum kegiatan kelas kedua (evaluasi hasil belajar kami tentang yang sudah kami pelajari tentang Metode Numerik sebelum UTS) berakhir, Pak Dai memberikan tugas mengenai simulasi perhitungan aljabar di Aplikasi OpenModelica. Kami diminta melaksanakan simulasi tersebut dengan menyelesaikan persamaan aljabar dan coding sederhana terkait nilai rata-rata sepuluh sampel. Maka saya mengambil tiga buah persamaan untuk diselesaikan, yaitu:
Aljabar tersebut dapat diselesaikan melalui OpenModelica yang telah terunggah pada gawai masing-masing mahasiswa. Pertama-tama, saya melakukan input pada aplikasi OpenModelica, dimana A dan C adalah input sedangkan B adalah faktor dari x1, x2, dan x3 yang akan dicari. Gambaran itu dapat disederhanakan dengan ilustrasi berikut.
Maka, pada simulasi OpenModelica ini, saya meng-input data A dan C seperti pada gambar berikut.
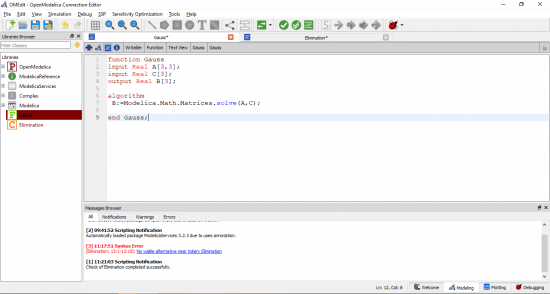
Pada gambar tersebut, A dituliskan sebagai A[3,3] yang artinya merupakan matriks 3x3. Kemudian, input C adalah matriks 3x1, maka ditulis C[3], dan yang terakhir adalah output, yakni nilai yang dicari, matriks B, yang merupakan matriks 3x1. Ketiga data tersebut disimpan pada fitur Function dengan nama "Gauss".
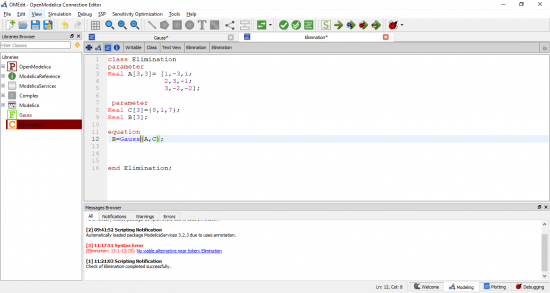
Setelah itu, untuk dapat mendapatkan hasil yang diinginkan, saya memasukkan matriks pada fitur Class dengan nama "Elimination". Pada fitur itu, nilai-nilai pada matriks dimasukkan menjadi coding sederhana seperti gambar berikut.
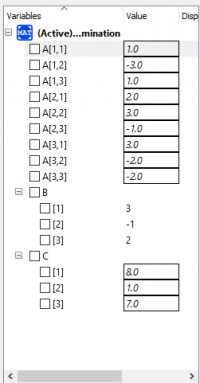
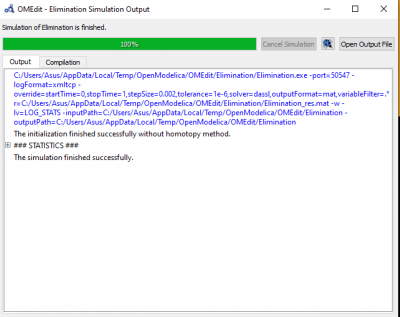
Tahap berikutnya adalah menjalankan formula dan data yang telah di-input dengan menklik fitur Simulate. Ketika sudah selesai, maka kita akan mendapatkan jawaban dari persamaan yang diinginkan. Hasil dari simulasi yang saya lakukan dapat dilihat melalui gambar di bawah ini.
Dapat disimpulkan bahwa jawaban dari persamaan yang di-input adalah x1=3, x2=-1, dan x3=2.
Sebagai bahan kelengkapan dari hasil simulasi OpenModelica ini, saya menyertakan Elimination Simulation Output dari simulasi ini.
Pertemuan 3: 23 November 2020
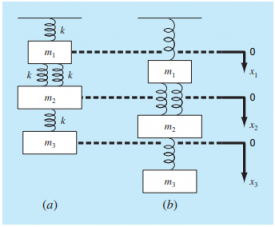
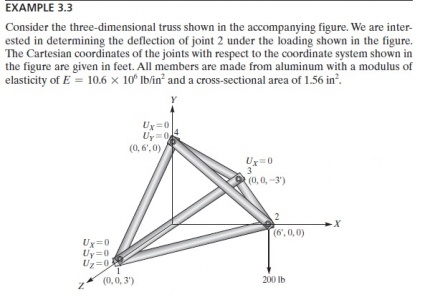
Kelas ketiga, tanggal 23 November 2020, kegiatan diawali dengan diskusi buku bab 12 (hal. 328) mengenai displacement pegas massa. Di bawah ini saya unggah foto dari buku textbook MK. Metoda Numerik tersebut.
Berangkat dari gambar tersebut, kami dipersilakan untuk membaca terlebih dahulu sebelum diskusi dimulai. Diskusi diawali dengan penjelasan peristiwa yang terjadi jika sebuah benda diberikan displacement. Melalui itu juga kami meneruskan pembahasan mengenai persamaannya.
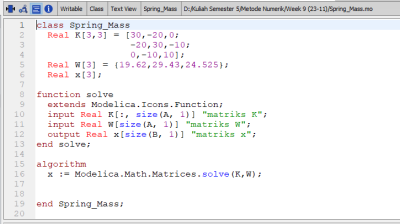
Sesi kelas dilanjutkan dengan sesi tanya jawab satu per satu mahasiswa oleh dosen Pak Dai. Kami menjelaskan mengenai progres pembelajaran kami di website air.eng.ui.ac.id. Namun, saya belum dapat kesempatan untuk menjelaskan progres pembelajaran saya. Sembari melakukan tanya jawab satu per satu, kami juga melakukan simulasi mengenai displacement dari suatu persoalan pegas massa yang terdapat pada textbook Metode Numerik halaman 330. Berikut gambaran dan penyelesaian simulasinya pada aplikasi OpenModelica.
Tidak berbeda jauh dari PR yang sudah diberikan sebelumnya, tahap awal simulasi dilakukan dengan meng-input data yang tersedia dan dikemas dalam bentuk matriks. Hal tersebut tercermin pada gambar di atas, dimana matriks K adalah matriks 3x3 dan matriks W (3x1) dengan nilainya yang sudah tertulis, serta matriks X (3x1) yang kita cari.
Melalui fitur Function, seperti yang digambar di atas, maka matriks yang dicari dapat ditentukan. Gambar di bawah ini adalah jawaban dari matriks yang ingin dicari.
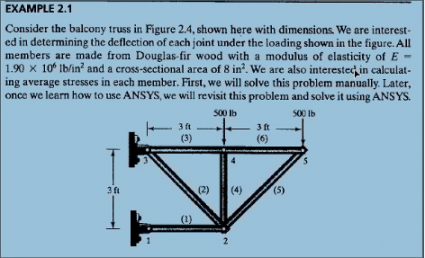
Sesaat sebelum kelas selesai, seperti biasa, kami diberikan tugas untuk mengerjakan soal tentang statika struktur dan disimulasikan pada OpenModelica. Berikut adalah gambar dari soal yang diberikan sebagai tugas kepada peserta didik kelas Metode Numerik 03.
Tugas 3
Melalui referensi yang saya gunakan, yaitu solusi dari buku terkait, soal tersebut dijawab dengan beberapa tahapan. Tahapan-tahapannya adalah sebagai berikut:
1. Mengubah permasalahan menjadi noda dan elemen
Mengubah soal statika struktur di atas menjadi noda dan elemen digambarkan dengan tabel berikut ini.
2. Tahap berikutnya adalah membuat asumsi solusi yang mendekati sifat elemen
Pada tahap ini kami menentukan asumsi untuk mendapatkan properties dari beam, yaitu k dengan rumus (AE)/L. L pada beam 1, 3, 4, dan 6 adalah 3 ft atau 36 inchi dan beam 2, 5 adalah 50.9 inchi (3 akar 2 ft)
3. Mengembangkan persamaan untuk menyelesaikan persamaan tiap elemen
Setiap elemen akan dianalisis berdasarkan posisi dan gaya reaksi yang terjadi pada elemennya. Analisis akan dimanifestasikand alam bentuk matriks. Berikut hasil analisis dari elemen beam-nya
- Elemen 1, 3, dan 6
- Elemen 4
- Elemen 2 dan 5
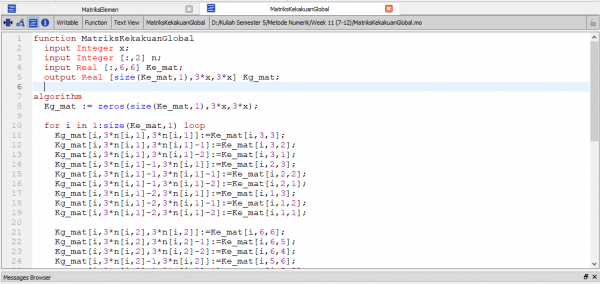
4. Penggabungan matriks
Setelah di atas kita melakukan analisis per golongan elemen, maka berikutnya adalah melakukan penggabungan matriks. Di bawah ini adalah hasil dari penggabungan tersebut.
5. Menentukan boundary condition
Berdasarkan solusi dari referensi yang ada, ditentukan beberapa kondisi batas:
U1(x)=U1(y)=U3(x)=U3(y)=0
F4(y) = -500 lb dan F5(y) = -500 lb
Dengan memasukkannya ke dalam matriks, maka menjadi:
6. Mencari solusi (OpenModelica)
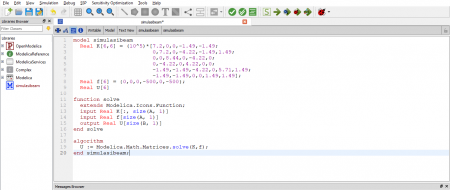
Tahap pencarian solusi inilah yang akan digunakan aplikasi OpenModelica. Input yang dilakukan pada aplikasi OpenModelica adalah seperti berikut.
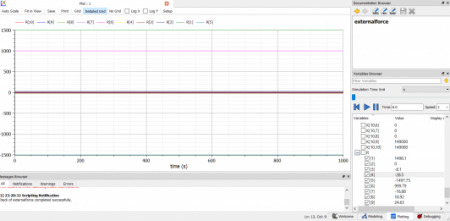
Ketika saya menggunakan fitur simulate, maka hasilnya akan digambarkan seperti ini.
7. Memperoleh besaran gaya-gaya
Proses pertama untuk mendapatkan besaran gaya yang ingin diukur adalah dengan input data pada matriks berikut.
dengan {u} adalah koordinat lokal, [U] koordinat global, dan [T] adalah matriks transformasi.
Melalui referensi yang digunakan, kita coba menghitung stress pada elemen beam 5. Berikut adalah perwujudannya dalam bentuk matriks.
Maka, saya melakukan simulasinya pada OpenModelica dan menghasilkan simulasi berikut.
Melalui formula coding yang telah dilakukan seperti diatas, saya mendapatkan hasil seperti di bawah ini.
Beberapa proses tersebut menghasilkan hasil defleksi dengan besaran U2(x)=-0.00976 inchi dan U6(x)=-0.01209 inchi.
Demikianlah besaran-besaran yang dapat didapatkan melalui OpenModelica dengan referensi yang diberikan.
Pertemuan 4: 30 November 2020
Seperti kelas biasanya, sesi kelas diawali dengan berdiskusi. Diskusi kali ini diawali dengan hal yang mendasar, yaitu berdiskusi mengenai pengertian perbedaan statika struktur dan dinamika struktur. Diskusi pun berjalan dengan hangat, dimana terjadi saling lempar jawaban dan tanggapan selama beberapa belas menit. Bisa disimpulkan bahwa mempelajari struktur pada dasarnya sama, hanya saja perbedaan mendasarnya terdapat pada situasi beban yang ada. Beban pada statika struktur adalah beban yang besarannya tidak berubah seiring waktu, sedangkan dinamika struktur adalah pembahasan struktur saat beban yang ada dapat berubah seiring waktu bahkan gaya reaksi yang terjadi pun berubah.
Tugas 4
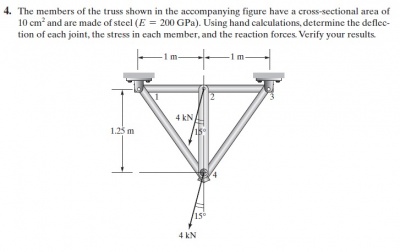
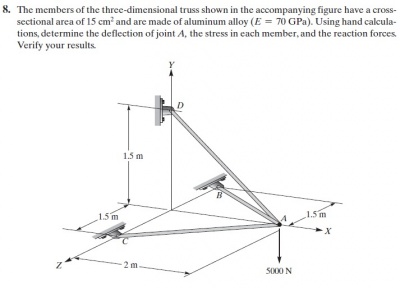
Pada tugas ini, tugas yang diberikan hampir sama seperti tugas sebelumnya, yaitu mengenai gaya reaksi dan internal pada struktur diam (struktur statis). Kali ini tugas yang berikan berjumlah dua, soal nomor 4 dan nomor 8. Berikut adalah gambar dari soal tersebut.
Soal No. 4:
Soal No. 8:
Pada hari yang sama, 30 November 2020, Pak Dai menyampaikan bahwa flowchart harus dikerjakan pada hari ini, sedangkan untuk pengerjaannya akan diserahkan dan diliput melalui air.eng.ui.ac.id pada pekan depan.
Berikut adalah flowchart yang saya buat untuk pengerjaan yang tenggat waktunya adalah pekan depan.
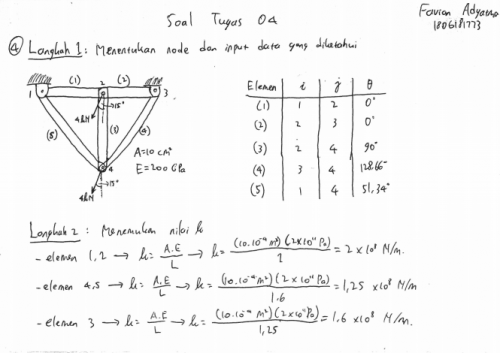
Sebagai tindak lanjut dari flow chart di atas, saya melakukan beberapa langkah penyelesaian di atas kertas.
Soal nomor 4
Setelah uraian di atas, maka tahap berikutnya adalah melakukan simulasi dengan aplikasi OpenModelica untuk menemuka values melalui eksekusi perhitungan matriks yang telah ditulis di kertas.
(permodelan di OpenModelica)
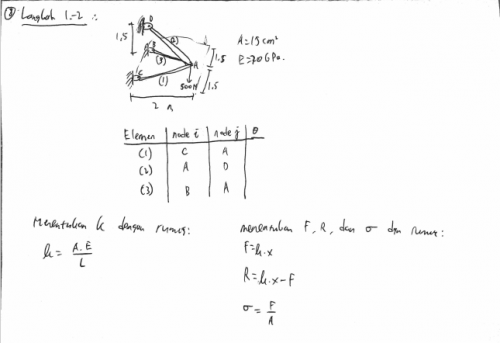
Soal nomor 8
Soal nomor 8 juga saya lakukan langkah-langkah sesuai dengan apa yang sudah tertera pada flow chart. Berikut adalah
Sedikit berbeda dengan nomor 4, nomor 8 ini memiliki alur pengerjaan yang lebih sesuai dengan rencana di flow chart. Setelah uraian di atas, maka tahap berikutnya adalah melakukan simulasi dengan aplikasi OpenModelica untuk menemukan values melalui eksekusi perhitungan matriks yang telah ditulis di kertas.
Pertemuan 5: 7 Desember 2020
Tugas Quiz 1
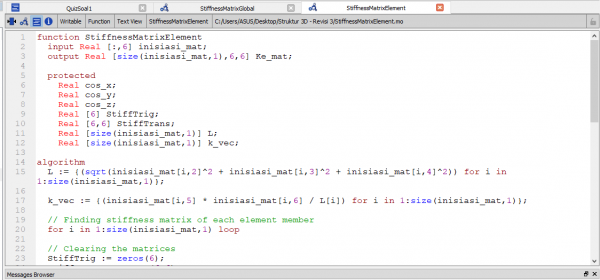
Pertemuan kelima dari kelas Metode Numerik 03 menyisakan tugas kepada kami sebagai tindaklanjut dari tugas sebelumnya. Sebagaimana kita tahu, bahwa tugas sebelumnya, kami ditugaskan untuk menghitung gaya reaksi pada elemen beam penyusun statika struktur. Dengan arahan Pak Dai, kami kembali diberikan tugas untuk mengembangkan sistem coding yang telah dirancang oleh rekan kami, Ahmad Mohammad Fahmi.
Maka dari itu, kami berdiskusi untuk mengembangkan serta menyempurnakan apa yang telah tersedia dari coding sebelumnya. Melalui platform ini, saya coba memaparkan apa yang telah saya dapat melalui diskusi yang telah kami lakukan. Kendati demikian, masih banyak yang belum saya mengerti dari apa yang saya akan tulis pada laman ini. Namun, saya tetap tuliskan karena telah dilakukan karena tetap merupakan progres dari diskusi yang dilakukan.
Di atas merupakan soal yang diberikan. Soal tersebut diminta kepada kami untuk dijawab berdasarkan pengembangan dari jawaban yang telah ada pembahasannya.
Berikut adalah link yang terintegrasi kepada berkas hasil pengerjaan perhitungan beam di OpenModelica:
https://drive.google.com/drive/folders/14SGfwkzNHtDlkqLvbO_ZxoGc9JmKBJM1?usp=sharing
Kemudian saya akan menyertakan beberapa bagian dari hasil pekerjaan tersebut di bawah ini.
Pada proses perhitungan yang dilakukan kali ini menggunakan tujuh function, untuk kemudian di-input pada class. Saya menggunakan fitur Class tersebut saat semua function sudah benar, sehingga dapat dilakukan panggilan pada Class.
Memasukkan rumus pertama kali dilakukan untuk kalkulasi pada tiap elemen beam (Matriks Elemen).
Berawal dari matriks tiap elemen, tahap berikutnya adalah melakukan perhitungan dengan cara input matriks global.
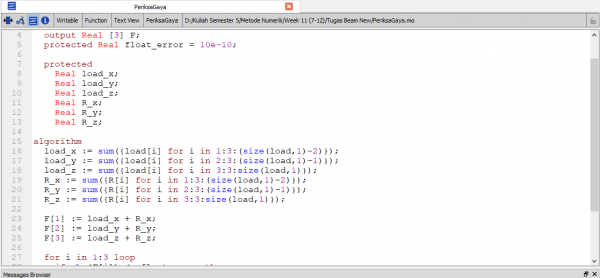
Tahap terus berlanjut, dimana diteruskan dengan perhitungan matriks total, menentukan boundary condition, penyelesaian dengan Gauss-Jordan, dan diakhiri dengan perhitungan gaya reaksi. Diantara proses tersebut, dilakukan juga perhitungan pemeriksaan gaya, dimana hal tersebut adalah tindaklanjut dari tugas yang diberikan Pak Dai. Tempo hari disampaikan kepada Ahmad dan teman sekelas bahwa kami harus menemukan formula untuk memastikan sigma F dari segala axis adalah 0. Maka, pemeriksaan gaya tersebut adalah result-nya.
Di bawah ini adalah tampilan dari coding pemeriksaan gaya.
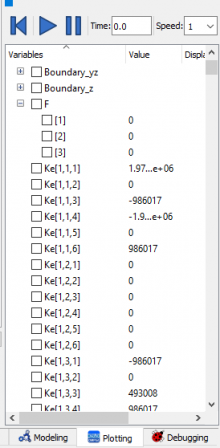
Kemudian, berikut adalah sedikit cuplikan dari hasil simulate Class yang diperoleh.
Hasil dari pengerjaan dapat dilihat melalui link drive di atas.
Pertemuan 6: 14 Desember 2020
Kelas keenam ini dibuka oleh Pak Ahmad Indra, ditambah dengan penjelasannya tentang optimasi perhitungan truss sederhana dengan menggunakan metode numerik. Metode numerik disebut memungkinkan untuk mempermudah kita mendapatkan data objektif yang diinginkan dari suatu sistem truss sederhana.
Pada penjelasan mengenai tugas besar dari dosen disebut bahwa kita diharapkan dapat menemukan stress atau tegangan yang maksimum dengan harga minimum. Aspek-aspek yang dapat diubah (variabel bebas) antara lain dimensi dari batangan truss. Untuk tahap akhir, kami diminta untuk membandingkan hasil stress dengan tabel properties.
Sesi kelas pun berlanjut dengan pendampingan simulasi oleh Bu Chandra mengenai sebuah kasus. Kasus tersebut diambil dari buku teks oleh Steven Chapra mengenai perhitungan Bracket Optimization Using Golden Ratio Method. Proses perhitungan tersebut diakhiri dengan membandingkan hasil simulasi OpenModelica dengan hasil riil di buku teks.
Tugas Besar Metnum
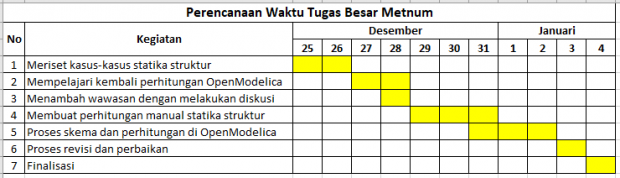
Tugas besar yang diberikan adalah optimasi perhitungan susunan statika struktur sederhana. Saya berprogres dengan merancang lini masa atau timeline untuk pengerjaan tugas besar ini. Saya pun masih memiliki kekurangan di sana sini dan memerlukan pembelajaran dari teman-teman yang lain.
Tabel di atas adalah lini masa yang saya buat untuk menuntaskan tugas besar yang diberikan ini.
Kelas 28 Desember 2020
Kelas ketujuh pada tanggal 28 Desember 2020 ini kami mengulas progres tugas besar dari peserta didik masing-masing didampingi oleh Pak Dai. Kami menjelaskan kendala-kendala yang dihadapi. Namun, kelas hanya dihadiri oleh beberapa peserta didik saja disebabkan adanya miskomunikasi tanggal merah. Sesi kelas tetap dilanjutkan dengan arahan untuk melanjutkan tugas besar yang telah diberikan. Sebagai tindaklanjutnya, kelas Metode Numerik 02 dan 03 akan mengadakan asistensi serta diskusi bersama demi kelancara tugas besar ini. Sementara ini, kami akan mempelajari coding dari Ahmad Fahmi yang telah dikirim ke Whatsapp Group kelas kami.
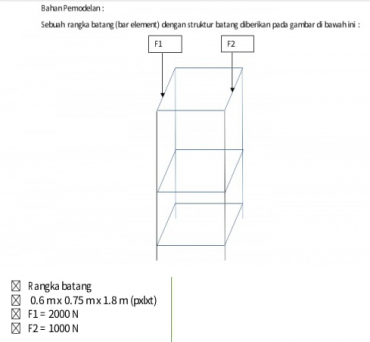
Tugas besar kali ini adalah tugas untuk mengoptimasi desain struktur sederhana. Berikut adalah model yang telah dibahas bersama oleh teman-teman sekelas beserta properties dari struktur tersebut.
Kemudian ada beberapa tujuan dari tugas besar ini, yaitu:
1. Membuat design optimum dengan biaya yang rendah
2. Membandingkan grafik terhadap
A) Y = Cost, X = Area variabel terikat. Variabel bebas = Material
B) Y = Cost, X = Material variabel terikat. Variabel bebas = Areal
Untuk mencapai tujuan tersebut, akan dilakukan proses perhitungan dengan tahap sebagai berikut.
Cara / Prosedur pengerjaan
1. Memilih bahan area dan material, dari data akan tersedia harga per satuan panjang
2. Konfigurasi: Panjang L, koordinat titik node
3. Melakukan perhitungan
4. melakukan verifikasi dan check antara stress/cost
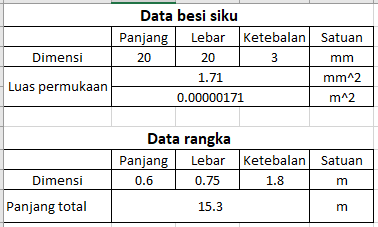
Data Material yang Dibutuhkan
Spesifikasi dan Harga Material
Permodelan Numerik
|
3D Trusses Model //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa) parameter Real Safety= (nilai yield/nilai stress) ; //Safety factor parameter Real Area= (nilai area) ; //Luas Besi Siku (Dimension=30x30x3mm) parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa) //define connection
parameter Integer C[:,2]=[1,5; // (Elemen 1)
2,6; // (Elemen 2)
3,7; // (Elemen 3)
4,8; // (Elemen 4)
5,6; // (Elemen 5)
6,7; // (Elemen 6)
7,8; // (Elemen 7)
5,8; // (Elemen 8)
5,9; // (Elemen 9)
6,10; // (Elemen 10)
7,11; // (Elemen 11)
8,12; // (Elemen 12)
9,10; // (Elemen 13)
10,11;// (Elemen 14)
11,12;// (Elemen 15)
9,12; // (Elemen 16)
9,13; // (Elemen 17)
10,14;// (Elemen 18)
11,15;// (Elemen 19)
12,16;// (Elemen 20)
13,14;// (Elemen 21)
14,15;// (Elemen 22)
15,16;// (Elemen 23)
13,16];//(Elemen 24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar;
|
Metode numerik curve fitting
|
Curve Fitting function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting; /* for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for;
|
Hasil dan Kesimpulan
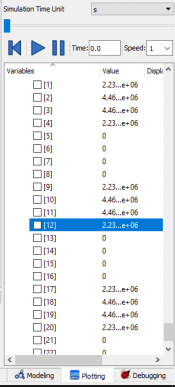
Walaupun coding yang mencakup formula telah di-input, saya belum dapat menyertakan hasilnya disebabkan oleh kendala teknis. Perangkat yang saya gunakan masih mengalami gangguan saat simulate.
Setelah beberapa saat, saya kembali mencoba untuk mendapatkan hasil yang diinginkan. Dari dua jenis material, yakni SS 304 dan SS 316L, saya mendapatkan hasil sebagai berikut.
Di atas adalah data-data yang didapat dari gaya reaksi, safety, hingga stress yang dialami oleh beam pada material SS304.
Berikut ini adalah hasil data-data sama yang dihasilkan dari SS316L.
[[File:HasilTumet363.PNG|185px]
Sama halnya dengan material SS304, simulasi dengan material SS316L memberikan hasil yang kurang lebih sama.
Ujian Akhir Semester Metnum 03
Soal 1
Soal 2
Soal 3
Soal 4
Soal 5
Soal 6
Soal 7
Soal nomor 7 telah dikirim via WhatsApp Pak Dai.
Berikut adalah coding yang saya tuliskan pada Ujian AKhir Semester Metoda Numerik.