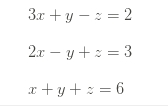Difference between revisions of "Metnum03-Muhammad Daffa Fachturrohman"

From ccitonlinewiki
Jump to: navigation, search
(→‎Tugas II)
 
(32 intermediate revisions by the same user not shown)
Line 62: Line 62:
 
=='''Tugas II'''==
 
=='''Tugas II'''==
  
−
Pada pertemuan kedua dengan pak [Ahmad Indra Siswantara], saya diberikan tugas untuk menyelesaikan simulasi dari persamaan-presamaan aljabar simultan yaitu seperti Gauss Elimination, Gauss-Seidel, dan lainnya didalam OpenModelica.
+
Pada pertemuan kedua dengan pak [[Ahmad Indra Siswantara]], saya diberikan tugas untuk menyelesaikan simulasi dari persamaan-presamaan aljabar simultan yaitu seperti Gauss Elimination, Gauss-Seidel, dan lainnya didalam OpenModelica.
  
 
Dengan demikian, saya menggunakan 3 persamaan aljabar yang ada sebagai berikut  
 
Dengan demikian, saya menggunakan 3 persamaan aljabar yang ada sebagai berikut  
  
−
[[File:1606107310523.jpg|600px]]
+
[[File:1606107310523.jpg|300px]]
  
 
Untuk menyelesaikan 3 persamaan tersebut, saya menggunakan Gauss Elimination. Didalam sistem OpenModelica sendiri, saya mengubahnya dalam bentuk matriks 3x3 yang dapat dilihat seperti kodingan saya dibawah ini
 
Untuk menyelesaikan 3 persamaan tersebut, saya menggunakan Gauss Elimination. Didalam sistem OpenModelica sendiri, saya mengubahnya dalam bentuk matriks 3x3 yang dapat dilihat seperti kodingan saya dibawah ini
Line 72: Line 72:
 
[[File:9981.jpg|600px]]
 
[[File:9981.jpg|600px]]
  
−
Untuk penyelesaiannya, saya mengugnakan perintah dari sistem OpenModelicanya sendiri, yaitu Modelica.Math.Matrices.solve(A,b) dan beberapa perintah baru yang saya pelajari dari beberapa sumber yang ada. Dan penyelesaiannya dari hasil simulasi saya adalah sebagai berikut
+
Untuk penyelesaiannya, saya menggugnakan perintah dari sistem OpenModelicanya sendiri, yaitu Modelica.Math.Matrices.solve(A,b) dan beberapa perintah baru yang saya pelajari dari beberapa sumber yang ada. Dan penyelesaiannya dari hasil simulasi saya adalah sebagai berikut
  
 
[[File:1606107125738.jpg|600px]]
 
[[File:1606107125738.jpg|600px]]
  
 
Sehingga ditemukan bahwa x = 1, y = 2, dan z = 3.
 
Sehingga ditemukan bahwa x = 1, y = 2, dan z = 3.
 +
 +
= '''Pertemuan Ketiga''' =
 +
Bismillahirrahmanirrahiim
 +
 +
Pada pertemuan kali ini, saya diminta untuk melakukan simulasi dalam modelica yang datanya didapat dari Numerical Methods for Engineers edisi ke-7.
 +
 +
Didalam buku ini di halaman 328, terdapat studi kasus pegas massa pada tabel 11.12, pada pertemuan ini saya diminta untuk membuktikan persamaan aljabar yang ada dengan menggunakan OpenModelica sebagai berikut :
 +
 +
[[File:1606114179693.jpg|300px]]
 +
 +
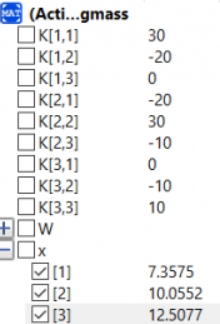
Lalu, saya menggunakan OpenModelica dengan memasukkan persamaan linier yang ada dengan menggunakan matriks 3x3 sebagai berikut dan juga saya
 +
 +
[[File:1606114928506.jpg|600px]]
 +
 +
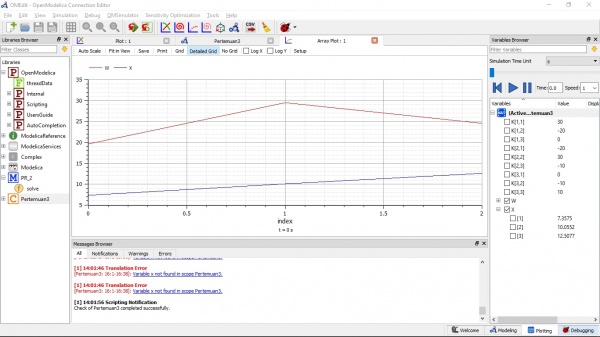
Lalu untuk penyelesaiannya, saya menggunakan perintah dari sistem OpenModelica yang ada seperti gambar berikut
 +
 +
[[File:1606115131055.jpg|600px]]
 +
 +
Dari hasil simulasi yang saya lakukan dengan OpenModelica, terdapat hasil yaitu x1 = 7.3575; x2 = 10.0552; x3 = 12.5077. Dan hasil tersebut sesuai dengan yang ada di buku Numerical Methods for Engineers edisi ke-7
 +
 +
 +
== '''Tugas III''' ==
 +
 +
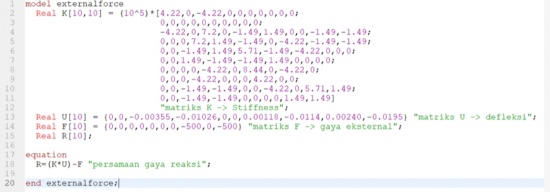
Pada pertemuan ini, Pak [[Ahmad Indra Siswantara]] memberikan tugas untuk mencari defleksi menggunakan matriks yang didapat dari buku Finite Element Analysis halaman 60-68, lalu saya melakukan koding dari soal yang ada sebagai berikut
 +
 +
[[File:414B09F8-8F1D-4AE2-8ADF-3296B789B723.png|550px]]
 +
 +
Dengan kodingan diatas, saya mendapatkan data sebagai berikut :
 +
 +
[[File:1606711313050.jpg|300px]]
 +
 +
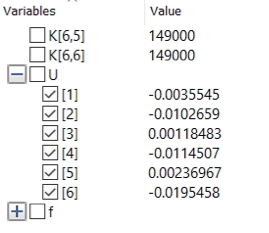
Lalu, untuk mendapatkan gaya reaksi, saya melakukan koding dan menghasilkan data sebagai berikut :
 +
 +
[[File:1606711713530.jpg|550px]]
 +
 +
[[File:1606711780530.jpg|300px]]
 +
 +
Lalu untuk mendapatkan defleksi total dari referensi yang ada dibuku juga, saya melakukan koding dan dapat dilihat pula hasilnya sebagai berikut :
 +
 +
[[File:1606711864417.jpg|550px]]
 +
 +
[[File:1606711905375.jpg|300px]]
 +
 +
Dari data diatas, didapatkan hasil U2x=-0.00976 inch dan U6x=-0.01209 inch
 +
 +
Lalu untuk internal force :
 +
 +
f ix = k(uix - ujx)
 +
f jx = k(ujx - uix)
 +
 +
dari persamaan diatas didapatkan internal force pada elemen-5 yaitu 696lb
 +
 +
Dan dengan persamaan normal stress :
 +
 +
[[File:1606712071490.jpg|200px]]
 +
 +
Lalu didapatkan normal stress sebesar 87lb/in^2
 +
 +
 +
= '''Pertemuan Ke Empat''' =
 +
 +
Pada pertemuan kali ini, pak [[Ahmad Indra Siswantara]] me remind tentang analisa Statik dan Dinamik
 +
 +
 +
== '''Excersice''' ==
 +
 +
Dari pertemuan kali ini, saya diberikan soal oleh Pak [[Ahmad Indra Siswantara]] seperti gambar dibawah ini :
 +
 +
[[File:1606735880652.jpg|500px]]
 +
[[File:WhatsApp_Image_2020-11-30_at_1.17.40_PM.jpeg|500px]]
 +
 +
Lalu dengan soal tersebut saya melakukan perhitungan sampai menemukan K dari setiap elemen yang ada yang bisa saya klasifikasikan. Lalu, saya menmbuat chart flow untuk mendapatkan defleksi dan juga gaya reaksi setelah perhitungan saya menggunakan OpenModelica sebagai berikut :
 +
 +
[[File:127384.jpg|550px]]
 +
 +
[[File:127385.jpg|550px]]
 +
 +
 +
== '''Lanjutan Exersice untuk Modelica''' ==
 +
 +
Saya melanjutkan data yang saya dapat diatas untuk dijadikan matriks seperti yang ada dibawah ini
 +
 +
[[File:1607427760636.jpg|500px]]
 +
 +
Dari matriks yang saya dapatkan diatas, saya mengimplementasikan matriks tersebut kedalam software OpenModelica
 +
 +
[[File:1607430295131.jpg|700px]]
 +
 +
dan berikut merupakan hasil simulasi dari matriks yang saya masukkan ke atas
 +
 +
[[File:1607499704841.jpg|700px]]
 +
 +
= '''Pertemuan Kelima''' =
 +
 +
Pada pertemuan tanggal 7 Desember 2020, saya di ajarkan Pak [[Ahmad Indra Siswantara]] tentang quiz no 4 dan 8 yang dibantu oleh teman saya Ahmad Mohammad Fahmi yang telah menyelesaikan kedua nomor pada quiz sebelumnya, ada beberapa tahapan dari setelah kita membuat flow chart seperti gambar yang terlampir pada laman ini, yang pertama adalah solve striffness, lalu menentukan matriks pada setiap elemen dan dilanjutkan dengan pengintegrasian ke matriks global dan boundary condition yang nantinya akan mendapatkan variable U (Defleksi).
 +
 +
Seperti yang sudah dijelaskan Fahmi pada asistensi hari minggu, setelah memasukkan setup code dari node-node, soal no.4 menggunakan solving stifftring cos^theta, sin^2theta, dan sin theta * cos theta. Lalu pada no.8 menggunakan (cos_x)^2, (cos_y)^2, (cos_z)^2, (cos_x*cos_y), (cos_x*cos_z), dan (cos_y*cos_z). Setelah memasukkan matriks element, dikerjakan matriks global yang mencakup semua nilai pada matriks lokal. Setelah itu, function GaussJordan digunakan untuk mendapat variabel U, R, dan check force. Lalu, fuction dimasukkan ke dalam class kembali. Setelah check model, dapat dilakukan simulasi yang didapatkan nilai U dan R pada masing-masing simulasi. Lalu, saya diberikan tugas oleh pak [[Ahmad Indra Siswantara]] yaitu soal berikut ini
 +
 +
[[File:ASD1.jpg|500px]]
 +
 +
 +
== '''Tugas IV''' ==
 +
 +
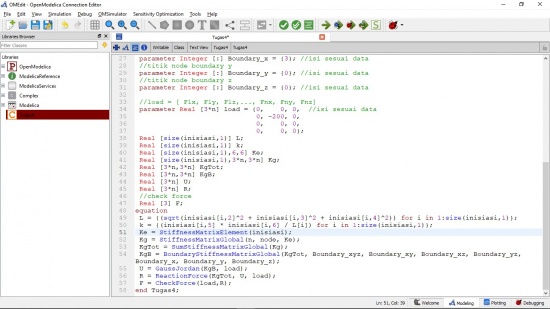
Dalam tugas ini, saya diminta untuk mencari matrix displacement dimana U = {U1x, U1y, U1z,..., Unx, Uny, Unz} ; matrix gaya reaksi dimana R = {R1x, R1y, R1z,...,Rnx, Rny, Rnz}; dan matrix gaya total pada sumbu x, y, dan z dan berikut merupakan coding yang saya lakukan didalam OpenModelica
 +
 +
[[File:Modelica_3bagol.jpg|550px]]
 +
[[File:MessageImage_1608187958042.jpg|550px]]
 +
 +
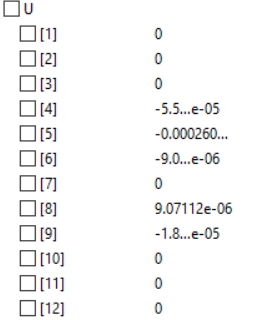
Dan berikut merupakan hasil simulasi saya untuk matrix displacement
 +
 +
[[File:Uuuuuuuuuuu.jpg|300px]]
 +
 +
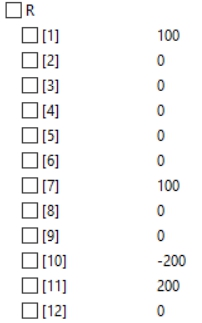
matrix gaya reaksi
 +
 +
[[File:Rrrrrrrrr.jpg|300px]]
 +
 +
matrix gaya total
 +
 +
[[File:Fffffff.jpg|300px]]
 +
 +
 +
= '''Pertemuan ke Enam''' =
 +
 +
Pada pertemuan ini, saya diminta Pak [[Ahmad Indra Siswantara]] untuk muhasabah diri terkait apa yang sudah saya pelajari dalam metode numerik ini
 +
 +
Menurut saya, pemahaman saya tentang metode numerik khususnya pada pengaplikasiannya di OpenModelica, saya sudah lumayan memahami OpenModelica karena saya sudah memiliki pemahaman sebelum UTS oleh Pak Engkos. Saya juga sudah lumayan memahami tentang suatu fenomena atau suatu benda kerja yang di input dalam pemodelan matematikanya. Menurut saya disini sangat dibantu dengan software seperti OpenModelica yang dapat membantu menyelesaikan pemodelan matematika yang harus saya kerjakan dalam pembelajaran Metoda Numerik ini.
 +
 +
 +
== '''Tugas Besar''' ==
 +
 +
Berikut merupakan soal dari tugas besar yang ada
 +
[[File:metnumafdhal46.png|500px]]
 +
 +
'''Flow Chart'''
 +
[[File:1609744201374.jpg|500px]]
 +
 +
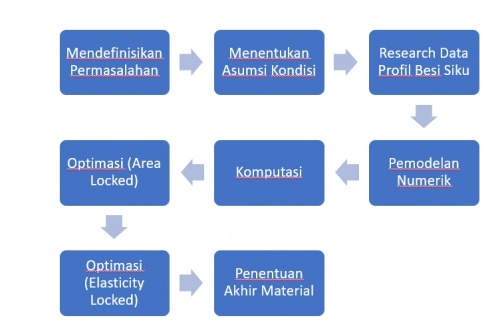
'''Mendefinisikan Permasalahan'''
 +
 +
Melakukan optimisasi pada rangka untuk mengetahui material apa yang memiliki kekuatan yang maksimal dengan harga yang minimum. Pertama-tama kita harus mengetahui profil dari besi siku dan rangka yang digunakan. Setelah itu kita juga harus menentukan elemen serta node pada rangka.
 +
 +
[[File:1609744333243.jpg|500px]]
 +
 +
'''Menentukan Asumsi dan Kondisi'''
 +
 +
Asumsi:
 +
- Diasumsikan tidak ada bending karena bersifat truss
 +
- Beban terdistribusi pada node
 +
- Safety Factor = 2
 +
- Batas displacement 0,001m sebelum terjadi buckling
 +
- Variabel bebas
 +
 +
Constraint"
 +
- Node 1,2,3,4 (lantai dasar) fixed
 +
- Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga:
 +
1. Node 13 & 16 = 1000N
 +
2. Node 14 & 15 = 500N
 +
 +
'''Research Data Profil Besi Siku'''
 +
 +
[[File:1609744461966.jpg|500px]]
 +
 +
'''Pemodelan Numerik'''
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''' 3D Trusses Model'''
 +
 +
//define initial variable
 +
 +
  parameter Integer Points=size(P,1); //Number of Points
 +
 +
  parameter Integer Trusses=size(C,1); //Number of Trusses
 +
 +
  parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa)
 +
 +
  parameter Real Area= (nilai area) ;  //Luas Besi Siku (Dimension=30x30x3mm)
 +
 +
  parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=[1,5;  // (Elemen 1)
 +
                          2,6;  // (Elemen 2)
 +
                          3,7;  // (Elemen 3)
 +
                          4,8;  // (Elemen 4)
 +
                          5,6;  // (Elemen 5)
 +
                          6,7;  // (Elemen 6)
 +
                          7,8;  // (Elemen 7)
 +
                          5,8;  // (Elemen 8)
 +
                          5,9;  // (Elemen 9)
 +
                          6,10; // (Elemen 10)
 +
                          7,11; // (Elemen 11)
 +
                          8,12; // (Elemen 12)
 +
                          9,10; // (Elemen 13)
 +
                          10,11;// (Elemen 14)
 +
                          11,12;// (Elemen 15)
 +
                          9,12; // (Elemen 16)
 +
                          9,13; // (Elemen 17)
 +
                          10,14;// (Elemen 18)
 +
                          11,15;// (Elemen 19)
 +
                          12,16;// (Elemen 20)
 +
                          13,14;// (Elemen 21)
 +
                          14,15;// (Elemen 22)
 +
                          15,16;// (Elemen 23)
 +
                          13,16];//(Elemen 24)
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[  0  ,0  ,0,1,1,1; //node 1
 +
                          0.75,0  ,0,1,1,1; //node 2
 +
                          0.75,0.6,0,1,1,1; //node 3
 +
                          0  ,0.6,0,1,1,1; //node 4
 +
                         
 +
                          0  ,0  ,0.3,0,0,0; //node 5
 +
                          0.75,0  ,0.3,0,0,0; //node 6
 +
                          0.75,0.6,0.3,0,0,0; //node 7
 +
                          0  ,0.6,0.3,0,0,0; //node 8
 +
                         
 +
                          0  ,0  ,1.05,0,0,0; //node 9
 +
                          0.75,0  ,1.05,0,0,0; //node 10 
 +
                          0.75,0.6,1.05,0,0,0; //node 11
 +
                          0  ,0.6,1.05,0,0,0; //node 12
 +
                         
 +
                          0  ,0  ,1.8,0,0,0; //node 13
 +
                          0.75,0  ,1.8,0,0,0;  //node 14
 +
                          0.75,0.6,1.8,0,0,0; //node 15
 +
                          0  ,0.6,1.8,0,0,0]; //node 16
 +
                         
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,-1000,
 +
                          0,0,-500,
 +
                          0,0,-500,
 +
                          0,0,-1000};
 +
//solution
 +
  Real displacement[N], reaction[N];
 +
  Real check[3];
 +
  Real stress1[Trusses];
 +
  Real safety[Trusses];
 +
  Real dis[3];
 +
  Real Str[3];
 +
protected
 +
  parameter Integer N=3*Points;
 +
  Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
  Real err=10e-15, ers=10e-8;
 +
algorithm
 +
  //Creating Global Matrix
 +
    G:=id;
 +
      for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
                end for;     
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                    cy*cx,cy^2,cy*cz;
 +
                    cz*cx,cz*cy,cz^2];
 +
    //Transforming to global matrix
 +
  g:=zeros(N,N);
 +
  for m,n in 1:3 loop
 +
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
  end for; 
 +
  G_star:=G+g;
 +
  G:=G_star;
 +
end for;
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
  if P[x,4] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-2,a]:=0;
 +
    G[(x*3)-2,(x*3)-2]:=1;
 +
  end for;
 +
end if;
 +
if P[x,5] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-1,a]:=0;
 +
    G[(x*3)-1,(x*3)-1]:=1;
 +
  end for;
 +
end if;
 +
if P[x,6] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[x*3,a]:=0;
 +
    G[x*3,x*3]:=1;
 +
  end for;
 +
  end if;
 +
end for;
 +
//Solving displacement
 +
    displacement:=Modelica.Math.Matrices.solve(G,F);
 +
//Solving reaction
 +
    reaction:=(G_star*displacement)-F;
 +
//Eliminating float error
 +
for i in 1:N loop
 +
  reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
  displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
//Checking Force
 +
  check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
  check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
  check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); 
 +
    for i in 1:3 loop
 +
      check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
    end for;
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
end for;     
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];   
 +
  Str:=(X*dis);
 +
  stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for;
 +
//Safety factor
 +
  for i in 1:Trusses loop
 +
  if stress1[i]>0 then
 +
    safety[i]:=Yield/stress1[i];
 +
  else
 +
    safety[i]:=0;
 +
  end if;
 +
  end for;
 +
end Trusses_3D_Tugas_Besar;
 +
|}
 +
 +
'''Komputasi'''
 +
 +
Dan berikut merupakan progres yang saya lakukan yang pertama saya mengisi data didalam excel untuk input dari catalog yang sudah saya dapatkan, dan disini saya menggunakan SS304
 +
 +
[[File:Asdadadada.jpg]]
 +
 +
Dan berikut merupakan coding dari curve fitting yang telah saya lakukan
 +
 +
[[File:1609741663978.jpg|500px]]
 +
[[File:1609741654787.jpg|500px]]
 +
 +
Dan berikut merupakan grafik yang saya dapat
 +
 +
[[File:1609742172512.jpg]]
 +
 +
= '''Jawaban UAS''' =
 +
 +
Berikut merupakan Jawaban uas saya
 +
 +
[[File:158040.jpg]]
 +
[[File:158041.jpg]]
 +
 +
Dan berikut merupakan pemodelan yang saya buat di OpenModelica
 +
 +
[[File:MessageImage_1610560683494.jpg|700px]]
 +
 +
[[File:1610560193145.jpg]]
 +
 +
Berikut merupakan hasil dari Stress 1, 2, dan 3 yang telah saya simulasikan
 +
 +
[[File:MessageImage_1610560426309.jpg]]

Latest revision as of 12:27, 14 January 2021

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Assalamualaikum wr. wb.


Biodata Diri

Muhammad Daffa Fachturrohman

Nama : Muhammad Daffa Fachturrohman

NPM : 1806181855

Agama : Islam

Program Studi : S1 Teknik Mesin Paralel



Pertemuan Pertama


Pada pertemuan pertama saya dengan Pak Ahmad Indra Siswantara, saya diminta untuk menginstall software OpenModelica yang bertujuan untuk mensimulasikan suatu sistem yang didistribusikan dalam bentuk kode sumber dan biner untuk penelitian.

Tugas I

Untuk Tugas Pertama yang saya dapat dari Pak Ahmad Indra Siswantara adalah membuat video pengaplikasian pada OpenModelica. Pada kesempatan kali ini, saya mengerjakan simulasi dari software OpenModelica ini bersumber dari buku yang saya gunakan selama pembelajaran Metode Numerik ini yaitu Numerical Methods for Engineers 7th Edition. Saya menerapkan regresi linear yang ada didalam buku tersebut yaitu di bab 17 tepatnya di example 17.1.

Disini saya hanya memasukkan data-data dari setiap variabel yang ada dan juga memasukkan formula-formula untuk menyelesaikan persamaan yang dibutuhkan yang datanya dari variabel yang telah saya masukkan kedalam sistem. Namun, ada sedikit kesalahan memasukkan data yang saya alami didalam video yang saya lampirkan dibawah. Tetapi OpenModelica ini sangat berguna untuk saya untuk menyelesaikan persamaan-persamaan yang ada didalam suatu sistem contohnya regresi linear yang saya kerjakan ini dibandingkan saya harus menghitungnya secara manual dan secara tertulis.

Berikut merupakan sumber yang saya gunakan dalam pengerjaan simulasi ini

Dari Buku 1.jpg Dari Buku 2.jpg

Link Video

Berikut merupakan link video penjelasan saya dalam pengerjaan simulasi diatas dalam OpenModelica

https://youtu.be/JNhN_M6N6p0

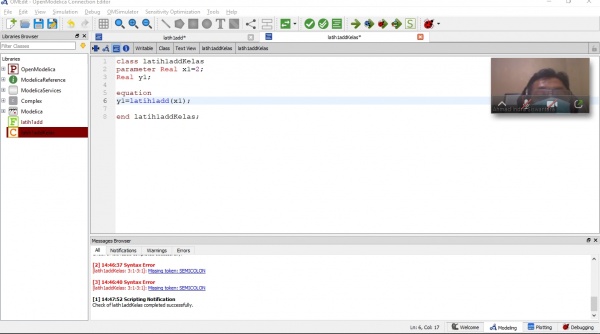
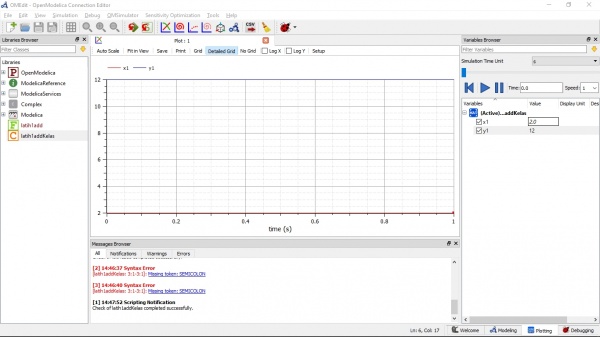
Pertemuan Kedua

Pada pertemuan kali ini, setiap mahasiswa mata kuliah metode numerik 03 diminta untuk menjelaskan progres dari PRnya masing-masing kepada Pak Ahmad Indra Siswantara, namun saya tidak dipanggil untuk diminta menjelaskan kembali progres PR saya karena saya sudah mensimulasikan melalui OpenModelica dan saya juga sudah mengunggah video saya di youtube channel saya sendiri.

Pada pertemuan ini saya juga diajarkan untuk mensimulasikan kembali di OpenModelica sesuai dengan instruksi dari Pak Ahmad Indra Siswantara. Saya memasukkan persamaan kedalam kelas modelica yang saya buat untuk tipe Class dan juga Function, disitu saya diminta untuk memasukkan variabel-variabel yang telah disebutkan oleh Pak Ahmad Indra Siswantara, dan variabel-variabel sampai hasil simulasinya adalah sebagai berikut :

Modelica 1.jpg Modelica 2.jpg Modelica 3.jpg

Tugas II

Pada pertemuan kedua dengan pak Ahmad Indra Siswantara, saya diberikan tugas untuk menyelesaikan simulasi dari persamaan-presamaan aljabar simultan yaitu seperti Gauss Elimination, Gauss-Seidel, dan lainnya didalam OpenModelica.

Dengan demikian, saya menggunakan 3 persamaan aljabar yang ada sebagai berikut

1606107310523.jpg

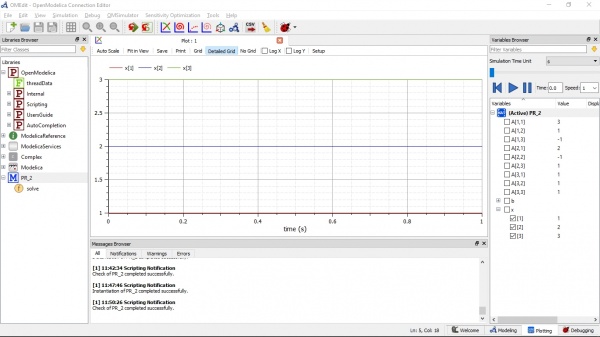
Untuk menyelesaikan 3 persamaan tersebut, saya menggunakan Gauss Elimination. Didalam sistem OpenModelica sendiri, saya mengubahnya dalam bentuk matriks 3x3 yang dapat dilihat seperti kodingan saya dibawah ini

9981.jpg

Untuk penyelesaiannya, saya menggugnakan perintah dari sistem OpenModelicanya sendiri, yaitu Modelica.Math.Matrices.solve(A,b) dan beberapa perintah baru yang saya pelajari dari beberapa sumber yang ada. Dan penyelesaiannya dari hasil simulasi saya adalah sebagai berikut

1606107125738.jpg

Sehingga ditemukan bahwa x = 1, y = 2, dan z = 3.

Pertemuan Ketiga

Bismillahirrahmanirrahiim

Pada pertemuan kali ini, saya diminta untuk melakukan simulasi dalam modelica yang datanya didapat dari Numerical Methods for Engineers edisi ke-7.

Didalam buku ini di halaman 328, terdapat studi kasus pegas massa pada tabel 11.12, pada pertemuan ini saya diminta untuk membuktikan persamaan aljabar yang ada dengan menggunakan OpenModelica sebagai berikut :

1606114179693.jpg

Lalu, saya menggunakan OpenModelica dengan memasukkan persamaan linier yang ada dengan menggunakan matriks 3x3 sebagai berikut dan juga saya

1606114928506.jpg

Lalu untuk penyelesaiannya, saya menggunakan perintah dari sistem OpenModelica yang ada seperti gambar berikut

1606115131055.jpg

Dari hasil simulasi yang saya lakukan dengan OpenModelica, terdapat hasil yaitu x1 = 7.3575; x2 = 10.0552; x3 = 12.5077. Dan hasil tersebut sesuai dengan yang ada di buku Numerical Methods for Engineers edisi ke-7


Tugas III

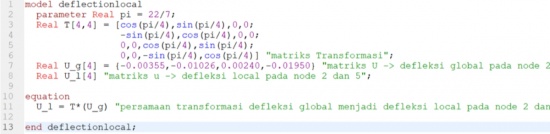
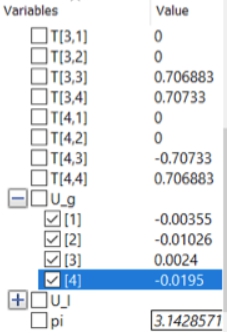
Pada pertemuan ini, Pak Ahmad Indra Siswantara memberikan tugas untuk mencari defleksi menggunakan matriks yang didapat dari buku Finite Element Analysis halaman 60-68, lalu saya melakukan koding dari soal yang ada sebagai berikut

414B09F8-8F1D-4AE2-8ADF-3296B789B723.png

Dengan kodingan diatas, saya mendapatkan data sebagai berikut :

1606711313050.jpg

Lalu, untuk mendapatkan gaya reaksi, saya melakukan koding dan menghasilkan data sebagai berikut :

1606711713530.jpg

1606711780530.jpg

Lalu untuk mendapatkan defleksi total dari referensi yang ada dibuku juga, saya melakukan koding dan dapat dilihat pula hasilnya sebagai berikut :

1606711864417.jpg

1606711905375.jpg

Dari data diatas, didapatkan hasil U2x=-0.00976 inch dan U6x=-0.01209 inch

Lalu untuk internal force :

f ix = k(uix - ujx) f jx = k(ujx - uix)

dari persamaan diatas didapatkan internal force pada elemen-5 yaitu 696lb

Dan dengan persamaan normal stress :

1606712071490.jpg

Lalu didapatkan normal stress sebesar 87lb/in^2


Pertemuan Ke Empat

Pada pertemuan kali ini, pak Ahmad Indra Siswantara me remind tentang analisa Statik dan Dinamik


Excersice

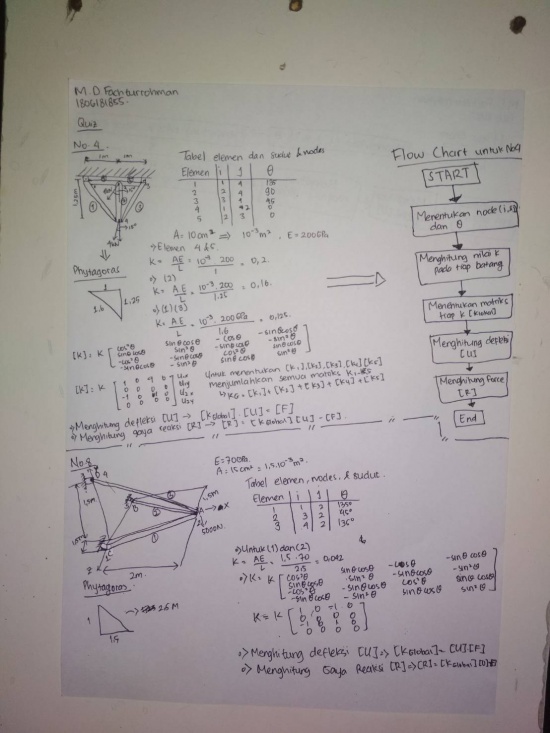
Dari pertemuan kali ini, saya diberikan soal oleh Pak Ahmad Indra Siswantara seperti gambar dibawah ini :

1606735880652.jpg WhatsApp Image 2020-11-30 at 1.17.40 PM.jpeg

Lalu dengan soal tersebut saya melakukan perhitungan sampai menemukan K dari setiap elemen yang ada yang bisa saya klasifikasikan. Lalu, saya menmbuat chart flow untuk mendapatkan defleksi dan juga gaya reaksi setelah perhitungan saya menggunakan OpenModelica sebagai berikut :

127384.jpg

127385.jpg


Lanjutan Exersice untuk Modelica

Saya melanjutkan data yang saya dapat diatas untuk dijadikan matriks seperti yang ada dibawah ini

1607427760636.jpg

Dari matriks yang saya dapatkan diatas, saya mengimplementasikan matriks tersebut kedalam software OpenModelica

1607430295131.jpg

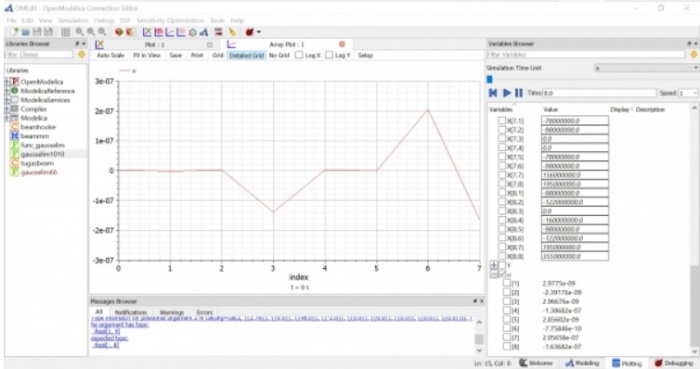
dan berikut merupakan hasil simulasi dari matriks yang saya masukkan ke atas

1607499704841.jpg

Pertemuan Kelima

Pada pertemuan tanggal 7 Desember 2020, saya di ajarkan Pak Ahmad Indra Siswantara tentang quiz no 4 dan 8 yang dibantu oleh teman saya Ahmad Mohammad Fahmi yang telah menyelesaikan kedua nomor pada quiz sebelumnya, ada beberapa tahapan dari setelah kita membuat flow chart seperti gambar yang terlampir pada laman ini, yang pertama adalah solve striffness, lalu menentukan matriks pada setiap elemen dan dilanjutkan dengan pengintegrasian ke matriks global dan boundary condition yang nantinya akan mendapatkan variable U (Defleksi).

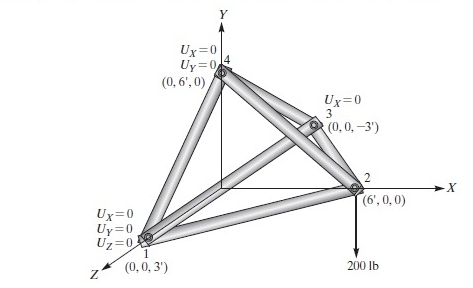
Seperti yang sudah dijelaskan Fahmi pada asistensi hari minggu, setelah memasukkan setup code dari node-node, soal no.4 menggunakan solving stifftring cos^theta, sin^2theta, dan sin theta * cos theta. Lalu pada no.8 menggunakan (cos_x)^2, (cos_y)^2, (cos_z)^2, (cos_x*cos_y), (cos_x*cos_z), dan (cos_y*cos_z). Setelah memasukkan matriks element, dikerjakan matriks global yang mencakup semua nilai pada matriks lokal. Setelah itu, function GaussJordan digunakan untuk mendapat variabel U, R, dan check force. Lalu, fuction dimasukkan ke dalam class kembali. Setelah check model, dapat dilakukan simulasi yang didapatkan nilai U dan R pada masing-masing simulasi. Lalu, saya diberikan tugas oleh pak Ahmad Indra Siswantara yaitu soal berikut ini

ASD1.jpg


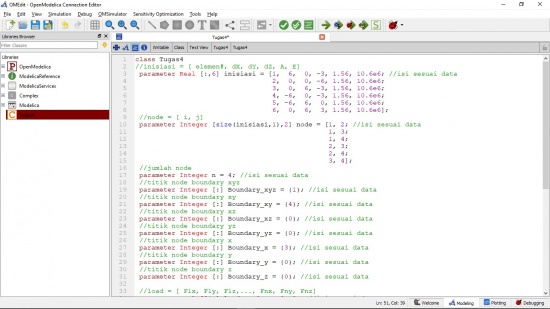
Tugas IV

Dalam tugas ini, saya diminta untuk mencari matrix displacement dimana U = {U1x, U1y, U1z,..., Unx, Uny, Unz} ; matrix gaya reaksi dimana R = {R1x, R1y, R1z,...,Rnx, Rny, Rnz}; dan matrix gaya total pada sumbu x, y, dan z dan berikut merupakan coding yang saya lakukan didalam OpenModelica

Modelica 3bagol.jpg MessageImage 1608187958042.jpg

Dan berikut merupakan hasil simulasi saya untuk matrix displacement

Uuuuuuuuuuu.jpg

matrix gaya reaksi

Rrrrrrrrr.jpg

matrix gaya total

Fffffff.jpg


Pertemuan ke Enam

Pada pertemuan ini, saya diminta Pak Ahmad Indra Siswantara untuk muhasabah diri terkait apa yang sudah saya pelajari dalam metode numerik ini

Menurut saya, pemahaman saya tentang metode numerik khususnya pada pengaplikasiannya di OpenModelica, saya sudah lumayan memahami OpenModelica karena saya sudah memiliki pemahaman sebelum UTS oleh Pak Engkos. Saya juga sudah lumayan memahami tentang suatu fenomena atau suatu benda kerja yang di input dalam pemodelan matematikanya. Menurut saya disini sangat dibantu dengan software seperti OpenModelica yang dapat membantu menyelesaikan pemodelan matematika yang harus saya kerjakan dalam pembelajaran Metoda Numerik ini.


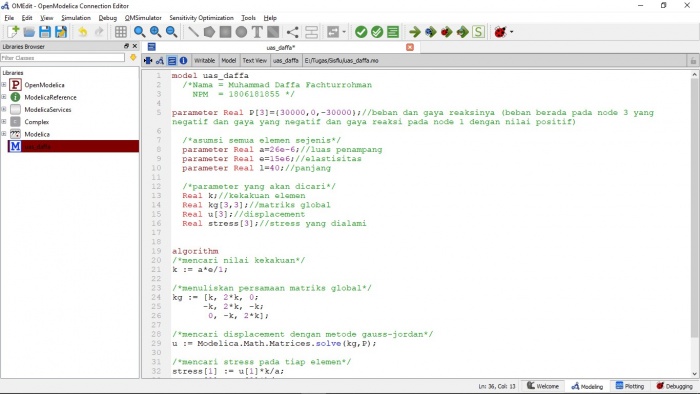
Tugas Besar

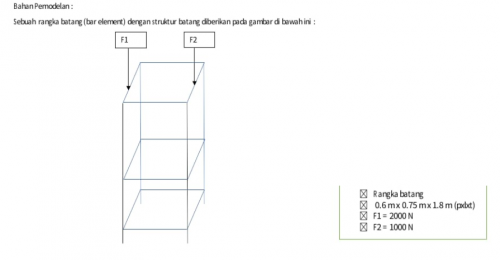
Berikut merupakan soal dari tugas besar yang ada Metnumafdhal46.png

Flow Chart 1609744201374.jpg

Mendefinisikan Permasalahan

Melakukan optimisasi pada rangka untuk mengetahui material apa yang memiliki kekuatan yang maksimal dengan harga yang minimum. Pertama-tama kita harus mengetahui profil dari besi siku dan rangka yang digunakan. Setelah itu kita juga harus menentukan elemen serta node pada rangka.

1609744333243.jpg

Menentukan Asumsi dan Kondisi

Asumsi: 

- Diasumsikan tidak ada bending karena bersifat truss
- Beban terdistribusi pada node
- Safety Factor = 2
- Batas displacement 0,001m sebelum terjadi buckling
- Variabel bebas

Constraint"
- Node 1,2,3,4 (lantai dasar) fixed
- Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga:
1. Node 13 & 16 = 1000N
2. Node 14 & 15 = 500N

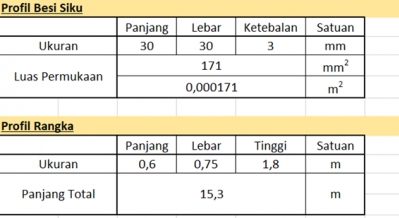
Research Data Profil Besi Siku

1609744461966.jpg

Pemodelan Numerik

3D Trusses Model 

//define initial variable

  parameter Integer Points=size(P,1);		//Number of Points

  parameter Integer Trusses=size(C,1); 		//Number of Trusses

  parameter Real Yield= (nilai yield) ;		//Yield Strength Material(Pa)

  parameter Real Area= (nilai area) ;   	//Luas Besi Siku (Dimension=30x30x3mm)

  parameter Real Elas= (nilai elastisitas) ;	//Elasticity Material (Pa)

//define connection
parameter Integer C[:,2]=[1,5;  // (Elemen 1)
                         2,6;  // (Elemen 2)
                         3,7;  // (Elemen 3)
                         4,8;  // (Elemen 4)
                         5,6;  // (Elemen 5)
                         6,7;  // (Elemen 6)
                         7,8;  // (Elemen 7)
                         5,8;  // (Elemen 8)
                         5,9;  // (Elemen 9)
                         6,10; // (Elemen 10)
                         7,11; // (Elemen 11)
                         8,12; // (Elemen 12)
                         9,10; // (Elemen 13)
                         10,11;// (Elemen 14)
                         11,12;// (Elemen 15)
                         9,12; // (Elemen 16)
                         9,13; // (Elemen 17)
                         10,14;// (Elemen 18)
                         11,15;// (Elemen 19)
                         12,16;// (Elemen 20)
                         13,14;// (Elemen 21)
                         14,15;// (Elemen 22)
                         15,16;// (Elemen 23)
                         13,16];//(Elemen 24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[   0   ,0  ,0,1,1,1;	//node 1
                          0.75,0  ,0,1,1,1;	//node 2
                          0.75,0.6,0,1,1,1;	//node 3
                          0   ,0.6,0,1,1,1;	//node 4
                          
                          0   ,0  ,0.3,0,0,0;	//node 5
                          0.75,0  ,0.3,0,0,0;	//node 6
                          0.75,0.6,0.3,0,0,0;	//node 7
                          0   ,0.6,0.3,0,0,0;	//node 8
                          
                          0   ,0  ,1.05,0,0,0;	//node 9
                          0.75,0  ,1.05,0,0,0;	//node 10  
                          0.75,0.6,1.05,0,0,0;	//node 11
                          0   ,0.6,1.05,0,0,0;	//node 12
                          
                          0   ,0  ,1.8,0,0,0;	//node 13
                          0.75,0  ,1.8,0,0,0;  //node 14
                          0.75,0.6,1.8,0,0,0;	//node 15
                          0   ,0.6,1.8,0,0,0];	//node 16
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,-1000, 
                          0,0,-500, 
                          0,0,-500, 
                          0,0,-1000}; 
//solution
  Real displacement[N], reaction[N];
  Real check[3];
  Real stress1[Trusses];
  Real safety[Trusses];
  Real dis[3];
  Real Str[3];
protected
 parameter Integer N=3*Points;
 Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 Real err=10e-15, ers=10e-8;
algorithm
 //Creating Global Matrix
    G:=id;
     for i in 1:Trusses loop
		for j in 1:3 loop
 			q1[j]:=P[C[i,1],j];
 			q2[j]:=P[C[i,2],j];
               end for;       
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                    cy*cx,cy^2,cy*cz;
                    cz*cx,cz*cy,cz^2];
   //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;   
 G_star:=G+g;
 G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
 if P[x,4] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-2,a]:=0;
    G[(x*3)-2,(x*3)-2]:=1;
  end for;
end if;
if P[x,5] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-1,a]:=0;
    G[(x*3)-1,(x*3)-1]:=1;
  end for;
end if;
if P[x,6] <> 0 then
  for a in 1:Points*3 loop
    G[x*3,a]:=0;
    G[x*3,x*3]:=1;
  end for;
 end if;
end for;
//Solving displacement
    displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
    reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
  check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
  check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
  check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});  
    for i in 1:3 loop
      check[i] := if abs(check[i])<=ers then 0 else check[i];
    end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;       
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
               cy*cx,cy^2,cy*cz;
               cz*cx,cz*cy,cz^2];    
  Str:=(X*dis);
  stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
 for i in 1:Trusses loop
  if stress1[i]>0 then
   safety[i]:=Yield/stress1[i];
  else
   safety[i]:=0;
  end if; 
 end for;
end Trusses_3D_Tugas_Besar;

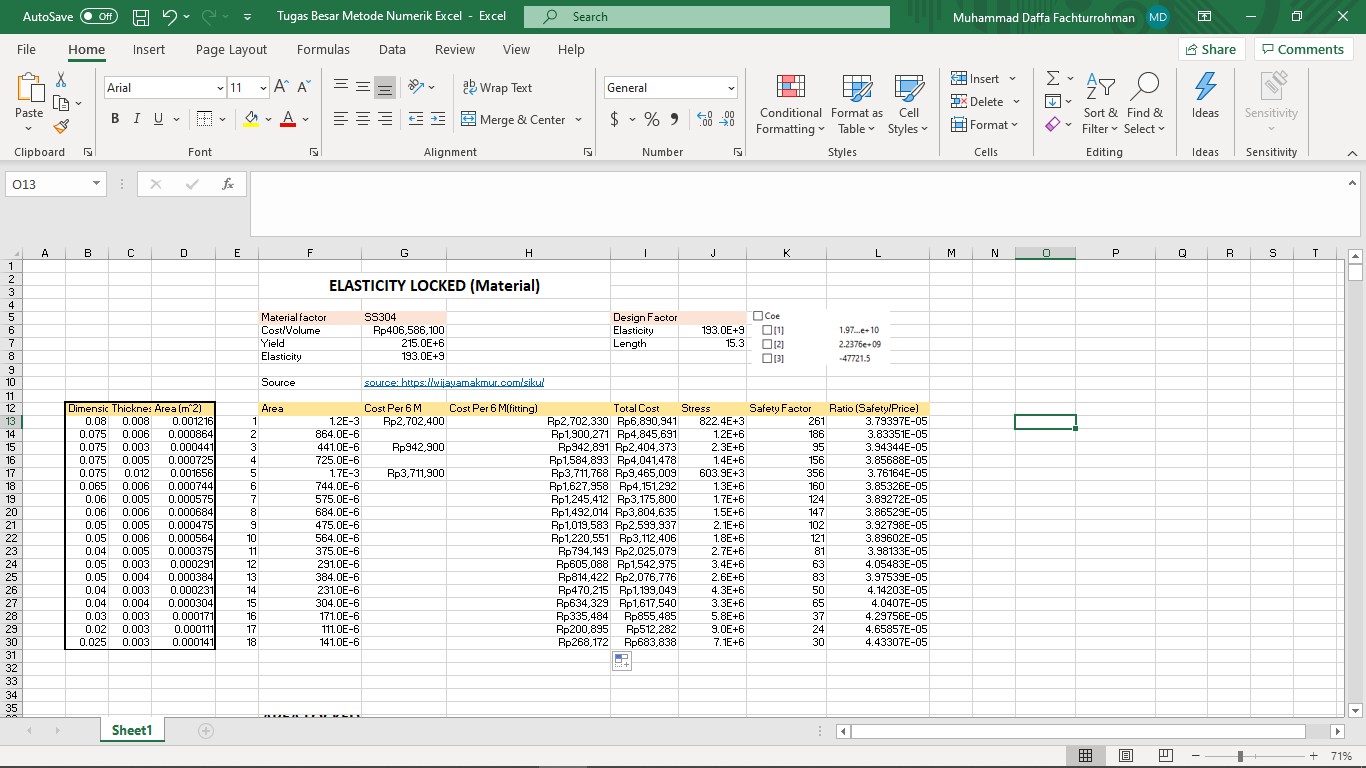
Komputasi

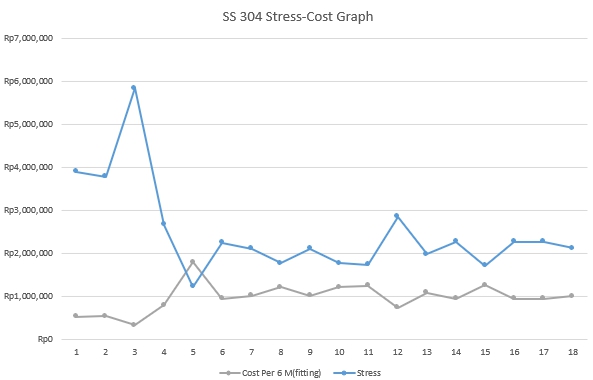
Dan berikut merupakan progres yang saya lakukan yang pertama saya mengisi data didalam excel untuk input dari catalog yang sudah saya dapatkan, dan disini saya menggunakan SS304

Asdadadada.jpg

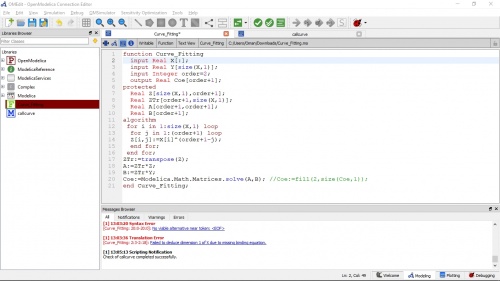
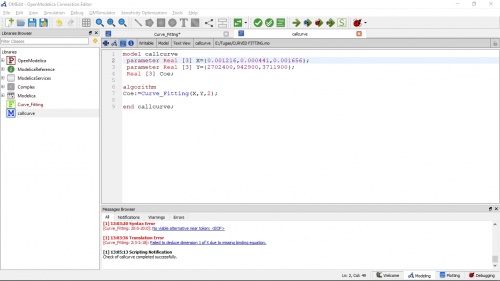
Dan berikut merupakan coding dari curve fitting yang telah saya lakukan

1609741663978.jpg 1609741654787.jpg

Dan berikut merupakan grafik yang saya dapat

1609742172512.jpg

Jawaban UAS

Berikut merupakan Jawaban uas saya

158040.jpg 158041.jpg

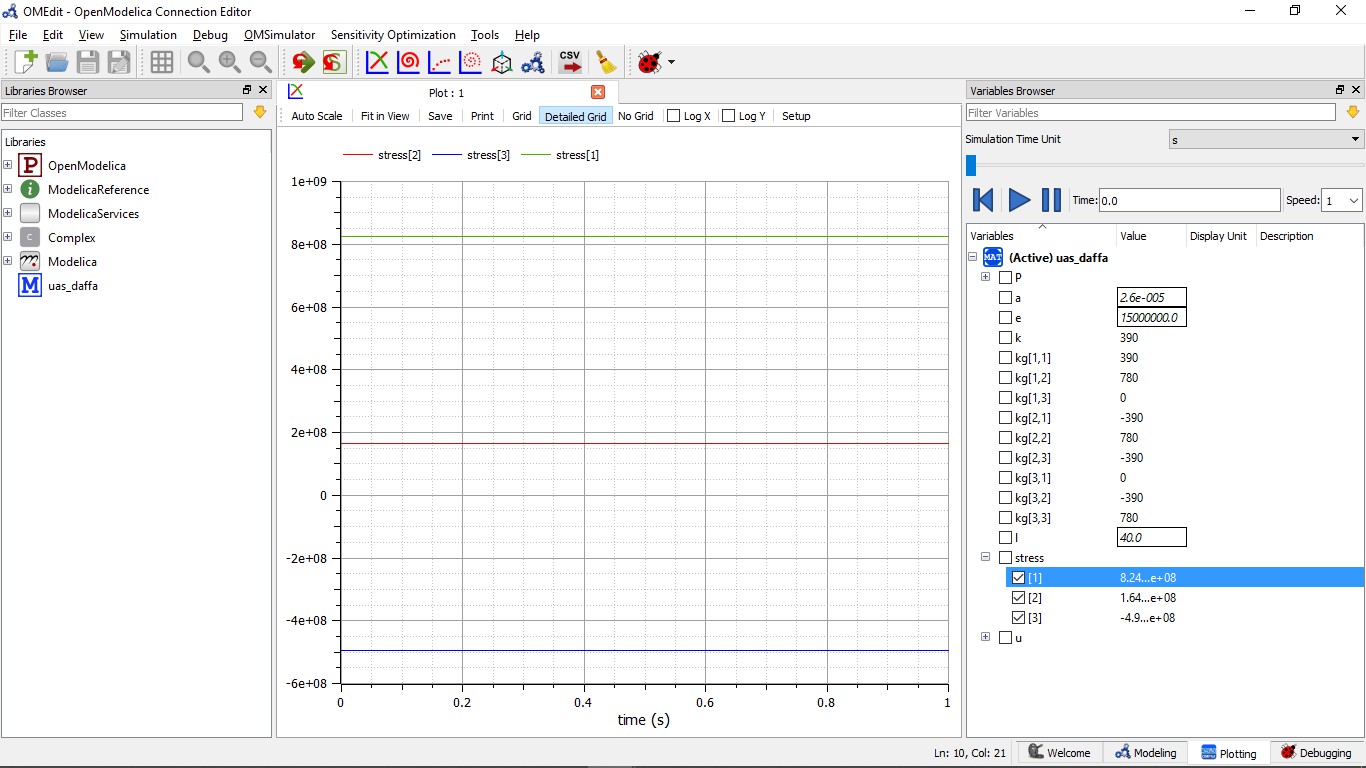
Dan berikut merupakan pemodelan yang saya buat di OpenModelica

MessageImage 1610560683494.jpg

1610560193145.jpg

Berikut merupakan hasil dari Stress 1, 2, dan 3 yang telah saya simulasikan

MessageImage 1610560426309.jpg

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03-Muhammad_Daffa_Fachturrohman&oldid=55855"