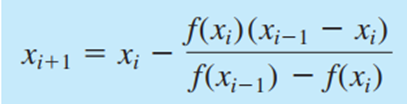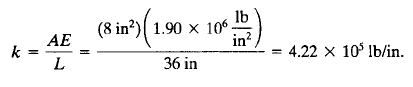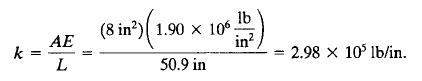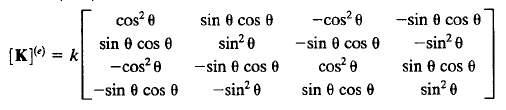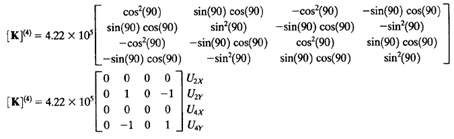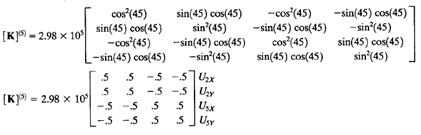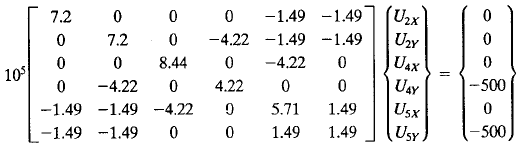Difference between revisions of "Metnum03-Dendy Dwi Rohma P J"

From ccitonlinewiki
Jump to: navigation, search
(→‎Pertemuan 2)
(→‎Jawaban UAS)
 
(43 intermediate revisions by the same user not shown)
Line 5: Line 5:
 
NPM: 1906435473
 
NPM: 1906435473
  
−
== Pertemuan 1 ==
+
= Pertemuan 1 =
 
'''1. Tugas_01_MetodeNumerik03'''
 
'''1. Tugas_01_MetodeNumerik03'''
  
Line 22: Line 22:
 
Dalam kesempatan kali ini saya akan membahas tentang metode secant.
 
Dalam kesempatan kali ini saya akan membahas tentang metode secant.
  
−
'''Pengertian Metode Secant'''
+
=='''Pengertian Metode Secant'''==
  
 
Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi
 
Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi
Line 33: Line 33:
 
3.  Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.
 
3.  Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.
  
−
'''SOAL 1'''
+
=='''SOAL 1'''==
  
 
Cari Akar Persamaan dari Persamaan f(x) dengan Metode Secant Method pada Literasi ke 4?
 
Cari Akar Persamaan dari Persamaan f(x) dengan Metode Secant Method pada Literasi ke 4?
Line 52: Line 52:
 
'''''Link Youtube :''''' https://www.youtube.com/watch?v=Bk_QtrInpks
 
'''''Link Youtube :''''' https://www.youtube.com/watch?v=Bk_QtrInpks
  
−
== Pertemuan 2 ==
+
= Pertemuan 2 =
  
 
[[File:LatihanMean2.png|700px|center]]
 
[[File:LatihanMean2.png|700px|center]]
Line 58: Line 58:
 
Melakukan latihan mencari nilai mean dari persamaan dan data sederhana.
 
Melakukan latihan mencari nilai mean dari persamaan dan data sederhana.
  
−
'''''PR Eliminasi Gauss'''''
+
=='''''PR Eliminasi Gauss'''''==
  
 
[[File:CodingGauss1.png|700px|center]]
 
[[File:CodingGauss1.png|700px|center]]
Line 65: Line 65:
  
 
[[File:ValidasiGauss.jpg|500px|center]]
 
[[File:ValidasiGauss.jpg|500px|center]]
 +
 +
 +
= Pertemuan 3 =
 +
'''3. Tugas_03_MetodeNumerik03'''
 +
 +
=='''''MASS SPRING ANALYSIS MATRIX'''''==
 +
 +
 +
=='''''TRUSS ANALYSIS MATRIX'''''==
 +
 +
Tugas kali ini disuruh mencari nilai defleksi/dX/U pada suatu truss yang disusun dan dikenai pembebanan dan tumpuan seperti pada soal dibawah ini. Lalu kemudian setelah kita menemukan nilai U lalu digunakan untuk mencari reaksi gaya (R) pada setiap elemen truss.
 +
 +
[[File:1_Soal_Truss.png]]
 +
 +
Berdasarkan susunan truss diatas, kita harus mampu menjabarkan setiap beam/ truss menjadi notasi element, tumpuan menjadi notasi node dan sudut element terhadap garis refrensi yg kita pilih (saya menggunakan X positif sbg sb.0 deg). Lalu setelah dilakukan penjabaran berdasarkan element, node dan sudut didapatkan Tabel 2.1 sebagai hubungannya.
 +
 +
[[File:2_Truss_MenjadiNode.png]]
 +
 +
Setelah itu dilakukan perkalian untuk mencari nilai kekakuan setiap truss/ element dengan rumus k=A.E/L. Namun sebelumnya dilakukan pengelompokan berdasarkan panjang batang/truss lalu didapatkan batang dengan panjang yang sama (1,3,4,6) dan batang (2,5). Namun untuk mendapatkan nilai K lokal nilai k(kekakuan) harus terlebih dahulu dikalikan dengan rumus K lokal dalam bentuk matrix 4x4.
 +
 +
[[File:3_KonstantaStiffness_1.3.4.6.png]]
 +
 +
[[File:3_KonstantaStiffness_2.5.png]]
 +
 +
Nah rumus K^e atau K lokal menurut pemahaman saya dapat berbeda-beda tergantung dengan susunan dari truss (sudut yang terbentuk dari sb. refrensi yang kita gunakan) atau batang dan tumpuan yang kita gunakan. Lalu untuk nilai k (kekakuan) hanya dipengaruhi dari cross section area (A), elastisitas (E) dan panjang batang (L)
 +
 +
[[File:4_RumusK.png]]
 +
 +
'''Analisa Batang 4'''
 +
 +
Analisa batang pada contoh soal ini jg dapat dikelompokan berdasarkan panjang batangnya. Jadi untuk analisa pertama batang (1,3,4,6) dan batang (2 dan 5). Pada batang (1,3,dan 6) memiliki sudut refrensi yang sama yaitu 0 derajat, namun ketiga element ini memiliki node yang berbeda sehingga akan berpengaruh pada peletakan hasil matrix 4x4 pada matrix global (K^G) 10x10.
 +
 +
[[File:5_1_AnalisaElemen4.png]]
 +
 +
Pada gambar dibawah ini hasil K^e (K lokal) dimasukan ke dalam matrix 10x10 K^G berdasarkan node arah sb. X dan sb. Y.
 +
 +
[[File:5_2_Elemen4_DiglobalMatrik.png]]
 +
 +
'''Analisa Batang 2'''
 +
 +
Kemudian dilakukan analisa batang (2 dan 5) dengan cara yang sama seperti gambar diatas dengan mengunakan rumus matrix K (4x4). Namun pada element 2 dan 5 hanya berbeda pada penggunaan sudut berdasarkan sumbu refrensi (element 2 : 135deg, element 5 : 45deg).
 +
 +
[[File:6_1_AnalisaElemen2.png]]
 +
 +
Pada gambar dibawah ini hasil K^e (K lokal) dimasukan ke dalam matrix 10x10 K^G berdasarkan node arah sb. X dan sb. Y.
 +
 +
[[File:6_1_Elemen2Global.png]]
 +
 +
'''Analisa Batang 5'''
 +
 +
[[File:6_2_AnalisaElemen5.png]]
 +
 +
[[File:6_2_Elemen5Global.png]]
 +
 +
Kemudian dilakukan penjumlahan matrik tersebut menjadi matrik global.
 +
 +
[[File:7_1_PenjumlahanK-Kglobal.png]]
 +
 +
Didapatkan hasil penjumlahan matrik lokal tersebut menjadi matrik global dengan jumlah 10x10.
 +
 +
[[File:7_2_Kglobal.png]]
 +
 +
Kemudian dilakukan batasan masalah seperti ada atau tidaknya fix point pada suatu susunan model truss. Berdasarkan soal didapatkan pada node 1 dan 3 adalah nilai U adalah 0 (U1x, U1y, U3x, U3y). Karena apabila tidak dilakukan permisalan maka susunan trus akan berotasi bila dikenai gaya.
 +
 +
[[File:8_1_Matrik6x6_PenerapanFixPoint.png]]
 +
 +
Berdasarkan rumus F=K.dX (F=K.U) kita disuruh untuk mencari nilai U pada tiap node berdasarkan sb. x dan sb. y. Maka untuk mencarinya kita dapat memanggil fungsi solve (A.x=B) untuk mencari nilai x atau U. Dengan memasukan koding 6x6 dibawah ini akan didapatkan nilai U pada node (2,4,5) berdasarkan sb.x dan sb.y.
 +
 +
[[File:8_2_Matrik6x6_Coding.png]]
 +
 +
Didapatkan nilai U adalah sama seperti contoh dibuku.
 +
 +
[[File:8_3_Matrik6x6_dXatauU.png]]
 +
 +
'''Analisa Reaksi Gaya pada Setiap Node'''
 +
 +
Pada analisa ini kita harus menuliskan kembali hasil perhitungan sebelumnya U kedalam parameter matriknya. Rumus reaksi adalah R = [K]^G.{U}-{F}. Dapat dikatakan bahwa R adalah reaksi yang terjadi pada setiap node dengan arah sb.x dan sb.y. Dengan metode matrik ini iibaratnya seperti perhitungan manual (FBD) gaya-gaya yang terjadi pada setiap titik tumpuan berdasarkan arah sumbu kerja (2D yaitu x,y).
 +
 +
[[File:9_ReaksiGaya.png]]
 +
 +
[[File:10_dXatauU_Matrik10x10.png]]
 +
 +
Pada U semua node, didaptkan bahwa nilai pada node 1 dan 3 adalah tetap 0 pada matix K^G untuk mencari nilai R seperti dibawah ini.
 +
 +
[[File:11_1_Matrik10x10_MencariReaksi(R).png]]
 +
 +
Untuk programnya hanya perlu mengalikan fungsi R=(K*U)-F seperti biasa. Tidak perlu memanggil program solve (gauss).
 +
 +
[[File:11_2_Matrik10x10_Coding.png]]
 +
 +
Kemudian untuk reaksi gayanya didapatkan nilai seperti ploting dibawah ini, dan dilakukan pembulatan pada node (3,4,5) karena nilai gayanya sangat kecil.
 +
 +
[[File:11_3_Matrik10x10_Reaksi(R).png]]
 +
 +
= Pertemuan 4 =
 +
=='''Quiz_1_MetodeNumerik03'''==
 +
 +
==='''Quiz_1_Truss2D'''===
 +
 +
[[File:1_Flow_Chart_Kuiz1.jpg|400px]]
 +
 +
[[File:2_FBD_Kuiz1.jpg|400px]]
 +
 +
[[File:3_K_Lokal.jpg|400px]]
 +
 +
[[File:4_K_Lokal.jpg|400px]]
 +
 +
[[File:Element1_2D_Dendy.png]]
 +
 +
[[File:Element5_2D_Dendy.png]]
 +
 +
[[File:KG_2D_DendyDwi.png]]
 +
 +
[[File:CodingU_Truss_2D_DendyDwi.png]]
 +
 +
[[File:CodingR_Truss_2D_DendyDwi.png]]
 +
 +
[[File:Nilai_U_R_2D_DendyDwi.png]]
 +
 +
==='''Quiz_1_Truss3D'''===
 +
 +
[[File:1_FBD_3D_DendyDwi.jpg]]
 +
 +
[[File:2_FBD_3D_DendyDwi.jpg]]
 +
 +
[[File:3_Element1_3D_Dendy.jpg]]
 +
 +
[[File:4_Element2_3D_Dendy.jpg]]
 +
 +
[[File:5_Element3_3D_Dendy.jpg]]
 +
 +
= Pertemuan 5 =
 +
=='''Tugas Metode Numerik'''==
 +
 +
[[File:Soal3D.jpeg|400px|center]]
 +
 +
[[File:1 Class.jpg|600px|center]]
 +
 +
[[File:2 U.jpg|300px|center]]
 +
 +
[[File:3 R.jpg|300px|center]]
 +
 +
[[File:4 F.jpg|300px|center]]
 +
 +
= Tugas Besar =
 +
 +
'''Soal'''
 +
 +
-Temukan Cost sebagai dengan variasi area dan material
 +
 +
'''Geometri Pemodelan dan Load'''
 +
 +
[[File:1-Soal-Tubes.jpg|300px|center]]
 +
 +
'''Diketahui'''
 +
 +
- Spesifikasi L (Panjang) dan geometri rangka truss
 +
 +
- Gaya beban terhadap struktur (1000 N dan 2000 N)
 +
 +
'''Asumsi'''
 +
 +
- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
 +
 +
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
 +
 +
[[File:Langkah Pengerjaan.jpg|500px|center]]
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Trusses Modelling''
 +
 +
model Trusses_3D_Tugas_Besar_Safety
 +
 +
//define initial variable
 +
parameter Integer Points=size(P,1);  //Number of Points
 +
parameter Integer Trusses=size(C,1); //Number of Trusses
 +
parameter Real Yield=250e6;          //Yield Strength (Pa)  Material ASTM A36
 +
parameter Real Area=3.75E-04;        //Area L Profile (0.04 x 0.04 x 0.005) (m2)
 +
parameter Real Elas=2e11;            //Elasticity ASTM A36  (Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=      [1,5;
 +
                                2,6;
 +
                                3,7;
 +
                                4,8;
 +
                                5,6;  //1st floor
 +
                                6,7;  //1st floor
 +
                                7,8;  //1st floor
 +
                                5,8;  //1st floor
 +
                                5,9;
 +
                                6,10;
 +
                                7,11;
 +
                                8,12;
 +
                                9,10; //2nd floor
 +
                                10,11;//2nd floor
 +
                                11,12;//2nd floor
 +
                                9,12; //2nd floor
 +
                                9,13;
 +
                                10,14;
 +
                                11,15;
 +
                                12,16;
 +
                                13,14;//3rd floor
 +
                                14,15;//3rd floor
 +
                                15,16;//3rd floor
 +
                                13,16];//3rd floor
 +
                                                             
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1;          //1
 +
                            -0.3,-0.375,0,1,1,1;    //2
 +
                            -0.3,0.375,0,1,1,1;    //3
 +
                            0.3,0.375,0,1,1,1;      //4
 +
                           
 +
                            0.3,-0.375,0.6,0,0,0;  //5
 +
                            -0.3,-0.375,0.6,0,0,0;  //6
 +
                            -0.3,0.375,0.6,0,0,0;  //7
 +
                            0.3,0.375,0.6,0,0,0;    //8
 +
                           
 +
                            0.3,-0.375,1.2,0,0,0;  //9
 +
                            -0.3,-0.375,1.2,0,0,0;  //10 
 +
                            -0.3,0.375,1.2,0,0,0;  //11
 +
                            0.3,0.375,1.2,0,0,0;    //12
 +
                           
 +
                            0.3,-0.375,1.8,0,0,0;  //13
 +
                            -0.3,-0.375,1.8,0,0,0;  //14
 +
                            -0.3,0.375,1.8,0,0,0;  //15
 +
                            0.3,0.375,1.8,0,0,0];  //16
 +
                           
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,-500,
 +
                            0,0,-1000,
 +
                            0,0,-1000,
 +
                            0,0,-500};
 +
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
 +
Real stress1[Trusses];
 +
Real safety[Trusses];
 +
Real dis[3];
 +
Real Str[3];
 +
 +
protected
 +
parameter Integer N=3*Points;
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-6;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                      cy*cx,cy^2,cy*cz;
 +
                      cz*cx,cz*cy,cz^2];
 +
 +
    //Transforming to global matrix
 +
    g:=zeros(N,N);
 +
    for m,n in 1:3 loop
 +
      g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
      g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
      g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
    end for; 
 +
 +
G_star:=G+g;
 +
G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
  if P[x,4] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-2,a]:=0;
 +
      G[(x*3)-2,(x*3)-2]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,5] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[(x*3)-1,a]:=0;
 +
      G[(x*3)-1,(x*3)-1]:=1;
 +
    end for;
 +
  end if;
 +
  if P[x,6] <> 0 then
 +
    for a in 1:Points*3 loop
 +
      G[x*3,a]:=0;
 +
      G[x*3,x*3]:=1;
 +
    end for;
 +
  end if;
 +
end for;
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F;
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
  check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
   
 +
    Str:=(X*dis);
 +
    stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for;
 +
 +
//Safety factor
 +
for i in 1:Trusses loop
 +
  if stress1[i]>0 then
 +
    safety[i]:=Yield/stress1[i];
 +
  else
 +
    safety[i]:=0;
 +
  end if;
 +
end for;
 +
 +
end Trusses_3D_Tugas_Besar_Safety;
 +
 +
 +
| style='border-style: solid solid none  none;'  |
 +
''Curve Fitting Function''
 +
 +
function Curve_Fitting
 +
 +
input Real X[:];
 +
input Real Y[size(X,1)];
 +
input Integer order=2;
 +
output Real Coe[order+1];
 +
 +
protected
 +
Real Z[size(X,1),order+1];
 +
Real ZTr[order+1,size(X,1)];
 +
Real A[order+1,order+1];
 +
Real B[order+1];
 +
 +
algorithm
 +
 +
for i in 1:size(X,1) loop
 +
  for j in 1:(order+1) loop
 +
  Z[i,j]:=X[i]^(order+1-j);
 +
  end for;
 +
end for;
 +
ZTr:=transpose(Z);
 +
 +
A:=ZTr*Z;
 +
B:=ZTr*Y;
 +
Coe:=Modelica.Math.Matrices.solve(A,B);
 +
 +
end Curve_Fitting;
 +
|}
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''model CurveFitting''
 +
 +
parameter Real X[3]={190e9,195e9,200e9}; // Input variabel X adalah data bebas
 +
parameter Real Y[3]={7850,8020,8075};  // Input variabel Y adalah data berikat
 +
 +
Real Coe[3];
 +
 +
algorithm
 +
Coe:=Curve_Fitting(X,Y,2);
 +
 +
end CurveFitting;
 +
 +
|}
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Optimasi Gold Area''
 +
 +
model Opt_Gold
 +
 +
parameter Real xd[:]={190e9,191e9,192e9,193e9,194e9,195e9,196e9,197e9}; //Area Lock masukkin Elasticity
 +
parameter Real yd[size(xd,1)]={2.19e-4,1.02e-4,6.50e-5,4.77e-5,4.77e-5,3.3e-5,2.99e-5,284e-5};//Ratio
 +
parameter Real xlo=190e9;// x Low pada variabel x
 +
parameter Real xhi=197e9; // x high pada variabel x
 +
parameter Integer N=100; // maximum iteration
 +
parameter Real es=0.0001; // maximum error
 +
 +
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
 +
Real xopt,  fx;
 +
protected
 +
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
 +
 +
algorithm
 +
xl := xlo;
 +
xu := xhi;
 +
y  := Curve_Fitting(xd,yd);
 +
 +
for i in 1:N loop
 +
d:= R*(xu-xl);
 +
x1[i]:=xl+d;
 +
x2[i]:=xu-d;
 +
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
 +
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
 +
xint:=xu-xl;
 +
 +
if f1[i]>f2[i] then
 +
  xl:=x2[i];
 +
  xopt:=x1[i];
 +
  fx:=f1[i];
 +
  else
 +
    xu:=x1[i];
 +
    xopt:=x2[i];
 +
    fx:=f2[i];
 +
end if;
 +
 +
ea[i]:=(1-R)*abs((xint)/xopt);
 +
if ea[i]<es then
 +
  break;
 +
end if;
 +
end for;
 +
 +
end Opt_Gold;
 +
 +
|}
 +
 +
[[File:Optimasi Gold Area.jpg]]
 +
 +
[[File:Material Lock Rev2.jpg]]
 +
 +
Nilai optimasi berdasarkan openmodelica pada Area Lock digunakan untuk menentukan penggunaan dimensi Siku L yang paling efisien berdasarkan asumsi penggunaan material simulasi (ASTM A36). Berdasarkan simulasi optimasi golden ratio openmodelica didapatkan luasan area paling efektif adalah 0.00030343. Apabila dicocokan dengan dimensi material yang dipilih maka didaptkankan area 0.00030343m^2 akan sama dengan dimensi siku L 40x40x4 mm.
 +
 +
Kesimpulannya berdasarkan optimasi golden rasio menggunakan openmodelica didapatkan dimensi material yang paling effisien adalah 40x40x4mm lalu kemudian dilakukan pemilihan material dengan mengguanakan optimasi golden ratio.
 +
 +
{| class="wikitable"
 +
|-
 +
| style='border-style: none  none  solid  solid;' |
 +
''Optimasi Gold Material''
 +
 +
model Opt_Gold_Mat
 +
 +
parameter Real xd[:]={111e-6,141e-6,171e-6,231e-6,304e-6,375e-6,344e-6,425e-6}; //Material Lock masukkin Area
 +
parameter Real yd[size(xd,1)]={269.3e-6,269.4e-6,269.6e-6,269.7e-6,269.8e-6,269.7e-6,269.8e-6,269.6e-6};//Ratio
 +
parameter Real xlo=111e-6;// x Low pada variabel x
 +
parameter Real xhi=425e-6; // x high pada variabel x
 +
parameter Integer N=100; // maximum iteration
 +
parameter Real es=0.0001; // maximum error
 +
 +
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
 +
Real xopt,  fx;
 +
protected
 +
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
 +
 +
algorithm
 +
xl := xlo;
 +
xu := xhi;
 +
y  := Curve_Fitting(xd,yd);
 +
 +
for i in 1:N loop
 +
d:= R*(xu-xl);
 +
x1[i]:=xl+d;
 +
x2[i]:=xu-d;
 +
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
 +
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
 +
xint:=xu-xl;
 +
 +
if f1[i]>f2[i] then
 +
  xl:=x2[i];
 +
  xopt:=x1[i];
 +
  fx:=f1[i];
 +
  else
 +
    xu:=x1[i];
 +
    xopt:=x2[i];
 +
    fx:=f2[i];
 +
end if;
 +
 +
ea[i]:=(1-R)*abs((xint)/xopt);
 +
if ea[i]<es then
 +
  break;
 +
end if;
 +
end for;
 +
 +
end Opt_Gold_Mat;
 +
 +
|}
 +
 +
[[File:Optimasi Gold Material.jpg]]
 +
 +
[[File:Area Lock Rev2.jpg]]
 +
 +
Nilai optimasi E didapatkan berdasarkan simulasi menggunakan openmodelica adalah E = 196.987GPa. Kemudian nilai E ini digunakan untuk mencocokan 3 material yang sudah kita pilih (SS400, SS304, dan SS316). Nilai E optimasi dicocokan dengan nilai E material dipasaran yang kita pilih.
 +
 +
Kesimpulan berdasarkan optimasi dengan golden ratio didapatkan material yang paling efisien (low cost) dalam rancangan rak adalah SS304 dengan dimensi (40x40x4 mm).
 +
 +
 +
= '''UAS''' =
 +
 +
==Jawaban UAS==
 +
 +
[[File:Jawaban_UAS03_1.jpg|600px|center]]
 +
 +
[[File:Jawaban_UAS03_2.jpg|600px|center]]
 +
 +
[[File:Jawaban_UAS03_3.jpg|600px|center]]
 +
 +
[[File:Jawaban_UAS03_4.jpg|600px|center]]
 +
 +
[[File:Jawaban_UAS03_5.jpg|center]]

Latest revision as of 02:39, 14 January 2021

Assalamualaikum Warahmatullahi Wabarakatuh

Nama:Dendy Dwi Rohma P J

NPM: 1906435473

Pertemuan 1

1. Tugas_01_MetodeNumerik03

Dalam mencari nilai suatu akar dari suatu persamaan atau permasalahan yang ada, berbagai macam cara dan metode, berikut ini bermacam-macam metode yang dapat kita gunakan dalam mencari nilai suatu akar persamaan :

1. Metode Bagi dua (Bisection)

2. Metode False Position

3. Metode Secant

4. Metode Iterasi Titik Tetap

5. Metode Newton Raphson

Dalam kesempatan kali ini saya akan membahas tentang metode secant.

Pengertian Metode Secant

Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f'(x). Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.

Algoritma Metode Secant 1. Definisikan fungsi F(x) 2. Definisikan torelansi error (e) dan iterasi maksimum (n) 3. Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.

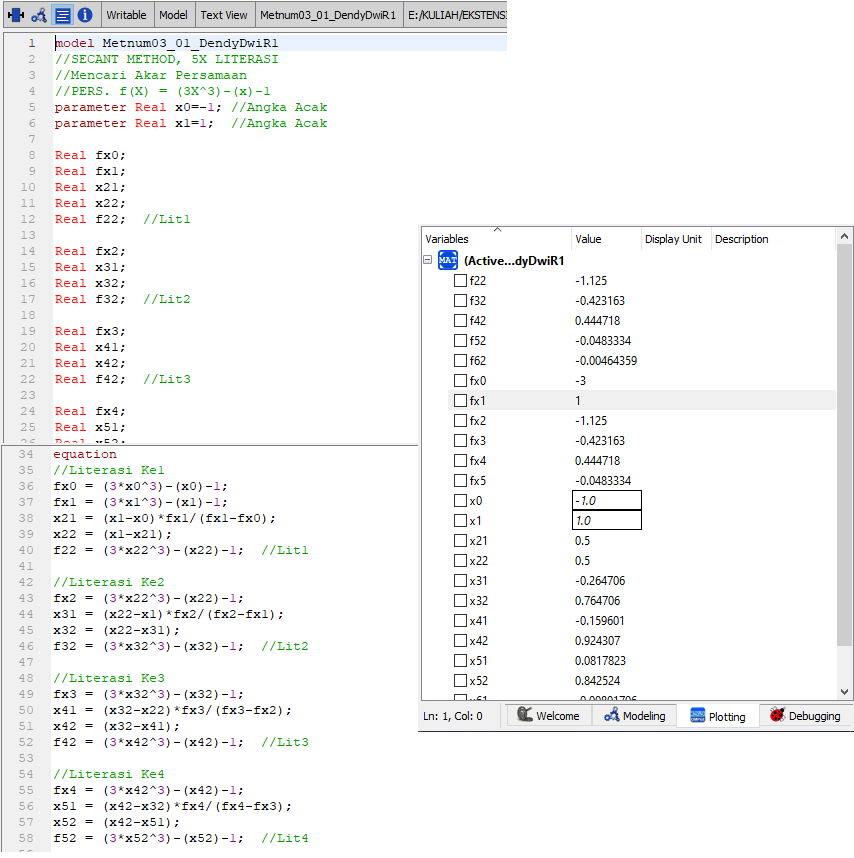
SOAL 1

Cari Akar Persamaan dari Persamaan f(x) dengan Metode Secant Method pada Literasi ke 4? f(x) = 3x^3 -x -1

Asumsi: 

       x0 = -1
       x  = 1
RumusSecant.png
HasilLiterasi.png
Code12.png

Penjelasan menganai pemrograman Secant Method menggunakan OpenModelica terlampir dalam Link dibawah ini:

Link Youtube : https://www.youtube.com/watch?v=Bk_QtrInpks

Pertemuan 2

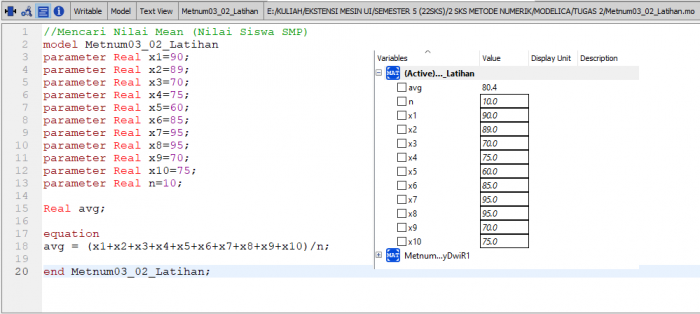
LatihanMean2.png

Melakukan latihan mencari nilai mean dari persamaan dan data sederhana.

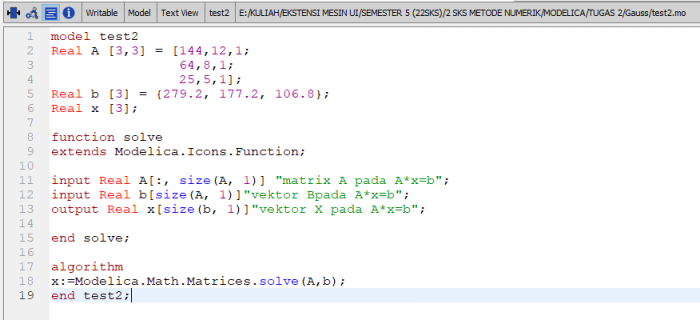
PR Eliminasi Gauss

CodingGauss1.png
PlotingGauss2.png
ValidasiGauss.jpg


Pertemuan 3

3. Tugas_03_MetodeNumerik03

MASS SPRING ANALYSIS MATRIX

TRUSS ANALYSIS MATRIX

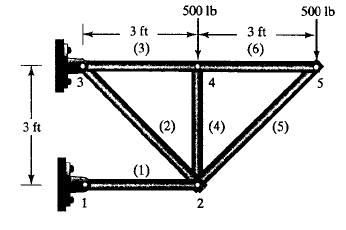
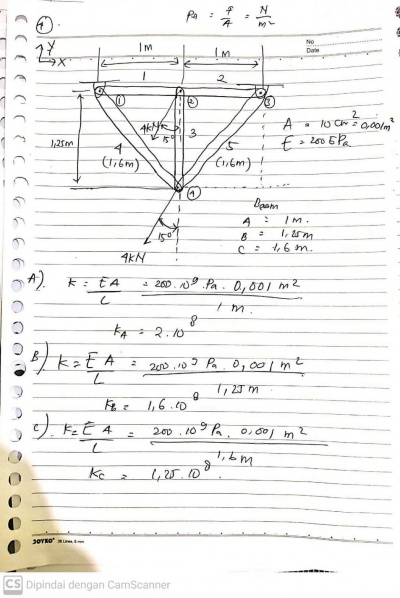
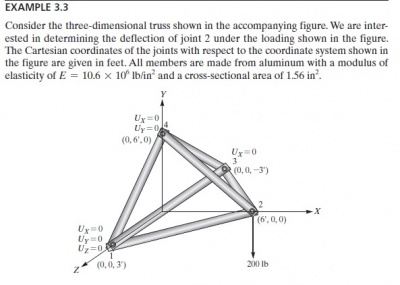
Tugas kali ini disuruh mencari nilai defleksi/dX/U pada suatu truss yang disusun dan dikenai pembebanan dan tumpuan seperti pada soal dibawah ini. Lalu kemudian setelah kita menemukan nilai U lalu digunakan untuk mencari reaksi gaya (R) pada setiap elemen truss.

1 Soal Truss.png

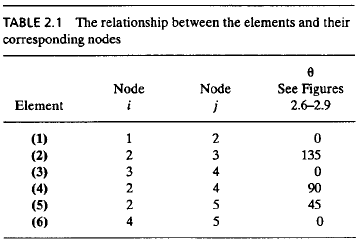
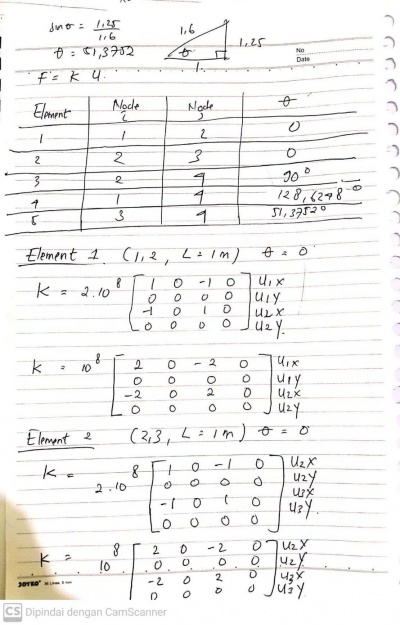
Berdasarkan susunan truss diatas, kita harus mampu menjabarkan setiap beam/ truss menjadi notasi element, tumpuan menjadi notasi node dan sudut element terhadap garis refrensi yg kita pilih (saya menggunakan X positif sbg sb.0 deg). Lalu setelah dilakukan penjabaran berdasarkan element, node dan sudut didapatkan Tabel 2.1 sebagai hubungannya.

2 Truss MenjadiNode.png

Setelah itu dilakukan perkalian untuk mencari nilai kekakuan setiap truss/ element dengan rumus k=A.E/L. Namun sebelumnya dilakukan pengelompokan berdasarkan panjang batang/truss lalu didapatkan batang dengan panjang yang sama (1,3,4,6) dan batang (2,5). Namun untuk mendapatkan nilai K lokal nilai k(kekakuan) harus terlebih dahulu dikalikan dengan rumus K lokal dalam bentuk matrix 4x4.

3 KonstantaStiffness 1.3.4.6.png

3 KonstantaStiffness 2.5.png

Nah rumus K^e atau K lokal menurut pemahaman saya dapat berbeda-beda tergantung dengan susunan dari truss (sudut yang terbentuk dari sb. refrensi yang kita gunakan) atau batang dan tumpuan yang kita gunakan. Lalu untuk nilai k (kekakuan) hanya dipengaruhi dari cross section area (A), elastisitas (E) dan panjang batang (L)

4 RumusK.png

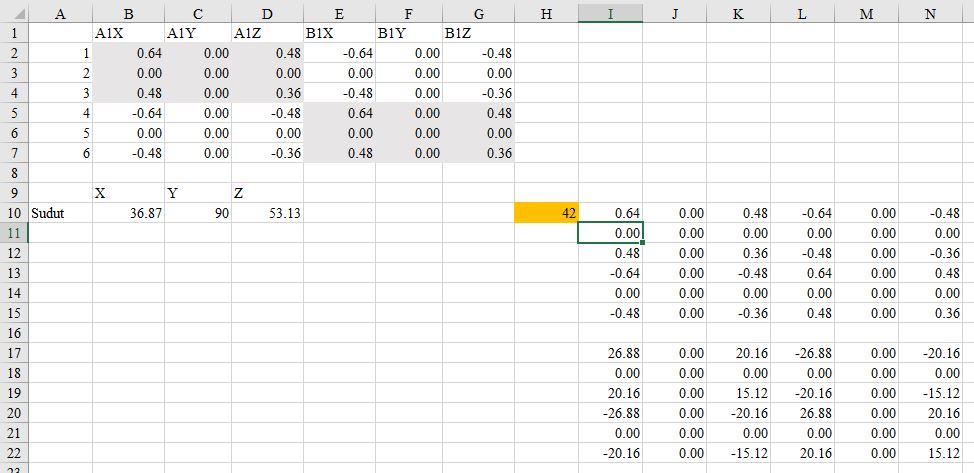
Analisa Batang 4

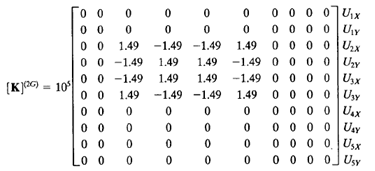
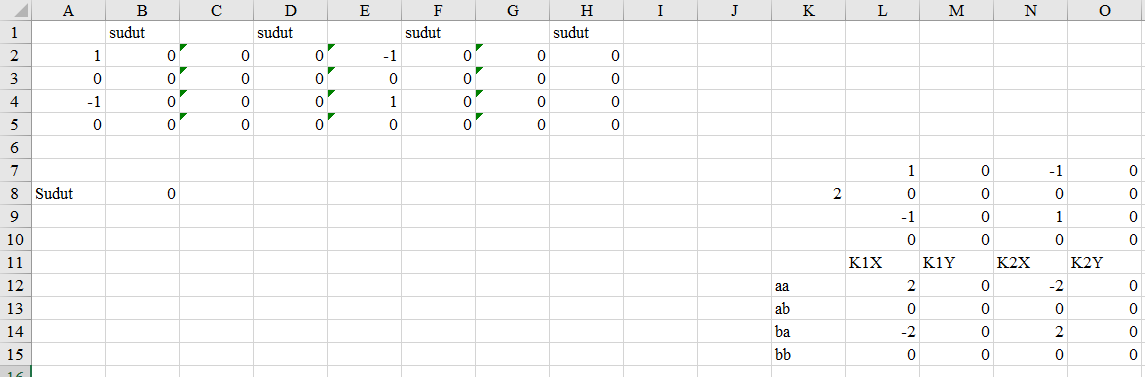
Analisa batang pada contoh soal ini jg dapat dikelompokan berdasarkan panjang batangnya. Jadi untuk analisa pertama batang (1,3,4,6) dan batang (2 dan 5). Pada batang (1,3,dan 6) memiliki sudut refrensi yang sama yaitu 0 derajat, namun ketiga element ini memiliki node yang berbeda sehingga akan berpengaruh pada peletakan hasil matrix 4x4 pada matrix global (K^G) 10x10.

5 1 AnalisaElemen4.png

Pada gambar dibawah ini hasil K^e (K lokal) dimasukan ke dalam matrix 10x10 K^G berdasarkan node arah sb. X dan sb. Y.

5 2 Elemen4 DiglobalMatrik.png

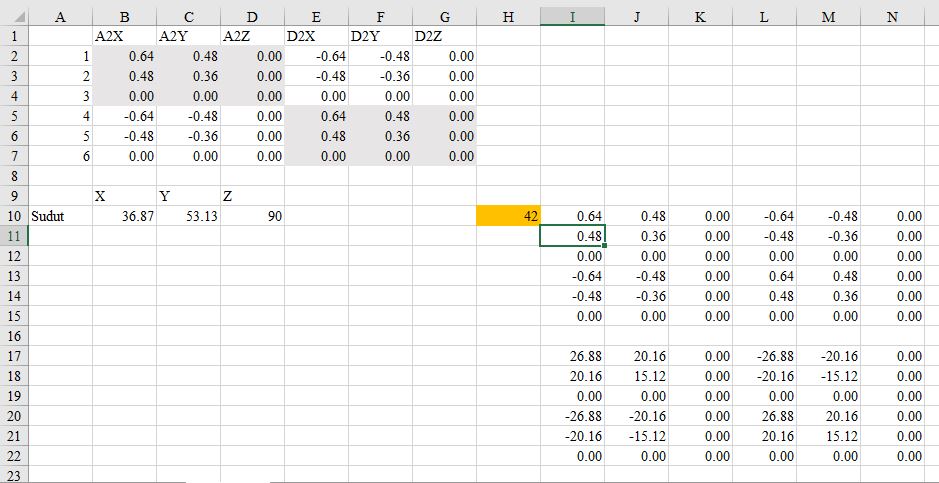
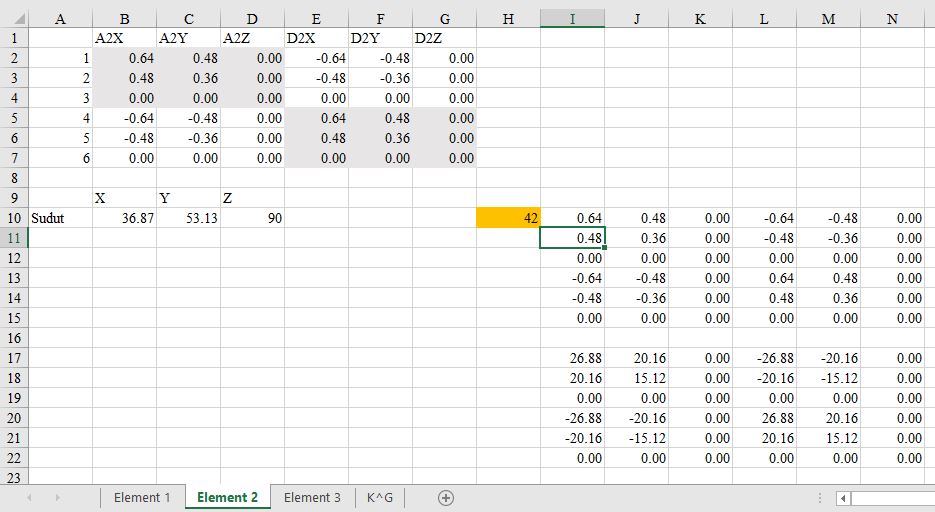
Analisa Batang 2

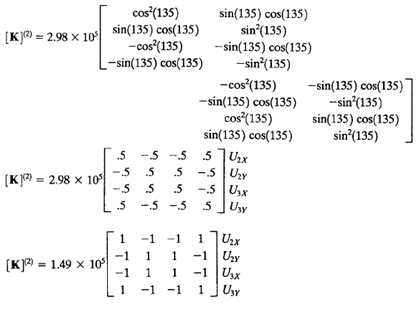
Kemudian dilakukan analisa batang (2 dan 5) dengan cara yang sama seperti gambar diatas dengan mengunakan rumus matrix K (4x4). Namun pada element 2 dan 5 hanya berbeda pada penggunaan sudut berdasarkan sumbu refrensi (element 2 : 135deg, element 5 : 45deg).

6 1 AnalisaElemen2.png

Pada gambar dibawah ini hasil K^e (K lokal) dimasukan ke dalam matrix 10x10 K^G berdasarkan node arah sb. X dan sb. Y.

6 1 Elemen2Global.png

Analisa Batang 5

6 2 AnalisaElemen5.png

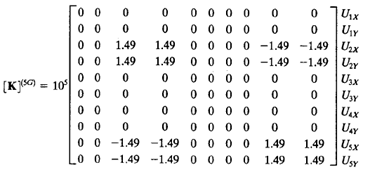
6 2 Elemen5Global.png

Kemudian dilakukan penjumlahan matrik tersebut menjadi matrik global.

7 1 PenjumlahanK-Kglobal.png

Didapatkan hasil penjumlahan matrik lokal tersebut menjadi matrik global dengan jumlah 10x10.

7 2 Kglobal.png

Kemudian dilakukan batasan masalah seperti ada atau tidaknya fix point pada suatu susunan model truss. Berdasarkan soal didapatkan pada node 1 dan 3 adalah nilai U adalah 0 (U1x, U1y, U3x, U3y). Karena apabila tidak dilakukan permisalan maka susunan trus akan berotasi bila dikenai gaya.

8 1 Matrik6x6 PenerapanFixPoint.png

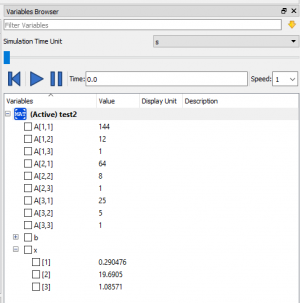
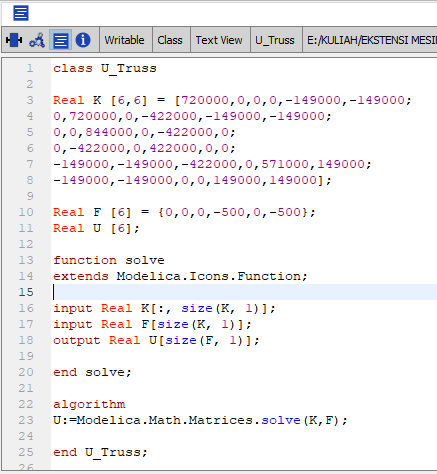
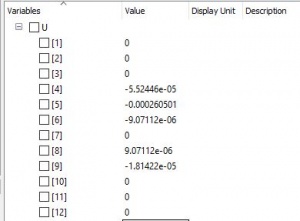
Berdasarkan rumus F=K.dX (F=K.U) kita disuruh untuk mencari nilai U pada tiap node berdasarkan sb. x dan sb. y. Maka untuk mencarinya kita dapat memanggil fungsi solve (A.x=B) untuk mencari nilai x atau U. Dengan memasukan koding 6x6 dibawah ini akan didapatkan nilai U pada node (2,4,5) berdasarkan sb.x dan sb.y.

8 2 Matrik6x6 Coding.png

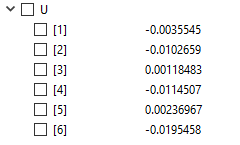
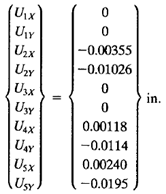
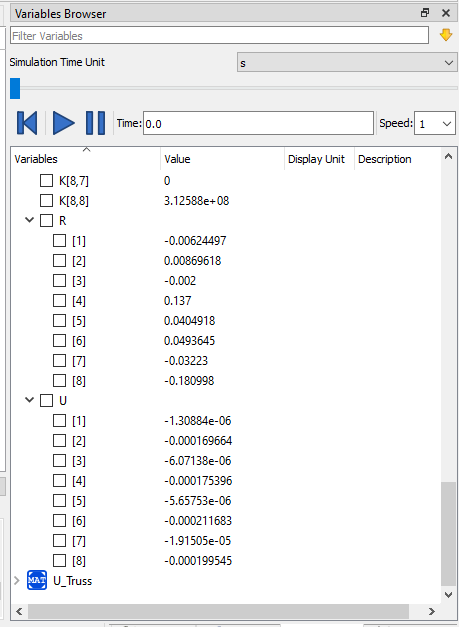
Didapatkan nilai U adalah sama seperti contoh dibuku.

8 3 Matrik6x6 dXatauU.png

Analisa Reaksi Gaya pada Setiap Node

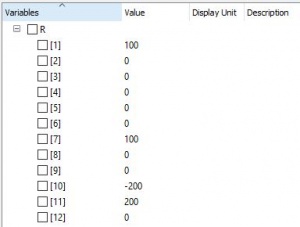
Pada analisa ini kita harus menuliskan kembali hasil perhitungan sebelumnya U kedalam parameter matriknya. Rumus reaksi adalah R = [K]^G.{U}-{F}. Dapat dikatakan bahwa R adalah reaksi yang terjadi pada setiap node dengan arah sb.x dan sb.y. Dengan metode matrik ini iibaratnya seperti perhitungan manual (FBD) gaya-gaya yang terjadi pada setiap titik tumpuan berdasarkan arah sumbu kerja (2D yaitu x,y).

9 ReaksiGaya.png

10 dXatauU Matrik10x10.png

Pada U semua node, didaptkan bahwa nilai pada node 1 dan 3 adalah tetap 0 pada matix K^G untuk mencari nilai R seperti dibawah ini.

11 1 Matrik10x10 MencariReaksi(R).png

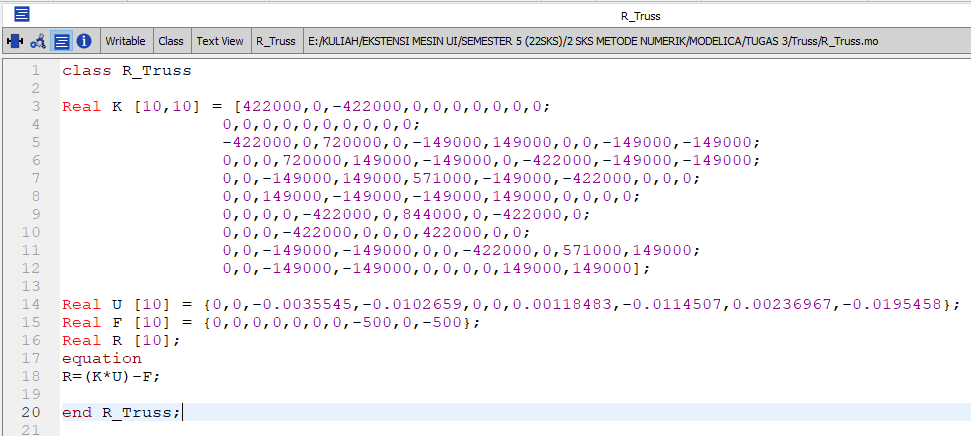
Untuk programnya hanya perlu mengalikan fungsi R=(K*U)-F seperti biasa. Tidak perlu memanggil program solve (gauss).

11 2 Matrik10x10 Coding.png

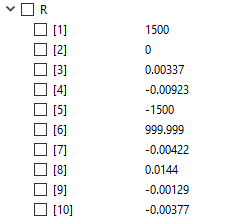
Kemudian untuk reaksi gayanya didapatkan nilai seperti ploting dibawah ini, dan dilakukan pembulatan pada node (3,4,5) karena nilai gayanya sangat kecil.

11 3 Matrik10x10 Reaksi(R).png

Pertemuan 4

Quiz_1_MetodeNumerik03

Quiz_1_Truss2D

1 Flow Chart Kuiz1.jpg

2 FBD Kuiz1.jpg

3 K Lokal.jpg

4 K Lokal.jpg

Element1 2D Dendy.png

Element5 2D Dendy.png

KG 2D DendyDwi.png

CodingU Truss 2D DendyDwi.png

CodingR Truss 2D DendyDwi.png

Nilai U R 2D DendyDwi.png

Quiz_1_Truss3D

1 FBD 3D DendyDwi.jpg

2 FBD 3D DendyDwi.jpg

3 Element1 3D Dendy.jpg

4 Element2 3D Dendy.jpg

5 Element3 3D Dendy.jpg

Pertemuan 5

Tugas Metode Numerik

Soal3D.jpeg
1 Class.jpg
2 U.jpg
3 R.jpg
4 F.jpg

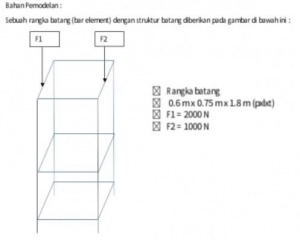
Tugas Besar

Soal

-Temukan Cost sebagai dengan variasi area dan material

Geometri Pemodelan dan Load

1-Soal-Tubes.jpg

Diketahui

- Spesifikasi L (Panjang) dan geometri rangka truss

- Gaya beban terhadap struktur (1000 N dan 2000 N)

Asumsi

- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.

- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)

Langkah Pengerjaan.jpg

Trusses Modelling

model Trusses_3D_Tugas_Besar_Safety

//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36 parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2) parameter Real Elas=2e11; //Elasticity ASTM A36 (Pa)

//define connection parameter Integer C[:,2]= [1,5; 

                               2,6;
                               3,7;
                               4,8;
                               5,6;  //1st floor
                               6,7;  //1st floor
                               7,8;  //1st floor
                               5,8;  //1st floor
                               5,9;
                               6,10;
                               7,11;
                               8,12;
                               9,10; //2nd floor
                               10,11;//2nd floor 
                               11,12;//2nd floor
                               9,12; //2nd floor
                               9,13;
                               10,14;
                               11,15;
                               12,16;
                               13,14;//3rd floor
                               14,15;//3rd floor
                               15,16;//3rd floor
                               13,16];//3rd floor

//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 

                           -0.3,-0.375,0,1,1,1;    //2
                           -0.3,0.375,0,1,1,1;     //3
                           0.3,0.375,0,1,1,1;      //4
                           
                           0.3,-0.375,0.6,0,0,0;   //5
                           -0.3,-0.375,0.6,0,0,0;  //6
                           -0.3,0.375,0.6,0,0,0;   //7
                           0.3,0.375,0.6,0,0,0;    //8
                           
                           0.3,-0.375,1.2,0,0,0;   //9
                           -0.3,-0.375,1.2,0,0,0;  //10  
                           -0.3,0.375,1.2,0,0,0;   //11
                           0.3,0.375,1.2,0,0,0;    //12
                           
                           0.3,-0.375,1.8,0,0,0;   //13
                           -0.3,-0.375,1.8,0,0,0;  //14
                           -0.3,0.375,1.8,0,0,0;   //15
                           0.3,0.375,1.8,0,0,0];   //16

//define external force (please put orderly) parameter Real F[Points*3]={0,0,0, 

                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,-500, 
                           0,0,-1000, 
                           0,0,-1000, 
                           0,0,-500};

//solution Real displacement[N], reaction[N]; Real check[3];

Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];

protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6;

algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop 

for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2];

   //Transforming to global matrix
   g:=zeros(N,N); 
   for m,n in 1:3 loop
     g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
     g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
   end for;  

G_star:=G+g;
G:=G_star;

end for;

//Implementing boundary for x in 1:Points loop 

 if P[x,4] <> 0 then
   for a in 1:Points*3 loop
     G[(x*3)-2,a]:=0;
     G[(x*3)-2,(x*3)-2]:=1;
   end for;
 end if;
 if P[x,5] <> 0 then
   for a in 1:Points*3 loop
     G[(x*3)-1,a]:=0;
     G[(x*3)-1,(x*3)-1]:=1;
   end for;
 end if;
 if P[x,6] <> 0 then
   for a in 1:Points*3 loop
     G[x*3,a]:=0;
     G[x*3,x*3]:=1;
   end for;
 end if;

end for;

//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction reaction:=(G_star*displacement)-F;

//Eliminating float error for i in 1:N loop 

reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];

end for;

//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});

for i in 1:3 loop 

 check[i] := if abs(check[i])<=ers then 0 else check[i];

end for;

//Calculating stress in each truss for i in 1:Trusses loop 

for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
                cy*cx,cy^2,cy*cz;
                cz*cx,cz*cy,cz^2];
   
   Str:=(X*dis);
   stress1[i]:=Modelica.Math.Vectors.length(Str);

end for;

//Safety factor for i in 1:Trusses loop 

 if stress1[i]>0 then
   safety[i]:=Yield/stress1[i];
 else
   safety[i]:=0;
 end if;

end for;

end Trusses_3D_Tugas_Besar_Safety;


Curve Fitting Function 

function Curve_Fitting

input Real X[:];
input Real Y[size(X,1)];
input Integer order=2;
output Real Coe[order+1];

protected
Real Z[size(X,1),order+1];
Real ZTr[order+1,size(X,1)];
Real A[order+1,order+1];
Real B[order+1];

algorithm

for i in 1:size(X,1) loop
 for j in 1:(order+1) loop
 Z[i,j]:=X[i]^(order+1-j);
 end for;
end for;
ZTr:=transpose(Z);

A:=ZTr*Z;
B:=ZTr*Y;
Coe:=Modelica.Math.Matrices.solve(A,B);

end Curve_Fitting;

model CurveFitting

parameter Real X[3]={190e9,195e9,200e9}; // Input variabel X adalah data bebas parameter Real Y[3]={7850,8020,8075}; // Input variabel Y adalah data berikat

Real Coe[3];

algorithm Coe:=Curve_Fitting(X,Y,2);

end CurveFitting;

Optimasi Gold Area

model Opt_Gold

parameter Real xd[:]={190e9,191e9,192e9,193e9,194e9,195e9,196e9,197e9}; //Area Lock masukkin Elasticity parameter Real yd[size(xd,1)]={2.19e-4,1.02e-4,6.50e-5,4.77e-5,4.77e-5,3.3e-5,2.99e-5,284e-5};//Ratio parameter Real xlo=190e9;// x Low pada variabel x parameter Real xhi=197e9; // x high pada variabel x parameter Integer N=100; // maximum iteration parameter Real es=0.0001; // maximum error

Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;

algorithm xl := xlo; xu := xhi; y  := Curve_Fitting(xd,yd);

for i in 1:N loop 

d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;

if f1[i]>f2[i] then
  xl:=x2[i];
  xopt:=x1[i];
  fx:=f1[i];
  else
    xu:=x1[i];
    xopt:=x2[i];
    fx:=f2[i];
end if;

ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
  break;
end if;

end for;

end Opt_Gold;

Optimasi Gold Area.jpg

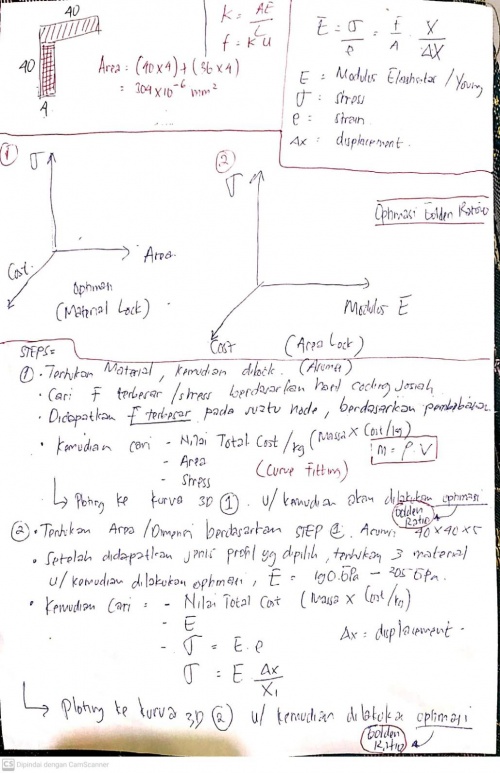
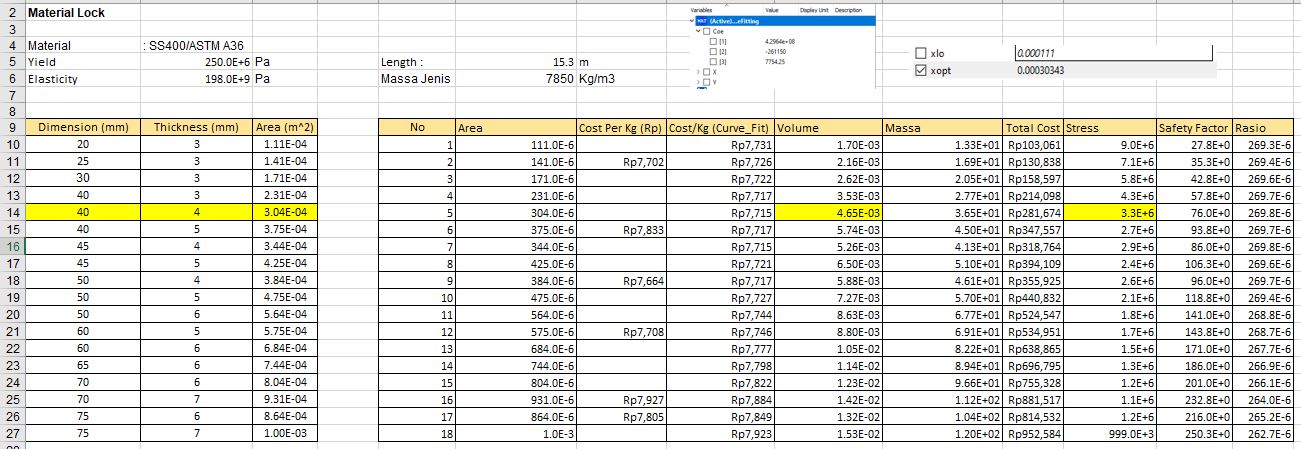
Material Lock Rev2.jpg

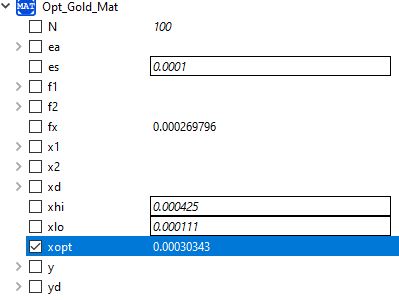
Nilai optimasi berdasarkan openmodelica pada Area Lock digunakan untuk menentukan penggunaan dimensi Siku L yang paling efisien berdasarkan asumsi penggunaan material simulasi (ASTM A36). Berdasarkan simulasi optimasi golden ratio openmodelica didapatkan luasan area paling efektif adalah 0.00030343. Apabila dicocokan dengan dimensi material yang dipilih maka didaptkankan area 0.00030343m^2 akan sama dengan dimensi siku L 40x40x4 mm.

Kesimpulannya berdasarkan optimasi golden rasio menggunakan openmodelica didapatkan dimensi material yang paling effisien adalah 40x40x4mm lalu kemudian dilakukan pemilihan material dengan mengguanakan optimasi golden ratio.

Optimasi Gold Material

model Opt_Gold_Mat

parameter Real xd[:]={111e-6,141e-6,171e-6,231e-6,304e-6,375e-6,344e-6,425e-6}; //Material Lock masukkin Area parameter Real yd[size(xd,1)]={269.3e-6,269.4e-6,269.6e-6,269.7e-6,269.8e-6,269.7e-6,269.8e-6,269.6e-6};//Ratio parameter Real xlo=111e-6;// x Low pada variabel x parameter Real xhi=425e-6; // x high pada variabel x parameter Integer N=100; // maximum iteration parameter Real es=0.0001; // maximum error

Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;

algorithm xl := xlo; xu := xhi; y  := Curve_Fitting(xd,yd);

for i in 1:N loop 

d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;

if f1[i]>f2[i] then
  xl:=x2[i];
  xopt:=x1[i];
  fx:=f1[i];
  else
    xu:=x1[i];
    xopt:=x2[i];
    fx:=f2[i];
end if;

ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
  break;
end if;

end for;

end Opt_Gold_Mat;

Optimasi Gold Material.jpg

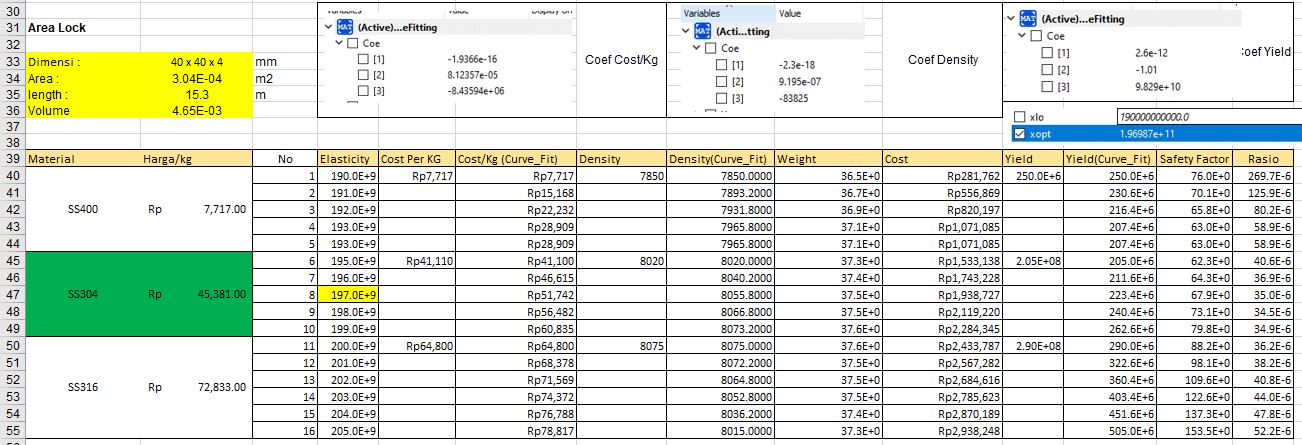
Area Lock Rev2.jpg

Nilai optimasi E didapatkan berdasarkan simulasi menggunakan openmodelica adalah E = 196.987GPa. Kemudian nilai E ini digunakan untuk mencocokan 3 material yang sudah kita pilih (SS400, SS304, dan SS316). Nilai E optimasi dicocokan dengan nilai E material dipasaran yang kita pilih.

Kesimpulan berdasarkan optimasi dengan golden ratio didapatkan material yang paling efisien (low cost) dalam rancangan rak adalah SS304 dengan dimensi (40x40x4 mm).


UAS

Jawaban UAS

Jawaban UAS03 1.jpg
Jawaban UAS03 2.jpg
Jawaban UAS03 3.jpg
Jawaban UAS03 4.jpg
Jawaban UAS03 5.jpg
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03-Dendy_Dwi_Rohma_P_J&oldid=55605"