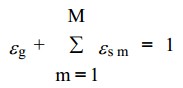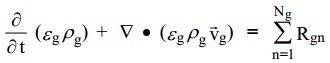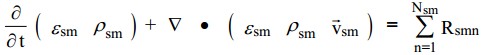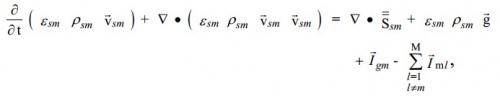Difference between revisions of "Hydrodynamic"
Agus.nuryadi (talk | contribs) (→Theory) |
Agus.nuryadi (talk | contribs) (→Conservation of Internal Energy =) |
||
| (18 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
the '''averaging approach''' to derive equations that describe interpenetrating continua, the point variables are averaged over a region that is large compared with the particle spacing but much smaller than the flow domain. New field variables, the phasic volume fractions, are introduced to track the fraction of the averaging volume occupied by various phases. These are denoted by '''ε'''g for the fluid phase (also known as the void fraction) and '''ε'''sm for the mth solids phase. These volume fractions are assumed to be continuous functions of space and time. | the '''averaging approach''' to derive equations that describe interpenetrating continua, the point variables are averaged over a region that is large compared with the particle spacing but much smaller than the flow domain. New field variables, the phasic volume fractions, are introduced to track the fraction of the averaging volume occupied by various phases. These are denoted by '''ε'''g for the fluid phase (also known as the void fraction) and '''ε'''sm for the mth solids phase. These volume fractions are assumed to be continuous functions of space and time. | ||
| − | [[File:1.eq_theory.jpg| | + | [[File:1.eq_theory.jpg|300px|thumb|centre|alt text]] |
M is the total number of solids phases. The effective (macroscopic) density of the gas phase is: | M is the total number of solids phases. The effective (macroscopic) density of the gas phase is: | ||
| − | [[File:2.eq_theory.jpg| | + | [[File:2.eq_theory.jpg|300px|thumb|centre|alt text]] |
The solids phase is | The solids phase is | ||
| − | [[File:3.eq_theory.jpg| | + | [[File:3.eq_theory.jpg|300px|thumb|centre|alt text]] |
the two-phase system is the same as the bulk density. Just as the actual (microscopic) densities appear in single-phase equations, these effective densities appear in all of the multiphase equations. | the two-phase system is the same as the bulk density. Just as the actual (microscopic) densities appear in single-phase equations, these effective densities appear in all of the multiphase equations. | ||
| − | ==Conservation of Mass== | + | ===Conservation of Mass=== |
| + | |||
| + | The continuity equation for the gas phase is: | ||
| + | |||
| + | [[File:4.eq_theory.jpg|500px|thumb|centre|alt text]] | ||
| + | |||
| + | There are M solids-phase continuity equations, each of the form. | ||
| + | |||
| + | [[File:5.eq_theory.jpg|500px|thumb|centre|alt text]] | ||
| + | |||
| + | The first term on the left in the equations above accounts for the rate of mass accumulation per unit volume and the second term is the net rate of convective mass flux. The term on the right accounts for interphase mass transfer because of chemical reactions or physical processes, such as evaporation. | ||
| + | |||
| + | ===Conservation of Momentum=== | ||
| + | |||
| + | The gas-phase momentum balance is expressed | ||
| + | |||
| + | [[File:6.eq_theory.jpg|500px|thumb|centre|alt text]] | ||
| + | |||
| + | |||
| + | '''Sg''' is the gas-phase stress tensor, '''Igm''' is an interaction force representing the momentum transfer between the gas phase and the '''m'''th solids phase, and '''f'''g is the flow resistance offered by internal porous surfaces. | ||
| + | |||
| + | [[File:7.eq_theory.jpg|500px|thumb|centre|alt text]] | ||
| + | |||
| + | |||
| + | The momentum equation for the mth solids phase is where '''S'''sm is the stress tensor for the '''m'''th solids phase. The term '''I'''lm is the interaction force between the '''m'''th and '''l'''th solids phases. | ||
| + | |||
| + | === Conservation of Internal Energy === | ||
| + | |||
| + | The internal energy balance for the fluid phase is written in terms of the fluid temperature: | ||
Latest revision as of 10:36, 1 December 2020
Hydrodynamic modelling has the remarkable ability to synthesize data from various, relatively simple experiments (for example, the drag on an isolated sphere or the volatilization rate measured using a single layer of coal particles) and, thereby, to describe the time-dependent distribution of fluid and solids volume fractions, velocities, pressure, temperatures, and species mass fractions in industrial reactors. With such power also come several limitations that the user must bear in mind.
1. The accuracy of the model's predictions may be limited for a variety of reasons: incomplete formulation of the governing equations, insufficient knowledge of the constitutive relations, unsatisfactory numerical treatment of the governing partial differential equations, insufficient information on initial and boundary conditions, and the impracticality of using a large number of nodes to resolve all the fine details of the flow.
2. A limitation of hydrodynamic modeling is that an expert user is needed to conduct simulations and to analyze results. To assist the user, the present code resolves many of the difficulties in setting up simulations by using a special NAMELIST format in the input data file that reports input errors and allows comment lines. There is no limitation on the number of initial and boundary conditions. The code also does much run-time error reporting and has a graphical post-processor.
3. hydrodynamic modeling requires significant computer resources, although supercomputer facilities are not required. The availability of faster and cheaper computers has made hydrodynamic modeling more affordable.
Contents
Theory
The averaging approach and the mixture theory approach. In the averaging approach, the equations are derived by space, time, or ensemble averaging of the local, instantaneous balances for each of the phases. In the mixture theory approach, equations that are generalizations of single phase equations are postulated. Both approaches yield a similar set of balance equations that must be closed by specifying several constitutive relations, such as a fluid-phase equation of state, fluid-solids and solids-solids momentum transfer and heat transfer, and fluid and solids phase stress tensors. The principle of material frame-indifference, the second axiom of thermodynamics, material symmetry, and over-all balance equations for the mixture yield several useful restrictions on such constitutive relations.
the averaging approach to derive equations that describe interpenetrating continua, the point variables are averaged over a region that is large compared with the particle spacing but much smaller than the flow domain. New field variables, the phasic volume fractions, are introduced to track the fraction of the averaging volume occupied by various phases. These are denoted by εg for the fluid phase (also known as the void fraction) and εsm for the mth solids phase. These volume fractions are assumed to be continuous functions of space and time.
M is the total number of solids phases. The effective (macroscopic) density of the gas phase is:
The solids phase is
the two-phase system is the same as the bulk density. Just as the actual (microscopic) densities appear in single-phase equations, these effective densities appear in all of the multiphase equations.
Conservation of Mass
The continuity equation for the gas phase is:
There are M solids-phase continuity equations, each of the form.
The first term on the left in the equations above accounts for the rate of mass accumulation per unit volume and the second term is the net rate of convective mass flux. The term on the right accounts for interphase mass transfer because of chemical reactions or physical processes, such as evaporation.
Conservation of Momentum
The gas-phase momentum balance is expressed
Sg is the gas-phase stress tensor, Igm is an interaction force representing the momentum transfer between the gas phase and the mth solids phase, and fg is the flow resistance offered by internal porous surfaces.
The momentum equation for the mth solids phase is where Ssm is the stress tensor for the mth solids phase. The term Ilm is the interaction force between the mth and lth solids phases.
Conservation of Internal Energy
The internal energy balance for the fluid phase is written in terms of the fluid temperature: