Difference between revisions of "Umar"
(→Ujian Akhir Semester) |
|||
| (105 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ | بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ | ||
| − | + | السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ | |
== '''Biodata Diri''' == | == '''Biodata Diri''' == | ||
[[File:Umar.jpg|200px|thumb|right]] | [[File:Umar.jpg|200px|thumb|right]] | ||
| Line 14: | Line 14: | ||
Saya adalah Mahasiswa Fakultas Teknik Universitas Indonesia, Program Studi Teknik Mesin angkatan 2018. Saat ini Saya sedang menempuh perkuliahan di semester 5, yang artinya sudah tahun ketiga pekuliahan. | Saya adalah Mahasiswa Fakultas Teknik Universitas Indonesia, Program Studi Teknik Mesin angkatan 2018. Saat ini Saya sedang menempuh perkuliahan di semester 5, yang artinya sudah tahun ketiga pekuliahan. | ||
| − | Alasan Saya mengambil Program Studi (Prodi) Teknik Mesin karena Prodi ini cukup luas prospeknya dan juga prodi yang mempelajari ilmu engineering yang lebih advance dari prodi teknik lainnya menurut Saya dan akan terus digunakan | + | Alasan Saya mengambil Program Studi (Prodi) Teknik Mesin karena Prodi ini cukup luas prospeknya dan juga prodi yang mempelajari ilmu engineering yang lebih advance dari prodi teknik lainnya menurut Saya dan akan terus digunakan di masa mendatang. |
__TOC__ | __TOC__ | ||
| − | == Pertemuan 1 (11 | + | == '''Pertemuan 1 (11 November 2020)''' == |
Setelah melewati pembelajaran selama paruh semester awal dengan Bapak Dr. Ir. Engkos A. Kosasih, M.T. dan melakukan Ujian Tengah Semester (UTS), kelas Metode Numerik - 02 berganti dosen menjadi Bapak Dr. Ir. Ahmad Indra Siswantara atau biasa disapa Pak Da'i. Pada pertemuan pertama setelah UTS ini, Pak Da'i meminta mahasiswa untuk membuat akun pada situs wiki air. Kami dijelaskan bagaimana cara - cara untuk menggunakan wiki air ini supaya lebih familiar dalam menggunakannya, karena tugas - tugas kedepannya akan dikerjakan di wiki air. Pak Da'i pada saat itu juga memaparkan kembali apa tujuan dari pembelajaran metode numerik ini, berikut tujuan - tujuan yang beliau sebutkan : | Setelah melewati pembelajaran selama paruh semester awal dengan Bapak Dr. Ir. Engkos A. Kosasih, M.T. dan melakukan Ujian Tengah Semester (UTS), kelas Metode Numerik - 02 berganti dosen menjadi Bapak Dr. Ir. Ahmad Indra Siswantara atau biasa disapa Pak Da'i. Pada pertemuan pertama setelah UTS ini, Pak Da'i meminta mahasiswa untuk membuat akun pada situs wiki air. Kami dijelaskan bagaimana cara - cara untuk menggunakan wiki air ini supaya lebih familiar dalam menggunakannya, karena tugas - tugas kedepannya akan dikerjakan di wiki air. Pak Da'i pada saat itu juga memaparkan kembali apa tujuan dari pembelajaran metode numerik ini, berikut tujuan - tujuan yang beliau sebutkan : | ||
| Line 26: | Line 26: | ||
* Mendapat nilai tambah/moral sehingga kita menjadi orang yang lebih beradab seperti yang sudah tertulis di sila ke-2 Pancasila. | * Mendapat nilai tambah/moral sehingga kita menjadi orang yang lebih beradab seperti yang sudah tertulis di sila ke-2 Pancasila. | ||
| − | Uniknya pada perkuliahan kemarin Saya mendapat suatu pelajaran hidup bahwa kita sebagai manusia punya limitasi terkait ilmu pengetahuan atau apapun itu, salah satu kasusnya dalam bidang matematika yaitu belum terpecahkan jawaban atau belum terdefinisi jawaban dari bilangan berapapun dibagi dengan 0 (n/0) walaupun menggunakan ''software'' sekalipun. Maka dari itu kita sebagai manusia tidak boleh merasa "tinggi" walaupun orang - orang menganggap kita orang hebat sekalipun. | + | Uniknya pada perkuliahan kemarin Saya mendapat suatu pelajaran hidup bahwa kita sebagai manusia punya limitasi terkait ilmu pengetahuan atau apapun itu, salah satu kasusnya dalam bidang matematika yaitu belum terpecahkan jawaban atau belum terdefinisi jawaban dari bilangan berapapun dibagi dengan 0 (n/0) walaupun menggunakan ''software'' sekalipun. Maka dari itu kita bisa petik hikmah bahwa sebagai manusia tidak boleh merasa "tinggi" walaupun orang - orang menganggap kita sebagai orang hebat sekalipun. |
| + | === '''Tugas Pertemuan 1''' === | ||
| + | |||
| + | Pada minggu pertama, setiap mahasiswa diminta untuk melihat dan mempraktikan tentang tutorial atau dasar Open Modellica dari youtube. Kemudian diharapkan untuk mengupload video tutorial singkat di Youtube. Berikut ini adalah video tutorial dasar dari saya untuk penghitungan volume langkah piston pada OpenModelica. | ||
| + | |||
| + | <youtube width="200" height="100">G9rTRXlE8UA</youtube> | ||
| + | |||
| + | == '''Pertemuan 2 (Rabu, 18 November 2020)''' == | ||
| + | Pak Dai menjelaskan bahwa menggunakan ''Software'' OpenModelica lebih nyaman dan sederhana dibanding ''Software'' atau program yang sejenis lainnya. Sangat cocok untuk digunakan oleh para ''Engineer'', karena dapat menyelesaikan persoalan perhitungan terkait masalah - masalah keteknikan atau permodelan desain (seperti : perpindahan kalor, sistem fluida, pengendalian sistem, dan rangkaian elektronika). Selain itu OpenModelica juga tidak rumit untuk seorang pemula untuk mempelajarinya. Kemudian Open Modelica tidak mempunyai bahasa program sendiri, itulah yang menyebabkan waktu simulasi permodelannya cukup lama. Open modelica memproses data lebih lama dikarenakan Open Modelica harus menerjemahkan perintah yang ditulis ke bahasa C++, setelah diproses baru akan muncul data - data perhitungan yang kita inginkan. | ||
| + | |||
| + | |||
| + | === '''Tugas Pertemuan 2''' === | ||
| + | |||
| + | Berikut tugas kedua yaitu pengaplikasian OpenModelica dengan ''class'' dan ''function'' dalam permasalahan matriks variabel array | ||
| + | |||
| + | <youtube width="200" height="100">hJ811iGIUig</youtube> | ||
| + | |||
| + | |||
| + | == '''Pertemuan 3 (25 November 2020)''' == | ||
| + | Pada awal-awal Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, pertama ada ''Computation Fluid Dynamics (CFD)'', lalu ''FInite Element Analysis (FEA)'', dan Metode Stokastik. ''CFD'' dan ''FEA'' berbasis ilmu fisika, kemudian metode stokastik berbasis data dan statistik. Ada lima langkah yang Pak Dai paparkan dalam mengaplikasikan metode numerik ke permasalahan teknik : | ||
| + | * Riset masalah tekniknya terlebih dahulu | ||
| + | * Menganalisis masalah (mendefinisikan variabel yang mau dicari dan mencari parameter fisikanya) | ||
| + | * Membuat model matematika | ||
| + | * Membuat model numerik | ||
| + | * Setelah itu cari penyelesaian dengan bantuan komputer untuk mendapatkan ''output'' yang diinginkan | ||
| + | |||
| + | Agar Kami bisa lebih paham tentang dasar-dasar metode numerik, Pak Dai menyuruh Kami untuk mencoba membuat fungsi untuk menyelesaikan Persamaan 9.12 di buku ''Numerical Methods for Engineers 7th Edition'' oleh Chapra dengan cara apapun (misalnya eliminasi gauss). Kedua, Kami disuru latihan menyelesaikan sistem persamaan dengan membuat fungsi penyelesaian dengan cara pseudocode 9.4 untuk menjawab soal 9.5 yang ada di buku yang sama juga. Latihan yang kedua ini dimaksudkan agar Kami paham dalam penggunaan ''array'' dalam penggunaan OpenModelica, yang dimana ''array'' ini dapat memudahkan mengumpulkan himpunan penyelesaian. Brikut adalah fungsi Gauss Jordan di OpenModelica | ||
| + | |||
| + | |||
| + | function GaussJordan | ||
| + | |||
| + | input Real [:,:] A; | ||
| + | output Real [:,:] B; | ||
| + | |||
| + | protected // untuk local variable | ||
| + | Integer h = 1; //pivot row | ||
| + | Integer k = 1; //pivot coloumn | ||
| + | Integer m = size(A,1); //Number of row | ||
| + | Integer n = size(A,2); //Number of column | ||
| + | Integer c = 0; | ||
| + | Integer max_row; // Row index of max number in pivot column | ||
| + | |||
| + | Real [:] pivot_column; | ||
| + | Real [:] pivot_row; | ||
| + | Real [:,:] temp_array; | ||
| + | Real r; | ||
| + | |||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | |||
| + | algorithm | ||
| + | |||
| + | //fungsi input A dan output B | ||
| + | B := A; | ||
| + | |||
| + | while h <= m and k <= n loop | ||
| + | |||
| + | for i in 1 : m loop | ||
| + | for j in 1 : n loop | ||
| + | if abs(B[i,j]) <= float_error then | ||
| + | B[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //Finding pivot | ||
| + | pivot_column:= {B[i,h] for i in h:m}; | ||
| + | |||
| + | //Mencari baris terbawah yang mempunyai nilai pivot tertinggi | ||
| + | c:=h-1; | ||
| + | for element in pivot_column loop | ||
| + | c:= c+1; | ||
| + | if abs(element)== max(abs(pivot_column)) then | ||
| + | max_row :=c; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya | ||
| + | if B[max_row,k] == 0 then | ||
| + | k:=k+1; | ||
| + | |||
| + | else | ||
| + | // tukar row h - max_row | ||
| + | temp_array := B; | ||
| + | temp_array[h] := B[max_row]; | ||
| + | temp_array[max_row] := B[h]; | ||
| + | B:= temp_array; | ||
| + | |||
| + | //devide pivot row by pivot number | ||
| + | B[h] := B[h]/B[h,k]; | ||
| + | |||
| + | for i in (h+1) :m loop | ||
| + | r := B[i,k]/B[h,k]; | ||
| + | |||
| + | B[i,k]:=0; | ||
| + | |||
| + | for j in (k+1) : n loop | ||
| + | B[i,j] := B[i,j]-B[h,j] * r; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //move ke pivot kolom dan row selanjutnya | ||
| + | h := h+1; | ||
| + | k := k+1; | ||
| + | |||
| + | end if; | ||
| + | |||
| + | end while; | ||
| + | |||
| + | // proses dari kanan atas | ||
| + | h :=m; | ||
| + | k :=n; | ||
| + | |||
| + | while h >=1 and k>=1 loop | ||
| + | |||
| + | //dealing with error | ||
| + | for i in 1:m loop | ||
| + | for j in 1:n loop | ||
| + | if abs(B[i,j]) <=float_error then | ||
| + | B[i,j]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //finding pivot | ||
| + | pivot_row := {B[h,i] for i in 1:k}; | ||
| + | |||
| + | //Get position index k of pivot | ||
| + | c := 0; | ||
| + | for element in pivot_row loop | ||
| + | c := c+1; | ||
| + | if element <> 0 then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | k:= c; | ||
| + | |||
| + | // no pivot in this row, move to next row | ||
| + | if B[h,k] == 0 then | ||
| + | h:= h-1; | ||
| + | |||
| + | else | ||
| + | //perform row operatation | ||
| + | for i in 1:(h-1) loop | ||
| + | r := B[i,k]; | ||
| + | B[i] := B[i] - B[h] *r; | ||
| + | end for; | ||
| + | |||
| + | //move to next pivot row dan column | ||
| + | h:=h+1; | ||
| + | k:=k+1; | ||
| + | |||
| + | end if; | ||
| + | |||
| + | end while; | ||
| + | |||
| + | |||
| + | end GaussJordan; | ||
| + | |||
| + | |||
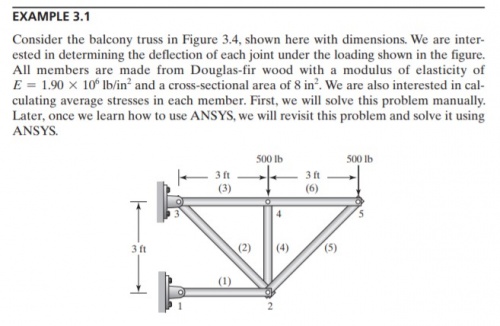
| + | === '''Contoh Soal Truss''' === | ||
| + | |||
| + | |||
| + | [[File:Example 3.1 RS.jpg|500px|thumb|centre]] | ||
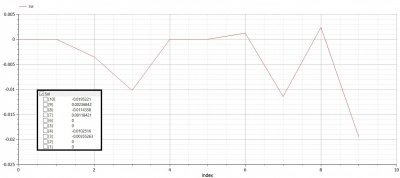
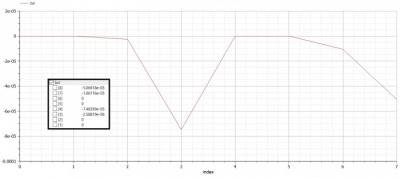
| + | [[File:Soal Trusses 1 Displacement RS.jpg|400px|thumb|right|Grafik Displacement]] | ||
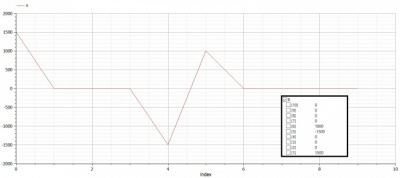
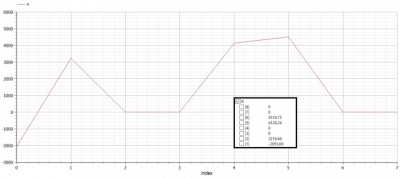
| + | [[File:Soal Trusses 1 Reaction RS.jpg|400px|thumb|right|Grafik Reaction Forces]] | ||
| + | |||
| + | '''Kodingan''' | ||
| + | |||
| + | model Trusses | ||
| + | |||
| + | parameter Integer N=10; //Global matrice = 2*points connected | ||
| + | parameter Real A=8; | ||
| + | parameter Real E=1.9e6; | ||
| + | Real G[N,N]; //global | ||
| + | Real Ginitial[N,N]; //global | ||
| + | Real Sol[N]; //global dispplacement | ||
| + | Real X[N]={0,0,0,0,0,0,0,-500,0,-500}; | ||
| + | Real R[N]; //global reaction force | ||
| + | Real SolMat[N,1]; | ||
| + | Real XMat[N,1]; | ||
| + | |||
| + | //boundary coundition | ||
| + | Integer b1=1; | ||
| + | Integer b2=3; | ||
| + | |||
| + | //truss 1 | ||
| + | parameter Real X1=0; //degree between truss | ||
| + | Real k1=A*E/36; | ||
| + | Real K1[4,4]; //stiffness matrice | ||
| + | Integer p1a=1; | ||
| + | Integer p1b=2; | ||
| + | Real G1[N,N]; | ||
| + | |||
| + | //truss 2 | ||
| + | parameter Real X2=135; //degree between truss | ||
| + | Real k2=A*E/50.912; | ||
| + | Real K2[4,4]; //stiffness matrice | ||
| + | Integer p2a=2; | ||
| + | Integer p2b=3; | ||
| + | Real G2[N,N]; | ||
| + | |||
| + | //truss 3 | ||
| + | parameter Real X3=0; //degree between truss | ||
| + | Real k3=A*E/36; | ||
| + | Real K3[4,4]; //stiffness matrice | ||
| + | Integer p3a=3; | ||
| + | Integer p3b=4; | ||
| + | Real G3[N,N]; | ||
| + | |||
| + | //truss 4 | ||
| + | parameter Real X4=90; //degree between truss | ||
| + | Real k4=A*E/36; | ||
| + | Real K4[4,4]; //stiffness matrice | ||
| + | Integer p4a=2; | ||
| + | Integer p4b=4; | ||
| + | Real G4[N,N]; | ||
| + | |||
| + | //truss 5 | ||
| + | parameter Real X5=45; //degree between truss | ||
| + | Real k5=A*E/50.912; | ||
| + | Real K5[4,4]; //stiffness matrice | ||
| + | Integer p5a=2; | ||
| + | Integer p5b=5; | ||
| + | Real G5[N,N]; | ||
| + | |||
| + | //truss 6 | ||
| + | parameter Real X6=0; //degree between truss | ||
| + | Real k6=A*E/36; | ||
| + | Real K6[4,4]; //stiffness matrice | ||
| + | Integer p6a=4; | ||
| + | Integer p6b=5; | ||
| + | Real G6[N,N]; | ||
| + | |||
| + | /* | ||
| + | for each truss, please ensure pXa is lower then pXb (X represents truss element number) | ||
| + | */ | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | //creating global matrice | ||
| + | K1:=Stiffness_Matrices(X1); | ||
| + | G1:=k1*Local_Global(K1,N,p1a,p1b); | ||
| + | |||
| + | K2:=Stiffness_Matrices(X2); | ||
| + | G2:=k2*Local_Global(K2,N,p2a,p2b); | ||
| + | |||
| + | K3:=Stiffness_Matrices(X3); | ||
| + | G3:=k3*Local_Global(K3,N,p3a,p3b); | ||
| + | |||
| + | K4:=Stiffness_Matrices(X4); | ||
| + | G4:=k4*Local_Global(K4,N,p4a,p4b); | ||
| + | |||
| + | K5:=Stiffness_Matrices(X5); | ||
| + | G5:=k5*Local_Global(K5,N,p5a,p5b); | ||
| + | |||
| + | K6:=Stiffness_Matrices(X6); | ||
| + | G6:=k6*Local_Global(K6,N,p6a,p6b); | ||
| + | |||
| + | G:=G1+G2+G3+G4+G5+G6; | ||
| + | Ginitial:=G; | ||
| + | |||
| + | //implementing boundary condition | ||
| + | for i in 1:N loop | ||
| + | G[2*b1-1,i]:=0; | ||
| + | G[2*b1,i]:=0; | ||
| + | G[2*b2-1,i]:=0; | ||
| + | G[2*b2,i]:=0; | ||
| + | end for; | ||
| + | |||
| + | G[2*b1-1,2*b1-1]:=1; | ||
| + | G[2*b1,2*b1]:=1; | ||
| + | G[2*b2-1,2*b2-1]:=1; | ||
| + | G[2*b2,2*b2]:=1; | ||
| + | |||
| + | //solving displacement | ||
| + | Sol:=Gauss_Jordan(N,G,X); | ||
| + | |||
| + | //solving reaction force | ||
| + | SolMat:=matrix(Sol); | ||
| + | XMat:=matrix(X); | ||
| + | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| + | |||
| + | end Trusses; | ||
| + | |||
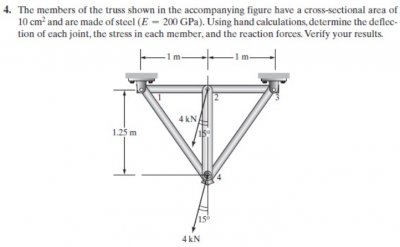
| + | === Tugas Pertemuan 3 === | ||
| + | Kami diberi tugas oleh Pak Dai untuk membuat program sederhana atau penyelesaian dari soal statika struktur dibawah ini dengan OpenModelica | ||
| + | [[File:soal statur.png|400px|thumb|center]] | ||
| + | |||
| + | '''Kodingan''' | ||
| + | [[File:Soal Trusses 2 Displacement RS.jpg|400px|thumb|right|Grafik Displacement]] | ||
| + | [[File:Soal Trusses 2 Reaction RS.jpg|400px|thumb|right|Grafik Reaction Forces]] | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | ''Persamaan'' | ||
| + | |||
| + | class Trusses_HW | ||
| + | |||
| + | parameter Integer N=8; //Global matrice = 2*points connected | ||
| + | parameter Real A=0.001; //Area m2 | ||
| + | parameter Real E=200e9; //Pa | ||
| + | Real G[N,N]; //global | ||
| + | Real Ginitial[N,N]; //global | ||
| + | Real Sol[N]; //global dispplacement | ||
| + | Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; | ||
| + | Real R[N]; //global reaction force | ||
| + | Real SolMat[N,1]; | ||
| + | Real XMat[N,1]; | ||
| + | |||
| + | //boundary condition | ||
| + | Integer b1=1; | ||
| + | Integer b2=3; | ||
| + | |||
| + | //truss 1 | ||
| + | parameter Real X1=0; //degree between truss | ||
| + | Real k1=A*E/1; | ||
| + | Real K1[4,4]; //stiffness matrice | ||
| + | Integer p1a=1; | ||
| + | Integer p1b=2; | ||
| + | Real G1[N,N]; | ||
| + | |||
| + | //truss 2 | ||
| + | parameter Real X2=0; //degree between truss | ||
| + | Real k2=A*E/1; | ||
| + | Real K2[4,4]; //stiffness matrice | ||
| + | Integer p2a=2; | ||
| + | Integer p2b=3; | ||
| + | Real G2[N,N]; | ||
| + | |||
| + | //truss 3 | ||
| + | parameter Real X3=90; //degree between truss | ||
| + | Real k3=A*E/1.25; | ||
| + | Real K3[4,4]; //stiffness matrice | ||
| + | Integer p3a=2; | ||
| + | Integer p3b=4; | ||
| + | Real G3[N,N]; | ||
| + | |||
| + | //truss 4 | ||
| + | parameter Real X4=90+38.6598; //degree between truss | ||
| + | Real k4=A*E/1.6; | ||
| + | Real K4[4,4]; //stiffness matrice | ||
| + | Integer p4a=1; | ||
| + | Integer p4b=4; | ||
| + | Real G4[N,N]; | ||
| + | |||
| + | //truss 5 | ||
| + | parameter Real X5=90-38.6598; //degree between truss | ||
| + | Real k5=A*E/1.6; | ||
| + | Real K5[4,4]; //stiffness matrice | ||
| + | Integer p5a=3; | ||
| + | Integer p5b=4; | ||
| + | Real G5[N,N]; | ||
| + | |||
| + | /* | ||
| + | for each truss, please ensure pXa is lower then pXb (X represents truss element number) | ||
| + | */ | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | //creating global matrice | ||
| + | K1:=Stiffness_Matrices(X1); | ||
| + | G1:=k1*Local_Global(K1,N,p1a,p1b); | ||
| + | |||
| + | K2:=Stiffness_Matrices(X2); | ||
| + | G2:=k2*Local_Global(K2,N,p2a,p2b); | ||
| + | |||
| + | K3:=Stiffness_Matrices(X3); | ||
| + | G3:=k3*Local_Global(K3,N,p3a,p3b); | ||
| + | |||
| + | K4:=Stiffness_Matrices(X4); | ||
| + | G4:=k4*Local_Global(K4,N,p4a,p4b); | ||
| + | |||
| + | K5:=Stiffness_Matrices(X5); | ||
| + | G5:=k5*Local_Global(K5,N,p5a,p5b); | ||
| + | |||
| + | G:=G1+G2+G3+G4+G5; | ||
| + | Ginitial:=G; | ||
| + | |||
| + | //implementing boundary condition | ||
| + | for i in 1:N loop | ||
| + | G[2*b1-1,i]:=0; | ||
| + | G[2*b1,i]:=0; | ||
| + | G[2*b2-1,i]:=0; | ||
| + | G[2*b2,i]:=0; | ||
| + | end for; | ||
| + | |||
| + | G[2*b1-1,2*b1-1]:=1; | ||
| + | G[2*b1,2*b1]:=1; | ||
| + | G[2*b2-1,2*b2-1]:=1; | ||
| + | G[2*b2,2*b2]:=1; | ||
| + | |||
| + | //solving displacement | ||
| + | Sol:=Gauss_Jordan(N,G,X); | ||
| + | |||
| + | //solving reaction force | ||
| + | SolMat:=matrix(Sol); | ||
| + | XMat:=matrix(X); | ||
| + | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| + | |||
| + | end Trusses_HW; | ||
| + | |} | ||
| + | |||
| + | '''Fungsi Panggil''' | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | ''Matrice Transformation'' | ||
| + | |||
| + | function Stiffness_Matrices | ||
| + | input Real A; | ||
| + | Real Y; | ||
| + | output Real X[4,4]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | final constant Real pi=2*Modelica.Math.asin(1.0); | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Y:=A/180*pi; | ||
| + | |||
| + | X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; | ||
| + | |||
| + | -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2]; | ||
| + | |||
| + | for i in 1:4 loop | ||
| + | for j in 1:4 loop | ||
| + | if abs(X[i,j]) <= float_error then | ||
| + | X[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end Stiffness_Matrices; | ||
| + | |||
| + | | style="width: 20cm;"| | ||
| + | ''Global Element Matrice'' | ||
| + | |||
| + | function Local_Global | ||
| + | input Real Y[4,4]; | ||
| + | input Integer B; | ||
| + | input Integer p1; | ||
| + | input Integer p2; | ||
| + | output Real G[B,B]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:B loop | ||
| + | for j in 1:B loop | ||
| + | G[i,j]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | G[2*p1,2*p1]:=Y[2,2]; | ||
| + | G[2*p1-1,2*p1-1]:=Y[1,1]; | ||
| + | G[2*p1,2*p1-1]:=Y[2,1]; | ||
| + | G[2*p1-1,2*p1]:=Y[1,2]; | ||
| + | |||
| + | G[2*p2,2*p2]:=Y[4,4]; | ||
| + | G[2*p2-1,2*p2-1]:=Y[3,3]; | ||
| + | G[2*p2,2*p2-1]:=Y[4,3]; | ||
| + | G[2*p2-1,2*p2]:=Y[3,4]; | ||
| + | |||
| + | G[2*p2,2*p1]:=Y[4,2]; | ||
| + | G[2*p2-1,2*p1-1]:=Y[3,1]; | ||
| + | G[2*p2,2*p1-1]:=Y[4,1]; | ||
| + | G[2*p2-1,2*p1]:=Y[3,2]; | ||
| + | |||
| + | G[2*p1,2*p2]:=Y[2,4]; | ||
| + | G[2*p1-1,2*p2-1]:=Y[1,3]; | ||
| + | G[2*p1,2*p2-1]:=Y[2,3]; | ||
| + | G[2*p1-1,2*p2]:=Y[1,4]; | ||
| + | |||
| + | end Local_Global; | ||
| + | |||
| + | | style="width: 20cm;"| | ||
| + | ''Reaction Matrice Equation'' | ||
| + | |||
| + | function Reaction_Trusses | ||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N,1]; | ||
| + | input Real C[N,1]; | ||
| + | Real X[N,1]; | ||
| + | output Real Sol[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=A*B-C; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i,1]) <= float_error then | ||
| + | X[i,1] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | Sol[i]:=X[i,1]; | ||
| + | end for; | ||
| + | |||
| + | end Reaction_Trusses; | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | == '''Pertemuan 4 (2 Desember 2020)''' == | ||
| + | |||
| + | === '''Kuis : Membuat class diagram dan flowchart setiap class''' === | ||
| + | |||
| + | [[File:Perhitungan.jpg|600px|thumb|center]] | ||
| + | [[File:Flowchartt.jpg|600px|thumb|center]] | ||
| + | [[File:supportingdiagramm.jpg|600px|thumb|center]] | ||
| + | |||
| + | === '''Tugas Pertemuan 4''' === | ||
| + | |||
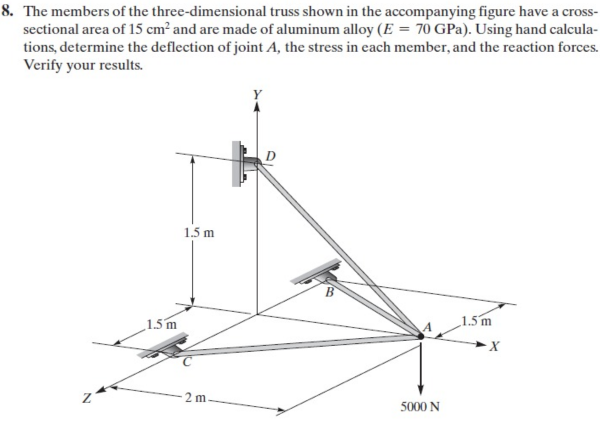
| + | === '''Soal''' === | ||
| + | [[File:pr4metnum.png|600px|thumb|center]] | ||
| + | |||
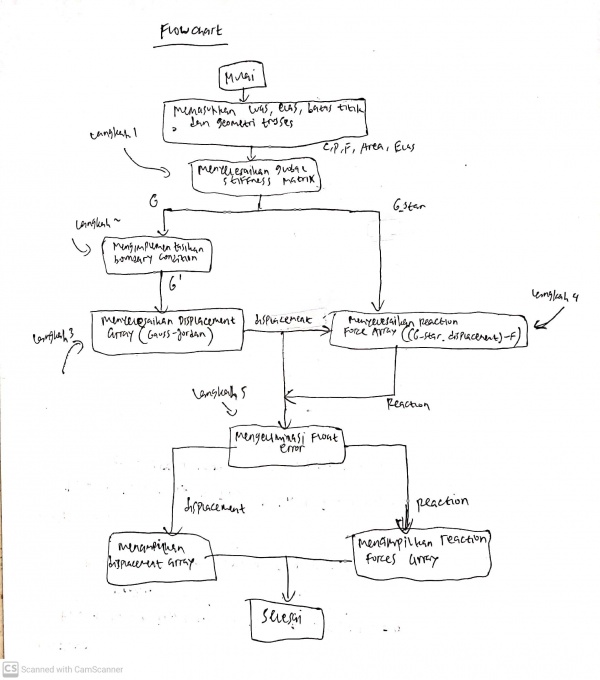
| + | === '''Flow Chart''' === | ||
| + | [[File:flowcharttt.jpg|600px|thumb|center]] | ||
| + | |||
| + | === '''Perhitungan di OpenModelica''' === | ||
| + | |||
| + | '''Berikut kodingannya :''' | ||
| + | |||
| + | class Trusses3D_Tes | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=4; //Number of Points | ||
| + | parameter Integer Trusses=3; //Number of Trusses | ||
| + | parameter Real Area=0.0015; //Area | ||
| + | parameter Real Elas=70e9; //Elasticity | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[Trusses,2]=[1,2; | ||
| + | 1,3; | ||
| + | 1,4]; | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[Points,3]=[2,0,0; | ||
| + | 0,0,1.5; | ||
| + | 0,0,-1.5; | ||
| + | 0,1.5,0]; | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,-5000,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0}; | ||
| + | |||
| + | //define boundary | ||
| + | parameter Integer b[:]={2,3,4}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, X[3,3]; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for i in boundary loop | ||
| + | for j in 1:N loop | ||
| + | G[i,j]:=id[i,j]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | end Trusses3D_Tes; | ||
| + | |||
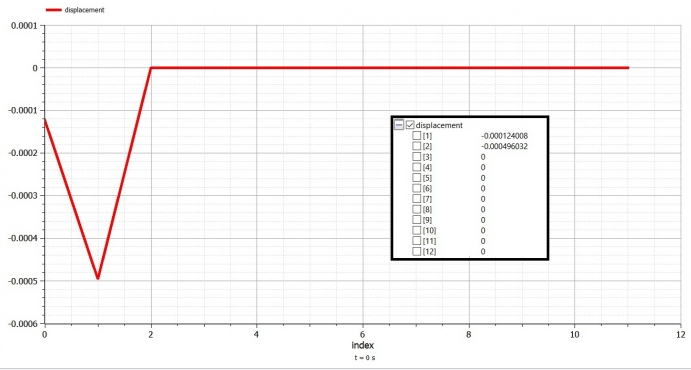
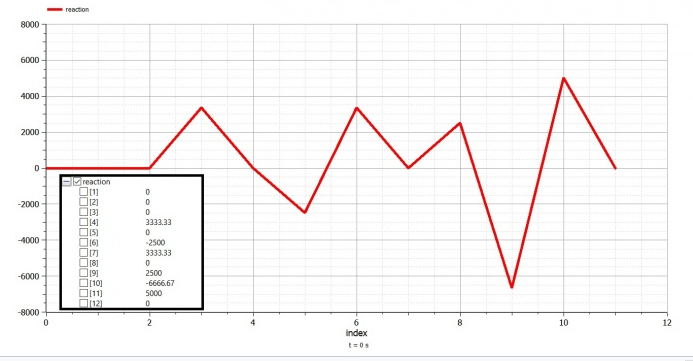
| + | [[File:3D grf1.png|700px|thumb|center]] | ||
| + | [[File:3D grf.png|700px|thumb|center]] | ||
| + | |||
| + | === '''Verifikasi Perhitungan''' === | ||
| + | [[File:Verifikasi.jpg|600px|thumb|center|]] | ||
| + | |||
| + | == '''Pertemuan 5 (16 Desember 2020)''' == | ||
| + | Pada pertemuan kelima, Kami diajarkan mengenai pengaplikasian metode numerik dalam optimasi sebuah sistem menggunakan OpenModelica. Materi ini dijelaskan melalui sebuah video oleh Bu Candra serta pseudocode dari persoalan tersebut, contoh persoalan tersebut adalah optimasi menggunakan metode Bracket. Berikut adalah pseudocode yang di OpenModelica : | ||
| + | |||
| + | '''FungsiObjek.mo''' | ||
| + | function FungsiObjek | ||
| + | |||
| + | input Real x; | ||
| + | output Real y; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | y:= 2*Modelica.Math.sin(x)-x^2/10; | ||
| + | |||
| + | end FungsiObjek; | ||
| + | |||
| + | Fungsi tersebut akan dipanggil di suatu file model | ||
| + | |||
| + | '''BracketOptimal.mo''' | ||
| + | model BracketOptimal | ||
| + | |||
| + | parameter Integer n = 8; | ||
| + | Real x1[n]; | ||
| + | Real x2[n]; | ||
| + | Real xup; | ||
| + | Real xlow; | ||
| + | Real f1[n]; | ||
| + | Real f2[n]; | ||
| + | Real xopt; | ||
| + | Real yopt; | ||
| + | Real d; | ||
| + | |||
| + | algorithm | ||
| + | xup := 4; | ||
| + | xlow := 0; | ||
| + | |||
| + | for i in 1:n loop | ||
| + | d:=((5^(1/2)-1)/2) * (xup-xlow); | ||
| + | x1[i] := xlow+d; | ||
| + | x2[i] := xup-d; | ||
| + | f1[i] := FungsiObjek(x1[i]); | ||
| + | f2[i] := FungsiObjek(x2[i]); | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xup := xup; | ||
| + | xlow := x2[i]; | ||
| + | xopt := xup; | ||
| + | yopt := f1[i]; | ||
| + | else | ||
| + | xlow :=xlow; | ||
| + | xup := x1[i]; | ||
| + | xopt := xup; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | |||
| + | end BracketOptimal; | ||
| + | |||
| + | == '''Pertemuan 6 (23 Desember 2020)''' == | ||
| + | |||
| + | === '''Tugas Besar''' === | ||
| + | |||
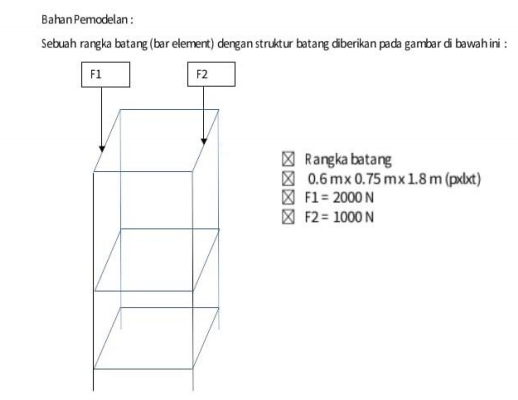
| + | Kami diberi tugas besar yaitu melakukan oprimasi rangka sederhana, dengan tujuan mendesain rangka yang ''reliable'' dengan biaya yang optimal. Geometri dan ''load'' sudah diberikan Pak Dai di grup whatsapp. Tugas besar ini harus mempertimbangkan tiga variabel bebas yaitu, biaya, material, ''area cross section truss''. Kemudian juga membuat kurva efisiensi biaya dengan ''curve fitting''. Berikut bahan permodelannya : | ||
| + | [[File:soaltubesumar.png|600px|thumb|center]] | ||
| + | |||
| + | '''Pendefinisian Masalah''' | ||
| + | |||
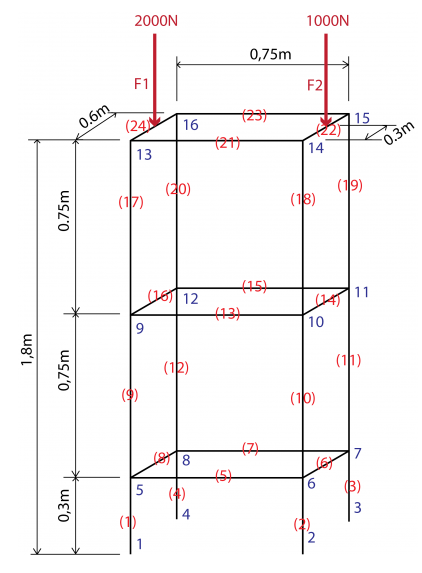
| + | Pertama - tama, Saya mendefinisikan node dan elemen pada struktur batang di soal. | ||
| + | [[File:strukturbatangumar.png|600px|thumb|center]] | ||
| + | |||
| + | '''Asumsi dan Batasan''' | ||
| + | |||
| + | Asumsi : | ||
| + | *Strukturnya sebagai truss, sehingga tidak ada bending. | ||
| + | *Beban terdistribusi pada node-node yang ada. | ||
| + | *Batas displacement 0,001m sebelum terjadi buckling. | ||
| + | |||
| + | Batasan : | ||
| + | *Node 1, 2, 3, dan 4 merupakan fixed. | ||
| + | *Beban F1 dan F2 terdistribusi ke node sekitarnya. | ||
| + | *Beban eksternal pada node 14 dan 15 sebesar 500N arah y negatif. | ||
| + | *Beban eksternal pada node 13 dan 16 sebesar 1000N arah y negatif. | ||
| + | |||
| + | '''Penentuan Penyelesaian yang akan dikerjakan''' | ||
| + | |||
| + | Data yang perlu dicari adalah variasi profil dari besi siku dengan suatu material dan variasi material dari besi siku dengan luas profil tertentu beserta dengan biayanya, karena yang ingin dicari adalah variasi material (elastisitas) dan luas profil dari besi siku yang optimum. Setelah mendapat seluruh data yang diperlukan, disusun dalam bentuk excel untuk proses perhitungan untuk sistem permodelan dan untuk 3D-trusses digunakan coding-an yang sudah dibuat oleh saudara Josiah, Christopher, dan Fahmi. Hasilnya berupa stress pada tiap truss yang terjadi pada elastisitas dan luas profil area tertentu. Kemudian untuk memenuhi data yang kurang digunakan permodelan Curve fitting untuk digunakan pada perhitungan dan komputasi nanti. | ||
| + | |||
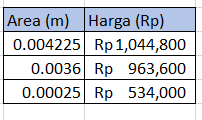
| + | '''Menentukan variasi material dan variasi luas penampang untuk menghitung optimasi''' | ||
| + | |||
| + | Material tetap, variasi luas | ||
| + | [[File:dataumar1.png|600px|thumb|center]] | ||
| + | [[File:dataumar2.png|600px|thumb|center]] | ||
| + | |||
| + | Luas penampang tetap, variasi material | ||
| + | [[File:dataumar3.png|600px|thumb|center]] | ||
| + | |||
| + | |||
| + | '''Membuat Codingan untuk Mencari nilai displacement, reaction force, dan melakukan optimasi | ||
| + | ---- | ||
| + | |||
| + | Berikut adalah coding hasil diskusi dua kelas yang dipimpin oleh Josiah, Fahmi, dan Christo | ||
| + | |||
| + | *Untuk perhitungan displacement, reaction force, stress, dan safety factor: | ||
| + | model TugasBesar_Umar_Metnum02 | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end TugasBesar_Umar_Metnum02; | ||
| + | |||
| + | |||
| + | *Untuk membuat kurva curve fitting: | ||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | |||
| + | |||
| + | * Untuk golden section: | ||
| + | model Opt_Gold | ||
| + | |||
| + | parameter Real xd[:]; | ||
| + | parameter Real yd[size(xd,1)]; | ||
| + | parameter Real xlo=87e-6; | ||
| + | parameter Real xhi=504e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Opt_Gold; | ||
| + | |||
| + | |||
| + | '''Hasil Perhitungan''' | ||
| + | |||
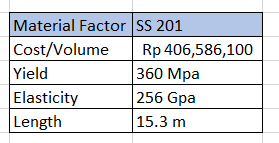
| + | *Nilai luas area penampang optimum untuk material SS201 adalah 283,81 mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 6m dan tebal 60mm. | ||
| + | |||
| + | [[File:ItunganUmar1.png|600px|thumb|center]] | ||
| + | |||
| + | *Material optimum yang dapat digunakan untuk luas penampang 360mm^2 adalah material dengan nilai elastisitas 15324000000000 N/m^2 atau material yang paling mendekati adalah SS316L | ||
| + | |||
| + | [[File:ItunganUmar2.png|600px|thumb|center]] | ||
| + | |||
| + | |||
| + | == '''Ujian Akhir Semester''' == | ||
| + | |||
| + | '''Nomor 1''' | ||
| + | [[File:nomer1umarr.jpg|600px|thumb|center]] | ||
| + | '''Nomor 2 & 3''' | ||
| + | [[File:nomer23umar.jpg|600px|thumb|center]] | ||
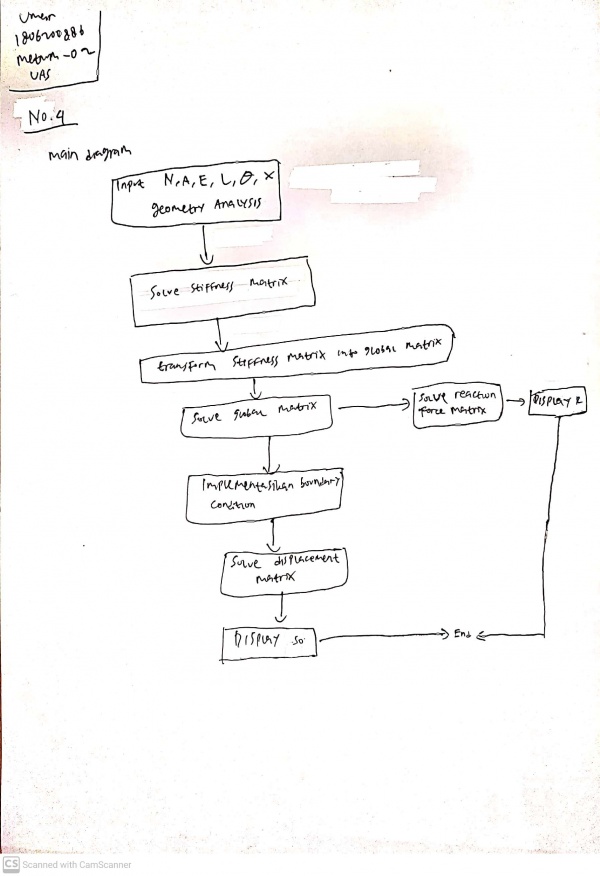
| + | '''Nomor 4''' | ||
| + | [[File:nomer4umar.jpg|600px|thumb|center]] | ||
| + | '''Nomor 5 & 6''' | ||
| + | [[File:nomer56umarr.jpg|600px|thumb|center]] | ||
| + | |||
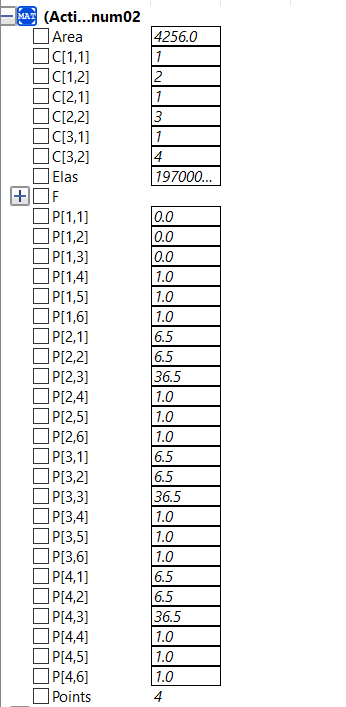
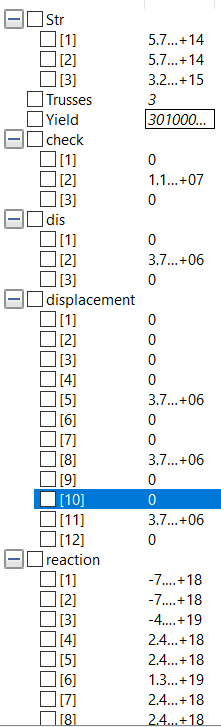
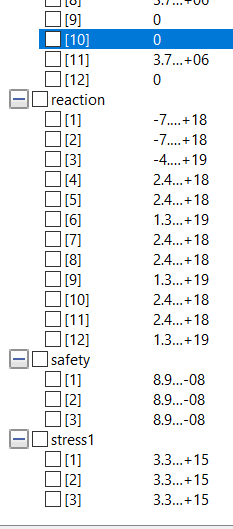
| + | '''Berikut adalah hasil pengerjaan di OpenModelica untuk nomor 7''' | ||
| + | |||
| + | model UAS_Umar_Metnum02 | ||
| + | //define initial variable | ||
| + | parameter Integer Points = size(P, 1); | ||
| + | //Number of Points | ||
| + | parameter Integer Trusses = size(C, 1); | ||
| + | //Number of Trusses | ||
| + | parameter Real Yield = 301e6; | ||
| + | //Yield Strength (Pa) | ||
| + | parameter Real Area = 4256; | ||
| + | //Area L Profile | ||
| + | parameter Real Elas = 197e9; | ||
| + | //Elasticity Stainless Steel 201 (Pa) | ||
| + | //define connection | ||
| + | parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4]; | ||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1 | ||
| + | 6.5, 6.5, 36.5, 1, 1, 1; //2 | ||
| + | 6.5, 6.5, 36.5, 1, 1, 1; //3 | ||
| + | 6.5, 6.5, 36.5, 1, 1, 1]; //4 | ||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points * 3] = {0,0,0,0,3708180,0,0,3708180,0,0,3708180,0}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N = 3 * Points; | ||
| + | Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] = identity(N), cx, cy, cz, L, X[3, 3]; | ||
| + | Real err = 10e-10, ers = 10e-4; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G := id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j] := P[C[i, 1], j]; | ||
| + | q2[j] := P[C[i, 2], j]; | ||
| + | end for; | ||
| + | L := Modelica.Math.Vectors.length(q2 - q1); | ||
| + | cx := (q2[1] - q1[1]) / L; | ||
| + | cy := (q2[2] - q1[2]) / L; | ||
| + | cz := (q2[3] - q1[3]) / L; | ||
| + | X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2]; | ||
| + | g := zeros(N, N); | ||
| + | for m, n in 1:3 loop | ||
| + | g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n]; | ||
| + | g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n]; | ||
| + | g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n]; | ||
| + | g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n]; | ||
| + | end for; | ||
| + | G_star := G + g; | ||
| + | G := G_star; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | //Transforming to global matrix | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x, 4] <> 0 then | ||
| + | for a in 1:Points * 3 loop | ||
| + | G[x * 3 - 2, a] := 0; | ||
| + | G[x * 3 - 2, x * 3 - 2] := 1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x, 5] <> 0 then | ||
| + | for a in 1:Points * 3 loop | ||
| + | G[x * 3 - 1, a] := 0; | ||
| + | G[x * 3 - 1, x * 3 - 1] := 1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x, 6] <> 0 then | ||
| + | for a in 1:Points * 3 loop | ||
| + | G[x * 3, a] := 0; | ||
| + | G[x * 3, x * 3] := 1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement := Modelica.Math.Matrices.solve(G, F); | ||
| + | //Solving reaction | ||
| + | reaction := G_star * displacement - F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i]; | ||
| + | displacement[i] := if abs(displacement[i]) <= err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in 1:3:N - 2}); | ||
| + | check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in 2:3:N - 1}); | ||
| + | check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in 3:3:N}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i]) <= ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j] := P[C[i, 1], j]; | ||
| + | q2[j] := P[C[i, 2], j]; | ||
| + | dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3 * (C[i, 2] - 1) + j]); | ||
| + | end for; | ||
| + | L := Modelica.Math.Vectors.length(q2 - q1); | ||
| + | cx := (q2[1] - q1[1]) / L; | ||
| + | cy := (q2[2] - q1[2]) / L; | ||
| + | cz := (q2[3] - q1[3]) / L; | ||
| + | X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2]; | ||
| + | Str := X * dis; | ||
| + | stress1[i] := Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i] > 0 then | ||
| + | safety[i] := Yield / stress1[i]; | ||
| + | else | ||
| + | safety[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end UAS_Umar_Metnum02; | ||
| + | |||
| + | [[File:ssmodelicaumar1.png|600px|thumb|center]] | ||
| + | [[File:ssmodelicaumar2.png|600px|thumb|center]] | ||
| + | [[File:ssmodelicaumar3.png|600px|thumb|center]] | ||
Latest revision as of 03:40, 14 January 2021
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Biodata Diri
Nama : Umar
NPM : 1806200886
TTL : Jakarta, 16 September 2000
Tempat Tinggal: Jakarta
Saya adalah Mahasiswa Fakultas Teknik Universitas Indonesia, Program Studi Teknik Mesin angkatan 2018. Saat ini Saya sedang menempuh perkuliahan di semester 5, yang artinya sudah tahun ketiga pekuliahan.
Alasan Saya mengambil Program Studi (Prodi) Teknik Mesin karena Prodi ini cukup luas prospeknya dan juga prodi yang mempelajari ilmu engineering yang lebih advance dari prodi teknik lainnya menurut Saya dan akan terus digunakan di masa mendatang.
Contents
Pertemuan 1 (11 November 2020)
Setelah melewati pembelajaran selama paruh semester awal dengan Bapak Dr. Ir. Engkos A. Kosasih, M.T. dan melakukan Ujian Tengah Semester (UTS), kelas Metode Numerik - 02 berganti dosen menjadi Bapak Dr. Ir. Ahmad Indra Siswantara atau biasa disapa Pak Da'i. Pada pertemuan pertama setelah UTS ini, Pak Da'i meminta mahasiswa untuk membuat akun pada situs wiki air. Kami dijelaskan bagaimana cara - cara untuk menggunakan wiki air ini supaya lebih familiar dalam menggunakannya, karena tugas - tugas kedepannya akan dikerjakan di wiki air. Pak Da'i pada saat itu juga memaparkan kembali apa tujuan dari pembelajaran metode numerik ini, berikut tujuan - tujuan yang beliau sebutkan :
- Memahami konsep dan prinsip dasar dalam Metode Numerik
- Mampu mengaplikasikan pemahaman dari konsep yang ada di dalam permodelan numerik
- Mampu mengaplikasikan metode numerik dalam persoalan teknik
- Mendapat nilai tambah/moral sehingga kita menjadi orang yang lebih beradab seperti yang sudah tertulis di sila ke-2 Pancasila.
Uniknya pada perkuliahan kemarin Saya mendapat suatu pelajaran hidup bahwa kita sebagai manusia punya limitasi terkait ilmu pengetahuan atau apapun itu, salah satu kasusnya dalam bidang matematika yaitu belum terpecahkan jawaban atau belum terdefinisi jawaban dari bilangan berapapun dibagi dengan 0 (n/0) walaupun menggunakan software sekalipun. Maka dari itu kita bisa petik hikmah bahwa sebagai manusia tidak boleh merasa "tinggi" walaupun orang - orang menganggap kita sebagai orang hebat sekalipun.
Tugas Pertemuan 1
Pada minggu pertama, setiap mahasiswa diminta untuk melihat dan mempraktikan tentang tutorial atau dasar Open Modellica dari youtube. Kemudian diharapkan untuk mengupload video tutorial singkat di Youtube. Berikut ini adalah video tutorial dasar dari saya untuk penghitungan volume langkah piston pada OpenModelica.
Pertemuan 2 (Rabu, 18 November 2020)
Pak Dai menjelaskan bahwa menggunakan Software OpenModelica lebih nyaman dan sederhana dibanding Software atau program yang sejenis lainnya. Sangat cocok untuk digunakan oleh para Engineer, karena dapat menyelesaikan persoalan perhitungan terkait masalah - masalah keteknikan atau permodelan desain (seperti : perpindahan kalor, sistem fluida, pengendalian sistem, dan rangkaian elektronika). Selain itu OpenModelica juga tidak rumit untuk seorang pemula untuk mempelajarinya. Kemudian Open Modelica tidak mempunyai bahasa program sendiri, itulah yang menyebabkan waktu simulasi permodelannya cukup lama. Open modelica memproses data lebih lama dikarenakan Open Modelica harus menerjemahkan perintah yang ditulis ke bahasa C++, setelah diproses baru akan muncul data - data perhitungan yang kita inginkan.
Tugas Pertemuan 2
Berikut tugas kedua yaitu pengaplikasian OpenModelica dengan class dan function dalam permasalahan matriks variabel array
Pertemuan 3 (25 November 2020)
Pada awal-awal Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, pertama ada Computation Fluid Dynamics (CFD), lalu FInite Element Analysis (FEA), dan Metode Stokastik. CFD dan FEA berbasis ilmu fisika, kemudian metode stokastik berbasis data dan statistik. Ada lima langkah yang Pak Dai paparkan dalam mengaplikasikan metode numerik ke permasalahan teknik :
- Riset masalah tekniknya terlebih dahulu
- Menganalisis masalah (mendefinisikan variabel yang mau dicari dan mencari parameter fisikanya)
- Membuat model matematika
- Membuat model numerik
- Setelah itu cari penyelesaian dengan bantuan komputer untuk mendapatkan output yang diinginkan
Agar Kami bisa lebih paham tentang dasar-dasar metode numerik, Pak Dai menyuruh Kami untuk mencoba membuat fungsi untuk menyelesaikan Persamaan 9.12 di buku Numerical Methods for Engineers 7th Edition oleh Chapra dengan cara apapun (misalnya eliminasi gauss). Kedua, Kami disuru latihan menyelesaikan sistem persamaan dengan membuat fungsi penyelesaian dengan cara pseudocode 9.4 untuk menjawab soal 9.5 yang ada di buku yang sama juga. Latihan yang kedua ini dimaksudkan agar Kami paham dalam penggunaan array dalam penggunaan OpenModelica, yang dimana array ini dapat memudahkan mengumpulkan himpunan penyelesaian. Brikut adalah fungsi Gauss Jordan di OpenModelica
function GaussJordan
input Real [:,:] A;
output Real [:,:] B;
protected // untuk local variable
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //Number of row
Integer n = size(A,2); //Number of column
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
//fungsi input A dan output B
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Mencari baris terbawah yang mempunyai nilai pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//move ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
Contoh Soal Truss
Kodingan
model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
Tugas Pertemuan 3
Kami diberi tugas oleh Pak Dai untuk membuat program sederhana atau penyelesaian dari soal statika struktur dibawah ini dengan OpenModelica
Kodingan
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
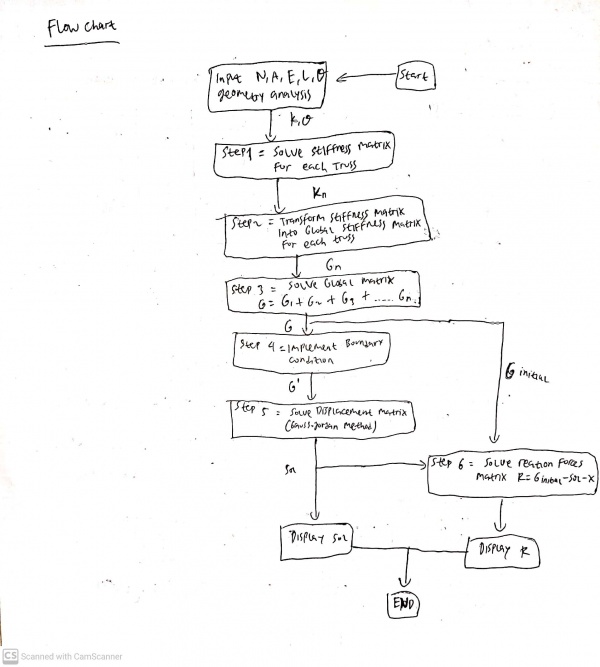
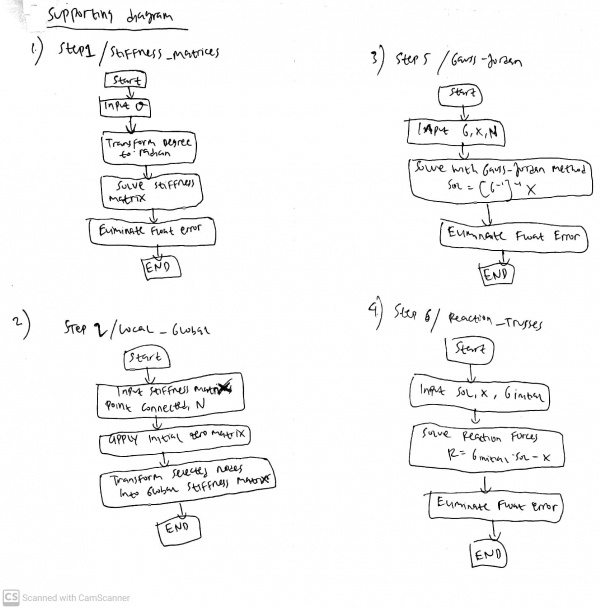
Pertemuan 4 (2 Desember 2020)
Kuis : Membuat class diagram dan flowchart setiap class
Tugas Pertemuan 4
Soal
Flow Chart
Perhitungan di OpenModelica
Berikut kodingannya :
class Trusses3D_Tes
//define initial variable
parameter Integer Points=4; //Number of Points
parameter Integer Trusses=3; //Number of Trusses
parameter Real Area=0.0015; //Area
parameter Real Elas=70e9; //Elasticity
//define connection
parameter Integer C[Trusses,2]=[1,2;
1,3;
1,4];
//define coordinates (please put orderly)
parameter Real P[Points,3]=[2,0,0;
0,0,1.5;
0,0,-1.5;
0,1.5,0];
//define external force (please put orderly)
parameter Real F[Points*3]={0,-5000,0,
0,0,0,
0,0,0,
0,0,0};
//define boundary
parameter Integer b[:]={2,3,4};
//solution
Real displacement[N], reaction[N];
protected
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, X[3,3];
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
end Trusses3D_Tes;
Verifikasi Perhitungan
Pertemuan 5 (16 Desember 2020)
Pada pertemuan kelima, Kami diajarkan mengenai pengaplikasian metode numerik dalam optimasi sebuah sistem menggunakan OpenModelica. Materi ini dijelaskan melalui sebuah video oleh Bu Candra serta pseudocode dari persoalan tersebut, contoh persoalan tersebut adalah optimasi menggunakan metode Bracket. Berikut adalah pseudocode yang di OpenModelica :
FungsiObjek.mo function FungsiObjek input Real x; output Real y; algorithm y:= 2*Modelica.Math.sin(x)-x^2/10; end FungsiObjek;
Fungsi tersebut akan dipanggil di suatu file model
BracketOptimal.mo
model BracketOptimal
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end BracketOptimal;
Pertemuan 6 (23 Desember 2020)
Tugas Besar
Kami diberi tugas besar yaitu melakukan oprimasi rangka sederhana, dengan tujuan mendesain rangka yang reliable dengan biaya yang optimal. Geometri dan load sudah diberikan Pak Dai di grup whatsapp. Tugas besar ini harus mempertimbangkan tiga variabel bebas yaitu, biaya, material, area cross section truss. Kemudian juga membuat kurva efisiensi biaya dengan curve fitting. Berikut bahan permodelannya :
Pendefinisian Masalah
Pertama - tama, Saya mendefinisikan node dan elemen pada struktur batang di soal.
Asumsi dan Batasan
Asumsi :
- Strukturnya sebagai truss, sehingga tidak ada bending.
- Beban terdistribusi pada node-node yang ada.
- Batas displacement 0,001m sebelum terjadi buckling.
Batasan :
- Node 1, 2, 3, dan 4 merupakan fixed.
- Beban F1 dan F2 terdistribusi ke node sekitarnya.
- Beban eksternal pada node 14 dan 15 sebesar 500N arah y negatif.
- Beban eksternal pada node 13 dan 16 sebesar 1000N arah y negatif.
Penentuan Penyelesaian yang akan dikerjakan
Data yang perlu dicari adalah variasi profil dari besi siku dengan suatu material dan variasi material dari besi siku dengan luas profil tertentu beserta dengan biayanya, karena yang ingin dicari adalah variasi material (elastisitas) dan luas profil dari besi siku yang optimum. Setelah mendapat seluruh data yang diperlukan, disusun dalam bentuk excel untuk proses perhitungan untuk sistem permodelan dan untuk 3D-trusses digunakan coding-an yang sudah dibuat oleh saudara Josiah, Christopher, dan Fahmi. Hasilnya berupa stress pada tiap truss yang terjadi pada elastisitas dan luas profil area tertentu. Kemudian untuk memenuhi data yang kurang digunakan permodelan Curve fitting untuk digunakan pada perhitungan dan komputasi nanti.
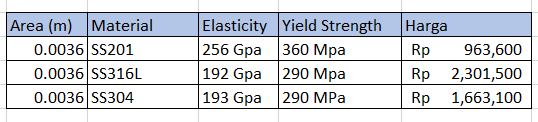
Menentukan variasi material dan variasi luas penampang untuk menghitung optimasi
Material tetap, variasi luas
Luas penampang tetap, variasi material
Membuat Codingan untuk Mencari nilai displacement, reaction force, dan melakukan optimasi
Berikut adalah coding hasil diskusi dua kelas yang dipimpin oleh Josiah, Fahmi, dan Christo
- Untuk perhitungan displacement, reaction force, stress, dan safety factor:
model TugasBesar_Umar_Metnum02
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end TugasBesar_Umar_Metnum02;
- Untuk membuat kurva curve fitting:
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
- Untuk golden section:
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Hasil Perhitungan
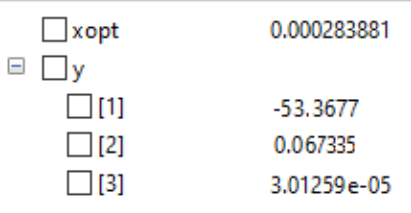
- Nilai luas area penampang optimum untuk material SS201 adalah 283,81 mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 6m dan tebal 60mm.
- Material optimum yang dapat digunakan untuk luas penampang 360mm^2 adalah material dengan nilai elastisitas 15324000000000 N/m^2 atau material yang paling mendekati adalah SS316L
Ujian Akhir Semester
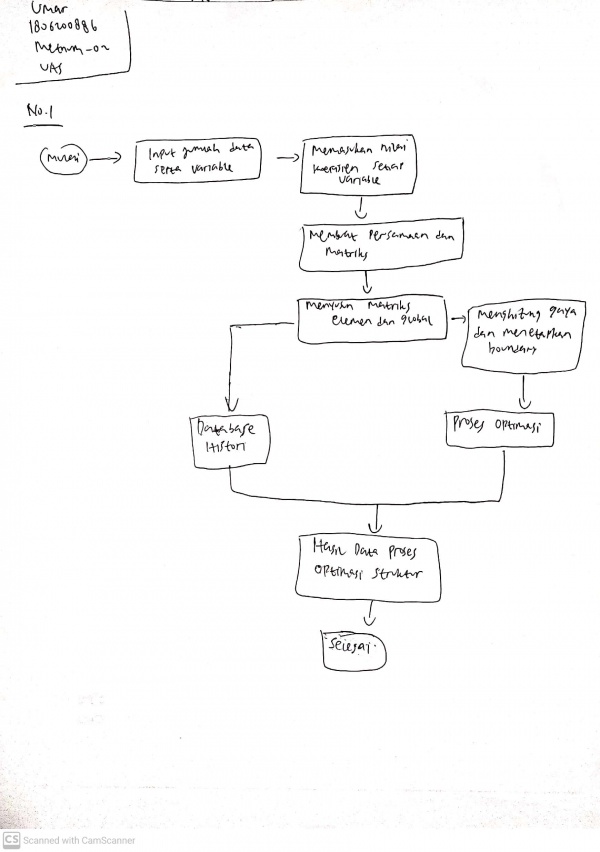
Nomor 1
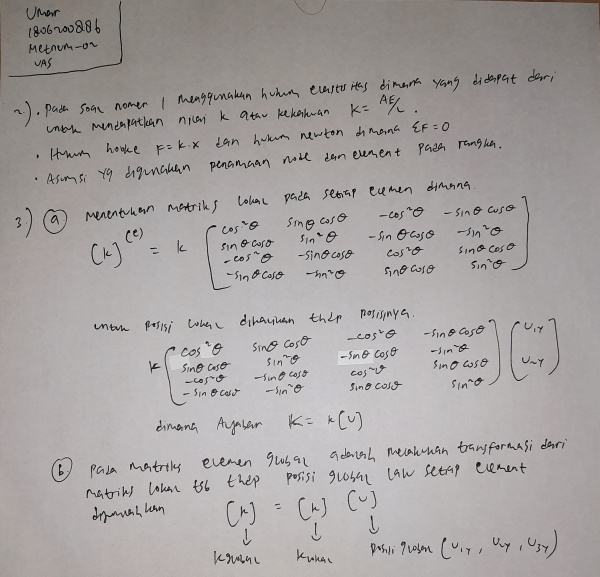
Nomor 2 & 3
Nomor 4
Nomor 5 & 6
Berikut adalah hasil pengerjaan di OpenModelica untuk nomor 7
model UAS_Umar_Metnum02
//define initial variable
parameter Integer Points = size(P, 1);
//Number of Points
parameter Integer Trusses = size(C, 1);
//Number of Trusses
parameter Real Yield = 301e6;
//Yield Strength (Pa)
parameter Real Area = 4256;
//Area L Profile
parameter Real Elas = 197e9;
//Elasticity Stainless Steel 201 (Pa)
//define connection
parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4];
//define coordinates (please put orderly)
parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1
6.5, 6.5, 36.5, 1, 1, 1; //2
6.5, 6.5, 36.5, 1, 1, 1; //3
6.5, 6.5, 36.5, 1, 1, 1]; //4
//define external force (please put orderly)
parameter Real F[Points * 3] = {0,0,0,0,3708180,0,0,3708180,0,0,3708180,0};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N = 3 * Points; Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] = identity(N), cx, cy, cz, L, X[3, 3]; Real err = 10e-10, ers = 10e-4;
algorithm
//Creating Global Matrix
G := id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
g := zeros(N, N);
for m, n in 1:3 loop
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n];
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n];
end for;
G_star := G + g;
G := G_star;
end for;
//Solving Matrix //Transforming to global matrix //Implementing boundary
for x in 1:Points loop
if P[x, 4] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 2, a] := 0;
G[x * 3 - 2, x * 3 - 2] := 1;
end for;
end if;
if P[x, 5] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 1, a] := 0;
G[x * 3 - 1, x * 3 - 1] := 1;
end for;
end if;
if P[x, 6] <> 0 then
for a in 1:Points * 3 loop
G[x * 3, a] := 0;
G[x * 3, x * 3] := 1;
end for;
end if;
end for;
//Solving displacement
displacement := Modelica.Math.Matrices.solve(G, F);
//Solving reaction
reaction := G_star * displacement - F;
//Eliminating float error
for i in 1:N loop reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i]; displacement[i] := if abs(displacement[i]) <= err then 0 else displacement[i]; end for;
//Checking Force
check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in 1:3:N - 2});
check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in 2:3:N - 1});
check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in 3:3:N});
for i in 1:3 loop
check[i] := if abs(check[i]) <= ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3 * (C[i, 2] - 1) + j]);
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
Str := X * dis;
stress1[i] := Modelica.Math.Vectors.length(Str);
end for;
//Solving Matrix //Safety factor
for i in 1:Trusses loop
if stress1[i] > 0 then
safety[i] := Yield / stress1[i];
else
safety[i] := 0;
end if;
end for;
end UAS_Umar_Metnum02;