Difference between revisions of "Diagy Alwan Irsyad"
m (→Solusi) |
|||
| (70 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
Alamat surel : diagya.irsyad29@gmail.com / diagy.alwan@ui.ac.id | Alamat surel : diagya.irsyad29@gmail.com / diagy.alwan@ui.ac.id | ||
| − | == Metode Numerik == | + | == Metode Numerik-02 == |
Pada semester gasal 2020/2021, saya mengambil mata kuliah Metode Numerik, tepatnya di kelas [[Kelas Metoda Numerik 02 Sem. Gasal 2020/21|Metode Numerik-02]]. | Pada semester gasal 2020/2021, saya mengambil mata kuliah Metode Numerik, tepatnya di kelas [[Kelas Metoda Numerik 02 Sem. Gasal 2020/21|Metode Numerik-02]]. | ||
| + | __TOC__ | ||
| − | [https://youtu.be/ | + | === Pertemuan I (11 November 2020) === |
| + | Pertemuan pertama bersama Pak Dai, saya dan mahasiswa lain diajak berpikir untuk bisa mengetahui hal-hal yang sudah kami ketahui dan yang belum. Dengan mengetahui hal yang belum diketahui, kami bisa mempelajari hal-hal tersebut. Selain itu, kami juga membahas tentang pengenalan aplikasi OpenModelica. | ||
| + | |||
| + | ==== Tugas 1 ==== | ||
| + | Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara penggunaan OpenModelica. | ||
| + | |||
| + | Berikut adalah video yang saya buat: | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <youtube width="200" height="100">https://youtu.be/hockvdJUJOg</youtube> | ||
| + | </div> | ||
| + | |||
| + | === Pertemuan II (18 November 2020) === | ||
| + | Pertemuan kedua bersama Pak Dai, saya dan mahasiswa lain diminta untuk bisa menjadi orang yang beruntung. Yang dimaksud orang yang beruntung adalah orang yang mampu menjadi pribadi yang lebih baik dibandingkan kemarin. Pak Dai mengingatkan agar kami jangan menjadi orang yang merugi, yaitu orang yang tidak memiliki perkembangan antara hari ini dengan kemarin. | ||
| + | |||
| + | Setelah mendapatkan pelajaran hidup yang berharga, kami diminta untuk mempresentasikan tugas kami yang telah dibuat sebelumnya. Tujuan dari presentasi ini adalah untuk menilai kemampuan mahasiswa dalam pemahaman penggunaan aplikasi OpenModelica. | ||
| + | |||
| + | Materi yang diberikan pada pertemuan ini adalah penggunaan ''class'' untuk memanggil sebuah ''function''. ''Function'' yang bisa dipanggil beragam jumlahnya, mulai dari penjumlahan sederhana sampai operasi eliminasi matriks. | ||
| + | |||
| + | ==== Tugas 2 ==== | ||
| + | Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara menyelesaikan persamaan aljabar simultan dengan OpenModelica. Metode yang digunakan menggunakan ''class'' untuk memanggil sebuah ''function'', seperti yang sudah diajarkan sebelumnya. | ||
| + | |||
| + | Berikut adalah video yang saya buat: | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <youtube width="200" height="100">https://youtu.be/pRDux7BR3F4</youtube> | ||
| + | </div> | ||
| + | |||
| + | === Pertemuan III (25 November 2020) === | ||
| + | Pertemuan ketiga bersama Pak Dai, saya dan mahasiswa lain membahas penggunaan metode numerik pada bidang teknik. Metode numerik bisa digunakan untuk menyelesaikan simulasi CFD dan menghitung gaya reaksi pada suatu rangkaian ''truss''. | ||
| + | |||
| + | Langkah yang diperlukan untuk menyelesaikan masalah di bidang teknik dengan metode numerik adalah: | ||
| + | # Melakukan analisis terhadap masalah | ||
| + | # Membuat model matematis penyelesaian masalah | ||
| + | # Menggunakan metode numerik yang sesuai untuk menyelesaikan masalah | ||
| + | |||
| + | Setelah langkah-langkah tersebut dilakukan, maka solusi dari masalah bisa ditemukan. Untuk pembelajaran di kelas, kami mempelajari rangkaian ''truss'' untuk sarana belajar metode numerik. | ||
| + | |||
| + | ==== Tugas 3 ==== | ||
| + | Di akhir kelas, kami diberi tugas untuk membuat program sederhana menggunakan aplikasi OpenModelica menggunakan fungsi penyelesaian aljabar untuk menyelesaikan soal berikut: | ||
| + | [[File:No4 d29..jpeg|700px|center]] | ||
| + | |||
| + | Berikut adalah program yang saya buat: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Class''''' | ||
| + | |||
| + | class Trusses_Tugas3_d29 | ||
| + | |||
| + | parameter Integer N=8; //Global matrice = 2*points connected | ||
| + | parameter Real A=0.001; //m^2 | ||
| + | parameter Real E=200e9; //Pa | ||
| + | Real G[N,N]; //global | ||
| + | Real Ginitial[N,N]; //global | ||
| + | Real Sol[N]; //global displacement | ||
| + | Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; | ||
| + | Real R[N]; //global reaction force | ||
| + | Real SolMat[N,1]; | ||
| + | Real XMat[N,1]; | ||
| + | |||
| + | //boundary condition | ||
| + | Integer b1=1; | ||
| + | Integer b2=3; | ||
| + | |||
| + | //truss 1 | ||
| + | parameter Real X1=0; //degree between trusses | ||
| + | Real k1=A*E/1; | ||
| + | Real K1[4,4]; //stiffness matrices | ||
| + | Integer p1a=1; | ||
| + | Integer p1b=2; | ||
| + | Real G1[N,N]; | ||
| + | |||
| + | //truss 2 | ||
| + | parameter Real X2=0; //degree between trusses | ||
| + | Real k2=A*E/1; | ||
| + | Real K2[4,4]; //stiffness matrices | ||
| + | Integer p2a=2; | ||
| + | Integer p2b=3; | ||
| + | Real G2[N,N]; | ||
| + | |||
| + | //truss 3 | ||
| + | parameter Real X3=90; //degree between trusses | ||
| + | Real k3=A*E/1.25; | ||
| + | Real K3[4,4]; //stiffness matrices | ||
| + | Integer p3a=2; | ||
| + | Integer p3b=4; | ||
| + | Real G3[N,N]; | ||
| + | |||
| + | //truss 4 | ||
| + | parameter Real X4=90+38.6598; //degree between trusses | ||
| + | Real k4=A*E/1.6; | ||
| + | Real K4[4,4]; //stiffness matrices | ||
| + | Integer p4a=1; | ||
| + | Integer p4b=4; | ||
| + | Real G4[N,N]; | ||
| + | |||
| + | //truss 5 | ||
| + | parameter Real X5=90-38.6598; //degree between trusses | ||
| + | Real k5=A*E/1.6; | ||
| + | Real K5[4,4]; //stiffness matrices | ||
| + | Integer p5a=3; | ||
| + | Integer p5b=4; | ||
| + | Real G5[N,N]; | ||
| + | |||
| + | /* | ||
| + | for each truss, ensure pXa is lower then pXb (X represents truss element number) | ||
| + | */ | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | //creating global matrice | ||
| + | K1:=Stiffness_Matrices(X1); | ||
| + | G1:=k1*Local_Global(K1,N,p1a,p1b); | ||
| + | |||
| + | K2:=Stiffness_Matrices(X2); | ||
| + | G2:=k2*Local_Global(K2,N,p2a,p2b); | ||
| + | |||
| + | K3:=Stiffness_Matrices(X3); | ||
| + | G3:=k3*Local_Global(K3,N,p3a,p3b); | ||
| + | |||
| + | K4:=Stiffness_Matrices(X4); | ||
| + | G4:=k4*Local_Global(K4,N,p4a,p4b); | ||
| + | |||
| + | K5:=Stiffness_Matrices(X5); | ||
| + | G5:=k5*Local_Global(K5,N,p5a,p5b); | ||
| + | |||
| + | G:=G1+G2+G3+G4+G5; | ||
| + | Ginitial:=G; | ||
| + | |||
| + | //implementing boundary condition | ||
| + | for i in 1:N loop | ||
| + | G[2*b1-1,i]:=0; | ||
| + | G[2*b1,i]:=0; | ||
| + | G[2*b2-1,i]:=0; | ||
| + | G[2*b2,i]:=0; | ||
| + | end for; | ||
| + | |||
| + | G[2*b1-1,2*b1-1]:=1; | ||
| + | G[2*b1,2*b1]:=1; | ||
| + | G[2*b2-1,2*b2-1]:=1; | ||
| + | G[2*b2,2*b2]:=1; | ||
| + | |||
| + | //solving displacement | ||
| + | Sol:=Gauss_Jordan(N,G,X); | ||
| + | |||
| + | //solving reaction force | ||
| + | SolMat:=matrix(Sol); | ||
| + | XMat:=matrix(X); | ||
| + | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| + | |||
| + | end Trusses_Tugas3_d29; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function Stiffness_Matrices''''' | ||
| + | |||
| + | function Stiffness_Matrices | ||
| + | |||
| + | input Real A; | ||
| + | Real Y; | ||
| + | output Real X[4,4]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | final constant Real pi=2*Modelica.Math.asin(1.0); | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Y:=A/180*pi; | ||
| + | |||
| + | X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; | ||
| + | |||
| + | -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2]; | ||
| + | |||
| + | for i in 1:4 loop | ||
| + | for j in 1:4 loop | ||
| + | if abs(X[i,j]) <= float_error then | ||
| + | X[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end Stiffness_Matrices; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function Gauss-Jordan''''' | ||
| + | function Gauss_Jordan | ||
| + | |||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N]; | ||
| + | output Real X[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i]) <= float_error then | ||
| + | X[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Gauss_Jordan; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function Reaction_Trusses''''' | ||
| + | function Reaction_Trusses | ||
| + | |||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N,1]; | ||
| + | input Real C[N,1]; | ||
| + | Real X[N,1]; | ||
| + | output Real Sol[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=A*B-C; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i,1]) <= float_error then | ||
| + | X[i,1] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | Sol[i]:=X[i,1]; | ||
| + | end for; | ||
| + | |||
| + | end Reaction_Trusses; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function Local_Global''''' | ||
| + | function Local_Global | ||
| + | |||
| + | input Real Y[4,4]; | ||
| + | input Integer B; | ||
| + | input Integer p1; | ||
| + | input Integer p2; | ||
| + | output Real G[B,B]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:B loop | ||
| + | for j in 1:B loop | ||
| + | G[i,j]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | G[2*p1,2*p1]:=Y[2,2]; | ||
| + | G[2*p1-1,2*p1-1]:=Y[1,1]; | ||
| + | G[2*p1,2*p1-1]:=Y[2,1]; | ||
| + | G[2*p1-1,2*p1]:=Y[1,2]; | ||
| + | |||
| + | G[2*p2,2*p2]:=Y[4,4]; | ||
| + | G[2*p2-1,2*p2-1]:=Y[3,3]; | ||
| + | G[2*p2,2*p2-1]:=Y[4,3]; | ||
| + | G[2*p2-1,2*p2]:=Y[3,4]; | ||
| + | |||
| + | G[2*p2,2*p1]:=Y[4,2]; | ||
| + | G[2*p2-1,2*p1-1]:=Y[3,1]; | ||
| + | G[2*p2,2*p1-1]:=Y[4,1]; | ||
| + | G[2*p2-1,2*p1]:=Y[3,2]; | ||
| + | |||
| + | G[2*p1,2*p2]:=Y[2,4]; | ||
| + | G[2*p1-1,2*p2-1]:=Y[1,3]; | ||
| + | G[2*p1,2*p2-1]:=Y[2,3]; | ||
| + | G[2*p1-1,2*p2]:=Y[1,4]; | ||
| + | |||
| + | end Local_Global; | ||
| + | |} | ||
| + | |||
| + | === Pertemuan IV (2 Desember 2020) === | ||
| + | Pertemuan keempat bersama Pak Dai, saya dan mahasiswa lain membahas tentang tugas yang diberikan di pekan sebelumnya, yaitu Tugas 3. Setelah membandingkan berbagai cara pengerjaan yang dipaparkan oleh beberapa teman saya, saya merasa masih perlu belajar lebih giat agar mampu memahami dan bisa mengerjakan jenis soal lainnya. | ||
| + | |||
| + | ==== Kuis ''Flowchart'' dan ''Class Diagram'' ==== | ||
| + | Kami diberi kuis untuk membuat ''flowchart'' proses penyelesaian soal Tugas 3. | ||
| + | |||
| + | Berikut adalah ''flowchart'' yang saya buat: | ||
| + | [[File:Kuis4 d29.jpg|700px|center]] | ||
| + | |||
| + | ==== Tugas 4 ==== | ||
| + | Di akhir kelas, kami diberi tugas untuk membuat ''flowchart'', ''class diagram'', dan program sederhana menggunakan aplikasi OpenModelica untuk menyelesaikan soal berikut: | ||
| + | [[File:No8 d29.jpeg|700px|center]] | ||
| + | |||
| + | Berikut adalah ''flowchart'' dan ''class diagram'' yang saya buat: | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[File:T4 class d29.jpg|600px|Displacement]][[File:T4 flow d29.jpg|600px|Displacement]] | ||
| + | </div> | ||
| + | |||
| + | Berikut adalah program yang saya buat: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Class''''' | ||
| + | |||
| + | class Tugas4_d29 | ||
| + | parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5; | ||
| + | 2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5; | ||
| + | 3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5]; | ||
| + | parameter Integer [:,2] node = [1, 2; | ||
| + | 1, 3; | ||
| + | 1, 4]; | ||
| + | parameter Integer y = size(node,1); | ||
| + | parameter Integer x = 3*(size(node_load,1)); | ||
| + | parameter Integer z = size(Boundary,1); | ||
| + | parameter Integer [:] Boundary = {2,3,4}; | ||
| + | parameter Real [:,4] node_load = [1, 0, -5000, 0; | ||
| + | 2, 0, 0, 0; | ||
| + | 3, 0, 0, 0; | ||
| + | 4, 0, 0, 0]; | ||
| + | parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; | ||
| + | Real [y] k; | ||
| + | Real [y,6,6] Ke; | ||
| + | Real [y,x,x] Kg; | ||
| + | Real [x,x] KgTot; | ||
| + | Real [x,x] KgB; | ||
| + | Real [x] U; | ||
| + | Real [x] R; | ||
| + | |||
| + | equation | ||
| + | k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y}; | ||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | ||
| + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | ||
| + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | ||
| + | U = GaussJordan(x, KgB, load); | ||
| + | R = ReactionForce(x, KgTot, U, load); | ||
| + | |||
| + | end Tugas4_d29; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function StiffnessMatrixElement''''' | ||
| + | |||
| + | function StiffnessMatrixElement | ||
| + | |||
| + | input Real [:,9] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | |||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real cos_z; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | |||
| + | algorithm | ||
| + | k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | |||
| + | // Finding stiffness matrix of each element member | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | |||
| + | // Clearing the matrices | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | |||
| + | // Converting degrees to radians | ||
| + | cos_x := inisiasi_mat[i,4]; | ||
| + | cos_y := inisiasi_mat[i,5]; | ||
| + | cos_z := inisiasi_mat[i,6]; | ||
| + | |||
| + | // {cos^2, sin^2, sincos} | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | |||
| + | // Construct stiffness transformation matrix | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | |||
| + | // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end for; | ||
| + | end StiffnessMatrixElement; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function StiffnessMatrixGlobal''''' | ||
| + | |||
| + | function StiffnessMatrixGlobal | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,6,6] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | |||
| + | algorithm | ||
| + | for i in 1:y loop | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | Kg_mat[i,a,b]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:y loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function SumStiffnessMatrixGlobal''''' | ||
| + | |||
| + | function SumStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,x,x] Kg_mat; | ||
| + | output Real [x,x] KgTot_mat; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end SumStiffnessMatrixGlobal; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function BoundaryStiffnessMatrixGlobal''''' | ||
| + | |||
| + | function BoundaryStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer z; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Integer[z] Boundary_met; | ||
| + | output Real [x,x] KgB_met; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:x loop | ||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_met[a])-b,i]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end BoundaryStiffnessMatrixGlobal; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function GaussJordan''''' | ||
| + | |||
| + | function GaussJordan | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgB_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] U_met; | ||
| + | |||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | |||
| + | for i in 1:x loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end GaussJordan; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function ReactionForce''''' | ||
| + | |||
| + | function ReactionForce | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Real [x] U_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] R_met; | ||
| + | |||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | end ReactionForce; | ||
| + | |} | ||
| + | |||
| + | Berikut adalah hasil jawaban dari soal, yaitu: | ||
| + | * U = displacement | ||
| + | * R = gaya reaksi | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[File:T4 U d29.png|300px|Displacement]][[File:T4 R d29.png|300px|Displacement]] | ||
| + | </div> | ||
| + | |||
| + | Berikut adalah video yang saya buat mengenai penjelasan setiap ''function'': | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <youtube width="200" height="100">https://youtu.be/PkWkfmgdOHs</youtube> | ||
| + | </div> | ||
| + | |||
| + | === Pertemuan V (16 Desember 2020) === | ||
| + | Pertemuan kelima bersama Pak Dai, saya dan mahasiswa lain membahas tentang pentingnya mencari wawasan dari berbagai sumber. Ilmu atau wawasan bisa didapatkan tidak hanya dari buku, tetapi juga dari alam sekitar kami. Maka dari itu, kami sebaiknya peka terhadap lingkungan sekitar kami agar mampu menambah pengetahuan dari alam sekitar. Setelah kami sudah mendapatkan ilmu, kami harus menerapkan dan mengajarkan ilmu yang kami miliki dalam kehidupan sehari-hari. | ||
| + | |||
| + | ==== Aplikasi Metode Numerik dalam Kasus Optimisasi ==== | ||
| + | Setelah mendapatkan ilmu dari Pak Dai, pembelajaran berlanjut membahas optimasi. Kali ini, kelas Metode Numerik-02 diajar oleh Bu Chandra. Beliau mengajarkan optimasi menggunakan OpenModelica dengan memberikan sebuah video sebagai pengantar sebelum kegiatan pembelajaran di kelas. Dari video tersebut, kami diminta mencoba membuat program sederhana untuk melakukan optimasi. Berikut adalah program yang diajarkan: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Model Bracket''''' | ||
| + | model bracket | ||
| + | parameter Integer n=8; | ||
| + | Real x1[n]; | ||
| + | Real x2[n]; | ||
| + | Real xup; | ||
| + | Real xlow; | ||
| + | Real d; | ||
| + | Real f1[n]; | ||
| + | Real f2[n]; | ||
| + | Real xopt; | ||
| + | Real yopt; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | xup :=4; | ||
| + | xlow:=0; | ||
| + | |||
| + | for i in (1:n) loop | ||
| + | d:= (5^(1/2)-1)/2*(xup-xlow); | ||
| + | x1[i]:= xlow+d; | ||
| + | x2[i]:= xup-d; | ||
| + | f1[i]:= obj(x1[i]); | ||
| + | f2[i]:= obj(x2[i]); | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xup:= xup; | ||
| + | xlow:= x2[i]; | ||
| + | xopt:= xup; | ||
| + | yopt:= f1[i]; | ||
| + | |||
| + | else | ||
| + | xlow:= xlow; | ||
| + | xup:= x1[i]; | ||
| + | xopt:= xup; | ||
| + | |||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end bracket; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Function obj''''' | ||
| + | function obj | ||
| + | import Modelica.Math; | ||
| + | input Real x; | ||
| + | output Real y; | ||
| + | |||
| + | algorithm | ||
| + | y:= 2*Math.sin(x)-x^2/10; | ||
| + | |||
| + | end obj; | ||
| + | |} | ||
| + | |||
| + | === Tugas Besar === | ||
| + | |||
| + | ==== Masalah ==== | ||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[File:Tugas besar d29.jpeg|600px|Displacement]][[File:Tugas besar 2 d29.jpeg|600px|Displacement]] | ||
| + | </div> | ||
| + | |||
| + | Kami diberi tugas besar berupa aplikasi metode numerik dalam optimasi desain statika struktur rangka sederhana (''space truss''/3D). | ||
| + | |||
| + | Kami diminta untuk mendesain suatu rangka dengan biaya serendah mungkin tetapi dengan kualitas yang maksimal. Terdapat beberapa variabel yang perlu diperhatikan, yaitu: | ||
| + | |||
| + | # Harga material | ||
| + | # Jenis material | ||
| + | # Luas penampang | ||
| + | # Penampang yang digunakan | ||
| + | |||
| + | Langkah selanjutnya adalah melakukan optimasi dan membentuk kurva efisiensi harga dengan ''curve fitting'' menggunakan metode numerik. | ||
| + | |||
| + | ==== Solusi ==== | ||
| + | Langkah pertama yang saya lakukan untuk menyelesaikan kasus ini adalah menentukan perbedaan pengaruh luas penampang dan jenis material. Untuk mengetahui pengaruh luas penampang, saya menggunakan lima (5) variasi luas penampang dengan material yang sama. Sedangkan untuk mengetahui pengaruh jenis material, saya menggunakan empat (4) variasi jenis material dengan luas penampang yang sama. Berikut adalah data yang saya gunakan: | ||
| + | |||
| + | [[File:SS304 1 d29.png]] | ||
| + | [[File:Material d29.png]] | ||
| + | |||
| + | Setelah diketahui data yang diperlukan, langkah kedua adalah menghitung pengaruh masing-masing variabel menggunakan OpenModelica untuk mencari ''safety factor'' dari setiap variasi. Berikut adalah program yang saya gunakan: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''Model tubes_safety_d29''''' | ||
| + | |||
| + | model tubes_safety_d29 | ||
| + | |||
| + | //mendefinisikan variabel | ||
| + | parameter Integer Points=size(P,1); //jumlah titik | ||
| + | parameter Integer Trusses=size(C,1); //jumlah trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000144; //Area L Profile (Dimension=0.02, Thickness=0,004)(m) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //mendefinisikan hubungan | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11; //2nd floor | ||
| + | 11,12; //2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14; //3rd floor | ||
| + | 14,15; //3rd floor | ||
| + | 15,16; //3rd floor | ||
| + | 13,16]; //3rd floor | ||
| + | |||
| + | //mendefinisikan koordinat (berurut) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //mendefinisikangaya eksternal (berurut) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end tubes_safety_d29; | ||
| + | |} | ||
| + | |||
| + | Berikut adalah hasil perhitungan dari OpenModelica: | ||
| + | |||
| + | [[File:Areahasil.png]] | ||
| + | [[File:Materialhasil.png]] | ||
| + | |||
| + | Langkah ketiga adalah mencari variasi yang paling optimal dengan optimasi Golden Ratio dan fungsi ''curve fitting''. Berikut adalah program yang saya gunakan: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''class GoldenRatio''''' | ||
| + | |||
| + | class GoldenRatio | ||
| + | |||
| + | //memasukan data pada xd,yd,xlo,xhi | ||
| + | parameter Real xd[:]={0.000144,0.000224,0.000275,0.000375}; | ||
| + | parameter Real yd[size(xd,1)]={845155,1269736,1554978,2147211}; | ||
| + | parameter Real xlo=0.000144; | ||
| + | parameter Real xhi=0.000375; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := CurveFitting(xd,yd); | ||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end GoldenRatio; | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | '''''function CurveFitting''''' | ||
| + | |||
| + | function CurveFitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end CurveFitting; | ||
| + | |} | ||
| + | |||
| + | * Berikut adalah hasil perhitungan untuk variasi area: | ||
| + | :[[File:Opt area d29.png]] | ||
| + | :Hasil <code>xopt</code> yang merupakan luas optimum menunjukkan nilai yang mendekati luas tertinggi. | ||
| + | :Kesimpulan yang bisa diambil adalah luas optimum yang bisa digunakan adalah luas tertinggi, yaitu 0,000375 m<sup>2</sup>. | ||
| + | |||
| + | * Berikut adalah hasil perhitungan untuk variasi material: | ||
| + | :[[File:Opt material d29.png]] | ||
| + | :Hasil <code>xopt</code> yang merupakan nilai elastisitas optimum menunjukkan nilai yang mendekati nilai elastisitas terendah. | ||
| + | :Kesimpulan yang bisa diambil adalah material optimum yang bisa digunakan adalah SS304 atau SS316. | ||
| + | |||
| + | === UAS (13 Januari 2021) === | ||
| + | |||
| + | Berikut adalah jawaban UAS milik saya yang ditulis di kertas: | ||
| + | |||
| + | [[File:Uas1 d29.jpg|840px]] | ||
| + | |||
| + | [[File:Uas2 d29.jpg|840px]] | ||
| + | |||
| + | [[File:Uas3 d29.jpg|840px]] | ||
| + | |||
| + | [[File:Uas4 d29.jpg|840px]] | ||
| + | |||
| + | [[File:Uas56 d29.jpg|840px]] | ||
| + | |||
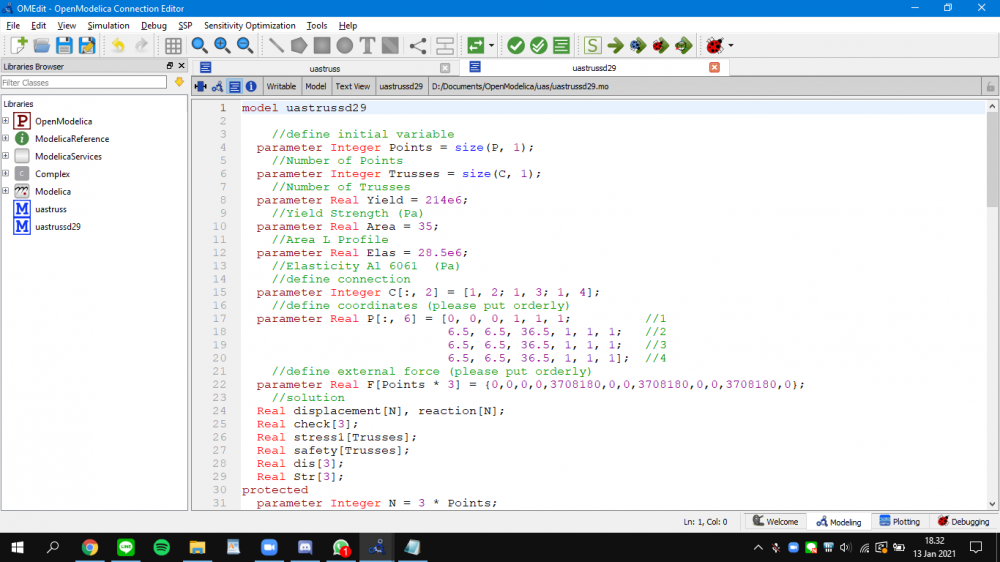
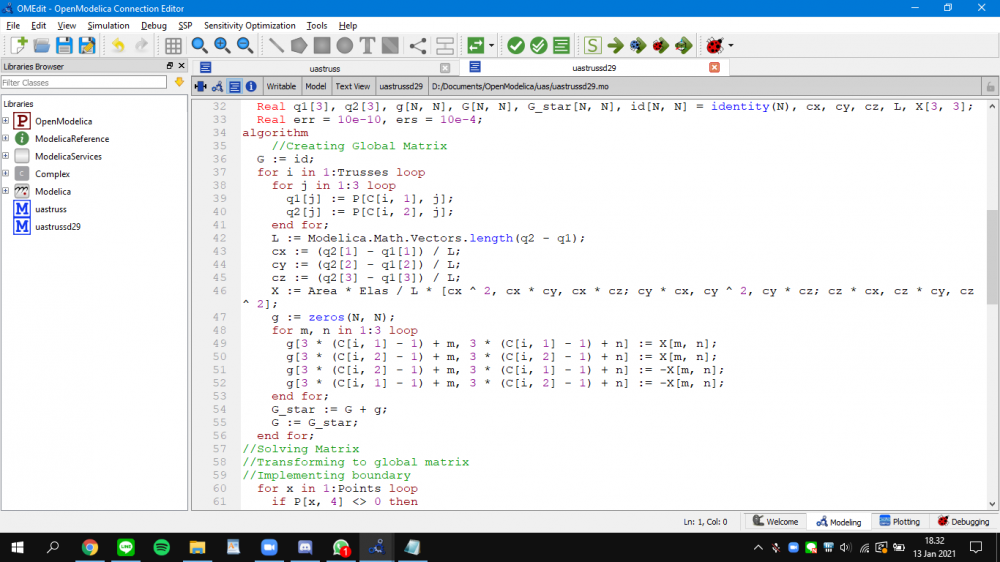
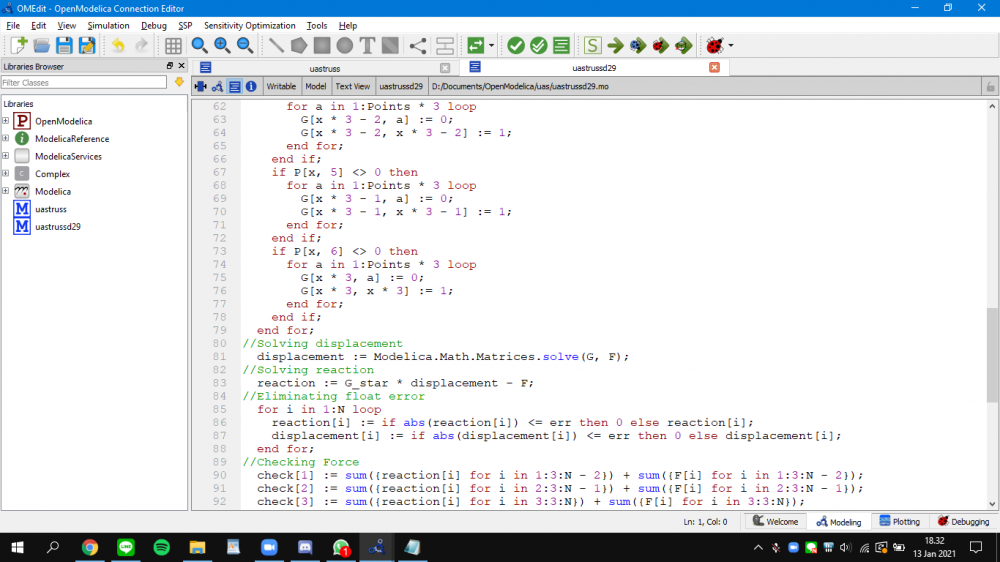
| + | Berikut adalah program untuk soal nomor 7: | ||
| + | |||
| + | [[File:Code1 d29.png|1000px]] | ||
| + | |||
| + | [[File:Code2 d29.png|1000px]] | ||
| + | |||
| + | [[File:Code3 d29.png|1000px]] | ||
| + | |||
| + | [[File:Code4 d29.png|1000px]] | ||
Latest revision as of 18:02, 14 January 2021
Biodata
Nama : Diagy Alwan Irsyad
NPM : 1906301154
Angkatan : 2019
Program Studi : Teknik Mesin, S1 Reguler
Tempat, tanggal lahir : Cepu, 29 April 2001
Jenis kelamin : Laki-laki
Alamat surel : diagya.irsyad29@gmail.com / diagy.alwan@ui.ac.id
Metode Numerik-02
Pada semester gasal 2020/2021, saya mengambil mata kuliah Metode Numerik, tepatnya di kelas Metode Numerik-02.
Contents
Pertemuan I (11 November 2020)
Pertemuan pertama bersama Pak Dai, saya dan mahasiswa lain diajak berpikir untuk bisa mengetahui hal-hal yang sudah kami ketahui dan yang belum. Dengan mengetahui hal yang belum diketahui, kami bisa mempelajari hal-hal tersebut. Selain itu, kami juga membahas tentang pengenalan aplikasi OpenModelica.
Tugas 1
Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara penggunaan OpenModelica.
Berikut adalah video yang saya buat:
Pertemuan II (18 November 2020)
Pertemuan kedua bersama Pak Dai, saya dan mahasiswa lain diminta untuk bisa menjadi orang yang beruntung. Yang dimaksud orang yang beruntung adalah orang yang mampu menjadi pribadi yang lebih baik dibandingkan kemarin. Pak Dai mengingatkan agar kami jangan menjadi orang yang merugi, yaitu orang yang tidak memiliki perkembangan antara hari ini dengan kemarin.
Setelah mendapatkan pelajaran hidup yang berharga, kami diminta untuk mempresentasikan tugas kami yang telah dibuat sebelumnya. Tujuan dari presentasi ini adalah untuk menilai kemampuan mahasiswa dalam pemahaman penggunaan aplikasi OpenModelica.
Materi yang diberikan pada pertemuan ini adalah penggunaan class untuk memanggil sebuah function. Function yang bisa dipanggil beragam jumlahnya, mulai dari penjumlahan sederhana sampai operasi eliminasi matriks.
Tugas 2
Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara menyelesaikan persamaan aljabar simultan dengan OpenModelica. Metode yang digunakan menggunakan class untuk memanggil sebuah function, seperti yang sudah diajarkan sebelumnya.
Berikut adalah video yang saya buat:
Pertemuan III (25 November 2020)
Pertemuan ketiga bersama Pak Dai, saya dan mahasiswa lain membahas penggunaan metode numerik pada bidang teknik. Metode numerik bisa digunakan untuk menyelesaikan simulasi CFD dan menghitung gaya reaksi pada suatu rangkaian truss.
Langkah yang diperlukan untuk menyelesaikan masalah di bidang teknik dengan metode numerik adalah:
- Melakukan analisis terhadap masalah
- Membuat model matematis penyelesaian masalah
- Menggunakan metode numerik yang sesuai untuk menyelesaikan masalah
Setelah langkah-langkah tersebut dilakukan, maka solusi dari masalah bisa ditemukan. Untuk pembelajaran di kelas, kami mempelajari rangkaian truss untuk sarana belajar metode numerik.
Tugas 3
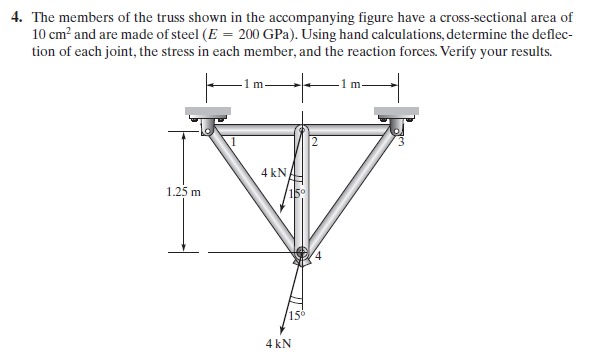
Di akhir kelas, kami diberi tugas untuk membuat program sederhana menggunakan aplikasi OpenModelica menggunakan fungsi penyelesaian aljabar untuk menyelesaikan soal berikut:
Berikut adalah program yang saya buat:
|
Class class Trusses_Tugas3_d29
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //m^2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global displacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between trusses
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrices
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between trusses
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrices
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between trusses
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrices
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between trusses
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrices
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between trusses
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrices
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_Tugas3_d29;
|
|
Function Stiffness_Matrices function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
|
Function Gauss-Jordan function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;
|
|
Function Reaction_Trusses function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
|
Function Local_Global function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
Pertemuan IV (2 Desember 2020)
Pertemuan keempat bersama Pak Dai, saya dan mahasiswa lain membahas tentang tugas yang diberikan di pekan sebelumnya, yaitu Tugas 3. Setelah membandingkan berbagai cara pengerjaan yang dipaparkan oleh beberapa teman saya, saya merasa masih perlu belajar lebih giat agar mampu memahami dan bisa mengerjakan jenis soal lainnya.
Kuis Flowchart dan Class Diagram
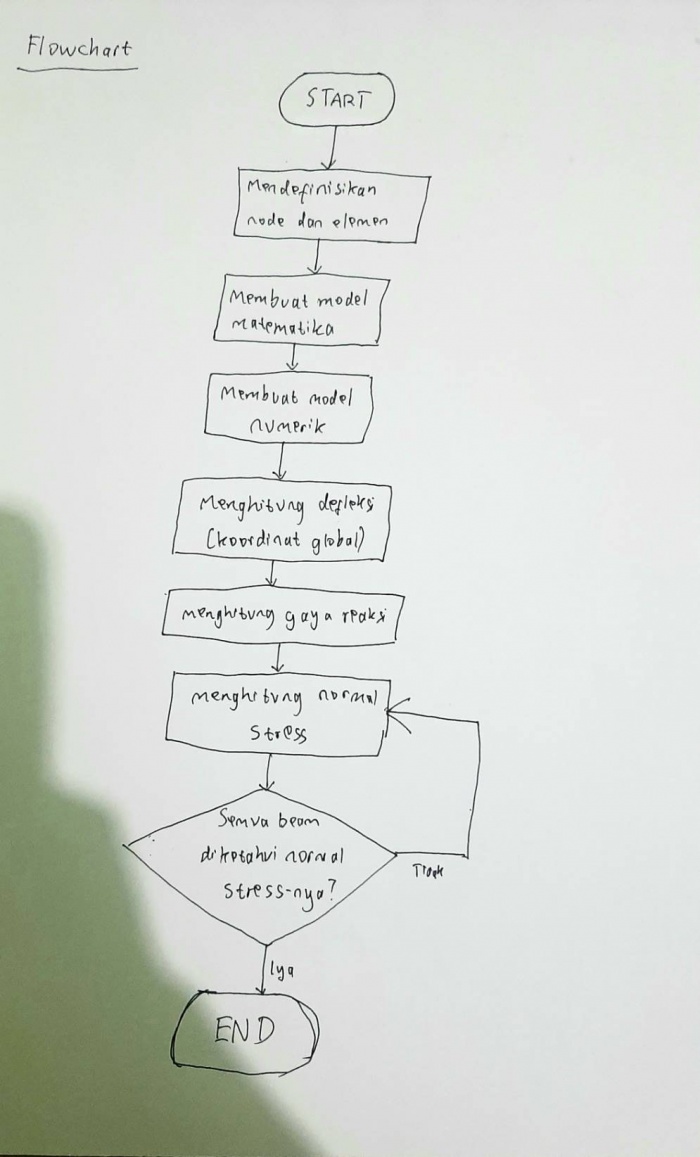
Kami diberi kuis untuk membuat flowchart proses penyelesaian soal Tugas 3.
Berikut adalah flowchart yang saya buat:
Tugas 4
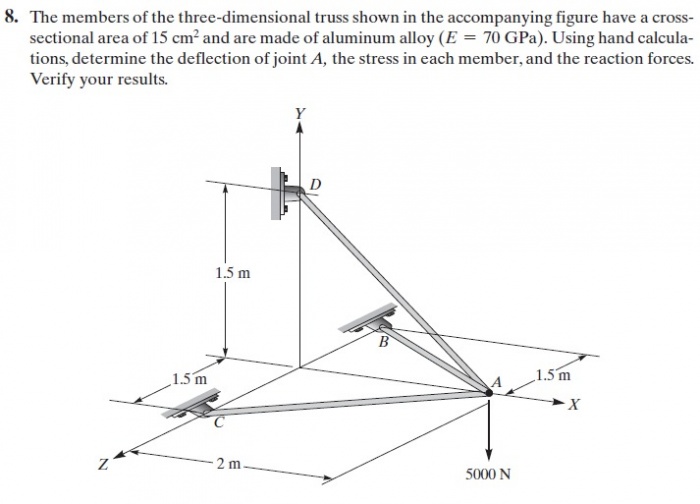
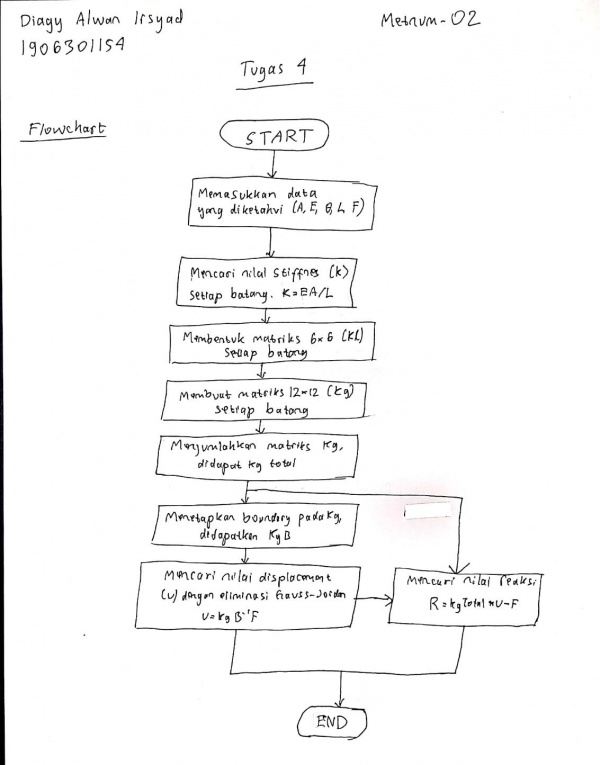
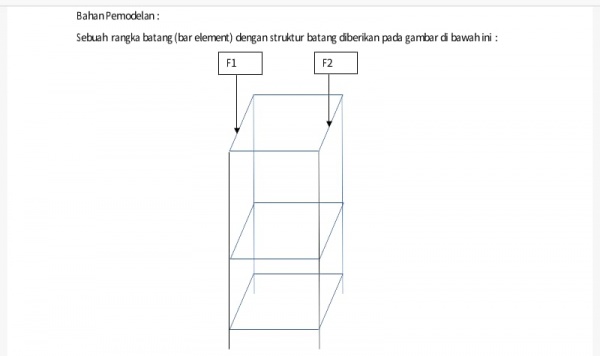
Di akhir kelas, kami diberi tugas untuk membuat flowchart, class diagram, dan program sederhana menggunakan aplikasi OpenModelica untuk menyelesaikan soal berikut:
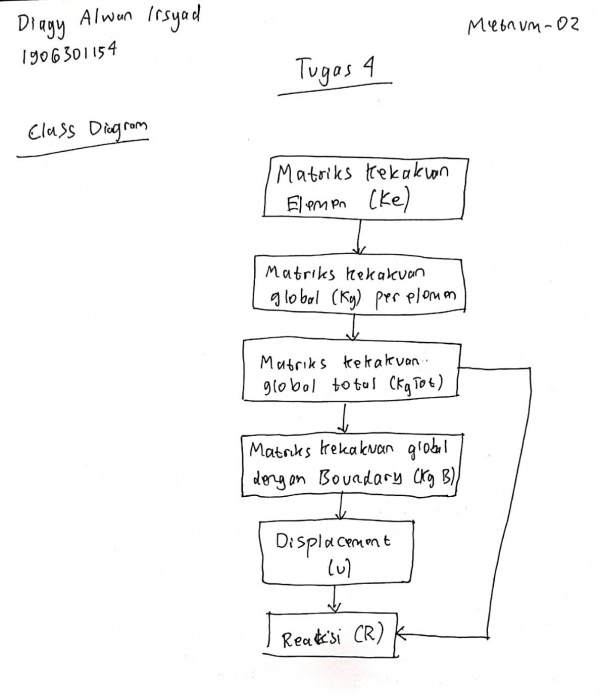
Berikut adalah flowchart dan class diagram yang saya buat:
Berikut adalah program yang saya buat:
|
Class class Tugas4_d29
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end Tugas4_d29;
|
|
Function StiffnessMatrixElement function StiffnessMatrixElement
input Real [:,9] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,4];
cos_y := inisiasi_mat[i,5];
cos_z := inisiasi_mat[i,6];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
|
|
Function StiffnessMatrixGlobal function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;
|
|
Function SumStiffnessMatrixGlobal function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
|
|
Function BoundaryStiffnessMatrixGlobal function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
|
|
Function GaussJordan function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
|
|
Function ReactionForce function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce; |
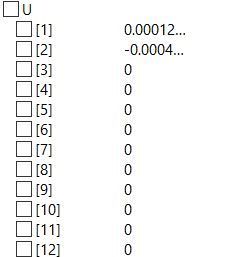
Berikut adalah hasil jawaban dari soal, yaitu:
- U = displacement
- R = gaya reaksi
Berikut adalah video yang saya buat mengenai penjelasan setiap function:
Pertemuan V (16 Desember 2020)
Pertemuan kelima bersama Pak Dai, saya dan mahasiswa lain membahas tentang pentingnya mencari wawasan dari berbagai sumber. Ilmu atau wawasan bisa didapatkan tidak hanya dari buku, tetapi juga dari alam sekitar kami. Maka dari itu, kami sebaiknya peka terhadap lingkungan sekitar kami agar mampu menambah pengetahuan dari alam sekitar. Setelah kami sudah mendapatkan ilmu, kami harus menerapkan dan mengajarkan ilmu yang kami miliki dalam kehidupan sehari-hari.
Aplikasi Metode Numerik dalam Kasus Optimisasi
Setelah mendapatkan ilmu dari Pak Dai, pembelajaran berlanjut membahas optimasi. Kali ini, kelas Metode Numerik-02 diajar oleh Bu Chandra. Beliau mengajarkan optimasi menggunakan OpenModelica dengan memberikan sebuah video sebagai pengantar sebelum kegiatan pembelajaran di kelas. Dari video tersebut, kami diminta mencoba membuat program sederhana untuk melakukan optimasi. Berikut adalah program yang diajarkan:
|
Model Bracket model bracket parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= obj(x1[i]); f2[i]:= obj(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket; |
|
Function obj function obj import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end obj; |
Tugas Besar
Masalah
Kami diberi tugas besar berupa aplikasi metode numerik dalam optimasi desain statika struktur rangka sederhana (space truss/3D).
Kami diminta untuk mendesain suatu rangka dengan biaya serendah mungkin tetapi dengan kualitas yang maksimal. Terdapat beberapa variabel yang perlu diperhatikan, yaitu:
- Harga material
- Jenis material
- Luas penampang
- Penampang yang digunakan
Langkah selanjutnya adalah melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan metode numerik.
Solusi
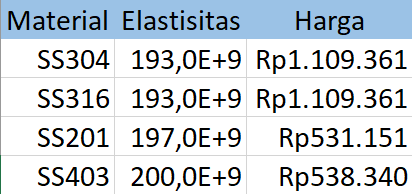
Langkah pertama yang saya lakukan untuk menyelesaikan kasus ini adalah menentukan perbedaan pengaruh luas penampang dan jenis material. Untuk mengetahui pengaruh luas penampang, saya menggunakan lima (5) variasi luas penampang dengan material yang sama. Sedangkan untuk mengetahui pengaruh jenis material, saya menggunakan empat (4) variasi jenis material dengan luas penampang yang sama. Berikut adalah data yang saya gunakan:
Setelah diketahui data yang diperlukan, langkah kedua adalah menghitung pengaruh masing-masing variabel menggunakan OpenModelica untuk mencari safety factor dari setiap variasi. Berikut adalah program yang saya gunakan:
|
Model tubes_safety_d29 model tubes_safety_d29
//mendefinisikan variabel
parameter Integer Points=size(P,1); //jumlah titik
parameter Integer Trusses=size(C,1); //jumlah trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000144; //Area L Profile (Dimension=0.02, Thickness=0,004)(m)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//mendefinisikan hubungan
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11; //2nd floor
11,12; //2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14; //3rd floor
14,15; //3rd floor
15,16; //3rd floor
13,16]; //3rd floor
//mendefinisikan koordinat (berurut)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//mendefinisikangaya eksternal (berurut)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end tubes_safety_d29;
|
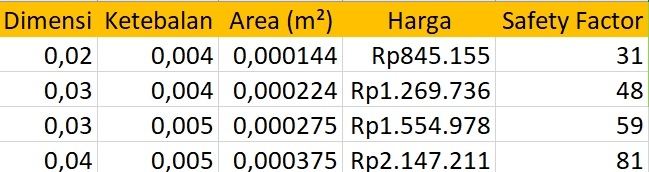
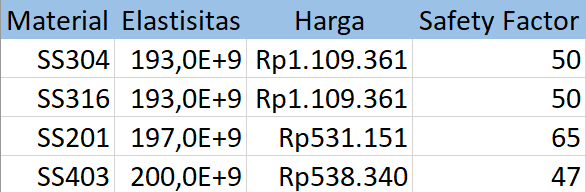
Berikut adalah hasil perhitungan dari OpenModelica:
Langkah ketiga adalah mencari variasi yang paling optimal dengan optimasi Golden Ratio dan fungsi curve fitting. Berikut adalah program yang saya gunakan:
|
class GoldenRatio class GoldenRatio
//memasukan data pada xd,yd,xlo,xhi
parameter Real xd[:]={0.000144,0.000224,0.000275,0.000375};
parameter Real yd[size(xd,1)]={845155,1269736,1554978,2147211};
parameter Real xlo=0.000144;
parameter Real xhi=0.000375;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := CurveFitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end GoldenRatio;
|
|
function CurveFitting function CurveFitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end CurveFitting; |
- Berikut adalah hasil perhitungan untuk variasi area:

- Hasil
xoptyang merupakan luas optimum menunjukkan nilai yang mendekati luas tertinggi. - Kesimpulan yang bisa diambil adalah luas optimum yang bisa digunakan adalah luas tertinggi, yaitu 0,000375 m2.
- Berikut adalah hasil perhitungan untuk variasi material:

- Hasil
xoptyang merupakan nilai elastisitas optimum menunjukkan nilai yang mendekati nilai elastisitas terendah. - Kesimpulan yang bisa diambil adalah material optimum yang bisa digunakan adalah SS304 atau SS316.
UAS (13 Januari 2021)
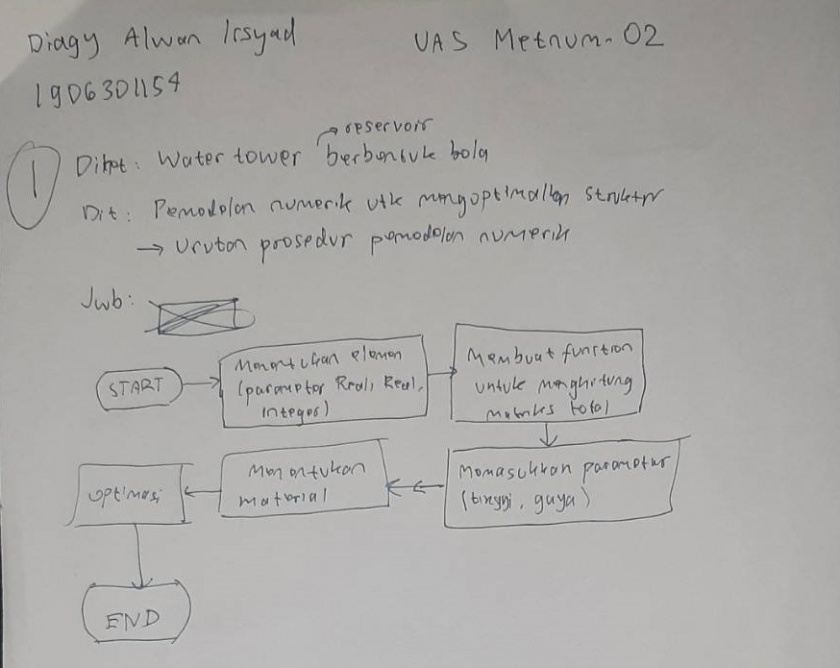
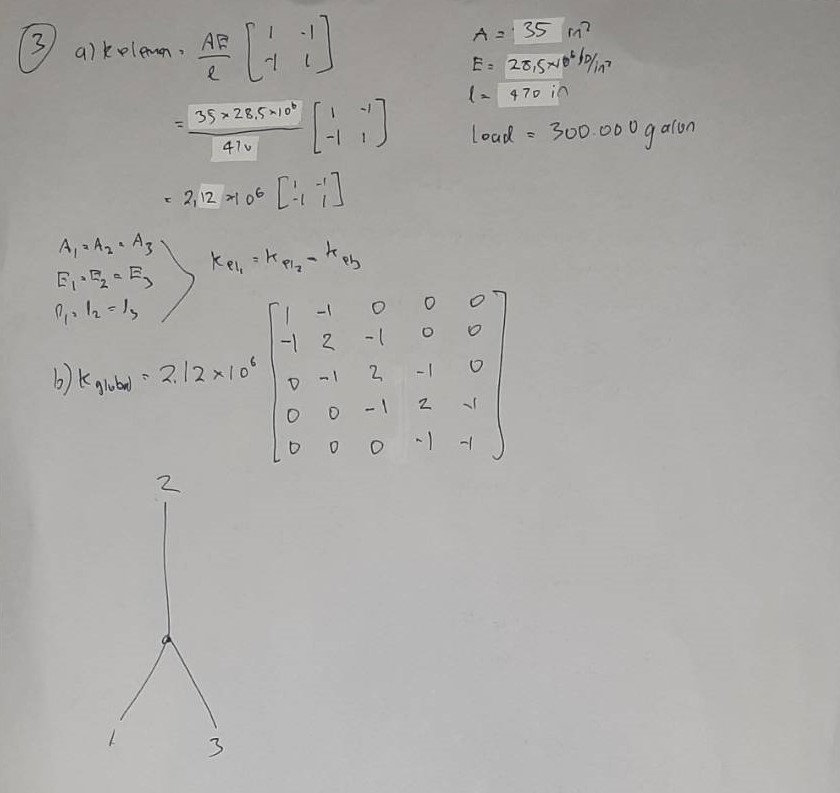
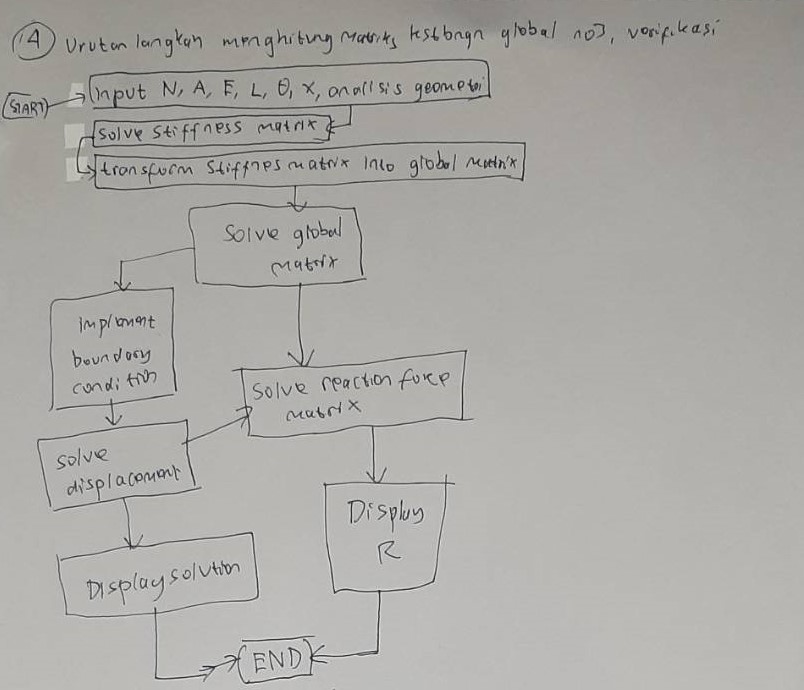
Berikut adalah jawaban UAS milik saya yang ditulis di kertas:
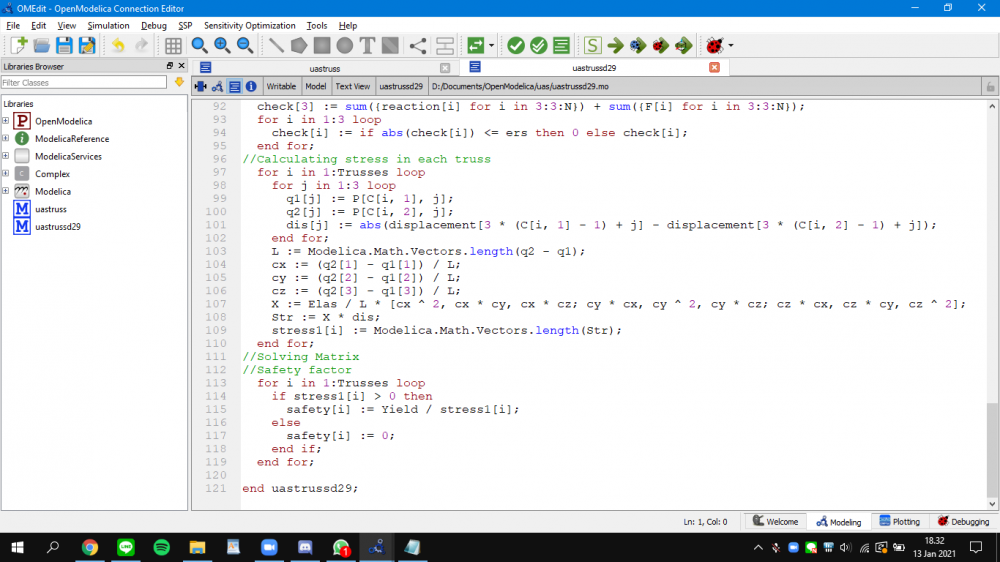
Berikut adalah program untuk soal nomor 7: