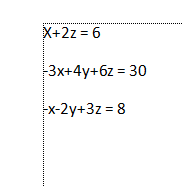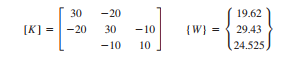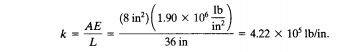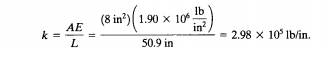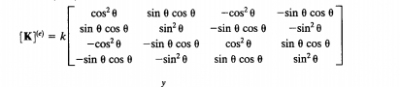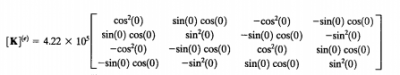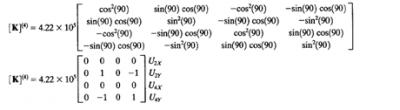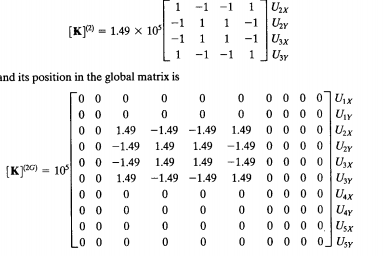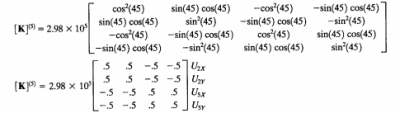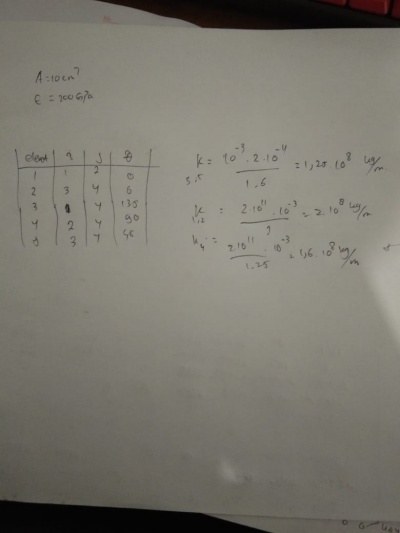Difference between revisions of "Metnum03-Trio Kurnia Ryplida"
(→Pertemuan Tanggal 16 November 2020) |
(→UAS) |
||
| (104 intermediate revisions by the same user not shown) | |||
| Line 40: | Line 40: | ||
Hari ini pak Dai memberikan petunjuk bagaimana cara membuat sebuah program sederhana | Hari ini pak Dai memberikan petunjuk bagaimana cara membuat sebuah program sederhana | ||
| − | + | contoh membuat hasil rata-rata senbagai berikut : | |
| − | 2. membuat hasil | + | |
| + | [[File:Latihan Ratarata.PNG|400px|thumb|center|rata-rata]] | ||
| + | [[File:Hasil rata.PNG|400px|thumb|center|Hasil rata-rata]] | ||
| + | |||
| + | |||
| + | Pr menyelesaikan masalah 3 aljabar sebagai berikut : | ||
| + | |||
| + | [[File:matrikstrio.png|200px]] | ||
| + | |||
| + | |||
| + | persamaan ini akan diselesaikan dengan menggunakan open modelica dengan metode Gauss Elimination. Maka persamaan ini akan diubah dalam bentuk matriks. | ||
| + | |||
| + | berikut bentuk penyelesaian dengan menggunakan open modelica : | ||
| + | |||
| + | [[File:fungsimatriks.png|500px|center]] | ||
| + | |||
| + | [[File:hasilmatriks1.png|500px|center]] | ||
| + | |||
| + | dapat dilihat bahwa hasil plotting tersebut menunjukkan penyelesaian dari permasalaha sistem persamaan yang telah ditunjukkan sebelumnya, yaitu x1=58, x2=-8, x3=-24. | ||
| + | |||
| + | |||
| + | == Pertemuan Tanggal 23 November 2020 == | ||
| + | |||
| + | Pada hari ini pak Dai memberikan sebuah latihan pada buku Metode Numerik edisi 7 karangan Steven C.Chapra dan Raymond P.Canel pada halamam 328 latihan 12.11 | ||
| + | |||
| + | dengan soal: [[File:soal_massspring1.png|300px]] | ||
| + | |||
| + | lalu pak Dai memberi kesempatan untuk menyelesaikan perssoalan dengan menggunakan Open Modelica | ||
| + | |||
| + | pada function coding | ||
| + | |||
| + | [[File:fungsi-massspring1.png|500px|center|thumb|function coding]] | ||
| + | |||
| + | lalu pada class coding | ||
| + | |||
| + | [[File:class-massspring1.png|500px|center|thumb|class coding]] | ||
| + | |||
| + | hasil simulasi | ||
| + | |||
| + | [[File:hasil-massspring1.png|500px|center|thumb|hasil simulasi]] | ||
| + | |||
| + | == PR3 menyelesaikan permasalahan pada example 2.1 == | ||
| + | |||
| + | |||
| + | [[File:example2.1Trio.png|400px|center|thumb|Example 2.1]] | ||
| + | |||
| + | Dari PR yang diberikan saya akan mencoba menggunakan aljabar simultan untuk mencari nilai displacement dan gaya reaksi disetiap join. Hal yang pertama dilakukan adalah menentukan node, sudut terhadap sumbu X positif dan element pada setiap batang. | ||
| + | |||
| + | [[File:node2.1Trio.png|400px|center|thumb|Node dan Element]] | ||
| + | |||
| + | Lalu menentukan nilai konstanta kekakuan dengan permusan k=AE/L.Dari soal sudah diketahui modulus elastisitas setiap batang E = luas penampang setiap batang sebesar 8inch persegi dan panjang batang 1, 3, 4 dan 6 adalah 3 feet atau sebesar 36 inch dan sudut antara batang 4 dengan batang 2 dan 5 adalah 45 derajat. Oleh karena itu kita dapat menghitung panjang batang 2 dan 5 dengan 36/cos45 = 50.9 inch. | ||
| + | |||
| + | k untuk batang 1, 3, 4 dan 6 adalah | ||
| + | |||
| + | [[File:k1,3,6,4.png|400px|center|thumb|Nilai k pada batang 1,3,4, dan 6]] | ||
| + | |||
| + | Pada batang 2 dan 5 | ||
| + | |||
| + | [[File:k2,5.png|400px|center|thumb|Nilai k pada batang 2 dan 5]] | ||
| + | |||
| + | Lalu memasukkan persamaan matriks untuk K pada setiap element.Dengan perumusan sebagai berikut | ||
| + | |||
| + | |||
| + | [[File:persamaanKmatrix.png|400px|center|thumb|Matiks K]] | ||
| + | |||
| + | '''Analisa Batang 1,3,dan 6''' | ||
| + | |||
| + | Untuk menyelesaikan masalah pada batang 1,3,dan 6 maka menggunakan nilai k = 4,22x10^5 dan sudut 0. | ||
| + | |||
| + | Maka matriks k pada persamaan ini adalah | ||
| + | |||
| + | [[File:Kmatriks1,3,6.png|400px|center|thumb|K matriks 1,3,dan 6]] | ||
| + | |||
| + | Lalu untuk penyelesaiaannya | ||
| + | |||
| + | [[File:analysaBatang1,3,6.png|center|400px|thumb|Analysa batang 1,3,dan 6]] | ||
| + | |||
| + | Lalu ketiga matriks diatas diinput kedalam matriks global sesuai dengan posisi U. | ||
| + | |||
| + | [[File:matriksGlobal1,3,6.png|400px|center|thumb|Matriks Global 1,3,dan 6]] | ||
| + | |||
| + | '''Analisa Batang 4''' | ||
| + | |||
| + | Pada batang 4 nilai k = 4,22 x 10^5 dengan sudut 90 derajat terhadap sumbu X.Berikut bentuk matrik k | ||
| + | |||
| + | [[File:element4.png|400px|center|thumb|Matrik k pada batang 4]] | ||
| + | |||
| + | Lalu menginput kedalam matrik global sesuai dengan posisi U | ||
| + | |||
| + | [[File:KglobalE4.png|400px|center|thumb|Matriks Global 4]] | ||
| + | |||
| + | '''Analisa Batang 2''' | ||
| + | |||
| + | Pada batang 2 nilai k yang digunakan adalah 2,98 x 10^5 dengan sudut 135 derajat terhadap sumbu X. Dengan bentuk matriks K sebagai berikut | ||
| + | |||
| + | [[File:Kmatrik2.png|400px|center|thumb|Matrik K 2]] | ||
| + | |||
| + | Lalu diinput dalam matriks global sesauai dengan posisi U | ||
| + | |||
| + | [[File:matriks global 2.png|400px|center|thumb|Matrik Global 2]] | ||
| + | |||
| + | '''Analisa Batang 5''' | ||
| + | |||
| + | Pada batang 5 nilai k yang digunakan 2,98 x 10^5 dengan sudut 45 derajat terhadap sumbu X. Berikut bentuk matriks k | ||
| + | |||
| + | [[File:matriksK5.png|400px|center|thumb|Matrik K batang 5]] | ||
| + | |||
| + | Lalu diinput kedalam matriks global sesuai dengan posisi U. | ||
| + | |||
| + | [[File:MatriksGlobal5.png|400px|center|thumb|Matriks Global Batang 5]] | ||
| + | |||
| + | Lalu melakukan poenjumlahan pada semua matriks global untuk menjadi Kglobal | ||
| + | |||
| + | [[File:PenjumlahanSeluruhK.png|400px|center|thumb|Penentuan Nilai Kglobal]] | ||
| + | |||
| + | Tentukan kondisi batas dan kondisi pembebanan pada struktur. Dari struktur kita dapat mengetahui bahwa U1x, U1y, U3x, U3y = 0 dan beban sebesar 500 kearah bawah pada titik tumpuan 4 dan 5 ke arah sumbu Y. Karena nilai U1x, U1y, U3x, U3y = 0 maka kita bisa mengeliminasi baris dan kolom 1, 2, 6 dan 7, sehingga nantinya akan didapatkan matrix berukuran 6 x 6. | ||
| + | |||
| + | [[File:matriks6x6.png|400px|center|thumb]] | ||
| + | |||
| + | Setekah itu menghitung nilai U dengan menggunakan Open Modelica. | ||
| + | |||
| + | [[File:Koding mencari U.png|600px|center|thumb|Coding untuk mencari nilai U]] | ||
| + | |||
| + | Hasil dari nilai U yang telah disimulasikan | ||
| + | |||
| + | [[File:nilai U.png|400px|center|thumb]] | ||
| + | |||
| + | Hasil dari simulasi OpenModelica adalah | ||
| + | |||
| + | U2x = -0.0035545 inch | ||
| + | |||
| + | U2y = -0.0102659 inch | ||
| + | |||
| + | U4x = 0.00118483 inch | ||
| + | |||
| + | U4y = -0.0114507 inch | ||
| + | |||
| + | U5x = 0.00236967 inch | ||
| + | |||
| + | U5y = -0.0195458 inch | ||
| + | |||
| + | karana niali U1x, U1y, U3x,dan U3y = 0 maka | ||
| + | |||
| + | [[File:nilai U final.png|400px|center|thumb|Nilai U]] | ||
| + | |||
| + | Setelah nilai U didapan maka kita bisa mencari nilai Rection Force dengan perumusan R=Kglobal x U - F dalam bentuk matriks. | ||
| + | |||
| + | [[File:RumusR.png|400px|center|thumb|Mencari R]] | ||
| + | |||
| + | setelah itu menggunakan Open Modelica untuk Mencari Nilai R | ||
| + | |||
| + | [[File:kodingR.png|600px|center|thumb|Coding untuk mencari nilai R]] | ||
| + | |||
| + | Hasil dari simulasi | ||
| + | |||
| + | [[File:HasilR.png|400px|center|thumb|Nilai R]] | ||
| + | |||
| + | Nilai R pada Buku | ||
| + | |||
| + | [[File:Nilai R.png|400px|center|thumb|]] | ||
| + | |||
| + | == Pertemuan Tanggal 30 November 2020 == | ||
| + | |||
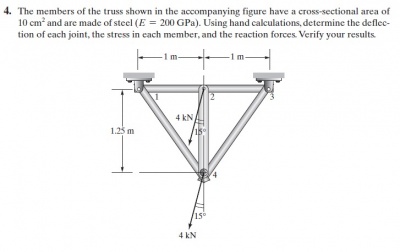
| + | Pada hari ini pak Dai memberikan quis dengan sola sebagai berikut : | ||
| + | |||
| + | [[File:quisno4.jpeg|400px|center]] | ||
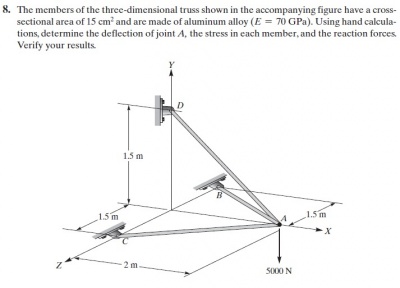
| + | |||
| + | [[File:quisno8.jpeg|400px|center]] | ||
| + | |||
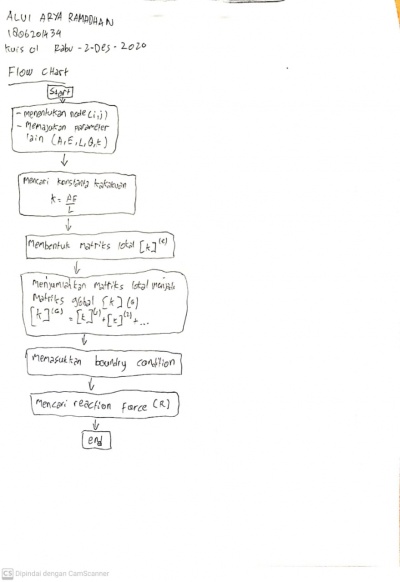
| + | Kami dimintak untuk membuat flowchart untuk mnyelesaikan permasalahan diatas. Flowchar sebagai berikut : | ||
| + | |||
| + | [[File:flowchart.jpeg|400px|center]] | ||
| + | |||
| + | Pembahasan No.4 | ||
| + | |||
| + | Penentuan nilai node dan K | ||
| + | |||
| + | [[File:Node dan K.jpeg|400px|center]] | ||
| + | |||
| + | Nilai K global | ||
| + | |||
| + | [[File:K global.jpeg|400px|center]] | ||
| + | |||
| + | Nilai U jika 1 dan 3 adalah tumpuan | ||
| + | |||
| + | [[File:Nilai U 4.jpeg|400px|center]] | ||
| + | |||
| + | Koding mencari Nilai U | ||
| + | |||
| + | [[File:kodingU 4.png|400px|center]] | ||
| + | |||
| + | Koding mencari Nilai R | ||
| + | |||
| + | [[File:nilaiR 4.png|400px|center]] | ||
| + | |||
| + | Nilai R | ||
| + | |||
| + | [[File:Nilai R 4.jpeg|400px|center]] | ||
| + | |||
| + | Nilai U dan R | ||
| + | |||
| + | [[File:Nilai UdanR.png|400px|center]] | ||
| + | |||
| + | |||
| + | == Pertemuan Tanggal 7 Desember 2020 == | ||
| + | |||
| + | Pada pertemuan kali ini Ahmda Mohammad Fahmi menjelaskan mengenai penyelesaian quiz 1 minggu lalu menggunakan aplikasi open modelica | ||
| + | |||
| + | '''PR Metode Numerik''' | ||
| + | |||
| + | [[File:Soal 3.3Trio.jpeg|600px|center]] | ||
| + | |||
| + | Cara penyelesaian | ||
| + | |||
| + | 1. Membuat class untuk menginpus semua yang diketahui dan ditanya | ||
| + | |||
| + | [[File:PRMetnum.png|500px|center]] | ||
| + | [[File:PRMetnum1.png|500px|center]] | ||
| + | |||
| + | 2. Membuat Fungsi matrik untuk K lokal | ||
| + | |||
| + | [[File:PRMetnum2.png|500px|center]] | ||
| + | |||
| + | 3. Membuat fungsi matriks untuk K global | ||
| + | |||
| + | [[File:PRMetnum3.png|500px|center]] | ||
| + | |||
| + | 4. Menjumlah kan semua K global | ||
| + | |||
| + | [[File:PRMetnum4.png|500px|center]] | ||
| + | |||
| + | 5. Mencari nilai U | ||
| + | |||
| + | [[File:PRMetnum5.png|500px|center]] | ||
| + | |||
| + | 6. Mencari nilai R | ||
| + | |||
| + | [[File:PRMetnum6.png|500px|center]] | ||
| + | |||
| + | Pada simulasi masih terjadi Error | ||
| + | |||
| + | [[File:PRMetnum7.png|500px|center]] | ||
| + | |||
| + | |||
| + | == Pertemuan Tanggal 14 Desember 2020 == | ||
| + | |||
| + | Pertemuan ini pak DAI menginstruksikan mahasiswanya untuk melakukan muhasabah diri. Muhasabah yang dilakukan dengan terkait dengan kemampuan dalam melakukan metode numerik secara individu. Muhasabah ini juga membuat para mahasiswa menilai diri sendiri berdasarkan kemampuan individual pemahaman metode numerik selama ini. | ||
| + | |||
| + | Selanjutnya Christo menjelaskan konsep berpikir dalam melakukan metode numerik dengan alur berfikir mengenai soal-soal yang telah diberikan dan menjelaskannya ke teman-teman yang ada di kelas menggunakan software OpenModelica. Lalu Enrico dan Fahmi menjelaskan perbedaan dari konsep koding mereka. Selanjutnya pak Dai meminta kita agar mengkombinasikan koding dari josiah dan fahmy untuk tugas besar 2 kelas secara bersama - sama. | ||
| + | |||
| + | == Tugas Besar == | ||
| + | |||
| + | '''Soal ''' | ||
| + | |||
| + | -Temukan Cost sebagai dengan variasi area dan material | ||
| + | |||
| + | '''Geometri dan Load''' | ||
| + | |||
| + | [[File:gambarTubes.png|400px|center]] | ||
| + | |||
| + | '''Diketahui''' | ||
| + | |||
| + | - Spesifikasi L (Panjang) dan geometri rangka truss | ||
| + | |||
| + | - Gaya beban terhadap struktur (1000 N dan 2000 N) | ||
| + | |||
| + | '''Asumsi''' | ||
| + | |||
| + | - Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya. | ||
| + | |||
| + | - Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss) | ||
| + | |||
| + | '''Model Trusses''' | ||
| + | |||
| + | model Trusses_3D_Tugas_Besar_Safety | ||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1);//Number of Trusses | ||
| + | parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36 | ||
| + | parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2) | ||
| + | parameter Real Elas=2e11; //Elasticity ASTM A36 (Pa) | ||
| + | //define connection parameter | ||
| + | Integer C[:,2]= [1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | //define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | //define external force (please put orderly) parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | //solution Real displacement[N], reaction[N]; Real check[3]; | ||
| + | Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; | ||
| + | protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6; | ||
| + | algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | //Implementing boundary for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | //Solving reaction reaction:=(G_star*displacement)-F; | ||
| + | //Eliminating float error for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i | ||
| + | in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Safety factor for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| + | |||
| + | '''Opt_GoldSection''' | ||
| + | |||
| + | model Opt_Gold | ||
| + | parameter Real xd[:]; | ||
| + | parameter Real yd[size(xd,1)]; | ||
| + | parameter Real xlo=87e-6; | ||
| + | parameter Real xhi=504e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Opt_Gold; | ||
| + | |||
| + | Pada pengerjaan tugas besar ini saya memilih material ASTM A36 yang akan digunakan pada penyelesaiaan untuk Material sama dengan area yang berbeda , berikut excel beserta koding yang dipakai : | ||
| + | |||
| + | [[File:Elas_LockTrio.png|1200px|center]] | ||
| + | |||
| + | pada table di atas dilakukan pencarian pada curve fitting untuk menentukan cost/kg pada masing masing ukuran dengan X adalah area dan Y adalah harga per kilogram siku, berikut kodingannya | ||
| + | |||
| + | [[File:Tubes_curvefitting1.jpg|500px|center]] | ||
| + | |||
| + | Hasiil dari kodingan diinput ke excel | ||
| + | |||
| + | [[File:Tubes_hasil_curvefitting1.jpg|500px|center]] | ||
| + | |||
| + | Nilai Optimasi pada elastisitas lock xd = Area dan yd = Rasion, maka dari hasil optimasi dimana hasilnya 3e-4 maka profil L yang digunakan 40 mm tebel 4mm | ||
| + | |||
| + | [[File:Opt_ElasLock1.png|500px|center]] | ||
| + | |||
| + | Lalu dilakukan perhitungan pada Area yang sama dengan material yang berbeda. Pada pengerjaan ini dilakukan 3 variasi material, SS400, SS304, SS316 dengan dimensi 40 mm x 40 mm x 5 mm. | ||
| + | |||
| + | [[File:Area_lockTrio1.png|1200px|center]] | ||
| + | |||
| + | Pada perhitungan area lock dilakukan curve fitting untuk nghasilkan nilai Cost/kg , Density, Yield strength. | ||
| + | |||
| + | Berikut kodingan unutk mencari cost/kg dengan X= Elasticity dan Y= cost/kg yang diketahui | ||
| + | |||
| + | [[File:Tubes_curvefitting2.jpg|500px|center]] | ||
| + | |||
| + | Hasil dari simulasi | ||
| + | |||
| + | [[File:Tubes_hasil_curvefitting2.jpg|500px|center]] | ||
| + | |||
| + | Berikut koding untuk mencari density, dengan X = Elasticity dan Y = Density yang diketahui | ||
| + | |||
| + | [[File:Tubes_curvefitting3.jpg|500px|center]] | ||
| + | |||
| + | Hasil dari simulasi | ||
| + | |||
| + | [[File:Tubes_hasil_curvefitting3.jpg|500px|center]] | ||
| + | |||
| + | Berikut koding untuk mencari Yield, dengan X = Elasticity dan Y = Yield yang diketahui | ||
| + | |||
| + | [[File:Tubes_curvefitting4.jpg|500px|center]] | ||
| + | |||
| + | Hasil dari simulasi | ||
| + | |||
| + | [[File:Tubes_hasil_curvefitting4.jpg|500px|center]] | ||
| + | |||
| + | Nilai Opt pada Area Lock dimana xd = Elastisitas dan yd = Rasio, dimana hasil dari optimasi 1.90019e-11 maka material yang dipilih adalah SS400 | ||
| + | |||
| + | [[File:Opt_ArealockTrio.png|500px|center]] | ||
| + | |||
| + | == UAS == | ||
| + | |||
| + | Nomor1 | ||
| + | [[File:UASMETNUM1.jpeg|400px|center]] | ||
| + | |||
| + | Nomor 2 | ||
| + | [[File:UASMETNUM2.jpeg|400px|center]] | ||
| + | |||
| + | Nomor 3 | ||
| + | [[File:UASMETNUM3.jpeg|400px|center]] | ||
| + | |||
| + | Nomor 4,5,6 | ||
| + | [[File:UASMETNUM4.jpeg|400px|center]] | ||
| + | |||
| + | Kodingan nomor 7 | ||
| + | |||
| + | class UAS | ||
| + | |||
| + | parameter Real [:,5] inisiasi = [1, 2, 40, 35e6, 480; | ||
| + | 2, 3, 40, 35e6, 480; | ||
| + | 3, 4, 40, 35e6, 480]; | ||
| + | |||
| + | |||
| + | parameter Integer [:,2] node = [1, 2; | ||
| + | 2, 3; | ||
| + | 3, 4]; | ||
| + | |||
| + | parameter Integer y = size(node,1); | ||
| + | |||
| + | parameter Integer x = 2*(size(node_load,1)); | ||
| + | |||
| + | parameter Integer z = size(Boundary,1); | ||
| + | |||
| + | parameter Integer [:] Boundary = {3}; | ||
| + | |||
| + | parameter Real [:,3] node_load = [1, 2503621.3356, 2503621.3356 ; | ||
| + | 2, 0, 0; | ||
| + | 3, 0, 0; | ||
| + | 4, 0, 0]; | ||
| + | parameter Real [2*(size(node_load,1))] load = {2503621.3356,0,0,0,0,0,0}; | ||
| + | Real [y] k; | ||
| + | Real [y,4,4] Ke; | ||
| + | Real [y,x,x] Kg; | ||
| + | Real [x,x] KgTot; | ||
| + | Real [x,x] KgB; | ||
| + | Real [x] U; | ||
| + | Real [x] R; | ||
| + | equation | ||
| + | k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)}; | ||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | ||
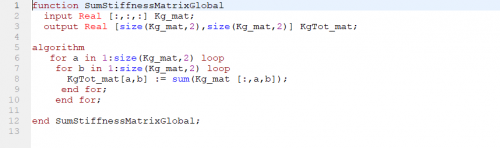
| + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | ||
| + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | ||
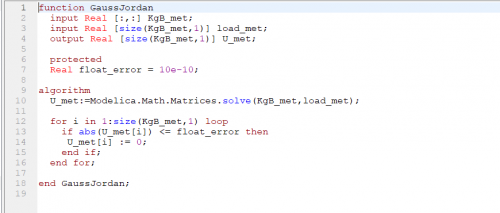
| + | U = GaussJordan(x, KgB, load); | ||
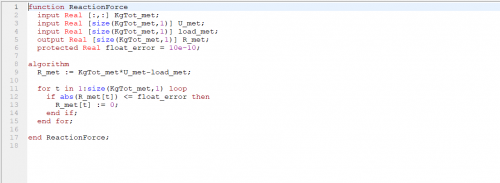
| + | R = ReactionForce(x, KgTot, U, load); | ||
| + | end UAS; | ||
| + | |||
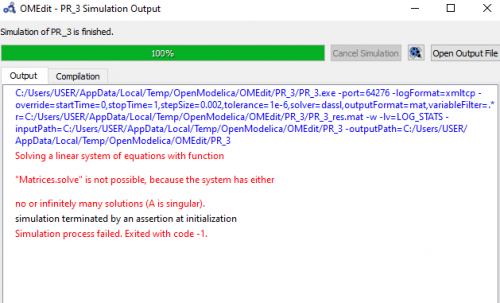
| + | dari koding ini simulasi saya masih error | ||
Latest revision as of 18:32, 13 January 2021
Alhamdulillah, segala puji bagi Allah SWT Tuhan semesta alam dan sholawat beserta salam kepada Nabi Muhammad SAW.
Contents
- 1 BIODATA
- 2 Pertemuan Tanggal 9 November 2020
- 3 Pertemuan Tanggal 16 November 2020
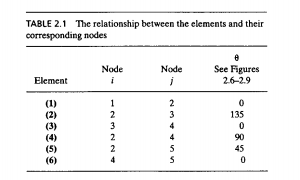
- 4 Pertemuan Tanggal 23 November 2020
- 5 PR3 menyelesaikan permasalahan pada example 2.1
- 6 Pertemuan Tanggal 30 November 2020
- 7 Pertemuan Tanggal 7 Desember 2020
- 8 Pertemuan Tanggal 14 Desember 2020
- 9 Tugas Besar
- 10 UAS
BIODATA
Nama :Trio Kurnia Ryplida
Npm : 1906435561
Agama : Islam
No.Telp : 085274017943
Pendidikan Terakhir: Diploma III
Tempat/Tgl lahir : Padang, 29 oktober 1997
Pertemuan Tanggal 9 November 2020
Pada pertemuan pertama Pak Dai memberikan PR, sebagai berikut :
1. apa saja yang sudah dipelajari di metode numerik?
2. Buatlah video tentang aplikasi Open Modelica.
Numerical Differentiation
pada kasus ini menggunakan perumusan :
Untuk vido tentang aplikasi OpenModelica terdapat pada link : https://www.youtube.com/watch?v=uxVO7iPxMKo
Pertemuan Tanggal 16 November 2020
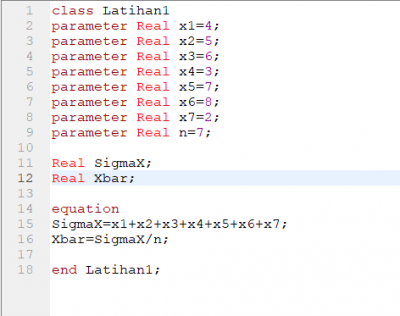
Hari ini pak Dai memberikan petunjuk bagaimana cara membuat sebuah program sederhana
contoh membuat hasil rata-rata senbagai berikut :
Pr menyelesaikan masalah 3 aljabar sebagai berikut :
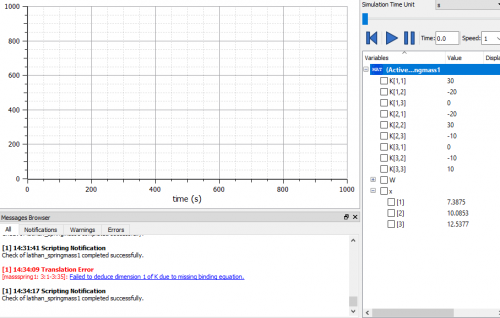
persamaan ini akan diselesaikan dengan menggunakan open modelica dengan metode Gauss Elimination. Maka persamaan ini akan diubah dalam bentuk matriks.
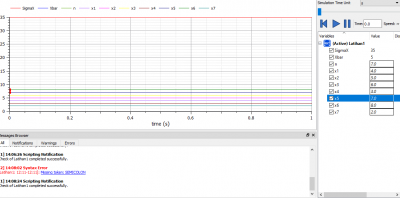
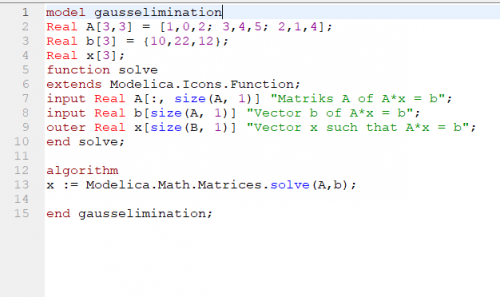
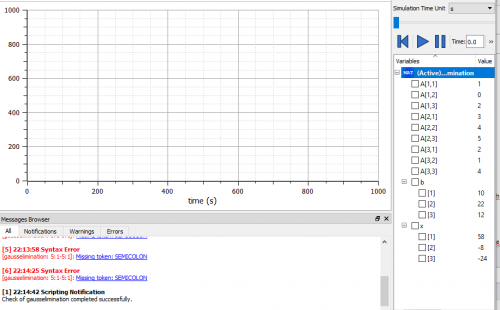
berikut bentuk penyelesaian dengan menggunakan open modelica :
dapat dilihat bahwa hasil plotting tersebut menunjukkan penyelesaian dari permasalaha sistem persamaan yang telah ditunjukkan sebelumnya, yaitu x1=58, x2=-8, x3=-24.
Pertemuan Tanggal 23 November 2020
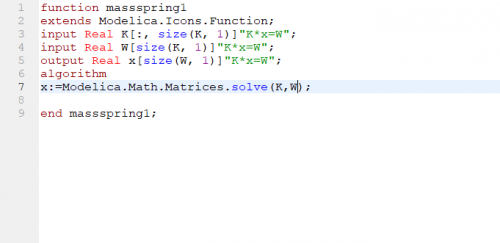
Pada hari ini pak Dai memberikan sebuah latihan pada buku Metode Numerik edisi 7 karangan Steven C.Chapra dan Raymond P.Canel pada halamam 328 latihan 12.11
lalu pak Dai memberi kesempatan untuk menyelesaikan perssoalan dengan menggunakan Open Modelica
pada function coding
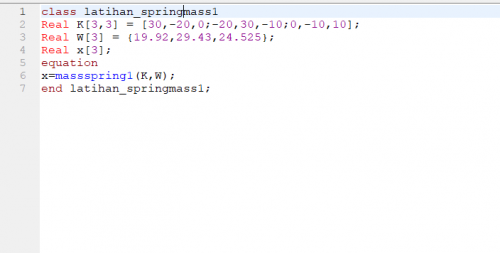
lalu pada class coding
hasil simulasi
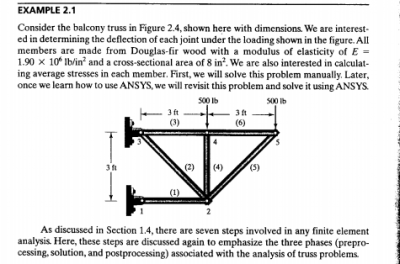
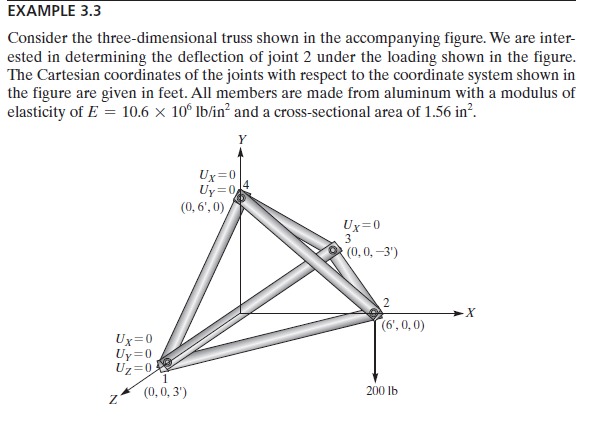
PR3 menyelesaikan permasalahan pada example 2.1
Dari PR yang diberikan saya akan mencoba menggunakan aljabar simultan untuk mencari nilai displacement dan gaya reaksi disetiap join. Hal yang pertama dilakukan adalah menentukan node, sudut terhadap sumbu X positif dan element pada setiap batang.
Lalu menentukan nilai konstanta kekakuan dengan permusan k=AE/L.Dari soal sudah diketahui modulus elastisitas setiap batang E = luas penampang setiap batang sebesar 8inch persegi dan panjang batang 1, 3, 4 dan 6 adalah 3 feet atau sebesar 36 inch dan sudut antara batang 4 dengan batang 2 dan 5 adalah 45 derajat. Oleh karena itu kita dapat menghitung panjang batang 2 dan 5 dengan 36/cos45 = 50.9 inch.
k untuk batang 1, 3, 4 dan 6 adalah
Pada batang 2 dan 5
Lalu memasukkan persamaan matriks untuk K pada setiap element.Dengan perumusan sebagai berikut
Analisa Batang 1,3,dan 6
Untuk menyelesaikan masalah pada batang 1,3,dan 6 maka menggunakan nilai k = 4,22x10^5 dan sudut 0.
Maka matriks k pada persamaan ini adalah
Lalu untuk penyelesaiaannya
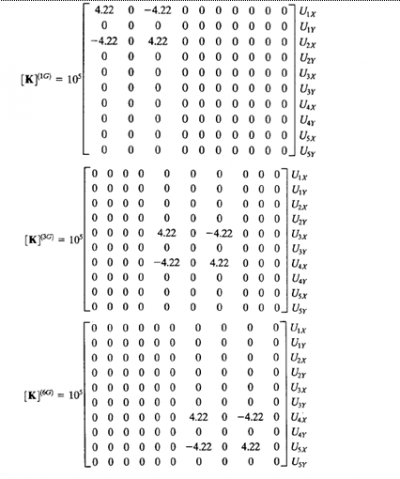
Lalu ketiga matriks diatas diinput kedalam matriks global sesuai dengan posisi U.
Analisa Batang 4
Pada batang 4 nilai k = 4,22 x 10^5 dengan sudut 90 derajat terhadap sumbu X.Berikut bentuk matrik k
Lalu menginput kedalam matrik global sesuai dengan posisi U
Analisa Batang 2
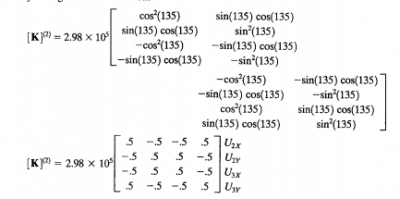
Pada batang 2 nilai k yang digunakan adalah 2,98 x 10^5 dengan sudut 135 derajat terhadap sumbu X. Dengan bentuk matriks K sebagai berikut
Lalu diinput dalam matriks global sesauai dengan posisi U
Analisa Batang 5
Pada batang 5 nilai k yang digunakan 2,98 x 10^5 dengan sudut 45 derajat terhadap sumbu X. Berikut bentuk matriks k
Lalu diinput kedalam matriks global sesuai dengan posisi U.
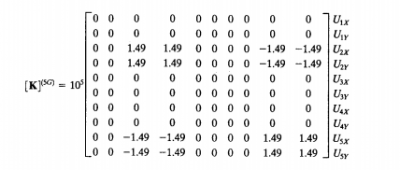
Lalu melakukan poenjumlahan pada semua matriks global untuk menjadi Kglobal
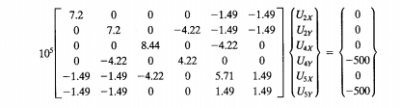
Tentukan kondisi batas dan kondisi pembebanan pada struktur. Dari struktur kita dapat mengetahui bahwa U1x, U1y, U3x, U3y = 0 dan beban sebesar 500 kearah bawah pada titik tumpuan 4 dan 5 ke arah sumbu Y. Karena nilai U1x, U1y, U3x, U3y = 0 maka kita bisa mengeliminasi baris dan kolom 1, 2, 6 dan 7, sehingga nantinya akan didapatkan matrix berukuran 6 x 6.
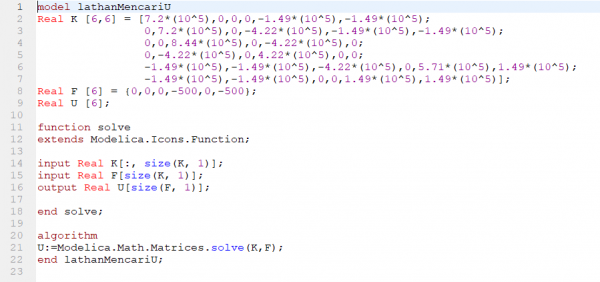
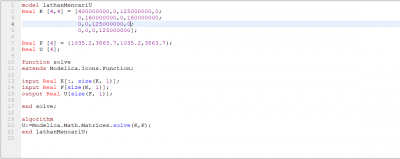
Setekah itu menghitung nilai U dengan menggunakan Open Modelica.
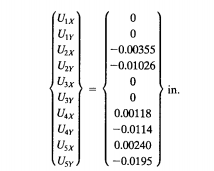
Hasil dari nilai U yang telah disimulasikan
Hasil dari simulasi OpenModelica adalah
U2x = -0.0035545 inch
U2y = -0.0102659 inch
U4x = 0.00118483 inch U4y = -0.0114507 inch
U5x = 0.00236967 inch
U5y = -0.0195458 inch
karana niali U1x, U1y, U3x,dan U3y = 0 maka
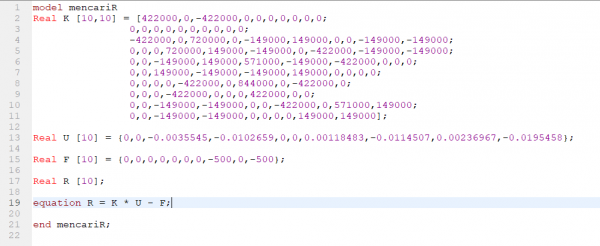
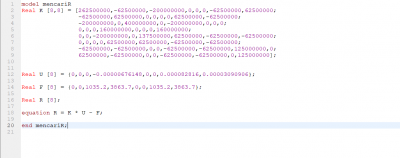
Setelah nilai U didapan maka kita bisa mencari nilai Rection Force dengan perumusan R=Kglobal x U - F dalam bentuk matriks.
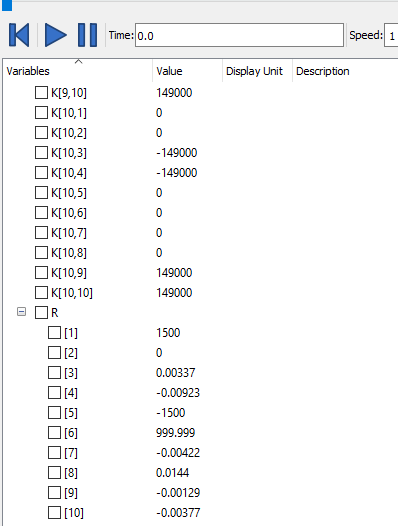
setelah itu menggunakan Open Modelica untuk Mencari Nilai R
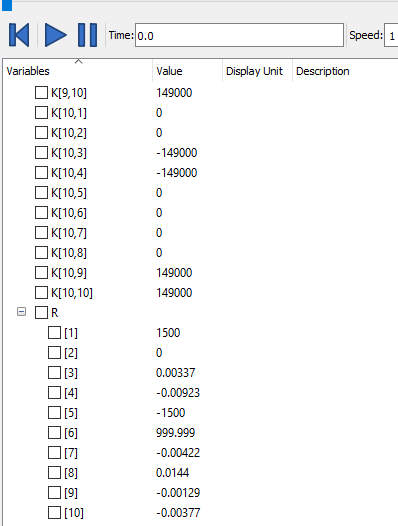
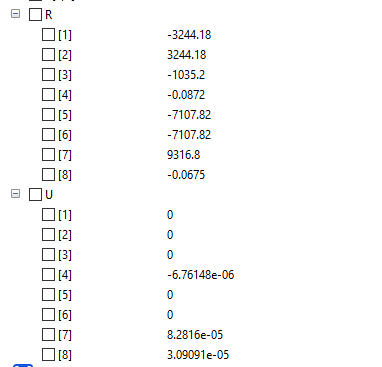
Hasil dari simulasi
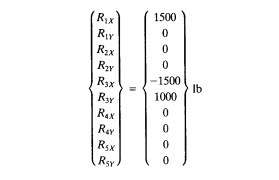
Nilai R pada Buku
Pertemuan Tanggal 30 November 2020
Pada hari ini pak Dai memberikan quis dengan sola sebagai berikut :
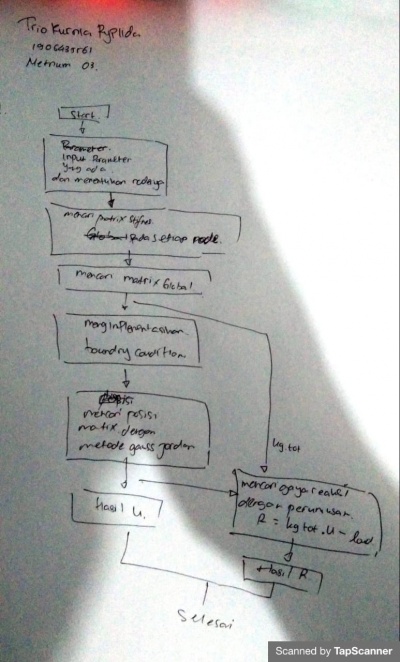
Kami dimintak untuk membuat flowchart untuk mnyelesaikan permasalahan diatas. Flowchar sebagai berikut :
Pembahasan No.4
Penentuan nilai node dan K
Nilai K global
Nilai U jika 1 dan 3 adalah tumpuan
Koding mencari Nilai U
Koding mencari Nilai R
Nilai R
Nilai U dan R
Pertemuan Tanggal 7 Desember 2020
Pada pertemuan kali ini Ahmda Mohammad Fahmi menjelaskan mengenai penyelesaian quiz 1 minggu lalu menggunakan aplikasi open modelica
PR Metode Numerik
Cara penyelesaian
1. Membuat class untuk menginpus semua yang diketahui dan ditanya
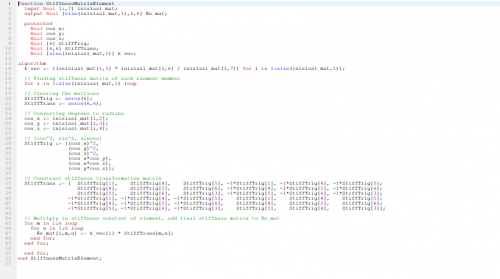
2. Membuat Fungsi matrik untuk K lokal
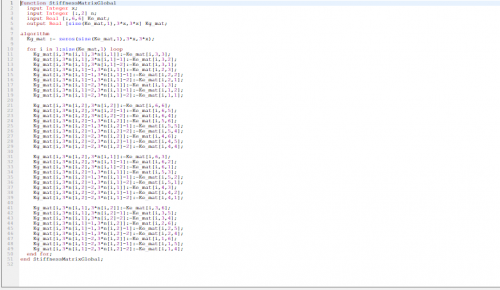
3. Membuat fungsi matriks untuk K global
4. Menjumlah kan semua K global
5. Mencari nilai U
6. Mencari nilai R
Pada simulasi masih terjadi Error
Pertemuan Tanggal 14 Desember 2020
Pertemuan ini pak DAI menginstruksikan mahasiswanya untuk melakukan muhasabah diri. Muhasabah yang dilakukan dengan terkait dengan kemampuan dalam melakukan metode numerik secara individu. Muhasabah ini juga membuat para mahasiswa menilai diri sendiri berdasarkan kemampuan individual pemahaman metode numerik selama ini.
Selanjutnya Christo menjelaskan konsep berpikir dalam melakukan metode numerik dengan alur berfikir mengenai soal-soal yang telah diberikan dan menjelaskannya ke teman-teman yang ada di kelas menggunakan software OpenModelica. Lalu Enrico dan Fahmi menjelaskan perbedaan dari konsep koding mereka. Selanjutnya pak Dai meminta kita agar mengkombinasikan koding dari josiah dan fahmy untuk tugas besar 2 kelas secara bersama - sama.
Tugas Besar
Soal
-Temukan Cost sebagai dengan variasi area dan material
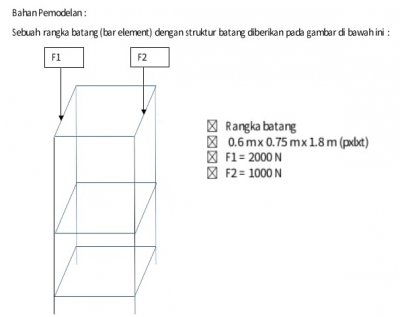
Geometri dan Load
Diketahui
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Asumsi
- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
Model Trusses
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1);//Number of Trusses
parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36
parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2)
parameter Real Elas=2e11; //Elasticity ASTM A36 (Pa)
//define connection parameter
Integer C[:,2]= [1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i
in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
Opt_GoldSection
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
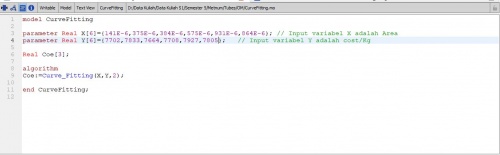
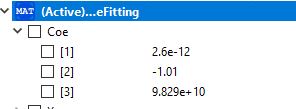
Pada pengerjaan tugas besar ini saya memilih material ASTM A36 yang akan digunakan pada penyelesaiaan untuk Material sama dengan area yang berbeda , berikut excel beserta koding yang dipakai :
pada table di atas dilakukan pencarian pada curve fitting untuk menentukan cost/kg pada masing masing ukuran dengan X adalah area dan Y adalah harga per kilogram siku, berikut kodingannya
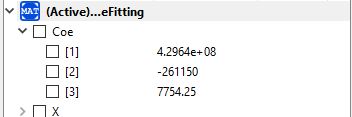
Hasiil dari kodingan diinput ke excel
Nilai Optimasi pada elastisitas lock xd = Area dan yd = Rasion, maka dari hasil optimasi dimana hasilnya 3e-4 maka profil L yang digunakan 40 mm tebel 4mm
Lalu dilakukan perhitungan pada Area yang sama dengan material yang berbeda. Pada pengerjaan ini dilakukan 3 variasi material, SS400, SS304, SS316 dengan dimensi 40 mm x 40 mm x 5 mm.
Pada perhitungan area lock dilakukan curve fitting untuk nghasilkan nilai Cost/kg , Density, Yield strength.
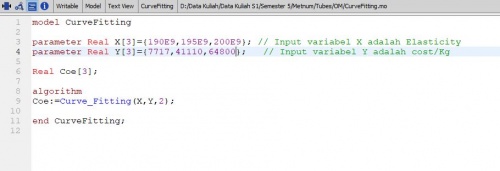
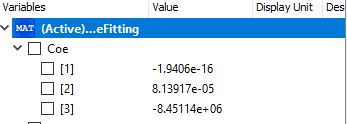
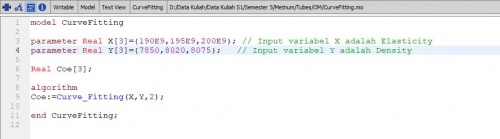
Berikut kodingan unutk mencari cost/kg dengan X= Elasticity dan Y= cost/kg yang diketahui
Hasil dari simulasi
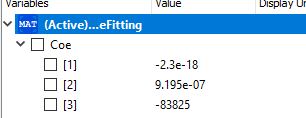
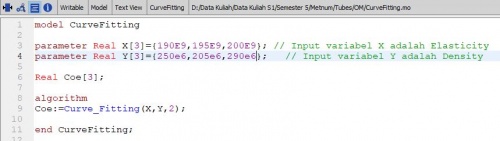
Berikut koding untuk mencari density, dengan X = Elasticity dan Y = Density yang diketahui
Hasil dari simulasi
Berikut koding untuk mencari Yield, dengan X = Elasticity dan Y = Yield yang diketahui
Hasil dari simulasi
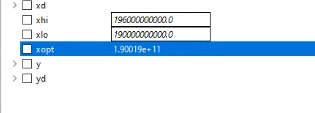
Nilai Opt pada Area Lock dimana xd = Elastisitas dan yd = Rasio, dimana hasil dari optimasi 1.90019e-11 maka material yang dipilih adalah SS400
UAS
Nomor1
Nomor 2
Nomor 3
Nomor 4,5,6
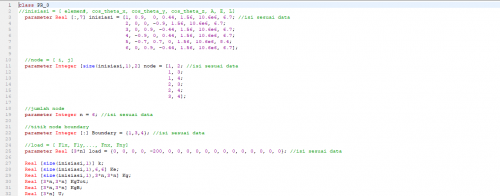
Kodingan nomor 7
class UAS
parameter Real [:,5] inisiasi = [1, 2, 40, 35e6, 480;
2, 3, 40, 35e6, 480;
3, 4, 40, 35e6, 480];
parameter Integer [:,2] node = [1, 2;
2, 3;
3, 4];
parameter Integer y = size(node,1);
parameter Integer x = 2*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {3};
parameter Real [:,3] node_load = [1, 2503621.3356, 2503621.3356 ;
2, 0, 0;
3, 0, 0;
4, 0, 0];
parameter Real [2*(size(node_load,1))] load = {2503621.3356,0,0,0,0,0,0};
Real [y] k;
Real [y,4,4] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
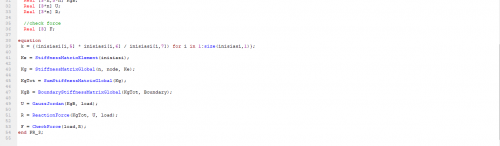
equation
k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end UAS;
dari koding ini simulasi saya masih error