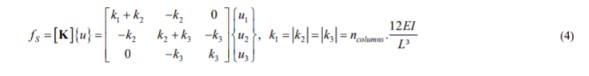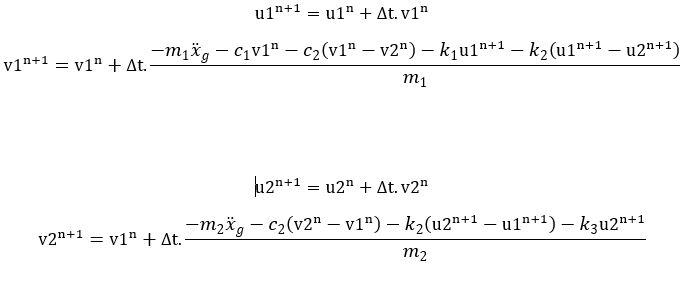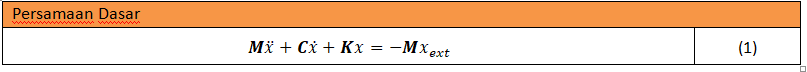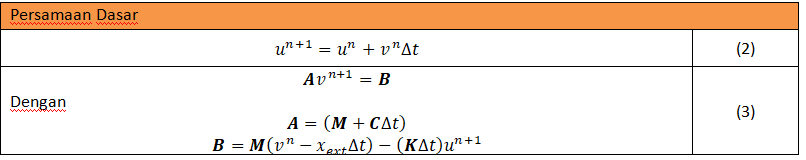Difference between revisions of "Simplified Finite Elements model to represent Mass-Spring structures in dynamic simulation by Rúbia M. Bosse, André Teófilo Beck"
(→Artikel Kolaborasi : USING EULER METHOD FOR 1-D OSCILLATING ANALYSIS arranged by Oldy Fahlovvi, Muchalis Zikramansyah Masuku, Ahmad Zikri, Muhammad Irfan Dzaky) |
Yusufraihan (talk | contribs) (→STUDI KASUS OSILASI GEDUNG DUA TINGKAT MENGGUNAKAN MODEL PEGAS-MASSA; Edo, Raihan, Jeri, Shabrina) |
||
| (49 intermediate revisions by 22 users not shown) | |||
| Line 84: | Line 84: | ||
==='''2. MODEL MASS-SPRING'''=== | ==='''2. MODEL MASS-SPRING'''=== | ||
| + | |||
| + | Diterjemahkan oleh : Mohamad Wafirul Hadi, Kania Dyah Nastiti, Maha Hidayatullah Akbar, Fajri Octadiansyah, Afitro Adam | ||
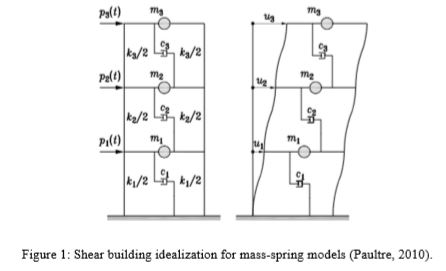
Analisis dinamis menggunakan model massa-pegas diskrit sangat umum dalam literatur dan menyajikan keuntungan sebagai alat sederhana untuk mengevaluasi respons dinamis struktur. Metode analisis ini memerlukan waktu pemrosesan yang sedikit, karena mereduksi struktur menjadi beberapa derajat kebebasan, dan karena jawabannya dapat diperoleh secara analitik dengan metode modal superposisi. Model MS tradisional berurusan dengan analisis linier, yaitu keseimbangan dihitung pada posisi awal, menyajikan matriks kekakuan konstan (Warburton, 1976 dan Paultre, 2010). Dalam makalah ini model bangunan geser dipertimbangkan. Idealisasi ini biasanya digunakan untuk mengevaluasi respons bangunan yang mengalami kegembiraan dinamis. Model bangunan geser biasanya mempertimbangkan bahwa massa kolom dapat diabaikan, dan massa lantai terkonsentrasi di lantai (titik massa). Juga, balok dan pelat dianggap kaku dalam arah longitudinal dan dalam lentur, kolom kaku untuk regangan aksial tetapi fleksibel secara transversal. Idealisasi bangunan geser mengasumsikan bahwa bangunan hanya menyajikan perpindahan horisontal, karena pembengkokan kolom. Mempertimbangkan kerangka bidang gambar 3 lantai yang tidak tertutup pada Gambar 1, model bangunan geser dapat dimodelkan dengan mendefinisikan massa dan pegas yang setara dan membuat matriks yang sesuai untuk solusi persamaan gerak. | Analisis dinamis menggunakan model massa-pegas diskrit sangat umum dalam literatur dan menyajikan keuntungan sebagai alat sederhana untuk mengevaluasi respons dinamis struktur. Metode analisis ini memerlukan waktu pemrosesan yang sedikit, karena mereduksi struktur menjadi beberapa derajat kebebasan, dan karena jawabannya dapat diperoleh secara analitik dengan metode modal superposisi. Model MS tradisional berurusan dengan analisis linier, yaitu keseimbangan dihitung pada posisi awal, menyajikan matriks kekakuan konstan (Warburton, 1976 dan Paultre, 2010). Dalam makalah ini model bangunan geser dipertimbangkan. Idealisasi ini biasanya digunakan untuk mengevaluasi respons bangunan yang mengalami kegembiraan dinamis. Model bangunan geser biasanya mempertimbangkan bahwa massa kolom dapat diabaikan, dan massa lantai terkonsentrasi di lantai (titik massa). Juga, balok dan pelat dianggap kaku dalam arah longitudinal dan dalam lentur, kolom kaku untuk regangan aksial tetapi fleksibel secara transversal. Idealisasi bangunan geser mengasumsikan bahwa bangunan hanya menyajikan perpindahan horisontal, karena pembengkokan kolom. Mempertimbangkan kerangka bidang gambar 3 lantai yang tidak tertutup pada Gambar 1, model bangunan geser dapat dimodelkan dengan mendefinisikan massa dan pegas yang setara dan membuat matriks yang sesuai untuk solusi persamaan gerak. | ||
[[File:afitrotgs3.jpg]] | [[File:afitrotgs3.jpg]] | ||
| + | |||
| + | |||
| + | [[File:4.3.9 1.jpg]] | ||
| + | |||
| + | [[File:4.3.9 2.jpg]] | ||
dengan M matriks massa diagonal sistem dengan massa lantai yang terkonsentrasi pada titik-massa, 𝑢̈ adalah | dengan M matriks massa diagonal sistem dengan massa lantai yang terkonsentrasi pada titik-massa, 𝑢̈ adalah | ||
vektor percepatan. | vektor percepatan. | ||
Paket karena redaman itu diperoleh sebagai: | Paket karena redaman itu diperoleh sebagai: | ||
| + | |||
| + | [[File:4.3.9 3.jpg]] | ||
di mana 𝑪 adalah matriks redaman, 𝑐 adalah koefisien redaman, 𝑢̇ adalah vektor kecepatan. | di mana 𝑪 adalah matriks redaman, 𝑐 adalah koefisien redaman, 𝑢̇ adalah vektor kecepatan. | ||
Kekuatan elastis dapat ditentukan sebagai: | Kekuatan elastis dapat ditentukan sebagai: | ||
| + | |||
| + | [[File:4.3.9 4.jpg]] | ||
dimana𝑲 adalah matriks kekakuan, | dimana𝑲 adalah matriks kekakuan, | ||
| Line 100: | Line 111: | ||
adalah koefisien kekakuan kolom dan 𝑢 adalah vektor perpindahan. | adalah koefisien kekakuan kolom dan 𝑢 adalah vektor perpindahan. | ||
Keseimbangan gerak dapat didefinisikan sebagai: | Keseimbangan gerak dapat didefinisikan sebagai: | ||
| + | |||
| + | [[File:4.3.9 5.jpg]] | ||
Untuk kasus beban gerakan tanah, vektor eksitasi diperoleh dengan mengalikan massa setiap derajat | Untuk kasus beban gerakan tanah, vektor eksitasi diperoleh dengan mengalikan massa setiap derajat | ||
| Line 105: | Line 118: | ||
sesuai dengan respons struktur dengan penyangga tetap, keluar oleh kekuatan eksternal dalam massanya; dan 𝑝 (𝑡) adalah | sesuai dengan respons struktur dengan penyangga tetap, keluar oleh kekuatan eksternal dalam massanya; dan 𝑝 (𝑡) adalah | ||
diadaptasi menjadi 𝑝 (𝑡) sebagai: | diadaptasi menjadi 𝑝 (𝑡) sebagai: | ||
| + | |||
| + | [[File:4.3.9 6.jpg]] | ||
di mana 𝑢̈ (𝑡) adalah vektor percepatan horizontal gempa bumi, 𝑟 adalah vektor dengan 𝑛 garis sama dengan jumlah bingkai | di mana 𝑢̈ (𝑡) adalah vektor percepatan horizontal gempa bumi, 𝑟 adalah vektor dengan 𝑛 garis sama dengan jumlah bingkai | ||
| Line 305: | Line 320: | ||
[[File : 2020-05-09 16_22_37-Spyder (Python 3.7).png || 500px ]] | [[File : 2020-05-09 16_22_37-Spyder (Python 3.7).png || 500px ]] | ||
| − | |||
| − | + | Untuk kasus yang dikerjakan adalah pada bangunan dengan penjalasan seperti pada laporan di bawah ini | |
| + | |||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | |||
| + | File:FEMBUILDINGSED (1).JPG | ||
| + | |||
| + | File:FEMBUILDINGSED (2).JPG | ||
| + | |||
| + | initial condition disini digambarkan bahwa, konstruksi rangka gedung dapat di modelkan sebagai batang kantilever dengan panjang (l) yang menerima gaya (F) arah lateral akibat gempa, sehingga akibat gaya F tersebut menyebabkan terjadinya displacement pada rangka tersebut sejauh x. | ||
| + | |||
| + | File:FEMBUILDINGSED (3).JPG | ||
| + | |||
| + | perpindahan posisi (displacement ) merupakan defleksi pada rangka. sehingga dapat dirumuskan besarnya displacennet sebagai persamaan defleksi pada batang kantilever. besarnya defleksi dipengaruhi oleh : bentuk penampang batang, panjang batang, gaya yang bekerja dan juga modulus elastistas material. | ||
| + | |||
| + | File:FEMBUILDINGSED (4).JPG | ||
| + | |||
| + | berdasrkan rumus defleksi tersebut didapatkan hasil perhitungan seperti pada grafik. dimana displacemnt yang terjadi akibat gaya F merupakan suatu bentuk osilsasi dengan simpangan terjauh mencapai 0.8 | ||
| + | |||
| + | File:FEMBUILDINGSED (5).JPG | ||
| + | |||
| + | File:FEMBUILDINGSED (6).JPG | ||
| + | |||
| + | File:FEMBUILDINGSED (7).JPG | ||
| + | |||
| + | File:FEMBUILDINGSED (8).JPG | ||
| + | |||
| + | File:FEMBUILDINGSED (9).JPG | ||
| + | |||
| + | </gallery> | ||
| + | |||
| + | '''slide 1 (judul)''' | ||
| + | |||
| + | '''slide 2 (FEM initial condition)''' | ||
| + | |||
| + | initial condition disini digambarkan bahwa, konstruksi rangka gedung dapat di modelkan sebagai batang kantilever dengan panjang (l) yang menerima gaya (F) arah lateral akibat gempa, sehingga akibat gaya F tersebut menyebabkan terjadinya displacement pada rangka tersebut sejauh x. | ||
| + | |||
| + | '''slide 3 (dasar teori defelksi untuk perhitungan manual-eksak)''' | ||
| + | |||
| + | perpindahan posisi (displacement ) merupakan defleksi pada rangka. sehingga dapat dirumuskan besarnya displacennet sebagai persamaan defleksi pada batang kantilever. besarnya defleksi dipengaruhi oleh : bentuk penampang batang, panjang batang, gaya yang bekerja dan juga modulus elastistas material. | ||
| + | |||
| + | '''slide 4 (hasil perhitungan manual)''' | ||
| + | |||
| + | berdasarkan rumus defleksi tersebut didapatkan hasil perhitungan seperti pada grafik. dimana displacemnt yang terjadi akibat gaya F merupakan suatu bentuk osilsasi dengan simpangan terjauh mencapai 0.8 | ||
| + | |||
| + | '''slide 5 (pemodelan FES)''' | ||
| + | |||
| + | pemodelan FES ini berangkat dari MS model, dimana FES ini merupakan bentuk sederhana dari FEM yang diberikan pembatasan-pembatasan, pergerakan kolom akibat gaya F dari gempa hanya ke arah horisontal saja sehingga mengabaikan gerakan vertikan maupun rotasi pada kolom. | ||
| + | |||
| + | '''slide 6 (hasil perhitungan FES)''' | ||
| + | |||
| + | hasil perhitungan dengan FES ini menunjukan simpangan terjauh dari kolom yang diakibatkan oleh gaya F dari gempa adalah sejauh 0.8 mm | ||
| + | |||
| + | '''slide 7 (pemodelan FEM)''' | ||
| − | + | '''slide 8 (hasil perhitungan FEM)''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | hasil perhitungan terdapat beberapa point dan cara yakni menggunakan FEM dan euler method | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''slide 9 (hasil dan kesimpulan)''' | |
| − | + | dari ketiga perhitungan tersebut (perhitungan manual-eksak, FES dan FEM) maka didapatkan hasil bahwa, perhitungan manual dana FES menunjukkan hasil yang hampir sama, yaitu terjadi simpangan dari pergerakan kolom arah laetral sejauh 0.8. | |
| − | + | sedangakan hasil perhitungan FEM amenunjukkan perbedaan yang cukup signifikan. perbedaan hasil tersebut kemungkinan besar disebabkan oleh adanya perbedaan input yang dilakukan dalam perhitungan, mengingat dalam FES dilakukan pembatasan-pembatasan, seperti pada gerakan akibat gaya F gempa terhadap kolom yang terjadi hanya pada arah hisontal. sedangkan pada kejadian sebenarnya tidaklah demikian. | |
| + | |||
| + | == Tugas Artikel Kania, Chandra, Dieter, Evi == | ||
| − | |||
<gallery mode="slideshow"> | <gallery mode="slideshow"> | ||
| − | File:Artikel Komputasi Teknik-1 USING EULER METHOD FOR 1-D OSCILLATING | + | File:Komptek_Artikel_Bangunan_page-0001.jpg |
| + | File:Komptek_Artikel_Bangunan_page-0002.jpg | ||
| + | File:Komptek_Artikel_Bangunan_page-0003.jpg | ||
| + | File:Komptek_Artikel_Bangunan_page-0004.jpg | ||
| + | File:Komptek_Artikel_Bangunan_page-0005.jpg | ||
| + | File:Komptek_Artikel_Bangunan_page-0006.jpg | ||
| + | File:Komptek_Artikel_Bangunan_page-0007.jpg | ||
| + | </gallery> | ||
| + | |||
| + | == Artikel Kolaborasi : ''USING MASS-SPRING (MS) MODEL FOR BUILDING ANALYSIS'' arranged by [http://air.eng.ui.ac.id/index.php?title=Oldy_Fahlovi Oldy Fahlovvi], [http://air.eng.ui.ac.id/index.php?title=Muchalis_Zikramansyah_Masuku Muchalis Zikramansyah Masuku], [http://air.eng.ui.ac.id/index.php?title=AHMAD_ZIKRI Ahmad Zikri], [http://air.eng.ui.ac.id/index.php?title=Muhammad_Irfan_Dzaky Muhammad Irfan Dzaky]== | ||
| + | |||
| + | Berikut ini kami lampirkan tugas kolaborasi tentang ''USING MASS-SPRING (MS) MODEL FOR BUILDING ANALYSIS'' dalam bentuk slideshow. | ||
| + | <gallery mode="slideshow"> | ||
| + | File:Artikel Komputasi Teknik-1 USING EULER METHOD FOR 1-D OSCILLATING ANALYSISS.jpg | ||
File:Artikel Komputasi Teknik-2 USING EULER METHOD FOR 1-D OSCILLATING ANALYSIS.jpg | File:Artikel Komputasi Teknik-2 USING EULER METHOD FOR 1-D OSCILLATING ANALYSIS.jpg | ||
File:Artikel Komputasi Teknik-3 USING EULER METHOD FOR 1-D OSCILLATING ANALYSIS.jpg | File:Artikel Komputasi Teknik-3 USING EULER METHOD FOR 1-D OSCILLATING ANALYSIS.jpg | ||
| Line 406: | Line 415: | ||
Persoalan | Persoalan | ||
| − | [[File:Artikel_4.1_judul2.jpg]] | + | [[File:Artikel_4.1_judul2.jpg|700px]] |
| − | [[File:Artikel_4.1_hal1.jpg]] | + | [[File:Artikel_4.1_hal1.jpg|700px]] |
Hasil | Hasil | ||
| + | [[File:Aghnia hasil.PNG|700px]] | ||
| + | |||
| + | Analisa | ||
| + | |||
| + | [[File:Analisa_daniel.jpg|700px]] | ||
| + | |||
| + | [[File:Analisa_daniel2.jpg|700px]] | ||
Berikut terlampir dokumen pendukung berupa Excel | Berikut terlampir dokumen pendukung berupa Excel | ||
| Line 417: | Line 433: | ||
https://drive.google.com/file/d/1Xvx7qlr-6vEFbYRVly7RprzASj8uwBfa/view?usp=sharing | https://drive.google.com/file/d/1Xvx7qlr-6vEFbYRVly7RprzASj8uwBfa/view?usp=sharing | ||
| − | == | + | |
| + | == Tugas Artikel Fajri, Kania Dyah, Maha, Wafirul == | ||
| + | |||
| + | |||
| + | [[File:D-1_pages-to-jpg-0001.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0002.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0003.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0004.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0005.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0006.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0007.jpg]] | ||
| + | |||
| + | [[File:D-1_pages-to-jpg-0008.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | == Tugas Artikel Adinda, Ilham Bagus, Adzanna, Maheka == | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | File:artikelsmo1.jpg | ||
| + | File:artikelsmo2.jpg | ||
| + | File:artikelsmo3.jpg | ||
| + | File:artikelsmo4.jpg | ||
| + | File:artikelsmo5.jpg | ||
| + | File:artikelsmo6.jpg | ||
| + | File:artikelsmo7.jpg | ||
| + | File:artikelsmo8a.jpg | ||
| + | </gallery> | ||
| + | |||
| + | == STUDI KASUS OSILASI GEDUNG DUA TINGKAT MENGGUNAKAN MODEL PEGAS-MASSA; Edo, Raihan, Jeri, Shabrina == | ||
| + | |||
| + | ''' Studi Kasus ''' | ||
| + | Bangunan Gedung merupakan salah satu sarana yang dibangun menggunakan pengetahuan Engineering yang kompleks. Hampir seluruh aspek dalam perekayasaan sebuah gedung memerlukan analisis khusus secara saintifik guna menghasilkan karya yang tepat guna, nyaman dan aman untuk digunakan. Agar suatu bangunan tersebut aman untuk digunakan, sistem struktur bangunan haruslah memiliki kriteria untuk dapat menahan beban dengan kekuatan tertentu. Salah satu jenis beban yang menjadi perhatian khusus dalam perancangan bangunan gedung adalah pengaruh eksitasi yang disebabkan oleh kondisi angin maupun gempa bumi. | ||
| + | Dalam menentukan respon suatu bangunan gedung terhadap eksitasi beban di atas, diperlukan proses komputasi terhadap fenomena yang akan terjadi. Untuk melakukan komputasi tersebut secara numerik, dapat dilakukan pendekatan menggunakan sistem pegas – massa maupun sistem finite element. Seperti yang dilakukan pada salah satu referensi yang diunggah oleh pak DAI mengenai simplified finite element, kami mencoba untuk melakukan studi kasus mengenai bangunan 2 tingkat yang diberikan gaya horizontal untuk diamati pengaruh gaya tersebut terhadap pergerakan osilasi gedung. | ||
| + | Contoh kasus yang kami uji adalah pada sebuah gedung 2 tingkat yang dikenakan gaya horizontal pada lantai dasar gedung untuk merepresentasikan gaya gempa bumi. Gaya gempa bumi direpresentasikan dengan percepatan lantai dasar yang dinotasikan dengan ẍg | ||
| + | |||
| + | ''' Modelling ''' | ||
| + | ''' Model Pegas-Massa ''' | ||
| + | Untuk dapat menghitung pergeseran dari bangunan dua lantai ketika dikenakan gaya horizontal pada tanah atau lantai dasar bangunan, kita bisa memodelkan bangunan tersebut menjadi model pegas-massa[1]. Berikut ini adalah konfirugasi permodelan pegas-massa pada bangunan dua lantai. | ||
| + | |||
| + | [[File:2lt.png]] | ||
| + | |||
| + | H1 dan H2 adalah tinggi masing-masing lantai, L adalah panjang lantai, c1 dan c2 adalah model damper untuk masing-masing lantai, m1 dan m2 adalah model massa untuk merepresentasikan massa masing-masing lantai, EIc1 dan EIc2 adalah kekakuan dari dinding masing-masing lantai, EIb1 dan EIb2 adalah kekakuan langit-langit masing-masing lantai, dan ẍg adalah percepatan tanah atau dasar bangunan. Model tersebut dapat dimodelkan ke dalam konfigurasi model pegas-massa yang umum kita temukan menjadi | ||
| + | |||
| + | [[File:4gbr.png]] | ||
| + | |||
| + | Figur b adalah model ketika kekakuan langit-langit lantai diasumsikan tak hingga, sehingga langit-langit tidak mengalami deformasi sama sekali. Figur tersebut dimodelkan ke dalam model pegas-massa menjadi seperti pada figur c. k1 dan k2 yang merupakan konstanta kekakuan pegas adalah fungsi dari EIc dan H. Figur d adalah kasus ketika langit-langit tidak diasumsikan memiliki kekakuan tak hingga, sehingga langit-langit juga mengalami deformasi. Pada kasus ini kekakuan langit-langit akan mempengaruhi nilai k1 dan k2 dan juga menambahkan model pegas baru dengan kekakuan k3 untuk merepresentasikan derajat kebebasan lateral dan rotasional, seperti yang dapat dilihat pada figur e. | ||
| + | Untuk kasus ini, kami memilih asumsi bahwa langit-langit tidak memiliki kekakuan tak hingga. Sehingga model pegas-massa yang kami gunakan adalah model pegas-massa pada figur e. Kemudian dari figur tersebut, kami akan melakukan analisis gaya untuk masing-masing massa. | ||
| + | Untuk massa 1, | ||
| + | [[File:Eq1jr.png]] | ||
| + | [[File:Eq2jr.png]] | ||
| + | Persamaan 1 dan 2 kemudian akan dihitung menggunakan metode numerik untuk mendapatkan nilai pergeseran lantai 1 dan lantai 2 (x1 dan x2). Konstanta pada persamaan tersebut akan diisi dengan nilai yang didapat dari jurnal referensi, yaitu sebagai berikut | ||
| + | m1 = 533,5 kg, m2 = 552,5 kg, c1 = 72,692 N.s/m, c2 = 68,688 N.s/m, k1 = 456,908 kN/m, k2 = 351.467 kN/m, k3 = -84,352 kN/m, ẍg = | ||
| + | |||
| + | Kondisi awal untuk x1, x2, ẋ1, dan ẋ2 adalah 0 | ||
| + | |||
| + | Untuk menyelesaikan persamaan dari sistem diatas, dapat diselesaiakn dengan menggunakan metode numerik untuk menyelesaikan persamaan differensial. Kami menggunakan metode Euler forward-backward untuk menyelesaikan dua persamaan differensial tersebut. Apabila x1 di misalkan sebagai u1 dan x2 dimisalkan dengan u2, maka: | ||
| + | |||
| + | v1 = du1/dt | ||
| + | |||
| + | v2 = du2/dt | ||
| + | |||
| + | Oleh karena itu, persamaan numeriknya menjadi: | ||
| + | |||
| + | [[File:Konsbang1.JPG]]] | ||
| + | |||
| + | Lalu, gaya eksitasi yang direpresentasikan oleh ẍg dibuat menjadi dua jenis kasus. Yaitu kasus gaya eksitasi konstan dan gaya eksitasi periodic. Dengan menggunakan excel, didapatkan bahwa hasil respons dari model di atas dapat dilihat sebagai berikut: | ||
| + | |||
| + | [[File:Konsbang2.JPG]] | ||
| + | |||
| + | [[File:Konsbang3.JPG]] | ||
| + | |||
| + | ''' Referensi ''' | ||
| + | [1] S. T. de La Cruz, M. A. Rodriguez, and V. Hernandez, “Using Spring-Mass Models to Determine the Dynamic Response of Two-Story Buildings Subjected to Lateral Loads,” 15th World Conf. Earthq. Eng., 2012. | ||
| + | |||
| + | == Menyelesaikan Kasus Osilasi pada Gedung n-Tingkat dengan Metode Komputasi. (Adhika, Fathur, Ali) == | ||
| + | |||
| + | |||
| + | '''Pendahuluan:''' | ||
| + | Artikel ini akan menjelaskan cara menyelesaikan kasus osilasi pada gedung n-tingkat yang dimodelkan dengan sistem pegas dan diselesaikan secara numerik. | ||
| + | |||
| + | |||
| + | '''Persamaan Dasar:''' | ||
| + | |||
| + | [[File:Komtek_Artikel3-k-AFA-Eq1.png]] | ||
| + | |||
| + | |||
| + | '''Penyelesaian:''' | ||
| + | Penyelesaian persamaan ini akan menggunakan metode Euler dengan skema forwards dan bacwards. Secara umum proses pemodelan dengan terknik ini akan menghasilkan persamaan: | ||
| + | |||
| + | [[File:Komtek_Artikel3-k-AFA-Eq2.png]] | ||
| + | |||
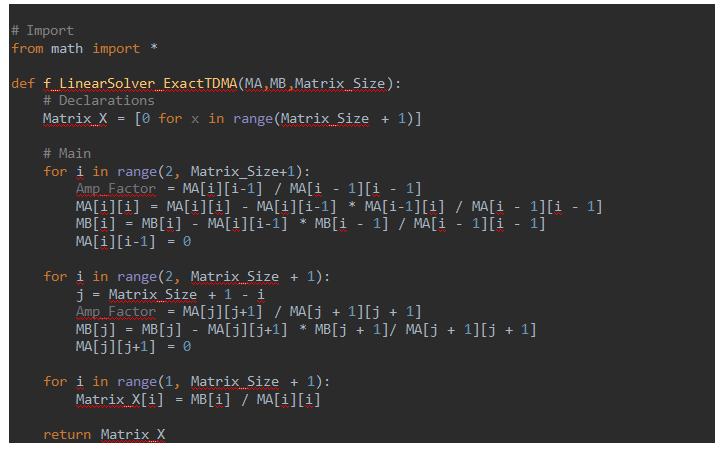
| + | Adapun untuk menyelesaikan persamaan kedua, matrix [A] akan diselesaikan dengan TDMA (Tri-Diagonal Matrix Algorithm). Seluruh penyelesaian kasus ini dilakukan dalam bahsa phyton. Berikut Source codenya: | ||
| + | |||
| + | [[File:Komtek_Artikel3-k-AFA-PIC1.png]] | ||
| + | |||
| + | [[File:Komtek_Artikel3-k-AFA-PIC2.png]] | ||
| + | |||
| + | |||
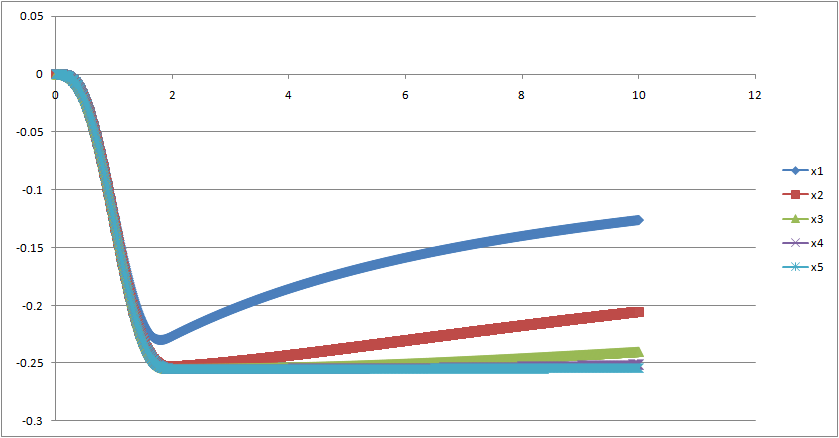
| + | '''Hasil:''' | ||
| + | Hasil dari perhitungan ini adalah sebagai berikut: | ||
| + | |||
| + | [[File:Komtek_Artikel3-k-AFA-PIC3.png]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Artikel Komputasi Teknik Sistem Pada Gedung Bertingkat Dengan 3 Model Strukstur (Adam, Aji, Alghi, Iqbal) == | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | |||
| + | File:Coverkomptek.jpg | ||
| + | File:lapafitro1.jpg|800px | ||
| + | File:lapafitro2.jpg|800px | ||
| + | File:lapafitro3.jpg|800px | ||
| + | File:lapafitro4.jpg|800px | ||
| + | File:lapafitro5.jpg|800px | ||
| + | File:lapafitro6.jpg|800px | ||
| + | File:lapafitro7.jpg|800px | ||
| + | File:lapafitro8.jpg|800px | ||
| + | File:lapafitro9.jpg|800px | ||
| + | File:lapafitro10.jpg|800px | ||
| + | File:lapafitro11.jpg|800px | ||
| + | File:lapafitro12.jpg|800px | ||
| + | File:lapafitro13.jpg|800px | ||
| + | File:lapafitro14.jpg|800px | ||
| + | File:lapafitro15.jpg|800px | ||
| + | File:lapafitro16.jpg|800px | ||
| + | File:lapafitro17.jpg|800px | ||
| + | File:lapafitro18.jpg|800px | ||
| + | File:lapafitro19a.jpg|800px | ||
| + | File:lapafitro20.jpg|800px | ||
| + | File:lapafitro21.jpg|800px | ||
| + | File:lapafitr022.jpg|800px | ||
| + | File:lapafitro23.jpg|800px | ||
| + | File:lapafitro24.jpg|800px | ||
| + | File:lapafitro25.jpg|800px | ||
| + | File:lapafitro26.jpg|800px | ||
| + | File:lapafitro27.jpg|800px | ||
| + | File:lapafitro28.jpg|800px | ||
| + | File:lapafitro29.jpg|800px | ||
| + | File:lapafitro30.jpg|800px | ||
| + | File:lapafitro31.jpg|800px | ||
| + | File:lapafitro32.jpg|800px | ||
| + | File:lapafitro33.jpg|800px | ||
| + | File:lapafitro34.jpg|800px | ||
| + | File:lapafitro35.jpg|800px | ||
| + | File:lapafitro36.jpg|800px | ||
| + | File:lapafitro37.jpg|800px | ||
| + | File:lapafitro38.jpg|800px | ||
| + | File:lapafitro39.jpg|800px | ||
| + | File:lapafitro40.jpg|800px | ||
| + | |||
| + | File:lapafitro1b.jpg|800px | ||
| + | File:lapafitro2b.jpg|800px | ||
| + | File:lapafitro3b.jpg|800px | ||
| + | |||
| + | </gallery> | ||
| + | |||
| + | |||
| + | == Artikel Komputasi Teknik ''1-Storey Frame Under an Impulse Force (Simulation by ANN)'' oleh [http://air.eng.ui.ac.id/index.php?title=Ardy.lefran Ardy], [http://air.eng.ui.ac.id/index.php?title=I_Gusti_Agung_Ayu_Desy_Wulandari Desy], [http://air.eng.ui.ac.id/index.php?title=Ronald_Akbar Ronald] dan [http://air.eng.ui.ac.id/index.php?title=Yophie.dikaimana Yophie] == | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | File:1-STOREY FRAME 01.jpg | ||
| + | File:1-STOREY FRAME 02.jpg | ||
| + | File:1-STOREY FRAME 03.jpg | ||
| + | File:1-STOREY FRAME 04.jpg | ||
| + | File:1-STOREY FRAME 05.jpg | ||
| + | File:1-STOREY FRAME 06.jpg | ||
| + | File:1-STOREY FRAME 07.jpg | ||
| + | File:1-STOREY FRAME 08.jpg | ||
| + | File:1-STOREY FRAME 09.jpg | ||
| + | </gallery> | ||
Latest revision as of 10:57, 8 June 2020
<- back to Studi kasus komputasi teknik
Contents
- 1 Knowledge Base
- 2 Case Study
- 3 Terjemahan
- 4 Artikel
- 5 Tugas Artikel Wisnu Harry Ichwan Fadli
- 6 Tugas Artikel Kania, Chandra, Dieter, Evi
- 7 Artikel Kolaborasi : USING MASS-SPRING (MS) MODEL FOR BUILDING ANALYSIS arranged by Oldy Fahlovvi, Muchalis Zikramansyah Masuku, Ahmad Zikri, Muhammad Irfan Dzaky
- 8 Tugas Artikel Aghnia, Daniel, Joko, Paskal
- 9 Tugas Artikel Fajri, Kania Dyah, Maha, Wafirul
- 10 Tugas Artikel Adinda, Ilham Bagus, Adzanna, Maheka
- 11 STUDI KASUS OSILASI GEDUNG DUA TINGKAT MENGGUNAKAN MODEL PEGAS-MASSA; Edo, Raihan, Jeri, Shabrina
- 12 Menyelesaikan Kasus Osilasi pada Gedung n-Tingkat dengan Metode Komputasi. (Adhika, Fathur, Ali)
- 13 Artikel Komputasi Teknik Sistem Pada Gedung Bertingkat Dengan 3 Model Strukstur (Adam, Aji, Alghi, Iqbal)
- 14 Artikel Komputasi Teknik 1-Storey Frame Under an Impulse Force (Simulation by ANN) oleh Ardy, Desy, Ronald dan Yophie
Knowledge Base
Case Study
Terjemahan
Terjemahan
Model Elemen Hingga Sederhana untuk Menggambarkan Struktur Mass-Spring dalam Simulasi Dinamis
Rúbia M. Bosse, André Teófilo Beck
University of São Paulo - Departemen Teknik Struktural, São Carlos, rubiabosse@usp.br, atbeck@sc.usp.br
Abstrak
Makalah ini menyajikan pendekatan langkah demi langkah, didaktik untuk membangun model elemen hingga yang disederhanakan (Finite Element/FE)mereproduksi hasil yang diperoleh dengan model mass-spring (MS) atau bangunan geser. Tujuan utamanya adalah untuk mengekspos keterbatasan masing-masing model, dan untuk memfasilitasi perbandingan antara hasil numerik yang diperoleh dengan model yang berbeda,sangat sering oleh penulis yang berbeda. Contoh aplikasi adalah sistem kontrol getaran, analisis model teoritis, mesin pemodelan komponen dan jaringan lunak. Makalah ini menyajikan hipotesis yang diperlukan untuk membangun hierarkis model, membahas pengaruh masing-masing asumsi / penyederhanaan dalam respons struktural. Dengan tujuan ini, komputer kode diimplementasikan untuk menyelesaikan struktur kerangka 2D di bawah beban dinamis dengan model pegas massal dan posisi model elemen hingga mempertimbangkan analisis geometrik nonlinier. Hasil penelitian menunjukkan bahwa hipotesis yang diajukan adalah cukup untuk mereproduksi dalam metode FE respon yang sama dari model MS mengalami impuls dan beban gempa.
Kata kunci: Model elemen hingga, model pegas massa, struktur kerangka 2D, beban dinamis.
1. PENDAHULUAN
Dua metodologi utama yang digunakan untuk mengevaluasi perilaku mekanik struktur seperti bangunan di bawah beban dinamis adalah model Mass-Spring (MS) dan model Finite Element (FE). Penerapan masing-masing teknik ini biasanya tergantung pada jenis struktur, keakuratan analisis yang diminta, dan kompleksitas struktur. Telah diketahui bahwa semua model menghadirkan ketidakpastian terkait kesetiaan untuk mewakili perilaku struktural yang nyata. Dalam hal ini, interpretasi kritis terhadap penyederhanaan dan keterbatasan model teknik diperlukan untuk analisis dan desain yang andal.
Secara umum, model massa-pegas memiliki pendekatan diskrit dan formulasi matematika sederhana. Massa terkonsentrasi dalam titik-massa dan terhubung satu sama lain dengan pegas linier yang mewakili kekuatan elastis internal yang bekerja di antara massa. Model MS sederhana karena menghasilkan sangat sedikit derajat kebebasan, di mana persamaan gerak dapat diselesaikan secara analitis dengan modal superposisi. Ini secara signifikan mengurangi waktu pemrosesan untuk analisis dinamis. Model massa-pegas populer karena secara konsep lebih sederhana dan lebih mudah diimplementasikan daripada model yang lebih konsisten secara fisik berdasarkan metode elemen hingga. Selain itu, model MS sangat fleksibel untuk perubahan topologi.
Formulasi ini biasanya diterapkan untuk mewakili struktur sebagai sistem kontrol getaran, bangunan dalam perilaku global, elemen mesin dan bahan jaringan lunak. Model MS juga sangat berlaku untuk melakukan analisis keandalan dan respon stokastik, di mana biaya komputasi merupakan masalah mendasar, karena struktur perlu dipecahkan secara berulang. Kelemahan utama dari model MS adalah bahwa mereka dianggap tidak tepat untuk memperkirakan perilaku mekanik struktur yang dapat dideformasi. Model MS mengabaikan persamaan konstitutif material, dan menghadirkan sejumlah derajat kebebasan yang mungkin terlalu kecil untuk jenis analisis tertentu.
Beberapa kemajuan telah dibuat dalam model MS untuk meningkatkan representasi realistis dari struktur yang dapat dideformasi. Beberapa penelitian mengusulkan metode baru untuk mendapatkan koefisien kekakuan pegas, yang lain telah menyarankan modifikasi model tradisional (Kuether dan Allen, 2012, Geethu et al., 2015), termasuk misalnya pegas nonlinear dan piezometrik dalam analisis sistem kontrol getaran (Harne, 2013), penggabungan pegas kontak kubik untuk mensimulasikan kehilangan kontak (Huajiang dan Guan, 2016) dan pemecah implisit cepat untuk model MS standar (Liu et al., 2013, Zheng et al., 2017)
Di sisi lain, metode elemen hingga (FE) berasal dari mekanika kontinum dan menjadi salah satu metode yang paling sering digunakan untuk memecahkan masalah sistem mekanik. Metode FE memerlukan penggunaan komputer secara intensif dan biaya komputasinya dapat menjadi penghalang untuk analisis skala besar. Namun, teknik ini mampu mensimulasikan sistem fisik yang kompleks, menyelesaikan masalah multi-dimensi dengan nonlinier (Dhatt, Touzot dan Legrançois, 2012).
Model FE mendiskritisasi struktur dalam elemen-elemen kecil untuk merepresentasikan perilaku berkelanjutan. Metode ini menggunakan pendekatan variabel yang tidak diketahui untuk mengubah persamaan diferensial parsial menjadi persamaan aljabar yang diselesaikan melalui metode numerik. Model FE cocok untuk mengevaluasi respons berbagai struktur, terutama karena undang-undang dasar material dipertimbangkan dalam formulasi matematika. Namun, kemajuan ini ada harganya: semakin halus modelnya, semakin kompleks solusinya, yang mengarah ke biaya komputasi yang besar.
Tantangan yang cukup besar di bidang metode FE adalah pertimbangan perpindahan besar dalam tubuh yang cacat. Upaya penelitian membahas pengembangan formulasi yang mempertimbangkan efek nonlinier dalam bahan konstitutif atau dalam kondisi batas (perpindahan atau rotasi besar). Dalam masalah perpindahan besar, deskripsi Total Lagrangian menunjukkan metode yang efisien untuk menyelesaikan masalah dinamis struktur padat, karena mempertimbangkan konfigurasi referensi yang unik dan tetap: matriks massa tetap konstan dan solusi keseimbangan dinamis diperoleh dengan lebih mudah. Solusi masalah yang mempertimbangkan analisis geometri nonlinear dengan deskripsi Total Lagrangian dapat diverifikasi dalam Mondkar dan Powell (1977), Wood dan Zienkiewicz (1977), Surana (1983), Coda dan Greco (2004). Pendekatan alternatif untuk merepresentasikan analisis nonlinier geometris menggunakan deskripsi Lagrangian total adalah model FE posisional. Dalam teknik ini, parameter nodal adalah koordinat nodal (posisi) dan dimungkinkan untuk menggunakan kinematika Reissner yang tepat dalam evaluasi perpindahan dan rotasi untuk struktur rangka. Contoh aplikasi dari formulasi ini dapat dilihat di Coda dan Paccola (2014), Reis dan Coda (2014), dan Siqueira dan Coda (2016, 2017).
Saat ini, dengan kemajuan teknik komputasi untuk meningkatkan waktu pemrosesan, model FE yang disempurnakan semakin dapat diterapkan untuk menyelesaikan masalah mekanis apa pun. Dalam makalah ini, kami bermaksud untuk mendefinisikan hipotesis yang berlaku untuk model FE untuk membuatnya mewakili hasil yang kompatibel dengan model massa-pegas dengan idealisasi kerangka geser. Ini juga merupakan tujuan untuk mengamati dan mengukur perbedaan yang disebabkan oleh hipotesis ini dalam respon struktur, mengevaluasi keuntungan dan keterbatasan masing-masing model untuk memperkirakan respon struktur yang terkena berbagai sumber beban dinamis.
Untuk melakukan analisis ini, kode komputasi diterapkan untuk kedua model: model FE posisional dan model MS. Contoh-contoh yang disajikan dalam makalah ini berkaitan dengan struktur rangka yang tidak terbungkus yang dapat mewakili bangunan. Contoh 1 dan 2 memperlihatkan struktur satu dan lima lantai yang tereksitasi oleh gaya impuls. Contoh ketiga berkaitan dengan struktur yang sama dari contoh 2 yang bersemangat dengan catatan Gempa Bumi El Centro. Respons dalam domain waktu dan frekuensi dipelajari.
2. MODEL MASS-SPRING
Diterjemahkan oleh : Mohamad Wafirul Hadi, Kania Dyah Nastiti, Maha Hidayatullah Akbar, Fajri Octadiansyah, Afitro Adam
Analisis dinamis menggunakan model massa-pegas diskrit sangat umum dalam literatur dan menyajikan keuntungan sebagai alat sederhana untuk mengevaluasi respons dinamis struktur. Metode analisis ini memerlukan waktu pemrosesan yang sedikit, karena mereduksi struktur menjadi beberapa derajat kebebasan, dan karena jawabannya dapat diperoleh secara analitik dengan metode modal superposisi. Model MS tradisional berurusan dengan analisis linier, yaitu keseimbangan dihitung pada posisi awal, menyajikan matriks kekakuan konstan (Warburton, 1976 dan Paultre, 2010). Dalam makalah ini model bangunan geser dipertimbangkan. Idealisasi ini biasanya digunakan untuk mengevaluasi respons bangunan yang mengalami kegembiraan dinamis. Model bangunan geser biasanya mempertimbangkan bahwa massa kolom dapat diabaikan, dan massa lantai terkonsentrasi di lantai (titik massa). Juga, balok dan pelat dianggap kaku dalam arah longitudinal dan dalam lentur, kolom kaku untuk regangan aksial tetapi fleksibel secara transversal. Idealisasi bangunan geser mengasumsikan bahwa bangunan hanya menyajikan perpindahan horisontal, karena pembengkokan kolom. Mempertimbangkan kerangka bidang gambar 3 lantai yang tidak tertutup pada Gambar 1, model bangunan geser dapat dimodelkan dengan mendefinisikan massa dan pegas yang setara dan membuat matriks yang sesuai untuk solusi persamaan gerak.
dengan M matriks massa diagonal sistem dengan massa lantai yang terkonsentrasi pada titik-massa, 𝑢̈ adalah vektor percepatan. Paket karena redaman itu diperoleh sebagai:
di mana 𝑪 adalah matriks redaman, 𝑐 adalah koefisien redaman, 𝑢̇ adalah vektor kecepatan. Kekuatan elastis dapat ditentukan sebagai:
dimana𝑲 adalah matriks kekakuan,
adalah koefisien kekakuan kolom dan 𝑢 adalah vektor perpindahan. Keseimbangan gerak dapat didefinisikan sebagai:
Untuk kasus beban gerakan tanah, vektor eksitasi diperoleh dengan mengalikan massa setiap derajat kebebasan dengan percepatan gempa dalam arah yang sesuai, untuk setiap langkah waktu. Dengan cara ini, analisis sesuai dengan respons struktur dengan penyangga tetap, keluar oleh kekuatan eksternal dalam massanya; dan 𝑝 (𝑡) adalah diadaptasi menjadi 𝑝 (𝑡) sebagai:
di mana 𝑢̈ (𝑡) adalah vektor percepatan horizontal gempa bumi, 𝑟 adalah vektor dengan 𝑛 garis sama dengan jumlah bingkai cerita. Vektor ini mewakili koefisien pengaruh dalam perpindahan nodal, ketika perpindahan kesatuan adalah dikenakan pada dukungan. Persamaan solving (5), respon dinamis linear dari struktur diperoleh, dikenakan beban dinamis. Menyelesaikan kesetimbangan dinamis analitis, metode modal superposisi dapat diterapkan; Metode ini didasarkan pada kenyataan bahwa, untuk model redaman tertentu, persamaan gerak 𝑛 ditambah dari sistem diskrit dapat dimodifikasi melalui a transformasi untuk koordinat modal dalam persamaan decoupled. Metode ini menggunakan sifat ortogonalitas dari mode getaran untuk memisahkan sistem persamaan; karenanya tanggapan diperoleh dengan menyelesaikan persamaan diferensial mirip dengan persamaan yang dikembangkan untuk satu derajat struktur kebebasan (Warburton, 1976, Clough and Penzien, 1993, dan Rao, 2010). Dalam tulisan ini, untuk menyederhanakan solusi dan membuat kode umum untuk semua jenis beban, linier keseimbangan persamaan gerak diselesaikan dengan menerapkan integrasi waktu Newmark, dengan mempertimbangkan rata-rata konstan akselerasi, menurut Paultre (2010). Model MS mempertimbangkan idealisasi bangunan geser sangat digunakan karena fleksibilitas untuk mewakili struktur yang berbeda topologi. Namun, untuk mewakili struktur ramping yang menghadirkan perilaku mampudeformasi, yang lebih fisik metodologi yang realistis mungkin diperlukan.
3. POSITIONAL FINITE ELEMENT
Analisis nonlinier geometris digunakan untuk menangani defleksi besar: posisi keseimbangan struktur dicari negara terlantar. Dalam apa yang disebut pendekatan FE posisional, ruang non-dimensi dibuat dan kelengkungan relatif elemen bingkai dihitung untuk konfigurasi awal dan untuk yang cacat (Coda dan Greco 2004). Itu Posisi keseimbangan adalah variabel utama yang tidak diketahui, dan diperoleh dari prinsip total potensial stasioner energi. Formulasi Lagrangian total digunakan, menggunakan konfigurasi referensi yang unik, posisi awal; di dalam konteksnya, matriks massa adalah konstan. Elemen frame dengan empat node dan pendekatan kubik digunakan. Untuk analisis nonlinier geometris, deskripsi rinci tentang kinematika elemen awalnya ditunjukkan dan prinsip energi stasioner digunakan untuk menulis persamaan keseimbangan dinamis. Sistem nonlinier persamaan diselesaikan dengan menggabungkan integrasi waktu Newmark dengan prosedur Newton-Raphson, mengikuti Coda dan Paccola (2014).
3.1 Finite Element Model pada Posisi Frame
Diterjemahkan Oleh : Ahmad Zikri, Muhammad Irfan Dzaky, Muchalis Zikramansyah Masuku, Oldy Fahlovvi
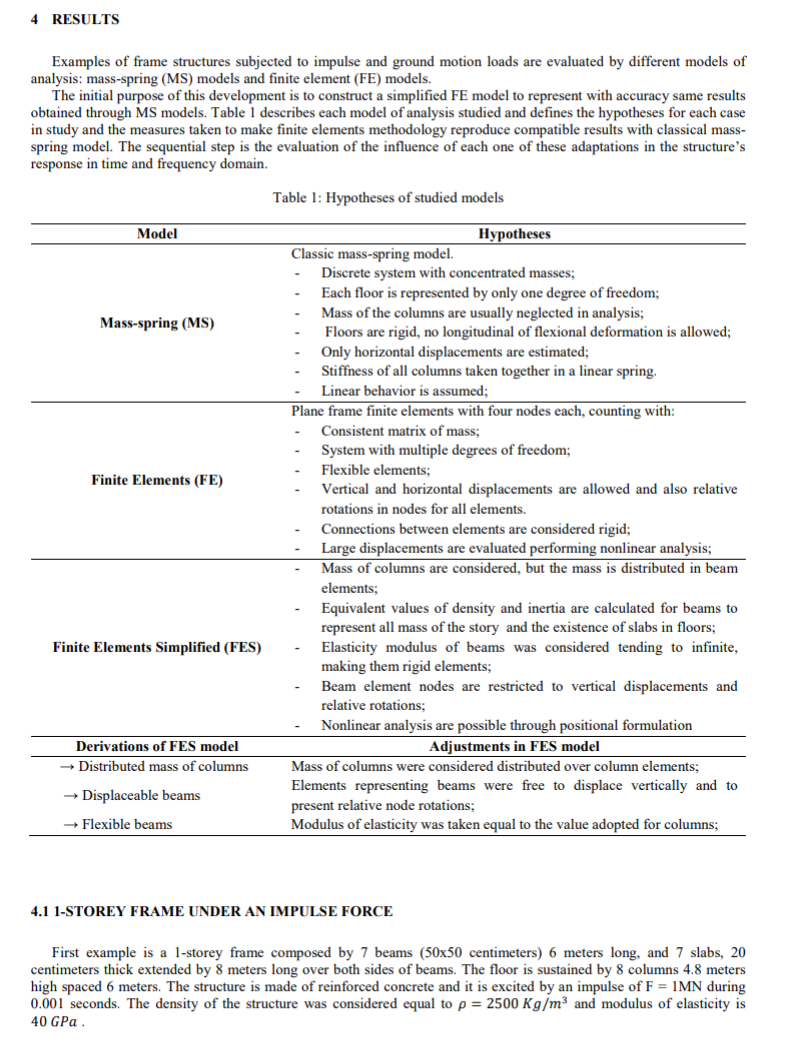
4. RESULTS
Dalam paper ini diperlihatkan berberapa hasil analisis yaitu dengan metode Mass-Spring (MS), dan Finite Element (FE) kepada sebuah struktur yang diberikan impuls dan gerakan pada bagian dasar. Tujuan awal dari paper ini adalah untuk mengembangkan model FE yang lebih sederhana yang tetap akurat sama dengan hasil yang diperoleh dari model MS. Tabel 1 memperlihatkan analisa dan hypothesis dari setiap model yang digunakan serta langkah-langkah yang diambil agar model FE yang disederhanakan tetap mempunyai hasil yang sebanding dengan model MS. Tahap sequential merupakan evaluasi dari setiap model pada response structure terhadap waktu dan secara frekuensi.
Tabel 1. Hypothesis dari model MS, FE, dan FES
Mass Spring (MS):
- Sistem diskrit dengan massa yang terkonsentrasi
- Setiap lantai diwakili oleh 1 degree of freedom
- Massa dari kolom/tiang vertical ccenderung diabaikan dalam analysis
- Lantai merupakan benda rigid. Tidak ada deformasi.
- Hanya mengestimasi pergerakan horizontal
- Stiffness dari kolom langsung diwakili oleh sebuah pegas linear
- Sistem diasumsikan berkerja secara linear
Finite Element(FE):
- Bidang terdiri dari 4 node
- Terdapat matrix massa
- System yang terbentuk mempunyai banyak degree of freedom
- Elementnya bergerak dengan flexible (Vertical, horizontal, serta putaran relatif)
- Koneksi antara elemen diasumsikan rigid
- Pergerakan yang besar dianalisa secara nonlinear
Finite Element Simplified (FES):
- Massa kolom ikut diperhitungkan, hanya saja massa ini dimodelkan dalam batang horizontal dengan distribusi secara merata. Pemodelan ini selain mempengaruhi massa dari batang horizontal, massa ini juga mempengaruhi pada densitas dan inertia.
- Modulus Elastisitas dari batang horizontal diasumsikan tak hingga, sehingga dapat dianggap rigid.
- Element dalam batang horizontal terrestriksi pada pergerakan secara vertical dan putaran relatif.
- Dapat terjadi nonlinear analysis
4.1. Rangka 1 Lantai Dibawah Sebuah Gaya Impuls
Diterjemahkan oleh: Ardy, Desy, Ronald, Yophie
Contoh pertama adalah sebuah kerangka bangunan 1 lantai yang terbentuk dari tujuh buah balok (50 x 50 cm) dengan panjang 6 meter, dan 7 lempengan, 20 cm ketebalan diperpanjang oleh panjang 8 meter pada kedua sisi dari balok. Lantai ditopang oleh 8 kolom dengan tinggi 4.8 meter berjarak 6 meter satu sama lain. Struktur tersebut terbuat dari beton yang diperkuat dan digemparkan oleh sebuah impuls dengan F = 1 MN selama 0.001 detik. Kepadatan dari struktur dipertimbangkan sama dengan ρ = 2500 kgm^-3, dan modulus elastisitasnya sebesar 40 GPa.
Kerangka ini telah dimodelkan sebagai model MS (Pegas-massa) dan model FE (Elemen hingga). Untuk model MS, struktur tersebut digambarkan sebagai sebuah massa m = 186900 kg (balok ditambah massa lempengan dengan mengabaikan massa kolom) terhubung ke suatu pegas linear dengan kekakuan K = 8 kolom. (12EI/L^3) = 181 MNm^-1, menghasilkan suatu sistem tidak teredam dengan satu derajat kebebasan.
Pada model FE, struktur tersebut didiskritisasi ke dalam 22 elemen rangka simpul 4, dihitung dengan 201 derajat kebebasan di mana semua hipotesis yang dikembangkan dalam Tab. 1 diuji. Untuk representasi struktur dalam model FE, sebuah momen equivalen inersia telah dihitung untuk set (balok + lempeng); juga nilai kepadatan equivalen telah dihitung untuk memperhitungkan semua hipotesis dengan memperhatikan massa dari struktur tersebut.
Respons dinamis dari struktur dievaluasi dalam model MS, FES dan FE melalui teknik integrasi waktu Newmark dengan perbedaan pada model FE dan FES sistem persamaan nonlinier dilinearisasi dengan prosedur Newton Raphson. Analisis dilakukan dalam total waktu 1,0 detik sebagai domain waktu dan hasil ini digunakan untuk membuat FFT (Fast Fourier Transform) pada respon studi frekuensi alami dari struktur.
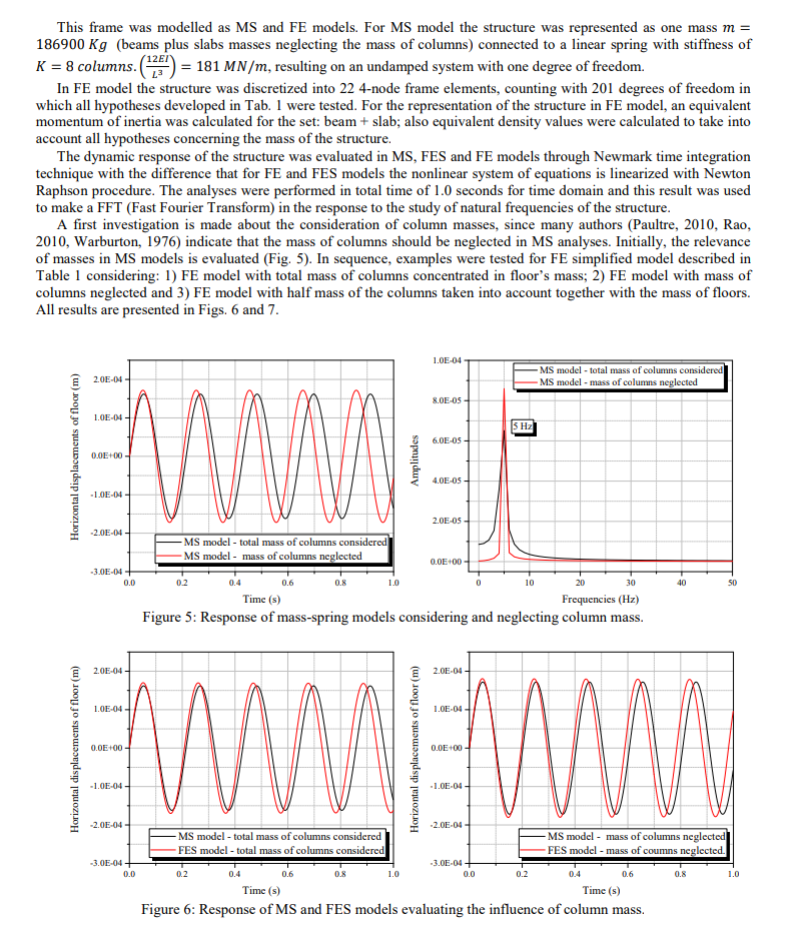
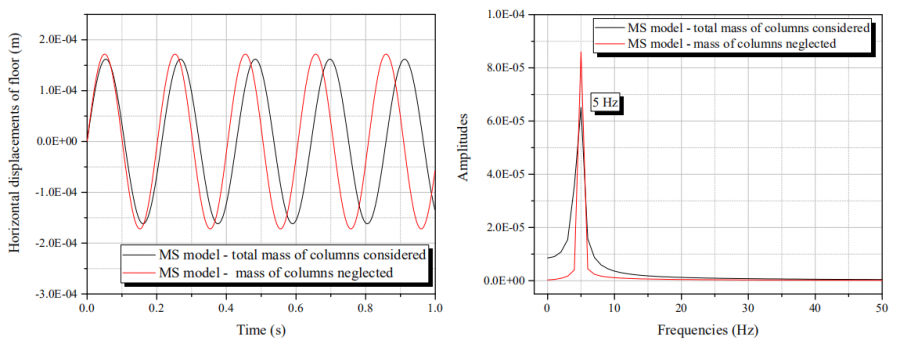
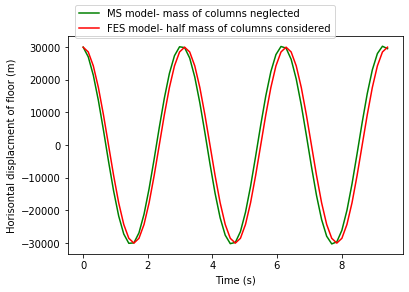
Investigasi pertama dibuat mengenai pertimbangan massa kolom, karena banyak penulis (Paultre, 2010, Rao, 2010, Warburton, 1976) yang menyatakan bahwa massa kolom harus diabaikan dalam analisis MS. Mula -mula relevansi massa dalam model MS dievaluasi (Gbr. 5). Secara berurutan, contoh-contoh diuji untuk FE model sederhana yang dijelaskan dalam Tabel 1 dengan mempertimbangkan: 1) model FE dengan massa total kolom terkonsentrasi pada massa lantai; 2) model FE dengan massa kolom diabaikan dan 3) model FE dengan setengah massa kolom diperhitungkan bersama dengan massa lantai. Semua hasil ditunjukkan pada Gbr. 6 dan 7.
Dari Gambar 5 dapat digaris bawahi bahwa pergeseran puncak respon dari struktur mengabaikan dan mempertimbangkan massa dari kolom model MS sekitar 5%. Pada frekuensi domain, frekuensi natural yang sama bisa dilihat di kedua kasus (5 Hz), dengan perbedaan hanya pada kedua amplitudo. Hasil ini memperlihatkan bahwa frekuensi bertentangan dengan estimasi, pertimbangan massa pada kolom analisis MS tidak relevan.
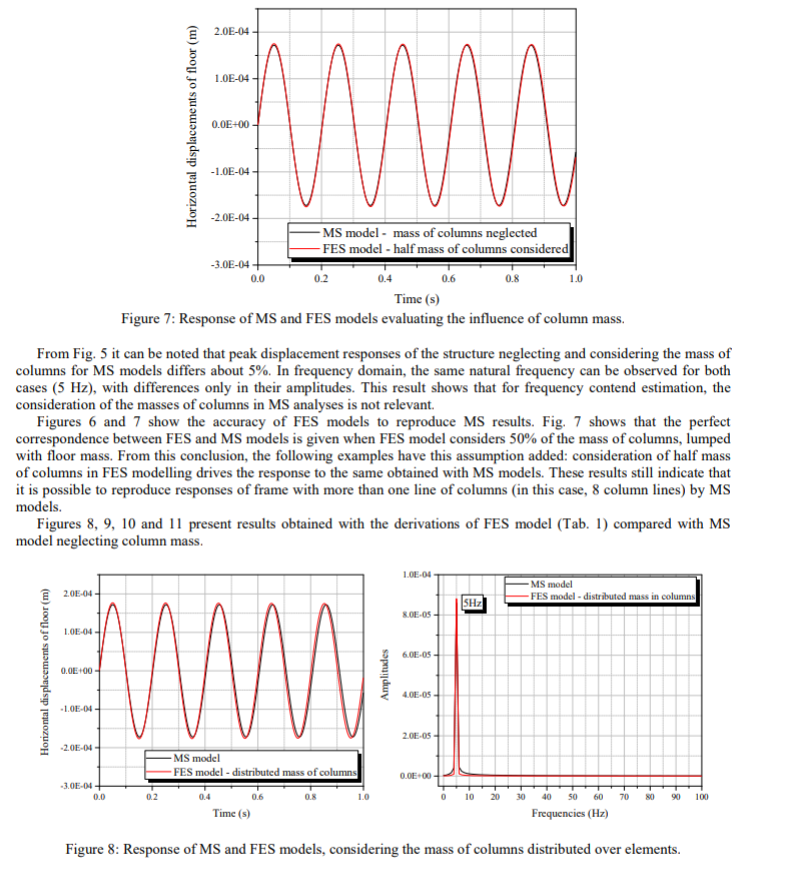
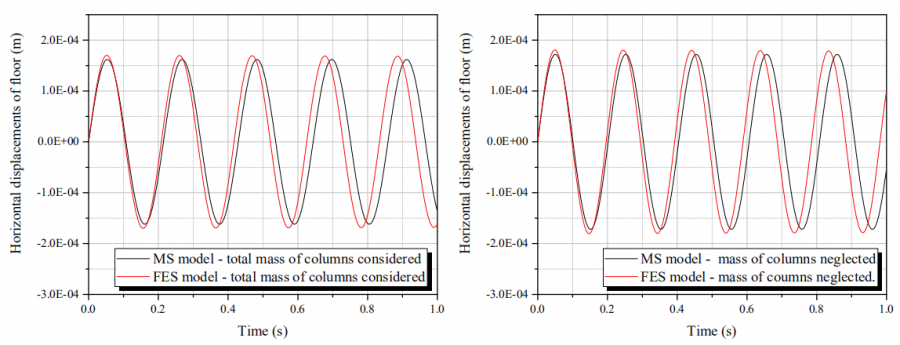
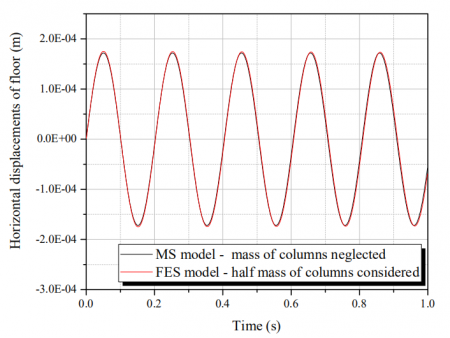
Gambar 6 dan 7 menunjukkan akurasi model FES untuk memproduksi hasil MS. Gambar 7 menunjukkan korespondensi sempurna antara model FES dan MS yang memiliki pertimbangan 50 % dari kolom massa, disatukan dengan massa dasar. Dari kesimpulan tersebut, contoh berikut ini mempunyai penambahan asumsi : pertimbangan dari setengah massa kolom pada model FES mendorong respons untuk mencapai hasil yang sama dengan model MS. Hasil ini mengindikasikan bahwa memungkinkan untuk memproduksi response frame dengan lebih dari satu baris kolom (pada kasus ini, 8 baris kolom. ) dengan model MS.
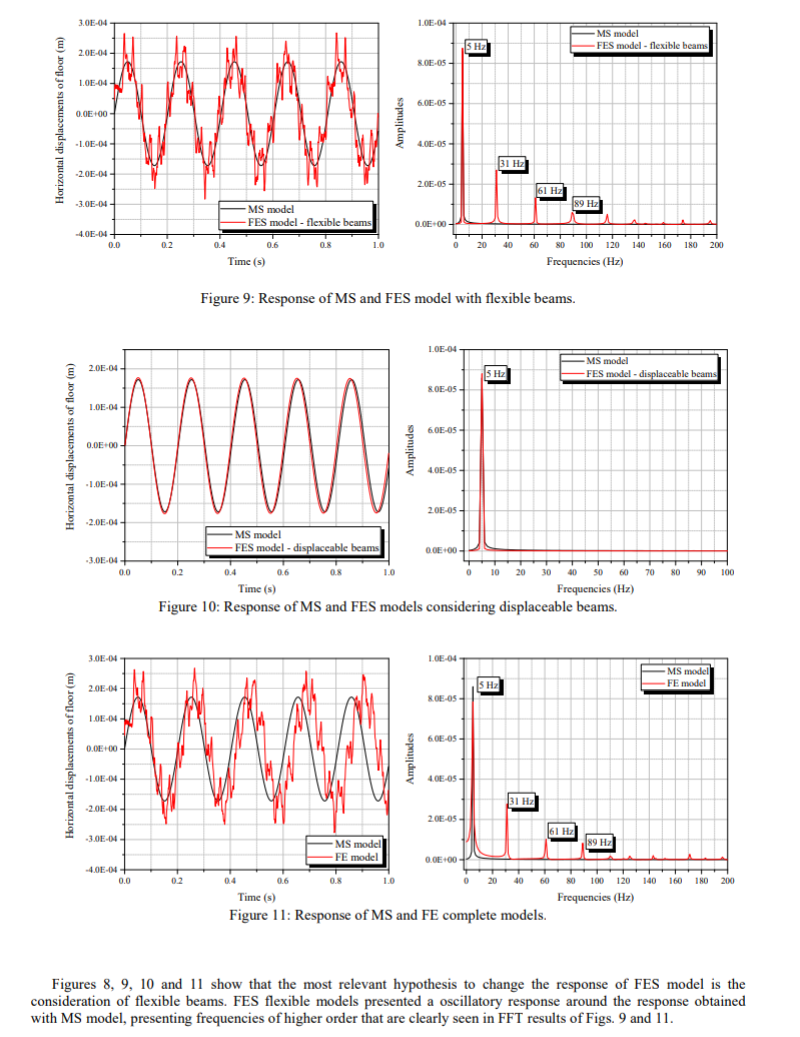
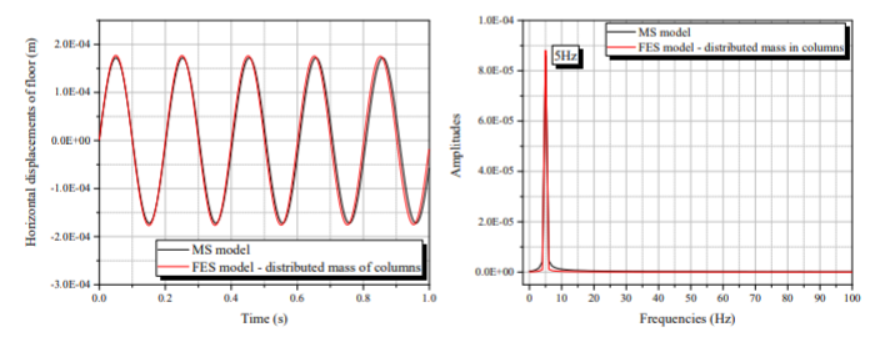
Gambar 8, 9, 10, dan 11 adalah hasil dari FES model (Tabel 1) dibandingkan dengan model MS dengan mengabaikan kolom massa.
Gambar 8, 9, 10, dan 11 menunjukkan bahwa perkiraan yang paling relevan untuk mengubah resspns dari model FES adalah pertimbangan dari balok flexible. Model fleksibel FES memperlihatkan sebuah respons osilasi di sekitar respons yang dihasilkan oleh model MS, terlihat frekuensi pada tingkatan lebih tinggi yang terlihat dengan jelas pada hasil FFT Gambar 9 dan 11.
Hasil dari Gambar 8 dan 10 menunjukkan pertimbangan dari distribusi massa pada kolom elemen, pergeseran pada arah vertical dan rotasi pada balok tidak menyebabkan perubahan yang signifikan pada hasil awal model FES, sangat mirip dengan hasil MS. Dapat dilihat juga bahwa esimasi dari frekuensi natural dari stukrur, semua model konvergen pada 5 Hz, menunjukkan bahwa frekuensi dari respons domain kurang sensitif pada asumsi model yang dibahas ini. Gambar 11 juga memperlihatkan bagaimana jarak dari respons pada model FE secara keseluruhan, tanpa simplifikasi, dan model MS : puncak respons amplitude lebih tinggi untuk model FE dan pada kasus ini perpindahan terjadi pada frekuensi yang tinggi.
4.2. Rangka 5 Lantai Terhadap Gaya Impuls
Diterjemahkan oleh : Edo, Shabrina, Jeri, dan Raihan
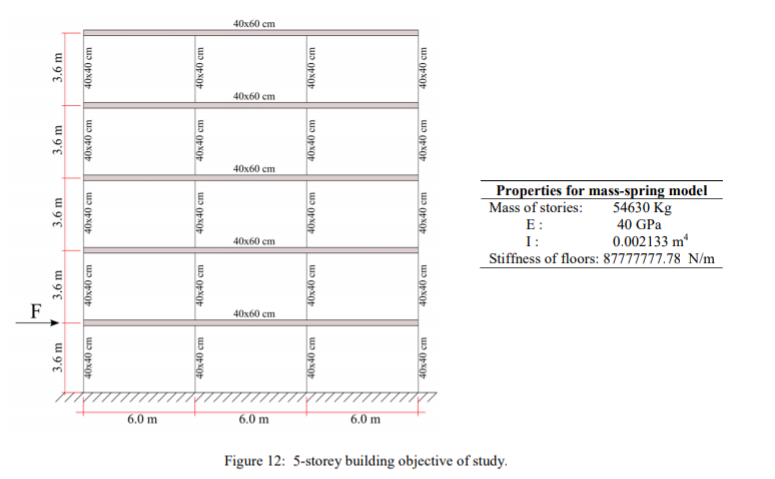
Contoh kedua menjabarkan tentang Rangka 5 lantai yang terbuat dari beton bertulang dengan dimensi yang tertera pada Figur 12. Struktur dikenakan gaya impuls F = 100 MN selama 0,001 detik. Gaya impuls diberikan pada lantai pertama dari struktur untuk menghindari efek non-linier dari model 'Finite Element'. Sebuah lempeng setebal 14 cm memanjang sejauh 6 meter pada tiap balok dipasangkan pada bangunan tersebut. Struktur ini dimodelkan sesuai dengan metodologi yang telah dideskripsikan pada Bagian 1.
Untuk model massa-pegas, struktur direpresentasikan oleh 5 susunan massa-pegas, menghasilkan 5 derajat kebebasan yang menjelaskan pergeseran horizontal lantai (massa lempeng dijumlahkan ke dalam total massa lantai). Dalam model FE dan FES, struktur didiskritisasi ke dalam lima puluh elemen bingkai 4-node, sehingga dihasilkan 150 derajat kebebasan yang menggambarkan translasi (horizontal dan vertikal) dan rotasi dalam vektor normal dari node. Untuk merepresentasikan lempeng, momen inersia ekuivalen dihitung untuk balok yang memiliki kekakuan balok ditambah lempeng; Densitas balok juga dikoreksi berdasarkan massa lempeng.
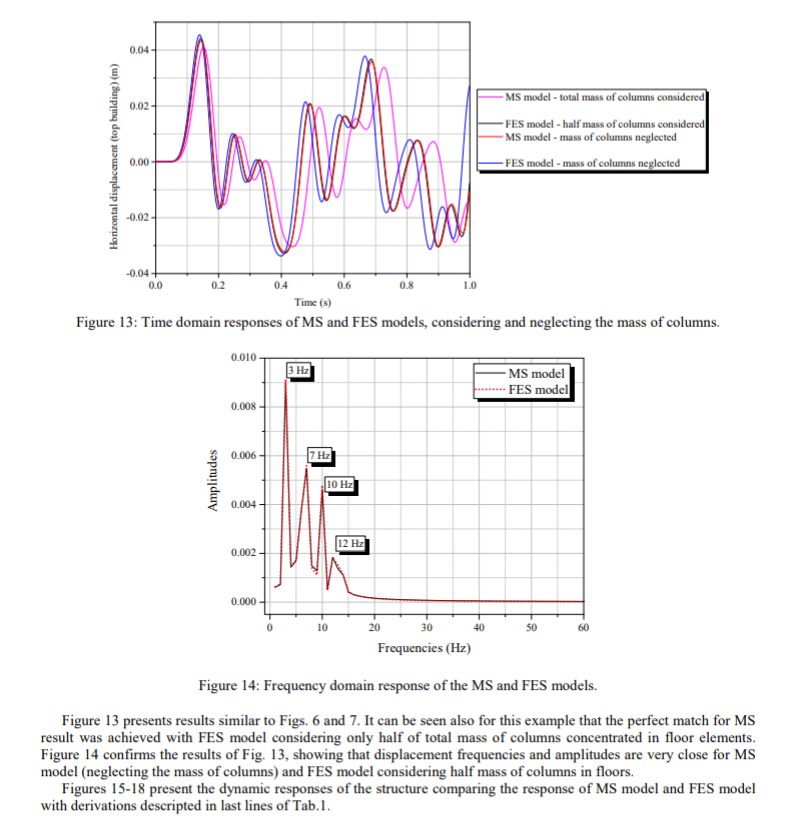
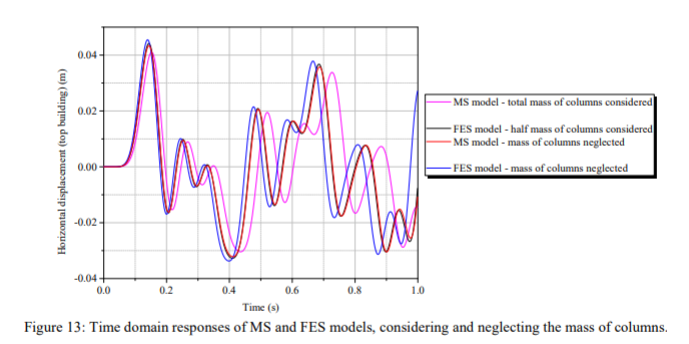
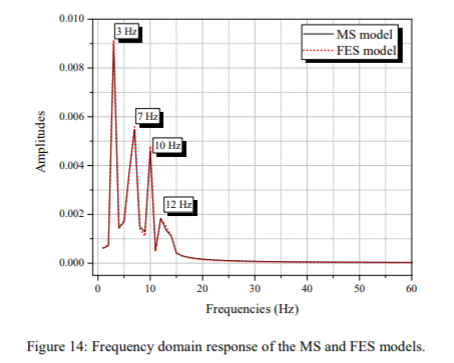
Gambar 13 dan 14 menunjukkan hasil awal di sekitar perkiraan massa dari kolom kolom untuk model MS dan FES dalam analisis yang dilakukan selama pergerakan satu detik
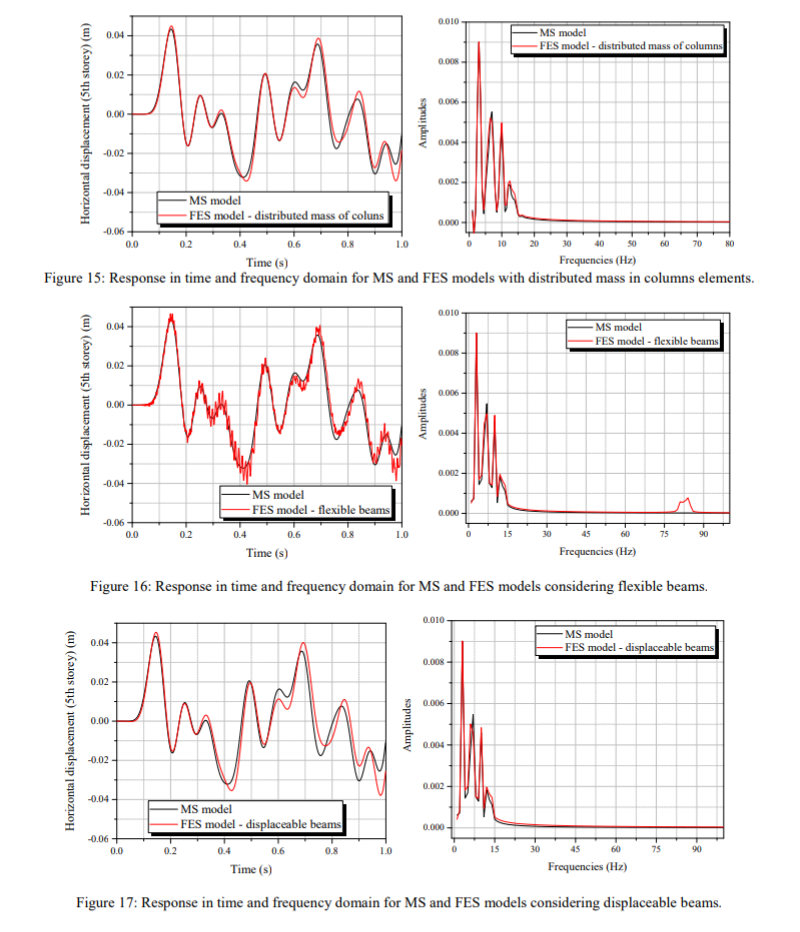
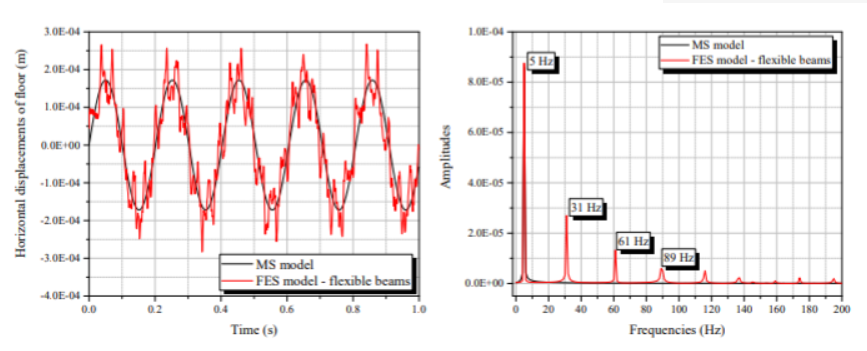
Gambar 13 menyajikan hasil yang mirip dengan gambar.6 dan 7. Dapat dilihat juga untuk contoh ini bahwa kecocokan sempurna untuk hasil MS dicapai dengan model FES mengingat hanya setengah dari total massa kolom terkonsentrasi di elemen lantai. Gambar 14 mengkonfirmasi hasil gambar 13, menunjukkan bahwa frekuensi perpindahan dan amplitudo sangat dekat untuk model MS (mengabaikan massa kolom) dan model FES mempertimbangkan setengah massa kolom di lantai. Gambar 15-18 menyajikan respons dinamis struktur yang membandingkan respons model MS dan model FES dengan derivasi yang dijelaskan dalam baris terakhir Tab.1
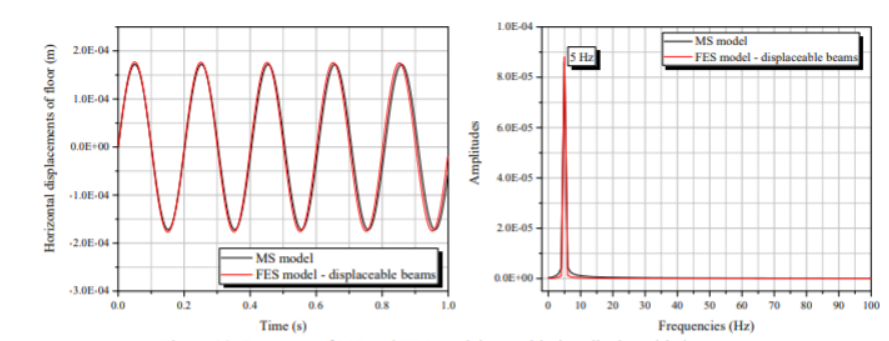
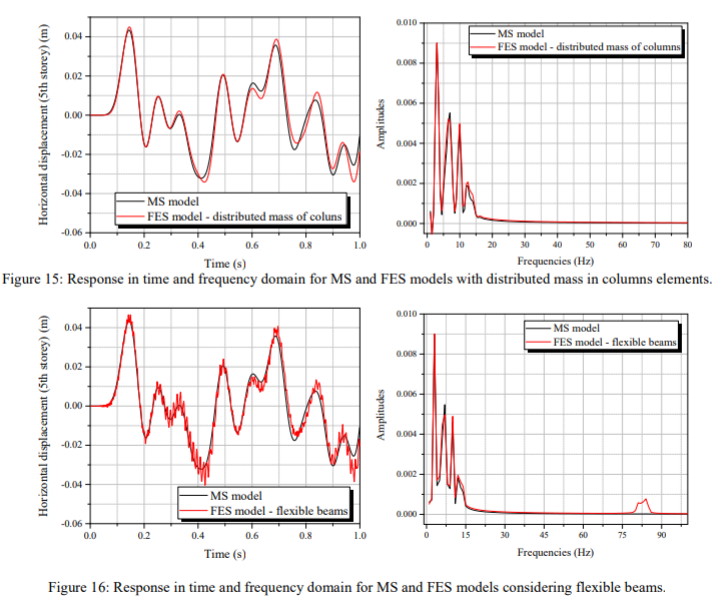
Gambar 15 mengindikasikan bahwa pertimbangan dari masa yang terdistribusi pada kolom-kolom sistem tidak terlalu berpengaruh terhadap response yang diberikan berdasarkan model FES yang disederhanakan. Seluruh nilai tertinggi/puncak dari frekuensi naturalnya cocok, dan amplitudo dari response yang diberikan juga serupa.
Gambar 16 menunjukkan bahwa response yang diperoleh berdasarkan model FES mempertimbangkan balok/beam flexible yang berosilasi dengan frekuensi yang tinggi di sekitar respons yang diberikan dari model MS. FFT membuktikan bahwa puncak-puncak dari frekuensi osilasi tersebut berkisar 80 Hz. Apabila dirata-ratakan, respons pergeseran/displacement yang diberikan dan frekuensi yang diberikan pada saat awal menghasilkan hasil yang relatif dekat terhadap response yang didapat berdasarkan model MS.
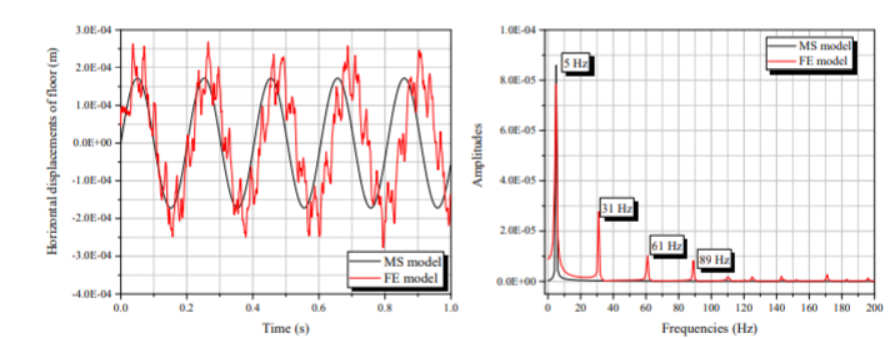
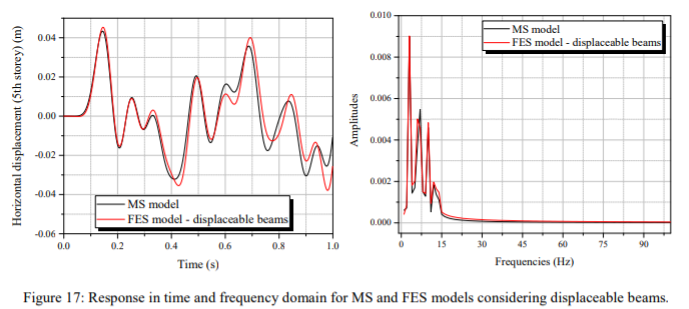
Gambar 17 membandingkan respons model MS dengan model FES dengan mempertimbangkan balok yang dapat dipindahkan. Asumsi perpindahan vertikal dan rotasi balok mempengaruhi sebagian perpindahan dan frekuensi respons pada struktur. Dalam FFT dapat dicatat bahwa hanya frekuensi natural kedua tidak sama dengan hasil yang ditunjukkan oleh model MS. Dalam analisis model FE lengkap, ditunjukkan pada gambar 18, dapat dicatat bahwa perpindahan yang terjadi berbeda dari model MS. Model FE menyajikan osilasi dengan frekuensi tinggi dan perpindahan puncak yang lebih tinggi, dibandingkan dengan hasil model MS; Namun, karakteristik perpindahan serupa, menghadirkan siklus frekuensi rendah dengan jumlah yang sama. Dalam domain frekuensi, perbedaan signifikan dalam puncak amplitudo dapat diamati, juga beberapa perbedaan dalam frekuensi natural. Frekuensi yang lebih tinggi muncul sekitar 80 Hz, memvalidasi perilaku osilasi yang diamati dalam respons perpindahan. Untuk semua kasus analisis bangunan, menunjukkan perilaku linier dalam analisis FE, mengambil sejumlah kecil iterasi untuk konvergensi solusi numerik.
4.3. Pergerakan Rangka 5-Lantai oleh Gempa Bumi
Kania, Evi, Chandra, Dieter
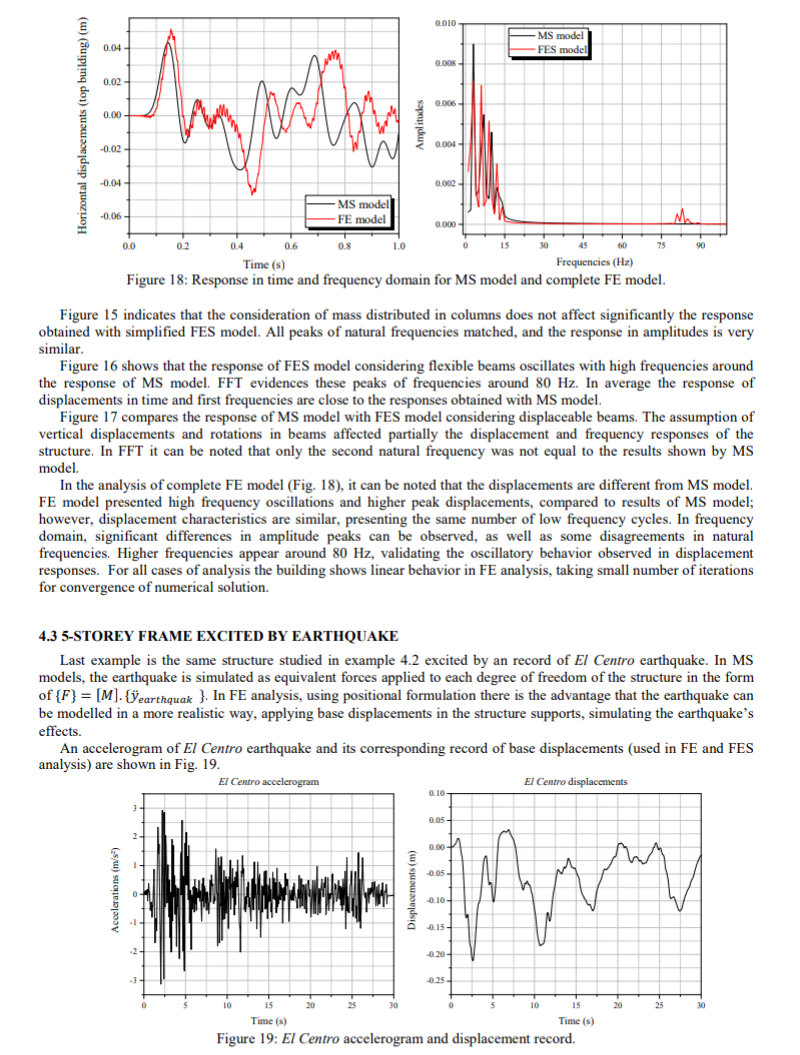
Contoh terakhir menggunakan struktur yang sama dan sudah dipelajari pada contoh 4.2 didapatkan dari rekaman gempa bumi EL Centro. Di MS model, gempa bumi disimulasikan sebagai gaya ekuivalen yang diterapkan ke setiap derajat kebebasan dari struktur dalam bentuk {F}=[M].{y ̈_earthquake}. Di dalam FE analisis, penggunaan persamaan posisi di sini memberikan keuntungan bahwa gempa bumi dapat dimodelkan dengan sedemikian rupa hingga terlihat lebih rill, penggunaan basis perpindahan dalam pendukung sturuktur, dan simulalsi efek yang terjadi akibat gempa bumi.
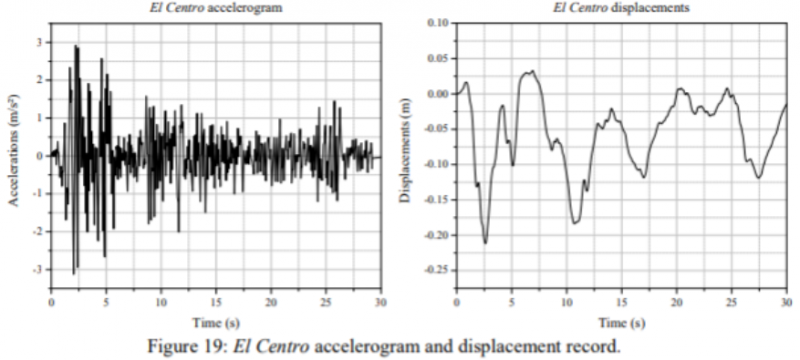
Accelerogram dari gempa bumi EL Centro dan berdasarkan rekaman dari basis perpindahan (digunakan dalam analisa FE dan FES) ditunjukan pada gambar 19.
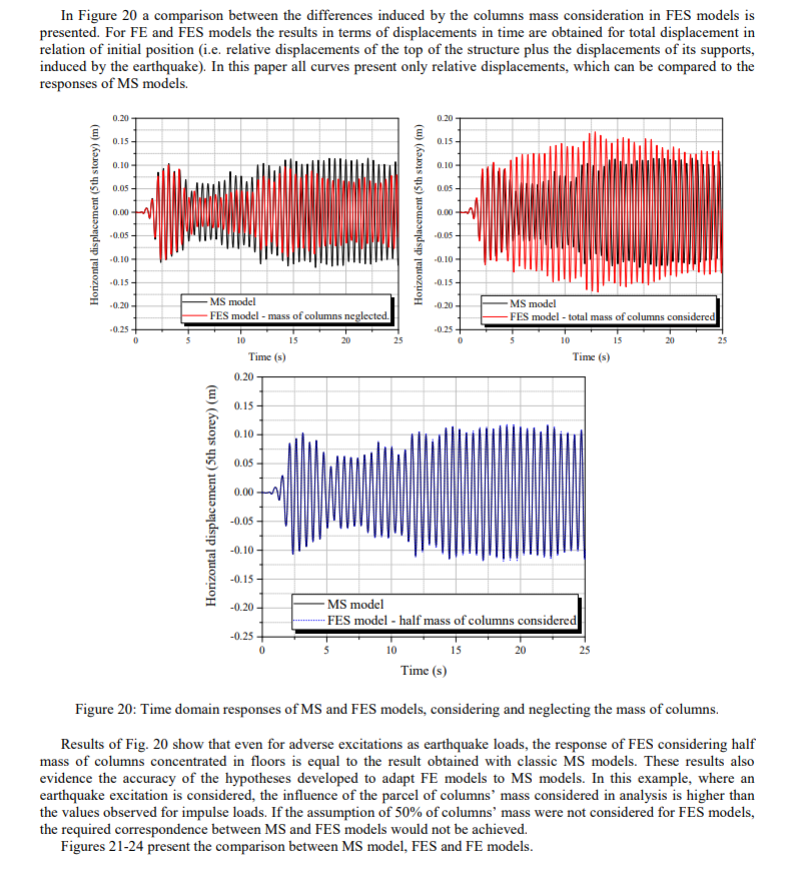
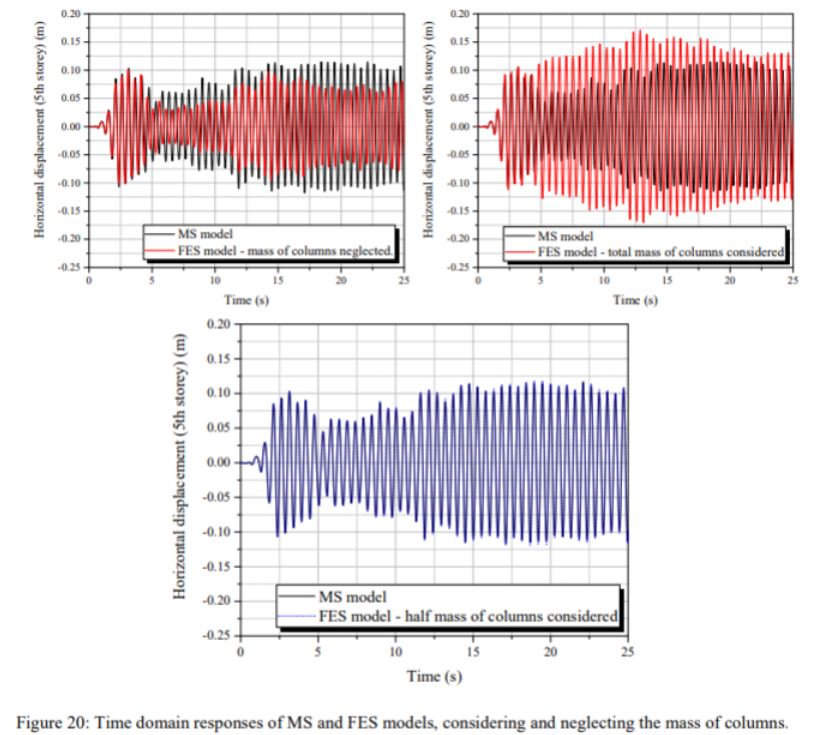
Gambar 20 menjelaskan sebuah perbandingan antara perbedaan-perbedaan yang disebabkan oleh perhitungan massa kolom dalam permodelan FES. Untuk model FE dan FES, hasil dalam hal perpindahan (displacement) terhadap waktu diperoleh untuk total perpindahan dalam kaitannya dengan initial position (i.e.perpindahan relatif pada struktur atas ditambah perpindahan pada struktur pendukungnya, yang disebabkan oleh gempa bumi). Pada studi ini, semua curve hanya menunjukkan perpindahan relatif, yang mana dapat dibandingkan dengan respons dari model MS.
Hasil dari Gambar 20 menunjukkan bahwa dengan adanya gangguan/eksitasi dalam bentuk gempa, respon dari FES pada permasalahan-½ massa kolom terpusat di lantai, memiliki hasil yang sama dengan penggunaan model MS dasar. Hal tersebut membuktikan keakuratan hipotesis yang sudah dibangun untuk menyelaraskan FE models dengan MS models. Pada contoh ini, dimana terdapat eksitasi berupa gempa, pengaruh dari bagian kolom masa dalam analisis adalah lebih tinggi daripada nila yang didapat dengan impulse loads. Jika diasumsikan 50% massa kolom diabaikan untuk FES models, maka hubungan antara MS dan FES models tidak mungkin didapat. Gambar 21-24 menunjuklan perbandingan antara MS models, FES dan FE models.
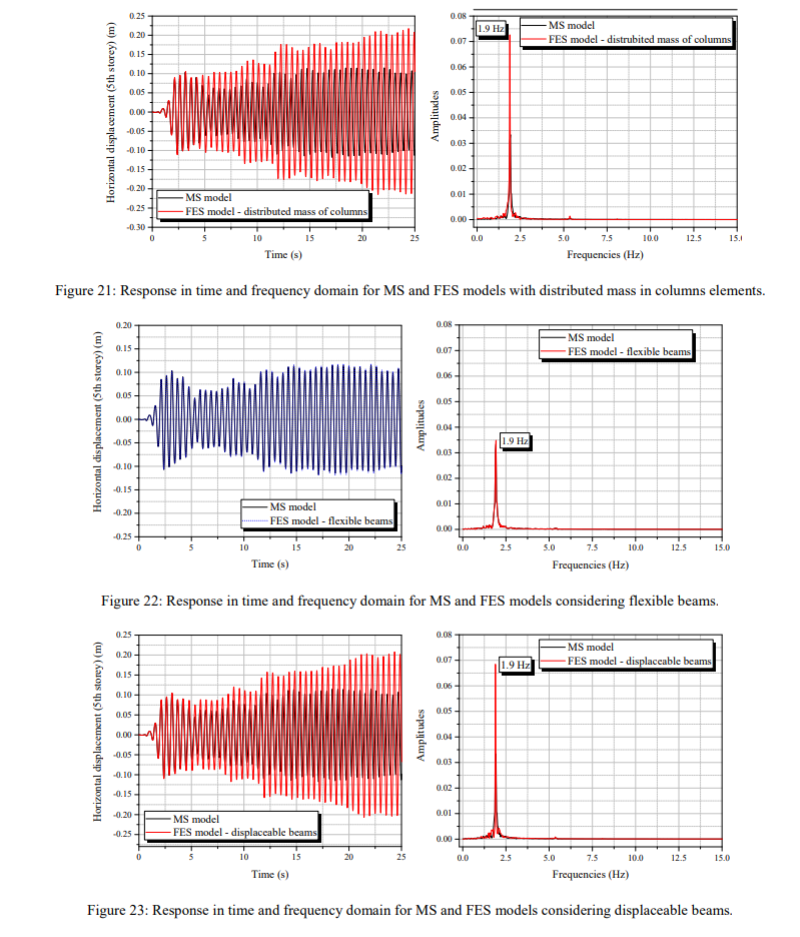
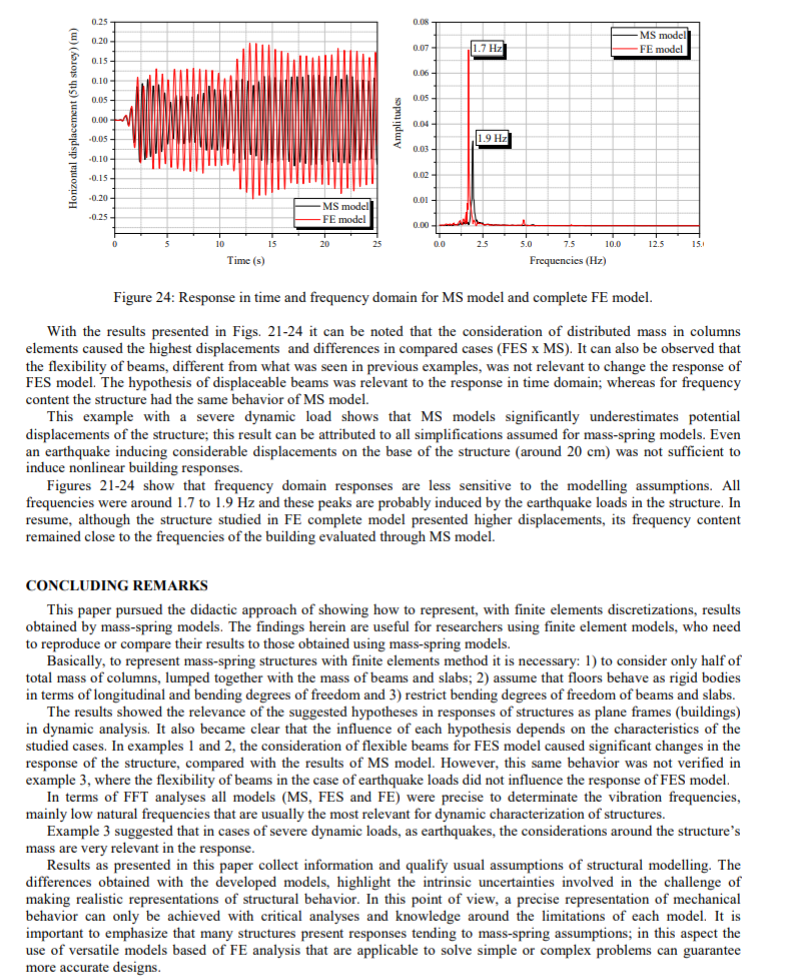
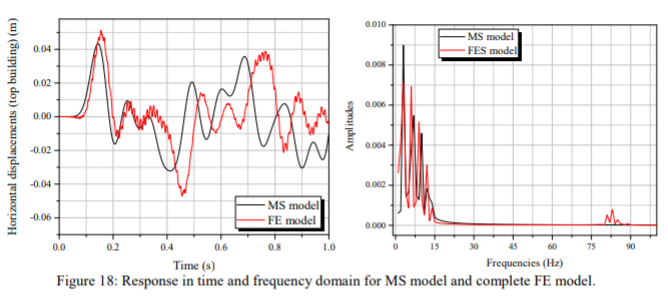
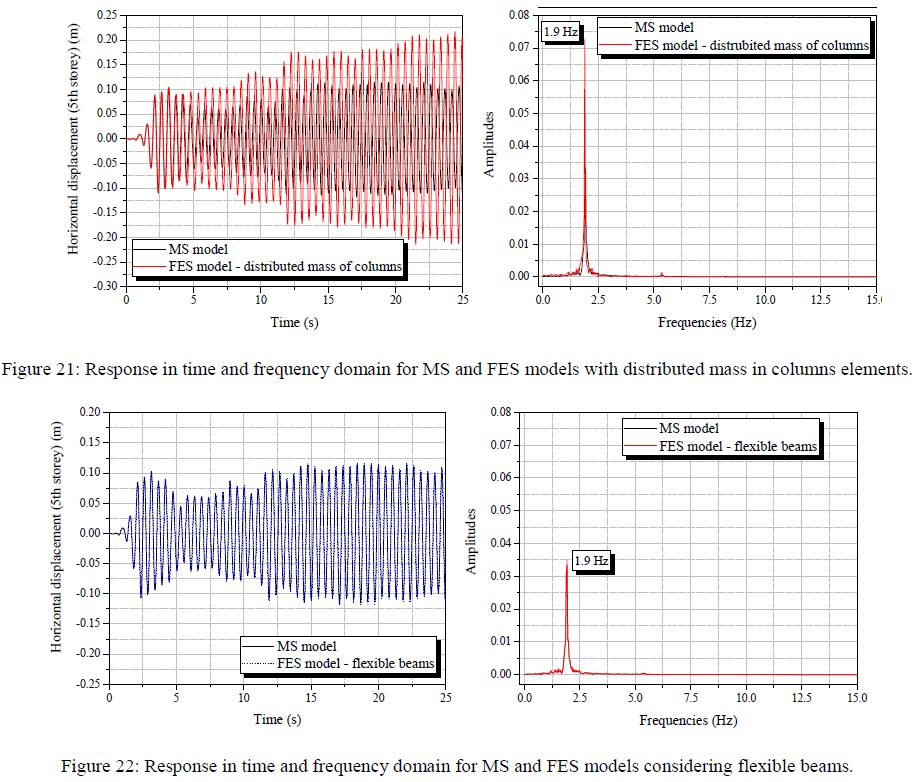
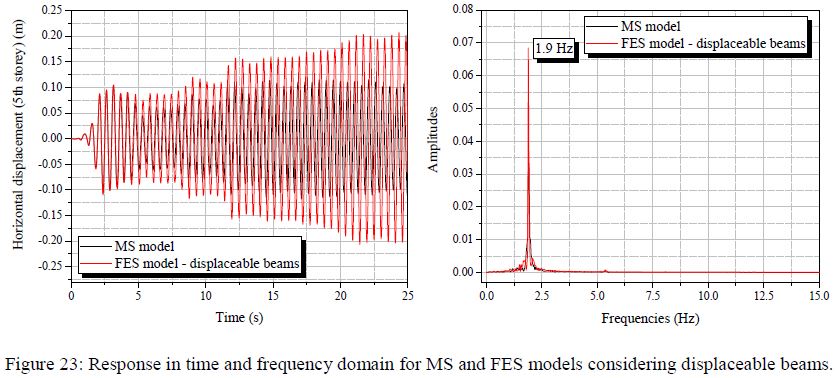
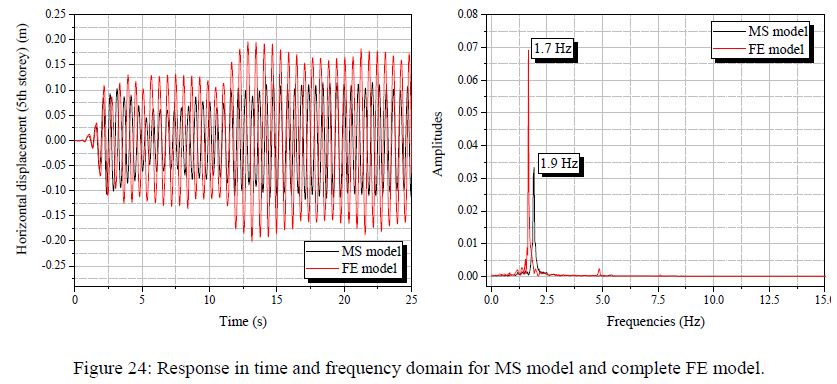
dengan hasil yang disajikan dalam gambar 21-24 dapat diketahui bahwa pertimbangan massa terdistribusi dalam elemen kolom menyebabkan perpindahan tertinggi dan perbedaan dalam kasus yang dibandingkan (FES x MS). Dapat juga diamati bahwa fleksibilitas balok, berbeda dari apa yang terlihat dalam contoh sebelumnya, dan hal ini perlu diperhatikan sebagai hal yang relevan untuk mengubah respons Model FES. Hipotesis balok yang dapat dipindahkan relevan dengan respons dalam domain waktu; sedangkan untuk konten frekuensi struktur memiliki perilaku yang sama dari model MS. Contoh ini dengan beban dinamis yang besar menunjukkan bahwa model MS secara signifikan tidak mementingkan potensi perpindahan struktur; hasil ini dapat dikaitkan dengan semua penyederhanaan yang diasumsikan untuk model pegas-massa. Bahkan gempa bumi yang menyebabkan perpindahan besar di dasar struktur (sekitar 20 cm) tidak cukup untuk memicu respons bangunan nonlinier. Gambar 21-24 menunjukkan bahwa respons domain frekuensi kurang sensitif terhadap asumsi pemodelan. Semua frekuensi sekitar 1,7 hingga 1,9 Hz dan puncak ini mungkin disebabkan oleh beban gempa dalam struktur. Dalam resume, meskipun struktur yang dipelajari dalam model FE menyajikan perpindahan yang lebih tinggi, konten frekuensinya tetap dekat dengan frekuensi bangunan yang dievaluasi melalui mode MS.
CONCLUDING REMARKS
Makalah ini mengupayakan pendekatan didaktik untuk menunjukkan bagaimana merepresentasikan, dengan diskritisasi elemen hingga, hasilnya diperoleh dengan model massa-pegas. Temuan di sini bermanfaat bagi para peneliti yang menggunakan model elemen hingga, yang membutuhkan untuk mereproduksi atau membandingkan hasilnya dengan yang diperoleh menggunakan model pegas massal.
Pada dasarnya, untuk merepresentasikan struktur pegas massa dengan metode elemen hingga, perlu: 1) mempertimbangkan hanya setengahnya massa total kolom, disatukan dengan massa balok dan pelat; 2) menganggap lantai berfungsi sebagai benda tegar dalam hal derajat kebebasan longitudinal dan lentur dan 3) membatasi derajat lentur kebebasan balok dan pelat.
Hasil penelitian menunjukkan relevansi hipotesis yang disarankan dalam respon struktur sebagai kerangka pesawat (bangunan) dalam analisis dinamis. Juga menjadi jelas bahwa pengaruh masing-masing hipotesis tergantung pada karakteristik mempelajari kasus. Dalam contoh 1 dan 2, pertimbangan balok fleksibel untuk model FES menyebabkan perubahan signifikan pada respon struktur, dibandingkan dengan hasil model MS. Namun, perilaku yang sama ini tidak diverifikasi di Contoh 3, di mana fleksibilitas balok dalam hal beban gempa tidak mempengaruhi respons model FES.
Dalam hal analisis FFT, semua model (MS, FES, dan FE) tepat untuk menentukan frekuensi getaran,terutama frekuensi alami rendah yang biasanya paling relevan untuk karakterisasi dinamis struktur.Contoh 3 menyarankan bahwa dalam kasus beban dinamis yang parah, seperti gempa bumi, pertimbangan di sekitar struktur Massa sangat relevan dalam respons.Hasil seperti yang disajikan dalam makalah ini mengumpulkan informasi dan memenuhi kualifikasi asumsi pemodelan struktural yang biasa. Itu perbedaan yang diperoleh dengan model yang dikembangkan, menyoroti ketidakpastian intrinsik yang terlibat dalam tantangan membuat representasi perilaku struktural yang realistis. Dalam sudut pandang ini, representasi mekanik yang tepat perilaku hanya dapat dicapai dengan analisis kritis dan pengetahuan di sekitar keterbatasan masing-masing model. ini penting untuk ditekankan bahwa banyak struktur menghadirkan respons yang cenderung pada asumsi pegas-massa; dalam aspek ini penggunaan model serbaguna berdasarkan analisis FE yang dapat diterapkan untuk memecahkan masalah sederhana atau kompleks dapat menjamin desain yang lebih akurat
Artikel
Tugas Artikel Wisnu Harry Ichwan Fadli
Menunjukkan bahwa korespondensi sempurna antara FES dan model MS diberikan ketika model FES mempertimbangkan 50% dari massa kolom, disamakan dengan massa lantai. Dari kesimpulan ini, contoh-contoh berikut memiliki asumsi ini ditambahkan: pertimbangan setengah massa kolom dalam pemodelan FES mendorong respons yang sama diperoleh dengan model MS. Hasil ini masih menunjukkan bahwa dimungkinkan untuk mereproduksi respons bingkai dengan lebih dari satu baris kolom (dalam hal ini, 8 baris kolom) oleh model MS.
Figure 7
Dari Gambar. 5 dapat dicatat bahwa respon perpindahan puncak struktur mengabaikan dan mempertimbangkan massa kolom untuk model MS berbeda sekitar 5%. Dalam domain frekuensi, frekuensi alami yang sama dapat diamati untuk kedua kasus (5 Hz), dengan perbedaan hanya dalam amplitudo mereka. Hasil ini menunjukkan bahwa untuk estimasi pertentangan frekuensi, pertimbangan massa kolom dalam analisis MS tidak relevan. Gambar 6 dan 7 menunjukkan keakuratan model FES untuk mereproduksi hasil MS. Gambar. 7 menunjukkan bahwa korespondensi sempurna antara FES dan model MS diberikan ketika model FES mempertimbangkan 50% dari massa kolom, disamakan dengan massa lantai. Dari kesimpulan ini, contoh-contoh berikut memiliki asumsi ini ditambahkan: pertimbangan setengah massa kolom dalam pemodelan FES mendorong respons yang sama diperoleh dengan model MS. Hasil ini masih menunjukkan bahwa dimungkinkan untuk mereproduksi respons bingkai dengan lebih dari satu baris kolom (dalam hal ini, 8 baris kolom) oleh model MS.
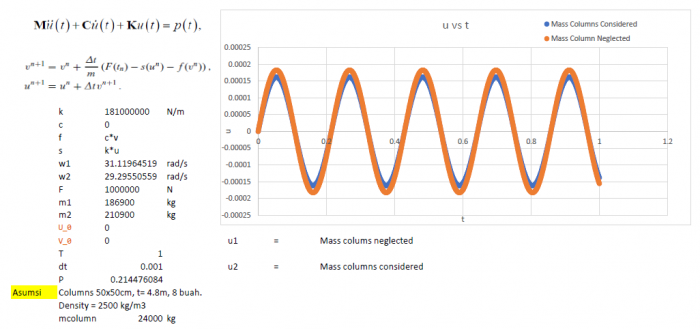
Untuk kasus yang dikerjakan adalah pada bangunan dengan penjalasan seperti pada laporan di bawah ini
slide 1 (judul)
slide 2 (FEM initial condition)
initial condition disini digambarkan bahwa, konstruksi rangka gedung dapat di modelkan sebagai batang kantilever dengan panjang (l) yang menerima gaya (F) arah lateral akibat gempa, sehingga akibat gaya F tersebut menyebabkan terjadinya displacement pada rangka tersebut sejauh x.
slide 3 (dasar teori defelksi untuk perhitungan manual-eksak)
perpindahan posisi (displacement ) merupakan defleksi pada rangka. sehingga dapat dirumuskan besarnya displacennet sebagai persamaan defleksi pada batang kantilever. besarnya defleksi dipengaruhi oleh : bentuk penampang batang, panjang batang, gaya yang bekerja dan juga modulus elastistas material.
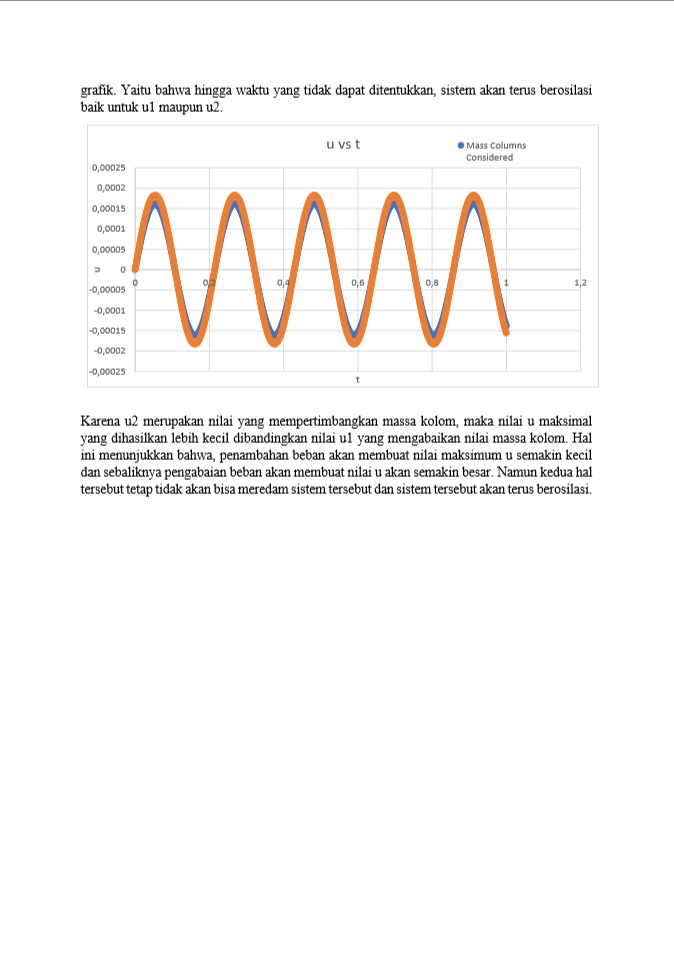
slide 4 (hasil perhitungan manual)
berdasarkan rumus defleksi tersebut didapatkan hasil perhitungan seperti pada grafik. dimana displacemnt yang terjadi akibat gaya F merupakan suatu bentuk osilsasi dengan simpangan terjauh mencapai 0.8
slide 5 (pemodelan FES)
pemodelan FES ini berangkat dari MS model, dimana FES ini merupakan bentuk sederhana dari FEM yang diberikan pembatasan-pembatasan, pergerakan kolom akibat gaya F dari gempa hanya ke arah horisontal saja sehingga mengabaikan gerakan vertikan maupun rotasi pada kolom.
slide 6 (hasil perhitungan FES)
hasil perhitungan dengan FES ini menunjukan simpangan terjauh dari kolom yang diakibatkan oleh gaya F dari gempa adalah sejauh 0.8 mm
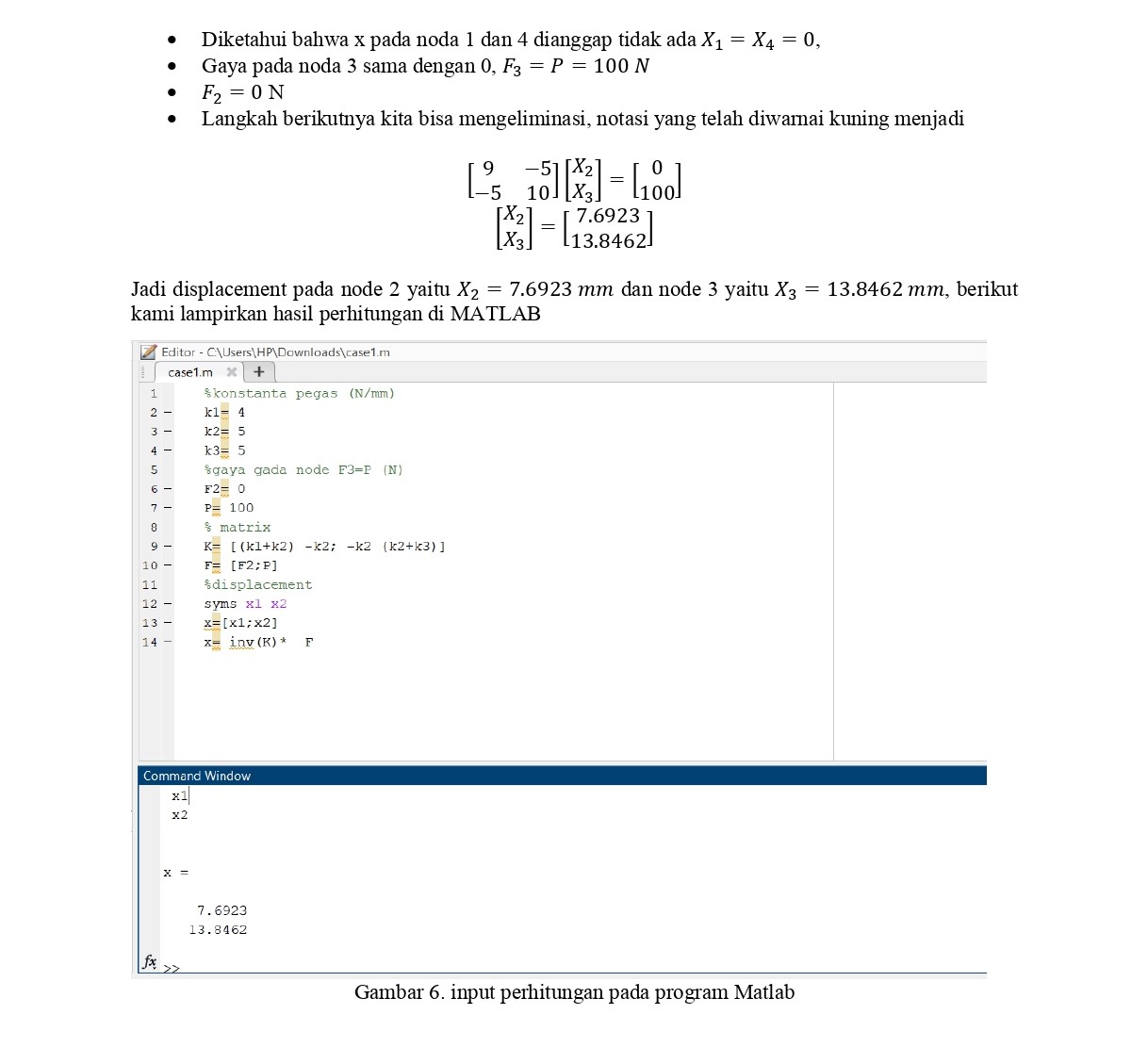
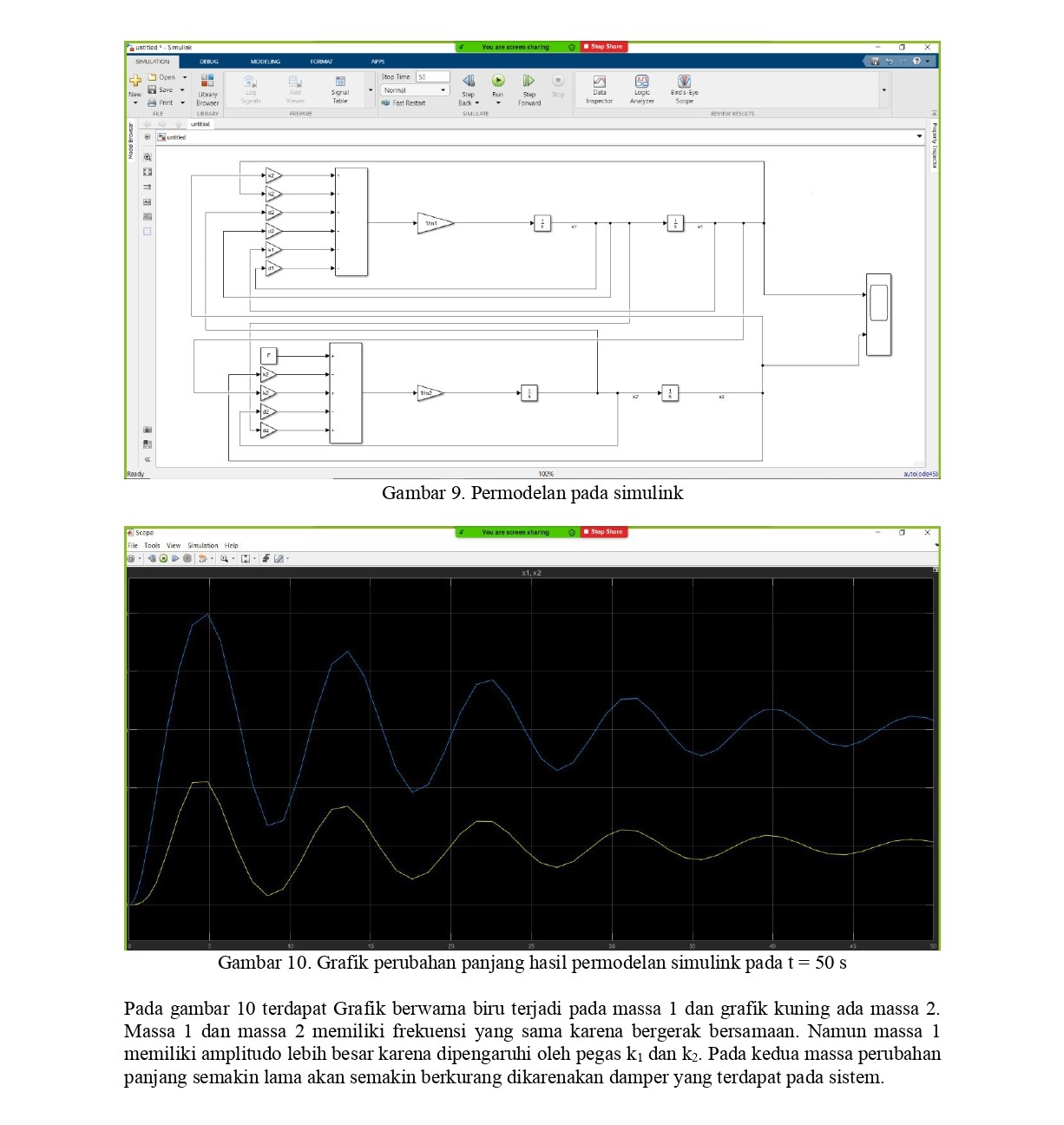
slide 7 (pemodelan FEM)
slide 8 (hasil perhitungan FEM)
hasil perhitungan terdapat beberapa point dan cara yakni menggunakan FEM dan euler method
slide 9 (hasil dan kesimpulan)
dari ketiga perhitungan tersebut (perhitungan manual-eksak, FES dan FEM) maka didapatkan hasil bahwa, perhitungan manual dana FES menunjukkan hasil yang hampir sama, yaitu terjadi simpangan dari pergerakan kolom arah laetral sejauh 0.8.
sedangakan hasil perhitungan FEM amenunjukkan perbedaan yang cukup signifikan. perbedaan hasil tersebut kemungkinan besar disebabkan oleh adanya perbedaan input yang dilakukan dalam perhitungan, mengingat dalam FES dilakukan pembatasan-pembatasan, seperti pada gerakan akibat gaya F gempa terhadap kolom yang terjadi hanya pada arah hisontal. sedangkan pada kejadian sebenarnya tidaklah demikian.
Tugas Artikel Kania, Chandra, Dieter, Evi
Artikel Kolaborasi : USING MASS-SPRING (MS) MODEL FOR BUILDING ANALYSIS arranged by Oldy Fahlovvi, Muchalis Zikramansyah Masuku, Ahmad Zikri, Muhammad Irfan Dzaky
Berikut ini kami lampirkan tugas kolaborasi tentang USING MASS-SPRING (MS) MODEL FOR BUILDING ANALYSIS dalam bentuk slideshow.
Tugas Artikel Aghnia, Daniel, Joko, Paskal
Persoalan
Hasil
Analisa
Berikut terlampir dokumen pendukung berupa Excel
https://drive.google.com/file/d/1Xvx7qlr-6vEFbYRVly7RprzASj8uwBfa/view?usp=sharing
Tugas Artikel Fajri, Kania Dyah, Maha, Wafirul
Tugas Artikel Adinda, Ilham Bagus, Adzanna, Maheka
STUDI KASUS OSILASI GEDUNG DUA TINGKAT MENGGUNAKAN MODEL PEGAS-MASSA; Edo, Raihan, Jeri, Shabrina
Studi Kasus Bangunan Gedung merupakan salah satu sarana yang dibangun menggunakan pengetahuan Engineering yang kompleks. Hampir seluruh aspek dalam perekayasaan sebuah gedung memerlukan analisis khusus secara saintifik guna menghasilkan karya yang tepat guna, nyaman dan aman untuk digunakan. Agar suatu bangunan tersebut aman untuk digunakan, sistem struktur bangunan haruslah memiliki kriteria untuk dapat menahan beban dengan kekuatan tertentu. Salah satu jenis beban yang menjadi perhatian khusus dalam perancangan bangunan gedung adalah pengaruh eksitasi yang disebabkan oleh kondisi angin maupun gempa bumi. Dalam menentukan respon suatu bangunan gedung terhadap eksitasi beban di atas, diperlukan proses komputasi terhadap fenomena yang akan terjadi. Untuk melakukan komputasi tersebut secara numerik, dapat dilakukan pendekatan menggunakan sistem pegas – massa maupun sistem finite element. Seperti yang dilakukan pada salah satu referensi yang diunggah oleh pak DAI mengenai simplified finite element, kami mencoba untuk melakukan studi kasus mengenai bangunan 2 tingkat yang diberikan gaya horizontal untuk diamati pengaruh gaya tersebut terhadap pergerakan osilasi gedung. Contoh kasus yang kami uji adalah pada sebuah gedung 2 tingkat yang dikenakan gaya horizontal pada lantai dasar gedung untuk merepresentasikan gaya gempa bumi. Gaya gempa bumi direpresentasikan dengan percepatan lantai dasar yang dinotasikan dengan ẍg
Modelling Model Pegas-Massa Untuk dapat menghitung pergeseran dari bangunan dua lantai ketika dikenakan gaya horizontal pada tanah atau lantai dasar bangunan, kita bisa memodelkan bangunan tersebut menjadi model pegas-massa[1]. Berikut ini adalah konfirugasi permodelan pegas-massa pada bangunan dua lantai.
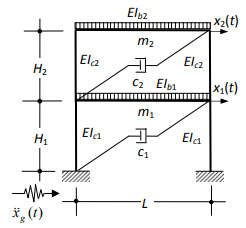
H1 dan H2 adalah tinggi masing-masing lantai, L adalah panjang lantai, c1 dan c2 adalah model damper untuk masing-masing lantai, m1 dan m2 adalah model massa untuk merepresentasikan massa masing-masing lantai, EIc1 dan EIc2 adalah kekakuan dari dinding masing-masing lantai, EIb1 dan EIb2 adalah kekakuan langit-langit masing-masing lantai, dan ẍg adalah percepatan tanah atau dasar bangunan. Model tersebut dapat dimodelkan ke dalam konfigurasi model pegas-massa yang umum kita temukan menjadi
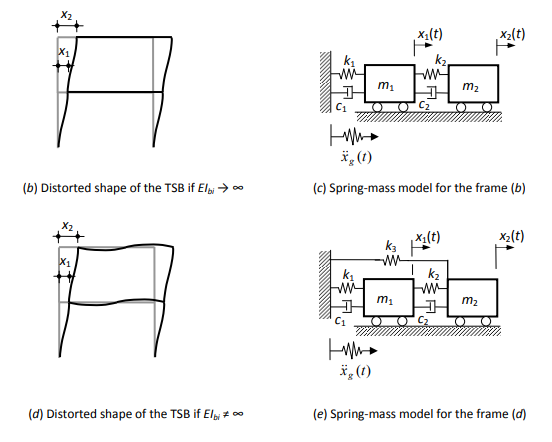
Figur b adalah model ketika kekakuan langit-langit lantai diasumsikan tak hingga, sehingga langit-langit tidak mengalami deformasi sama sekali. Figur tersebut dimodelkan ke dalam model pegas-massa menjadi seperti pada figur c. k1 dan k2 yang merupakan konstanta kekakuan pegas adalah fungsi dari EIc dan H. Figur d adalah kasus ketika langit-langit tidak diasumsikan memiliki kekakuan tak hingga, sehingga langit-langit juga mengalami deformasi. Pada kasus ini kekakuan langit-langit akan mempengaruhi nilai k1 dan k2 dan juga menambahkan model pegas baru dengan kekakuan k3 untuk merepresentasikan derajat kebebasan lateral dan rotasional, seperti yang dapat dilihat pada figur e.
Untuk kasus ini, kami memilih asumsi bahwa langit-langit tidak memiliki kekakuan tak hingga. Sehingga model pegas-massa yang kami gunakan adalah model pegas-massa pada figur e. Kemudian dari figur tersebut, kami akan melakukan analisis gaya untuk masing-masing massa.
Untuk massa 1,
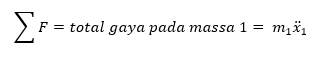
 Persamaan 1 dan 2 kemudian akan dihitung menggunakan metode numerik untuk mendapatkan nilai pergeseran lantai 1 dan lantai 2 (x1 dan x2). Konstanta pada persamaan tersebut akan diisi dengan nilai yang didapat dari jurnal referensi, yaitu sebagai berikut
m1 = 533,5 kg, m2 = 552,5 kg, c1 = 72,692 N.s/m, c2 = 68,688 N.s/m, k1 = 456,908 kN/m, k2 = 351.467 kN/m, k3 = -84,352 kN/m, ẍg =
Persamaan 1 dan 2 kemudian akan dihitung menggunakan metode numerik untuk mendapatkan nilai pergeseran lantai 1 dan lantai 2 (x1 dan x2). Konstanta pada persamaan tersebut akan diisi dengan nilai yang didapat dari jurnal referensi, yaitu sebagai berikut
m1 = 533,5 kg, m2 = 552,5 kg, c1 = 72,692 N.s/m, c2 = 68,688 N.s/m, k1 = 456,908 kN/m, k2 = 351.467 kN/m, k3 = -84,352 kN/m, ẍg =
Kondisi awal untuk x1, x2, ẋ1, dan ẋ2 adalah 0
Untuk menyelesaikan persamaan dari sistem diatas, dapat diselesaiakn dengan menggunakan metode numerik untuk menyelesaikan persamaan differensial. Kami menggunakan metode Euler forward-backward untuk menyelesaikan dua persamaan differensial tersebut. Apabila x1 di misalkan sebagai u1 dan x2 dimisalkan dengan u2, maka:
v1 = du1/dt
v2 = du2/dt
Oleh karena itu, persamaan numeriknya menjadi:
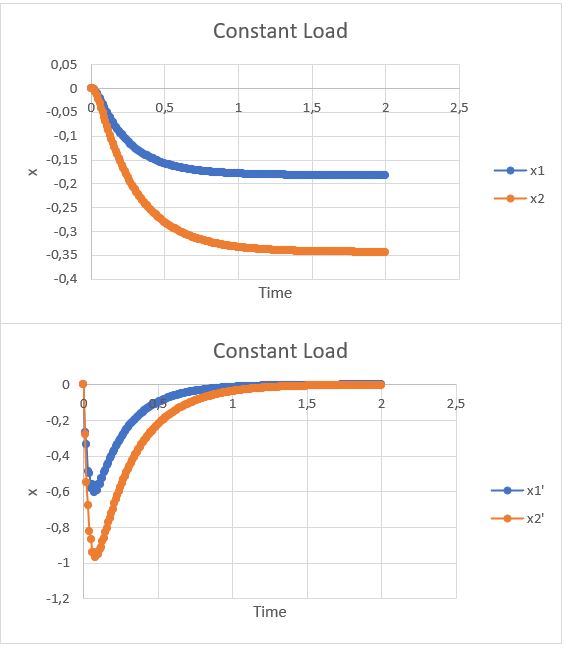
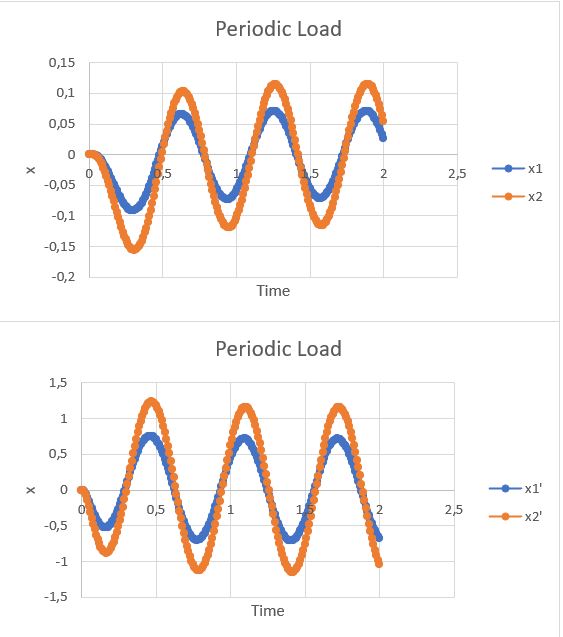
Lalu, gaya eksitasi yang direpresentasikan oleh ẍg dibuat menjadi dua jenis kasus. Yaitu kasus gaya eksitasi konstan dan gaya eksitasi periodic. Dengan menggunakan excel, didapatkan bahwa hasil respons dari model di atas dapat dilihat sebagai berikut:
Referensi [1] S. T. de La Cruz, M. A. Rodriguez, and V. Hernandez, “Using Spring-Mass Models to Determine the Dynamic Response of Two-Story Buildings Subjected to Lateral Loads,” 15th World Conf. Earthq. Eng., 2012.
Menyelesaikan Kasus Osilasi pada Gedung n-Tingkat dengan Metode Komputasi. (Adhika, Fathur, Ali)
Pendahuluan: Artikel ini akan menjelaskan cara menyelesaikan kasus osilasi pada gedung n-tingkat yang dimodelkan dengan sistem pegas dan diselesaikan secara numerik.
Persamaan Dasar:
Penyelesaian:
Penyelesaian persamaan ini akan menggunakan metode Euler dengan skema forwards dan bacwards. Secara umum proses pemodelan dengan terknik ini akan menghasilkan persamaan:
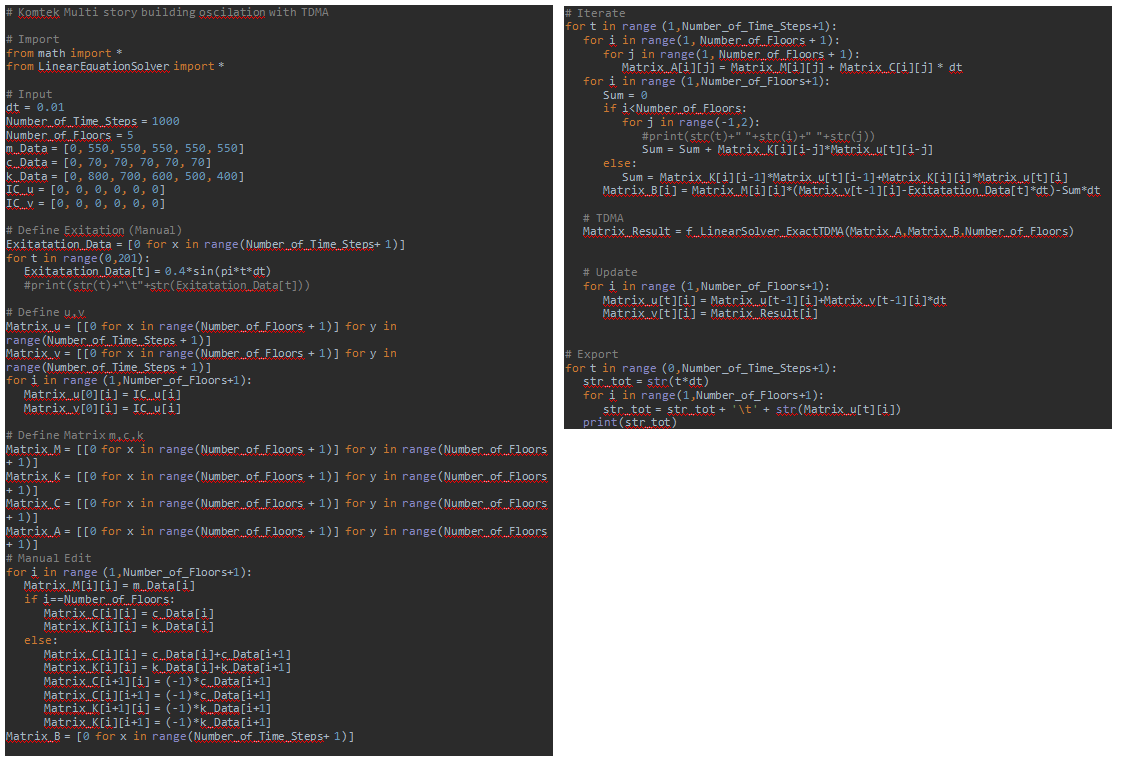
Adapun untuk menyelesaikan persamaan kedua, matrix [A] akan diselesaikan dengan TDMA (Tri-Diagonal Matrix Algorithm). Seluruh penyelesaian kasus ini dilakukan dalam bahsa phyton. Berikut Source codenya:
Hasil:
Hasil dari perhitungan ini adalah sebagai berikut:
Artikel Komputasi Teknik Sistem Pada Gedung Bertingkat Dengan 3 Model Strukstur (Adam, Aji, Alghi, Iqbal)