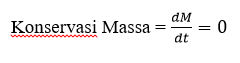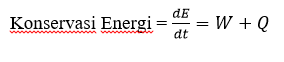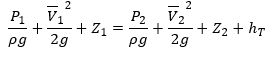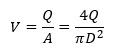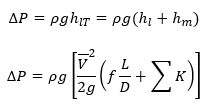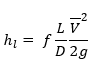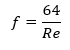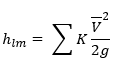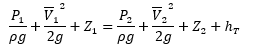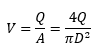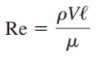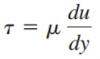Difference between revisions of "Dendy Dwi Rohma P J"
(→Pertemuan ke Simulasi Eksternal Flow Car Body) |
|||
| (81 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Ddy.jpg|150px|thumb|right|Dendy Dwi Rohma P J.S1 Teknik Mesin 2019 Ekstensi.Universitas Indonesia]] | [[File:Ddy.jpg|150px|thumb|right|Dendy Dwi Rohma P J.S1 Teknik Mesin 2019 Ekstensi.Universitas Indonesia]] | ||
| − | |||
| − | |||
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ | بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ | ||
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ | السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ | ||
| − | BIODATA DIRI | + | |
| + | '''BIODATA DIRI''' | ||
Nama : Dendy Dwi Rohma Prahara Jaya | Nama : Dendy Dwi Rohma Prahara Jaya | ||
NPM : 1906435473 | NPM : 1906435473 | ||
| + | |||
| + | Pendidikan Terakhir : Diploma III | ||
| + | |||
| + | Email : jaya.dendy1@gmail.com / dendy.dwi@ui.ac.id | ||
Fakultas/ Jurusan : Teknik/ Teknik Mesin | Fakultas/ Jurusan : Teknik/ Teknik Mesin | ||
| Line 61: | Line 64: | ||
| − | == '''Pertemuan | + | == '''Pertemuan Kedua''' == |
---- | ---- | ||
'''Hari, Tanggal : Rabu 1 April 2020''' | '''Hari, Tanggal : Rabu 1 April 2020''' | ||
| Line 85: | Line 88: | ||
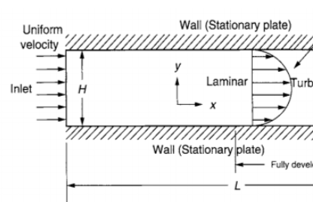
[[File:FullyDeveloped.png|center|Gambar.Fully Developed]] | [[File:FullyDeveloped.png|center|Gambar.Fully Developed]] | ||
| − | Soal Simulasi CFD: | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == '''Pertemuan Keempat''' == | ||
| + | ---- | ||
| + | '''Hari, Tanggal : Rabu 08 April 2020''' | ||
| + | |||
| + | Aliran suatu fluida dibedakan menjadi dua tipe, yaitu aliran laminar dan aliran turbulent. Aliran dikatakan laminar apabila partikel-partikel fluida yang bergerak secara teratur dalam lapisan-lapisan, sedangkan aliran disebut turbulent apabila tiap partikel fluida bergerak secara acak. Aliran laminar dan turbulent diilustrasikan pada gambar 2.5. A dan B. | ||
| + | |||
| + | [[File:AliranLaminerTurbulen.png|center]] | ||
| + | |||
| + | Kondisi aliran laminar atau turbulent dapat dinyatakan dengan bilangan Reynolds. Bilangan Reynolds pada ducting dirumuskan pada persamaan 2.1. | ||
| + | |||
| + | [[File:Re12.png|center]] | ||
| + | |||
| + | Dimana : | ||
| + | Re = Bilangan Reynold | ||
| + | V = Kecepatan Statis dan Dinamis (m/s) | ||
| + | D = Diameter Saluran Masuk (m) | ||
| + | μ = Viskositas Dinamsis Fluida (Nm/s) | ||
| + | |||
| + | == '''Pertemuan Keenam''' == | ||
| + | ---- | ||
| + | '''Hari, Tanggal : Rabu 15 April 2020''' | ||
| + | |||
| + | '''Head Loss''' | ||
| + | |||
| + | Aliran fluida di dalam pipa mengikuti persamaan Bernouli, yang ditunjukkan pada persamaan dibawah ini: | ||
| + | |||
| + | [[File:PersBernoulli.png|center]] | ||
| + | |||
| + | Dimana P1 adalah tekanan upstream, P2 adalah tekanan downstream, ¯V adalah kecepatan rata-rata upstream. ¯V adalah kecepatan rata-rata downstream. ¯V didapatkan dengan membagi debit dengan luas penampang pipa. Z adalah elevasi pipa dalam m, dan hl adalah headloss. Kecepatan fluida dalam pipa didapatkan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:KecFluida.png|center]] | ||
| + | |||
| + | Dimana Q adalah debit fluida dalam m3/s, A adalah cross sectional pipa dalam m2, D adalah diameter dalam pipa dalam meter. Total head loss adalah penjumlahan major loss dan minor loss, dirumuskan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:HeadLossTotal.png|center]] | ||
| + | |||
| + | Pressure drop pada segment pipa dapat dirumuskan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:pressdrop12.png|center]] | ||
| + | |||
| + | Dimana ΔP adalah pressure drop, hl adalah major headloss, f adalah friction factor, L adalah panjang pipa, D adalah diameter dalam pipa, dan K adalah loss coefficient pada fitting. | ||
| + | |||
| + | |||
| + | '''Head Loss Major (hl)''' | ||
| + | |||
| + | Major losses terjadi akibat gesekan fluida dengan permukaan pipa.Major losses dapat dirumuskan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:MajorLosses12.png|center]] | ||
| + | |||
| + | Dimana ΔP adalah pressure drop, hl adalah major headloss, f adalah friction factor, L adalah panjang pipa, dan D adalah diameter dalam pipa. Besar nilai Re menentukan jenis aliran fluida. Jika Re≤2000 maka aliran laminar. Jika 2000>Re<4000 maka aliran transisi. Sedangkan jika Re>4000 maka aliran turbulent. Nilai Re dirumuskan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:Re12.png|center]] | ||
| + | |||
| + | Dimana Re adalah reynold number, V adalah kecepatan aliran fluida dalam m/s, D adalah diameter dalam pipa dalam m, ρ adalah massa jenis fluida dalam kg/m3, dan μ adalah viskositas fluida dalam N.s/m2. Nilai f pada aliran laminar dan turbulen ditunjukkan oleh persamaan dibawah ini: | ||
| + | |||
| + | [[File:flaminer.png|center]] | ||
| + | |||
| + | [[File:fturbulen.png|center]] | ||
| + | |||
| + | Nilai f juga dapat ditemukan pada Moody’s Diagram yang ditunjukkan pada Gambar 2.9.Dimana nilai roughness (ε) ditunjukkan pada Tabel 2. | ||
| + | |||
| + | Tabel 2.1 Nilai Roughness (ε) pada Berbagai Material | ||
| + | |||
| + | [[File:TabelRoughness.png|center]] | ||
| + | |||
| + | [[File:Moody'sChart12.png|center]] | ||
| + | |||
| + | |||
| + | == '''Pertemuan Ketujuh''' == | ||
| + | ---- | ||
| + | '''Hari, Tanggal : Selasa 21 April 2020''' | ||
| + | |||
| + | '''Head Loss Minor''' | ||
| + | |||
| + | Pada sistem pipa, fluida akan melalui fitting, bend, atau valve sehingga terjadi minor losses. Minor losses dapat dirumuskan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:Headlossminor12.png|center]] | ||
| + | |||
| + | Dimana K adalah loss coefficient dan Le adalah equivalent lenght pipa dalam m. Loss coefficient (KL) pada valve dan fitting ditunjukkan pada Tabel 2.1. | ||
| + | |||
| + | '''Tabel 2.2 Loss Coefficient pada Valve dan Fitting''' | ||
| + | |||
| + | [[File:TabelValveFitting.png|center]] | ||
| + | |||
| + | == '''Soal Simulasi CFD: Laminar Parallel Plate Flow - ARTIKEL 2''' == | ||
[[File:SoalP2.png|1000px|thumb|center]] | [[File:SoalP2.png|1000px|thumb|center]] | ||
| − | Hasil Simulasi: | + | '''Hasil Simulasi:''' |
| + | |||
'''Jawaban A.1:''' | '''Jawaban A.1:''' | ||
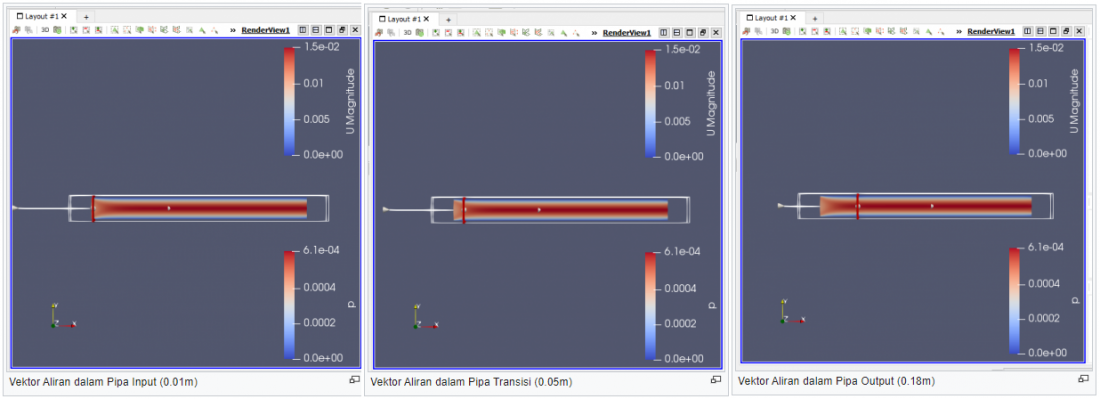
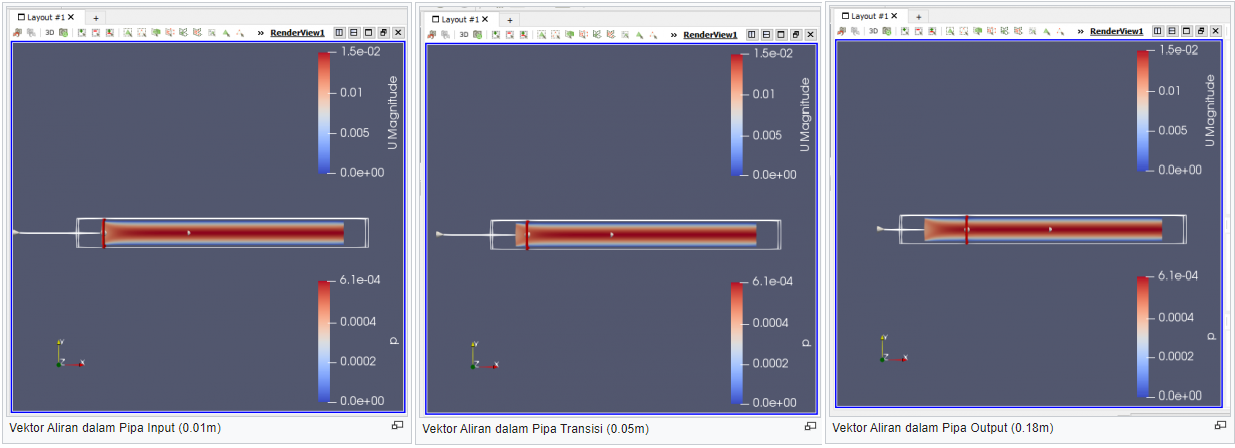
| − | [[File:AliranpadaSb.X0.01.png| | + | [[File:AliranpadaSb.X0.18,0.05,0.01.png|1100px]] |
| − | + | Pada gambar diatas ditunjukkan hasil potongan dari simulasi dengan Uin: 0.01m/s (sama) namun dengan variasi dynamic viscosity (berbeda). Dapat diketahui berdasarkan sebaran warna kecepatan aliran pada pipa lurus berbeda. Kecepatan pipa akan cenderung lebih besar jika mendekati pusat pipa sedangkan akan cenderung mengalami penurunan atau dapat dikatakan u=0 jika mendekati dinding pipa. Hal berdasarkan prinsip tegangan geser yang timbul antara dinding pipa dan aliran fluida. | |
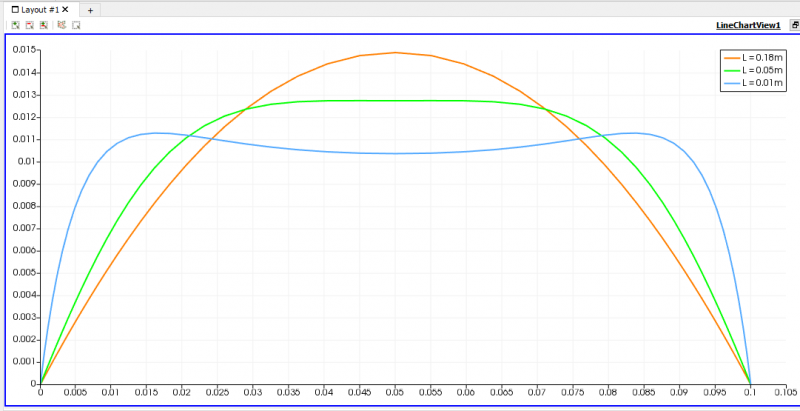
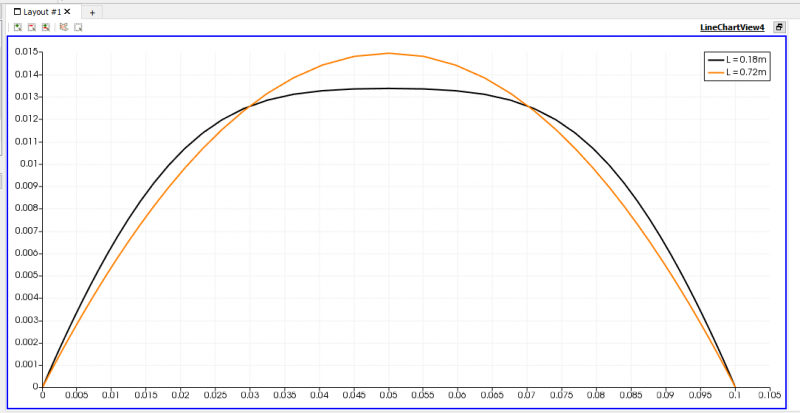
| − | [[File: | + | [[File:GrafikUdanDpada0.18,0.05,0.01.png|thumb|center|800px|Perbandingan velocity profile 0.01, 0.05 dan 0.18m]] |
| − | + | Nilai velocity profile dengan =0,00004 kg/m.s pada setiap potongan dapat dilihat seperti gambar diatas. Dapat kita ketahui bahwa nilai kecepatan pada inlet sangat bervariasi, itu menandakan bahwa di bagian entrance region aliran akan memiliki kecepatan yang bervariasi. Namun setelah aliran melewati pipa sejauh Le aliran akan mengalami fully developed condition. | |
'''Jawaban A.2:''' | '''Jawaban A.2:''' | ||
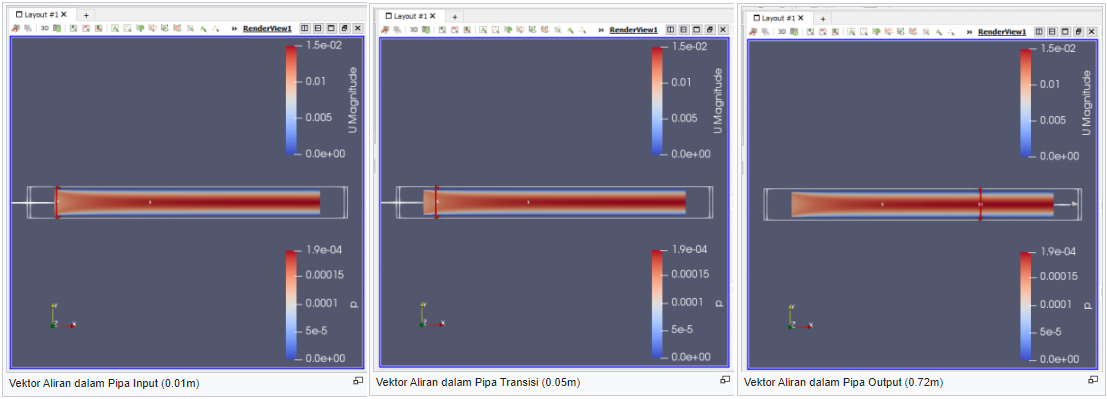
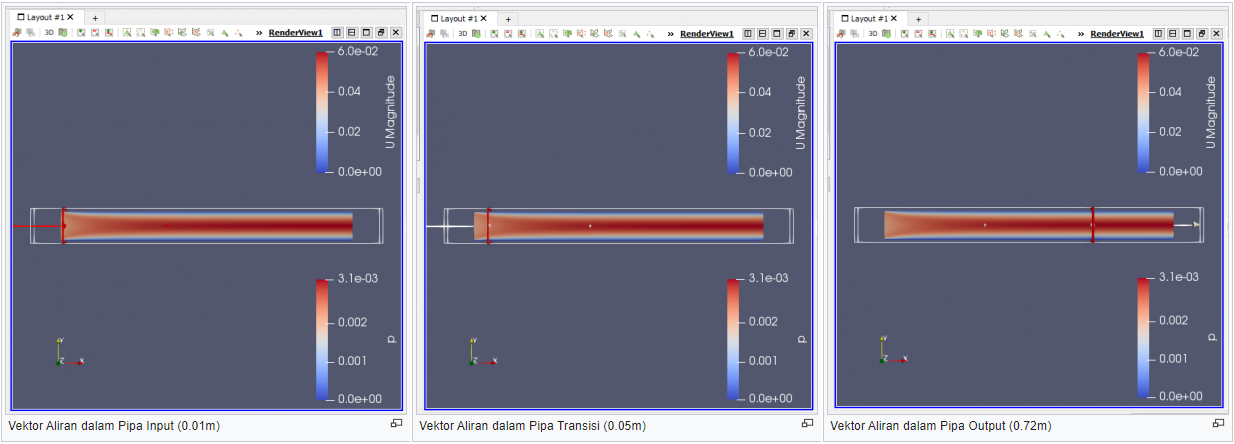
| + | [[File:AliranpadaSb.X(0.72,0.05,0.01m)A2.png]] | ||
| + | |||
| + | Pada gambar diatas ditunjukkan hasil potongan dari simulasi dengan Uin: 0.01m/s (sama) namun dengan variasi dynamic viscosity (berbeda), sama seperti jawaban soal A1. Dapat diketahui berdasarkan sebaran warna kecepatan aliran pada pipa lurus berbeda. Kecepatan pipa akan cenderung lebih besar jika mendekati pusat pipa sedangkan akan cenderung mengalami penurunan atau dapat dikatakan u=0 jika mendekati dinding pipa. Hal berdasarkan prinsip tegangan geser yang timbul antara dinding pipa dan aliran fluida. | ||
| + | |||
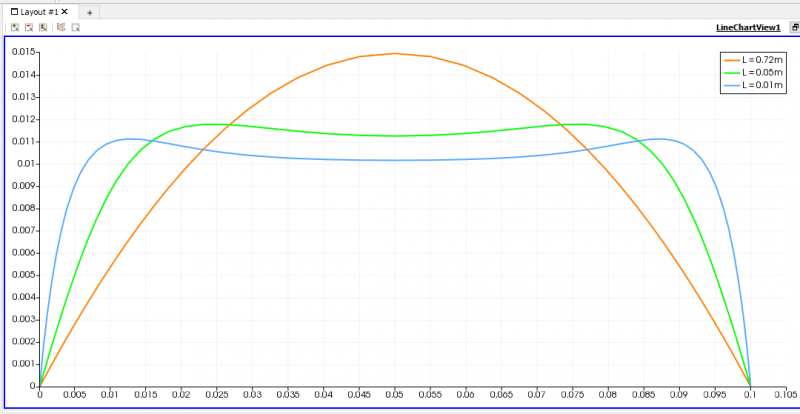
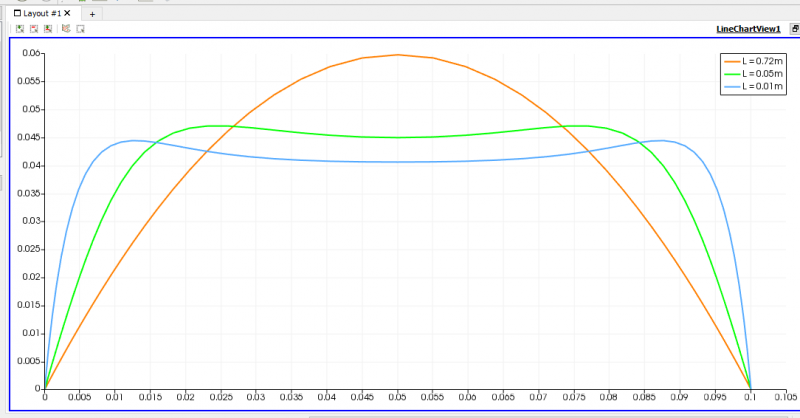
| + | [[File:GrafikUdanDpada(0.72,0.05,0.01m).png|thumb|center|800px|Perbandingan velocity profile 0.01, 0.05 dan 0.72m]] | ||
| + | [[File:GrafikUdanDpada(0.72,0.18m).png|thumb|center|800px|Perbandingan velocity profile 0.18m dan 0.72m]] | ||
| + | |||
| + | Nilai velocity profile dengan =0,00001 kg/m.s pada setiap potongan dapat dilihat seperti gambar diatas. Dapat kita ketahui bahwa nilai kecepatan pada inlet sangat bervariasi, itu menandakan bahwa di bagian entrance region aliran akan memiliki kecepatan yang bervariasi. Namun setelah aliran melewati pipa sejauh Le aliran akan mengalami fully developed condition. Kita juga dapat melihat bentuk kurva pada aliran fluida setelah menjadi fully developed. Bentuk kurvanya akan cenderung sama, namun beda dikecepatan dipusat pipa. Hal tersebut berdasarkan prinsip tegangan geser dinding pipa dengan aliran fluida. | ||
| + | |||
| + | '''Jawaban B.1:''' | ||
| + | [[File:AliranpadaSb.X(0.18,0.05,0.01m)B1.png]] | ||
| + | [[File:GrafikUdanDpada(0.18,0.05,0.01m)B1.png|thumb|center|800px|Perbandingan velocity profile 0.01, 0.05 dan 0.18m]] | ||
| − | [[File:AliranpadaSb.X(0.01m).png|thumb| | + | '''Jawaban B.2:''' |
| + | [[File:AliranpadaSb.X(0.72,0.05,0.01m)B2.png]] | ||
| + | [[File:GrafikUdanD(0.72, 0.05,0.01m)B2.png|thumb|center|800px|Perbandingan velocity profile 0.01, 0.05 dan 0.72m]] | ||
| − | [[File: | + | == '''Soal Simulasi CFD: Turbulent Parallel Plate Flow - ARTIKEL 3''' == |
| + | [[File:SoalPlatDatarTurbulent.png|thumb|center|800px]] | ||
| − | [[File: | + | '''Hasil Simulasi:''' |
| + | '''Contoh Hasil Slice pada Uin=0.02''' | ||
| + | [[File:PotonganUin0.02.png|thumb|center|800px]] | ||
| − | [[File: | + | '''Jawaban A.1:''' |
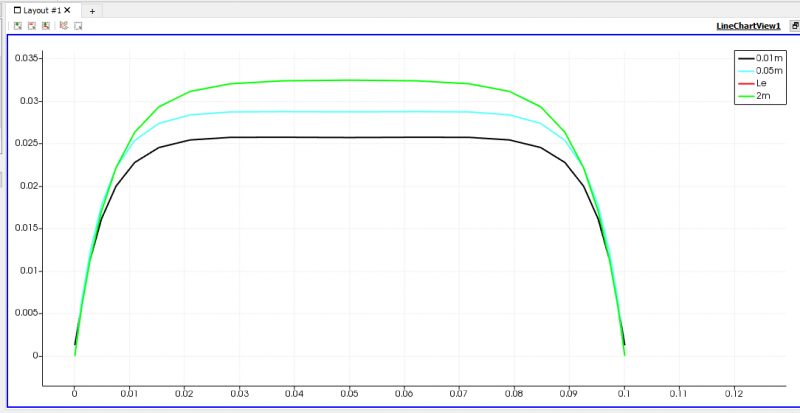
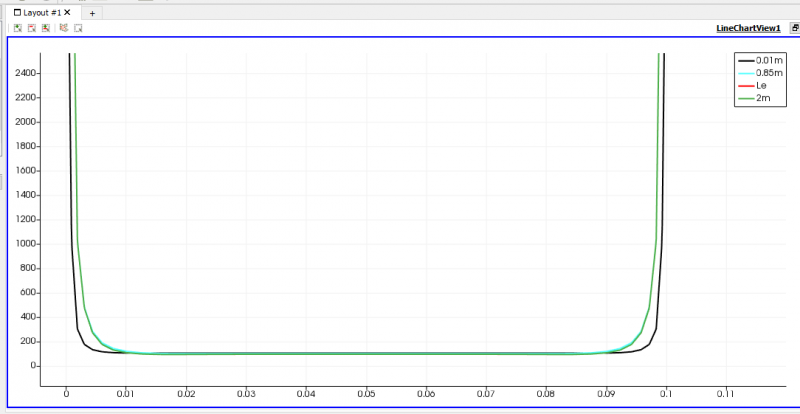
| + | [[File:GrafikUBerbagaiTitik,Uin(0,02).png|thumb|center|800px|Perbandingan velocity profile 0.01, 0.05, Le dan 2m]] | ||
| − | [[File: | + | '''Jawaban A.2:''' |
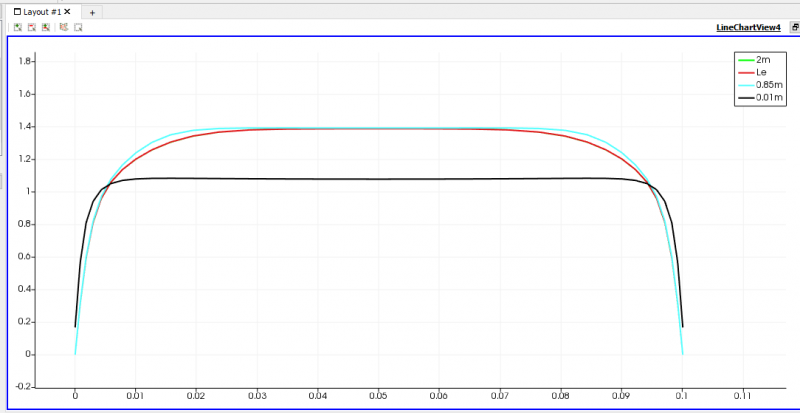
| + | [[File:GrafikUBerbagaiTitik,Uin(1).png|thumb|center|800px|Perbandingan velocity profile 0.01, 0.85, Le dan 2m]] | ||
'''Jawaban B.1:''' | '''Jawaban B.1:''' | ||
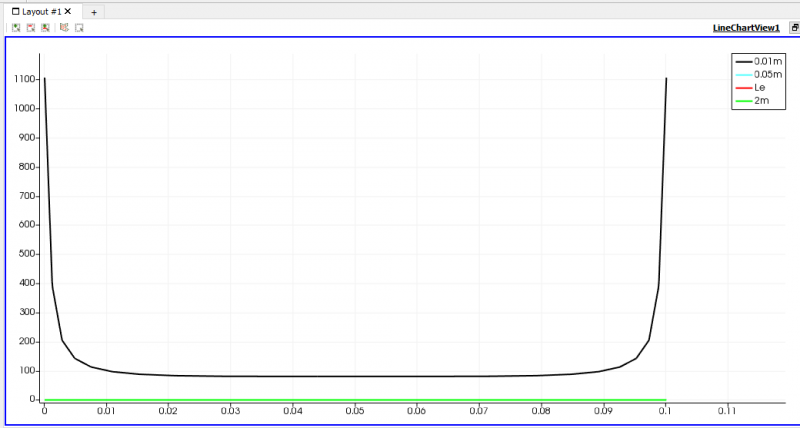
| − | + | [[File:GrafikViskositasBebagaiTitik,Uin(0.02).png|thumb|center|800px|Perbandingan viscosity profile 0.01, 0.05, Le dan 2m]] | |
| − | [[File: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Perbandingan | ||
| − | |||
'''Jawaban B.2:''' | '''Jawaban B.2:''' | ||
| + | [[File:GrafikViskositasBebagaiTitik,Uin(1).png|thumb|center|800px|Perbandingan viscosity profile 0.01, 0.85, Le dan 2m]] | ||
| + | |||
| + | == '''Soal Simulasi CFD: Soal jawab mekanika fluida, munson, example 8.2 laminar pipe flow - ARTIKEL 4''' == | ||
| + | '''Soal Pressure Drop pada Aliran Laminer dalam Pipa''' | ||
| + | [[File:Soal_PressureDrop_Laminer_Pipa.png|thumb|center|800px|Soal PressureDrop Laminer Pipa]] | ||
| + | |||
| + | '''Hasil Simulasi''' | ||
| + | [[File:ParaView_parameter.png|thumb|center|600px|ParaView Parameter]] | ||
| + | |||
| + | '''Inlet Slice (0,06, 1, 2.16, 4)m''' | ||
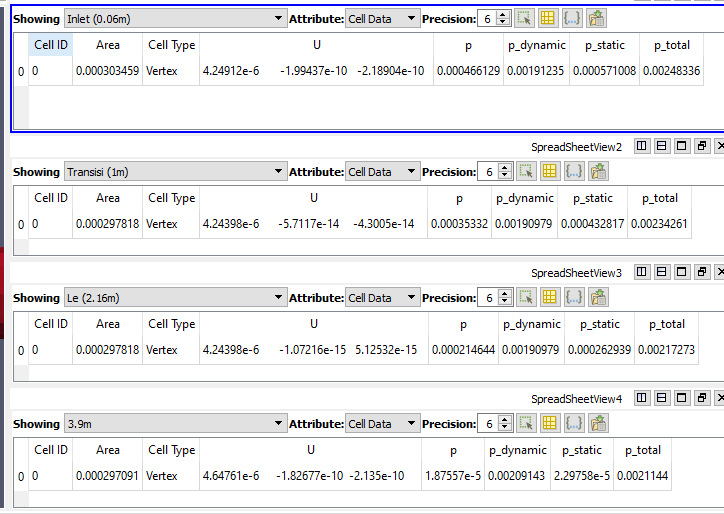
| + | [[File:p_total_Inlet_Slice_0,06,1,2.16,4.png|thumb|center|1000px|p total Inlet Slice_(0.06, 1, 2.16 ,4)m]] | ||
| + | |||
| + | Aliran fluida di dalam pipa mengikuti persamaan Bernouli, yang ditunjukkan pada persamaan dibawah ini: | ||
| + | |||
| + | [[File:Bernoulli1.png]] | ||
| + | |||
| + | Dimana P1 adalah tekanan upstream, P2 adalah tekanan downstream, ¯V adalah kecepatan rata-rata upstream. ¯V adalah kecepatan rata-rata downstream. ¯V didapatkan dengan membagi debit dengan luas penampang pipa. Z adalah elevasi pipa dalam m, dan hl adalah headloss. Kecepatan fluida dalam pipa didapatkan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:KecepatanFluida.png]] | ||
| + | |||
| + | Dimana Q adalah debit fluida dalam m3/s, A adalah cross sectional pipa dalam m2, D adalah diameter dalam pipa dalam meter. Total head loss adalah penjumlahan major loss dan minor loss, dirumuskan dengan persamaan dibawah ini: | ||
| + | |||
| + | [[File:HeatLossTotal.png]] | ||
| + | |||
| + | '''Pressure Drop pada (0,06, 1, 2.16, 4)m''' | ||
| + | [[File:p_static_dynamic_total(0.06,1,2.16,3.9m).png|thumb|center|800px|Hasil Simulasi Pressure Drop Pipa Laminer]] | ||
| + | |||
| + | Berdasarkan hasil simulasi didapatkan hasil pressure total (p_static+p_dynamic) mengalami penurunan dari inltet menuju outlet. Maka dalam internal flow pipa panjang perlu dipikirkan besaran heat loss mayor dari suatu aliran. Hal ini dapat diatasi dengan penggunaan pompa pada jarak pipa tertentu agar aliran fluida dapat sampai pada tempatnya. | ||
| + | |||
| + | == '''QUIZ 1: Mekanika Fluida''' == | ||
| + | '''Soal No 4''' | ||
| + | |||
| + | '''''A.Pengaruh Panjang Pipa pada Aliran Pipa Laminar Horizontal Terhadap Pressure Drop.''''' | ||
| + | |||
| + | •Jenis aliran pada pipa ada 2 yaitu aliran laminar dan turbulen. Aliran didalam pipa dikatakan laminar jika nilai Re<2100. | ||
| + | |||
| + | [[File:Re1.png|thumb|center|100px|Rumus Re]] | ||
| + | |||
| + | •Turunnya tekanan total pada pipa horizontal akibat adanya gesekan pada dinding pipa. Nilai gesekan tersebut berdasarkan perkalian viskositas dinamik fluida dengan kecepatan fluida tersebut pada suatu titik. (Gambar. Rumus Gaya Gesek Fluida). Arah gaya gesek fluida dengan dinding pipa berlawanan dengan arah aliran fluida dan nilai gaya gesek paling besar terdapat pada aliran fluida yang dekat dengan dinding pipa. (Gambar. Aliran Laminar dalam Pipa). Sesuai dengan Hk. konservasi energi, energi tidak dapat dimusnahkan tapi hanya berubah bentuk. Pada kasus pressure drop pada aliran laminar gaya gesek yang timbul antara fluida dengan dinding pipa tersbut menjadikan energi panas. | ||
| + | |||
| + | [[File:ShearStress.png|thumb|center|100px|Rumus ShearStress Fluida]] | ||
| + | |||
| + | [[File:AliranLaminerDalamPipa.png|thumb|center|500px|Aliran Laminer dalam Pipa]] | ||
| + | |||
| + | Tekanan pada fluida ada 3 jenis yaitu: | ||
| + | •Tekanan Statik = tekanan yang diberikan oleh partikel fluida saat dalam kondisi diam atau statis ke segala arah. | ||
| + | •Tekanan Dinamis = tekanan yang diakibatkan oleh pergerakan dari partikel fluida yang dipengaruhi oleh kecepatan dari partikel fluida itu sendiri. | ||
| + | •Tekanan Hydrostatik = tekanan yang diakibatkan dari ketinggian fluida dari fluida terhadap titik steady statenya. | ||
| + | Pada kasus aliran laminar dalam pipa horizontal nilai tekanan hidrostatik diabaikan karena ΔZ = 0. | ||
| + | |||
| + | '''''B.Pengaruh adanya sudut θ pada aliran pipa laminar terhadap pressure drop (Δp).''''' | ||
| + | |||
| + | •Kita ketahui aliran fluida memiliki 3 tekanan, yaitu tekanan static, tekanan dinamik, dan tekanan hidrostatik. Pada kasus aliran laminar pada pipa bersudut θ tekanan hidrostatiknya akan memiliki nilai. | ||
| + | |||
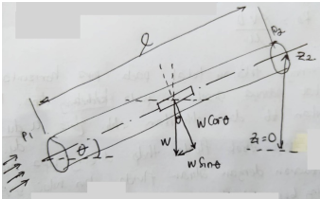
| + | [[File:AliranPadaPipaBersudutθ.png|thumb|center|500px|Aliran pada Pipa Bersudut θ]] | ||
| + | |||
| + | •Pada aliran laminar pipa bersudut θ, pressure drop dapat dihitung dari perbedaan ketinggian pada titik 1 (p1) dengan titik 2 (p2). Nilai p1>p2. | ||
| + | |||
| + | [[File:RumusBedaTekanan.png|thumb|center|100px|Rumus Pressure Drop h]] | ||
| + | |||
| + | [[File:RumusBedaKettinggian.png|thumb|center|400px|Rumus Beda Ketinggian]] | ||
| + | |||
| + | '''Soal No 5''' | ||
| + | |||
| + | '''''A.Pengaruh Ketebalan Sublapisan Viskos Terhadap Pressure Drop''''' | ||
| + | |||
| + | •Aliran turbulen adalah aliran yang memiliki Re tinggi. Karakteristik aliran turbulen dalam pipa horizontal memiliki Le yang pendek, tegangan geser yang besar pada dinding pipa, energi panas dihasilkan tinggi, kecepatan aliran pada center yang lebih rendah daripada aliran laminar dalam pipa horizontal. Dengan kecepatan inlet sama, diameter pipa sama, namun densitas fluida yang melalui pipa berbeda akan menjadinkan aliran fluida yang memiliki density tinggi akan memiliki Re yang lebih tinggi (Gambar. Rumus Re). Re kental> Re cair. Pada aliran turbulen terdapat suatu lapisan semu tipis akibat tegangan geser yang dinamakan sublapis viskos. Sublapisan viskos ini yang menimbulkan pressure drop. Sublapisan viskos besarnya di tentukan oleh viskositas, density fluida, dan tegangan geser disekitar dinding pipa. Semakin besar tegangan geser pada permukaan pipa maka semakin besar viskositas fluida sehingga semakin besar pula sublapisan viskosnya (Gambar. Rumus Tegangan Geser). Inilah hal yang nantinya akan membuat pressure drop pada aliran turbulen akan semakin besar. | ||
| + | |||
| + | [[File:Re2.png|thumb|center|150px|Rumus Re]] | ||
| + | |||
| + | [[File:ShearStress.png|thumb|center|100px|Rumus ShearStress]] | ||
| + | |||
| + | •Maka pressure drop akan berbanding lurus dengan sublapisan viskos. | ||
| + | |||
| + | '''Soal No 2''' | ||
| + | |||
| + | '''''A.Hubungan Antara Beda Viskositas Dinamik pada Aliran Laminer Terhadap Panjang Entrance Length''''' | ||
| + | |||
| + | •Aliran laminar adalah nilai bilangan Reynold dibawah 2100. Untuk menentukan jenis aliran dapat ditentukan dengan menentukan nilai bilangan reynoldnya dengan persamaan: | ||
| + | |||
| + | [[File:Re1.png|thumb|center|100px|Rumus Re]] | ||
| + | |||
| + | Pada kasus A ini aliran diketahui adalah aliran laminar. Kemudian diberikan 𝜇1 = 4x10-5 kg/m.s dan 𝜇2 = 10-5 kg/m.s dengan Uin yang sama. Menurut saya Re dari 𝜇1 pada entrance region akan lebih kecil dari 𝜇2. Sehingga nilai Le1 dari 𝜇1 akan lebih pendek jika dibandingkan dengan Le2. Hal tersebut karena tegangan geser dari 𝜇1 lebih besar daripada tegangan geser 𝜇2. Rumus mengukur tegangan geser adalah: | ||
| + | |||
| + | [[File:ShearStress.png|thumb|center|100px|Rumus ShearStress]] | ||
| + | |||
| + | Posisi entrance region dapat ditentukan dengan menghitung jarak entrance length dengan persamaan: | ||
| + | |||
| + | [[File:Le1.png|thumb|center|100px|Rumus Le]] | ||
| + | |||
| + | Dengan kata lain dapat disimpulkan bahwa 𝜇 (viskositas dinamik) akan mempengaruhi entrance region dari suatu aliran. Semakin tinggi nilai 𝜇 maka nilai entrance region akan semakin kecil karena dipengaruhi oleh tegangan geser yang juga semakin meningkat. | ||
| + | |||
| + | '''''B.Hubungan Antara Beda Kecepatan Inlet (Uin) pada Aliran Laminer Terhadap Panjang Entrance Length''''' | ||
| + | |||
| + | •Pada aliran laminar akan terbentuk daerah entrance region antara entrance/ inlet dengan awal posisi fully developed. Jika diketahui nilai 𝜇 (viskositas dinamik) yang sama pada penggunaan kecepatan inlet yang berbeda U1 =0.01m/s dan U2 =0.04m/s. Maka untuk kedua penggunaan kecepatan inlet tersebut akan menghasilkan panjang entrance region yang berbeda. Entrance region akan semakin panjang/ membutuhkan waktu yang lama apabila aliran fluida masuk lebih besar. Karena dengan viskositas yang sama dan density (jenis fluida mengalir sama) nilai tegangan geser pada aliran dengan kecepatan inlet yang berbeda akan bernilai sama. Hal tersebut berdasarkan rumus tegangan geser dibawah ini. | ||
| + | |||
| + | [[File:ShearStress.png|thumb|center|100px|Rumus ShearStress]] | ||
| + | |||
| + | Maka dapat disimpulkan entrance region akan semakin panjang/ semakin lama waktu yang dibutuhkan untuk mencapai fully developed jika kecepatan masuk pada suatu aliran ditingkatkan. | ||
| + | |||
| + | '''Soal No 3''' | ||
| + | |||
| + | '''''A.Hubungan Antara Beda Kecepatan Inlet (Uin) Terhadap Jenis Aliran yang Akan Terjadi (Laminer atau Turbulen)''''' | ||
| + | |||
| + | •Kecepatan merupakan sebuah vector. Sama halnya yang terjadi pada aliran fluida pada jenis turbulen. Aliran turbulen adalah aliran yang partikel - partikel nya bergerak secara acak, menghasilkan vector aliran yang kesegala arah. Sehingga resultan aliran terhadap sumbu. X pada kasus soal 3 akan semakin kecil jika dibandingkan dengan aliran laminer. Cara untuk menghitung kecepatan aliran turbulen tidak sama dengan cara menghitung kecepatan aliran laminar. Jika aliran laminar kita hanya perlu menghitung kecepatan rata rata 𝑢̅ nya saja (arah vector searah sb. x) dan dianggap semua titik memiliki kecepatan yang sama dengan kecepatan rata rata. Sedangkan untuk aliran turbulen kita harus mencari kecepatan rata rata 𝑢̅ dan kecepatan fluktuasi di titik tertentu u’(u total A = 𝑢̅ A + u’A). | ||
| + | |||
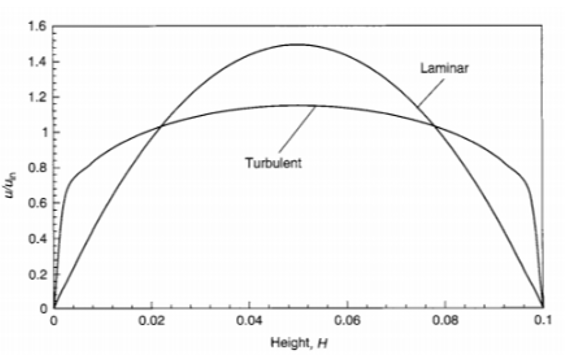
| + | [[File:NormalisasiUpadaAliranLaminerdanTurbulen.png|thumb|center|600px|Normalisasi U/Uin pada Aliran Laminer dan Turbulen]] | ||
| + | |||
| + | •Besarnya kecepatan pada aliran turbulen menyebabkan energi kinetiknya juga semakin besar yang nantinya akan menyebabkan sublapisan viskos semakin tebal dan energi panas yang dihasilkan pada aliran turbulen juga semakin besar. | ||
| + | |||
| + | '''Soal No 6''' | ||
| + | |||
| + | '''''A.Manipulasi Jenis Aliran (Laminer dan Turbulen) dengan Properties Fluida Masuk yang Sama''''' | ||
| + | |||
| + | •Pada kompetisi motor balap (road race) berbahan bakar bensin. Para mekanik akan meracik motor yang akan dipertandingkan sebaik mungkin. Pada kompetisi biasanya diatur cc motor yang akan dipertandingkan, tidak boleh motor kelas 200cc diturunkan pada ajang 150cc. Sehingga mekanik akan melakukan improvisasi agar motor dengan kelas yang sama memiliki performa yang tinggi. Salah satunya adalah dengan memanipulasi campuran bahan bakar dengan udara yang akan masuk ruang bakar. Pada motor biasa akan kita jumpai jenis manifold karburator/ inejksi yang halus pada permukaannya. Hal tersebut menjadikan besin dan udara tidak bisa tercampur maksimal. Akibatnya performa motor tidak dapat maksimal. Agar lebih maksimal dilakukan porting pada dinding manifold agar campuran bensin dan udara dapat tercampur maksimal. | ||
| + | |||
| + | [[File:PortingIntakeManifold.png|thumb|center|600px|Porting Golf pada Intake Manifold Motor]] | ||
| + | |||
| + | Berdasarkan karakteristik aliran turbulen, aliran ini akan memiliki bentuk aliran yang berputar ke segala arah. | ||
| + | |||
| + | [[File:Re2.png|thumb|center|100px|Rumus Re]] | ||
| + | |||
| + | [[File:ShearStress.png|thumb|center|100px|Rumus ShearStress]] | ||
| + | |||
| + | Dengan memberikan motif bola golf pada permukaan manifold, maka luasan dari permuaakan manifold akan meningkat/ dapat dikatakan tambah kasar. Sehingga aliran fluida yang melewati permukaan manifold tersebut akan mengalami tegangan geser yang lebih besar. Atau dapat dikatakan nilai dari 𝜇 (viskositas dinamik) akan lebih tinggi daripada penggunaan permukaan halus. Sehingga Re pada 𝜇 pada permukaan kasar lebih tinggi (Aliran Turbulen). | ||
| + | |||
| + | '''Soal No 1''' | ||
| + | |||
| + | '''''A.Aliran Fluida Jenis Laminer pada Plat Datar (2D)''''' | ||
| + | |||
| + | •Dalam mempelajari mekanika fluida kita mempelajari 3 hukum dasar atau biasa disebut governing equation: | ||
| + | •Hukum Konservasi Energi | ||
| + | dE/dt = W+Q | ||
| + | •Hukum Konservasi Massa | ||
| + | dm/ dt = 0 | ||
| + | •Hukum Konservasi Momentum | ||
| + | m.dv/ dt = ƩF | ||
| + | Pada aliran laminar dalam plat datar digunakan hukum dasar hukum konservasi momentum dengan kecepatan searah sumbu x. Dengan asumsi kecepatan arah sb. Y disetiap titik dianggap nol dan kecepatan arah sb. Z nol/ kosong (karena hanya 2D). | ||
| + | |||
| + | == '''Soal Simulasi CFD: Soal jawab mekanika fluida, Minor Losses Ex.8.6 - ARTIKEL 7''' == | ||
| + | '''Soal Ex.8.6 Munson''' | ||
| + | |||
| + | '''Soal Minor Losses Artikel 7''' | ||
| + | [[File:SoalMinorLossesEx8.6.png|thumb|center|800px|Soal Minor Losses Ex.8.6 Munson]] | ||
| + | |||
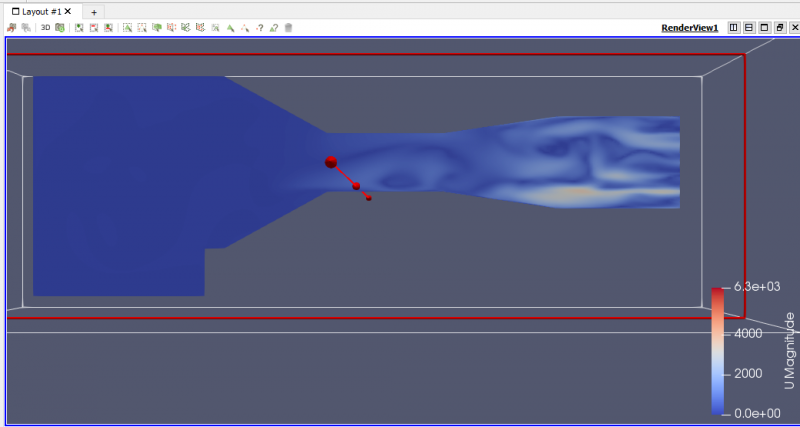
| + | '''Potongan Melintang Fenomena Cortex''' | ||
| + | [[File:SliceMelintang.png|thumb|center|800px|Potongan Melintang pada Wind Tunnel]] | ||
| + | |||
| + | '''Potongan Sepanjang Sb.-Z Fenomena Cortex''' | ||
| + | [[File:SliceMemotong(4.8,4.5,4,3.3,2.8,2.1,1.6,1,0.5)m.png|thumb|center|800px|Potongan Sepanjang Sb.-Z (4.8, 4.5, 4, 3.3, 2.8, 2.1, 1.6, 1, 0.5)m]] | ||
| + | |||
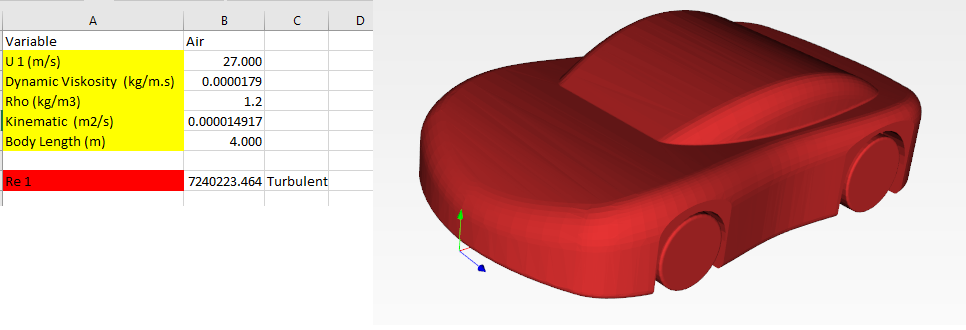
| + | '''Calculator''' | ||
| + | [[File:ParameterPD.png|thumb|center|800px|Calculator]] | ||
| + | |||
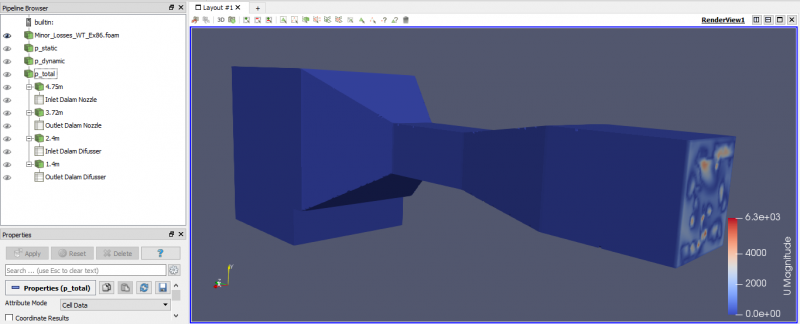
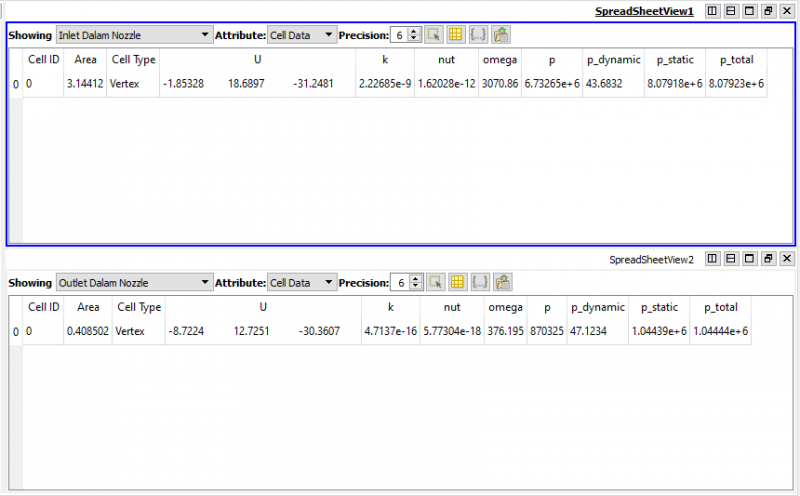
| + | '''Hasil Perhitungan Pressure Drop Dalam Nozzle''' | ||
| + | [[File:PressureDropDalamNozzle.png|thumb|center|800px|Pressure Drop Dalam Nozzle]] | ||
| + | |||
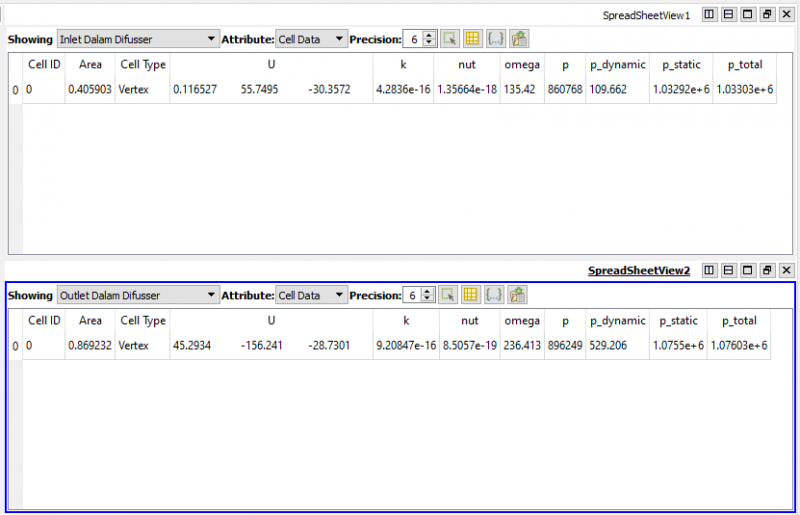
| + | '''Hasil Perhitungan Pressure Drop Dalam Difusser''' | ||
| + | [[File:PressureDropDalamDifusser.png|thumb|center|800px|Pressure Drop Dalam Difusser]] | ||
| + | |||
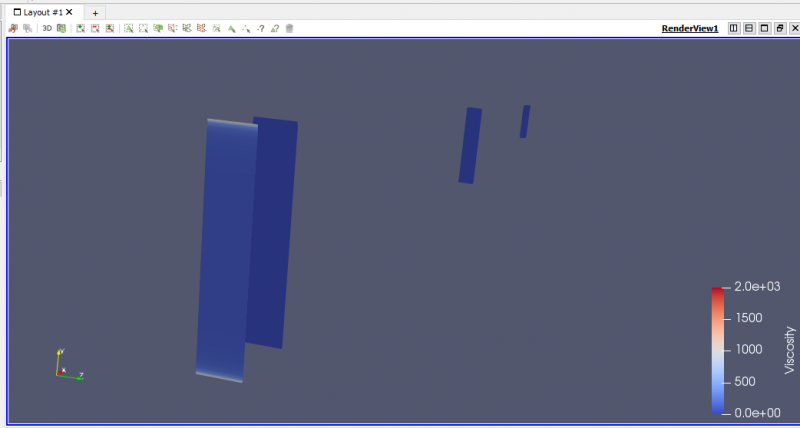
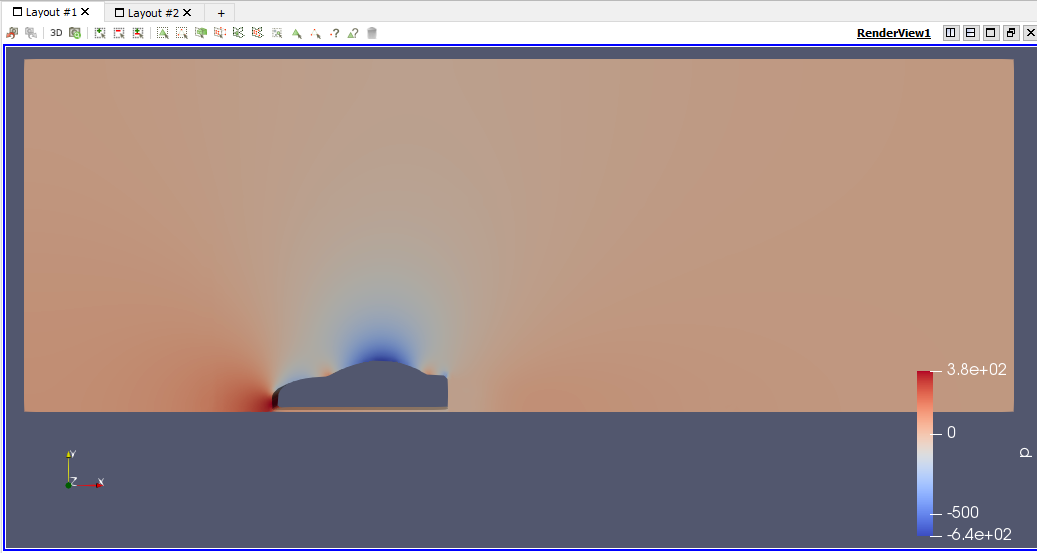
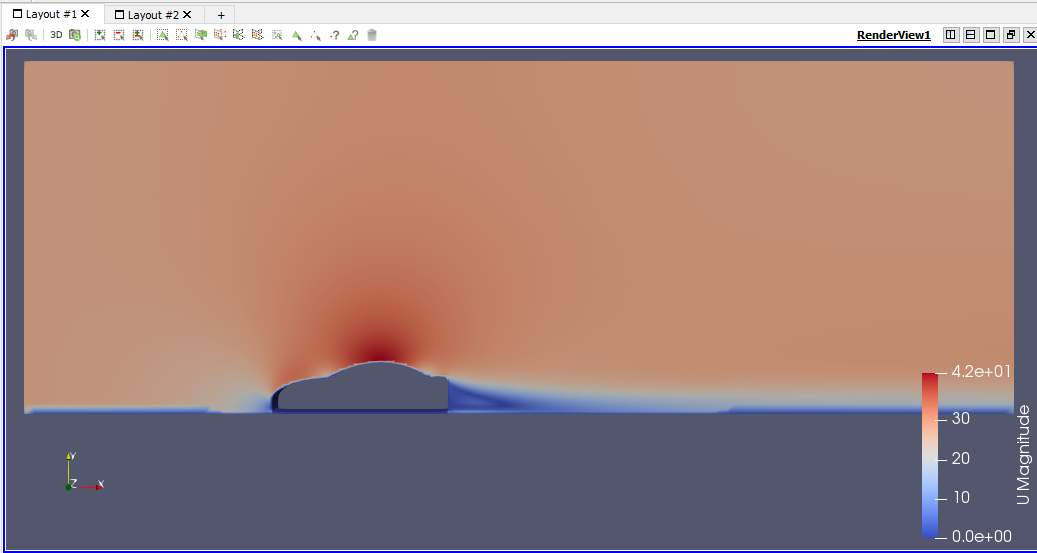
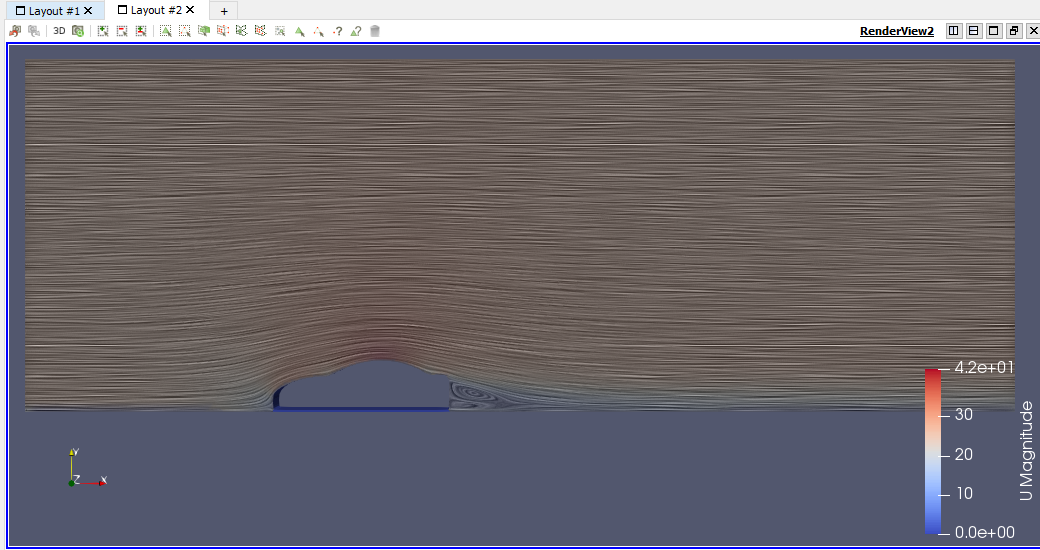
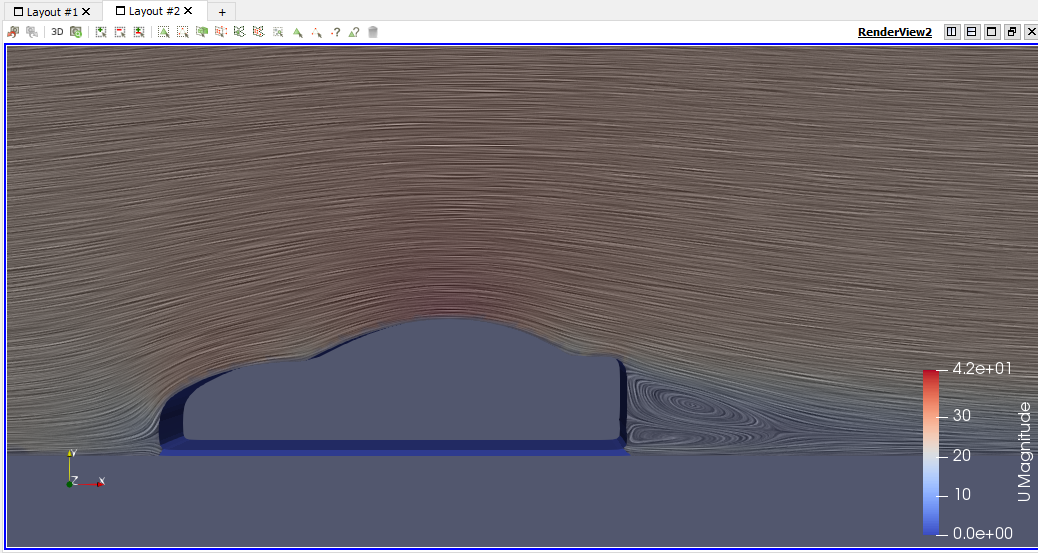
| + | == '''Pertemuan Kesepuluh Simulasi Eksternal Flow Car Body''' == | ||
| + | [[File:SoalCarBody.png]] | ||
| + | [[File:CarMesh.png]] | ||
| + | [[File:SebaranP.png]] | ||
| + | [[File:SebaranU.png]] | ||
| + | [[File:VortexU100.png]] | ||
| + | [[File:VortexU100zoom.png]] | ||
| + | |||
| + | == '''Tugas Besar - Analisa Profil Permuakaan (Surface Roughness) yang Berbeda pada Properties Fluida Masuk yang Sama pada Intake Manifold Karburator''' == | ||
| − | + | Pada kompetisi balap berbahan bakar bensin. Mekanik akan meracik kendaraan yang akan dipertandingkan sebaik mungkin. Pada kompetisi biasanya ada regulasi seperti pembatasan cc motor disetiap kelasnya, tidak boleh motor kelas 200cc diturunkan pada ajang 150cc. Sehingga mekanik akan melakukan improvisasi agar motor dengan kelas yang sama memiliki performa yang tinggi. Salah satunya adalah dengan memanipulasi campuran bahan bakar dengan udara yang akan masuk ruang bakar. Pada motor/ mobil biasa akan kita jumpai jenis manifold karburator/ inejksi yang halus pada permukaannya. Hal tersebut menjadikan besin dan udara tidak bisa tercampur maksimal atau dapat dikatakan campuran udara dan bahan bakar masih kasar. Akibatnya performa motor tidak dapat maksimal. Agar lebih maksimal dilakukan porting pada dinding manifold agar campuran bensin dan udara dapat tercampur maksimal. Porting adalah melakukan profiling pada dinding intake manifold agar surface rougnessnya lebih kasar. Diharapkan dengan dilakukannya profilling pada dinding manifold dapat menjadikan campuran udara dan bahan bakar lebih baik. | |
| − | + | [[File:IntakeManifold.png|500px|Intake Manifold]] | |
| − | + | [[File:PortingProfil.png|550px|Porting dan Polish]] | |
| − | |||
| − | |||
| − | [[File: | ||
| − | |||
| − | [[File: | ||
Latest revision as of 08:55, 16 June 2020
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
BIODATA DIRI
Nama : Dendy Dwi Rohma Prahara Jaya
NPM : 1906435473
Pendidikan Terakhir : Diploma III
Email : jaya.dendy1@gmail.com / dendy.dwi@ui.ac.id
Fakultas/ Jurusan : Teknik/ Teknik Mesin
Kelas Mekanika Fluida 02
Contents
- 1 Pertemuan Pertama
- 2 Pertemuan Kedua
- 3 Pertemuan Keempat
- 4 Pertemuan Keenam
- 5 Pertemuan Ketujuh
- 6 Soal Simulasi CFD: Laminar Parallel Plate Flow - ARTIKEL 2
- 7 Soal Simulasi CFD: Turbulent Parallel Plate Flow - ARTIKEL 3
- 8 Soal Simulasi CFD: Soal jawab mekanika fluida, munson, example 8.2 laminar pipe flow - ARTIKEL 4
- 9 QUIZ 1: Mekanika Fluida
- 10 Soal Simulasi CFD: Soal jawab mekanika fluida, Minor Losses Ex.8.6 - ARTIKEL 7
- 11 Pertemuan Kesepuluh Simulasi Eksternal Flow Car Body
- 12 Tugas Besar - Analisa Profil Permuakaan (Surface Roughness) yang Berbeda pada Properties Fluida Masuk yang Sama pada Intake Manifold Karburator
Pertemuan Pertama
Hari, Tanggal : Rabu 31 Maret 2020 Oleh : Dr. Ahmad Indra dan Bang Edo
Pertemuan pertama pada hari ini dimulai dengan pemberian materi oleh bang Muhammad Hilman Gumelar atau akrab disapa bang Edo. Materi tersebut berisi tentang penjelasan aliran viskos di dalam pipa, pressure drop, hubungan dari jenis aliran viskos dengan pressure drop dan simulasi aliran didalam pipa menggunakan software CFDSOF.
Aliran viskos adalah aliran dimana kekentalan yang melewati suatu ruangan nilainya diperhitungkan. Jenis aliran viskos dalam pipa ditentukan dari bilangan Reynold nya. Re besar (Re>4000) maka jenis alirannya turbulen, sedangkan Re kecil (Re<2100) maka jenis alirannya laminar. Bilangan reynold adalah rasio gaya inersia suatu fluida terhadap gaya viskos fluida tersebut.
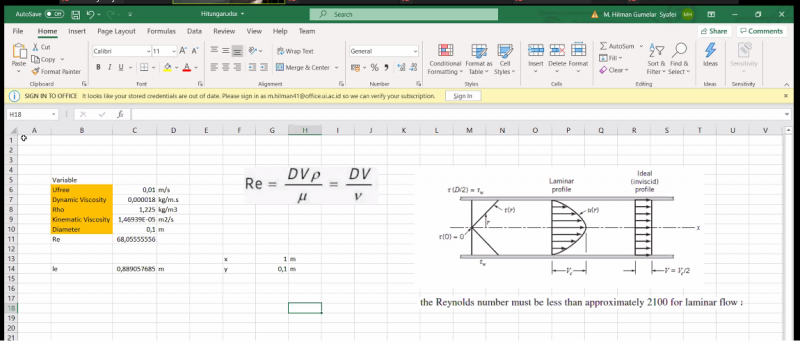
Re = (ρ*v*D)/μ
dimana :
v = Kecepatan aliran
D = Diameter pipa
ρ = massa jenis
μ = viskositas dinamik
Pada pertemuan ini bang Edo juga memberikan simulasi terkait penggunaan aplikasi CFD yang mana akan digunakan untuk mensimulasikan rangkaian aliran.Berikut hasil latihan dari penggunaan software CFDSOF.
Data simulasi yang akan digunakan pada software CFDSOF. Simulasi aliran udara pada bidang 2D.
Hasil simulasi aliran udara pada bidang 2D.
Kemudian bang edo memberikan beberapa pertanyaan tentang pengertian yaitu:
1. Apa yang dimaksud dengan entrance region ?
2. Apa yang dimaksud dengan aliran berkembang sempurna ?
3. Bagaimana hubungan entrance region dengan aliran berkembang sempurna ?
4. Apa yang mempengaruhi pressure drop ?
5. Apa pengaruh viskositas terhadap aliran ?
Pertemuan Kedua
Hari, Tanggal : Rabu 1 April 2020 Oleh : Dr. Ahmad Indra dan Bang Edo
Pada ini dijelaskan tentang aplikasi mekanika fluidamisalnya aliran fluida dalam pipa. Ada 3 tahapan konservasi yang harus dipahami dalam mekanika fluida. Ketiga konservasi tersebut adalah sebagai berikut:
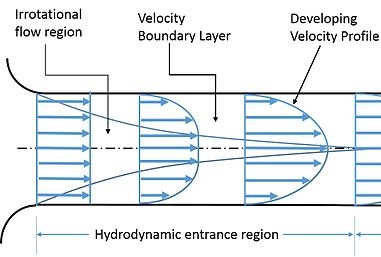
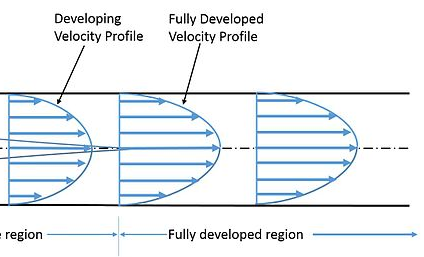
Kemudian dijelaskan tentang fenomena pada Entrance Region, terjadinya aliran Fully Developed pada pipa. Pada entarance region terdapat entrance length (Le) dimana entrance length dipengaruhi oleh U dan μ. Semakin tinggi kecepatan semakin panjang pula jarak Le dari Entrance Point dan μ (density) tinggi menjadikan Le yang pendek. Gambar dibawah ini adalah contoh Entrance Region dan Fully Developed:
1. Entrance Region
2. Fully Developed
Pertemuan Keempat
Hari, Tanggal : Rabu 08 April 2020
Aliran suatu fluida dibedakan menjadi dua tipe, yaitu aliran laminar dan aliran turbulent. Aliran dikatakan laminar apabila partikel-partikel fluida yang bergerak secara teratur dalam lapisan-lapisan, sedangkan aliran disebut turbulent apabila tiap partikel fluida bergerak secara acak. Aliran laminar dan turbulent diilustrasikan pada gambar 2.5. A dan B.
Kondisi aliran laminar atau turbulent dapat dinyatakan dengan bilangan Reynolds. Bilangan Reynolds pada ducting dirumuskan pada persamaan 2.1.
Dimana : Re = Bilangan Reynold V = Kecepatan Statis dan Dinamis (m/s) D = Diameter Saluran Masuk (m) μ = Viskositas Dinamsis Fluida (Nm/s)
Pertemuan Keenam
Hari, Tanggal : Rabu 15 April 2020
Head Loss
Aliran fluida di dalam pipa mengikuti persamaan Bernouli, yang ditunjukkan pada persamaan dibawah ini:
Dimana P1 adalah tekanan upstream, P2 adalah tekanan downstream, ¯V adalah kecepatan rata-rata upstream. ¯V adalah kecepatan rata-rata downstream. ¯V didapatkan dengan membagi debit dengan luas penampang pipa. Z adalah elevasi pipa dalam m, dan hl adalah headloss. Kecepatan fluida dalam pipa didapatkan dengan persamaan dibawah ini:
Dimana Q adalah debit fluida dalam m3/s, A adalah cross sectional pipa dalam m2, D adalah diameter dalam pipa dalam meter. Total head loss adalah penjumlahan major loss dan minor loss, dirumuskan dengan persamaan dibawah ini:
Pressure drop pada segment pipa dapat dirumuskan dengan persamaan dibawah ini:
Dimana ΔP adalah pressure drop, hl adalah major headloss, f adalah friction factor, L adalah panjang pipa, D adalah diameter dalam pipa, dan K adalah loss coefficient pada fitting.
Head Loss Major (hl)
Major losses terjadi akibat gesekan fluida dengan permukaan pipa.Major losses dapat dirumuskan dengan persamaan dibawah ini:
Dimana ΔP adalah pressure drop, hl adalah major headloss, f adalah friction factor, L adalah panjang pipa, dan D adalah diameter dalam pipa. Besar nilai Re menentukan jenis aliran fluida. Jika Re≤2000 maka aliran laminar. Jika 2000>Re<4000 maka aliran transisi. Sedangkan jika Re>4000 maka aliran turbulent. Nilai Re dirumuskan dengan persamaan dibawah ini:
Dimana Re adalah reynold number, V adalah kecepatan aliran fluida dalam m/s, D adalah diameter dalam pipa dalam m, ρ adalah massa jenis fluida dalam kg/m3, dan μ adalah viskositas fluida dalam N.s/m2. Nilai f pada aliran laminar dan turbulen ditunjukkan oleh persamaan dibawah ini:
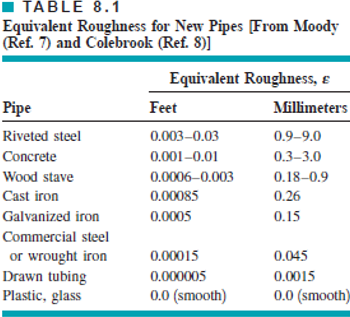
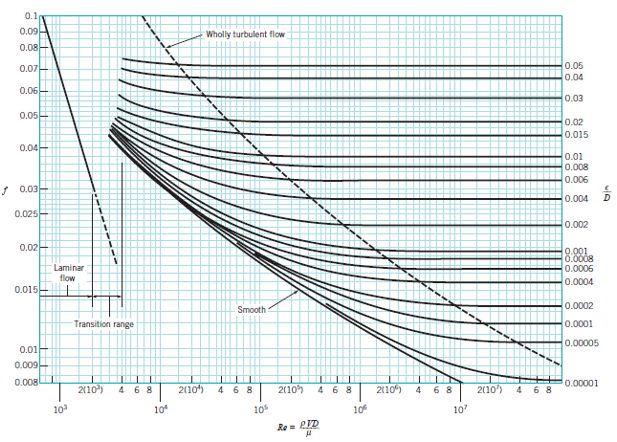
Nilai f juga dapat ditemukan pada Moody’s Diagram yang ditunjukkan pada Gambar 2.9.Dimana nilai roughness (ε) ditunjukkan pada Tabel 2.
Tabel 2.1 Nilai Roughness (ε) pada Berbagai Material
Pertemuan Ketujuh
Hari, Tanggal : Selasa 21 April 2020
Head Loss Minor
Pada sistem pipa, fluida akan melalui fitting, bend, atau valve sehingga terjadi minor losses. Minor losses dapat dirumuskan dengan persamaan dibawah ini:
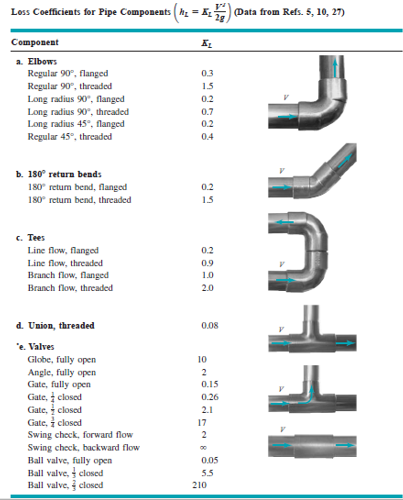
Dimana K adalah loss coefficient dan Le adalah equivalent lenght pipa dalam m. Loss coefficient (KL) pada valve dan fitting ditunjukkan pada Tabel 2.1.
Tabel 2.2 Loss Coefficient pada Valve dan Fitting
Soal Simulasi CFD: Laminar Parallel Plate Flow - ARTIKEL 2
Hasil Simulasi:
Pada gambar diatas ditunjukkan hasil potongan dari simulasi dengan Uin: 0.01m/s (sama) namun dengan variasi dynamic viscosity (berbeda). Dapat diketahui berdasarkan sebaran warna kecepatan aliran pada pipa lurus berbeda. Kecepatan pipa akan cenderung lebih besar jika mendekati pusat pipa sedangkan akan cenderung mengalami penurunan atau dapat dikatakan u=0 jika mendekati dinding pipa. Hal berdasarkan prinsip tegangan geser yang timbul antara dinding pipa dan aliran fluida.
Nilai velocity profile dengan =0,00004 kg/m.s pada setiap potongan dapat dilihat seperti gambar diatas. Dapat kita ketahui bahwa nilai kecepatan pada inlet sangat bervariasi, itu menandakan bahwa di bagian entrance region aliran akan memiliki kecepatan yang bervariasi. Namun setelah aliran melewati pipa sejauh Le aliran akan mengalami fully developed condition.
Pada gambar diatas ditunjukkan hasil potongan dari simulasi dengan Uin: 0.01m/s (sama) namun dengan variasi dynamic viscosity (berbeda), sama seperti jawaban soal A1. Dapat diketahui berdasarkan sebaran warna kecepatan aliran pada pipa lurus berbeda. Kecepatan pipa akan cenderung lebih besar jika mendekati pusat pipa sedangkan akan cenderung mengalami penurunan atau dapat dikatakan u=0 jika mendekati dinding pipa. Hal berdasarkan prinsip tegangan geser yang timbul antara dinding pipa dan aliran fluida.
Nilai velocity profile dengan =0,00001 kg/m.s pada setiap potongan dapat dilihat seperti gambar diatas. Dapat kita ketahui bahwa nilai kecepatan pada inlet sangat bervariasi, itu menandakan bahwa di bagian entrance region aliran akan memiliki kecepatan yang bervariasi. Namun setelah aliran melewati pipa sejauh Le aliran akan mengalami fully developed condition. Kita juga dapat melihat bentuk kurva pada aliran fluida setelah menjadi fully developed. Bentuk kurvanya akan cenderung sama, namun beda dikecepatan dipusat pipa. Hal tersebut berdasarkan prinsip tegangan geser dinding pipa dengan aliran fluida.
Soal Simulasi CFD: Turbulent Parallel Plate Flow - ARTIKEL 3
Hasil Simulasi: Contoh Hasil Slice pada Uin=0.02
Jawaban A.1:
Jawaban A.2:
Jawaban B.1:
Jawaban B.2:
Soal Simulasi CFD: Soal jawab mekanika fluida, munson, example 8.2 laminar pipe flow - ARTIKEL 4
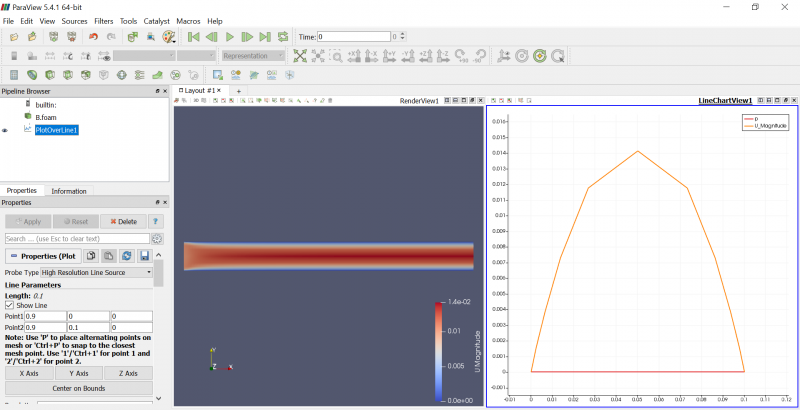
Soal Pressure Drop pada Aliran Laminer dalam Pipa
Hasil Simulasi
Inlet Slice (0,06, 1, 2.16, 4)m
Aliran fluida di dalam pipa mengikuti persamaan Bernouli, yang ditunjukkan pada persamaan dibawah ini:
Dimana P1 adalah tekanan upstream, P2 adalah tekanan downstream, ¯V adalah kecepatan rata-rata upstream. ¯V adalah kecepatan rata-rata downstream. ¯V didapatkan dengan membagi debit dengan luas penampang pipa. Z adalah elevasi pipa dalam m, dan hl adalah headloss. Kecepatan fluida dalam pipa didapatkan dengan persamaan dibawah ini:
Dimana Q adalah debit fluida dalam m3/s, A adalah cross sectional pipa dalam m2, D adalah diameter dalam pipa dalam meter. Total head loss adalah penjumlahan major loss dan minor loss, dirumuskan dengan persamaan dibawah ini:
Pressure Drop pada (0,06, 1, 2.16, 4)m
Berdasarkan hasil simulasi didapatkan hasil pressure total (p_static+p_dynamic) mengalami penurunan dari inltet menuju outlet. Maka dalam internal flow pipa panjang perlu dipikirkan besaran heat loss mayor dari suatu aliran. Hal ini dapat diatasi dengan penggunaan pompa pada jarak pipa tertentu agar aliran fluida dapat sampai pada tempatnya.
QUIZ 1: Mekanika Fluida
Soal No 4
A.Pengaruh Panjang Pipa pada Aliran Pipa Laminar Horizontal Terhadap Pressure Drop.
•Jenis aliran pada pipa ada 2 yaitu aliran laminar dan turbulen. Aliran didalam pipa dikatakan laminar jika nilai Re<2100.
•Turunnya tekanan total pada pipa horizontal akibat adanya gesekan pada dinding pipa. Nilai gesekan tersebut berdasarkan perkalian viskositas dinamik fluida dengan kecepatan fluida tersebut pada suatu titik. (Gambar. Rumus Gaya Gesek Fluida). Arah gaya gesek fluida dengan dinding pipa berlawanan dengan arah aliran fluida dan nilai gaya gesek paling besar terdapat pada aliran fluida yang dekat dengan dinding pipa. (Gambar. Aliran Laminar dalam Pipa). Sesuai dengan Hk. konservasi energi, energi tidak dapat dimusnahkan tapi hanya berubah bentuk. Pada kasus pressure drop pada aliran laminar gaya gesek yang timbul antara fluida dengan dinding pipa tersbut menjadikan energi panas.
Tekanan pada fluida ada 3 jenis yaitu: •Tekanan Statik = tekanan yang diberikan oleh partikel fluida saat dalam kondisi diam atau statis ke segala arah. •Tekanan Dinamis = tekanan yang diakibatkan oleh pergerakan dari partikel fluida yang dipengaruhi oleh kecepatan dari partikel fluida itu sendiri. •Tekanan Hydrostatik = tekanan yang diakibatkan dari ketinggian fluida dari fluida terhadap titik steady statenya. Pada kasus aliran laminar dalam pipa horizontal nilai tekanan hidrostatik diabaikan karena ΔZ = 0.
B.Pengaruh adanya sudut θ pada aliran pipa laminar terhadap pressure drop (Δp).
•Kita ketahui aliran fluida memiliki 3 tekanan, yaitu tekanan static, tekanan dinamik, dan tekanan hidrostatik. Pada kasus aliran laminar pada pipa bersudut θ tekanan hidrostatiknya akan memiliki nilai.
•Pada aliran laminar pipa bersudut θ, pressure drop dapat dihitung dari perbedaan ketinggian pada titik 1 (p1) dengan titik 2 (p2). Nilai p1>p2.
Soal No 5
A.Pengaruh Ketebalan Sublapisan Viskos Terhadap Pressure Drop
•Aliran turbulen adalah aliran yang memiliki Re tinggi. Karakteristik aliran turbulen dalam pipa horizontal memiliki Le yang pendek, tegangan geser yang besar pada dinding pipa, energi panas dihasilkan tinggi, kecepatan aliran pada center yang lebih rendah daripada aliran laminar dalam pipa horizontal. Dengan kecepatan inlet sama, diameter pipa sama, namun densitas fluida yang melalui pipa berbeda akan menjadinkan aliran fluida yang memiliki density tinggi akan memiliki Re yang lebih tinggi (Gambar. Rumus Re). Re kental> Re cair. Pada aliran turbulen terdapat suatu lapisan semu tipis akibat tegangan geser yang dinamakan sublapis viskos. Sublapisan viskos ini yang menimbulkan pressure drop. Sublapisan viskos besarnya di tentukan oleh viskositas, density fluida, dan tegangan geser disekitar dinding pipa. Semakin besar tegangan geser pada permukaan pipa maka semakin besar viskositas fluida sehingga semakin besar pula sublapisan viskosnya (Gambar. Rumus Tegangan Geser). Inilah hal yang nantinya akan membuat pressure drop pada aliran turbulen akan semakin besar.
•Maka pressure drop akan berbanding lurus dengan sublapisan viskos.
Soal No 2
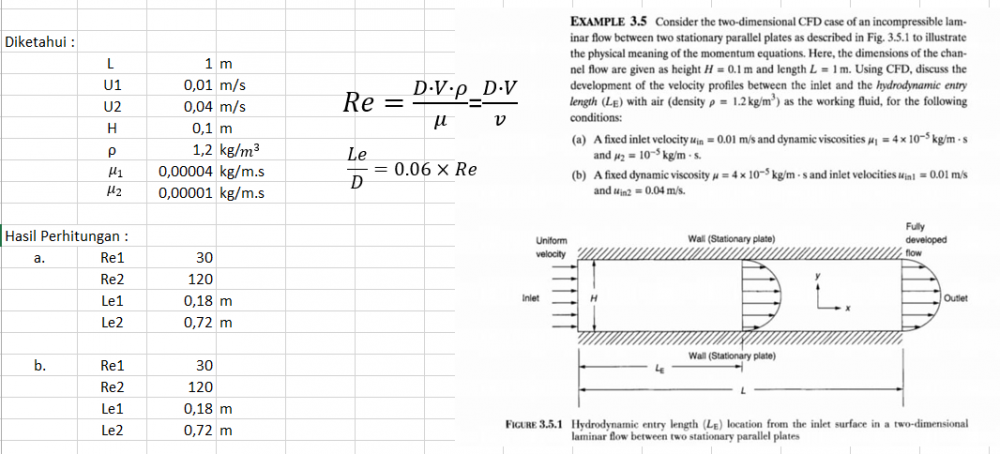
A.Hubungan Antara Beda Viskositas Dinamik pada Aliran Laminer Terhadap Panjang Entrance Length
•Aliran laminar adalah nilai bilangan Reynold dibawah 2100. Untuk menentukan jenis aliran dapat ditentukan dengan menentukan nilai bilangan reynoldnya dengan persamaan:
Pada kasus A ini aliran diketahui adalah aliran laminar. Kemudian diberikan 𝜇1 = 4x10-5 kg/m.s dan 𝜇2 = 10-5 kg/m.s dengan Uin yang sama. Menurut saya Re dari 𝜇1 pada entrance region akan lebih kecil dari 𝜇2. Sehingga nilai Le1 dari 𝜇1 akan lebih pendek jika dibandingkan dengan Le2. Hal tersebut karena tegangan geser dari 𝜇1 lebih besar daripada tegangan geser 𝜇2. Rumus mengukur tegangan geser adalah:
Posisi entrance region dapat ditentukan dengan menghitung jarak entrance length dengan persamaan:
Dengan kata lain dapat disimpulkan bahwa 𝜇 (viskositas dinamik) akan mempengaruhi entrance region dari suatu aliran. Semakin tinggi nilai 𝜇 maka nilai entrance region akan semakin kecil karena dipengaruhi oleh tegangan geser yang juga semakin meningkat.
B.Hubungan Antara Beda Kecepatan Inlet (Uin) pada Aliran Laminer Terhadap Panjang Entrance Length
•Pada aliran laminar akan terbentuk daerah entrance region antara entrance/ inlet dengan awal posisi fully developed. Jika diketahui nilai 𝜇 (viskositas dinamik) yang sama pada penggunaan kecepatan inlet yang berbeda U1 =0.01m/s dan U2 =0.04m/s. Maka untuk kedua penggunaan kecepatan inlet tersebut akan menghasilkan panjang entrance region yang berbeda. Entrance region akan semakin panjang/ membutuhkan waktu yang lama apabila aliran fluida masuk lebih besar. Karena dengan viskositas yang sama dan density (jenis fluida mengalir sama) nilai tegangan geser pada aliran dengan kecepatan inlet yang berbeda akan bernilai sama. Hal tersebut berdasarkan rumus tegangan geser dibawah ini.
Maka dapat disimpulkan entrance region akan semakin panjang/ semakin lama waktu yang dibutuhkan untuk mencapai fully developed jika kecepatan masuk pada suatu aliran ditingkatkan.
Soal No 3
A.Hubungan Antara Beda Kecepatan Inlet (Uin) Terhadap Jenis Aliran yang Akan Terjadi (Laminer atau Turbulen)
•Kecepatan merupakan sebuah vector. Sama halnya yang terjadi pada aliran fluida pada jenis turbulen. Aliran turbulen adalah aliran yang partikel - partikel nya bergerak secara acak, menghasilkan vector aliran yang kesegala arah. Sehingga resultan aliran terhadap sumbu. X pada kasus soal 3 akan semakin kecil jika dibandingkan dengan aliran laminer. Cara untuk menghitung kecepatan aliran turbulen tidak sama dengan cara menghitung kecepatan aliran laminar. Jika aliran laminar kita hanya perlu menghitung kecepatan rata rata 𝑢̅ nya saja (arah vector searah sb. x) dan dianggap semua titik memiliki kecepatan yang sama dengan kecepatan rata rata. Sedangkan untuk aliran turbulen kita harus mencari kecepatan rata rata 𝑢̅ dan kecepatan fluktuasi di titik tertentu u’(u total A = 𝑢̅ A + u’A).
•Besarnya kecepatan pada aliran turbulen menyebabkan energi kinetiknya juga semakin besar yang nantinya akan menyebabkan sublapisan viskos semakin tebal dan energi panas yang dihasilkan pada aliran turbulen juga semakin besar.
Soal No 6
A.Manipulasi Jenis Aliran (Laminer dan Turbulen) dengan Properties Fluida Masuk yang Sama
•Pada kompetisi motor balap (road race) berbahan bakar bensin. Para mekanik akan meracik motor yang akan dipertandingkan sebaik mungkin. Pada kompetisi biasanya diatur cc motor yang akan dipertandingkan, tidak boleh motor kelas 200cc diturunkan pada ajang 150cc. Sehingga mekanik akan melakukan improvisasi agar motor dengan kelas yang sama memiliki performa yang tinggi. Salah satunya adalah dengan memanipulasi campuran bahan bakar dengan udara yang akan masuk ruang bakar. Pada motor biasa akan kita jumpai jenis manifold karburator/ inejksi yang halus pada permukaannya. Hal tersebut menjadikan besin dan udara tidak bisa tercampur maksimal. Akibatnya performa motor tidak dapat maksimal. Agar lebih maksimal dilakukan porting pada dinding manifold agar campuran bensin dan udara dapat tercampur maksimal.
Berdasarkan karakteristik aliran turbulen, aliran ini akan memiliki bentuk aliran yang berputar ke segala arah.
Dengan memberikan motif bola golf pada permukaan manifold, maka luasan dari permuaakan manifold akan meningkat/ dapat dikatakan tambah kasar. Sehingga aliran fluida yang melewati permukaan manifold tersebut akan mengalami tegangan geser yang lebih besar. Atau dapat dikatakan nilai dari 𝜇 (viskositas dinamik) akan lebih tinggi daripada penggunaan permukaan halus. Sehingga Re pada 𝜇 pada permukaan kasar lebih tinggi (Aliran Turbulen).
Soal No 1
A.Aliran Fluida Jenis Laminer pada Plat Datar (2D)
•Dalam mempelajari mekanika fluida kita mempelajari 3 hukum dasar atau biasa disebut governing equation: •Hukum Konservasi Energi dE/dt = W+Q •Hukum Konservasi Massa dm/ dt = 0 •Hukum Konservasi Momentum m.dv/ dt = ƩF Pada aliran laminar dalam plat datar digunakan hukum dasar hukum konservasi momentum dengan kecepatan searah sumbu x. Dengan asumsi kecepatan arah sb. Y disetiap titik dianggap nol dan kecepatan arah sb. Z nol/ kosong (karena hanya 2D).
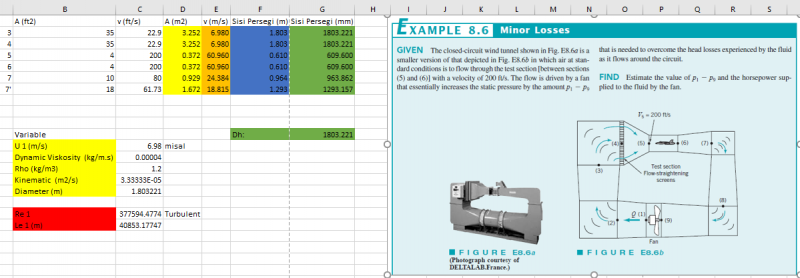
Soal Simulasi CFD: Soal jawab mekanika fluida, Minor Losses Ex.8.6 - ARTIKEL 7
Soal Ex.8.6 Munson
Soal Minor Losses Artikel 7
Potongan Melintang Fenomena Cortex
Potongan Sepanjang Sb.-Z Fenomena Cortex
Calculator
Hasil Perhitungan Pressure Drop Dalam Nozzle
Hasil Perhitungan Pressure Drop Dalam Difusser
Pertemuan Kesepuluh Simulasi Eksternal Flow Car Body
Tugas Besar - Analisa Profil Permuakaan (Surface Roughness) yang Berbeda pada Properties Fluida Masuk yang Sama pada Intake Manifold Karburator
Pada kompetisi balap berbahan bakar bensin. Mekanik akan meracik kendaraan yang akan dipertandingkan sebaik mungkin. Pada kompetisi biasanya ada regulasi seperti pembatasan cc motor disetiap kelasnya, tidak boleh motor kelas 200cc diturunkan pada ajang 150cc. Sehingga mekanik akan melakukan improvisasi agar motor dengan kelas yang sama memiliki performa yang tinggi. Salah satunya adalah dengan memanipulasi campuran bahan bakar dengan udara yang akan masuk ruang bakar. Pada motor/ mobil biasa akan kita jumpai jenis manifold karburator/ inejksi yang halus pada permukaannya. Hal tersebut menjadikan besin dan udara tidak bisa tercampur maksimal atau dapat dikatakan campuran udara dan bahan bakar masih kasar. Akibatnya performa motor tidak dapat maksimal. Agar lebih maksimal dilakukan porting pada dinding manifold agar campuran bensin dan udara dapat tercampur maksimal. Porting adalah melakukan profiling pada dinding intake manifold agar surface rougnessnya lebih kasar. Diharapkan dengan dilakukannya profilling pada dinding manifold dapat menjadikan campuran udara dan bahan bakar lebih baik.