Difference between revisions of "Muhammad Yusuf Raihan"
Yusufraihan (talk | contribs) (→Draft Paper Proyek Komputasi Teknik) |
Yusufraihan (talk | contribs) |
||
| (23 intermediate revisions by the same user not shown) | |||
| Line 274: | Line 274: | ||
Image:MYR Draft Paper 4.jpg | Image:MYR Draft Paper 4.jpg | ||
</gallery> | </gallery> | ||
| + | |||
| + | =='''Optimasi Pengaturan Infill pada Cetak Tiga Dimensi untuk Fabrikasi Tangan Prostetik Murah - Muhammad Yusuf Raihan'''== | ||
| + | |||
| + | '''Abstrak''' | ||
| + | |||
| + | Tangan prostetik adalah alat bantu medis yang berfungsi untuk menggantikan tangan yang hilang. Alat ini sangat membantu para penyandang disabilitas karena dapat membantu melakukan kegiatan-kegiatan yang membutuhkan penggunaan tangan. Sayangnya, tangan prostetik yang tersedia secara komersil masih memiliki harga yang sangat tinggi. Hal ini dikarenakan komponen-komponen pada tangan prostetik memiliki bentuk yang rumit dan skala produksinya kecil sehingga investasi alat untuk membuat produk tersebut menjadi cukup tinggi. Solusi dari mahalnya harga tangan prostetik adalah dengan mengganti metode manufaktur konvensional menjadi metode manufaktur aditif menggunakan pencetak tiga dimensi. Metode manufaktur ini mampu memproduksi barang dengan ukuran dan bentuk yang rumit dan lebih ekonomis jika digunakan untuk memproduksi dalam skala kecil. | ||
| + | |||
| + | Selain bentuk dan ukuran, pencetak tiga dimensi juga memiliki fleksibilitas dalam melakukan fabrikasi karena terdapat opsi pengaturan pencetakan yang beragam. Salah satu opsi pengaturan pencetakan adalah pengaturan infill. Infill adalah pengaturan mengenai isi dari suatu objek. Infill 100% berarti objek pejal sedangkan infill 0% berarti objek hollow. Pengaturan infill juga termasuk pengaturan pola pencetakan infill. Pada penelitian ini akan dilakukan optimasi pengaturan infill pada proses pencetakan tiga dimensi untuk mendapatkan hasil cetakan yang kuat namun tetap hemat material sehingga biaya produksi bisa lebih murah. Optimasi dilakukan dengan permodelan matematika mengenai pengaruh densitas dan pola infill terhadap kekuatan struktur tangan prostetik. Data kekuatan struktur didapatkan melalui simulasi pada peranti lunak menggunakan metode finite element. Hasil yang diharapkan dari penelitian ini adalah model matematika yang dapat digunakan untuk menentukan pengaturan infill seperti apa yang paling optimal baik dari segi kekuatan maupun harga. | ||
| + | |||
| + | <comments/> | ||
| + | |||
| + | =='''Kuis Komputasi Teknik – Permodelan Sistem Osilasi Satu Dimensi Menggunakan Metode Euler'''== | ||
| + | |||
| + | Soal : Hitung posisi dan kecepatan massa m seiring waktu (dari detik 0 sampai 10) menggunakan metode analitik dan numerik! | ||
| + | |||
| + | [[File:OsilasiMYR.PNG|600px]] | ||
| + | |||
| + | Jawab : | ||
| + | |||
| + | '''Initial Thinking dan Modelling''' | ||
| + | |||
| + | Gambar di atas adalah sistem di mana terdapat gerobak beroda yang dikaitkan terhadap pegas yang menempel pada suatu dinding. Pada sistem tersebut, ketka gerobak ditarik atau didorong ke luar dari kesetimbangan, maka gerobak akan bergerak bolak balik secara harmonik. Gerakan tersebut sering disebut sebagai osilasi. Sistem tersebut bisa dimodelkan menjadi sistem osilasi satu dimensi. Sistem osilasi satu dimensi adalah sistem yang berosilasi dalam satu dimensi ruang. Pada kasus ini, sistem dapat dimodelkan ke dalam satu dimensi ruang horizontal (X), dengan mengasumsikan tidak terdapat gaya lain yang memiliki arah ke dimensi lain (Y atau Z). Dengan demikian, menggunakan persamaan kesetimbangan gaya, kita dapat memodelkan sistem tersebut menjadi sistem osilasi satu dimensi. Asumsi lain yang digunakan pada kasus ini adalah tidak terdapat gesekan pada dasar roda, dan arah kanan positif arah kiri negatif. | ||
| + | |||
| + | Dari sistem di atas, apabila gerobak ditarik menjauhi dinding, bisa kita modelkan menjadi | ||
| + | |||
| + | [[File:1MYR.PNG|100px]] | ||
| + | |||
| + | Persamaan tersebut menggambarkan bahwa ketika gerobak ditarik kemudian dilepas, sistem mengalami gaya pegas ke arah kiri (-kx) sehingga mengalami percepatan (x”). Persamaan tersebut dapat ditulis ulang menjadi | ||
| + | |||
| + | [[File:2MYR.PNG|100px]] | ||
| + | |||
| + | dengan cara memindahkan –kx ke ruas kanan dan membagi kedua ruas dengan m. Omega pada persamaan tersebut adalah rumus frekuensi osilasi pada sistem pegas yaitu ω=√(k⁄m) | ||
| + | Persamaan di atas adalah persamaan diferensial biasa (ODE) orde dua. Karena orde dua, maka diperlukan dua initial condition agar dapat mendapatkan solusi eksak. Initial condition pada sistem ini adalah x(0) = X0 dan x’(0) = 0, di mana X0 merupakan posisi awal ketika gerobak selesai ditarik, dan karena sistem awalnya diam maka kecepatan awal (x’(0)) bernilai 0. Dari sini kita bisa mendapatkan solusi eksak dari persamaan yaitu X(t)=X_A cosωt di mana XA adalah amplitudo atau simpangan terjauh dari sistem, amplitudo dari sistem ini sama dengan simpangan awal X0. Dari persamaan tersebut kita bisa mengetahui posisi, kecepatan, serta percepatan dari sistem seiring waktu. | ||
| + | Namun ada cara lain selain metode eksak untuk menghitung posisi, kecepatan, dan percepatan yaitu menggunakan metode euler. Metode euler adalah metode numerik sederhana dengan memperkirakan nilai suatu titik dengan cara menambahkan nilai pada titik sebelumnya dengan besar slope dikali interval. Metode ini bisa dilakukan dengan menerapkan sedikit modifikasi dari persamaan ODE yang sebelumnya telah didapat. Modifikasi dilakukan dengan memperkenalkan dua variabel baru yaitu u dan v, di mana u = x dan v = x’ = u’, yang juga dapat diturunkan menjadi v’=x’’. Dari persamaan ODE di atas, kita bisa mendapatkan nilai x’’ yaitu ’’=-ω^2 x , kita bisa mengubah variabel pada persamaan tersebut menjadi u dan v sehingga persamaannya menjadi | ||
| + | |||
| + | [[File:3MYR.PNG|100px]] | ||
| + | |||
| + | Hal selanjutnya yang dilakukan adalah penulisan ulang persamaan tersebut. Penulisan ulang dilakukan dengan mengganti notasi kutip menjadi notasi d/dt. Sehingga persamaannya menjadi | ||
| + | |||
| + | du/dt=v | ||
| + | |||
| + | dv/dt=-ω^2u | ||
| + | |||
| + | Hal selanjutnya adalah hal krusial dalam melakukan metode numerik, yaitu proses diskritisasi. Diskritisasi adalah proses mengubah variabel yang kontinu menjadi nilai nilai pecah atau diskrit. Sehingga pada proses ini d diganti menjadi delta. Menandakan bahwa d yang merupakan selisih yang sangat sangat kecil diubah menjadi selisih yang diskrit yaitu delta. Oleh karena itu persamaan berubah menjadi | ||
| + | |||
| + | [[File:4MYR.PNG|200px]] | ||
| + | |||
| + | Dengan menulis ulang persamaan tersebut, kita bisa mendapatkan persamaan baru yaitu | ||
| + | |||
| + | [[File:5MYR.PNG|200px]] | ||
| + | |||
| + | Persamaan inilah yang akan digunakan untuk melakukan metode euler. Metode euler mengharuskan kita menentukan nilai delta t. Pada metode euler, semakin kecil delta t seharusnya menghasilkan hasil yang lebih akurat. Simulasi perhitungan baik menggunakan metode eksak maupun euler akan di bahas pada bab selanjutnya | ||
| + | |||
| + | '''Simulasi''' | ||
| + | |||
| + | Pada kasus ini, simulasi perhitungan dilakukan menggunakan bantuan peranti lunak Microsoft Excel. Dalam simulasi ini kita akan menghitung nilai posisi dan kecepatan seiring waktu baik menggunakan metode eksak maupun metode euler. Selanjutnya kita akan membandingkan hasil kedua metode tersebut. Perbandingan hasil tersebut dikenal dengan nama proses ''''verifikasi'''. | ||
| + | |||
| + | Pada kasus ini, ''boundary'' dan ''initial condition'' yang digunakan adalah | ||
| + | |||
| + | ω=2 rad | ||
| + | X_0=5 m | ||
| + | 〖x'〗_0=0 m/s | ||
| + | |||
| + | 1. Metode eksak | ||
| + | |||
| + | Untuk dapat menghitung nilai posisi dan kecepatan sistem tersebut menggunakan metode eksak pada Ms excel, kita perlu membuat dua kolom masing masing untuk posisi dan kecepatan. Pada kolom posisi, kita memasukkan rumus posisi yaitu x(t)=X_0 cosωt. Sedangkan pada kolom kecepatan kita masukkan rumus kecepatan yang merupakan turunan dari rumus posisi yaitu x"(t)=〖-X〗_A ωsinωt. Kemudian masukkan nilai t dengan membuat kolom baru. | ||
| + | |||
| + | 2. Metode Euler | ||
| + | |||
| + | Pada metode euler, kolom posisi dan kecepatan diisi dengan rumus | ||
| + | |||
| + | [[File:5MYR.PNG|200px]] | ||
| + | |||
| + | Pada kasus ini, saya akan memvariasikan besar delta t, yaitu delta t = 0.1 , 0.05, dan 0.01. | ||
| + | |||
| + | 3. Hasil | ||
| + | |||
| + | [[File:0.1MYR.PNG|400px]] | ||
| + | [[File:0.05MYR.PNG|400px]] | ||
| + | [[File:0.01MYR.PNG|400px]] | ||
| + | |||
| + | '''Verifikasi''' | ||
| + | |||
| + | Verifikasi adalah proses membandingkan nilai hasil simulasi permodelan dengan hasil ideal atau teoritis. Pada kasus ini, nilai teoritis adalah nilai dari hasil metode eksak, sedangkan hasil permodelan adalah hasil metode euler. Pada tahap ini, kita membandingkan nilai dari kedua metode tersebut. Perbandingan nilai akan disajikan dengan tabel data error untuk variabel posisi dan kecepatan. Nilai error berupa selisih mutlak antara nilai pada metode eksak dan metode euler. Berikut ini nilai error untuk masing-masing variasi delta t. | ||
| + | |||
| + | [[File:E 0.1MYR.PNG|400px]] | ||
| + | [[File:E 0.05MYR.PNG|400px]] | ||
| + | [[File:E 0.01MYR.PNG|400px]] | ||
| + | |||
| + | Dari grafik di atas jelas terlihat bahwa semakin kecil nilai delta t maka semakin kecil error. Pola lain yang juga jelas terlihat adalah semakin besar nilai t maka error semakin besar, berapapun besar delta t nya. Hal ini menandakan bahwa metode euler yang diterapkan pada kasus ini sudah terverifikasi, di mana metode euler dengan delta t 0.01 merupakan metode yang paling terverifikasi karena nilai error yang paling kecil. Namun metode euler bisa menjadi tidak terverifikasi ketika nilai t yang digunakan besar misalkan perhitungan dilakukan hingga t = 1000. Untuk dapat menerapkan metode euler pada kasus tersebut maka dibutuhkan besar delta t yang sangat kecil untuk dapat menghindari error yang besar. Pada proses permodelan, hal yang harus dilakukan setelah verifikasi adalah validasi. Validasi merupakan proses penilaian apakah model yang dibuat sesuai dengan kondisi aktual. Namun pada kasus ini karena tidak terdapat data aktual untuk dibandingkan dengan data hasil simulasi maka proses validasi tidak dapat dilakukan sehingga proses permodelan hanya berhenti di tahap verifikasi. Dan hasil permodelan yang didapatkan adalah bahwa model numerik menggunakan metode euler dengan besar delta t sebesar 0.01 sudah terverifikasi. | ||
| + | |||
| + | '''Kesimpulan''' | ||
| + | |||
| + | Komputasi teknik merupakan metode penyelesaian masalah-masalah teknik menggunakan bantuan komputasi. Salah satu metode komputasi yang umum digunakan adalah metode numerik. Permasalahan teknik yang bisa diselesaikan dengan metode numerik salah satunya adalah kasus sistem osilasi satu dimensi, di mana kita ingin mengetahui posisi dan kecepatan sistem seiring waktu. Pada kasus ini, metode numerik yang digunakan adalah metode euler dengan besar interval waktu 0.1, 0.05, dan 0.01. Persamaan yang digunakan untuk metode euler didapat dari analisis kesetimbangan gaya dari sistem dengan asumsi bahwa tidak terdapat gaya lain selain gaya pegas dalam arah x. Dengan menghitung posisi dan kecepatan sistem dari waktu 0 detik sampai 10 detik, metode euler berhasil menghitung dengan cukup baik, dengan hasil terbaik ketika nilai interval waktu paling kecil yaitu 0.01. Dari sini kita dapat mempelajari bahwa metode numerik dapat sangat membantu kita dalam menyelesaikan permasalahan teknik ketika kita tidak dapat menyelesaikan permasalahan tersebut dengan metode analitik. | ||
| + | |||
| + | == ''' Kasus Pressure Drop '''== | ||
| + | |||
| + | [[File:MYRPRESSUREDROP1.jpg|600px]] [[File:MYRPRESSUREDROP2.jpg|600px]] | ||
| + | |||
| + | [[File:MYRPRESSUREDROP3.jpg|600px]] [[File:MYRPRESSUREDROP4.jpg|600px]] | ||
| + | |||
| + | == ''' Ujian Akhir Semester ''' == | ||
| + | |||
| + | ==== '''Kasus Perhitungan Laju Mobil Toyota Agya''' ==== | ||
| + | |||
| + | Pada Ujian Akhir Semester kuliah Komputasi Teknik ini, kami diminta untuk menghitung waktu yang dibutuhkan oleh suatu mobil untuk mencapai kecepatan maksimumnya dari keadaan diam, ketika diketahui nilai-nilai spesifikasi seperti daya mesin, torsi, massa mobil dan hambatan udara. Pada kasus ini, saya akan mengambil Toyota Agya sebagai contoh perhitungan. Segala data spesifikasi terkait mobil Toyota Agya didapat dari website [https://www.toyota.astra.co.id/product/agya?utm_source=google&utm_medium=cpc&utm_campaign=toyota_thrive_sem_clicks_all-city_all-gender_18-65__all-device_sem-agya_hatchback_new-agya_&utm_content=product_text_keyword_agya-product_product&gclid=CjwKCAjw5vz2BRAtEiwAbcVIL5tGcDfc13jwVPB_ttcgo9VE-b4HATnIDMfYJFGNbpj7Uv1Fsw0VqhoCZ9gQAvD_BwE website Toyota]. Spesifikasi mobil tersebut adalah sebagai berikut | ||
| + | |||
| + | [[File:SpekAgyaMYR.PNG|700px]] | ||
| + | |||
| + | Pada kasus ini saya akan menerapkan ''Rule of Thumb'' komputasi teknik yang dahulu pernah diajarkan oleh Pak Dai. Pertama tama kita akan mulai dengan tahap ''Initial Thinking''. | ||
| + | |||
| + | ''' Initial Thinking ''' | ||
| + | |||
| + | Agar dapat menghitung waktu tercapainya kecepatan maksimum (''top speed''), kita perlu tahu seberapa besar akselerasi dari mobil tersebut. Relasi antara akselerasi, kecepatan, dan kecepatan maksimum dapat dijelaskan melalui persamaan kinematika yaitu v = v0 + at, di mana v adalah kecepatan akhir, v0 adalah kecepatan awal, a adalah akselerasi, dan t adalah waktu tempuh. Nilai v0 sudah kita ketahui yakni 0, karena mobil mulai dari keadaan diam. Sedangkan nilai v merupakan kecepatan maksimum mobil, nilai ini bisa didapat dari melihat spesifikasi mobil, namun kita juga bisa mendapatkan nilai v dengan melakukan komputasi. Agar dapat menghitung nilai t atau waktu tempuh, kita tinggal menghitung nilai a yaitu akselerasi. | ||
| + | |||
| + | Akselerasi suatu benda terkait erat dengan gaya-gaya yang bekerja pada benda tersebut. Seperti yang kita tahu hukum gerakan newton menyatakan bahwa F=m.a yang juga berarti bahwa akselerasi suatu benda disebabkan oleh gaya yang dialami oleh benda tersebut. Melalui hukum tersebut, kita dapat menghitung nilai a dengan menghitung resultan gaya yang dialami oleh mobil. | ||
| + | |||
| + | Sebelum lanjut ke tahap ''modelling'', kita perlu menyatakan asumsi apa saja yang diperlukan untuk dapat menghitung variabel yang kita inginkan. Asumsi pertama adalah mobil bergerak dengan selalu menggunakan daya maksimum (daya konstan dan tidak bervariasi terhadap waktu), kemudian mobil hanya mengalami gaya dalam arah sumbu x, dan luas penampang mobil (yang terhambat laju udara) dianggap berbentuk persegi panjang. Setelah asumsi telah dinyatakan, kita dapat memulai pada tahap ''modelling''. | ||
| + | |||
| + | ''' Modelling ''' | ||
| + | |||
| + | Pada tahap ini, kita akan menganalisis gaya-gaya yang bekerja pada mobil. Berikut ini adalah diagram yang menggambarkan gaya-gaya tersebut | ||
| + | |||
| + | [[File:ModellingmobilMYR.PNG|500px]] | ||
| + | |||
| + | Dapat kita lihat bahwa terdapat tiga gaya yang mempengaruhi gerakan mobil, gaya pertama adalah gaya dorong dari mesin yang dinotasikan dengan Fm, gaya ini adalah gaya utama yang menyebabkan mobil bergerak. Selanjutnya ada gaya Fg yaitu gaya gesek antara mobil dengan jalan, gaya ini adalah gaya yang menghambat laju mobil namun juga penting agar roda mobil dapat mendorong mobil maju. Yang terakhir adalah gaya Fa yaitu gaya hambatan udara. Gaya hambatan udara terjadi akibat luas penampang mobil yang tidak mengizinkan udara untuk mengalir dengan bebas (tak terhalang), sehingga perubahan momentum udara berakibat pada gaya yang menghambat gerakan mobil tersebut. Besar gaya ini tergantung oleh densitas udara, luas penampang mobil, kecepatan udara relatif dengan mobil, dan koefisien hambatan udara yang juga dikenal dengan nama ''drag coefficient''. Nilai ''drag coefficient'' berbeda-beda untuk tiap mobil, semakin aerodinamis suatu mobil maka semakin kecil nilai koefisien tersebut. Pada kasus Toyota Agya ini saya tidak menemukan nilai ''drag coefficient'' yang tepat, oleh karena itu saya akan menggunakan nilai ''drag coefficient'' yang umum untuk mobil dengan desain sejenis yaitu sebesar kira-kira 0,3. | ||
| + | |||
| + | Gaya dorong mobil (Fm) dihitung dengan rumus Fm=torsi(tau)/jari-jari roda mobil(r), sedangkan torsi didapat dari torsi=daya/kecepatan putar mesin. Sementara itu gaya gesek didapat dari rumus Fg=miu*gaya normal, di mana miu diasumsikan sebesar 0,12. Sedangkan rumus untuk gaya hambatan udara adalah sebagai berikut | ||
| + | |||
| + | [[File:Drag-force-formulaMYR.png]] | ||
| + | |||
| + | Dari persamaan-persamaan tersebut kita mendapatkan rumus untuk akselerasi mobil sebagai berikut | ||
| + | |||
| + | [[File:PercepatanmobilMYR.PNG]] | ||
| + | |||
| + | Dari persamaan kinematik v=v0+at, maka didapatkan rumus waktu tempuh untuk mencapai kecepatan maksimum sebagai berikut | ||
| + | |||
| + | [[File:WaktutempuhMYR.PNG]] | ||
| + | |||
| + | Dilihat dari rumus tersebut, ada satu variabel yang menyebabkan kita tidak dapat langsung menggunakan rumus tersebut, variabel tersebut adalah v atau kecepatan mobil. Hal ini dikarenakan nilai v bervariasi terhadap waktu. Fenomena ini juga dijelaskan oleh fakta bahwa besar hambatan angin akan semakin besar apabila kecepatan relatif udara juga makin besar. Untuk itu kita perlu menggunakan metode numerik untuk menghitung nilai kecepatan dan percepatan yang terus berubah sepanjang waktu. | ||
| + | |||
| + | Perhitungan numerik dilakukan dengan menghitung nilai percepatan dan kecepatan untuk setiap detik sesuai interval. Pada t=0, nilai percepatan dihitung dengan rumus semula (tidak bermasalah karena gaya hambat = 0), sedangkan nilai kecepatan = 0 karena bermula dari kondisi diam. Pada interval selanjutnya, hitung kecepatan berdasarkan nilai percepatan pada detik sebelumnya. Gunakan rumus vt=v0+at. Kemudian hitung percepatan dengan rumus percepatan dan masukkan nilai kecepatan yang baru saja didapatkan. Lakukan langkah-langkah perhitungan tersebut hingga didapatkan kecepatan yang konstan (''top speed'') atau percepatan sama dengan nol, kemudian catat waktu yang ditempuh. | ||
| + | |||
| + | Jika langkah-langkah tersebut diterjemahkan ke dalam rumus numerik, maka rumus numeriknya adalah sebagai berikut | ||
| + | |||
| + | [[File:NumerikmobilMYR.PNG]] | ||
| + | |||
| + | Nilai vn awal, atau v0 adalah 0 karena mobil mulai dari keadaan diam. | ||
| + | |||
| + | ''' Simulasi ''' | ||
| + | |||
| + | Rumus numerik tersebut akan disimulasikan menggunakan aplikasi Microsoft Excel. Simulasi dilakukan untuk interval waktu 1 detik. Berikut ini adalah tabel perhitungan dari simulasi pada Microsoft Excel | ||
| + | |||
| + | [[File:ExcelmobilMYR.PNG|700px]] | ||
| + | |||
| + | Dari hasil perhitungan tersebut didapatkan grafik percepatan dan kecepatan seperti berikut ini | ||
| + | |||
| + | [[File:Grafik percepatanMYR.PNG|600px]] [[File:GrafikkecepatanMYR.PNG|600px]] | ||
| + | |||
| + | Dari grafik tersebut kita bisa menentukan waktu yang dibutuhkan mobil Toyota Agya untuk mencapai kecepatan maksimum. Kecepatan maksimum dapat dilihat dari laju kecepatan yang mulai konstan yang juga berarti nilai percepatan yang mendekati 0. Dari grafik tersebut kecepatan maksimum diraih pada waktu 140 detik. Di mana kecepatan maksimum Toyota Agya adalah sebesar 178 km/jam. | ||
| + | |||
| + | ''' Verifikasi dan Validasi ''' | ||
| + | |||
| + | Untuk dapat menilai kebenaran dari perhitungan tersebut maka perlu dilakukan tahap verifikasi dan validasi. Verifikasi dilakukan dengan menilik ulang apakah perhitungan telah dilakukan tanpa kesalahan hitung dan juga dihitung pada asumsi-asumsi yang telah ditentukan. Dari proses ini maka perhitungan tersebut telah terverifikasi. Proses validasi dilakukan dengan membandingkan hasil perhitungan dengan spesifikasi mobil. Berdasarkan situs [https://otomotifnet.gridoto.com/read/231148018/test-drive-si-bengal-toyota-agya-12-trd-s-at-2017 otomotifnet] kecepatan maksimum Toyota Agya adalah 180 km/jam. Dari perbandingan ini ternyata hasil yang saya dapat cukup akurat. Error atau perbedaan hasil perhitungan dengan realita dapat disebabkan oleh asumsi-asumsi yang digunakan, semisal besar koefisien gesek, luas penampang mobil yang dianggap persegi dan juga penggunaan daya maksimum yang konstan. | ||
| + | |||
| + | ''' Kesimpulan ''' | ||
| + | |||
| + | Mobil bergerak diakibatkan gaya dorong dari mesin namun dihambat oleh gaya gesek dengan jalanan dan gaya hambat udara. Gaya hambat udara akan semakin besar ketika kecepatan mobil semakin besar. Hal ini menyebabkan suatu saat kecepatan mobil tidak akan bertambah lagi. Pada kasus mobil Toyota Agya, melalui analisis gaya pada mobil dan perhitungan menggunakan metode numerik, didapatkan bahwa kecepatan maksimum mobil adalah sebesar 178 km/jam dan ditempuh pada waktu selama 140 detik. Dari kasus ini kita belajar bahwa kita dapat memprediksi kecepatan maksimum mobil dan waktu tempuhnya berdasarkan spesifikasi mobil dan perhitungan menggunakan hukum-hukum fisika. | ||
| + | |||
| + | ==== ''' Muhasabah Diri ''' ==== | ||
| + | |||
| + | Selama satu semeter kuliah komputasi teknik, Alhamdulillah saya belajar banyak hal penting. Saya belajar mengenai langkah-langkah melakukan komputasi teknik (Initial thinking, modelling, simulation, verification, validation), istilah-istilah penting dalam komputasi, metode-metode komputasi yang sangat aplikatif seperti Euler Method, Runge-Kutta, Heun Method, Finite Element Method, Spring-mass modelling, hingga diperkenalkan dengan metode Artificial Neural Network. Yang tidak kalah penting adalah saya diingatkan bahwa dalam melakukan komputasi, dasar pemahaman kita terhadap fenomena fisik yang sedang dianalisis juga harus baik, inilah mengapa sering dilakukan diskusi fisika dasar contohnya seperti fenomena pressure drop. Saya juga belajar tentang bagaimana mengaplikasikan komputasi teknik pada kasus nyata seperti kasus pada skripsi, kasus laju korosi, kasus shockbreaker motor, kasus konsumsi energi harian, dan kasus getaran pada bangunan. Dalam kuliah ini saya tidak hanya didorong untuk dapat menggunakan metode-metode komputasi saja, tapi juga didorong untuk dapat memahami konsep di balik metode-metode tersebut. Seluruh hasil pembelajaran saya selama satu semester tercatat baik pada halaman wiki saya, sehingga akan selalu bermanfaat untuk masa-masa yang akan datang dan juga untuk orang lain, InsyaAllah Aamiin.. | ||
| + | |||
| + | Selama kuliah, saya belajar dengan serius dengan cara serius dalam mengerjakan tugas-tugas, baik yang berupa tulisan maupun video presentasi. Saya juga berkontribusi dengan baik pada tugas kelompok dengan cara mengerjakan bagian modelling dari studi kasus yang sedang dipelajari. Sementara untuk diskusi seperti pada grup WhatsApp dan pada wiki, saya jujur tidak terlalu aktif dikarenakan saya merasa ilmu saya terkait topik yang sedang didiskusikan masih sangat kurang. Namun saya selalu berusaha untuk membaca dan mengikuti jalannya diskusi sehingga saya bisa menjadi paham terhadap apa yang sedang didiskusikan. | ||
| + | |||
| + | Dari usaha dan pemahaman yang selama ini saya dapatkan di kelas komputasi teknik, mudah-mudahan saya bisa mendapatkan nilai 77 hingga 84 atau B+ hingga A-. Semoga apa yang selama ini saya pelajari di kelas komputasi teknik dapat terus berbekas dalam kehidupan saya dan dapat diaplikasikan untuk menyelesaikan masalah keteknikkan yang riil sehingga dapat bermanfaat untuk orang banyak. Aamiin | ||
Latest revision as of 23:21, 10 June 2020
Contents
- 1 Data Diri dan Pengenalan Singkat
- 2 Pemahaman terkini tentang Komputasi Teknik
- 3 Sinopsis Skripsi
- 4 Istilah-istilah dalam Komputasi Teknik
- 5 Permodelan Matematika Antropometri Tangan Manusia untuk Membantu Proses Perancangan Tangan Prostetik Indonesia
- 6 Pertemuan 4
- 7 Abstrak Studi Numerik Permasalahan Dalam Skripsi
- 8 "Pembukuan Energi Harian"
- 9 Rule of Thumb dari Komputasi Teknik
- 10 Tugas Pengganti UTS
- 11 Optimasi Pengaturan Infill pada Cetak Tiga Dimensi untuk Fabrikasi Tangan Prostetik Murah - Muhammad Yusuf Raihan
- 12 Kuis Komputasi Teknik – Permodelan Sistem Osilasi Satu Dimensi Menggunakan Metode Euler
- 13 Kasus Pressure Drop
- 14 Ujian Akhir Semester
Data Diri dan Pengenalan Singkat
Nama : Muhammad Yusuf Raihan
NPM : 1606835185
Program Studi : S2 Teknik Mesin
Peminatan : Sistem Manufaktur dan Otomasi
Email : muhammad.yusuf63@ui.ac.id
Perkenalkan, nama saya Muhammad Yusuf Raihan, teman-teman biasa memanggil saya Raihan. Saya tinggal di Bumi, Tata Surya, Lengan Orion, Galaksi Bima Sakti, Local Group, Virgo Supercluster, Alam Semesta. Terlahir sebagai debu bintang di antah berantah alam yang raya membangkitkan rasa penasaran saya terhadap dunia tempat tinggal kita yang luas dan penuh rahasia. Rasa penasaran ini mendekatkan saya dengan sains. Sejak kecil, sains menjadi kapal andalan saya dalam mengarungi samudera ilmu. Dengan sains, sedikit demi sedikit kotak hitam alam ini telah terbongkar. Kapal kita sudah mengantar ke peti harta karun berisi asal usul dan sejarah umat manusia dan dunia. Tapi pertanyaan sekarang adalah, apa selanjutnya? ke mana lagi kapal kita akan berlayar?
Rupanya di dalam peti harta karun tersebut terdapat petunjuk mengenai tujuan kita selanjutnya. Umat manusia diizinkan untuk melangkahkan kaki masuk ke dunia lain, ke dunia ciptaannya sendiri. Manusia mulai membuka pintu masuk ke dalam dunia digital dan mulai tinggal bersamanya. Revolusi Industri 4.0 adalah peta baru dalam ekspedisi umat manusia.
Tentunya saya ingin memiliki peran dalam ekspedisi ini. Kecintaan saya terhadap sains mendorong saya untuk menjadi seorang peneliti dan dosen. Sebagai peneliti, saya ingin memiliki kesempatan untuk memegang setir kapal ekspedisi Revolusi Industri 4.0. Sekarang, saya sedang mengambil program Fast Track di jurusan Teknik Mesin, Peminatan Sistem Manufaktur dan Otomasi, Universitas Indonesia angkatan 2016. Dan harapannya saya dapat melanjutkan kuliah doktoral dalam bidang Intelligent Machine. Kali ini saya sedang mengerjakan proyek perancangan tangan prostetik, dibimbing oleh Pak Agung Shamsuddin Saragih, S.T., MS.Eng., Ph.D.
Pemahaman terkini tentang Komputasi Teknik
Perkenalan pertama saya dengan komputasi teknik adalah ketika mengambil mata kuliah Metode Numerik pada semester 5 dulu di Teknik Mesin Universitas Indonesia. Metode numerik adalah alternatif solusi untuk memecahkan permasalahan matematika, di samping solusi lainnya yang lebih umum yaitu metode analitik. Perbedaan utama dari kedua metode tersebut adalah jenis hasil yang didapatkan. Metode analitik menghasilkan solusi exact atau pasti benar sedangkan metode numerik menghasilkan approximation atau pendekatan. Metode numerik muncul sebagai alternatif karena keterbatasan kemampuan metode analitik dalam memecahkan beberapa masalah. Keterbatasan tersebut biasanya berupa model persamaan yang rumit sehingga sulit didapat persamaan solusinya dan memerlukan waktu yang cukup lama untuk menyelesaikan masalah tersebut. Dengan metode numerik, kita bisa cukup melakukan hasil aproksimasi dari model rumit tersebut, sehingga didapat hasil yang cukup akurat namun dengan waktu yang jauh lebih singkat. Metode numerik semakin memiliki keunggulan juga dikarenakan meningkatnya teknologi komputasi, sehingga pendekatan yang dihasilkan menjadi jauh lebih akurat dan didapatkan dalam waktu yang sangat cepat.
Kuliah Metode Numerik pada semester 5 lalu mengenalkan saya dengan metode metode seperti Euler dan Runge-Kutta untuk menyelesaikan ODE (Ordinary Differential Equation), Numerical Integration dengan metode Newton-cotes, Trapezoidal, dan Simpsons, serta membahas sedikit tentang regresi dan interpolasi. Metode metode tersebut biasa dikerjakan dengan menggunakan bantuan software MATLAB. Namun mata kuliah ini masih belum membahas mengenai aplikasi nyata dari penggunaan metode metode tersebut. Sehingga saya masih belum merasakan manfaat langsung dari perkuliahan tersebut.
Harapan saya pada mata kuliah Komputasi Teknik adalah mendapatkan penjelasan lebih lanjut mengenai aplikasi Metode Numerik pada kasus nyata dunia teknik. Metode Numerik mungkin hanya salah satu metode dari banyak metode lain yang bisa dipakai dalam menyelesaikan permasalahan teknik, sehingga saya berharap dapat mempelajari teori dan prinsip-prinsip lain yang menjadi dasar dalam melakukan komputasi teknik. Selain itu saya juga berharap bisa belajar menggunakan software selain MATLAB untuk melakukan komputasi teknik, contohnya EES.
Sinopsis Skripsi
Saat ini saya sedang mengerjakan proyek perancangan tangan prostetik murah berbasis 3D Printing. Saya mencoba merancang tangan prostetik yang murah karena saat ini di Indonesia ketersediaan tangan prostetik masih sangat minim. Tangan prostetik komersil yang ada di Indonesia hanya tangan buatan Ottobock, perusahaan prostetik dari Jerman. Harga produk buatan Ottobock masih sangat mahal, untuk tangan prostetik dengan fungsi terbatas dihargai sebesar kira-kira Rp150.000.000,- sedangkan tangan prostetik yang berfungsi penuh berharga kira-kira Rp.1.500.000.000,-. Selain itu ukuran dari tangan prostetik tersebut masih terbatas, hanya tersedia dalam ukuran kecil, sedang, dan besar. Pilihan ukuran yang terbatas tersebut akan mengurangi nilai estetika dari tangan prostetik tersebut. Munculnya teknologi 3D Printing menjadi solusi dari permasalahan tersebut. Dengan teknologi 3D Printing, kita dapat memfabrikasi barang tanpa batasan bentuk dan dengan harga yang relatif murah. Harapannya hasil dari proyek ini dapat menjadi solusi kurangnya persediaan tangan prostetik di Indonesia.
Dalam perancangan ini, saya banyak menggunakan software CAD yaitu Autodesk Inventor. Autodesk Inventor digunakan untuk membuat desain tiga dimensi dari tangan prostetik. Hasil desain tiga dimensi tersebut kemudian akan diproduksi menggunakan 3D Printing sehingga dibutuhkan juga penggunaan software slicer untuk menentukan pengaturan 3D Printing. Sampai saat ini, saya belum menerapkan konsep komputasi teknik dalam mengerjakan proyek ini. Namun sepertinya komputasi teknik akan bermanfaat dalam proses analisis kekuatan struktur, optimasi penggunaan daya pada aktuator, serta optimasi penggunaan material pada proses 3D Printing.
Istilah-istilah dalam Komputasi Teknik
Stokastik dan Deterministik
Stokastik dan Deterministik adalah dua jenis permodelan yang umum dijumpai pada proses komputasi teknik. Perbedaan utama antara keduanya adalah pada kepastian hasil. Model stokastik adalah model yang memasukkan elemen keacakan atau randomness sehingga hasil yang didapatkan cenderung berbeda-beda walaupun parameter dan initial condition-nya sama persis. Pada model stokastik, randomness biasa dihitung dalam bentuk probabilitas. Sedangkan pada model deterministik, kesamaan parameter dan initial condition pasti menghasilkan angka yang sama.
Dalam memodelkan suatu kasus, model stokastik adalah model yang umumnya lebih tepat. Hal ini dikarenakan pada setiap kasus banyak terdapat variabel yang tidak kita ketahui. Model stokastik biasa digunakan ketika tidak dibutuhkan model kuantitatif yang menyatakan hubungan antar variabel, model ini lebih cocok digunakan ketika kita ingin menjelaskan suatu fenomena berdasarkan probabilitas dari variabel-variabel yang memiliki pengaruh. Walau lebih akurat dalam memodelkan suatu fenomena, model ini kurang tepat jika kita menginginkan nilai pasti dari suatu model. Maka dari itu model deterministik hadir sebagai alternatif. Dalam model deterministik, kita mengasumsikan kita paham betul mengenai variabel-variabel serta pengaruhnya, sehingga kita dapat memastikan hasil kuantitatif dari model yang dibuat.
Contoh dari model deterministik adalah analisis kekuatan struktur dengan mengasumsikan properti mekanikal dari bahan yang digunakan dan juga mengasumsikan beban yang diberikan. Dengan asumsi, kita bisa mendapatkan hasil dengan angka yang pasti. Namun pada kenyataannya, properti mekanikal dari suatu bahan bisa saja tidak uniform untuk keseluruhan komponen, sehingga terdapat aspek randomness pada variabel properti mekanikal, begitu pula dengan variabel beban yang diterima, belum tentu kenyataannya beban yang diterima selalu sama dengan apa yang sebelumnya diasumsikan pada model deterministik, contohnya yaitu beban yang diterima oleh suatu jembatan, besar beban pasti memiliki aspek randomness bergantung pada apa saja yang melewati jembatan tersebut.
Karena memiliki fungsi dan keunggulan masing-masing, maka pemahaman terkait kedua model perlu untuk dimiliki. Saya berharap dalam kuliah Komputasi Teknik kita dapat belajar lebih dalam mengenai cara membuat permodelan stokastik dan deterministik.
Validasi dan Verifikasi
Validasi dan Verifikasi adalah dua istilah yang sekilas terdengar mirip, namun keduanya memiliki perbedaan yang cukup signifikan. Dalam permodelan matematika, validasi adalah proses perbandingan hasil dari model matematika dengan kenyataan, semakin mirip dengan kenyataan, semakin valid sebuah model matematika. Dalam kata lain, validitas adalah ukuran kualitas dari sebuah model matematika. Berbeda dengan verifikasi, verifikasi adalah proses pengecekan dalam pelaksanaan atau penghitungan suatu model matematika atau algortima. Sebuah perhitungan dianggap terverifikasi apabila perhitungan tersebut dilakukan dengan benar. Perhitungan numerik yang terverifikasi belum pasti valid, model matematik yang valid juga belum tentu terverifikasi, tergantung dari pelaksanaan model matematik tersebut. Validasi menilai apakah modelnya benar, sedangkan verifikasi menilai apakah penggunaan modelnya benar.
Dalam penggunaan aplikasi pembantu permodelan numerik, contohnya MATLAB, proses verifikasi sudah dilakukan oleh engineer yang membuat software tersebut, jika terdapat hitungan yang tidak terverifikasi maka kesalahan ada di software. Sedangkan validasi hanya bisa dilakukan oleh pengguna aplikasi, karena validasi terkait dengan model matematika yang pengguna buat, sehingga akurasi model pasti ditentukan oleh sang pembuat model.
Regresi
Regresi adalah metode analisis statistik untuk menilai pengaruh dari suatu variabel yang memiliki hubungan kausalitas dengan variabel lain.
Ekstrapolasi
Ekstrapolasi adalah proses estimasi menggunakan nilai regresi dari dua variabel ke luar jangkauan data yang ada
Interpolasi
Interpolasi adalah metode penambahan data baru ke dalam interval antara dua data diskrit menggunakan metode estimasi. Interpolasi dibutuhkan karena dalam suatu studi seringkali ditemukan data diskrit. Data diskrit dapat menjadi masalah ketika kita menginginkan data lain yang berada di luar data point dari data tersebut. Terdapat beberapa metode interpolasi di antaranya adalah interpolasi constant piecewise, interpolasi linear, interpolasi polinomial dan interpolasi spline. Berikut ini contoh pengunaan dari masing-masing metode interpolasi
Anggap kita memiliki data diskrit seperti berikut ini
Interpolasi Constant Piecewise
Interpolasi constant piecewise bekerja dengan mengestimasi nilai interpolasi konstan terhadap data point terdekat. Kita memberikan nilai yang sama pada data baru sesuai dengan data terdekat dari data baru tersebut. Data terdekat bisa dihitung lewat selisih nilai pada sumbu x untuk data baru dan dua data di sampingnya. Data dengan selisih nilai x yang lebih kecil dijadikan nilai dari data baru tersebut. Constant piecewise bisa digambarkan lewat grafik berikut ini
Interpolasi Linear
Interpolasi linear mengasumsikan kontinuum antara dua data yang berdekatan berupa garis lurus. Untuk itu diperlukan persamaan garis lurus antara dua titik. Persamaan garis lurus didapatkan dengan menggunakan rumus persamaan garis lurus pada dua data yang berdekatan tersebut. Persamaan garis yang dihasilkan kemudian dapat dijadikan rumus untuk mengestimasi nilai data point baru yang berada di antara dua data yang dijadikan garis. Interpolasi linear bisa digambarkan lewat grafik berikut ini
Interpolasi Polinomial
Jika interpolasi linear mengasumsikan kontinuum berupa garis lurus, interpolasi ini mengasumsikan kontinuum berupa garis polinomial. Sehingga dibutuhkan persamaan polinomial dari data diskrit yang sudah dimiliki. Berbeda dengan interpolasi linear yang memiliki persamaan garis berbeda untuk tiap pasangan data yang berbeda, interpolasi polinomial hanya memiliki satu persamaan polinomial tapi harus mencakup semua data diskrit yang ada. Proses ini adalah proses perhitungan yang berat. Interpolasi polinomial bisa digambarkan lewat grafik berikut ini
Interpolasi Spline
Interpolasi spline mirip dengan interpolasi polinomial namun persamaan polinomial yang digunakan berbeda untuk tiap pasangan data. Interpolasi spline mirip dengan interpolasi linear namun dengan persamaan polinomial orde rendah. Persamaan polinomial yang dibentuk satu pasangan data sebisa mungkin dapat menciptakan kurva yang mulus jika digabungkan dengan persamaan polinomial di sebelahnya. Sehingga akan terbentuk garis yang mirip dengan interpolasi polinomial namun sedikit berbeda. Interpolasi spline dapat digambarkan lewat grafik berikut ini
Permodelan Matematika Antropometri Tangan Manusia untuk Membantu Proses Perancangan Tangan Prostetik Indonesia
Pendahuluan
Manusia memiliki ukuran dan bentuk tangan yang berbeda-beda tiap individu. Namun perbedaan tersebut tidak begitu besar. Secara umum, ukuran dan bentuk tangan manusia memiliki kemiripan. Sehingga ukuran dan bentuk tangan manusia bisa diperkirakan dan digambarkan dengan permodelan matematika. Model matematika adalah alat untuk menggambarkan suatu fenomena menggunakan persamaan matematika dengan tujuan untuk membantu proses analisis maupun rekayasa.
Model matematika untuk ukuran dan bentuk tangan manusia dapat dimanfaatkan untuk perancangan tangan prostetik. Saat ini tangan prostetik yang tersedia secara komersil hanya menyediakan ukuran tangan terbatas yakni S (kecil), M (sedang), dan L (besar). Hal ini kurang baik dalam hal antropomorfisme atau kemiripan dengan manusia karena tangan manusia lebih variatif dibanding tiga ukuran tersebut. Model matematika yang menggambarkan ukuran dan bentuk tangan orang Indonesia akan sangat membantu proses perancangan tangan prostetik Indonesia. Model matematika tersebut nantinya dapat dimasukkan ke dalam software CAD (Computer-Aided Design) sehingga proses penyesuaian ukuran dalam perancangan dapat berlangsung cepat dan otomatis.
Model matematika akan dibuat berdasarkan tabel antropometri yaitu sebuah tabel yang berisikan ukuran dari tubuh manusia. Karena tujuan dari permodelan matematika ini adalah untuk membantu perancangan tangan prostetik di Indonesia, maka tabel antropometri yang digunakan sebaiknya juga berasal dari Indonesia atau setidaknya dari ras yang sama sehingga didapatkan model matematika yang lebih akurat. Pada kasus ini, tabel antropometri yang dipakai adalah milik Eko Nurmianto.
Tabel Antropometri
Di bawah ini dilampirkan tabel antropometri orang Indonesia dari Eko Nurmianto
Metode
Permodelan matematika dilakukan dengan asumsi bahwa semua parameter ukuran tangan memiliki korelasi dengan parameter panjang tangan (Hand Length, parameter dengan nomor 1 pada tabel). Dari asumsi ini, dibuat model matematika yang menjelaskan besar nilai parameter ukuran lainnya terhadap ukuran panjang tangan. Sehingga didapat persamaan satu variabel berjumlah 21, sesuai jumlah parameter pada tabel tersebut. Berikut ini metode yang dilakukan dalam permodelan matematika untuk bentuk dan ukuran tangan orang Indonesia :
1. Buat rasio antara parameter target dengan parameter “Hand Length” untuk ketiga persentil dan semua parameter.
2. Lakukan regresi untuk nilai ratio dari ketiga persentil untuk parameter yang sama (Contoh : “Hand width”, 5%, 50%, 95%). Gunakan tipe regresi yang memiliki nilai R kuadrat terbesar.
3. Lakukan langkah 2 untuk semua parameter. 4. Buat persamaan baru untuk mengkonversi nilai panjang tangan menjadi persentil. Persamaan dibuat dengan meregresikan nilai persentil dengan nilai panjang tangan. Gunakan tipe regresi dengan nilai R kuadrat terbesar.
5. Setelah didapatkan persamaan konversi nilai panjang tangan menjadi persentil dan persamaan nilai parameter target terhadap parameter “Hand Length”, gabungkan keduanya dengan memasukkan persamaan konversi panjang tangan ke persentil ke dalam persamaan parameter target.
6. Permodelan matematika selesai. Didapatkan 21 persamaan dengan 1 variabel bebas di mana variabel bebas tersebut adalah nilai panjang tangan atau “Hand Length”.
Hasil
Berikut ini tabel hasil akhir dari permodelan matematika untuk ukuran dan bentuk tangan orang Indonesia
Dari rumus tersebut, kita bisa menghasilkan panjang dari bagian-bagian tangan hanya dengan mengetahui nilai panjang tangan. Hal ini dapat membantu proses perancangan tangan prostetik dengan cara memasukkan rumus tersebut ke dalam software CAD (Computer-Aided Design) sehingga proses penyesuaian ukuran bisa dilakukan secara otomatis dan cepat.
Pada beberapa kasus, terdapat amputee yang tidak memiliki tangan sama sekali. Hal ini dapat diselesaikan dengan membuat persamaan baru untuk mengkonversi nilai ukuran panjang anggota tubuh lain (contoh : tinggi badan) menjadi ukuran panjang tangan. Sehingga model matematika ini masih bisa diterapkan pada amputee yang tidak memiliki tangan.
Pertemuan 4
Pada pertemuan keempat kelas komputasi teknik, diadakan kuis untuk mengukur pengetahuan dari para mahasiswa. Hal yang menarik dari kuis ini adalah pertanyaan mengenai persamaan matematika dan makna fisik dari persamaan tersebut. Pertanyaan tersebut mengingatkan kembali bahwa dalam melakukan komputasi teknik dibutuhkan pemahaman yang baik mengenai persamaan matematika karena tanpa pemahaman tersebut kita akan kesulitan dalam melakukan analisis dari hasil komputasi teknik. Selain itu, persamaan matematika dalam bidang keteknikan bukan hanya susunan dan formasi dari variabel belaka, namun juga memiliki koherensi dengan dunia fisik. Persamaan matematika teknik seharusnya menggambarkan sifat/kelakuan dari zat dan energi dari sebuah sistem. Karena sifat inilah persamaan matematika menjadi sangat bermanfaat karena sebagai seorang engineer, persamaan matematika dapat membantu kita merekayasa sebuah sistem. Proses rekayasa dan manipulasi dari suatu sistem merupakan hal yang tidak mudah dilakukan sehingga akan sangat membantu jika terdapat tools yang dapat memudahkan proses ini. Komputasi teknik adalah tools tersebut. Dengan komputasi teknik kita dapat mensimulasikan persamaan matematika yang diketahui sehingga dapat memprediksi sifat dari suatu sistem tanpa harus kesulitan memecahkan persamaan tersebut secara manual. Penerapan komputasi teknik dalam memecahkan masalah keteknikan adalah subjek dari bagian kedua kuis. Pada bagian kedua kuis, mahasiswa diminta untuk menjelaskan masalah yang ingin diselesaikan beserta pendekatan komputasi apa yang dipilih untuk membantu proses penyelesaian masalah tersebut. Dari kuis ini diharapkan mahasiswa dapat mengetahui seberapa jauh pemahamannya akan komputasi teknik sehingga dapat melakukan proses pembelajaran yang lebih efektif lagi untuk kedepannya.
Abstrak Studi Numerik Permasalahan Dalam Skripsi
Abstrak 1
Permodelan Matematika Antropometri Tangan Manusia untuk Perancangan Parametrik Tangan Prostetik Indonesia
Secara komersil, tangan prostetik biasanya dibuat dalam tiga ukuran umum, yaitu S (kecil), M (sedang), dan L (besar). Keterbatasan ukuran tangan prostetik tersebut berdampak pada kurang baiknya proporsi ukuran tangan prostetik dengan penggunanya. Teknologi 3D Printing memungkinkan pengembangan tangan prostetik dengan bentuk dan ukuran yang sesuai dengan pengguna. Desain tangan prostetik yang dapat menyesuaikan ukuran pengguna dapat dicapai dengan memanfaatkan data antropometri, yaitu data yang berisi ukuran dari bagian-bagian anggota tubuh, termasuk tangan. Data dari tabel antropometri dapat dimodelkan sehingga dihasilkan model matematika yang menjelaskan hubungan antar ukuran bagian-bagian tangan. Pembuatan model matematika dilakukan dengan metode regresi polinomial. Model matematika tersebut kemudian akan dimasukkan ke dalam software CAD (Computer-Aided Design) untuk dijadikan dasar dari metode perancangan parametrik. Metode perancangan parametrik akan sangat mempermudah proses pengembangan tangan prostetik dengan ukuran yang dapat menyesuaikan pengguna.
Permodelan matematika untuk menjelaskan hubungan ukuran antara bagian-bagian tangan dilakukan dengan asumsi awal bahwa seluruh ukuran dari bagian-bagian tangan memiliki korelasi terhadap total panjang tangan (dari pergelangan tangan ke ujung jari tengah). Dari asumsi ini, kita dapat melakukan permodelan matematika dengan membandingkan ukuran dari bagian-bagian lain pada tangan terhadap total panjang tangan. Perbandingan dilakukan dengan membagi langsung antara panjang tangan dengan ukuran bagian lain sehingga didapat sebuah ratio yang menjelaskan perbandingan antara kedua data tersebut. Data antropometri biasanya disajikan dalam tiga persentil untuk setiap ukuran bagian-bagian tangan. Persamaan regresi digunakan untuk mencari hubungan antara ratio-ratio dari ketiga persentil pada ukuran bagian tangan tertentu, sehingga didapatkan persamaan yang dapat menjelaskan pengaruh ukuran panjang tangan terhadap bagian lain dari tangan. Hasil yang akan diperoleh berupa kumpulan persamaan yang menjelaskan hubungan tiap-tiap ukuran bagian tangan terhadap panjang tangan. Persamaan tersebut yang kemudian akan dimasukkan ke dalam software CAD untuk membantu proses desain parametrik.
Abstrak 2
Simulasi Finite Element Method untuk Penentuan Ukuran dan Material Komponen Link Pada Tangan Prostetik
Komponen link adalah komponen yang umum digunakan pada tangan prostetik. Komponen ini menghubungkan ruas jari distal phalanx dengan pemberi gerakan pada telapak tangan sehingga gaya yang dihasilkan aktuator pada telapak tangan dapat bertransmisi ke ruas jari ujung (distal phalankx). Komponen ini adalah komponen yang paling rentan patah ketika tangan prostetik terkena beban berat. Jika patah, maka jari tempat komponen tersebut patah tidak dapat berfungsi lagi. Akibat vitalnya komponen ini maka analisis untuk mengetahui kekuatan komponen tersebut menjadi patut dilakukan. Hal ini semakin menjadi perhatian ketika teknik produksi yang utama digunakan pada perancangan tangan prostetik ini berupa 3D Printing dengan bahan filamen polylacticacid (PLA). Bahan tersebut memiliki kekuatan yang relatif rendah jika dibandingkan dengan bahan-bahan lain yang umum digunakan pada tangan prostetik, seperti aluminium dan titanium.
Analisis kekuatan dilakukan menggunakan metode simulasi Finite Element Method (FEM) pada software Ansys Workbench. Simulasi yang dilakukan berupa pembebanan statik (static load). Alasan dari pemilihan metode simulasi ini adalah karena tujuan utama simulasi hanya untuk mencari tahu kekuatan link tersebut ketika dikenakan beban besar, bukan beban yang berubah-ubah terhadap waktu. Tujuan akhir dari simulasi ini adalah untuk mengambil keputusan berupa pengubahan ukuran maupun material untuk komponen link pada tangan prostetik berbasis 3D Printing. Jika hasil yang didapatkan adalah link tersebut patah ketika diberikan beban besar maka pengubahan ukuran maupun material akan dilakukan, kemudian dilakukan uji simulasi kembali untuk verifikasi.
"Pembukuan Energi Harian"
Energi adalah sesuatu yang diperlukan agar suatu hal dapat melakukan kerja. Tak terkecuali manusia, manusia juga butuh energi untuk melakukan sesuatu. Sehari-hari, kita pasti mengkonsumsi energi. Walaupun kekal, energi itu terbatas, energi yang dapat kita gunakan tidak tak terhingga. Ditambah lagi besar porsi dari sumber energi kita adalah energi tak ramah lingkungan. Hal ini berarti besar energi yang dikonsumsi berkorelasi terhadap besar dampak lingkungan yang diberikan. Agar dapat memanfaatkan keterbatasan energi dengan baik maka diperlukan pencatatan mengenai pemasukan energi dan pengeluaran energi. Pencatatan ini dilakukan dengan tujuan menemui keseimbangan antara ketersediaan dan kebutuhan. Namun kita sebagai manusia, biasanya melakukan sesuatu yang lebih dari butuh, kita sebut hal ini dengan "keinginan", dan keinginan juga ikut mengkonsumsi energi, sehingga kita juga perlu memperhitungkan keinginan kita ketika melakukan pencatatan energi. Pencatatan akan pemasukan dan pengeluaran energi dilihat dari ketersediaan, kebutuhan dan keinginan akan energi untuk aktivitas sehari-hari, akan saya sebut sebagai "Pembukuan Energi Harian".
Dalam Pembukuan Energi Harian saya akan mencatat pekerjaan apa saja yang dilakukan setiap hari dan berapa besar nominal energi (Joule) yang dibutuhkan untuk melakukan pekerjaan tersebut. Nominal energi akan saya bagi dua menjadi energi yang dibutuhkan dan energi yang diinginkan. Pemasukan energi dicatat dengan menuliskan aktivitas apa saja yang menyediakan energi beserta nominal energinya. Di samping nominal energi masukan, nominal tersebut juga akan dikonversi menjadi satuan mata uang (Rupiah) untuk menggambarkan berapa besar biaya yang saya keluarkan untuk menyediakan energi sehari-hari saya. Proses konversi nominal energi menjadi mata uang dilakukan berdasarkan jenis energi yang digunakan. Pencatatan akan dilakukan untuk 7 hari selama seminggu sehingga didapat 7 data untuk masing masing aktivitas harian. Tujuh data ini kemudian akan diplot ke dalam grafik dan dilakukan Regresi untuk mendapatkan break-even point . Dari pencatatan ini diharapkan bahwa saya akan mendapatkan sense mengenai konsumsi energi saya dibandingkan dengan kebutuhan dan biaya yang dikeluarkan, hasil dari Pembukuan Energi Harian ini akan menjadi bahan refleksi saya untuk dapat lebih menghargai serta menghemat energi sebagai wujud aktivitas peduli lingkungan.
Konsumsi Energi
Sementara ini, pembukuan energi yang dilakukan baru berupa pencatatan konsumsi energi selama satu minggu. Pencatatan konsumsi energi dilakukan untuk tiga jenis konsumsi yaitu makanan, bensin, dan listrik. Energi dicatat dalam satuan Kalori kemudian dilakukan regresi untuk melihat kecenderungan konsumsi energi dalam satu minggu.
Dari grafik tersebut dapat tergambarkan bahwa dari ketiga jenis energi, konsumsi paling banyak adalah konsumsi listrik, dan pada hari sabtu dan minggu terlihat kenaikan nilai konsumsi listrik dibandingkan dengan hari kerja yang mungkin disebabkan oleh lebih lamanya penggunaan AC. Dari hasil regresi terlihat bahwa konsumsi listrik dan makan cenderung naik sedangkan bensin cenderung turun. Kecenderungan turun dari konsumsi bensin dikarenakan pada hari jumat sabtu minggu tidak ada penggunaan bensin. Sedangkan kecenderungan naik untuk listrik dan makan disebabkan konsumsi yang lebih pada hari sabtu dan minggu.
Rule of Thumb dari Komputasi Teknik
Rule of thumb adalah suatu set prosedur yang dapat memudahkan kita untuk melakukan suatu aktivitas. Suatu rule of thumb tidak harus selalu tepat untuk segala situasi namun adanya rule of thumb akan sangat meningkatkan efisiensi dari suatu aktivitas. Sebagai sesuatu aktivitas yang bisa dibilang kompleks dan butuh banyak pertimbangan, aktivitas komputasi teknik akan sangat terbantu jika terdapat rule of thumb yang dapat dijadikan acuan. Pada pertemuan keenam kuliah komputasi teknik, Pak Dai memberikan kami sebuah rule of thumb komputasi teknik yang cukup sederhana namun sangat membantu. Rule of thumb tersebut adalah sebagai berikut
Dalam melakukan komputasi teknik, berikut adalah prosedur yang sebaiknya dilakukan :
1. Initial Thinking / Pemahaman akan masalah
Karena komputasi teknik hanyalah sebuah tools untuk menyelesaikan suatu masalah, maka hal yang paling penting untuk dilakukan terlebih dahulu adalah memahami apa yang menjadi masalah dan apa tujuan dari penyelesaian masalah tersebut. Pada tahap ini, kita akan menganalisis sistem hingga kita mendapatkan apa saja yang kita ketahui, dan yang lebih penting, apa yang belum kita ketahui terkait hal-hal yang diperlukan untuk mencapai tujuan yang kita tentukan. Hasil dari tahap ini adalah faktor-faktor yang berpengaruh terhadap tujuan akhir kita. Faktor-faktor ini nantinya akan menjadi variabel bebas dan tujuan kita akan menjadi variabel terikat. Faktor-faktor yang berpengaruh dalam suatu sistem bisa jadi terlalu banyak untuk dapat kita perhitungkan seluruhnya, untuk itu pada tahap ini juga diperlukan merumuskan apa saja variabel yang akan kita hitung dan apa saja yang tidak. Variabel yang diputuskan untuk tidak dihitung biasa disebut dengan "asumsi". Hubungan antar variabel-variabel ini akan dijelaskan pada tahap selanjutnya yaitu
2. Modelling
Modelling adalah proses merumuskan variabel-variabel yang sebelumnya sudah ditentukan menjadi sebuah persamaan yang dapat menjelaskan pengaruh variabel tersebut terhadap hasil/tujuan. Hasil dari tahap ini adalah sebuah model matematika yang, jika sesuai asumsi, diharapkan dapat menggambarkan dengan baik realitas dari sistem yang sedang kita analisis. Model matematika yang tepat menggambarkan suatu sistem adalah model matematika yang valid. Model matematika yang valid akan sangat membantu kita untuk memahami bahkan merekayasa suatu sistem. Karena manfaat yang besar dari model matematika yang valid, maka pencarian akan validitas suatu model menjadi salah satu fokus utama dalam melakukan komputasi teknik. Validitas dapat dicari dengan melakukan tahap-tahap selanjutnya yaitu
3. Simulation
Simulation(simulasi) adalah proses eksekusi dari model matematika yang dibuat dengan cara menentukan nilai dari variabel bebas dan memasukkan batas-batas dari asumsi yang telah awal disepakati. Pada tahap ini hasil akhir yang merupakan tujuan dari analisis akan didapatkan. Namun hasil yang didapatkan belum tentu benar karena model matematika yang dieksekusi belum diketahui validitasnya, bahkan kita belum juga tahu apakah kita mengeksekusi model tersebut dengan benar, sehingga dibutuhkan tahap selanjutnya yaitu
4. Verification
Verifikasi adalah proses peninjauan ulang mengenai eksekusi dari model matematika. Dalam proses verifikasi, kita menilai apakah kita sudah menerapkan model matematika sesuai dengan tujuan atau fungsi dari model tersebut. Proses ini juga mengecek ulang apakah kita sudah memperhatikan batas-batas atau asumsi yang diterapkan pada model tersebut. Dalam perhitungan manual (tanpa bantuan komputer), proses verifikasi juga termasuk dalam pengecekan ulang untuk menemukan apakah terdapat kesalahan pengoperasian matematika. Secara singkat, verifikasi adalah proses peninjauan seberapa benar kita melakukan suatu perhitungan. Verification is about whether we are solving the equation right
5. Validation
Proses terakhir yang bisa jadi merupakan proses yang paling krusial dalam menilai validitas suatu model adalah proses validasi itu sendiri. Jika verifikasi adalah " are we solving the equation right? " maka validasi adalah " are we solving the right question? ". Proses ini bisa dilakukan dengan membandingkan hasil simulasi dengan realita. Validasi bisa dilakukan dengan terus menerus membandingkan hasil simulasi dengan realita sehingga didapatkan tingkat validitas dari model tersebut. Kita dapat menentukan seberapa besar tingkat validitas yang diperlukan untuk menilai apakah model yang kita buat sudah cukup baik. Jika validitas model yang dibuat masih di bawah batas yang ditentukan maka perlu dilakukan pengulangan dari tahap-tahap pada rule of thumb ini. Jika model dinilai sudah cukup valid maka proses permodelan matematika sudah selesai sehingga model yang dihasilkan bisa digunakan untuk proses komputasi teknik.
Tugas Pengganti UTS
Video Presentasi Belajar Mingguan
Pertemuan 1
Pertemuan 2
Pertemuan 3
Pertemuan 4
Pertemuan 5
Pertemuan 6
Laporan Progres Tugas Optimasi Energi Harian
Energi adalah sesuatu yang diperlukan agar suatu hal dapat melakukan kerja. Tak terkecuali manusia, manusia juga butuh energi untuk melakukan sesuatu. Sehari-hari, kita pasti mengkonsumsi energi. Walaupun kekal, energi itu terbatas, energi yang dapat kita gunakan tidak tak terhingga. Ditambah lagi besar porsi dari sumber energi kita adalah energi tak ramah lingkungan. Hal ini berarti besar energi yang dikonsumsi berkorelasi terhadap besar dampak lingkungan yang diberikan. Agar dapat memanfaatkan keterbatasan energi dengan baik maka diperlukan pencatatan mengenai pemasukan energi dan pengeluaran energi. Pencatatan ini dilakukan dengan tujuan menemui keseimbangan antara ketersediaan dan kebutuhan. Namun kita sebagai manusia, biasanya melakukan sesuatu yang lebih dari butuh, kita sebut hal ini dengan "keinginan", dan keinginan juga ikut mengkonsumsi energi, sehingga kita juga perlu memperhitungkan keinginan kita ketika melakukan pencatatan energi. Pencatatan akan pemasukan dan pengeluaran energi dilihat dari ketersediaan, kebutuhan dan keinginan akan energi untuk aktivitas sehari-hari, akan saya sebut sebagai "Pembukuan Energi Harian".
Dalam Pembukuan Energi Harian saya akan mencatat pekerjaan apa saja yang dilakukan setiap hari dan berapa besar nominal energi (Joule) yang dibutuhkan untuk melakukan pekerjaan tersebut. Nominal energi akan saya bagi dua menjadi energi yang dibutuhkan dan energi yang diinginkan. Pemasukan energi dicatat dengan menuliskan aktivitas apa saja yang menyediakan energi beserta nominal energinya. Di samping nominal energi masukan, nominal tersebut juga akan dikonversi menjadi satuan mata uang (Rupiah) untuk menggambarkan berapa besar biaya yang saya keluarkan untuk menyediakan energi sehari-hari saya. Proses konversi nominal energi menjadi mata uang dilakukan berdasarkan jenis energi yang digunakan. Pencatatan akan dilakukan untuk 7 hari selama seminggu sehingga didapat 7 data untuk masing masing aktivitas harian. Tujuh data ini kemudian akan diplot ke dalam grafik dan dilakukan Regresi untuk mendapatkan break-even point . Dari pencatatan ini diharapkan bahwa saya akan mendapatkan sense mengenai konsumsi energi saya dibandingkan dengan kebutuhan dan biaya yang dikeluarkan, hasil dari Pembukuan Energi Harian ini akan menjadi bahan refleksi saya untuk dapat lebih menghargai serta menghemat energi sebagai wujud aktivitas peduli lingkungan.
Konsumsi Energi
Sementara ini, pembukuan energi yang dilakukan baru berupa pencatatan konsumsi energi selama satu minggu. Pencatatan konsumsi energi dilakukan untuk tiga jenis konsumsi yaitu makanan, bensin, dan listrik. Energi dicatat dalam satuan Kalori kemudian dilakukan regresi untuk melihat kecenderungan konsumsi energi dalam satu minggu.
Dari grafik tersebut dapat tergambarkan bahwa dari ketiga jenis energi, konsumsi paling banyak adalah konsumsi listrik, dan pada hari sabtu dan minggu terlihat kenaikan nilai konsumsi listrik dibandingkan dengan hari kerja yang mungkin disebabkan oleh lebih lamanya penggunaan AC. Dari hasil regresi terlihat bahwa konsumsi listrik dan makan cenderung naik sedangkan bensin cenderung turun. Kecenderungan turun dari konsumsi bensin dikarenakan pada hari jumat sabtu minggu tidak ada penggunaan bensin. Sedangkan kecenderungan naik untuk listrik dan makan disebabkan konsumsi yang lebih pada hari sabtu dan minggu.
Draft Paper Proyek Komputasi Teknik
Optimasi Pengaturan Infill pada Cetak Tiga Dimensi untuk Fabrikasi Tangan Prostetik Murah - Muhammad Yusuf Raihan
Abstrak
Tangan prostetik adalah alat bantu medis yang berfungsi untuk menggantikan tangan yang hilang. Alat ini sangat membantu para penyandang disabilitas karena dapat membantu melakukan kegiatan-kegiatan yang membutuhkan penggunaan tangan. Sayangnya, tangan prostetik yang tersedia secara komersil masih memiliki harga yang sangat tinggi. Hal ini dikarenakan komponen-komponen pada tangan prostetik memiliki bentuk yang rumit dan skala produksinya kecil sehingga investasi alat untuk membuat produk tersebut menjadi cukup tinggi. Solusi dari mahalnya harga tangan prostetik adalah dengan mengganti metode manufaktur konvensional menjadi metode manufaktur aditif menggunakan pencetak tiga dimensi. Metode manufaktur ini mampu memproduksi barang dengan ukuran dan bentuk yang rumit dan lebih ekonomis jika digunakan untuk memproduksi dalam skala kecil.
Selain bentuk dan ukuran, pencetak tiga dimensi juga memiliki fleksibilitas dalam melakukan fabrikasi karena terdapat opsi pengaturan pencetakan yang beragam. Salah satu opsi pengaturan pencetakan adalah pengaturan infill. Infill adalah pengaturan mengenai isi dari suatu objek. Infill 100% berarti objek pejal sedangkan infill 0% berarti objek hollow. Pengaturan infill juga termasuk pengaturan pola pencetakan infill. Pada penelitian ini akan dilakukan optimasi pengaturan infill pada proses pencetakan tiga dimensi untuk mendapatkan hasil cetakan yang kuat namun tetap hemat material sehingga biaya produksi bisa lebih murah. Optimasi dilakukan dengan permodelan matematika mengenai pengaruh densitas dan pola infill terhadap kekuatan struktur tangan prostetik. Data kekuatan struktur didapatkan melalui simulasi pada peranti lunak menggunakan metode finite element. Hasil yang diharapkan dari penelitian ini adalah model matematika yang dapat digunakan untuk menentukan pengaturan infill seperti apa yang paling optimal baik dari segi kekuatan maupun harga.
Kuis Komputasi Teknik – Permodelan Sistem Osilasi Satu Dimensi Menggunakan Metode Euler
Soal : Hitung posisi dan kecepatan massa m seiring waktu (dari detik 0 sampai 10) menggunakan metode analitik dan numerik!
Jawab :
Initial Thinking dan Modelling
Gambar di atas adalah sistem di mana terdapat gerobak beroda yang dikaitkan terhadap pegas yang menempel pada suatu dinding. Pada sistem tersebut, ketka gerobak ditarik atau didorong ke luar dari kesetimbangan, maka gerobak akan bergerak bolak balik secara harmonik. Gerakan tersebut sering disebut sebagai osilasi. Sistem tersebut bisa dimodelkan menjadi sistem osilasi satu dimensi. Sistem osilasi satu dimensi adalah sistem yang berosilasi dalam satu dimensi ruang. Pada kasus ini, sistem dapat dimodelkan ke dalam satu dimensi ruang horizontal (X), dengan mengasumsikan tidak terdapat gaya lain yang memiliki arah ke dimensi lain (Y atau Z). Dengan demikian, menggunakan persamaan kesetimbangan gaya, kita dapat memodelkan sistem tersebut menjadi sistem osilasi satu dimensi. Asumsi lain yang digunakan pada kasus ini adalah tidak terdapat gesekan pada dasar roda, dan arah kanan positif arah kiri negatif.
Dari sistem di atas, apabila gerobak ditarik menjauhi dinding, bisa kita modelkan menjadi
Persamaan tersebut menggambarkan bahwa ketika gerobak ditarik kemudian dilepas, sistem mengalami gaya pegas ke arah kiri (-kx) sehingga mengalami percepatan (x”). Persamaan tersebut dapat ditulis ulang menjadi
dengan cara memindahkan –kx ke ruas kanan dan membagi kedua ruas dengan m. Omega pada persamaan tersebut adalah rumus frekuensi osilasi pada sistem pegas yaitu ω=√(k⁄m) Persamaan di atas adalah persamaan diferensial biasa (ODE) orde dua. Karena orde dua, maka diperlukan dua initial condition agar dapat mendapatkan solusi eksak. Initial condition pada sistem ini adalah x(0) = X0 dan x’(0) = 0, di mana X0 merupakan posisi awal ketika gerobak selesai ditarik, dan karena sistem awalnya diam maka kecepatan awal (x’(0)) bernilai 0. Dari sini kita bisa mendapatkan solusi eksak dari persamaan yaitu X(t)=X_A cosωt di mana XA adalah amplitudo atau simpangan terjauh dari sistem, amplitudo dari sistem ini sama dengan simpangan awal X0. Dari persamaan tersebut kita bisa mengetahui posisi, kecepatan, serta percepatan dari sistem seiring waktu. Namun ada cara lain selain metode eksak untuk menghitung posisi, kecepatan, dan percepatan yaitu menggunakan metode euler. Metode euler adalah metode numerik sederhana dengan memperkirakan nilai suatu titik dengan cara menambahkan nilai pada titik sebelumnya dengan besar slope dikali interval. Metode ini bisa dilakukan dengan menerapkan sedikit modifikasi dari persamaan ODE yang sebelumnya telah didapat. Modifikasi dilakukan dengan memperkenalkan dua variabel baru yaitu u dan v, di mana u = x dan v = x’ = u’, yang juga dapat diturunkan menjadi v’=x’’. Dari persamaan ODE di atas, kita bisa mendapatkan nilai x’’ yaitu ’’=-ω^2 x , kita bisa mengubah variabel pada persamaan tersebut menjadi u dan v sehingga persamaannya menjadi
Hal selanjutnya yang dilakukan adalah penulisan ulang persamaan tersebut. Penulisan ulang dilakukan dengan mengganti notasi kutip menjadi notasi d/dt. Sehingga persamaannya menjadi
du/dt=v
dv/dt=-ω^2u
Hal selanjutnya adalah hal krusial dalam melakukan metode numerik, yaitu proses diskritisasi. Diskritisasi adalah proses mengubah variabel yang kontinu menjadi nilai nilai pecah atau diskrit. Sehingga pada proses ini d diganti menjadi delta. Menandakan bahwa d yang merupakan selisih yang sangat sangat kecil diubah menjadi selisih yang diskrit yaitu delta. Oleh karena itu persamaan berubah menjadi
Dengan menulis ulang persamaan tersebut, kita bisa mendapatkan persamaan baru yaitu
Persamaan inilah yang akan digunakan untuk melakukan metode euler. Metode euler mengharuskan kita menentukan nilai delta t. Pada metode euler, semakin kecil delta t seharusnya menghasilkan hasil yang lebih akurat. Simulasi perhitungan baik menggunakan metode eksak maupun euler akan di bahas pada bab selanjutnya
Simulasi
Pada kasus ini, simulasi perhitungan dilakukan menggunakan bantuan peranti lunak Microsoft Excel. Dalam simulasi ini kita akan menghitung nilai posisi dan kecepatan seiring waktu baik menggunakan metode eksak maupun metode euler. Selanjutnya kita akan membandingkan hasil kedua metode tersebut. Perbandingan hasil tersebut dikenal dengan nama proses 'verifikasi.
Pada kasus ini, boundary dan initial condition yang digunakan adalah
ω=2 rad X_0=5 m 〖x'〗_0=0 m/s
1. Metode eksak
Untuk dapat menghitung nilai posisi dan kecepatan sistem tersebut menggunakan metode eksak pada Ms excel, kita perlu membuat dua kolom masing masing untuk posisi dan kecepatan. Pada kolom posisi, kita memasukkan rumus posisi yaitu x(t)=X_0 cosωt. Sedangkan pada kolom kecepatan kita masukkan rumus kecepatan yang merupakan turunan dari rumus posisi yaitu x"(t)=〖-X〗_A ωsinωt. Kemudian masukkan nilai t dengan membuat kolom baru.
2. Metode Euler
Pada metode euler, kolom posisi dan kecepatan diisi dengan rumus
Pada kasus ini, saya akan memvariasikan besar delta t, yaitu delta t = 0.1 , 0.05, dan 0.01.
3. Hasil
Verifikasi
Verifikasi adalah proses membandingkan nilai hasil simulasi permodelan dengan hasil ideal atau teoritis. Pada kasus ini, nilai teoritis adalah nilai dari hasil metode eksak, sedangkan hasil permodelan adalah hasil metode euler. Pada tahap ini, kita membandingkan nilai dari kedua metode tersebut. Perbandingan nilai akan disajikan dengan tabel data error untuk variabel posisi dan kecepatan. Nilai error berupa selisih mutlak antara nilai pada metode eksak dan metode euler. Berikut ini nilai error untuk masing-masing variasi delta t.
Dari grafik di atas jelas terlihat bahwa semakin kecil nilai delta t maka semakin kecil error. Pola lain yang juga jelas terlihat adalah semakin besar nilai t maka error semakin besar, berapapun besar delta t nya. Hal ini menandakan bahwa metode euler yang diterapkan pada kasus ini sudah terverifikasi, di mana metode euler dengan delta t 0.01 merupakan metode yang paling terverifikasi karena nilai error yang paling kecil. Namun metode euler bisa menjadi tidak terverifikasi ketika nilai t yang digunakan besar misalkan perhitungan dilakukan hingga t = 1000. Untuk dapat menerapkan metode euler pada kasus tersebut maka dibutuhkan besar delta t yang sangat kecil untuk dapat menghindari error yang besar. Pada proses permodelan, hal yang harus dilakukan setelah verifikasi adalah validasi. Validasi merupakan proses penilaian apakah model yang dibuat sesuai dengan kondisi aktual. Namun pada kasus ini karena tidak terdapat data aktual untuk dibandingkan dengan data hasil simulasi maka proses validasi tidak dapat dilakukan sehingga proses permodelan hanya berhenti di tahap verifikasi. Dan hasil permodelan yang didapatkan adalah bahwa model numerik menggunakan metode euler dengan besar delta t sebesar 0.01 sudah terverifikasi.
Kesimpulan
Komputasi teknik merupakan metode penyelesaian masalah-masalah teknik menggunakan bantuan komputasi. Salah satu metode komputasi yang umum digunakan adalah metode numerik. Permasalahan teknik yang bisa diselesaikan dengan metode numerik salah satunya adalah kasus sistem osilasi satu dimensi, di mana kita ingin mengetahui posisi dan kecepatan sistem seiring waktu. Pada kasus ini, metode numerik yang digunakan adalah metode euler dengan besar interval waktu 0.1, 0.05, dan 0.01. Persamaan yang digunakan untuk metode euler didapat dari analisis kesetimbangan gaya dari sistem dengan asumsi bahwa tidak terdapat gaya lain selain gaya pegas dalam arah x. Dengan menghitung posisi dan kecepatan sistem dari waktu 0 detik sampai 10 detik, metode euler berhasil menghitung dengan cukup baik, dengan hasil terbaik ketika nilai interval waktu paling kecil yaitu 0.01. Dari sini kita dapat mempelajari bahwa metode numerik dapat sangat membantu kita dalam menyelesaikan permasalahan teknik ketika kita tidak dapat menyelesaikan permasalahan tersebut dengan metode analitik.
Kasus Pressure Drop
Ujian Akhir Semester
Kasus Perhitungan Laju Mobil Toyota Agya
Pada Ujian Akhir Semester kuliah Komputasi Teknik ini, kami diminta untuk menghitung waktu yang dibutuhkan oleh suatu mobil untuk mencapai kecepatan maksimumnya dari keadaan diam, ketika diketahui nilai-nilai spesifikasi seperti daya mesin, torsi, massa mobil dan hambatan udara. Pada kasus ini, saya akan mengambil Toyota Agya sebagai contoh perhitungan. Segala data spesifikasi terkait mobil Toyota Agya didapat dari website website Toyota. Spesifikasi mobil tersebut adalah sebagai berikut
Pada kasus ini saya akan menerapkan Rule of Thumb komputasi teknik yang dahulu pernah diajarkan oleh Pak Dai. Pertama tama kita akan mulai dengan tahap Initial Thinking.
Initial Thinking
Agar dapat menghitung waktu tercapainya kecepatan maksimum (top speed), kita perlu tahu seberapa besar akselerasi dari mobil tersebut. Relasi antara akselerasi, kecepatan, dan kecepatan maksimum dapat dijelaskan melalui persamaan kinematika yaitu v = v0 + at, di mana v adalah kecepatan akhir, v0 adalah kecepatan awal, a adalah akselerasi, dan t adalah waktu tempuh. Nilai v0 sudah kita ketahui yakni 0, karena mobil mulai dari keadaan diam. Sedangkan nilai v merupakan kecepatan maksimum mobil, nilai ini bisa didapat dari melihat spesifikasi mobil, namun kita juga bisa mendapatkan nilai v dengan melakukan komputasi. Agar dapat menghitung nilai t atau waktu tempuh, kita tinggal menghitung nilai a yaitu akselerasi.
Akselerasi suatu benda terkait erat dengan gaya-gaya yang bekerja pada benda tersebut. Seperti yang kita tahu hukum gerakan newton menyatakan bahwa F=m.a yang juga berarti bahwa akselerasi suatu benda disebabkan oleh gaya yang dialami oleh benda tersebut. Melalui hukum tersebut, kita dapat menghitung nilai a dengan menghitung resultan gaya yang dialami oleh mobil.
Sebelum lanjut ke tahap modelling, kita perlu menyatakan asumsi apa saja yang diperlukan untuk dapat menghitung variabel yang kita inginkan. Asumsi pertama adalah mobil bergerak dengan selalu menggunakan daya maksimum (daya konstan dan tidak bervariasi terhadap waktu), kemudian mobil hanya mengalami gaya dalam arah sumbu x, dan luas penampang mobil (yang terhambat laju udara) dianggap berbentuk persegi panjang. Setelah asumsi telah dinyatakan, kita dapat memulai pada tahap modelling.
Modelling
Pada tahap ini, kita akan menganalisis gaya-gaya yang bekerja pada mobil. Berikut ini adalah diagram yang menggambarkan gaya-gaya tersebut
Dapat kita lihat bahwa terdapat tiga gaya yang mempengaruhi gerakan mobil, gaya pertama adalah gaya dorong dari mesin yang dinotasikan dengan Fm, gaya ini adalah gaya utama yang menyebabkan mobil bergerak. Selanjutnya ada gaya Fg yaitu gaya gesek antara mobil dengan jalan, gaya ini adalah gaya yang menghambat laju mobil namun juga penting agar roda mobil dapat mendorong mobil maju. Yang terakhir adalah gaya Fa yaitu gaya hambatan udara. Gaya hambatan udara terjadi akibat luas penampang mobil yang tidak mengizinkan udara untuk mengalir dengan bebas (tak terhalang), sehingga perubahan momentum udara berakibat pada gaya yang menghambat gerakan mobil tersebut. Besar gaya ini tergantung oleh densitas udara, luas penampang mobil, kecepatan udara relatif dengan mobil, dan koefisien hambatan udara yang juga dikenal dengan nama drag coefficient. Nilai drag coefficient berbeda-beda untuk tiap mobil, semakin aerodinamis suatu mobil maka semakin kecil nilai koefisien tersebut. Pada kasus Toyota Agya ini saya tidak menemukan nilai drag coefficient yang tepat, oleh karena itu saya akan menggunakan nilai drag coefficient yang umum untuk mobil dengan desain sejenis yaitu sebesar kira-kira 0,3.
Gaya dorong mobil (Fm) dihitung dengan rumus Fm=torsi(tau)/jari-jari roda mobil(r), sedangkan torsi didapat dari torsi=daya/kecepatan putar mesin. Sementara itu gaya gesek didapat dari rumus Fg=miu*gaya normal, di mana miu diasumsikan sebesar 0,12. Sedangkan rumus untuk gaya hambatan udara adalah sebagai berikut
Dari persamaan-persamaan tersebut kita mendapatkan rumus untuk akselerasi mobil sebagai berikut
Dari persamaan kinematik v=v0+at, maka didapatkan rumus waktu tempuh untuk mencapai kecepatan maksimum sebagai berikut
Dilihat dari rumus tersebut, ada satu variabel yang menyebabkan kita tidak dapat langsung menggunakan rumus tersebut, variabel tersebut adalah v atau kecepatan mobil. Hal ini dikarenakan nilai v bervariasi terhadap waktu. Fenomena ini juga dijelaskan oleh fakta bahwa besar hambatan angin akan semakin besar apabila kecepatan relatif udara juga makin besar. Untuk itu kita perlu menggunakan metode numerik untuk menghitung nilai kecepatan dan percepatan yang terus berubah sepanjang waktu.
Perhitungan numerik dilakukan dengan menghitung nilai percepatan dan kecepatan untuk setiap detik sesuai interval. Pada t=0, nilai percepatan dihitung dengan rumus semula (tidak bermasalah karena gaya hambat = 0), sedangkan nilai kecepatan = 0 karena bermula dari kondisi diam. Pada interval selanjutnya, hitung kecepatan berdasarkan nilai percepatan pada detik sebelumnya. Gunakan rumus vt=v0+at. Kemudian hitung percepatan dengan rumus percepatan dan masukkan nilai kecepatan yang baru saja didapatkan. Lakukan langkah-langkah perhitungan tersebut hingga didapatkan kecepatan yang konstan (top speed) atau percepatan sama dengan nol, kemudian catat waktu yang ditempuh.
Jika langkah-langkah tersebut diterjemahkan ke dalam rumus numerik, maka rumus numeriknya adalah sebagai berikut
Nilai vn awal, atau v0 adalah 0 karena mobil mulai dari keadaan diam.
Simulasi
Rumus numerik tersebut akan disimulasikan menggunakan aplikasi Microsoft Excel. Simulasi dilakukan untuk interval waktu 1 detik. Berikut ini adalah tabel perhitungan dari simulasi pada Microsoft Excel
Dari hasil perhitungan tersebut didapatkan grafik percepatan dan kecepatan seperti berikut ini
Dari grafik tersebut kita bisa menentukan waktu yang dibutuhkan mobil Toyota Agya untuk mencapai kecepatan maksimum. Kecepatan maksimum dapat dilihat dari laju kecepatan yang mulai konstan yang juga berarti nilai percepatan yang mendekati 0. Dari grafik tersebut kecepatan maksimum diraih pada waktu 140 detik. Di mana kecepatan maksimum Toyota Agya adalah sebesar 178 km/jam.
Verifikasi dan Validasi
Untuk dapat menilai kebenaran dari perhitungan tersebut maka perlu dilakukan tahap verifikasi dan validasi. Verifikasi dilakukan dengan menilik ulang apakah perhitungan telah dilakukan tanpa kesalahan hitung dan juga dihitung pada asumsi-asumsi yang telah ditentukan. Dari proses ini maka perhitungan tersebut telah terverifikasi. Proses validasi dilakukan dengan membandingkan hasil perhitungan dengan spesifikasi mobil. Berdasarkan situs otomotifnet kecepatan maksimum Toyota Agya adalah 180 km/jam. Dari perbandingan ini ternyata hasil yang saya dapat cukup akurat. Error atau perbedaan hasil perhitungan dengan realita dapat disebabkan oleh asumsi-asumsi yang digunakan, semisal besar koefisien gesek, luas penampang mobil yang dianggap persegi dan juga penggunaan daya maksimum yang konstan.
Kesimpulan
Mobil bergerak diakibatkan gaya dorong dari mesin namun dihambat oleh gaya gesek dengan jalanan dan gaya hambat udara. Gaya hambat udara akan semakin besar ketika kecepatan mobil semakin besar. Hal ini menyebabkan suatu saat kecepatan mobil tidak akan bertambah lagi. Pada kasus mobil Toyota Agya, melalui analisis gaya pada mobil dan perhitungan menggunakan metode numerik, didapatkan bahwa kecepatan maksimum mobil adalah sebesar 178 km/jam dan ditempuh pada waktu selama 140 detik. Dari kasus ini kita belajar bahwa kita dapat memprediksi kecepatan maksimum mobil dan waktu tempuhnya berdasarkan spesifikasi mobil dan perhitungan menggunakan hukum-hukum fisika.
Muhasabah Diri
Selama satu semeter kuliah komputasi teknik, Alhamdulillah saya belajar banyak hal penting. Saya belajar mengenai langkah-langkah melakukan komputasi teknik (Initial thinking, modelling, simulation, verification, validation), istilah-istilah penting dalam komputasi, metode-metode komputasi yang sangat aplikatif seperti Euler Method, Runge-Kutta, Heun Method, Finite Element Method, Spring-mass modelling, hingga diperkenalkan dengan metode Artificial Neural Network. Yang tidak kalah penting adalah saya diingatkan bahwa dalam melakukan komputasi, dasar pemahaman kita terhadap fenomena fisik yang sedang dianalisis juga harus baik, inilah mengapa sering dilakukan diskusi fisika dasar contohnya seperti fenomena pressure drop. Saya juga belajar tentang bagaimana mengaplikasikan komputasi teknik pada kasus nyata seperti kasus pada skripsi, kasus laju korosi, kasus shockbreaker motor, kasus konsumsi energi harian, dan kasus getaran pada bangunan. Dalam kuliah ini saya tidak hanya didorong untuk dapat menggunakan metode-metode komputasi saja, tapi juga didorong untuk dapat memahami konsep di balik metode-metode tersebut. Seluruh hasil pembelajaran saya selama satu semester tercatat baik pada halaman wiki saya, sehingga akan selalu bermanfaat untuk masa-masa yang akan datang dan juga untuk orang lain, InsyaAllah Aamiin..
Selama kuliah, saya belajar dengan serius dengan cara serius dalam mengerjakan tugas-tugas, baik yang berupa tulisan maupun video presentasi. Saya juga berkontribusi dengan baik pada tugas kelompok dengan cara mengerjakan bagian modelling dari studi kasus yang sedang dipelajari. Sementara untuk diskusi seperti pada grup WhatsApp dan pada wiki, saya jujur tidak terlalu aktif dikarenakan saya merasa ilmu saya terkait topik yang sedang didiskusikan masih sangat kurang. Namun saya selalu berusaha untuk membaca dan mengikuti jalannya diskusi sehingga saya bisa menjadi paham terhadap apa yang sedang didiskusikan.
Dari usaha dan pemahaman yang selama ini saya dapatkan di kelas komputasi teknik, mudah-mudahan saya bisa mendapatkan nilai 77 hingga 84 atau B+ hingga A-. Semoga apa yang selama ini saya pelajari di kelas komputasi teknik dapat terus berbekas dalam kehidupan saya dan dapat diaplikasikan untuk menyelesaikan masalah keteknikkan yang riil sehingga dapat bermanfaat untuk orang banyak. Aamiin







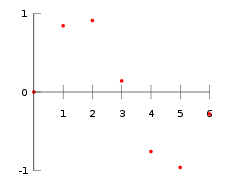
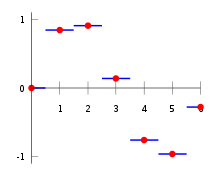
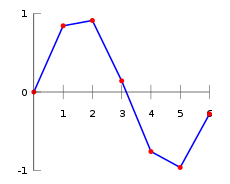
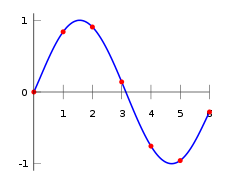
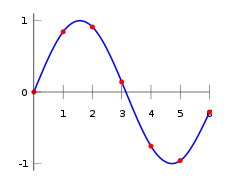
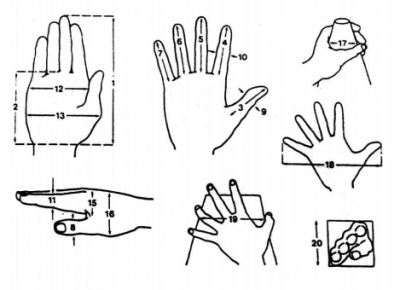
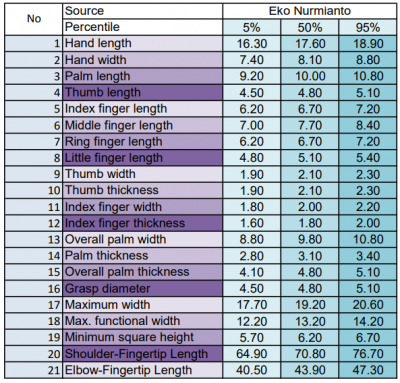
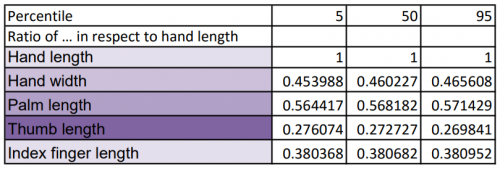
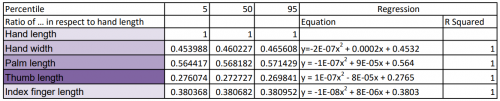
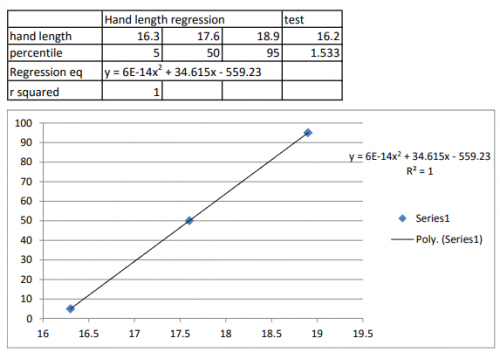

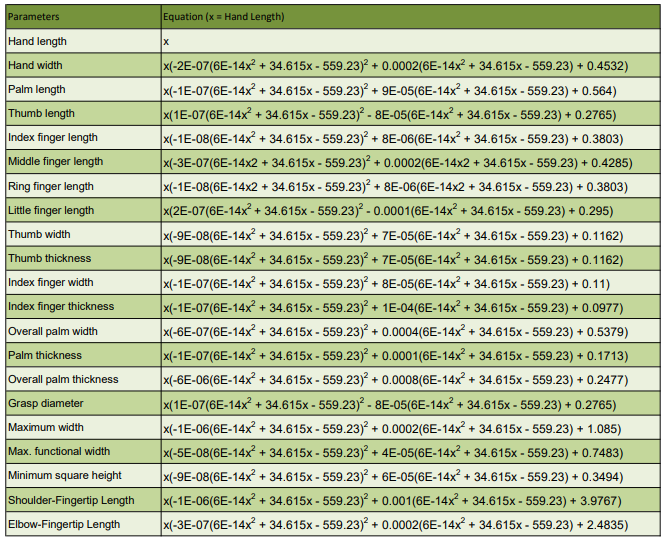
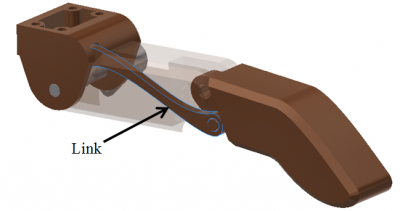
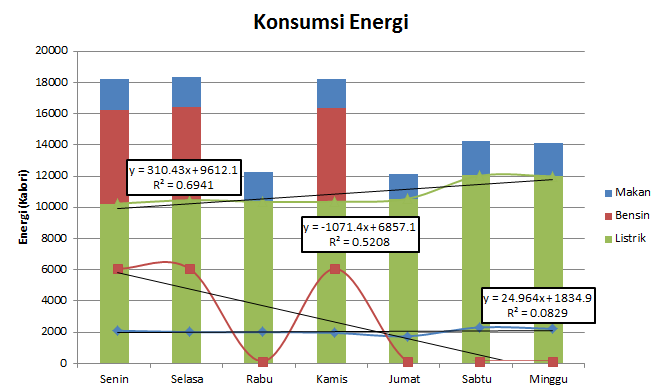




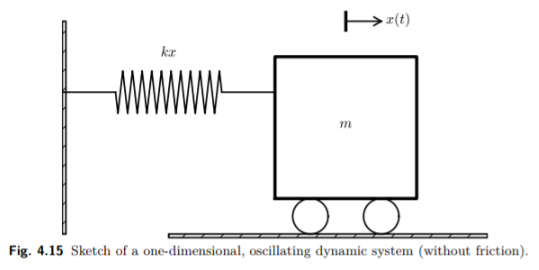
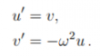
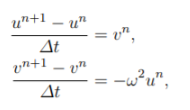
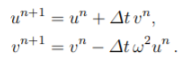
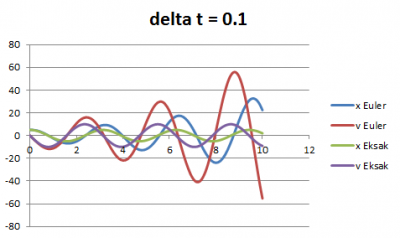
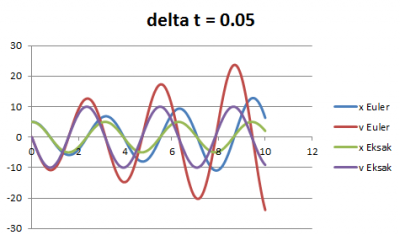
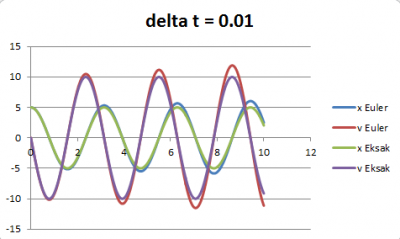
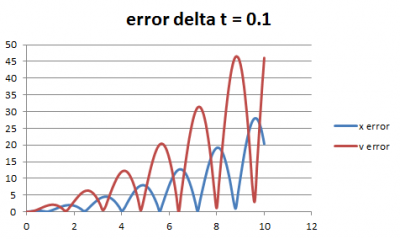
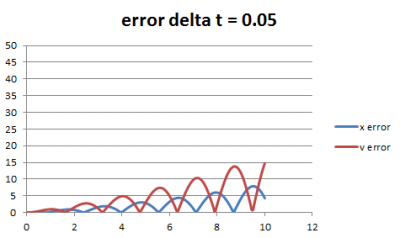
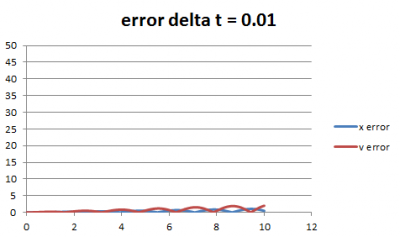





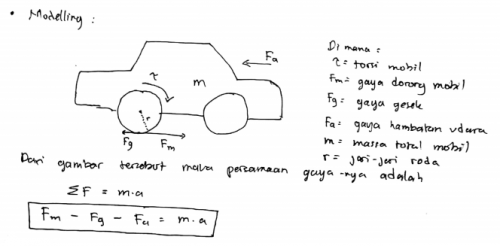
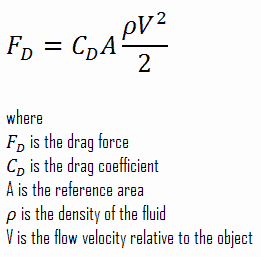
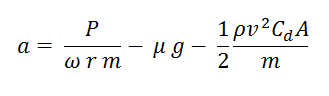
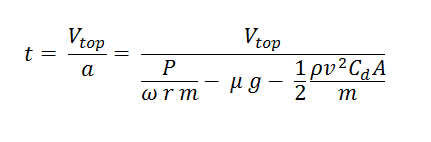
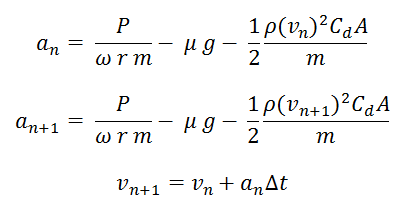
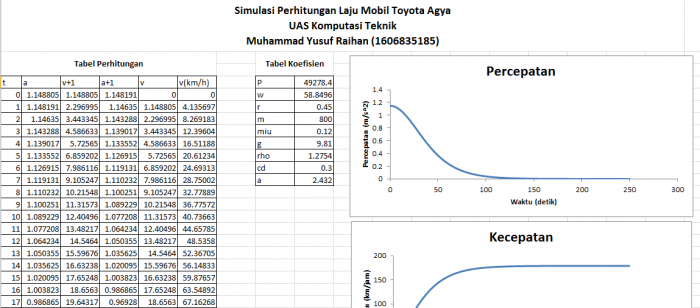
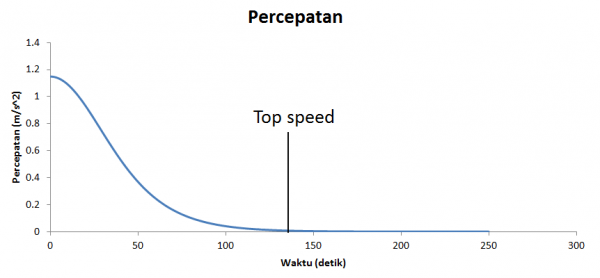
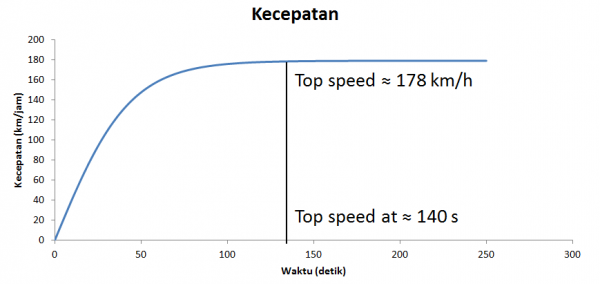
Enable comment auto-refresher
Yusufraihan
Permalink |