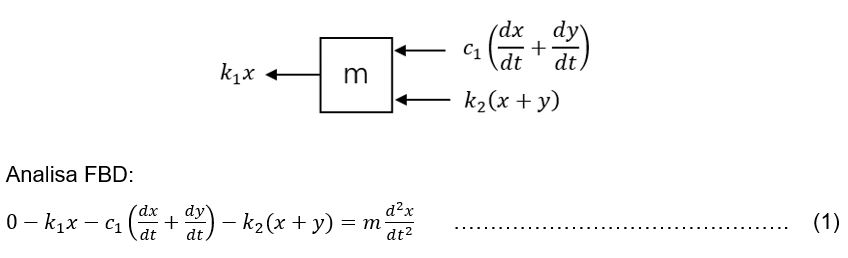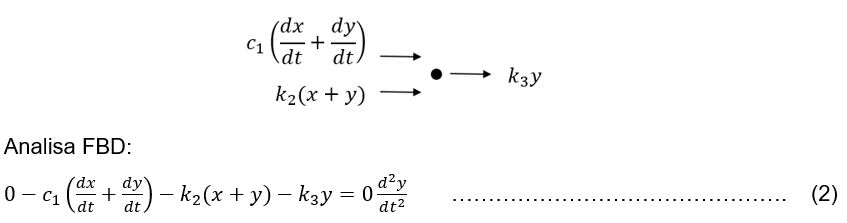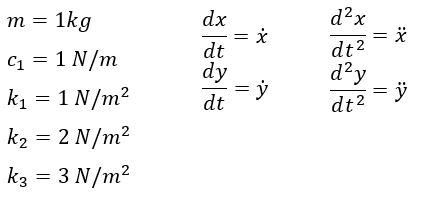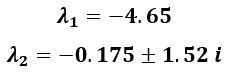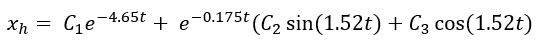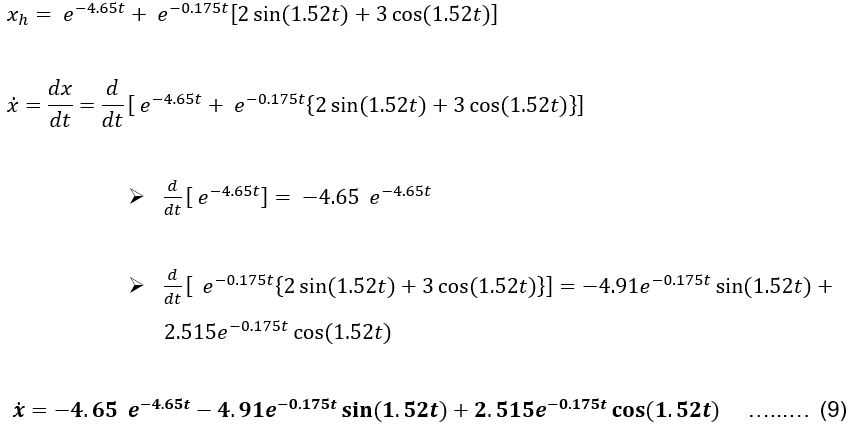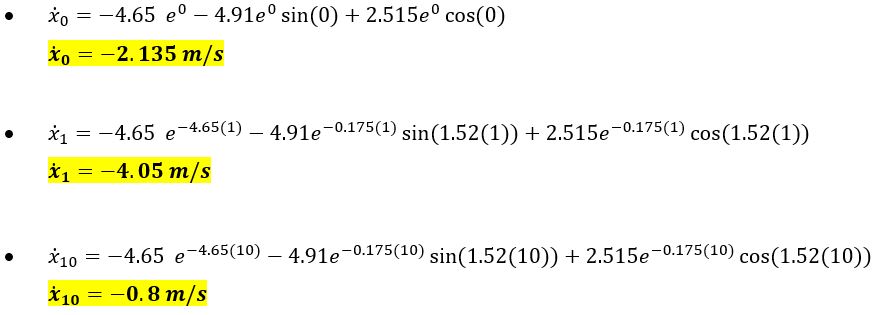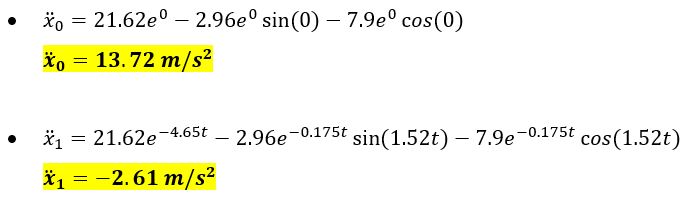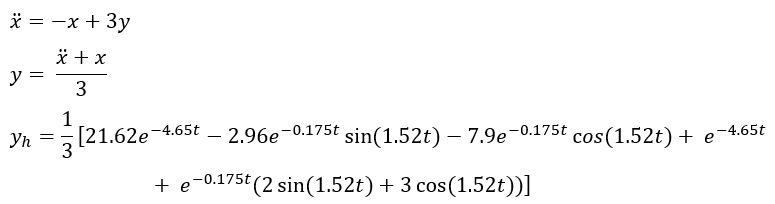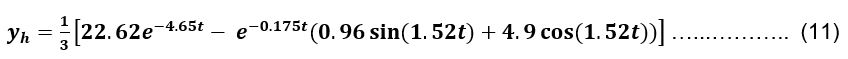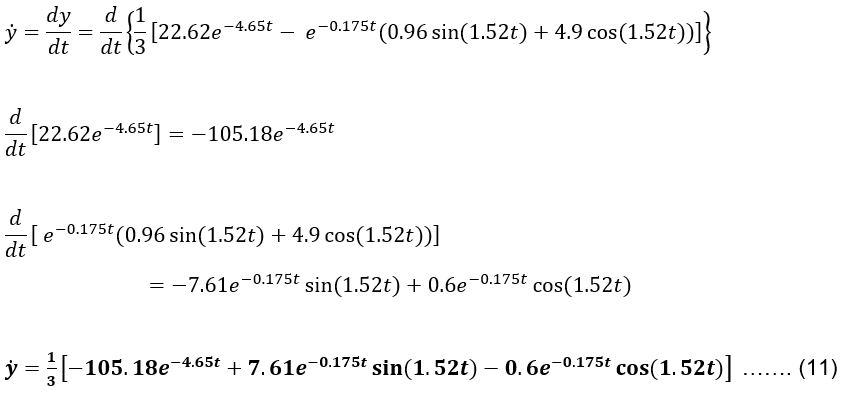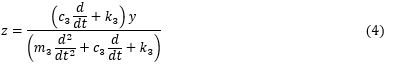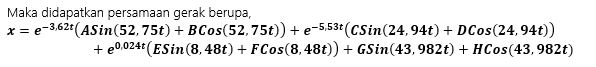Difference between revisions of "Chandra Simanjuntak"
| (48 intermediate revisions by the same user not shown) | |||
| Line 48: | Line 48: | ||
3. Ilmu bagaikan tetesan air yang jatuh di lautan, langsung menyatu menjadi bagian dari lautan itu sendiri. Yang perlu dipahami disini adalah bagaimana ilmu mekanika fisika yang kita miliki harus selalu bersatu dengan Pancasila, dan nasionalisme. Salah satu upaya yang dapat dilakukan untuk menjadikannya satu adalah dengan analisis. Dimana analisis dapat diartikan suatu proses untuk menghasilkan suatu prosedur pemceahan masalah atau mendapatkan langkah-langkah solusi. | 3. Ilmu bagaikan tetesan air yang jatuh di lautan, langsung menyatu menjadi bagian dari lautan itu sendiri. Yang perlu dipahami disini adalah bagaimana ilmu mekanika fisika yang kita miliki harus selalu bersatu dengan Pancasila, dan nasionalisme. Salah satu upaya yang dapat dilakukan untuk menjadikannya satu adalah dengan analisis. Dimana analisis dapat diartikan suatu proses untuk menghasilkan suatu prosedur pemceahan masalah atau mendapatkan langkah-langkah solusi. | ||
| − | === Tugas Sinopsis Skripsi === | + | === Tugas: Sinopsis Skripsi === |
Judul penelitian: Studi Eksperimental Karakteristik Aliran Fluida Melintasi Silinder Teriris Tipe I di Dekat Plat Datar Untuk Tebal Lapis Batas Laminar dan Turbulent | Judul penelitian: Studi Eksperimental Karakteristik Aliran Fluida Melintasi Silinder Teriris Tipe I di Dekat Plat Datar Untuk Tebal Lapis Batas Laminar dan Turbulent | ||
| Line 54: | Line 54: | ||
Hingga saat ini penelitian tentang pengaruh dinding terhadap aliran yang melintasi silinder sudah banyak dikembangkan. Berbagai variasi untuk mengetahui pengaruh dinding telah dilakukan untuk memperoleh data-data mengenai karakteristik aliran fluida yang terbentuk di sekeliling benda uji tersebut. Hasil dari penelitian ini banyak diaplikasikan dalam pengembangan dunia industri, sebagai contoh penyusunan shell and tube dalam penukar kalor, perpipaan bawah laut serta contoh-contoh yang lain. Berdasarkan pemikiran di atas maka akan dilakukan penelitian tentang pengaruh dinding terhadap aliran fluida melintasi silinder teriris tipe I. Penelitian ini dilakukan secara eksperimental dalam sebuah wind tunnel, dimana benda uji yang digunakan adalah silinder tipe I dengan sudut iris (θs) 53° dan 65° yang diletakkan dekat dengan suatu plat datar. Variasi Gap Rasio(G/D) sebesar 1,200 ; 1,267 ; 1,333 pada lapis batas laminar dan turbulent. Karakteristik aliran fluida yang diteliti adalah distribusi koefisien tekanan (Cp), koefisien drag (CD), koefisien lift (CL), profil kecepatan di belakang silinder dan melakukan visualisasi menggunakan metode oil flow picture pada subsonic wind tunnel pada Re= 5,3x104. Diharapkan penelitian ini akan mampu menjelaskan pengaruh lapisan batas dinding terhadap aliran pada silinder serta menjelaskan fenomena wake yang terjadi pada silinder teriris tipe I. | Hingga saat ini penelitian tentang pengaruh dinding terhadap aliran yang melintasi silinder sudah banyak dikembangkan. Berbagai variasi untuk mengetahui pengaruh dinding telah dilakukan untuk memperoleh data-data mengenai karakteristik aliran fluida yang terbentuk di sekeliling benda uji tersebut. Hasil dari penelitian ini banyak diaplikasikan dalam pengembangan dunia industri, sebagai contoh penyusunan shell and tube dalam penukar kalor, perpipaan bawah laut serta contoh-contoh yang lain. Berdasarkan pemikiran di atas maka akan dilakukan penelitian tentang pengaruh dinding terhadap aliran fluida melintasi silinder teriris tipe I. Penelitian ini dilakukan secara eksperimental dalam sebuah wind tunnel, dimana benda uji yang digunakan adalah silinder tipe I dengan sudut iris (θs) 53° dan 65° yang diletakkan dekat dengan suatu plat datar. Variasi Gap Rasio(G/D) sebesar 1,200 ; 1,267 ; 1,333 pada lapis batas laminar dan turbulent. Karakteristik aliran fluida yang diteliti adalah distribusi koefisien tekanan (Cp), koefisien drag (CD), koefisien lift (CL), profil kecepatan di belakang silinder dan melakukan visualisasi menggunakan metode oil flow picture pada subsonic wind tunnel pada Re= 5,3x104. Diharapkan penelitian ini akan mampu menjelaskan pengaruh lapisan batas dinding terhadap aliran pada silinder serta menjelaskan fenomena wake yang terjadi pada silinder teriris tipe I. | ||
| − | ===Tugas Rencana Skripsi dengan Menggunakan Komputasi Teknik=== | + | ===Tugas: Rencana Skripsi dengan Menggunakan Komputasi Teknik=== |
Hal bisa dilakukan terhadap tugas akhir S1 dengan metode komputasi teknik adalah dengan meng-aplikasikan software CFD yang antara lain bertujuan untuk: | Hal bisa dilakukan terhadap tugas akhir S1 dengan metode komputasi teknik adalah dengan meng-aplikasikan software CFD yang antara lain bertujuan untuk: | ||
| Line 79: | Line 79: | ||
Komputasi teknik merupakan proses melakukan studi dengan pemodelan matematis yang tidak dapat dipecahkan dengan perhitungan manual. | Komputasi teknik merupakan proses melakukan studi dengan pemodelan matematis yang tidak dapat dipecahkan dengan perhitungan manual. | ||
| − | ===Tugas Pemodelan dengan Menggunakan Komputasi Teknik=== | + | ===Tugas: Pemodelan dengan Menggunakan Komputasi Teknik=== |
Judul Skripsi: Studi Eksperimental Tentang Karakteristik Aliran Fluida Melintasi Silinder Teriris Tipe I di Dekat Plat Datar Untuk Tebal Lapis Batas Laminar dan Turbulen G/D 1,2 sd 1.33. | Judul Skripsi: Studi Eksperimental Tentang Karakteristik Aliran Fluida Melintasi Silinder Teriris Tipe I di Dekat Plat Datar Untuk Tebal Lapis Batas Laminar dan Turbulen G/D 1,2 sd 1.33. | ||
| Line 104: | Line 104: | ||
=='''PERTEMUAN 4 ( 23 Februari 2020 )'''== | =='''PERTEMUAN 4 ( 23 Februari 2020 )'''== | ||
| − | ===Tugas Membuat Extended Abstrak Proyek Skripsi=== | + | ===Tugas: Membuat Extended Abstrak Proyek Skripsi=== |
Name: Chandra R. M. Simanjuntak | Name: Chandra R. M. Simanjuntak | ||
| Line 115: | Line 115: | ||
=='''PERTEMUAN 5 ( 2 Maret 2020 )'''== | =='''PERTEMUAN 5 ( 2 Maret 2020 )'''== | ||
| − | ===Tugas Optimasi Kebutuhan Energi Manusia=== | + | ===Tugas: Optimasi Kebutuhan Energi Manusia=== |
Energi sangat diperlukan manusia untuk melakukan aktifitas sehari hari. Baik itu energi yang didapat dari makanan lalu diproses oleh tubuh untuk dikonversi menjadi gerak, panas, dan sinyal, maupun energi yang tersedia dalam bentuk listrik, dan panas di sekitar kita. Energi diperlukan oleh setiap individu akan berbeda-beda tergantung pada beban aktivitas harian yang dilakukan. | Energi sangat diperlukan manusia untuk melakukan aktifitas sehari hari. Baik itu energi yang didapat dari makanan lalu diproses oleh tubuh untuk dikonversi menjadi gerak, panas, dan sinyal, maupun energi yang tersedia dalam bentuk listrik, dan panas di sekitar kita. Energi diperlukan oleh setiap individu akan berbeda-beda tergantung pada beban aktivitas harian yang dilakukan. | ||
| Line 153: | Line 153: | ||
=='''PERTEMUAN 6 ( 9 Maret 2020 )'''== | =='''PERTEMUAN 6 ( 9 Maret 2020 )'''== | ||
| − | ===Tugas Rule Of Term Engineering Computation=== | + | ===Tugas: Rule Of Term Engineering Computation=== |
Pada pertemuan ini saya izin tidak mengikuti kelas dikarenakan adanya proses persalinan istri. Namun mengacu dari referensi wiki rekan-rekan, dengan menggunakan pemahaman pribadi saya akan mencoba menuliskan hal-hal yang menjadi poin penting pada perkuliahan kali ini. Wiki yang dijadikan acuan adalah Muchalis Zikramansyah Masuku, Evi Elisa Ambarita, dan Oldy Fahlovi. | Pada pertemuan ini saya izin tidak mengikuti kelas dikarenakan adanya proses persalinan istri. Namun mengacu dari referensi wiki rekan-rekan, dengan menggunakan pemahaman pribadi saya akan mencoba menuliskan hal-hal yang menjadi poin penting pada perkuliahan kali ini. Wiki yang dijadikan acuan adalah Muchalis Zikramansyah Masuku, Evi Elisa Ambarita, dan Oldy Fahlovi. | ||
| Line 178: | Line 178: | ||
| − | ==''' | + | =='''UJIAN TENGAH SEMESTER'''== |
| + | |||
| + | ===Tugas: Membuat laporan hasil tugas optimasi kebutuhan energi manusia=== | ||
| + | Klik panah (kiri-kanan)untuk mengganti halaman dokumen | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | File:UTS_Optimasi_1.jpg | ||
| + | File:2.Optimasi_Energi_Chandra-002.jpg | ||
| + | File:2.Optimasi_Energi_Chandra-003.jpg | ||
| + | File:2.Optimasi_Energi_Chandra-004.jpg | ||
| + | </gallery> | ||
| + | |||
| + | ===Tugas: Menyiapkan draft paper project komputasi teknik=== | ||
| + | Klik panah (kiri-kanan)untuk mengganti halaman dokumen | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | File:3.Draft_Proyek_Komputasi_Teknik-001.jpg | ||
| + | File:3.Draft_Proyek_Komputasi_Teknik-002.jpg | ||
| + | File:3.Draft_Proyek_Komputasi_Teknik-003.jpg | ||
| + | </gallery> | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | File:PaperCh_(1).JPG | ||
| + | File:PaperCh_(2).JPG | ||
| + | File:PaperCh_(3).JPG | ||
| + | File:PaperCh_(4).JPG | ||
| + | File:PaperCh_(5).JPG | ||
| + | File:PaperCh_(6).JPG | ||
| + | File:PaperCh_(7).JPG | ||
| + | File:PaperCh_(8).JPG | ||
| + | File:PaperCh_(9).JPG | ||
| + | File:PaperCh_(10).JPG | ||
| + | </gallery> | ||
| + | |||
| + | =='''PERTEMUAN 8 (6 April 2020)'''== | ||
| + | |||
| + | Pada pertemuan ini dilakukan presentasi proyek komputasi teknik oleh Wisnu Indrawan & Adhika Satyadharma | ||
| + | |||
| + | |||
| + | =='''PERTEMUAN 9 (13 April 2020)'''== | ||
| + | |||
| + | ===Oscillating 1-D Dynamic System=== | ||
| + | |||
| + | Mahasiswa diberi penjelasan terkait rule of term of engineering (pertemuan 6), dimana proses ini dilakukan untuk mendapatkan solusi komputasi teknik. Pada kesempatan ini dijelaskan konsep tersebut dimulai dari initial thinking, pemodelan matematis, sampai dengan verifikasi, dan validasi. Pada tahap initial thinking perlu diyakinkan semua konsep, data, dan referensi yang dihadapi sudah didapat dan dimengerti. Kemudian dibentuk model matematis yang diharapkan dapat mendekati kondis aktual. Setelah itu dilakukan simulasi perhitungan, lalu verifikasi. Pengertian verifikasi yaitu memastikan perhitungan yang dilakukan dengan komputer sudah benar dan sesuai kondisi ideal. Sedangkan validasi memiliki makna memastikan model matematika yang dibangun sudah mendekati aktual, atau umumnya dilakukan eksperimen untuk membandingkan hasil yang didapat. | ||
| + | |||
| + | Adapun materi oscillating dynamic system ini diberikan sebagai pengetahuan bagi mahasiswa mengenai bagaimana melakukan verifikasi perhitungan. Penyelesaian matematis yang dapat dilakukan untuk sistem dinamik tersebut antara lain dengan metode analitik, metode numerik, dan metode yang dinamakan "a magic fix for numerical method". Bagian yang disebut paling akhir ini disebut memiliki hasil dengan error yang paling kecil. | ||
| + | |||
| + | ===Quiz: Oscillating 1-D Dynamic System=== | ||
| + | |||
| + | Terdapat 2 metode numerik yang akan digunakan, yakni standard numerical solution (persamaan 4.47 dan 4.48) dan a magic fix of a numerical method (persamaan 4.49 dan 4.50). Suatu benda dengan massa m (sesuai gambar 4.15) melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan. Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) body (penampang m) kembali dan bekerja "melawan" gerakan, misalkan x (t) adalah posisi body pada sumbu x, dimana body bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya terjadi posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (misal gesekan). Hukum kedua Newton menyatakan F=ma kemudian memiliki F=-kx dan a=x ̈, | ||
| + | |||
| + | -kx=mx ̈ (4.41) | ||
| + | |||
| + | sehingga dapat dituliskan | ||
| + | |||
| + | x ̈+ω^2 x=0 (4.42) | ||
| + | |||
| + | Persamaan (4.42) adalah persamaan diferensial orde kedua, dan oleh karena itu kita memerlukan dua kondisi awal, satu pada posisi x (0) dan satu pada kecepatan x’ (0). | ||
| + | |||
| + | x (0) = 1,5 dan x’ (0) = 0 | ||
| + | |||
| + | Cara yang dapat kita tuliskan pada persamaan 4.42 merupakan sistem orde pertama dari 2 persamaan turunan, untuk mengendalikan turunan orde dua. Kita memperkenalkan u=x dan v=x^'=u' sebagai 2 fungsi baru yang tidak diketahui. Dua persamaan yang sesuai muncul dari definisi v=u' dan persamaan asal (4.42): | ||
| + | |||
| + | u^'=v (4.43) | ||
| + | |||
| + | v^'=-ω²u (4.44) | ||
| + | |||
| + | maka u^''=v' untuk menghilangkan turunan orde kedua dari hukum kedua newton. Dengan menggunakan metode numerik pertama, yakni standard numerical solution dengan persamaan-persamaan berikut: | ||
| + | |||
| + | u^(n+1)=u^n+∆t v^n (4.47) | ||
| + | |||
| + | v^(n+1)=v^n-∆t 〖ω^2 u〗^n (4.48) | ||
| + | |||
| + | Selain itu, terdapat juga metode numerik kedua yang anggap lebih akurat, disebut a magic fix of the numerical method dengan mengganti u^n untuk persamaan kedua menjadi u^(n+1) dari persamaan pertama, sehingga: | ||
| + | |||
| + | u^(n+1)=u^n+∆t v^n (4.49) | ||
| + | |||
| + | v^(n+1)=v^n-∆t 〖ω^2 u〗^(n+1) (4.50) | ||
| + | |||
| + | dimana diketahui ω = 2,5 rad/s dan ∆t = 0,05 s, maka dilakukan perhitungan yang dapat dilihat di lampiran (ms.excel). | ||
| + | |||
| + | Selanjutnya dilakukan verifikasi antara setiap metode numerik diatas terhadap metode analitik, dimana persamaan-persamaan untuk metode analitik adalah sebagai berikut: | ||
| + | |||
| + | u=x cosωt | ||
| + | |||
| + | v=- x ω cosωt | ||
| + | |||
| + | yang perhitungan detail nya dapat juga dilihat pada lampiran (ms.excel). Sehingga diperoleh hasil yang merupakan grafik sebagai berikut: | ||
| + | |||
| + | Dari kedua grafik diatas dapat dilihat jelas bahwa metode numerik yang standard dengan menggunakan persamaan 4.47 dan 4.48 jauh dari kata akurat, dikarenakan hasil yang didapat dari metode ini (grafik biru) sangat berbeda dengan hasil dari metode analitik (grafik abu-abu). Oleh karena itu, metode numerik yang disebut a magic fix for a numerical method perlu dilakukan, dengan hasil sebagai berikut: | ||
| + | |||
| + | Dari kedua grafik diatas, dapat dilihat bahwa metode numerik ini (grafik kuning) memiliki tingkat keakurasian yang sangat baik dengan pemverifikasian terhadap metode analitik (grafik hijau). Dengan demikian, disimpulkan bahwa a magic fix for a numerical method telah terverifikasi terhadap metode analitik yang mana dapat mewakili metode analitik. untuk menentukan nilai u dan v. | ||
| + | |||
| + | Klik panah (kiri-kanan)untuk mengganti halaman dokumen | ||
| + | |||
| + | <gallery mode="slideshow"> | ||
| + | File:Q2C_1.jpg | ||
| + | File:Q2C_2.jpg | ||
| + | File:Q2C_3.jpg | ||
| + | File:Q2C_4.jpg | ||
| + | File:Q2C_5.jpg | ||
| + | File:Q2C_6.jpg | ||
| + | File:Q2C_7.jpg | ||
| + | File:Q2C_8.jpg | ||
| + | File:Q2C_9.jpg | ||
| + | </gallery> | ||
| + | |||
| + | =='''PERTEMUAN 10 (20 April 2020)'''== | ||
| + | |||
| + | Inti dari komputasi teknik adalah agar kita mampu menerjemahkan persoalan fisik menjadi model matematis yang akan diselesaikan dengan komputer. Secara garis besar tahapannya yaitu: | ||
| + | |||
| + | 1. Terjemahkan real case ke dalam model | ||
| + | |||
| + | 2. Buat model sederhana dengan initial thinking dan asumsi. Disini sudah didapat konsep pemikirannya, setelah itu dapat ditentukan judul topik yang sesuai. | ||
| + | a.Contoh asumsi: tidak ada gesekan pada model yang dianalisa, dst. | ||
| + | b.Jadilah model matematis yang dapat diselesaikan dengan metode-metode komputasi teknik. Misal Forward Euler, Runge Kutta. | ||
| + | c.Ketika ditemui adanya keterbatasan pada model tsb, maka dapat dikembangkan dengan: | ||
| + | -finite difference | ||
| + | -finite element / volume (deterministik) | ||
| + | -ANN (stokastik) / GA (survival for the fittest) | ||
| + | d. Bandingkan hasil dari metode pada point "c" terhadap point "d" | ||
| + | |||
| + | Pada pertemuan ini tiap kelompok berdiskusi mengenai tugas komputasi teknik seperti pada tugas sebelumnya, yang ditambahkan dengan pembahasanan terkait artificial neural network atau finite elemen design. Untuk kelompok kami akan mengambil topik tambahan artificial neural network. | ||
| + | |||
| + | ===Tugas: Artificial Neural Network pada Oscillating 1-D Dynamic System=== | ||
| + | |||
| + | ====Pendahuluan==== | ||
| + | |||
| + | Artikel ini akan membahas penyelesaian permasalahan oscillating 1-D dynamic system pada system damping sesuai gambar di bawah. Pada system di bawah terdapat sebuah massa yang dihubungkan dengan 3 spring, dan 1 dashpot. System tersebut fix pada 2 boundary sisi kiri dan kanan. | ||
| + | |||
| + | [[File:Artikelkomtekevi1.JPG]] | ||
| + | |||
| + | Penyelesaian dari permasalahan tersebut akan dilakukan dengan 3 metode, yang kemudian akan dibandingkan hasil dari perhitungan pada tiap metode tersebut. Metode yang digunakan yaitu: analitikal, numerik, dan simulasi. Pada metode analitikal dilakukan tinjauan gaya aksi – reaksi pada free body diagram (FBD) yang muncul dari eksitasi yang diberikan. Kemudian untuk penyelesaian metode numerik akan dilakukan iterasi dengan bantuan software Microsoft Excel menggunakan Forward Euler. Sedangkan untuk proses simulasi akan dilakukan dengan bantuan software MATLAB. | ||
| + | |||
| + | ====Metode==== | ||
| + | |||
| + | '''Metode Analitik''' | ||
| + | |||
| + | Free Body Diagram (FBD): | ||
| + | |||
| + | • Tinjauan massa: | ||
| + | |||
| + | [[File:Artikelkomtekevi2.JPG]] | ||
| + | |||
| + | • Tinjauan titik: (diantara c1, k2, dan k3) | ||
| + | |||
| + | [[File:Artikelkomtekevi3.JPG]] | ||
| + | |||
| + | ''Diketahui:'' | ||
| + | |||
| + | [[File:Artikelkomtekevi4.JPG]] | ||
| + | |||
| + | Maka persamaan 1 dan 2 dapat dituliskan kembali menjadi; | ||
| + | |||
| + | Persamaan 1 | ||
| + | |||
| + | [[File:Artikelkomtekevi5.JPG]] | ||
| + | |||
| + | Persamaan 2 | ||
| + | |||
| + | [[File:Artikelkomtekevi6.JPG]] | ||
| + | |||
| + | ''Penyelesaian'' | ||
| + | |||
| + | Asumsi | ||
| + | |||
| + | [[File:Artikelkomtekevi7.JPG]] | ||
| + | |||
| + | Karena pada persamaan 5 masih terdapat ̇ y maka subtitusi persamaan 6 ke persamaan 5, sehingga didapatkan nilai ̇ z sebagai berikut; | ||
| + | |||
| + | [[File:Artikelkomtekevi8.JPG]] | ||
| + | |||
| + | Penyelesaian menggunakan matrix; | ||
| + | |||
| + | [[File:Artikelkomtekevi9.JPG]] | ||
| + | |||
| + | Maka didapatkan nilai λ sebesar | ||
| + | |||
| + | [[File:Artikelkomtekevi10.JPG]] | ||
| + | |||
| + | Sehingga didapatkan persamaan | ||
| + | |||
| + | [[File:Artikelkomtekevi11.JPG]] | ||
| + | |||
| + | Jika diasumsikan nilai C1,C2,dan C3 adalah 1, 2 dan 3 maka; | ||
| + | |||
| + | [[File:Artikelkomtekevi12.JPG]] | ||
| + | |||
| + | Nilai x untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi13.JPG]] | ||
| + | |||
| + | Mencari nilai yh dengan mensubtitusi nilai xh ke dalam persamaan ̇ z=-x+3y, di mana nilai ̇ z = ̈ x. | ||
| + | |||
| + | Mencari nilai ̇x; | ||
| + | |||
| + | [[File:Artikelkomtekevi14.JPG]] | ||
| + | |||
| + | Nilai ̇ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi15.JPG]] | ||
| + | |||
| + | Mencari nilai ̈ x; | ||
| + | |||
| + | [[File:Artikelkomtekevi16.JPG]] | ||
| + | |||
| + | Persamaan ̈ x di atas dapat disederhanakan menjadi; | ||
| + | |||
| + | [[File:Artikelkomtekevi17.JPG]] | ||
| + | |||
| + | Nilai ̈ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi18.JPG]] | ||
| + | |||
| + | Mencari nilai y; | ||
| + | |||
| + | [[File:Artikelkomtekevi19.JPG]] | ||
| + | |||
| + | Persamaan yh dapat disederhanakan menjadi; | ||
| + | |||
| + | [[File:Artikelkomtekevi20.JPG]] | ||
| + | |||
| + | Nilai y untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi21.JPG]] | ||
| + | |||
| + | Mencari nilai ̇ y; | ||
| + | |||
| + | [[File:Artikelkomtekevi22.JPG]] | ||
| + | |||
| + | Nilai ̇ y ketika t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi23.JPG]] | ||
| + | |||
| + | |||
| + | '''Metode Numerik''' | ||
| + | |||
| + | Metode ini dilakukan dengan menggunakan software Microsoft Excel. Parameter input yang harus diketahui yaitu x pada t = 0 s, y pada t = 0 s, dan selisih penambahan waktu (∆t). Parameter input x dan y ini dapat juga disebut dengan initial condition. Lalu kemudian dilakukan iterasi sesuai dengan ∆t sampai waktu yang ditentukan. Nilai parameter input tersebut didapat dengan cara analitis seperti sudah disebut di atas, yaitu x((t=0))=4 m; y((t=0))=5.9 m; dan selisih waktu ∆t=0.1 second. | ||
| + | |||
| + | Seperti sudah disebutkan sebelumnya bahwa penyelesaiannya menggunakan Forward Euler, yaitu sebagai berikut: | ||
| + | |||
| + | [[File:Artikelkomtekevi24.JPG]] | ||
| + | |||
| + | '''Simulasi''' | ||
| + | |||
| + | Simulasi dilakukan dengan bantuan software MATLAB. Adapun agar simulasi dapat berjalan, maka perlu diberikan input coding pada software MATLAB yang isinya sebagai berikut. | ||
| + | |||
| + | % Calculates the position, velocity, and acceleration as a function of time | ||
| + | % of a system of carts connected by springs and dashpots. Euler's Method is | ||
| + | % used to solve the equations of motion numerically. | ||
| + | clear all; close all; clc; | ||
| + | tic | ||
| + | |||
| + | % Problem parameters | ||
| + | k1=1; % cart 1 spring constant (N/m) | ||
| + | k2=2; % cart 1 spring constant (N/m) | ||
| + | b1=1; % cart 1 viscous damping coefficient (kg/s) | ||
| + | m1=1; % cart 1 mass (kg) | ||
| + | k3=3; % cart 1 spring constant (N/m) | ||
| + | x10=4; % cart 1 initial position (m) | ||
| + | x20=5.9; % y movement initial position (m) | ||
| + | v10=-2.135; % cart 1 initial velocity (m/s) | ||
| + | v20=-35.36; % cart 2 initial velocity (m/s) | ||
| + | |||
| + | % Set time step stuff | ||
| + | simTime=60; % simulation time (s) | ||
| + | tStep=0.1; % simulation time step | ||
| + | iterations=simTime/tStep; | ||
| + | t=0:iterations; | ||
| + | |||
| + | % Pre-allocate variables for speed and add initial conditions | ||
| + | x1=zeros(iterations,1); | ||
| + | x1(1,:)=x10; | ||
| + | x2=zeros(iterations,1); | ||
| + | x2(1,:)=x20; | ||
| + | v1=zeros(iterations,1); | ||
| + | v1(1,:)=v10; | ||
| + | v2=zeros(iterations,1); | ||
| + | v2(1,:)=v20; | ||
| + | a1=zeros(iterations,1); | ||
| + | a1(1,:)=((0-(k1*x10)-b1*(v10+v20)-k2*(x20+x10))/m1); | ||
| + | |||
| + | % Solve the ODE's with Euler's Method | ||
| + | for n=2:(iterations+1) | ||
| + | x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position | ||
| + | x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position | ||
| + | v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity | ||
| + | v2(n,:)=-(2*x1(n,:)+5*x2(n,:)+v1(n,:)) | ||
| + | % Find cart accelerations | ||
| + | a1(n,:)=((0-k1*x1(n,:))-b1*(v1(n,:)+v2(n,:))-k2*(x2(n,:)+x1(n,:))/m1); | ||
| + | end | ||
| + | |||
| + | % Plot results | ||
| + | subplot(3,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | plot(t',x2,'m') | ||
| + | ylabel('Position (m)') | ||
| + | title('Position, Velocity, & Acceleration as a Function of Time') | ||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | subplot(3,1,2) | ||
| + | hold on; | ||
| + | plot(t',v1,'b') | ||
| + | plot(t',v2,'c') | ||
| + | ylabel('Velocity (m/s)') | ||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | subplot(3,1,3) | ||
| + | hold on; | ||
| + | plot(t',a1,'g') | ||
| + | ylabel('Acceleration (m/s^2)') | ||
| + | xlabel('time (1 = 0.01 detik)') | ||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | |||
| + | toc | ||
| + | |||
| + | |||
| + | ====Hasil==== | ||
| + | |||
| + | [[File:Artikelkomtekevi25.JPG]] | ||
| + | |||
| + | Gambar 2. Grafik velocity (dx/dt) perbandingan analitik, numerik, dan simulasi | ||
| + | |||
| + | [[File:Artikelkomtekevi26.JPG]] | ||
| + | |||
| + | Gambar 3. Grafik acceleration (d^2x/dt^2) perbandingan analitik, numerik, dan simulasi | ||
| + | |||
| + | [[File:Artikelkomtekevi27.JPG]] | ||
| + | |||
| + | Gambar 4. Grafik velocity (dy/dt) perbandingan analitik, numerik, dan simulasi | ||
| + | |||
| + | Selanjutnya, untuk memverifikasi hasil numerik menggunakan metode euler yang dijelaskan diatas, digunakan metode Artificial Neural Networks (ANN) pada perangkat lunak matlab. Berikut sedikit pengenalan tentang ANN yang dapat kita temui dari beberapa sumber di internet. ANN adalah beberapa lapisan jaringan saraf (neural network) yang terhubung secara keseluruhan yang dapat dilihat dari gambar dibawah ini. Setiap node pada setiap lapisan terhubung ke setiap node dari lapisan selanjutnya. Jaringan dibuat lebih dalam dengan menambah jumlah lapisan tersembunyi (hidden layer). | ||
| + | |||
| + | [[File:Artikelkomtekevi28.JPG]] | ||
| + | |||
| + | Jika salah satu hidden layer atau node output diperbesar, maka akan ditemukan gambar dibawah ini. | ||
| + | |||
| + | [[File:Artikelkomtekevi29.JPG]] | ||
| + | |||
| + | Node tertentu mengambil jumlah bobot dari inputnya, dan meneruskannya melalui fungsi aktivasi non-linear. Ini merupakan output dari node yang kemudian menjadi input dari node yang lain pada layer selanjutnya. Sinyal mengalir dari kiri ke kanan, dan output akhir dihitung dengan cara melakukan prosedur ini untuk semua node. Melatih jaringan saraf berarti mempelajari bobot yang terkait dengan semua edge. | ||
| + | |||
| + | Metode ANN ini digunakan untuk melatih data-data yang didapat dari numerik, dimana nilai posisi pada sumbu x dan y digunakan sebagai nilai input, dan nilai kecepatan pada sumbu x (u) dan sumbu y (v) yang merupakan hasil diferensial dari posisi digunakan sebagai nilai target. Data yang di training sebanyak 400 data. | ||
| + | |||
| + | [[File:Artikelkomtekevi30.JPG]] | ||
| + | |||
| + | Dengan demikian, diperoleh hasil yang dapat dilihat pada gambar diatas, dengan nilai R sebesar 0,99996 yang berarti data yang didapat dari metode Euler terverifikasi secara baik dengan persamaan yang dihasilkan dari metode ANN pada matlab. | ||
| + | |||
| + | ====Kesimpulan==== | ||
| + | |||
| + | Dari hasil yang sudah didapat untuk metode analitik, numerik, dan simulasi berikut beberapa hal yang dapat disimpulkan: | ||
| + | a) Hasil perhitungan numerik terhadap simulasi memiliki nilai yang berimpit. Hal ini dikarenakan, pada dasarnya simulasi yang dilakukan dengan MATLAB, menggunakan cara yang sama dengan numerik, hanya saja pada numerik persamaan-persamaannya harus dirubah menjadi 3 persamaan dengan orde 1. Sedangan pada simulasi, persamaan dari FBD langsung menjadi input pada MATLAB. | ||
| + | b) Hasil perhitungan numerik dan simulasi berbeda dengan metode analitik. Seperti sudah disebutkan pada materi perkuliahan sebelum ini, bahwa pada metode Forward Euler terdapat hal yang harus diperhatikan pada perkembangan amplitudonya. | ||
| + | c) Hasil metode forward euler telah terverifikasi dengan metode Artificial Neural Networks (ANN) yang dapat dilihat dari nilai R sebesar 0,99996 (mendekati 1) dari persamaan output metode ANN menggunakan software matlab. | ||
| + | |||
| + | =='''PERTEMUAN 11 (27 April 2020)'''== | ||
| + | |||
| + | |||
| + | Agenda pada hari ini yaitu evaluasi individu: | ||
| + | |||
| + | 1. Memahami konsep, prinsip, thinking concept komputasi | ||
| + | |||
| + | 2. Penerapan konsep/skill dalam komputasi | ||
| + | |||
| + | 3. Dengan belajar, dapat lebih mengenal diri | ||
| + | |||
| + | |||
| + | Cara: | ||
| + | |||
| + | 1. Menunjukkan kontribusi diri | ||
| + | |||
| + | 2. Menunjukkan pemahaman diri dalam komputasi | ||
| + | |||
| + | 3. Menunjukkan skill/ketrampilan dalam komputasi | ||
| + | |||
| + | |||
| + | Perbedaan presisi dan akurat: | ||
| + | |||
| + | -Presisi: nilainya berdekatan meskipun diluar target | ||
| + | |||
| + | -Akurat: Pasti sesuai target, namun nilainya tidak harus berdekatan | ||
| + | |||
| + | |||
| + | Inti dari evaluasi diri, agar kita semua lebih serius belajar untuk dapat lebih mengenal diri dan pencipta. | ||
| + | |||
| + | =='''PERTEMUAN 12 (4 Mei 2020)'''== | ||
| + | |||
| + | Pada hari ini kembali lagi dilakukan evaluasi belajar agar mahasiswa mampu mengenali diri sendiri dalam sasarannya terhadap: | ||
| + | |||
| + | 1. Value | ||
| + | |||
| + | 2. Understanding of indulage | ||
| + | |||
| + | 3. Skill/performa | ||
| + | |||
| + | |||
| + | ===Tugas: Mass Spring Damping System=== | ||
| + | |||
| + | Kasus ini menjelaskan sebuah sistem 2 cart spring-mass-damper. Persamaan gerak untuk system 2 degree of freedom yang digunakan adalah Newtonian mechanics dan diselesaikan secara numerik pada matlab. | ||
| + | |||
| + | [[File:FBD-MS-FES.jpg|1000px]] | ||
| + | |||
| + | % Calculates the position, velocity, and acceleration as a function of time | ||
| + | % of a system of carts connected by springs and dashpots. Euler's Method is | ||
| + | % used to solve the equations of motion numerically. | ||
| + | clear all; close all; clc; | ||
| + | tic | ||
| + | |||
| + | % Problem parameters | ||
| + | k1=50; % cart 1 spring constant (N/m) | ||
| + | k2=50; % cart 2 spring constant (N/m) | ||
| + | b1=3; % cart 1 viscous damping coefficient (kg/s) | ||
| + | b2=3; % cart 2 viscous damping coefficient (kg/s) | ||
| + | m1=5; % cart 1 mass (kg) | ||
| + | m2=5; % cart 2 mass (kg) | ||
| + | x10=1; % cart 1 initial position (m) | ||
| + | x20=-1; % cart 2 initial position (m) | ||
| + | v10=0; % cart 1 initial velocity (m/s) | ||
| + | v20=0; % cart 2 initial velocity (m/s) | ||
| + | |||
| + | % Set time step stuff | ||
| + | simTime=10; % simulation time (s) | ||
| + | tStep=0.001; % simulation time step | ||
| + | iterations=simTime/tStep; | ||
| + | t=0:iterations; | ||
| + | |||
| + | % Pre-allocate variables for speed and add initial conditions | ||
| + | x1=zeros(iterations,1); | ||
| + | x1(1,:)=x10; | ||
| + | x2=zeros(iterations,1); | ||
| + | x2(1,:)=x20; | ||
| + | v1=zeros(iterations,1); | ||
| + | v1(1,:)=v10; | ||
| + | v2=zeros(iterations,1); | ||
| + | v2(1,:)=v20; | ||
| + | a1=zeros(iterations,1); | ||
| + | a1(1,:)=-(b1*v10-b2*(v20-v10)+k1*x10-k2*(x20-x10))/m1; | ||
| + | a2=zeros(iterations,1); | ||
| + | a2(1,:)=-(b2*(v20-v10)+k2*(x20-x10))/m2; | ||
| + | |||
| + | % Solve the ODE's with Euler's Method | ||
| + | for n=2:(iterations+1) | ||
| + | x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position | ||
| + | x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position | ||
| + | v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity | ||
| + | v2(n,:)=v2(n-1,:)+a2(n-1,:)*tStep; % cart 2 velocity | ||
| + | % Find cart accelerations | ||
| + | a1(n,:)=-(b1*v1(n,:)-b2*(v2(n,:)-v1(n,:))+k1*x1(n,:)-k2*(x2(n,:)-x1(n,:)))/m1; | ||
| + | a2(n,:)=-(b2*(v2(n,:)-v1(n,:))+k2*(x2(n,:)-x1(n,:)))/m2; | ||
| + | end | ||
| + | |||
| + | % Plot results | ||
| + | subplot(3,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | plot(t',x2,'m') | ||
| + | ylabel('Position (m)') | ||
| + | title('Position, Velocity, & Acceleration as a Function of Time') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | subplot(3,1,2) | ||
| + | hold on; | ||
| + | plot(t',v1,'b') | ||
| + | plot(t',v2,'c') | ||
| + | ylabel('Velocity (m/s)') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | subplot(3,1,3) | ||
| + | hold on; | ||
| + | plot(t',a1,'g') | ||
| + | plot(t',a2,'y') | ||
| + | ylabel('Acceleration (m/s^2)') | ||
| + | xlabel('time (iterations)') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | |||
| + | toc | ||
| + | |||
| + | [[File:Artikelkeduaevi.jpg]] | ||
| + | |||
| + | Akan tetapi pada kasus ini, pembahasan yang dilakukan masih dengan Mass-Spring method. Untuk Finite Element Simplified (FES), akan diupdate pada kesempatan selanjutnya. | ||
| + | |||
| + | Source: https:// www.youtube.com/ watch?v=N524t6wdlcM&feature=youtu.be | ||
| + | |||
| + | |||
| + | =='''PERTEMUAN 13 (11 Mei 2020)'''== | ||
| + | |||
| + | ===Tugas: Analisis Mass Spring Pada Bangunan=== | ||
| + | |||
| + | ====Pendahuluan==== | ||
| + | |||
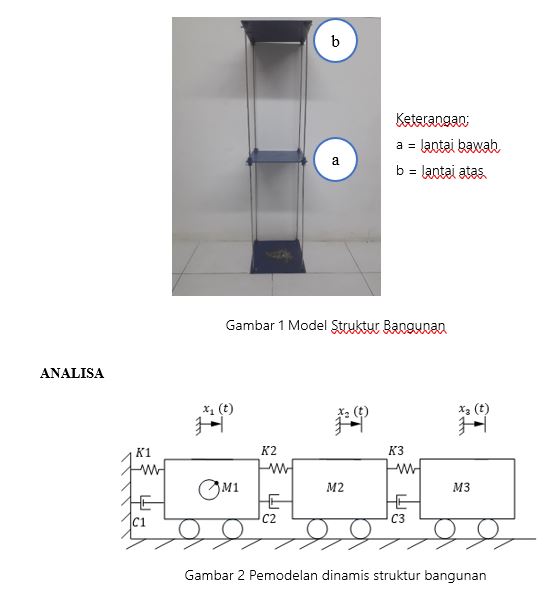
| + | Sistem pemodelan yang digunakan dalam struktur bangunan ini adalah pemodelan tiga derajat kebebasan (3 DOF). Gambar 1 menunjukkan model struktur bangunan bertingkat yang ditandai dengan adanya perpindahan sebesar x2 dan x3 karena pengaruh beban input gaya eksitasi dari shaking table. Sedangkan untuk pemodelan matematis, diperoleh persamaan dari free body diagram sistem yang akan dianalisa. | ||
| + | |||
| + | [[File:Bangunanevi1.JPG]] | ||
| + | |||
| + | |||
| + | ====Analisis==== | ||
| + | |||
| + | Untuk free body diagram dan persamaan massa shaking table (M1) adalah : | ||
| + | |||
| + | [[File:Bangunanevi2.JPG]] | ||
| + | |||
| + | [[File:Bangunanevi3.JPG]] | ||
| + | |||
| + | Setelah mendapatkan nilai parameter yang dibutuhkan untuk simulasi, Input yang digunakan yaitu input sinusoidal dengan frekuensi operasi 7 Hz atau 43,982 rad/s. | ||
| + | |||
| + | Untuk menyelesaikan persamaan gerak di atas maka dilakukan penyederhanaan persamaan menjadi 1 persamaan orde 6, dengan mengasumsikan x1 sebagai x, x2 sebagai y, dan x3 sebagai z, sehingga diperoleh persamaan, | ||
| + | |||
| + | [[File:Bangunanevi4.JPG]] | ||
| + | |||
| + | Persamaan 4 disubtitusikan kepersamaan 2 sehingga didapatkan persamaan, | ||
| + | |||
| + | [[File:Bangunanevi5.JPG]] | ||
| + | |||
| + | Untuk mencari nilai akar-akar dari persamaan di atas maka digunakan matlab untuk mempermudah perhitungan, | ||
| + | |||
| + | p=[1.154 21.059 4153.743 42436.977 2396974.157 2858796.484 151595214.4]; | ||
| + | r=roots(p) | ||
| + | r = | ||
| + | -3.6221 +52.7481i | ||
| + | -3.6221 -52.7481i | ||
| + | -5.5262 +24.9446i | ||
| + | -5.5262 -24.9446i | ||
| + | 0.0239 + 8.4846i | ||
| + | 0.0239 - 8.4846i | ||
| + | |||
| + | [[File:Bangunanevi6.JPG]] | ||
| + | |||
| + | Lalu dengan mengasumsikan nilai konstanta, | ||
| + | A=-0.0005 | ||
| + | B=0.0001 | ||
| + | C=0.0001 | ||
| + | D=-0.0002 | ||
| + | E=0.00032 | ||
| + | F=-0.009 | ||
| + | G=0.00008 | ||
| + | H=0.00001 | ||
| + | |||
| + | Maka dengan menggunakan software MATLAB dapat dibuat grafik posisi terhadap waktu. Berikut coding yang menjadi input dalam MATLAB: | ||
| + | |||
| + | syms x t A B C D E F | ||
| + | A=-0.0005 | ||
| + | B=0.0001 | ||
| + | C=0.0001 | ||
| + | D=-0.0002 | ||
| + | E=0.00032 | ||
| + | F=-0.009 | ||
| + | G=0.00008 | ||
| + | H=0.00001 | ||
| + | |||
| + | t=(1:100)/10 | ||
| + | x1 = exp(-3.62*t)*(A*sin(52.75*t) + B*cos(52.75*t)) + exp(5.53*t)* | ||
| + | (C*sin(24.94*t) + D*cos(24.94*t)) + exp(0.024*t)*(E*sin(8.48*t) + | ||
| + | F*cos(8.48*t)) + G*sin(43.982*t) + H*cos(43.982*t) | ||
| + | % Plot results | ||
| + | subplot(1,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | ylabel('Position (m)') | ||
| + | |||
| + | [[File:Bangunanevi7.JPG]] | ||
| + | |||
| + | Gambar 5 Grafik respon posisi terhadap waktu | ||
| + | |||
| + | Grafik di atas menunjukan pengaruh getaran pada bagian bawah struktur pemodelan bangunan di mana perubahan arah gerak pada bagian bawah struktur membentuk pola sinusoidal yang menandakan adanya gerak bolak-balik pada struktur tersebut. | ||
| + | |||
| + | ====Kesimpulan==== | ||
| + | |||
| + | Dalam permasalahan analisis gerak (perubahan arah, kecepatan dan percepatan) dapat dilakukan dengan metode lain berupa FES, namun pada artikel ini pemodelan FES belum dilakukan. Artikel ini hanya membahan mass-spring (MS) model yang terjadi pada suatu sistem pemodelan bangunan yang diberikan getaran. Sehingga dapat dilihat perilaku gerak bangunan sebagai respon dari adanya getaran yang diberikan. | ||
| + | |||
| + | '''REFERENSI''' | ||
| + | |||
| + | • Syaldiles Putri Indahdinata, Analisis Pengaruh Perubahan Cross Sectional Area Dan Posisi Peletakan Tuned Liquid Column Damper Terhadap Respon Dinamis Model Struktur Bangunan Bertingkat, Departemen Teknik Mesin FTI-ITS Surabaya, 2018. | ||
| + | |||
| + | |||
| + | =='''UJIAN AKHIR SEMESTER (8 Juni 2020)'''== | ||
| + | |||
| + | Pada ujian akhir semester komputasi teknik 2020, diberikan persoalan mengenai linear dynamic pada mobil, dengan data yang ditentukan sendiri. Penyelesaiannya dilakukan dengan metode numerik (dalam hal ini diselesaikan dengan metode 4th order Runge-Kutta) dibantu oleh software MATLAB. | ||
| + | |||
| + | [[File:UAS_Chandra-001.jpg]] | ||
| + | [[File:UAS_Chandra-002.jpg]] | ||
| + | [[File:UAS_Chandra-004.jpg]] | ||
| + | [[File:UAS_Chandra-005.jpg]] | ||
| + | |||
| + | END | ||
Latest revision as of 22:09, 10 June 2020
Contents
[hide]- 1 BIODATA
- 2 PERTEMUAN 1 ( 3 Februari 2020 )
- 3 PERTEMUAN 2 ( 10 Februari 2020 )
- 4 PERTEMUAN 3 ( 17 Februari 2020 )
- 5 PERTEMUAN 4 ( 23 Februari 2020 )
- 6 PERTEMUAN 5 ( 2 Maret 2020 )
- 7 PERTEMUAN 6 ( 9 Maret 2020 )
- 8 UJIAN TENGAH SEMESTER
- 9 PERTEMUAN 8 (6 April 2020)
- 10 PERTEMUAN 9 (13 April 2020)
- 11 PERTEMUAN 10 (20 April 2020)
- 12 PERTEMUAN 11 (27 April 2020)
- 13 PERTEMUAN 12 (4 Mei 2020)
- 14 PERTEMUAN 13 (11 Mei 2020)
- 15 UJIAN AKHIR SEMESTER (8 Juni 2020)
BIODATA
Nama : Chandra R. M. Simanjuntak
Jurusan : Teknik Mesin - Konversi Energi
NPM : 1906324012
Email : chandra.sijuntak@gmail.com
PERTEMUAN 1 ( 3 Februari 2020 )
Komputasi teknik merupakan suatu metode yang digunakan untuk menyelesaikan permasalahan matematis secara cepat dan lebih ringkas dengan memanfaatkan kemampuan komputer. Penggunaan komputasi teknik sudah sangat luas di bidang keteknikan, dengan berbagai variasi kemampuan serta output yang dihasilkan. Software konmputasi teknik antara lain, CFDSOF, Microsoft Excel, dll.
Komputasi teknik memiliki 3 tahapan utama yaitu Input - Proses - Output. Dimulai dari user yang harus memahami permasalahan, kemudian menerjemahkannya dalam bahasa yang dapat diproses komputer. Bahasa ini lah yang menjadi input bagi komputer. Lalu dengan menggunakan engine dari software komputer, input-an ini akan diproses sesuai kapabilitas software. Oleh karena itu komputasi teknik menjadi penting untuk dipelajari bagi orang yang menggeluti permasalahan teknik, sehingga dapat mempermudah simulasi perhitungan serta visualisasi, sampai akhirnya didapat output yang sesuai untuk menjawab permasalahannya.
Adapun sampai saat ini penerapan komputasi teknik lebih banyak didapat penulis dari penggunaan software Microsoft Excel.
PERTEMUAN 2 ( 10 Februari 2020 )
Di pertemuan ke-2 ini Pak DAI memberikan materi yang bertujuan untuk pengembangan diri mahasiswa, antara lain :
1. Belajar bukan hanya proses untuk menjadi tahu apa yang sebelumnya tidak diketahui, melainkan yang terpenting adalah bagaimana mendapatkan pelajaran unntuk belajar.
2. Untuk menunjang hal tersebut, perlu dimaknai bagaimana inersia setiap pribadi dalam kehidupan sehari-hari. Yang dimaksud disini adalah bagaimana memicu diri sendiri untuk berniat dan bekerja keras dalam belajar. Sehingga pada akhirnya mahasiswa terlatih untuk memiliki inersia diri yang besar.
3. Ilmu bagaikan tetesan air yang jatuh di lautan, langsung menyatu menjadi bagian dari lautan itu sendiri. Yang perlu dipahami disini adalah bagaimana ilmu mekanika fisika yang kita miliki harus selalu bersatu dengan Pancasila, dan nasionalisme. Salah satu upaya yang dapat dilakukan untuk menjadikannya satu adalah dengan analisis. Dimana analisis dapat diartikan suatu proses untuk menghasilkan suatu prosedur pemceahan masalah atau mendapatkan langkah-langkah solusi.
Tugas: Sinopsis Skripsi
Judul penelitian: Studi Eksperimental Karakteristik Aliran Fluida Melintasi Silinder Teriris Tipe I di Dekat Plat Datar Untuk Tebal Lapis Batas Laminar dan Turbulent
Hingga saat ini penelitian tentang pengaruh dinding terhadap aliran yang melintasi silinder sudah banyak dikembangkan. Berbagai variasi untuk mengetahui pengaruh dinding telah dilakukan untuk memperoleh data-data mengenai karakteristik aliran fluida yang terbentuk di sekeliling benda uji tersebut. Hasil dari penelitian ini banyak diaplikasikan dalam pengembangan dunia industri, sebagai contoh penyusunan shell and tube dalam penukar kalor, perpipaan bawah laut serta contoh-contoh yang lain. Berdasarkan pemikiran di atas maka akan dilakukan penelitian tentang pengaruh dinding terhadap aliran fluida melintasi silinder teriris tipe I. Penelitian ini dilakukan secara eksperimental dalam sebuah wind tunnel, dimana benda uji yang digunakan adalah silinder tipe I dengan sudut iris (θs) 53° dan 65° yang diletakkan dekat dengan suatu plat datar. Variasi Gap Rasio(G/D) sebesar 1,200 ; 1,267 ; 1,333 pada lapis batas laminar dan turbulent. Karakteristik aliran fluida yang diteliti adalah distribusi koefisien tekanan (Cp), koefisien drag (CD), koefisien lift (CL), profil kecepatan di belakang silinder dan melakukan visualisasi menggunakan metode oil flow picture pada subsonic wind tunnel pada Re= 5,3x104. Diharapkan penelitian ini akan mampu menjelaskan pengaruh lapisan batas dinding terhadap aliran pada silinder serta menjelaskan fenomena wake yang terjadi pada silinder teriris tipe I.
Tugas: Rencana Skripsi dengan Menggunakan Komputasi Teknik
Hal bisa dilakukan terhadap tugas akhir S1 dengan metode komputasi teknik adalah dengan meng-aplikasikan software CFD yang antara lain bertujuan untuk:
1.Melakukan simulasi dan visualisasi aliran di sekitar benda uji sehingga didapat gambaran distribusi tekanan di sepanjang penampang benda uji
2.Mencari nilai optimum dari G/D sehingga dapat lebih diketahui sejauh apa dampaknya terhadap gaya lift dan drag yang dihasilkan.
PERTEMUAN 3 ( 17 Februari 2020 )
Kelas dimulai dengan presentasi tugas sinopsis.
Lalu dilanjutkan dengan pembahasan terkait masalah dalam diri kita masing-masing. Masalah terutama dari manusia adalah Ketidaktahuan, Egois, dan Malas. Jika dengan segala upaya kita mampu memberantas sifat ini, maka kita akan mendapat nilai tambah.
Komputasi teknik merupakan proses melakukan studi dengan pemodelan matematis yang tidak dapat dipecahkan dengan perhitungan manual.
Tugas: Pemodelan dengan Menggunakan Komputasi Teknik
Judul Skripsi: Studi Eksperimental Tentang Karakteristik Aliran Fluida Melintasi Silinder Teriris Tipe I di Dekat Plat Datar Untuk Tebal Lapis Batas Laminar dan Turbulen G/D 1,2 sd 1.33.
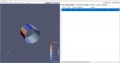
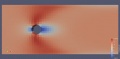
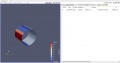
Pada tugas akhir S1 dilakukan eksperimental dalam windtunnel dimana benda uji silinder teriris dijadika sebagai objek percobaan. Pada percobaan tersebut dilakukan pengukuran koefisien tekanan melalui pressure tab yang ditempeli di sekeliling benda uji. Pada proyek kali ini dilakukan upaya simulasi visualisasi aliran di sekitar silinder dengan menggunakan piranti lunak CFD. Adapun pemodelan matematis dilakukan saat perhitungan gaya drag. Simplikasi dari pemodelan matematis dalam software adalah dengan memasukkan persamaan Gaya Drag = Pressure x Kecepatan di sepanjang sumbu.
Jarak silinder terhadap dinding : 5 cm
Jarak silinder terhadap dinding : 27 cm
PERTEMUAN 4 ( 23 Februari 2020 )
Tugas: Membuat Extended Abstrak Proyek Skripsi
Name: Chandra R. M. Simanjuntak
Title: Modeling of Flow Characteristic Around Circular Cylinder Near a Flat Plate
In 1976, an oil company found their subsea pipeline floating off the north east coast of Scotland 1½ miles from its original location. Effort has been made before the incident to protect the pipe, such as dredging and trenching the sea-bed. At that time it is believed that hydrodynamic force and the interaction between pipe and seabed was the root cause of these tragedy. Until nowadays flow characteristics around a bluff body have been widely investigated, whether to study the body-shape itself or to find the effect of the gap between bluff body and an artificial base. This further study will be focused on the drag pressure resulting from varying the gap and also the flow visualization around the body. With the assistance of computational fluid dynamic (CFD) software, external flow around the body will be simulated. The body would be in circular shape, and there would be a flat plate nearby with a certain gap. In order to do the simulation, the mesh modeling of the environment around the object shall be made. Several data and approach has to be decided. Thereafter in the simulation process the software will do the calculation and iteration, then emerge visualization of the flow. In certain gap to diameter ratios (G/D) the drag force started to decrease with the gap reduction. The minimum value reached when the gap was reduced to zero. The flow visualization shown an region behind the body as we known as wake.
PERTEMUAN 5 ( 2 Maret 2020 )
Tugas: Optimasi Kebutuhan Energi Manusia
Energi sangat diperlukan manusia untuk melakukan aktifitas sehari hari. Baik itu energi yang didapat dari makanan lalu diproses oleh tubuh untuk dikonversi menjadi gerak, panas, dan sinyal, maupun energi yang tersedia dalam bentuk listrik, dan panas di sekitar kita. Energi diperlukan oleh setiap individu akan berbeda-beda tergantung pada beban aktivitas harian yang dilakukan. Manusia telah membuat berbagai metode teknik pendekatan untuk mengetahui penggunaan energi setiap harinya. Salah satu tujuannya adalah untuk mengoptimasi energi yang dimasukkan ke tubuh, sehingga dapat lebih selektif dan tidak berlebihan dalam mengkonsumsi makanan.
Untuk mendapatkan perkiraan biaya yang dikeluarkan dari energi yang digunakan tiap individu, maka ada 2 variabel penggunaan energi yang perlu dicari, yaitu: energi yang digunakan dari aktivitas harian; dan energi yang digunakan dari penggunaan listrik atau panas. Hasil dari energi ini kemudian dikonversikan menjadi satuan Rupiah dengan mengalikan terhadap harga listrik PLN per kWh. Diasumsikan daya listrik rumah non-subsidi terendah, 1300 Watt maka biaya listrik nya adalah Rp 1,467 / kWh.
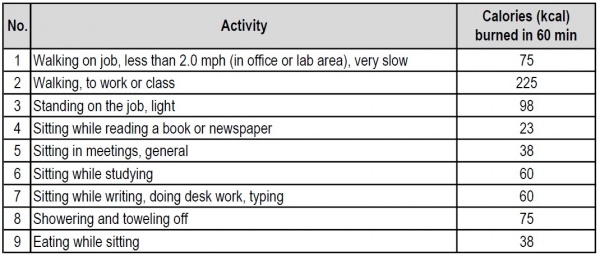
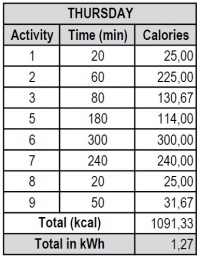
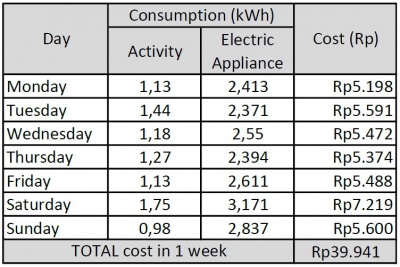
Contoh pada tabel 4, di hari Kamis aktivitas individu menggunakan 1,27 kWh dan penggunaan listrik 2,39 kWh. Maka biaya energi yang digunakan pada hari Kamis: (1,27+2,394)kWh x Rp 1467/kWh = Rp 5,374.00.
Di bawah ini beberapa proses perhitungan yang dilakukan:
Tabel 1, daftar kegiatan harian yang saya lakukan, dimana nilai kalori yang dicantumkan, didapat dari referensi [1]
Tabel 2, contoh perhitungan penggunaan energi ditinjau dari aktivitas yang dilakukan pada hari Kamis.
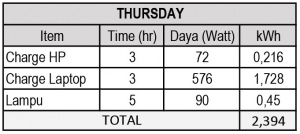
Tabel 3, contoh perhitungan penggunaan energi ditinjau dari penggunaan peralatan listrik pada hari Kamis.
Tabel 4, total penggunaan energi dari hari Senin - Minggu.
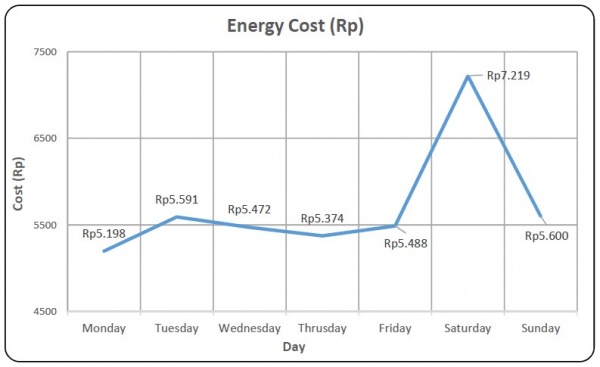
Grafik 1, grafik biaya yang dikeluarkan untuk penggunaan energi dari Senin - Minggu
PERTEMUAN 6 ( 9 Maret 2020 )
Tugas: Rule Of Term Engineering Computation
Pada pertemuan ini saya izin tidak mengikuti kelas dikarenakan adanya proses persalinan istri. Namun mengacu dari referensi wiki rekan-rekan, dengan menggunakan pemahaman pribadi saya akan mencoba menuliskan hal-hal yang menjadi poin penting pada perkuliahan kali ini. Wiki yang dijadikan acuan adalah Muchalis Zikramansyah Masuku, Evi Elisa Ambarita, dan Oldy Fahlovi.
Perkuliahan membahas kerangka proses kerja dalam melakukan dan menyelesaikan permasalahan dengan komputasi teknik. Hal yang menjadi rule of term dari proses ini yaitu:
1. Initial thinking. Proses identifikasi permasalahan dimana disini diperlukan konsep dan informasi terkait sebanyak-banyaknya. Diupayakan proses ini sudah 60% mengarah ke solusi yang ingin dicapai.
2. Permodelan matematis. Dengan konsep dan referensi yang ada, dikembangkan model matematis yang berisi variable-variabel yang akan dianalisa. Selain itu juga perlu dimasukkan asumsi-asumsi agar hasil dari pemodelan matematis dapat sedekat mungkin sesuai dengan kondisi aktual. Asumsi ini kembali pada pengetahuan dan pengalaman pribadi.
3. Pengumpulan data. Data yang didapat akan digunakan dalam penyelesaian model matematis.
4. Simulasi. Proses menjalankan atau mengeksekusi model yang sudah buat.
5. Verifikasi (resolve the equation right). Proses menguji apakah model yang dilakukan tidak terdapat kesalahan numerik, misalnya kesalahan pada proses meshing.
6. Validasi (resolve the right equation). Proses menguji kebenaran dari hasil simulasi.
7. Result dan discussion. Mendiskusikan hasil yang sudah didapat.
8. Recommendation. Proses memberikan masukan perbaikan terhadap penelitian tersebut, dan upaya untuk mencari celah improvisasi untuk penelitian berikutnya.
9.Reporting. Membuat laporan penelitian agar dapat dijadikan pengetahuan dan referensi bersama.
UJIAN TENGAH SEMESTER
Tugas: Membuat laporan hasil tugas optimasi kebutuhan energi manusia
Klik panah (kiri-kanan)untuk mengganti halaman dokumen
Tugas: Menyiapkan draft paper project komputasi teknik
Klik panah (kiri-kanan)untuk mengganti halaman dokumen
PERTEMUAN 8 (6 April 2020)
Pada pertemuan ini dilakukan presentasi proyek komputasi teknik oleh Wisnu Indrawan & Adhika Satyadharma
PERTEMUAN 9 (13 April 2020)
Oscillating 1-D Dynamic System
Mahasiswa diberi penjelasan terkait rule of term of engineering (pertemuan 6), dimana proses ini dilakukan untuk mendapatkan solusi komputasi teknik. Pada kesempatan ini dijelaskan konsep tersebut dimulai dari initial thinking, pemodelan matematis, sampai dengan verifikasi, dan validasi. Pada tahap initial thinking perlu diyakinkan semua konsep, data, dan referensi yang dihadapi sudah didapat dan dimengerti. Kemudian dibentuk model matematis yang diharapkan dapat mendekati kondis aktual. Setelah itu dilakukan simulasi perhitungan, lalu verifikasi. Pengertian verifikasi yaitu memastikan perhitungan yang dilakukan dengan komputer sudah benar dan sesuai kondisi ideal. Sedangkan validasi memiliki makna memastikan model matematika yang dibangun sudah mendekati aktual, atau umumnya dilakukan eksperimen untuk membandingkan hasil yang didapat.
Adapun materi oscillating dynamic system ini diberikan sebagai pengetahuan bagi mahasiswa mengenai bagaimana melakukan verifikasi perhitungan. Penyelesaian matematis yang dapat dilakukan untuk sistem dinamik tersebut antara lain dengan metode analitik, metode numerik, dan metode yang dinamakan "a magic fix for numerical method". Bagian yang disebut paling akhir ini disebut memiliki hasil dengan error yang paling kecil.
Quiz: Oscillating 1-D Dynamic System
Terdapat 2 metode numerik yang akan digunakan, yakni standard numerical solution (persamaan 4.47 dan 4.48) dan a magic fix of a numerical method (persamaan 4.49 dan 4.50). Suatu benda dengan massa m (sesuai gambar 4.15) melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan. Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) body (penampang m) kembali dan bekerja "melawan" gerakan, misalkan x (t) adalah posisi body pada sumbu x, dimana body bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya terjadi posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (misal gesekan). Hukum kedua Newton menyatakan F=ma kemudian memiliki F=-kx dan a=x ̈,
-kx=mx ̈ (4.41)
sehingga dapat dituliskan
x ̈+ω^2 x=0 (4.42)
Persamaan (4.42) adalah persamaan diferensial orde kedua, dan oleh karena itu kita memerlukan dua kondisi awal, satu pada posisi x (0) dan satu pada kecepatan x’ (0).
x (0) = 1,5 dan x’ (0) = 0
Cara yang dapat kita tuliskan pada persamaan 4.42 merupakan sistem orde pertama dari 2 persamaan turunan, untuk mengendalikan turunan orde dua. Kita memperkenalkan u=x dan v=x^'=u' sebagai 2 fungsi baru yang tidak diketahui. Dua persamaan yang sesuai muncul dari definisi v=u' dan persamaan asal (4.42):
u^'=v (4.43)
v^'=-ω²u (4.44)
maka u^=v' untuk menghilangkan turunan orde kedua dari hukum kedua newton. Dengan menggunakan metode numerik pertama, yakni standard numerical solution dengan persamaan-persamaan berikut:
u^(n+1)=u^n+∆t v^n (4.47)
v^(n+1)=v^n-∆t 〖ω^2 u〗^n (4.48)
Selain itu, terdapat juga metode numerik kedua yang anggap lebih akurat, disebut a magic fix of the numerical method dengan mengganti u^n untuk persamaan kedua menjadi u^(n+1) dari persamaan pertama, sehingga:
u^(n+1)=u^n+∆t v^n (4.49)
v^(n+1)=v^n-∆t 〖ω^2 u〗^(n+1) (4.50)
dimana diketahui ω = 2,5 rad/s dan ∆t = 0,05 s, maka dilakukan perhitungan yang dapat dilihat di lampiran (ms.excel).
Selanjutnya dilakukan verifikasi antara setiap metode numerik diatas terhadap metode analitik, dimana persamaan-persamaan untuk metode analitik adalah sebagai berikut:
u=x cosωt
v=- x ω cosωt
yang perhitungan detail nya dapat juga dilihat pada lampiran (ms.excel). Sehingga diperoleh hasil yang merupakan grafik sebagai berikut:
Dari kedua grafik diatas dapat dilihat jelas bahwa metode numerik yang standard dengan menggunakan persamaan 4.47 dan 4.48 jauh dari kata akurat, dikarenakan hasil yang didapat dari metode ini (grafik biru) sangat berbeda dengan hasil dari metode analitik (grafik abu-abu). Oleh karena itu, metode numerik yang disebut a magic fix for a numerical method perlu dilakukan, dengan hasil sebagai berikut:
Dari kedua grafik diatas, dapat dilihat bahwa metode numerik ini (grafik kuning) memiliki tingkat keakurasian yang sangat baik dengan pemverifikasian terhadap metode analitik (grafik hijau). Dengan demikian, disimpulkan bahwa a magic fix for a numerical method telah terverifikasi terhadap metode analitik yang mana dapat mewakili metode analitik. untuk menentukan nilai u dan v.
Klik panah (kiri-kanan)untuk mengganti halaman dokumen
PERTEMUAN 10 (20 April 2020)
Inti dari komputasi teknik adalah agar kita mampu menerjemahkan persoalan fisik menjadi model matematis yang akan diselesaikan dengan komputer. Secara garis besar tahapannya yaitu:
1. Terjemahkan real case ke dalam model
2. Buat model sederhana dengan initial thinking dan asumsi. Disini sudah didapat konsep pemikirannya, setelah itu dapat ditentukan judul topik yang sesuai.
a.Contoh asumsi: tidak ada gesekan pada model yang dianalisa, dst.
b.Jadilah model matematis yang dapat diselesaikan dengan metode-metode komputasi teknik. Misal Forward Euler, Runge Kutta.
c.Ketika ditemui adanya keterbatasan pada model tsb, maka dapat dikembangkan dengan:
-finite difference
-finite element / volume (deterministik)
-ANN (stokastik) / GA (survival for the fittest)
d. Bandingkan hasil dari metode pada point "c" terhadap point "d"
Pada pertemuan ini tiap kelompok berdiskusi mengenai tugas komputasi teknik seperti pada tugas sebelumnya, yang ditambahkan dengan pembahasanan terkait artificial neural network atau finite elemen design. Untuk kelompok kami akan mengambil topik tambahan artificial neural network.
Tugas: Artificial Neural Network pada Oscillating 1-D Dynamic System
Pendahuluan
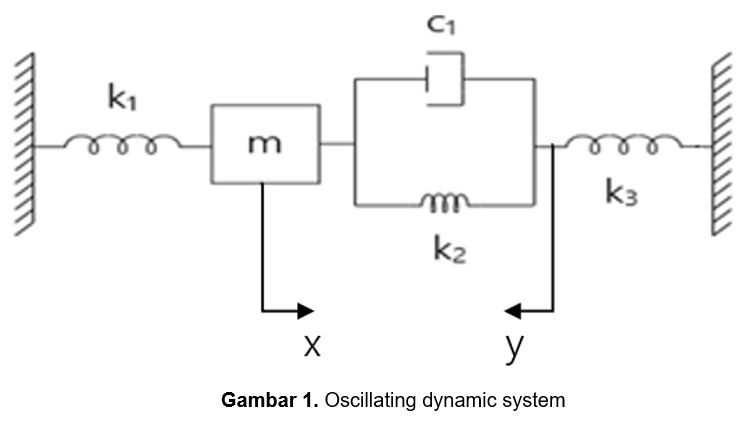
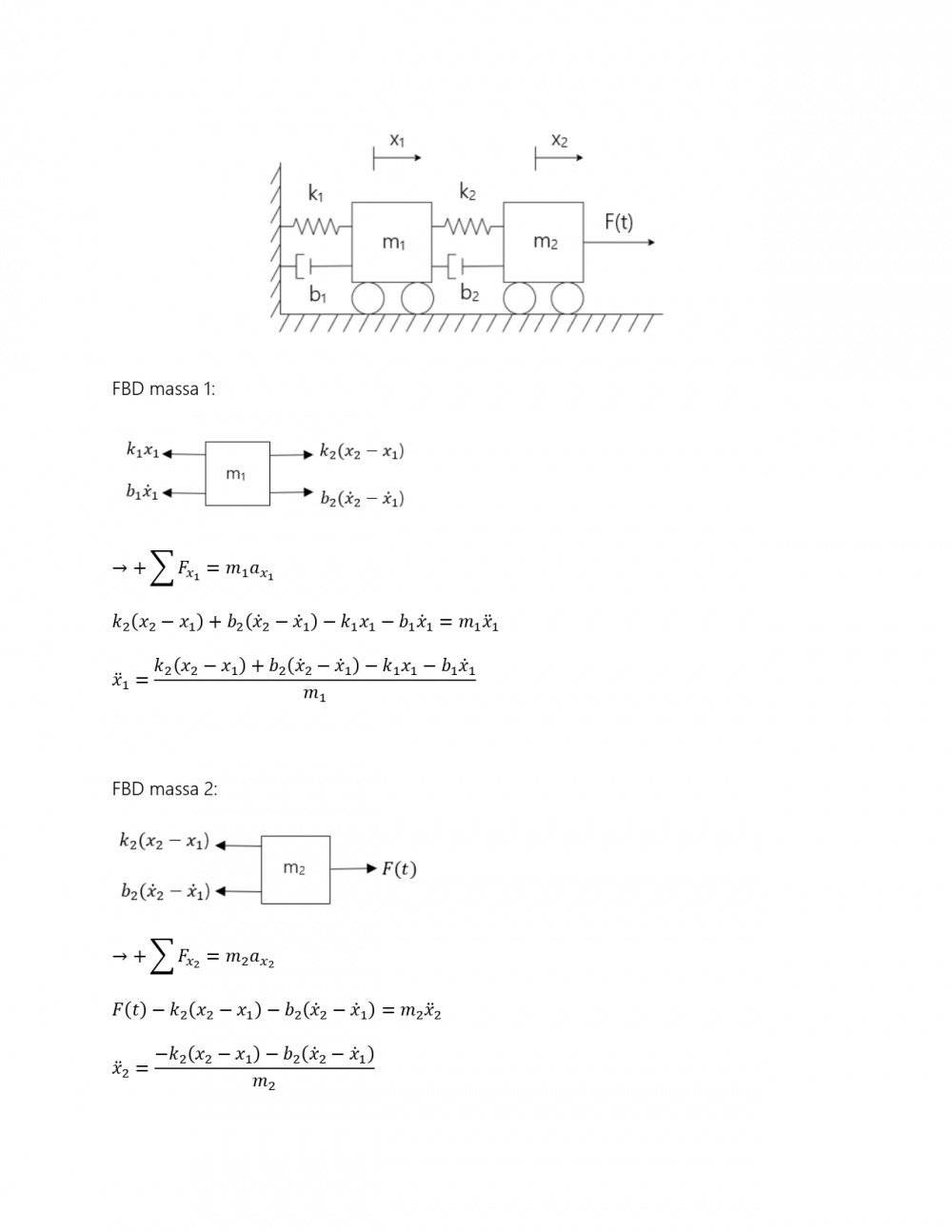
Artikel ini akan membahas penyelesaian permasalahan oscillating 1-D dynamic system pada system damping sesuai gambar di bawah. Pada system di bawah terdapat sebuah massa yang dihubungkan dengan 3 spring, dan 1 dashpot. System tersebut fix pada 2 boundary sisi kiri dan kanan.
Penyelesaian dari permasalahan tersebut akan dilakukan dengan 3 metode, yang kemudian akan dibandingkan hasil dari perhitungan pada tiap metode tersebut. Metode yang digunakan yaitu: analitikal, numerik, dan simulasi. Pada metode analitikal dilakukan tinjauan gaya aksi – reaksi pada free body diagram (FBD) yang muncul dari eksitasi yang diberikan. Kemudian untuk penyelesaian metode numerik akan dilakukan iterasi dengan bantuan software Microsoft Excel menggunakan Forward Euler. Sedangkan untuk proses simulasi akan dilakukan dengan bantuan software MATLAB.
Metode
Metode Analitik
Free Body Diagram (FBD):
• Tinjauan massa:
• Tinjauan titik: (diantara c1, k2, dan k3)
Diketahui:
Maka persamaan 1 dan 2 dapat dituliskan kembali menjadi;
Persamaan 1
Persamaan 2
Penyelesaian
Asumsi
Karena pada persamaan 5 masih terdapat ̇ y maka subtitusi persamaan 6 ke persamaan 5, sehingga didapatkan nilai ̇ z sebagai berikut;
Penyelesaian menggunakan matrix;
Maka didapatkan nilai λ sebesar
Sehingga didapatkan persamaan
Jika diasumsikan nilai C1,C2,dan C3 adalah 1, 2 dan 3 maka;
Nilai x untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai yh dengan mensubtitusi nilai xh ke dalam persamaan ̇ z=-x+3y, di mana nilai ̇ z = ̈ x.
Mencari nilai ̇x;
Nilai ̇ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai ̈ x;
Persamaan ̈ x di atas dapat disederhanakan menjadi;
Nilai ̈ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai y;
Persamaan yh dapat disederhanakan menjadi;
Nilai y untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai ̇ y;
Nilai ̇ y ketika t = 0 s, t = 1 s, dan t = 10 s adalah
Metode Numerik
Metode ini dilakukan dengan menggunakan software Microsoft Excel. Parameter input yang harus diketahui yaitu x pada t = 0 s, y pada t = 0 s, dan selisih penambahan waktu (∆t). Parameter input x dan y ini dapat juga disebut dengan initial condition. Lalu kemudian dilakukan iterasi sesuai dengan ∆t sampai waktu yang ditentukan. Nilai parameter input tersebut didapat dengan cara analitis seperti sudah disebut di atas, yaitu x((t=0))=4 m; y((t=0))=5.9 m; dan selisih waktu ∆t=0.1 second.
Seperti sudah disebutkan sebelumnya bahwa penyelesaiannya menggunakan Forward Euler, yaitu sebagai berikut:
Simulasi
Simulasi dilakukan dengan bantuan software MATLAB. Adapun agar simulasi dapat berjalan, maka perlu diberikan input coding pada software MATLAB yang isinya sebagai berikut.
% Calculates the position, velocity, and acceleration as a function of time % of a system of carts connected by springs and dashpots. Euler's Method is % used to solve the equations of motion numerically. clear all; close all; clc; tic
% Problem parameters k1=1; % cart 1 spring constant (N/m) k2=2; % cart 1 spring constant (N/m) b1=1; % cart 1 viscous damping coefficient (kg/s) m1=1; % cart 1 mass (kg) k3=3; % cart 1 spring constant (N/m) x10=4; % cart 1 initial position (m) x20=5.9; % y movement initial position (m) v10=-2.135; % cart 1 initial velocity (m/s) v20=-35.36; % cart 2 initial velocity (m/s)
% Set time step stuff simTime=60; % simulation time (s) tStep=0.1; % simulation time step iterations=simTime/tStep; t=0:iterations;
% Pre-allocate variables for speed and add initial conditions x1=zeros(iterations,1); x1(1,:)=x10; x2=zeros(iterations,1); x2(1,:)=x20; v1=zeros(iterations,1); v1(1,:)=v10; v2=zeros(iterations,1); v2(1,:)=v20; a1=zeros(iterations,1); a1(1,:)=((0-(k1*x10)-b1*(v10+v20)-k2*(x20+x10))/m1);
% Solve the ODE's with Euler's Method for n=2:(iterations+1) x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity v2(n,:)=-(2*x1(n,:)+5*x2(n,:)+v1(n,:)) % Find cart accelerations a1(n,:)=((0-k1*x1(n,:))-b1*(v1(n,:)+v2(n,:))-k2*(x2(n,:)+x1(n,:))/m1); end
% Plot results
subplot(3,1,1)
hold on;
plot(t',x1,'r')
plot(t',x2,'m')
ylabel('Position (m)')
title('Position, Velocity, & Acceleration as a Function of Time')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
subplot(3,1,2)
hold on;
plot(t',v1,'b')
plot(t',v2,'c')
ylabel('Velocity (m/s)')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
subplot(3,1,3)
hold on;
plot(t',a1,'g')
ylabel('Acceleration (m/s^2)')
xlabel('time (1 = 0.01 detik)')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
toc
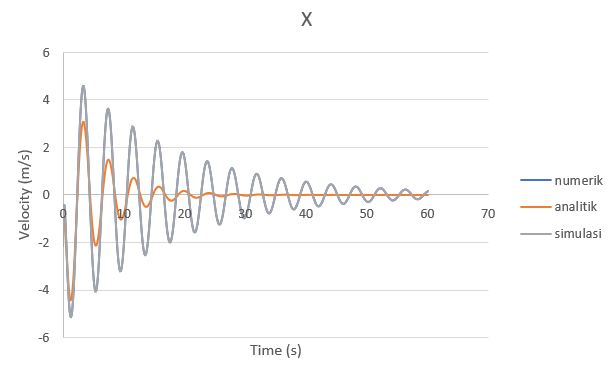
Hasil
Gambar 2. Grafik velocity (dx/dt) perbandingan analitik, numerik, dan simulasi
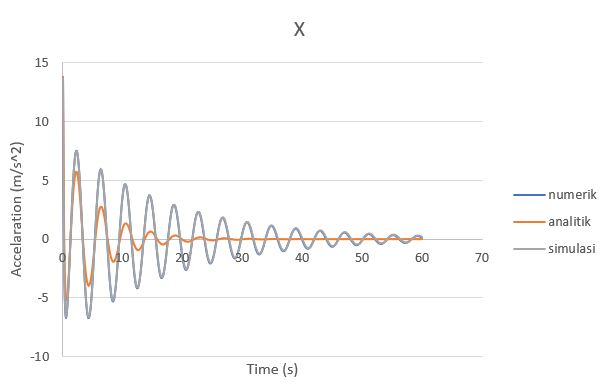
Gambar 3. Grafik acceleration (d^2x/dt^2) perbandingan analitik, numerik, dan simulasi
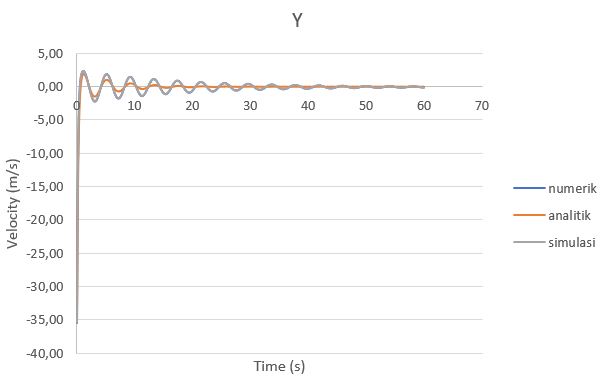
Gambar 4. Grafik velocity (dy/dt) perbandingan analitik, numerik, dan simulasi
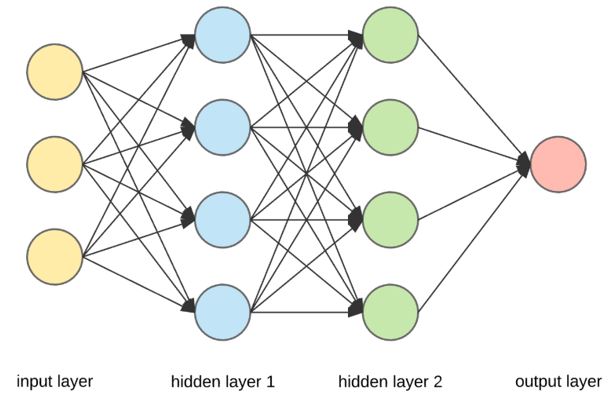
Selanjutnya, untuk memverifikasi hasil numerik menggunakan metode euler yang dijelaskan diatas, digunakan metode Artificial Neural Networks (ANN) pada perangkat lunak matlab. Berikut sedikit pengenalan tentang ANN yang dapat kita temui dari beberapa sumber di internet. ANN adalah beberapa lapisan jaringan saraf (neural network) yang terhubung secara keseluruhan yang dapat dilihat dari gambar dibawah ini. Setiap node pada setiap lapisan terhubung ke setiap node dari lapisan selanjutnya. Jaringan dibuat lebih dalam dengan menambah jumlah lapisan tersembunyi (hidden layer).
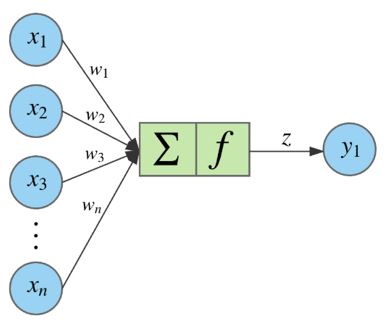
Jika salah satu hidden layer atau node output diperbesar, maka akan ditemukan gambar dibawah ini.
Node tertentu mengambil jumlah bobot dari inputnya, dan meneruskannya melalui fungsi aktivasi non-linear. Ini merupakan output dari node yang kemudian menjadi input dari node yang lain pada layer selanjutnya. Sinyal mengalir dari kiri ke kanan, dan output akhir dihitung dengan cara melakukan prosedur ini untuk semua node. Melatih jaringan saraf berarti mempelajari bobot yang terkait dengan semua edge.
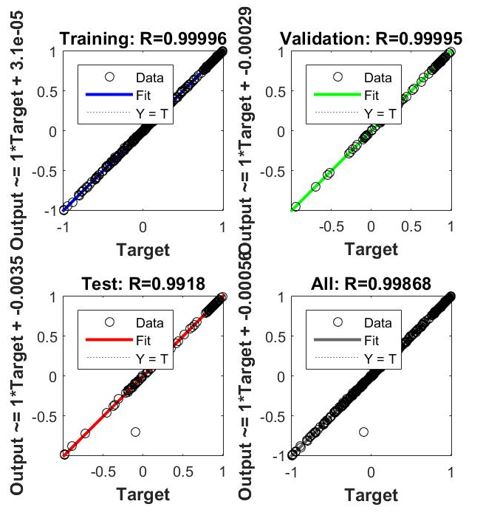
Metode ANN ini digunakan untuk melatih data-data yang didapat dari numerik, dimana nilai posisi pada sumbu x dan y digunakan sebagai nilai input, dan nilai kecepatan pada sumbu x (u) dan sumbu y (v) yang merupakan hasil diferensial dari posisi digunakan sebagai nilai target. Data yang di training sebanyak 400 data.
Dengan demikian, diperoleh hasil yang dapat dilihat pada gambar diatas, dengan nilai R sebesar 0,99996 yang berarti data yang didapat dari metode Euler terverifikasi secara baik dengan persamaan yang dihasilkan dari metode ANN pada matlab.
Kesimpulan
Dari hasil yang sudah didapat untuk metode analitik, numerik, dan simulasi berikut beberapa hal yang dapat disimpulkan: a) Hasil perhitungan numerik terhadap simulasi memiliki nilai yang berimpit. Hal ini dikarenakan, pada dasarnya simulasi yang dilakukan dengan MATLAB, menggunakan cara yang sama dengan numerik, hanya saja pada numerik persamaan-persamaannya harus dirubah menjadi 3 persamaan dengan orde 1. Sedangan pada simulasi, persamaan dari FBD langsung menjadi input pada MATLAB. b) Hasil perhitungan numerik dan simulasi berbeda dengan metode analitik. Seperti sudah disebutkan pada materi perkuliahan sebelum ini, bahwa pada metode Forward Euler terdapat hal yang harus diperhatikan pada perkembangan amplitudonya. c) Hasil metode forward euler telah terverifikasi dengan metode Artificial Neural Networks (ANN) yang dapat dilihat dari nilai R sebesar 0,99996 (mendekati 1) dari persamaan output metode ANN menggunakan software matlab.
PERTEMUAN 11 (27 April 2020)
Agenda pada hari ini yaitu evaluasi individu:
1. Memahami konsep, prinsip, thinking concept komputasi
2. Penerapan konsep/skill dalam komputasi
3. Dengan belajar, dapat lebih mengenal diri
Cara:
1. Menunjukkan kontribusi diri
2. Menunjukkan pemahaman diri dalam komputasi
3. Menunjukkan skill/ketrampilan dalam komputasi
Perbedaan presisi dan akurat:
-Presisi: nilainya berdekatan meskipun diluar target
-Akurat: Pasti sesuai target, namun nilainya tidak harus berdekatan
Inti dari evaluasi diri, agar kita semua lebih serius belajar untuk dapat lebih mengenal diri dan pencipta.
PERTEMUAN 12 (4 Mei 2020)
Pada hari ini kembali lagi dilakukan evaluasi belajar agar mahasiswa mampu mengenali diri sendiri dalam sasarannya terhadap:
1. Value
2. Understanding of indulage
3. Skill/performa
Tugas: Mass Spring Damping System
Kasus ini menjelaskan sebuah sistem 2 cart spring-mass-damper. Persamaan gerak untuk system 2 degree of freedom yang digunakan adalah Newtonian mechanics dan diselesaikan secara numerik pada matlab.
% Calculates the position, velocity, and acceleration as a function of time
% of a system of carts connected by springs and dashpots. Euler's Method is
% used to solve the equations of motion numerically.
clear all; close all; clc;
tic
% Problem parameters
k1=50; % cart 1 spring constant (N/m)
k2=50; % cart 2 spring constant (N/m)
b1=3; % cart 1 viscous damping coefficient (kg/s)
b2=3; % cart 2 viscous damping coefficient (kg/s)
m1=5; % cart 1 mass (kg)
m2=5; % cart 2 mass (kg)
x10=1; % cart 1 initial position (m)
x20=-1; % cart 2 initial position (m)
v10=0; % cart 1 initial velocity (m/s)
v20=0; % cart 2 initial velocity (m/s)
% Set time step stuff
simTime=10; % simulation time (s)
tStep=0.001; % simulation time step
iterations=simTime/tStep;
t=0:iterations;
% Pre-allocate variables for speed and add initial conditions
x1=zeros(iterations,1);
x1(1,:)=x10;
x2=zeros(iterations,1);
x2(1,:)=x20;
v1=zeros(iterations,1);
v1(1,:)=v10;
v2=zeros(iterations,1);
v2(1,:)=v20;
a1=zeros(iterations,1);
a1(1,:)=-(b1*v10-b2*(v20-v10)+k1*x10-k2*(x20-x10))/m1;
a2=zeros(iterations,1);
a2(1,:)=-(b2*(v20-v10)+k2*(x20-x10))/m2;
% Solve the ODE's with Euler's Method
for n=2:(iterations+1)
x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position
x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position
v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity
v2(n,:)=v2(n-1,:)+a2(n-1,:)*tStep; % cart 2 velocity
% Find cart accelerations
a1(n,:)=-(b1*v1(n,:)-b2*(v2(n,:)-v1(n,:))+k1*x1(n,:)-k2*(x2(n,:)-x1(n,:)))/m1;
a2(n,:)=-(b2*(v2(n,:)-v1(n,:))+k2*(x2(n,:)-x1(n,:)))/m2;
end
% Plot results
subplot(3,1,1)
hold on;
plot(t',x1,'r')
plot(t',x2,'m')
ylabel('Position (m)')
title('Position, Velocity, & Acceleration as a Function of Time')
legend('Cart 1','Cart 2')
subplot(3,1,2)
hold on;
plot(t',v1,'b')
plot(t',v2,'c')
ylabel('Velocity (m/s)')
legend('Cart 1','Cart 2')
subplot(3,1,3)
hold on;
plot(t',a1,'g')
plot(t',a2,'y')
ylabel('Acceleration (m/s^2)')
xlabel('time (iterations)')
legend('Cart 1','Cart 2')
toc
Akan tetapi pada kasus ini, pembahasan yang dilakukan masih dengan Mass-Spring method. Untuk Finite Element Simplified (FES), akan diupdate pada kesempatan selanjutnya.
Source: https:// www.youtube.com/ watch?v=N524t6wdlcM&feature=youtu.be
PERTEMUAN 13 (11 Mei 2020)
Tugas: Analisis Mass Spring Pada Bangunan
Pendahuluan
Sistem pemodelan yang digunakan dalam struktur bangunan ini adalah pemodelan tiga derajat kebebasan (3 DOF). Gambar 1 menunjukkan model struktur bangunan bertingkat yang ditandai dengan adanya perpindahan sebesar x2 dan x3 karena pengaruh beban input gaya eksitasi dari shaking table. Sedangkan untuk pemodelan matematis, diperoleh persamaan dari free body diagram sistem yang akan dianalisa.
Analisis
Untuk free body diagram dan persamaan massa shaking table (M1) adalah :
Setelah mendapatkan nilai parameter yang dibutuhkan untuk simulasi, Input yang digunakan yaitu input sinusoidal dengan frekuensi operasi 7 Hz atau 43,982 rad/s.
Untuk menyelesaikan persamaan gerak di atas maka dilakukan penyederhanaan persamaan menjadi 1 persamaan orde 6, dengan mengasumsikan x1 sebagai x, x2 sebagai y, dan x3 sebagai z, sehingga diperoleh persamaan,
Persamaan 4 disubtitusikan kepersamaan 2 sehingga didapatkan persamaan,
Untuk mencari nilai akar-akar dari persamaan di atas maka digunakan matlab untuk mempermudah perhitungan,
p=[1.154 21.059 4153.743 42436.977 2396974.157 2858796.484 151595214.4]; r=roots(p) r = -3.6221 +52.7481i -3.6221 -52.7481i -5.5262 +24.9446i -5.5262 -24.9446i 0.0239 + 8.4846i 0.0239 - 8.4846i
Lalu dengan mengasumsikan nilai konstanta, A=-0.0005 B=0.0001 C=0.0001 D=-0.0002 E=0.00032 F=-0.009 G=0.00008 H=0.00001
Maka dengan menggunakan software MATLAB dapat dibuat grafik posisi terhadap waktu. Berikut coding yang menjadi input dalam MATLAB:
syms x t A B C D E F A=-0.0005 B=0.0001 C=0.0001 D=-0.0002 E=0.00032 F=-0.009 G=0.00008 H=0.00001
t=(1:100)/10
x1 = exp(-3.62*t)*(A*sin(52.75*t) + B*cos(52.75*t)) + exp(5.53*t)*
(C*sin(24.94*t) + D*cos(24.94*t)) + exp(0.024*t)*(E*sin(8.48*t) +
F*cos(8.48*t)) + G*sin(43.982*t) + H*cos(43.982*t)
% Plot results
subplot(1,1,1)
hold on;
plot(t',x1,'r')
ylabel('Position (m)')
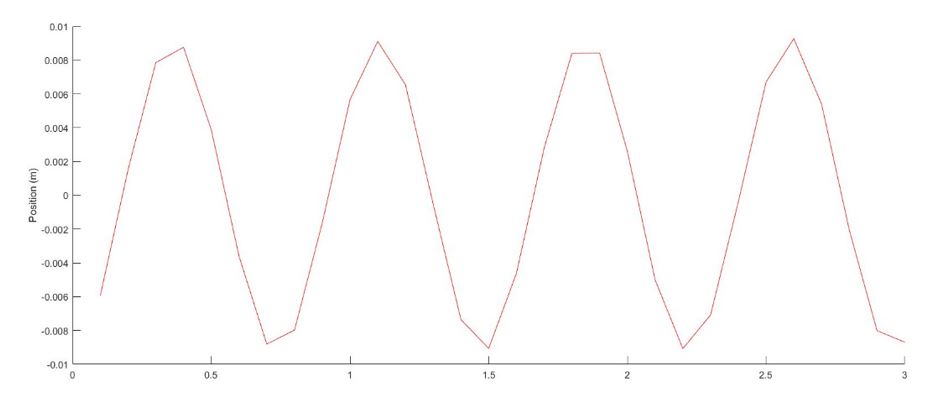
Gambar 5 Grafik respon posisi terhadap waktu
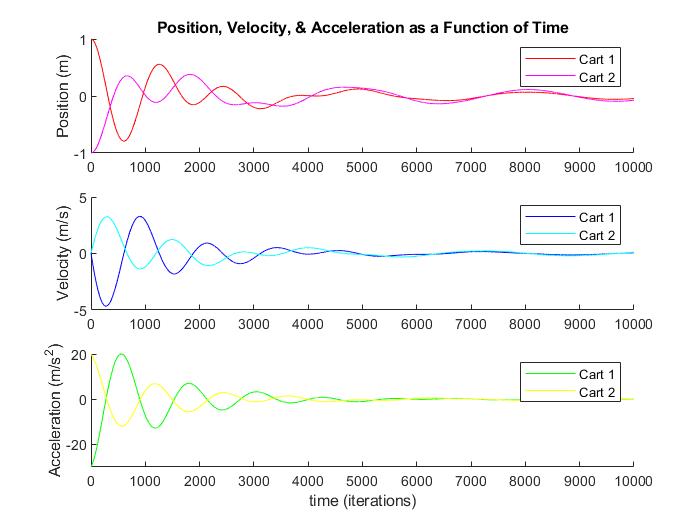
Grafik di atas menunjukan pengaruh getaran pada bagian bawah struktur pemodelan bangunan di mana perubahan arah gerak pada bagian bawah struktur membentuk pola sinusoidal yang menandakan adanya gerak bolak-balik pada struktur tersebut.
Kesimpulan
Dalam permasalahan analisis gerak (perubahan arah, kecepatan dan percepatan) dapat dilakukan dengan metode lain berupa FES, namun pada artikel ini pemodelan FES belum dilakukan. Artikel ini hanya membahan mass-spring (MS) model yang terjadi pada suatu sistem pemodelan bangunan yang diberikan getaran. Sehingga dapat dilihat perilaku gerak bangunan sebagai respon dari adanya getaran yang diberikan.
REFERENSI
• Syaldiles Putri Indahdinata, Analisis Pengaruh Perubahan Cross Sectional Area Dan Posisi Peletakan Tuned Liquid Column Damper Terhadap Respon Dinamis Model Struktur Bangunan Bertingkat, Departemen Teknik Mesin FTI-ITS Surabaya, 2018.
UJIAN AKHIR SEMESTER (8 Juni 2020)
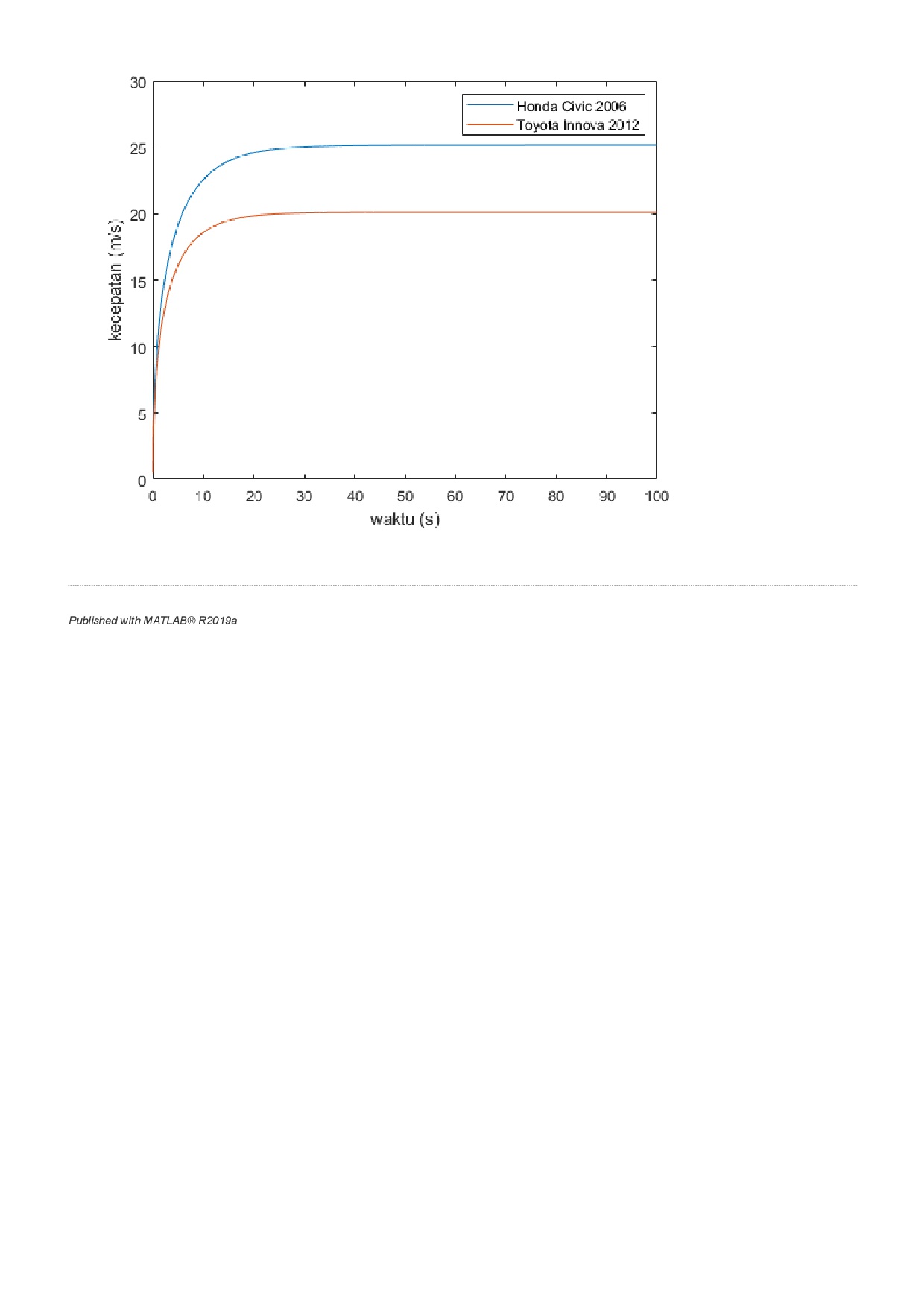
Pada ujian akhir semester komputasi teknik 2020, diberikan persoalan mengenai linear dynamic pada mobil, dengan data yang ditentukan sendiri. Penyelesaiannya dilakukan dengan metode numerik (dalam hal ini diselesaikan dengan metode 4th order Runge-Kutta) dibantu oleh software MATLAB.
END