Difference between revisions of "Apri melianes febri"
(→PERTEMUAN 6) |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 223: | Line 223: | ||
| + | |||
| + | Tugas Initial Value problem | ||
| + | |||
| + | |||
| + | Sebuah truk memiliki posisi awal 0 pada t=0 dan dihitung jarak pada waktu yang diinginkan yaitu pada 0.05 detik. Dengan metode Runge-Kutta dengan cepat kita bisa mendapatkan hasil yang diinginkan hanya dengan memasukkan waktu yang diperlukan untuk setiap pergerakan si mobil truk tersebut, Berikut penyelesaian dengan metode Runge-Kutta : | ||
| + | |||
| + | |||
| + | [[File:IVP cuy.png|500px]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Tugas Boundary Value Problem | ||
| + | |||
| + | |||
| + | Hambatan ini dibatasi oleh kecepatan tertetu yaitu yang saya ambil pada 5 m/s, 6 m/s, 7 m/s, 8 m/s, dan 9 m/s dan didapat regresi berikut ini : | ||
| + | |||
| + | [[File:BVPcuy.png|500px]] | ||
==PERTEMUAN 6== | ==PERTEMUAN 6== | ||
| Line 228: | Line 247: | ||
https://www.youtube.com/channel/UCc6DFXRJHPRFa3XgDVOuoTw?view_as=subscriber | https://www.youtube.com/channel/UCc6DFXRJHPRFa3XgDVOuoTw?view_as=subscriber | ||
| + | |||
| + | |||
| + | Tugas 8 | ||
| + | Optimasi sebuah balok | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Apri optmasi.png|200px]] | ||
| + | |||
| + | ==UTS METODE NUMERIK== | ||
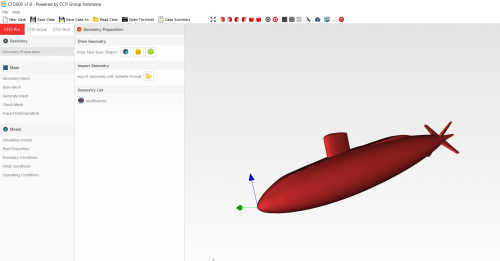
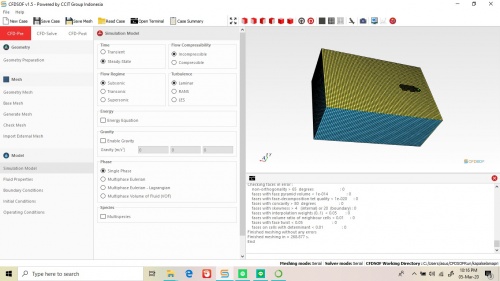
| + | Berikut ini adalah tugas simulasi AUV saya pada Software CFDSOft beserta regresi linearnya. | ||
| + | |||
| + | https://www.youtube.com/watch?v=tA7AIKps9sM&t=304s (part1) | ||
| + | |||
| + | https://www.youtube.com/watch?v=mWCZJtBIp2Q&t=227s (part2) | ||
Latest revision as of 14:48, 24 July 2020
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُFull Name : Apri Melianes Febri
Sex : Male
Place/Date of Birth : Padang, 19 april 1998
Address : wisma dwika jalan mandor goweng n0.65 rt4rw5 kukusan beji depok
Phone No. : 085278069287
email : aprimelianes@gmail.com
programming knowledge: Semasa di sma saya pernah belajar basic pascal. selain itu saya juga bisa MS office dan beberapa aplikasi design yang berhubungan dengan kapal seperti maxsurf dan autocad serta autodesk inventor
Contents
[hide]pertemuan 1
7 februari 2020
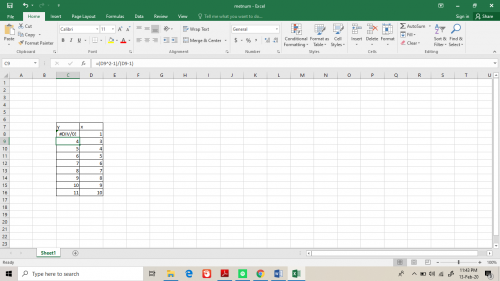
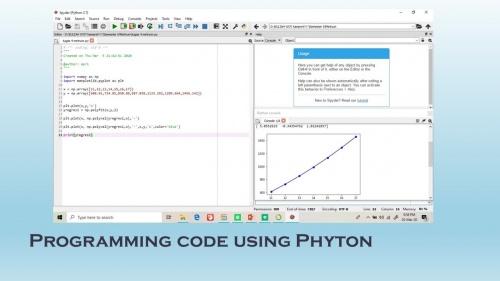
jadi sebelumnya kita diberi tugas oleh Pak dai yaitu membuat fungsi F(x) = x^2-1/x-1 lalu menjalankan fungsi tersebut pada pemograman. pada awalnya saya menggunakan cara manual yaitu dengan menggunakan rumus tersebut pada ms excel. akan tetapi pada nilai x=0, formula tersebut tidak berfungsi dengan baik atau 0/0. oleh sebab itu, fungsi ini diubah dalam bentuk limit agar diapatkan hasil yang mendekati limit.
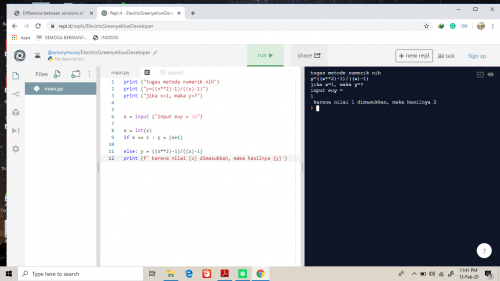
oleh karena itu saya menggunakan formula ini pada aplikasi phyton online yang dapat memproses formula tersebut. terlebih dahulu saya buat bahasa pemograman supaya bisa dijalankan. hasilnya ternyata berhasil ketika x=1 maka hasil y=2. programming ini berhasil.
Pertemuan 2
14 februari 2020
Tugas 2
pada pertemuan kali ini kita diminta oleh pak dai untuk selalu ingat apa tujuan kita belajar metode numerik. hal yang membuat sesorang tidak maju karena KEM( ketidaktahuan egois dan malas). pada pertemuan ini pula kita diminta untuk berlatih pada soal soal yang ada dibuku dan menerapkannya pada software programming phyton.
selain berlatih soal kita juga diajarkan untuk belatih pada bab 7 yaitu initial value problem
Data-informasi-pengetahuan-ilmu yang bermakna-hikmah-hidayah
data= merupakan angka, nama, huruf ata variable yang mempunyai nilai numerik atau karakter. contoh a=1, angka 1, 1 apel
analisis berasal dari
1. Statistikal-- berupa data dsikrit
2. Determinitik-- berupa persamaan differensial
TUgas 2.1
pada tugas 2.1 ini saya memilih soal pada bab 2 yaitu menggunakan metode choleski untuk dekomposisi matrix. sebelumnya disajikan soal dengan sbgai berikut. saya menggunakan metode invers untuk mnegetahui nilai masing masing x pada matriks. ini merupakan cara penyelasaian yang sangat sederhana pada umumnya karena masih tergolong matrix 3x3.
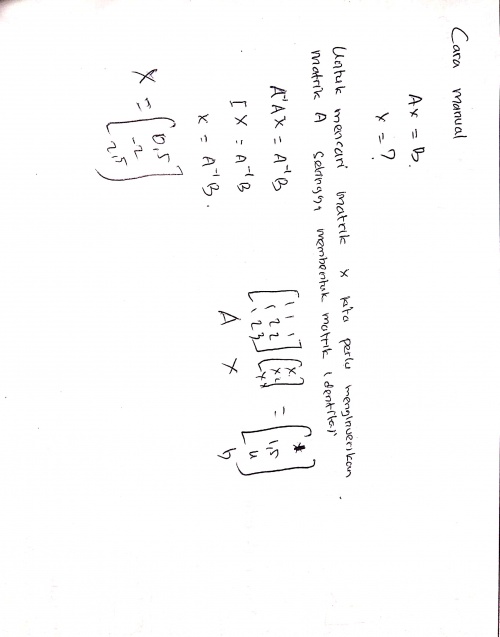
kemudian saya mencoba metode choleski untuk dekomposisi matrix sesuai dengan contoh yang diberikan pada buku. akan tetapi sebelum memulai kodingan terhadap matrixnya, kita perlu membuat kodingan choleskinya dulu pada file yang berbeda. sehingga terbentuklah programing seperti gambar dibawah ini. penggunaan programing ini juga bisa digunakan untuk matrix dengan ukuran 3x3 keatas dan tidak perlu menentukan daerah adjoinnya.
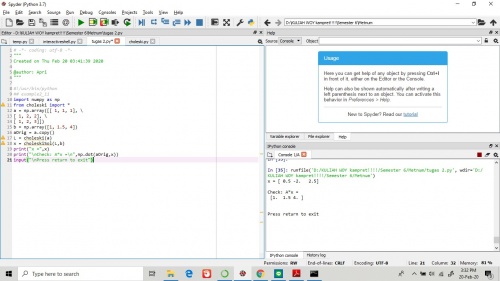
Tugas 2.2
initial value problem
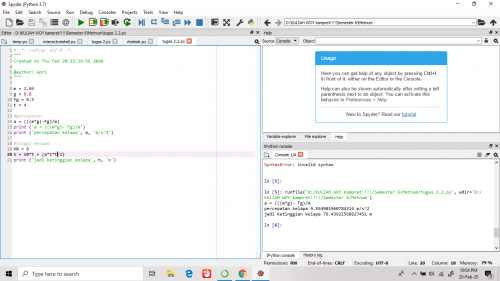
pada tugas 2.2 ini kita diminta oleh pak dai untuk menyelesaikan permasalahan inital value problem. dimana kasus kali ini adalah kita menentukan berapa ketinggian sebuah kelapa dengan data data yang telah disajikan dan hubungannya dengan diferrensial
berikut adalah hasil setelah melakukan kodingan terhadap kasus tersebut.
Tugas 2.3
Asistensi /selasa, 25 februari 2020
tugas 3 inital value problem dengan runge kutta method
Pertemuan 4
28 Februari 2020
Pada Pertemuan kali ini kita belajar mesimulasikan kapal dan menghitung hambatannya pada beberapa kecepatan yang berbeda. Untuk mesimulasikan itu kita menggunakan CFDSOF v1.5 powered by CCIT Group Indonesia
setelah itu kita membuat proses regresi linear dengan menggunakan program phyton(tercantum di laporan asistensi)
Laporan Asistensi
3 Maret 2020
Asisten: Michael Ahli, Teknik Kapal 2017
PERTEMUAN KE 5
pada pertemuan kali ini kita membahas tentang perbedaan initial value problem dan boundary value problem serta contoh kejadiannya
ASISTENSI KE 3
10 MARET 2020
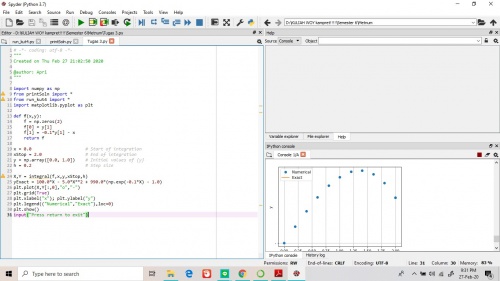
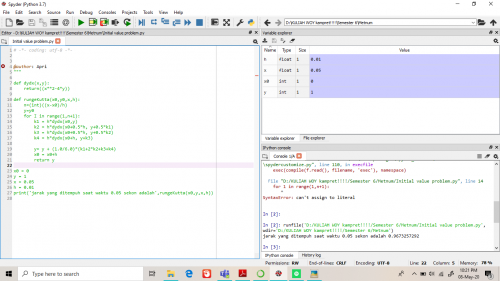
Tugas Initial Value problem
Sebuah truk memiliki posisi awal 0 pada t=0 dan dihitung jarak pada waktu yang diinginkan yaitu pada 0.05 detik. Dengan metode Runge-Kutta dengan cepat kita bisa mendapatkan hasil yang diinginkan hanya dengan memasukkan waktu yang diperlukan untuk setiap pergerakan si mobil truk tersebut, Berikut penyelesaian dengan metode Runge-Kutta :
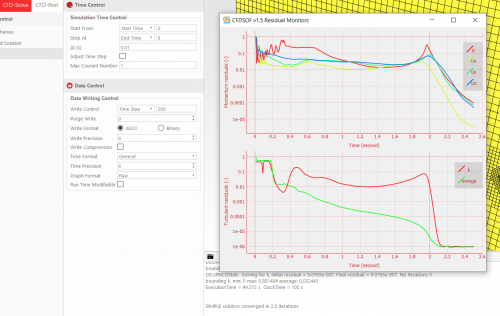
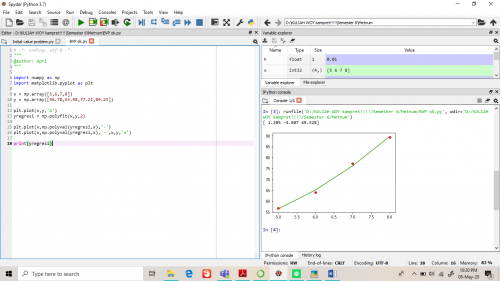
Tugas Boundary Value Problem
Hambatan ini dibatasi oleh kecepatan tertetu yaitu yang saya ambil pada 5 m/s, 6 m/s, 7 m/s, 8 m/s, dan 9 m/s dan didapat regresi berikut ini :
PERTEMUAN 6
TUGAS OPTIMASI
https://www.youtube.com/channel/UCc6DFXRJHPRFa3XgDVOuoTw?view_as=subscriber
Tugas 8
Optimasi sebuah balok
UTS METODE NUMERIK
Berikut ini adalah tugas simulasi AUV saya pada Software CFDSOft beserta regresi linearnya.