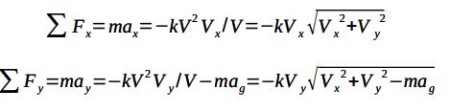Difference between revisions of "Memahami Initial Value dan Boundary Value Problem"
Cheater123an (talk | contribs) |
Saddamabdul (talk | contribs) (→Contoh Kasus dan Penyelesaiannya (Individu)) |
||
| (89 intermediate revisions by 24 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | == Tugas Kolaborasi == |
Bismillah, berikut ini adalah rangkuman dari apa yang sudah kami pelajari mengenai Initial Value dan Boundary Value Problem. | Bismillah, berikut ini adalah rangkuman dari apa yang sudah kami pelajari mengenai Initial Value dan Boundary Value Problem. | ||
| + | == Contoh Kasus dan Penyelesaiannya (Individu) == | ||
| + | 1. Fahmi Aqwa | ||
| − | --- | + | - Initial Value Problem : Menetukan Waktu yang dibutuhkan tandon air untuk terisi pada ketinggian tertentu |
| − | ''' | + | |
| + | - Boundary Value Problem : Pengantaran Panas pada sebuah balok | ||
| + | |||
| + | - Penyelesaiaan : [[Fahmi Aqwa]] | ||
| + | |||
| + | 2. Gigin Rizki Novrian | ||
| + | |||
| + | Initial value problem : | ||
| + | Sebuah gelombang berosilasi dengan persamaan F(x, y) = y"+4yy'^2, jika y(0)=0 maka tentukan nilai y'(0) | ||
| + | |||
| + | Boundary Value Problem : | ||
| + | Sebuah gelombang berosilasi dengan persamaan F(x, y) = y"+4yy'^2, dan y(0)=0 dan y(3)=1, maka y'(0) adalah | ||
| + | |||
| + | Penyelesaian: [[Gigin rizki novrian]] | ||
| + | |||
| + | 3. Sultan Alif Zidane | ||
| + | |||
| + | Initial value problem: | ||
| + | Diketahui persamaan sebuah kecepatan motor y = 100x - 5x^2 + 990(e^-0.1x - 1) jika percepatan y''= -0.1y'-x ; y(0)=0 ; y'(0)=1 | ||
| + | dari x=0 to 2 dan menggunakan metode euler h=0.05 | ||
| + | |||
| + | Boundary value problem: | ||
| + | Sebuah prototipe kapal selam yang memiliki bentuk seperti kapal selam uss albacore memiliki kecepatan yang beragam. Berapakah hambatan yang diterima kapal jika kecepetannya berkisar antara 11 m/s-15 m/s | ||
| + | |||
| + | Penyelesaian: [[Sultan alif zidane]] | ||
| + | |||
| + | 4. Muhammad Attaritsabitsah Gibran | ||
| + | |||
| + | - Initial Value Problem : Menentukan gaya sebuah pegas | ||
| + | |||
| + | - Boundary Value Problem : Menentukan drag pada objek rudal air | ||
| + | |||
| + | Penyelesaian : [[Muhammad Attaritsabitsah Gibran]] | ||
| + | |||
| + | 5. Naufal Aziz Putra | ||
| + | |||
| + | - Intial Value Problem : Menghitung kecepatan Pesawat Ketika Jatuh | ||
| + | |||
| + | - Boundary Value Problem : Hambatan udara pada sebuah mobil | ||
| + | |||
| + | Penyelesaian : [[Naufal Aziz Putra]] | ||
| + | |||
| + | 6. Vinia Permata Kusuma | ||
| + | - Initial Value: Penyelesaian pada hambatan loop listrik | ||
| + | |||
| + | - Boundary Value Problem : hambatan kapal selam pada 3 kecepatn yaitu, 11,13, dan 15 m/s | ||
| + | |||
| + | Penyelesaian : [[Vinia Permata Kusuma]] | ||
| + | |||
| + | 7. Mochammad Afrinaldi | ||
| + | |||
| + | - Initial Value Problem : penyelesaian persamaan fungsi turunan pada getaran nonlinear | ||
| + | |||
| + | - Boundary Value Problem : menentukan percepatan pada kapal dengan waktu tertentu | ||
| + | |||
| + | Penyelesaian : [[Mochammad afrinaldi]] | ||
| + | |||
| + | 8. Ferdy Yacobus Santoso | ||
| + | |||
| + | - Initial Value Problem : penyelesaian osilasi | ||
| + | |||
| + | - Boundary Value Problem : penyelesaian untuk mencari knots kapal | ||
| + | |||
| + | Penyelesaian : [[Ferdy yacobus santoso]] | ||
| + | |||
| + | 9. Niyar Nurfarikhah | ||
| + | |||
| + | - Initial Value Problem : Menetukan Waktu yang dibutuhkan mengisi ember untuk terisi pada kecepatan dan ketinggian tertentu | ||
| + | |||
| + | - Boundary Value Problem : Menghitung Hambatan kapal selam pada kecepatan 11 sampai 15 | ||
| + | |||
| + | Penyelesaian : [[Niyar Nurfarikhah]] | ||
| + | |||
| + | 10. Saddam Abdul Azziz | ||
| + | |||
| + | - Initial Value Problem : menentukan ketinggian sebuah apel yang jatuh dari pohon setinggi 800m pada waktu t = 5s | ||
| + | |||
| + | - Boundary Value Problem : mencari hambatan sebuah kapal selam pada kecepatan 16 m/s hingga 20 m/s | ||
| + | |||
| + | Penyelesaian : [[Saddam abdul azziz]] | ||
| + | |||
| + | == Definisi == | ||
[[File:Fotoinj.jpeg|500px|thumb|left]] | [[File:Fotoinj.jpeg|500px|thumb|left]] | ||
| − | + | [[File:Boundary_and_initial_value.PNG|500px|thumb|left|penggambaran singkat boundary dan initial value]] | |
| + | |||
| + | '''Boundary value problem''' memiliki kondisi yang ditentukan oleh suatu variabel independen dalam persamaan sedangkan pada initial value problem memiliki semua kondisi awal yang ditentukan pada nilai yang sama demi mendapatkan hasil secara spesifik yang diinginkan. untuk contoh penggunaan pada boundary value problem seperti pada persamaan gelombang ataupun komputasi yang hampir mendekati tak hingga. Sedangkan pada '''initial value problem''' suatu permasalahan dengan kondisi jelas demi mendaptkan suatu hasil kondisi sesuai dengan keadaan awal tersebut. | ||
| + | |||
| + | Singkatnya, Initial value problem adalah masalah yang memiliki nilai awal, yang ingin dicari batasnya hingga kembali ke posisi semula atau mencapai nilai maksimum. Kemudian dengan modal nilai awal tersebut dapat dihasilkan satu solusi. boundary value problem adalah persoalan yang memiliki nilai batas, jadi suatu permasalahan yang sebenarnya infinit dapat diperhitungkan dengan batasan batasan yang ada. Karena banyak variasi nilai yang kita ambil, solusi yang didapatkan bisa saja bervariasi. | ||
| + | |||
| + | Initial Value Problem itu adalah penyelesaian suatu kondisi masalah yang di ukur dari tinjauan yang sama. Sementara, Boundary Value Problem adalah penyelesaian suatu kondisi masalah yang diukur dari tinjauan berbeda. | ||
| + | |||
| + | Intial Value Problems tidak perlu menentukan nilai pada batas, melainkan membutuhkan nilai selama kondisi awal. Ini biasanya berlaku untuk sistem dinamis yang berubah seiring waktu seperti dalam Fisika. Pada initial value problems, diberikan fungsi nilai yaitu: | ||
| + | |||
| + | y(x)y(x) dan turunannya yaitu y′(x)y′(x) pada ( initial point ). | ||
| + | |||
| + | Pada x=0x=0 i.e y(0)=xi1y(0)=xi1 dan y′(0)=x2y′(0)=x2. | ||
| + | |||
| + | Sedangkan Boundary Value Problems adalah sebaliknya. Boundary value problems tidak selalu digunakan untuk sistem dinamis. Sebaliknya, ini sangat berguna untuk sistem yang memiliki batas ruang. | ||
| + | Pada boundary value problems, fungsi nilainya yaitu: | ||
| + | |||
| + | y(x)y(x) di titik yang berbeda i.e y(a)=x1y(a)=x1 and y(b)=x2y(b)=x2. | ||
| + | |||
| + | Jadi secara jelas perbandingan rumus dari initial dan boundary adalah | ||
| + | |||
| + | Initial Value Problem : | ||
| + | |||
| + | Masalah yang memiliki nilai awal, F(x,y) , y’(a),y(a) yang memiliki fungsi x dan y yang berbeda. | ||
| + | Contoh: mencari nilai kecepatan awal pada benda yang jatuh bebas | ||
| + | |||
| + | Boundary Value Problem : | ||
| + | |||
| + | Digunakan dalam mencari nilai yang ditentukan oleh batas yang diinginkan sendiri, F(x,y) , y(a) , y(b) yang memiliki fungsi x berbeda dan y sama. | ||
| + | Contoh: mencari nilai hambatan pada kapal selam | ||
| + | |||
| + | |||
| + | Contoh pada suatu akselerasi itu merupakan turunan dari fungsi kecepatan dan kecepatan sediri turunan dari fungsi posisi. Jadi dari posisi kita bisa kembangkan menjadi suatu percepatan, hal itu disebut '''initial value problem'''. Sedangkan boundary value itu menyelesaikan masalah yg unlimited dengan batasan-batasan yang diketahui. Contohnya hambatan kapal dan kecepatan kapal yg kita cari pakai CFD, itu fluida yg kita gunakan adalah air laut dan luasnya unlimited. Tapi kita hanya fokus pada fluida yg nyentuh kapalnya | ||
| + | Boundary Value Problem merupakan sistem persamaan diferensial dengan penyelesaian dan nilai penurunan yang spesifik lebih dari satu fokus, Biasanya, penyelesaian dan penurunan ditunjukan hanya untuk dua titik (the boundaries) yang menjelaskan sebuah two-point value problems (Ian Gladwell, scholarpedia.org) | ||
| + | Initial Problem ditunjukan untuk penyelesaian pada initial condition y(t0)=A, Penyelesaian mengharapkan bahwa F(t,y) akan terus lanjut pada bagian yang melibatkan A dan turunan sebagian ∂Fi/∂yj yang terikat, dengan asumsi dimana initial value problem memilki penyelesaian | ||
| + | Boundary Value Problem menujukan penyelesaian, dengan memperlihatkan kondisi lebih dari satu titik, Blasius Problem merupakan persamaan diferensial y‴=−yy″/2 dengan adanya boundary condition y(0)=0,y′(0)=0,y′(∞)=1 (Vita Puspita) | ||
| − | + | IVB tidak perlu menentukan nilai pada batas, melainkan membutuhkan nilai selama kondisi awal. Ini biasanya berlaku untuk sistem dinamis yang berubah seiring waktu seperti dalam Fisika. Contoh, untuk menyelesaikan posisi partikel dalam persamaan diferensial, kita memerlukan posisi awal dan juga kecepatan awal. Tanpa nilai awal ini, kita tidak dapat menentukan posisi akhir dari persamaan. | |
| − | |||
| − | + | BVB : Sebaliknya, masalah nilai batas tidak selalu digunakan untuk sistem dinamis. Sebaliknya, ini sangat berguna untuk sistem yang memiliki batas ruang. Contohnya adalah bentuk dari masalah bayangan dalam visi komputer. Untuk menentukan gradien permukaan dari PDE, kita harus memaksakan nilai batas pada wilayah yang diinginkan. | |
| − | |||
| − | + | Masalah nilai awal adalah masalah yang terkait dengan kondisi awal pertanyaan dan tidak ada batasan yang digunakan. Sementara masalah boundry vaue adalah masalah di mana batas digunakan yaitu interval diberikan | |
| − | |||
| − | + | == Perbedaan == | |
| − | |||
| − | + | ===Initial Value Problems=== | |
| − | 1. | + | 1. Bila nilai variabel tak bebas atau turunannya diketahui pada kondisi nilai mula-mula. |
2. Hanya memiliki satu penyelesaian. | 2. Hanya memiliki satu penyelesaian. | ||
| − | 3. | + | 3. Merupakan penggambaran pada suatu fungsi persamaan dan turunan fungsi persamaan. Contohnya bisa berupa jarak, kecepatan, maupun percepatan |
| + | |||
| + | 4. Memiliki indikator awal yang digunakan untuk mencari hasil penyelesaiannya. | ||
| + | |||
| + | 5. Masalah nilai awal tidak perlu menentukan nilai pada batas, melainkan membutuhkan nilai selama kondisi awal, biasanya digunakan pada sistem dinamis | ||
| + | |||
| + | 6. Initial Value problem dilakukan pada operasi yang tidak memiliki batas, tidak ada nilai maksimal didalamnya, selama ada kenaikan variabel bebas, juga akan mengalami perubahan variabel terikat | ||
| + | |||
| + | 7. Initial value problem itu diketahui semua kondisi awalnya | ||
| + | f(xo) =... | ||
| + | f’(xo)=... | ||
| + | F(x,y)=... | ||
| − | + | 8. suatu masalah dengan kondisi atau suatu ketetapan yang sudah tentukan (hanya satu ketetapan). | |
| − | + | ===Boundary Value Problems=== | |
| + | 1. Bila nilai variabel tak bebas atau turunannya diketahui lebih dari satu nilai variabel bebasnya | ||
2. Memiliki lebih dari satu kemungkinan solusi | 2. Memiliki lebih dari satu kemungkinan solusi | ||
| Line 42: | Line 168: | ||
4. Merupakan variabel bebas yang berfungsi sebagai batasan pada fungsi persamaan. Contohnya seperti variabel waktu sebagai batasan jarak, kecepatan, atau percepatan | 4. Merupakan variabel bebas yang berfungsi sebagai batasan pada fungsi persamaan. Contohnya seperti variabel waktu sebagai batasan jarak, kecepatan, atau percepatan | ||
| − | |||
| − | |||
| − | + | 5. BVP tidak digunakan pada sistem dinamis, melainkan pada sistem yang memiliki batas ruang | |
| + | |||
| + | 6. Boundary Value Problem dilakukan pada sistem yang memiliki batas, biasanya dalam bentuk batas minimal atau maksimal | ||
| + | |||
| + | 7. Kalau boundary diketahui kondisi pada sebuah boundary | ||
| + | f(xo)=... | ||
| + | f(x1)=... | ||
| + | F(x,y)=.... | ||
| + | |||
| + | 8. Suatu masalah dengan kondisi penyelesaian suatu masalah dengan berbagai kondisi atau berbagai ketetapan. | ||
| + | |||
| + | == Aplikasi Pada Submarine == | ||
| + | |||
| + | ===Aplikasi Initial Value Problems=== | ||
| + | |||
| + | *Bagaimana kapal selam bisa tenggelam pada suatu kedalaman | ||
| + | |||
| + | *Ketika tenaga dari mesin kapal selam tidak sesuai dengan laju yang dihasilkan, ini terjadi karena ada nya pengaruh dari viskositas air pada daerah pelayaran kapal selam | ||
| + | |||
| + | *Bagaimana kapal selam mampu bergerak dengan kecepatan tertentu ketika badan kapal berbentuk silindris. | ||
| + | |||
| + | *Pada suatu kapal selam dikeatahui kondisi awalnya, lalu kemudian melakukan pergerakan hingga mencapai kecepatan optimumnya. | ||
| + | |||
| + | *Bila diketahui submarine dengan kecepatan awal v, kemudian kita bisa mencari atau memprediksi kecepatan saat waktu t. Dengan mempertimbangkan nilai gaya hambatan air yang telah diketahui pula, maka didapatkan kecepatan akhir saat waktu t yang diinginkan. | ||
| + | |||
| + | *Kapal selam mengalami initial value problem disaat kapal tersebut tidak mendapatkan pengaruh gaya apapun dari luar kapal selam tsb. karena pengaruh dari luar dapat banyak hasil seperti gelombang, hewan laut yang menempel itu semua pengaruh dari luar kapal yang menyebabkan hambatan pada kapal banyak faktornya, initial value problem tidak dapat mendapatkan hasil lebih dari 1. Initial value problem, contoh yang terjadi pada kapal selam adalah ketika tenaga dari mesin kapal selam tidak sesuai dengan laju yang dihasilkan, ini terjadi karena ada nya pengaruh dari viskositas air pada daerah pelayaran kapal selam | ||
| + | |||
| + | *Kapal salam yang awalnya diam kemudian melaju kedepan dengan kecepatan yang telah ditentukan maka kita bisa mengetahui berapa jarak yang ditempuh oleh kapal selam | ||
| + | |||
| + | *Submarine bergerak misalkan selama waktu yang di tentukan, lalu dari waktu tersebut kita mendapatkan jarak dan kecepatan akhir dari submarine tersebut, contoh= Kapal bergerak percepatan 1m/s, tentukan kecepatan kapal dan jarak yang di tempuh ketika kapal sudah berjalan selama 30 detik. | ||
| + | |||
| + | *Initial value dapat digunakan untuk mencari persamaan seperti perubahan kecepatan, kedalaman kapal selam, dan perubahan properties fluida kerja. | ||
| + | |||
| + | *Diharapkan untuk mencari nilai kecepatan kapal ketika di laut natuna dan kecepatan kapal di laut antartika adalah 10. y = x^2 + 100. Maka, x adalah lebar dari lautanya. | ||
| + | |||
| + | *Drag dari submarine pada kecepatan tertentu (misalnya hanya pada v = 11m/s) | ||
| + | |||
| + | *Kapal selam melakukan operasi pergi ke suatu tempat, kapal selam berjalan dari posisi x pada t = 0 dan diketahui kecepatan v pada t=0. dari data tersebut kita dapat mengetahui posisi akhir dari persamaan yang didapat dari F(x,v,t) | ||
| + | |||
| + | *Pada Kapal selam initial value problem terletak pada fungsi posisi, kecepatan dan waktu | ||
| + | |||
| + | *Mencari drag dari submarine pada 3 kecepatan yang berbeda | ||
| + | |||
| + | ===Aplikasi Boundary Value Problem=== | ||
| + | |||
| + | [[File:Submarine.jpeg]] | ||
| + | |||
| + | *Bagaimana kapal selam dapat tenggelam pada kecepatan, waktu dan kondisi tertentu. | ||
| + | |||
| + | *Bagaimana tekanan dapat mempengaruhi perlakuan badan kapal. Apa efek yang terjadi ketika semakin dalam kapal menyelam. | ||
| + | |||
| + | *Kapal selam bergerak didalam laut mengalami kecepatan penyelaman sepersekian m/s berapakah kedalaman yang dicapai kapal selam dalam waktu 15 menit. Kecepatan penyelaman dapat divariasikan sesuai keinginan operator | ||
| + | |||
| + | *Pada submarine dapat diambil dari spesimen yang berdekatan dengan plat submarine tersebut. Dengan melihat batas-batas tersebut, kemudian didapatkan nilai dan perilaku yang berbeda setiap spesimen. Maka dari itu nilai-nilai tersebut dapat menghasilkan banyak solusi yang beragam/banyak. Solusi yang banyak tersebut bersifat unik satu sama lain. | ||
| + | |||
| + | *Dalam kasus gerak kapal selam, banyak aturan tambahan atau boundary conditions yang berlaku. Salah satunya adalah ukuran geometri dan bentuk hull dari kapal selam yang mempengaruhi karakteristik dan motion kapal selam. Contoh yang kedua yakni adalah komponen hydroplane yang tersusun pada bagian after body kapal selam, sehingga untuk mencapai karakteristik yang baik diperlukan perancangan ulang sistem kendali hydroplane. Perhitungan ini sendiri termasuk ke dalam Boundary Value Problem, dan perhitungan gaya hidrodinamika dan momen kapal selam tersebut dapat dilakukan secara numerik dengan menggunakan cfdsoft. | ||
| + | |||
| + | *Kapal selam tersebut mendapat gaya dari luar kapal. Mengapa demikian disaat kondisi tambahan itu ada maka hasil yang akan keluar juga akan banyak. karena hasil dari boundary value problem itu bisa lebih dari 1. | ||
| + | |||
| + | *Pada suatu kapal yang memiliki kecepatan tertentu kita dapat menentukan besaran hambatan kapal yang dialami oleh badan kapal selam tersebut | ||
| + | |||
| + | *Perubahan hambatan/drag force dari setiap kecepatan submarine tersebut, misalkan menentukan hambatan pada saat kecepatan 5m/s sampai dengsn 10m/s. sehingga variable x dalam permasalahan ini adalah kecepatan dari kapal selam tersebut. | ||
| + | |||
| + | *Sebuah kapal selam naik ke permukaan dengan kecepatan 10km/jam; kenaikan 2m/s; pada sudut 20 derajat. Kapal awalnya berada pada kedalaman 150m. Boundary value dapat digunakan untuk mencari nilai hambatan yang dihasilkan oleh kapal selam tersebut. | ||
| + | |||
| + | *Kapal selam yang memiliki hambatan atau tekanan yang terjadi pada kapal yang bervariasi. Untuk menentukan gradien permukaan dari PDE, kita harus memaksakan nilai batas pada wilayah yang diinginkan. Contoh batas nya adalah jumlah air yang tercelup mengenai kapal selam. Contoh kasus, untuk menyelesaikan posisi kapal selam dalam persamaan diferensial, kita memerlukan posisi awal dan juga kecepatan awal. Tanpa nilai awal ini, kita tidak dapat menentukan posisi akhir dari persamaan. | ||
| − | + | *Drag dari submarine dari berbagai variasi kecepatan. Maka dari itu tugas kita adalah membuat regresi dari hubungan hambatan (drag) dengan variasi kecepatan yang telah kita tentukan sebelumnya. Karena realitanya nanti di dunia kerja, kebanyakan masalah yang kita selesaikan adalah menurut berbagai tinjauan atau ukuran dan kita tentukan sendiri batasnya (boundary nya). | |
| − | |||
| − | + | *Kapal selam melakukan operasi pergi ke suatu tempat, kapal selam berjalan dari posisi x pada t = 0 dan diketahui kecepatan v pada t=0. kemudian diketahui pada jarak x t=10 kapal selam sudah mencapai kecepatan maksimal v pada t=10. kita dapat menentukan nilai kecepatan dan jarak dari batas-batas tersebut, selama ada didalam operasi | |
| − | |||
| − | + | *Kapal selam nilai boundary value problem terletak pada besar nilai froude number kapal pada kecepatan awal kapal selam, sampai kecepatan normal | |
| − | + | == Contoh Kasus Lain == | |
| − | |||
| − | |||
| − | + | === Initial value problem === | |
| − | |||
| − | + | *Mengukur posisi bola baseball pada waktu tertentu dan diketahui kecepatan awalnya | |
| − | + | *Mengukur posisi benda yang mengalami jatuh bebas dengan atau tanpa gaya hambatan udara dan mencari posisi jatuhnya benda tersebut terhadap perubahan waktu yang terjadi berdasarkan keadaan awal yang telah ditentukan. - Miftah D.F. | |
| − | + | *sistem redam pada pegas berdasarkan oleh konstanta, massa, dan gaya | |
| − | |||
| − | + | *menghitung loop pad listrik | |
| − | |||
| − | |||
| − | + | *Mobil bergerak dengan kecepatan tertentu | |
| − | + | *Untuk menghitung panjang lintasan bisbol yang dilempar dari bidang tengah lapangan bisbol ke home asumsikan bahwa outfielder melepaskan bola delapan meter di atas tanah dan bisbol yang memiliki kecepatan awal yang memiliki sudut = dengan horizontal.ingatlah bahwa perjalanan bisbol melalui udara, udara akan menyebabkan gaya gesek pada bola menentang kecepatan bola. Kekuatan tarik dapat ditunjukkan bervariasi dengan kuadrat kecepatan. Keseimbangan gaya pada bola di kedua arah x dan y hasil dalam | |
| − | |||
| − | |||
| − | * | + | *Suatu sepeda motor bergerak dari keadaan diam hingga mencapai jarak 100 meter dalam waktu 10 detik, berapa kecepatan motor tersebut |
| − | |||
| − | * | + | *Sebuah robot lengan otomatis melempar jarum dart menuju papan target di tengah dengan jarak, energi, dan masssa dart yang telah diperhitungkan (percobaan dilakukan diruang dimana hambatan udara tidak mempengaruhi jarum dart) |
| − | |||
| − | + | [[file:Capture2.JPG|450px|]] | |
| − | |||
| − | + | [[file:Capture.JPG|450px|]] | |
| − | + | *Diketahui persamaan y = 100x - 5x^2 + 990(e^-0.1x - 1) jika y''= -0.1y'-x ; y(0)=0 ; y'(0)=1 | |
| + | dari x=0 to 2 dan menggunakan metode euler h=0.05 | ||
| − | + | *Untuk menghitung panjang lintasan bisbol yang dilempar dari bidang tengah lapangan ke outfielder dengan kecepatan dan sudut horizontal yang ditentukan (Vita P) | |
| + | *posisi partikel dalam persamaan diferensial, kita memerlukan posisi awal dan juga kecepatan awal. Tanpa nilai awal ini, kita tidak dapat menentukan posisi akhir dari persamaan. x(0) dan v(0) | ||
| − | + | *Mengukur waktu tempuh sepeda motor dengan diketahui jarak dan kecepatan | |
| − | |||
| − | |||
| − | |||
| − | Boundary value problem | + | === Boundary value problem === |
| − | |||
| + | [[File:IVP111.PNG|400px|thumb|contoh initial value problem sumber:numerical methods in engineering with python jaan kiusalaas.|right]] | ||
| − | + | [[File:BVP222.PNG|400px|thumb|contoh initial value problem sumber:numerical methods in engineering with python jaan kiusalaas.|right]] | |
| − | |||
| + | *Menghitung kondisi besar hambatan gelombang pada kecepatan tinggi dan rendah | ||
| − | + | *'''Kondisi batas Dirichlet'''. Dalam mekanika fluida komputasi, kondisi batas Dirichlet klasik terdiri dari nilai kecepatan dan/atau tekanan yang akan diambil oleh set node tertentu. Adalah umum untuk merujuk pada beberapa kondisi seperti, (1)slip boundary condition: kecepatan normal ke batas diatur ke nol, sedangkan kecepatan paralel ke batas dibiarkan bebas (2)no-slip boundary condition: kecepatan normal ke batas dan paralel kecepatan ke batas ditetapkan sama dengan nol. | |
| − | + | *Mobil bergerak menuju ke tempat tujuan dengan waktu, kondisi dan kecepatan yang berbeda | |
| − | |||
| − | |||
| − | + | *Menghitung kondisi drag balok yang mengalami pendinginan agar mengetahui nilai kecepatan pendinginan perbagian dari balok tersebut - Miftah DF. | |
| − | |||
| − | |||
| − | + | *'''Hydrofoil pada kapal'''. Hydrofoil adalah sebuah penerapan foil pada lambung sebuah kapal. Hydrofoil menghasilkan gaya lift yang mengangkat lambung kapal tersebut keluar dari permukaan air. Gaya lift tersebut harus lebih besar dari gaya berat kapal tersebut, dan gaya lift tersebut hanya akan dihasilkan ketika kapal mencapai kecepatan/velocity tertentu. Kasus ini adalah sebuah boundary value problem karena adanya boundary conditions dari kasus tersebut, yang menghasilkan hasil yang berbeda beda dari tiap hydrofoil tergantung dari bentuk geometri dan ukuran foil tersebut. | |
| − | |||
| − | + | *Seseorang melempar jarum dart dengan tingkat keakurasian sebesar 0.83 per jarak 100m | |
| − | |||
| − | + | *Sebuah torpedo yang memiliki bentuk seperti kapal selam uss albacore memiliki kecepatan yang beragam. Berapakah hambatan yang diterima kapal jika kecepetannya berkisar antara 11 m/s-15 m/s | |
| − | |||
| − | + | *Software test, dengan menggunakan boundary value problem yang dimana menggunakan nilai maksimun dan nilai minimun untuk mendapatkan nilai valid. (Vita Puspita) | |
| − | + | *G (0) = 0, G '(0) = 0 I, C (kondisi awal). G (2) = 4, G '(1) = 3 B, C (Kondisi batas) | |
| − | + | *Gaya Drag pada airfoil | |
| − | |||
| − | + | == Manfaat == | |
| − | |||
| − | + | *Agar kita dapat mengelompokkan masalah sesuai dengan salah satu dari dua pilihan tersebut sehingga kita dapat lebih efektif dan efisien dalam mengerjakan masalah. | |
| − | + | *Agar kita mengenal lebih jauh atas indahnya ciptaan sang pencipta, kemudian kita dapat bersyukur. | |
| − | |||
| − | |||
| − | |||
---- | ---- | ||
| − | |||
| − | + | ||
| + | |||
| + | Kembali ke halaman [[Kelas Metode Numerik Teknik Perkapalan 2020]] | ||
Latest revision as of 19:18, 22 March 2020
Contents
Tugas Kolaborasi
Bismillah, berikut ini adalah rangkuman dari apa yang sudah kami pelajari mengenai Initial Value dan Boundary Value Problem.
Contoh Kasus dan Penyelesaiannya (Individu)
1. Fahmi Aqwa
- Initial Value Problem : Menetukan Waktu yang dibutuhkan tandon air untuk terisi pada ketinggian tertentu
- Boundary Value Problem : Pengantaran Panas pada sebuah balok
- Penyelesaiaan : Fahmi Aqwa
2. Gigin Rizki Novrian
Initial value problem : Sebuah gelombang berosilasi dengan persamaan F(x, y) = y"+4yy'^2, jika y(0)=0 maka tentukan nilai y'(0)
Boundary Value Problem : Sebuah gelombang berosilasi dengan persamaan F(x, y) = y"+4yy'^2, dan y(0)=0 dan y(3)=1, maka y'(0) adalah
Penyelesaian: Gigin rizki novrian
3. Sultan Alif Zidane
Initial value problem: Diketahui persamaan sebuah kecepatan motor y = 100x - 5x^2 + 990(e^-0.1x - 1) jika percepatan y= -0.1y'-x ; y(0)=0 ; y'(0)=1 dari x=0 to 2 dan menggunakan metode euler h=0.05
Boundary value problem: Sebuah prototipe kapal selam yang memiliki bentuk seperti kapal selam uss albacore memiliki kecepatan yang beragam. Berapakah hambatan yang diterima kapal jika kecepetannya berkisar antara 11 m/s-15 m/s
Penyelesaian: Sultan alif zidane
4. Muhammad Attaritsabitsah Gibran
- Initial Value Problem : Menentukan gaya sebuah pegas
- Boundary Value Problem : Menentukan drag pada objek rudal air
Penyelesaian : Muhammad Attaritsabitsah Gibran
5. Naufal Aziz Putra
- Intial Value Problem : Menghitung kecepatan Pesawat Ketika Jatuh
- Boundary Value Problem : Hambatan udara pada sebuah mobil
Penyelesaian : Naufal Aziz Putra
6. Vinia Permata Kusuma - Initial Value: Penyelesaian pada hambatan loop listrik
- Boundary Value Problem : hambatan kapal selam pada 3 kecepatn yaitu, 11,13, dan 15 m/s
Penyelesaian : Vinia Permata Kusuma
7. Mochammad Afrinaldi
- Initial Value Problem : penyelesaian persamaan fungsi turunan pada getaran nonlinear
- Boundary Value Problem : menentukan percepatan pada kapal dengan waktu tertentu
Penyelesaian : Mochammad afrinaldi
8. Ferdy Yacobus Santoso
- Initial Value Problem : penyelesaian osilasi
- Boundary Value Problem : penyelesaian untuk mencari knots kapal
Penyelesaian : Ferdy yacobus santoso
9. Niyar Nurfarikhah
- Initial Value Problem : Menetukan Waktu yang dibutuhkan mengisi ember untuk terisi pada kecepatan dan ketinggian tertentu
- Boundary Value Problem : Menghitung Hambatan kapal selam pada kecepatan 11 sampai 15
Penyelesaian : Niyar Nurfarikhah
10. Saddam Abdul Azziz
- Initial Value Problem : menentukan ketinggian sebuah apel yang jatuh dari pohon setinggi 800m pada waktu t = 5s
- Boundary Value Problem : mencari hambatan sebuah kapal selam pada kecepatan 16 m/s hingga 20 m/s
Penyelesaian : Saddam abdul azziz
Definisi
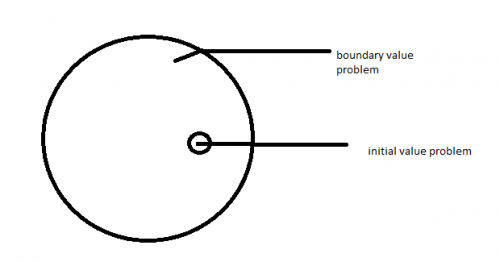
Boundary value problem memiliki kondisi yang ditentukan oleh suatu variabel independen dalam persamaan sedangkan pada initial value problem memiliki semua kondisi awal yang ditentukan pada nilai yang sama demi mendapatkan hasil secara spesifik yang diinginkan. untuk contoh penggunaan pada boundary value problem seperti pada persamaan gelombang ataupun komputasi yang hampir mendekati tak hingga. Sedangkan pada initial value problem suatu permasalahan dengan kondisi jelas demi mendaptkan suatu hasil kondisi sesuai dengan keadaan awal tersebut.
Singkatnya, Initial value problem adalah masalah yang memiliki nilai awal, yang ingin dicari batasnya hingga kembali ke posisi semula atau mencapai nilai maksimum. Kemudian dengan modal nilai awal tersebut dapat dihasilkan satu solusi. boundary value problem adalah persoalan yang memiliki nilai batas, jadi suatu permasalahan yang sebenarnya infinit dapat diperhitungkan dengan batasan batasan yang ada. Karena banyak variasi nilai yang kita ambil, solusi yang didapatkan bisa saja bervariasi.
Initial Value Problem itu adalah penyelesaian suatu kondisi masalah yang di ukur dari tinjauan yang sama. Sementara, Boundary Value Problem adalah penyelesaian suatu kondisi masalah yang diukur dari tinjauan berbeda.
Intial Value Problems tidak perlu menentukan nilai pada batas, melainkan membutuhkan nilai selama kondisi awal. Ini biasanya berlaku untuk sistem dinamis yang berubah seiring waktu seperti dalam Fisika. Pada initial value problems, diberikan fungsi nilai yaitu:
y(x)y(x) dan turunannya yaitu y′(x)y′(x) pada ( initial point ).
Pada x=0x=0 i.e y(0)=xi1y(0)=xi1 dan y′(0)=x2y′(0)=x2.
Sedangkan Boundary Value Problems adalah sebaliknya. Boundary value problems tidak selalu digunakan untuk sistem dinamis. Sebaliknya, ini sangat berguna untuk sistem yang memiliki batas ruang. Pada boundary value problems, fungsi nilainya yaitu:
y(x)y(x) di titik yang berbeda i.e y(a)=x1y(a)=x1 and y(b)=x2y(b)=x2.
Jadi secara jelas perbandingan rumus dari initial dan boundary adalah
Initial Value Problem :
Masalah yang memiliki nilai awal, F(x,y) , y’(a),y(a) yang memiliki fungsi x dan y yang berbeda. Contoh: mencari nilai kecepatan awal pada benda yang jatuh bebas
Boundary Value Problem :
Digunakan dalam mencari nilai yang ditentukan oleh batas yang diinginkan sendiri, F(x,y) , y(a) , y(b) yang memiliki fungsi x berbeda dan y sama. Contoh: mencari nilai hambatan pada kapal selam
Contoh pada suatu akselerasi itu merupakan turunan dari fungsi kecepatan dan kecepatan sediri turunan dari fungsi posisi. Jadi dari posisi kita bisa kembangkan menjadi suatu percepatan, hal itu disebut initial value problem. Sedangkan boundary value itu menyelesaikan masalah yg unlimited dengan batasan-batasan yang diketahui. Contohnya hambatan kapal dan kecepatan kapal yg kita cari pakai CFD, itu fluida yg kita gunakan adalah air laut dan luasnya unlimited. Tapi kita hanya fokus pada fluida yg nyentuh kapalnya
Boundary Value Problem merupakan sistem persamaan diferensial dengan penyelesaian dan nilai penurunan yang spesifik lebih dari satu fokus, Biasanya, penyelesaian dan penurunan ditunjukan hanya untuk dua titik (the boundaries) yang menjelaskan sebuah two-point value problems (Ian Gladwell, scholarpedia.org) Initial Problem ditunjukan untuk penyelesaian pada initial condition y(t0)=A, Penyelesaian mengharapkan bahwa F(t,y) akan terus lanjut pada bagian yang melibatkan A dan turunan sebagian ∂Fi/∂yj yang terikat, dengan asumsi dimana initial value problem memilki penyelesaian Boundary Value Problem menujukan penyelesaian, dengan memperlihatkan kondisi lebih dari satu titik, Blasius Problem merupakan persamaan diferensial y‴=−yy″/2 dengan adanya boundary condition y(0)=0,y′(0)=0,y′(∞)=1 (Vita Puspita)
IVB tidak perlu menentukan nilai pada batas, melainkan membutuhkan nilai selama kondisi awal. Ini biasanya berlaku untuk sistem dinamis yang berubah seiring waktu seperti dalam Fisika. Contoh, untuk menyelesaikan posisi partikel dalam persamaan diferensial, kita memerlukan posisi awal dan juga kecepatan awal. Tanpa nilai awal ini, kita tidak dapat menentukan posisi akhir dari persamaan.
BVB : Sebaliknya, masalah nilai batas tidak selalu digunakan untuk sistem dinamis. Sebaliknya, ini sangat berguna untuk sistem yang memiliki batas ruang. Contohnya adalah bentuk dari masalah bayangan dalam visi komputer. Untuk menentukan gradien permukaan dari PDE, kita harus memaksakan nilai batas pada wilayah yang diinginkan.
Masalah nilai awal adalah masalah yang terkait dengan kondisi awal pertanyaan dan tidak ada batasan yang digunakan. Sementara masalah boundry vaue adalah masalah di mana batas digunakan yaitu interval diberikan
Perbedaan
Initial Value Problems
1. Bila nilai variabel tak bebas atau turunannya diketahui pada kondisi nilai mula-mula.
2. Hanya memiliki satu penyelesaian.
3. Merupakan penggambaran pada suatu fungsi persamaan dan turunan fungsi persamaan. Contohnya bisa berupa jarak, kecepatan, maupun percepatan
4. Memiliki indikator awal yang digunakan untuk mencari hasil penyelesaiannya.
5. Masalah nilai awal tidak perlu menentukan nilai pada batas, melainkan membutuhkan nilai selama kondisi awal, biasanya digunakan pada sistem dinamis
6. Initial Value problem dilakukan pada operasi yang tidak memiliki batas, tidak ada nilai maksimal didalamnya, selama ada kenaikan variabel bebas, juga akan mengalami perubahan variabel terikat
7. Initial value problem itu diketahui semua kondisi awalnya f(xo) =... f’(xo)=... F(x,y)=...
8. suatu masalah dengan kondisi atau suatu ketetapan yang sudah tentukan (hanya satu ketetapan).
Boundary Value Problems
1. Bila nilai variabel tak bebas atau turunannya diketahui lebih dari satu nilai variabel bebasnya
2. Memiliki lebih dari satu kemungkinan solusi
3. Hasil solusi lebih banyak daripada initial value problem
4. Merupakan variabel bebas yang berfungsi sebagai batasan pada fungsi persamaan. Contohnya seperti variabel waktu sebagai batasan jarak, kecepatan, atau percepatan
5. BVP tidak digunakan pada sistem dinamis, melainkan pada sistem yang memiliki batas ruang
6. Boundary Value Problem dilakukan pada sistem yang memiliki batas, biasanya dalam bentuk batas minimal atau maksimal
7. Kalau boundary diketahui kondisi pada sebuah boundary f(xo)=... f(x1)=... F(x,y)=....
8. Suatu masalah dengan kondisi penyelesaian suatu masalah dengan berbagai kondisi atau berbagai ketetapan.
Aplikasi Pada Submarine
Aplikasi Initial Value Problems
- Bagaimana kapal selam bisa tenggelam pada suatu kedalaman
- Ketika tenaga dari mesin kapal selam tidak sesuai dengan laju yang dihasilkan, ini terjadi karena ada nya pengaruh dari viskositas air pada daerah pelayaran kapal selam
- Bagaimana kapal selam mampu bergerak dengan kecepatan tertentu ketika badan kapal berbentuk silindris.
- Pada suatu kapal selam dikeatahui kondisi awalnya, lalu kemudian melakukan pergerakan hingga mencapai kecepatan optimumnya.
- Bila diketahui submarine dengan kecepatan awal v, kemudian kita bisa mencari atau memprediksi kecepatan saat waktu t. Dengan mempertimbangkan nilai gaya hambatan air yang telah diketahui pula, maka didapatkan kecepatan akhir saat waktu t yang diinginkan.
- Kapal selam mengalami initial value problem disaat kapal tersebut tidak mendapatkan pengaruh gaya apapun dari luar kapal selam tsb. karena pengaruh dari luar dapat banyak hasil seperti gelombang, hewan laut yang menempel itu semua pengaruh dari luar kapal yang menyebabkan hambatan pada kapal banyak faktornya, initial value problem tidak dapat mendapatkan hasil lebih dari 1. Initial value problem, contoh yang terjadi pada kapal selam adalah ketika tenaga dari mesin kapal selam tidak sesuai dengan laju yang dihasilkan, ini terjadi karena ada nya pengaruh dari viskositas air pada daerah pelayaran kapal selam
- Kapal salam yang awalnya diam kemudian melaju kedepan dengan kecepatan yang telah ditentukan maka kita bisa mengetahui berapa jarak yang ditempuh oleh kapal selam
- Submarine bergerak misalkan selama waktu yang di tentukan, lalu dari waktu tersebut kita mendapatkan jarak dan kecepatan akhir dari submarine tersebut, contoh= Kapal bergerak percepatan 1m/s, tentukan kecepatan kapal dan jarak yang di tempuh ketika kapal sudah berjalan selama 30 detik.
- Initial value dapat digunakan untuk mencari persamaan seperti perubahan kecepatan, kedalaman kapal selam, dan perubahan properties fluida kerja.
- Diharapkan untuk mencari nilai kecepatan kapal ketika di laut natuna dan kecepatan kapal di laut antartika adalah 10. y = x^2 + 100. Maka, x adalah lebar dari lautanya.
- Drag dari submarine pada kecepatan tertentu (misalnya hanya pada v = 11m/s)
- Kapal selam melakukan operasi pergi ke suatu tempat, kapal selam berjalan dari posisi x pada t = 0 dan diketahui kecepatan v pada t=0. dari data tersebut kita dapat mengetahui posisi akhir dari persamaan yang didapat dari F(x,v,t)
- Pada Kapal selam initial value problem terletak pada fungsi posisi, kecepatan dan waktu
- Mencari drag dari submarine pada 3 kecepatan yang berbeda
Aplikasi Boundary Value Problem
- Bagaimana kapal selam dapat tenggelam pada kecepatan, waktu dan kondisi tertentu.
- Bagaimana tekanan dapat mempengaruhi perlakuan badan kapal. Apa efek yang terjadi ketika semakin dalam kapal menyelam.
- Kapal selam bergerak didalam laut mengalami kecepatan penyelaman sepersekian m/s berapakah kedalaman yang dicapai kapal selam dalam waktu 15 menit. Kecepatan penyelaman dapat divariasikan sesuai keinginan operator
- Pada submarine dapat diambil dari spesimen yang berdekatan dengan plat submarine tersebut. Dengan melihat batas-batas tersebut, kemudian didapatkan nilai dan perilaku yang berbeda setiap spesimen. Maka dari itu nilai-nilai tersebut dapat menghasilkan banyak solusi yang beragam/banyak. Solusi yang banyak tersebut bersifat unik satu sama lain.
- Dalam kasus gerak kapal selam, banyak aturan tambahan atau boundary conditions yang berlaku. Salah satunya adalah ukuran geometri dan bentuk hull dari kapal selam yang mempengaruhi karakteristik dan motion kapal selam. Contoh yang kedua yakni adalah komponen hydroplane yang tersusun pada bagian after body kapal selam, sehingga untuk mencapai karakteristik yang baik diperlukan perancangan ulang sistem kendali hydroplane. Perhitungan ini sendiri termasuk ke dalam Boundary Value Problem, dan perhitungan gaya hidrodinamika dan momen kapal selam tersebut dapat dilakukan secara numerik dengan menggunakan cfdsoft.
- Kapal selam tersebut mendapat gaya dari luar kapal. Mengapa demikian disaat kondisi tambahan itu ada maka hasil yang akan keluar juga akan banyak. karena hasil dari boundary value problem itu bisa lebih dari 1.
- Pada suatu kapal yang memiliki kecepatan tertentu kita dapat menentukan besaran hambatan kapal yang dialami oleh badan kapal selam tersebut
- Perubahan hambatan/drag force dari setiap kecepatan submarine tersebut, misalkan menentukan hambatan pada saat kecepatan 5m/s sampai dengsn 10m/s. sehingga variable x dalam permasalahan ini adalah kecepatan dari kapal selam tersebut.
- Sebuah kapal selam naik ke permukaan dengan kecepatan 10km/jam; kenaikan 2m/s; pada sudut 20 derajat. Kapal awalnya berada pada kedalaman 150m. Boundary value dapat digunakan untuk mencari nilai hambatan yang dihasilkan oleh kapal selam tersebut.
- Kapal selam yang memiliki hambatan atau tekanan yang terjadi pada kapal yang bervariasi. Untuk menentukan gradien permukaan dari PDE, kita harus memaksakan nilai batas pada wilayah yang diinginkan. Contoh batas nya adalah jumlah air yang tercelup mengenai kapal selam. Contoh kasus, untuk menyelesaikan posisi kapal selam dalam persamaan diferensial, kita memerlukan posisi awal dan juga kecepatan awal. Tanpa nilai awal ini, kita tidak dapat menentukan posisi akhir dari persamaan.
- Drag dari submarine dari berbagai variasi kecepatan. Maka dari itu tugas kita adalah membuat regresi dari hubungan hambatan (drag) dengan variasi kecepatan yang telah kita tentukan sebelumnya. Karena realitanya nanti di dunia kerja, kebanyakan masalah yang kita selesaikan adalah menurut berbagai tinjauan atau ukuran dan kita tentukan sendiri batasnya (boundary nya).
- Kapal selam melakukan operasi pergi ke suatu tempat, kapal selam berjalan dari posisi x pada t = 0 dan diketahui kecepatan v pada t=0. kemudian diketahui pada jarak x t=10 kapal selam sudah mencapai kecepatan maksimal v pada t=10. kita dapat menentukan nilai kecepatan dan jarak dari batas-batas tersebut, selama ada didalam operasi
- Kapal selam nilai boundary value problem terletak pada besar nilai froude number kapal pada kecepatan awal kapal selam, sampai kecepatan normal
Contoh Kasus Lain
Initial value problem
- Mengukur posisi bola baseball pada waktu tertentu dan diketahui kecepatan awalnya
- Mengukur posisi benda yang mengalami jatuh bebas dengan atau tanpa gaya hambatan udara dan mencari posisi jatuhnya benda tersebut terhadap perubahan waktu yang terjadi berdasarkan keadaan awal yang telah ditentukan. - Miftah D.F.
- sistem redam pada pegas berdasarkan oleh konstanta, massa, dan gaya
- menghitung loop pad listrik
- Mobil bergerak dengan kecepatan tertentu
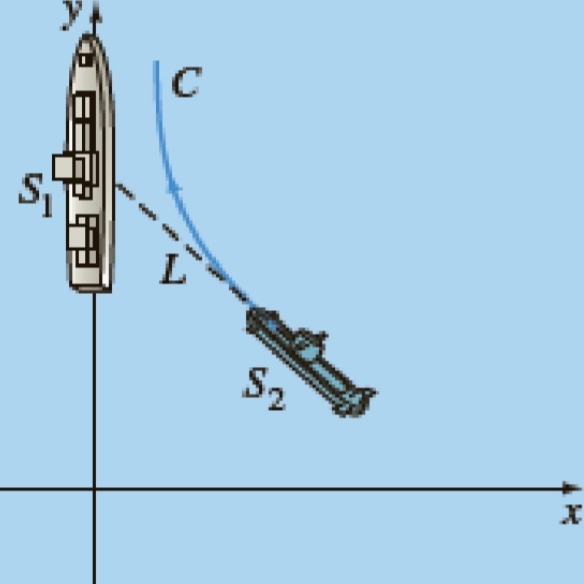
- Untuk menghitung panjang lintasan bisbol yang dilempar dari bidang tengah lapangan bisbol ke home asumsikan bahwa outfielder melepaskan bola delapan meter di atas tanah dan bisbol yang memiliki kecepatan awal yang memiliki sudut = dengan horizontal.ingatlah bahwa perjalanan bisbol melalui udara, udara akan menyebabkan gaya gesek pada bola menentang kecepatan bola. Kekuatan tarik dapat ditunjukkan bervariasi dengan kuadrat kecepatan. Keseimbangan gaya pada bola di kedua arah x dan y hasil dalam
- Suatu sepeda motor bergerak dari keadaan diam hingga mencapai jarak 100 meter dalam waktu 10 detik, berapa kecepatan motor tersebut
- Sebuah robot lengan otomatis melempar jarum dart menuju papan target di tengah dengan jarak, energi, dan masssa dart yang telah diperhitungkan (percobaan dilakukan diruang dimana hambatan udara tidak mempengaruhi jarum dart)
- Diketahui persamaan y = 100x - 5x^2 + 990(e^-0.1x - 1) jika y= -0.1y'-x ; y(0)=0 ; y'(0)=1
dari x=0 to 2 dan menggunakan metode euler h=0.05
- Untuk menghitung panjang lintasan bisbol yang dilempar dari bidang tengah lapangan ke outfielder dengan kecepatan dan sudut horizontal yang ditentukan (Vita P)
- posisi partikel dalam persamaan diferensial, kita memerlukan posisi awal dan juga kecepatan awal. Tanpa nilai awal ini, kita tidak dapat menentukan posisi akhir dari persamaan. x(0) dan v(0)
- Mengukur waktu tempuh sepeda motor dengan diketahui jarak dan kecepatan
Boundary value problem
- Menghitung kondisi besar hambatan gelombang pada kecepatan tinggi dan rendah
- Kondisi batas Dirichlet. Dalam mekanika fluida komputasi, kondisi batas Dirichlet klasik terdiri dari nilai kecepatan dan/atau tekanan yang akan diambil oleh set node tertentu. Adalah umum untuk merujuk pada beberapa kondisi seperti, (1)slip boundary condition: kecepatan normal ke batas diatur ke nol, sedangkan kecepatan paralel ke batas dibiarkan bebas (2)no-slip boundary condition: kecepatan normal ke batas dan paralel kecepatan ke batas ditetapkan sama dengan nol.
- Mobil bergerak menuju ke tempat tujuan dengan waktu, kondisi dan kecepatan yang berbeda
- Menghitung kondisi drag balok yang mengalami pendinginan agar mengetahui nilai kecepatan pendinginan perbagian dari balok tersebut - Miftah DF.
- Hydrofoil pada kapal. Hydrofoil adalah sebuah penerapan foil pada lambung sebuah kapal. Hydrofoil menghasilkan gaya lift yang mengangkat lambung kapal tersebut keluar dari permukaan air. Gaya lift tersebut harus lebih besar dari gaya berat kapal tersebut, dan gaya lift tersebut hanya akan dihasilkan ketika kapal mencapai kecepatan/velocity tertentu. Kasus ini adalah sebuah boundary value problem karena adanya boundary conditions dari kasus tersebut, yang menghasilkan hasil yang berbeda beda dari tiap hydrofoil tergantung dari bentuk geometri dan ukuran foil tersebut.
- Seseorang melempar jarum dart dengan tingkat keakurasian sebesar 0.83 per jarak 100m
- Sebuah torpedo yang memiliki bentuk seperti kapal selam uss albacore memiliki kecepatan yang beragam. Berapakah hambatan yang diterima kapal jika kecepetannya berkisar antara 11 m/s-15 m/s
- Software test, dengan menggunakan boundary value problem yang dimana menggunakan nilai maksimun dan nilai minimun untuk mendapatkan nilai valid. (Vita Puspita)
- G (0) = 0, G '(0) = 0 I, C (kondisi awal). G (2) = 4, G '(1) = 3 B, C (Kondisi batas)
- Gaya Drag pada airfoil
Manfaat
- Agar kita dapat mengelompokkan masalah sesuai dengan salah satu dari dua pilihan tersebut sehingga kita dapat lebih efektif dan efisien dalam mengerjakan masalah.
- Agar kita mengenal lebih jauh atas indahnya ciptaan sang pencipta, kemudian kita dapat bersyukur.
Kembali ke halaman Kelas Metode Numerik Teknik Perkapalan 2020