Difference between revisions of "Abdul Aziz Ananta"

From ccitonlinewiki
Jump to: navigation, search
(→‎UAS METODE NUMERIK - OPTIMASI STIFFNER)
 
(45 intermediate revisions by the same user not shown)
Line 1: Line 1:
 +
 +
== Tugas Metode Numerik 1 ==
 +
 
'''6 Februari 2018'''
 
'''6 Februari 2018'''
  
 
'''Hingga Paling Dasar'''
 
'''Hingga Paling Dasar'''
  
−
Sebagai pembelajar ilmu menjadi tujuan utama hasil yang didapatkan, namun yang jadi pertanyaan adalah apakah ilmu yang kita dapatkan sudah benar-benar didapatkan? maksudnya hingga paling dasar.
+
Sebagai pembelajar, ilmu adalah tujuan utama dari hasil belajar, namun yang jadi pertanyaan adalah apakah ilmu yang kita dapatkan sudah benar-benar didapatkan? maksudnya hingga paling dasar.
  
 
Contohnya =  (X^2-1)/(X-1) ,  dengan x = 1 seperti yang dicontohkan di papan tulis pada mata kuliah Metode Numerik. Pertanyaannya mengapa x=1 tidak bisa langsung dimasukkan?, banyak yang menjawab karena harus di-diferensialkan dan disederhanakan terlebih dahulu, namun banyak yang tidak tahu mengapa hal itu harus dilakukan dan apa penyebabnya?. Nah inilah yang dimaksud mengambil ilmu setengah-setengah.
 
Contohnya =  (X^2-1)/(X-1) ,  dengan x = 1 seperti yang dicontohkan di papan tulis pada mata kuliah Metode Numerik. Pertanyaannya mengapa x=1 tidak bisa langsung dimasukkan?, banyak yang menjawab karena harus di-diferensialkan dan disederhanakan terlebih dahulu, namun banyak yang tidak tahu mengapa hal itu harus dilakukan dan apa penyebabnya?. Nah inilah yang dimaksud mengambil ilmu setengah-setengah.
Line 12: Line 15:
  
 
-Abdul Aziz Ananta-
 
-Abdul Aziz Ananta-
 +
 +
 +
----
 +
 +
== Tugas Metode Numerik 2 ==
 +
 +
'''13 Februari 2019'''
 +
 +
'''Tugas Metode Numerik 2'''
 +
 +
ax + by = c dan px + qy =r dengan a,b,c,d,p,g,r adalah koeffisien dan x,y adalah variabel. buatlah algoritma dan flowchart dengan outputnya adalah syntax dengan 7-9 instruksi.
 +
 +
import numpy as np
 +
 +
A=np.array([
 +
 +
[a,b,c]
 +
])
 +
 +
B=np.array([
 +
 +
[p,q,r]
 +
])
 +
 +
Print A+B print A-B
 +
 +
 +
----
 +
 +
== Pertemuan 3 Kelas Metode Numerik ==
 +
 +
'''20 Februari 2019'''
 +
 +
penggunaan python yaitu untuk pengoprasian matematika yang lebih kompleks. seperi dari matrix n x n (anggap 50 x 50)
 +
 +
Materi : pengoprasian pengubahan matrix 3x3 diubah menjadi matrix segitiga bawah 0, dengan metode Gauss.
 +
Notasi :
 +
n : Jumlah baris/kolom
 +
i : Baris ke ..
 +
j : kolom
 +
k : pivot
 +
 +
Python memiliki bahasa sendiri, dan harus dipelajari sendiri di buku python BAB 1.
 +
contoh bahasa :
 +
for k in range (0, n-1) :
 +
  for i in range (k+1,n) :
 +
 +
if a[i,k] != 0.0:
 +
  lam = a[i,k]/a[k,k] (lam=lamda, dan a[i,k]=U1]
 +
  a[i,k+l:n] = a[i,k+1:n] - lam*a[k,k+1:n]
 +
  b[i] = b[i] - lam*b[k]
 +
 +
penggunaan "if" ialah menjadi pengecualian.
 +
 +
 +
----
 +
 +
 +
== Tugas Metode Numerik 3 ==
 +
 +
'''20 Februari 2019'''
 +
 +
'''Latihan Eliminasi Gauss'''
 +
 +
 +
 +
[[File:C--Users-lenovo-Pictures-Screenshots-Screenshot (201).png]]
 +
 +
 +
[[File:Screenshot (202).png]]
 +
 +
 +
----
 +
 +
 +
== Pertemuan 4 Metode Numerik ==
 +
 +
'''Rabu, 27 Februari 2019'''
 +
 +
Install numpy! command prompt -> pip install numphy
 +
 +
Fungsi-fungsi :
 +
 +
  array    : berfungsi mendefinisakan sebuah matrix
 +
  [ ]      : berfungsi untuk memberi batasan pada matrix
 +
  print(A) : berfungsi untuk menampilkan matrix A
 +
  np      : berfungsi untuk komando memanggil kode seperti
 +
  array,dll np juga sebagai library dari python
 +
  ' (kutip): berfungsi untuk menampilkan teks yang dikutip
 +
  #        : notes/catatan yang diinginkan
 +
  len      : berfungsi untuk membaca panjang array
 +
  for      : tidak sejajar dengan yang lain
 +
 +
  range(o,n-1) -> x=baris, y=kolom
 +
 +
contoh matrix A = [U11, U12, U13], [U21, U22, U23], [U31, U32, U33]
 +
agar menjadikan segitiga 0 bawah, ialah dengan langkah-langkah, seperti;
 +
 +
  langkah I :
 +
  U21-Lam*U11=0, dengan Lamda = U21/U11
 +
  U31-Lam*U11=0
 +
 +
  Langkah II :
 +
  U32-Lam*U22=0
 +
  dst
 +
 +
salah satu fungsi Eliminasi gauss dalam python adalah mencari nilai X tiap kolomnya.
 +
 +
[[File:Screenshot (203).png]]
 +
 +
[[File:Screenshot (204).png]]
 +
 +
 +
----
 +
 +
== Pertemuan 5 Metode Numerik ==
 +
 +
'''Rabu, 6 Maret 2019'''
 +
 +
Menghitung Persamaan
 +
Pada perhitungan struktural sederhana (pada pegas)
 +
|
 +
buat persamaan
 +
|
 +
pecahkan
 +
 +
Contoh kasus 1 :
 +
Ada bangunan dan memiliki 4 titik secara berurutan, titik 1 diatas dan titik 4 paling bawah, maka tentukan tegangan dan regangan paling tinggi.
 +
 +
hasil : tegangan terjadi pada titik 1
 +
        regangan, terjadi pada titik 4
 +
 +
Contoh kasus 2 :
 +
kerjakan menggunakan python persamaan berikut "
 +
  2x-2y=1
 +
  4x-6y=1
 +
 +
hasil : tidak bisa diselesaikan karena tidak memiliki titik temu. maka pelajaran yang bisa diambil ialah bahwa sebelum mengoprasikan dengan python maka harus ditelaah terlebih dahulu apakah persamaan bisa diselesaikan atau hanya mengecoh.
 +
 +
----
 +
 +
== Tugas 5 Metode Numerik ==
 +
 +
'''Aplikasi Eliminasi gauss pada sistem pegas seri'''
 +
 +
Jika Diketahui konstanta pegas 1,2 dan 3 serta gaya yang bekerja pada pegas :
 +
 +
[[File:soalpegas.png]]
 +
 +
Pengaplikasian gaya pegas seri pada python :
 +
 +
[[File:Pegas1.0.png]]
 +
 +
[[File:Pegas2.png]]
 +
 +
[[File:Pegas3.png]]
 +
 +
Hasil running :
 +
 +
[[File:Pegas4.png]]
 +
 +
 +
----
 +
 +
== Pertemuan 6 Metode Numerik ==
 +
 +
'''Rabu, 13 Maret 2019'''
 +
 +
Pelajari Hal 20 Linear spring as a finite Element
 +
 +
"Ada gambar batang". Hitung tegangan pada titik 1,2 &3
 +
 +
Tugas :
 +
1. Buat Flowchart --> Program Pegas
 +
2. Buat program Numerik (Python) untuk analisis struktur bilangan satu dimensi
 +
 +
----
 +
 +
== Tugas 6 Metode Numerik ==
 +
 +
'''Tugas 1 : Flowchart Program Pegas Seri'''
 +
 +
[[File:bandi1.jpg]]
 +
 +
[[File:bandi2.jpg]]
 +
 +
'''Tugas 2 : Program Numerik Analisis struktur bilangan satu dimensi'''
 +
 +
[[File:PegasBatang.png]]
 +
 +
'''Link Video : Youtube'''
 +
 +
[https://youtu.be/BUridbdiuTc]
 +
 +
https://youtu.be/BUridbdiuTc
 +
 +
----
 +
 +
 +
== UAS METODE NUMERIK - OPTIMASI STIFFNER ==
 +
 +
Berikut adalah Video lampiran UAS Metode Numerik, dengan topik Optimasi Stiffner.
 +
 +
'''Link Video : Youtube'''
 +
 +
[https://youtu.be/c6U2gKfXrr4]
 +
 +
https://youtu.be/c6U2gKfXrr4
 +
 +
'''PPT UAS METNUM'''
 +
 +
[https://drive.google.com/file/d/1hhq7qBbjTnFI_bOsfoVjOC-qkVEmx2CA/view?usp=sharing]
 +
 +
https://drive.google.com/file/d/1hhq7qBbjTnFI_bOsfoVjOC-qkVEmx2CA/view?usp=sharing
 +
 +
'''FILE PYTHON'''
 +
 +
[https://drive.google.com/file/d/1cb8PSQtaU0u31ffIYywwmsNJOnu8JX4A/view?usp=sharing]
 +
 +
https://drive.google.com/file/d/1cb8PSQtaU0u31ffIYywwmsNJOnu8JX4A/view?usp=sharing
 +
 +
CODING :
 +
 +
import math
 +
def bracket(f,x1,h):
 +
    c = 1.618033989
 +
    f1 = f(x1)
 +
    x2 = x1 + h; f2 = f(x2)
 +
    if f2 > f1:
 +
        h = -h
 +
        x2 = x1 + h; f2 = f(x2)
 +
        if f2 > f1: return x2,x1 - h
 +
    for i in range (100):
 +
        h = c*h
 +
        x3 = x2 + h; f3 = f(x3)
 +
        if f3 > f2: return x1,x3
 +
        x1 = x2; x2 = x3
 +
        f1 = f2; f2 = f3
 +
    print("Bracket did not find a minimum")
 +
def search(f,a,b,tol=1.0e-9):
 +
    nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
 +
    print(nIter)
 +
   
 +
    R = 0.618033989
 +
    C = 1.0 - R
 +
    x1 = R*a + C*b; x2 = C*a + R*b
 +
    f1 = f(x1); f2 = f(x2)
 +
    for i in range(nIter):
 +
        if f1 > f2:
 +
            a = x1
 +
            x1 = x2; f1 = f2
 +
            x2 = C*a + R*b; f2 = f(x2)
 +
        else:
 +
            b = x2
 +
            x2 = x1; f2 = f1
 +
            x1 = R*a + C*b; f1 = f(x1)
 +
    if f1 < f2: return x1,f1
 +
    else: return x2,f2
 +
print("Aplikasi Optimasi tinggi komponen vertikal I stiffner")
 +
b2 = eval(input("Nilai lebar tampak bawah :"))
 +
b1 = eval(input("Nilai lebar tampak atas :"))
 +
H = eval(input("Nilai tinggi I Stiffner :"))
 +
def f(x):
 +
    A1 = b1*(H-x)/2
 +
    A2 = b2*x
 +
    A3 = b1*(H-x)/2
 +
    d1 = 1/2*(H-x)/2
 +
    d2 = 1/2*x+(H-x)
 +
    d3 = 3/2*(H-x)+x
 +
    I1 = 1/12*b1*(H-x)**3
 +
    I2 = 1/12*b2*x**3
 +
    I3 = 1/12*b1*(H-x)**3
 +
    dc = (d1*A1+d2*A2+d3*A3)/(A1+A2+A3)
 +
    I = I1-A1*(dc-d1)**2+I2-A2*(dc-d2)**2+I3-A3*(dc-d3)**2
 +
    Z = I/dc         
 +
    return Z
 +
xStart = 0.0
 +
h = 1.0       
 +
x1,x2 = bracket(f,xStart,h)
 +
x,fMin = search(f,x1,x2)
 +
print("x =",x)
 +
print("optional sectional area =",-fMin)
 +
print("sectional area awal" , f(H))
 +
A = (-fMin/f(H))*100
 +
print("Efisiensi yang didapat sebesar =",A,"%")

Latest revision as of 19:00, 29 May 2019

Tugas Metode Numerik 1

6 Februari 2018

Hingga Paling Dasar

Sebagai pembelajar, ilmu adalah tujuan utama dari hasil belajar, namun yang jadi pertanyaan adalah apakah ilmu yang kita dapatkan sudah benar-benar didapatkan? maksudnya hingga paling dasar.

Contohnya = (X^2-1)/(X-1) , dengan x = 1 seperti yang dicontohkan di papan tulis pada mata kuliah Metode Numerik. Pertanyaannya mengapa x=1 tidak bisa langsung dimasukkan?, banyak yang menjawab karena harus di-diferensialkan dan disederhanakan terlebih dahulu, namun banyak yang tidak tahu mengapa hal itu harus dilakukan dan apa penyebabnya?. Nah inilah yang dimaksud mengambil ilmu setengah-setengah.

Pada kelas Metode Numerik, Aki DAI mengatakan bahwa pada saat belajar kita harus selalu menyertakan pertanyaan-pertanyaan sampai paling mendasar hingga pertanyaan tersebut habis. Sehingga kita dapat paham sepenuhnya dengan dicerna dan tidak menelan ilmu mentah-mentah. Dengan begitu proses belajar menjadi lebih banyak manfaat dan jika ada pertanyaan-pertanyaan seputar pelajaran tsb, kita dapat menjawab hingga ke akar layaknya seorang ahli.

Mudah-mudahan kita sebagai mahasiswa dapat selalu menerapkan proses pembelajaran seperti ini, dan selalu menjadi orang yang merasa bodoh sehingga selalu penasaran dengan hal-hal yang belum diketahui serta tidak malu untuk bertanya.

-Abdul Aziz Ananta-


Tugas Metode Numerik 2

13 Februari 2019

Tugas Metode Numerik 2

ax + by = c dan px + qy =r dengan a,b,c,d,p,g,r adalah koeffisien dan x,y adalah variabel. buatlah algoritma dan flowchart dengan outputnya adalah syntax dengan 7-9 instruksi.

import numpy as np

A=np.array([ 

[a,b,c] 
])

B=np.array([ 

[p,q,r] 
])

Print A+B print A-B


Pertemuan 3 Kelas Metode Numerik

20 Februari 2019

penggunaan python yaitu untuk pengoprasian matematika yang lebih kompleks. seperi dari matrix n x n (anggap 50 x 50)

Materi : pengoprasian pengubahan matrix 3x3 diubah menjadi matrix segitiga bawah 0, dengan metode Gauss. Notasi : n : Jumlah baris/kolom i : Baris ke .. j : kolom k : pivot

Python memiliki bahasa sendiri, dan harus dipelajari sendiri di buku python BAB 1. contoh bahasa : 

for k in range (0, n-1) :
  for i in range (k+1,n) :

if a[i,k] != 0.0: 
  lam = a[i,k]/a[k,k] (lam=lamda, dan a[i,k]=U1]
  a[i,k+l:n] = a[i,k+1:n] - lam*a[k,k+1:n]
  b[i] = b[i] - lam*b[k]

penggunaan "if" ialah menjadi pengecualian.



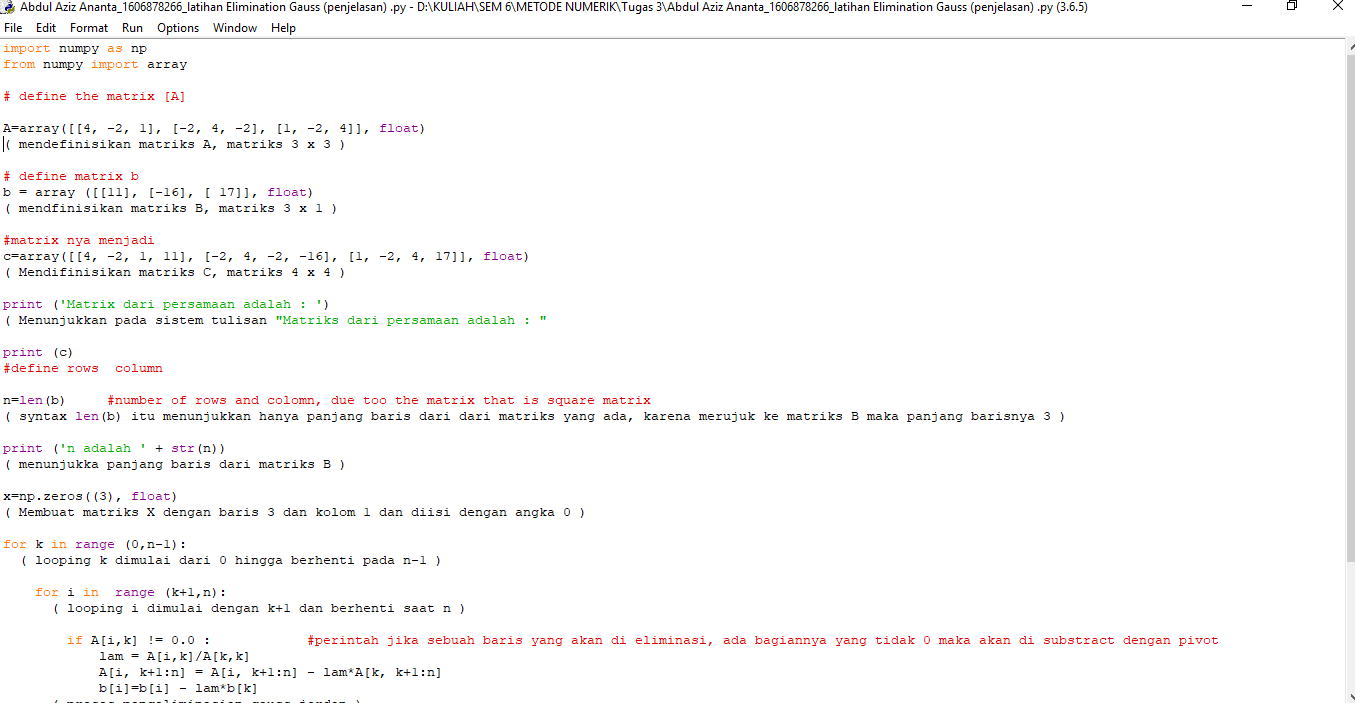
Tugas Metode Numerik 3

20 Februari 2019

Latihan Eliminasi Gauss


C--Users-lenovo-Pictures-Screenshots-Screenshot (201).png


Screenshot (202).png



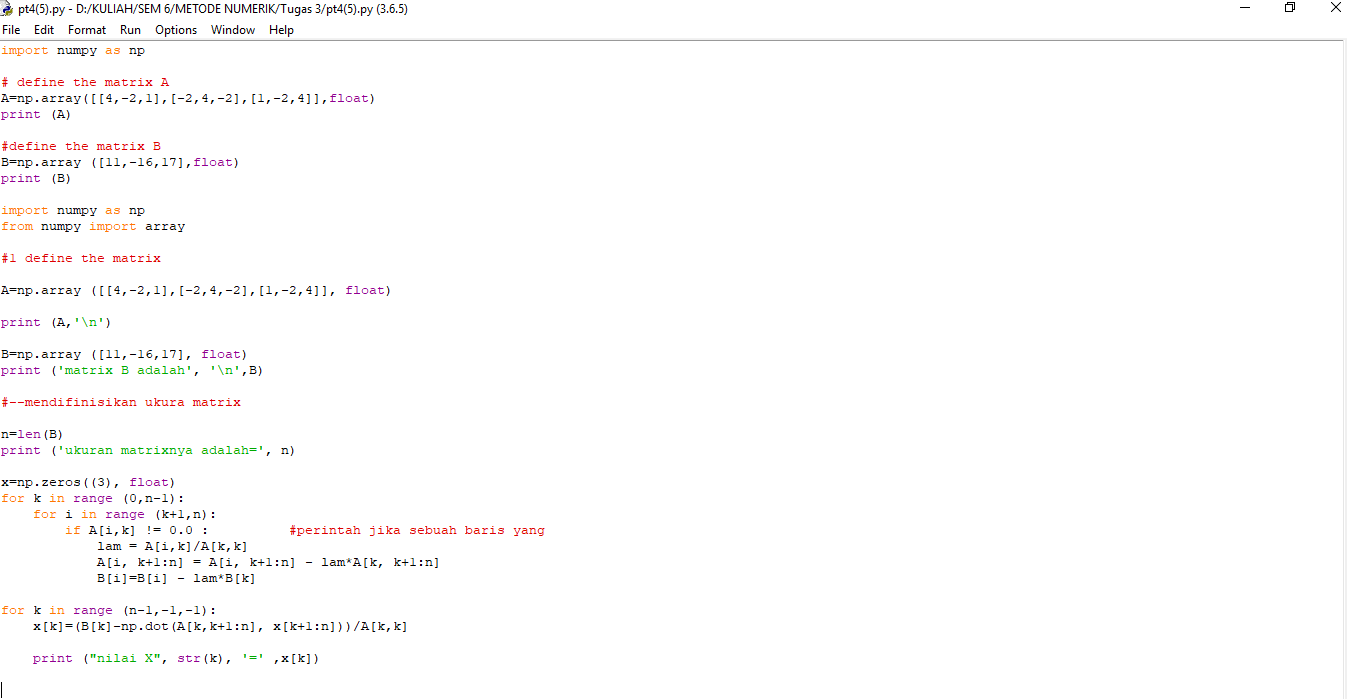
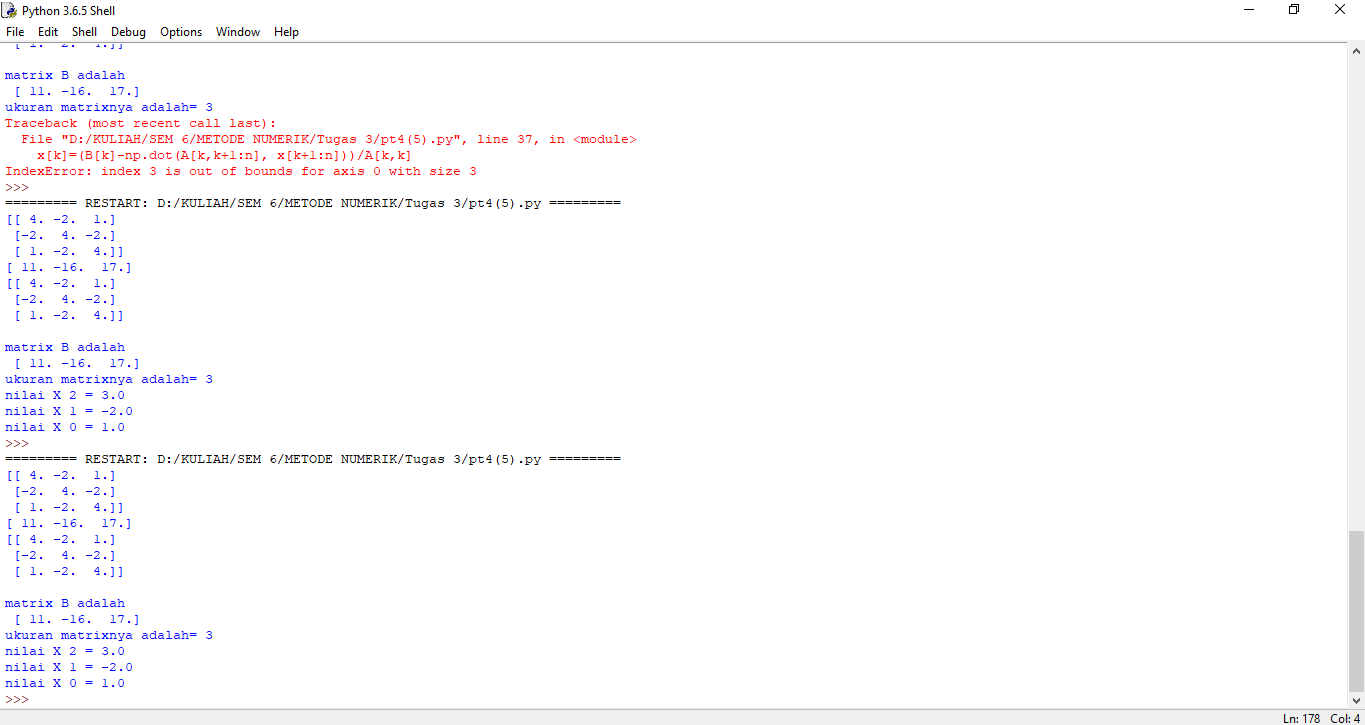
Pertemuan 4 Metode Numerik

Rabu, 27 Februari 2019

Install numpy! command prompt -> pip install numphy

Fungsi-fungsi : 

  array    : berfungsi mendefinisakan sebuah matrix
  [ ]      : berfungsi untuk memberi batasan pada matrix
  print(A) : berfungsi untuk menampilkan matrix A
  np       : berfungsi untuk komando memanggil kode seperti 
  array,dll np juga sebagai library dari python
  ' (kutip): berfungsi untuk menampilkan teks yang dikutip
  #        : notes/catatan yang diinginkan
  len      : berfungsi untuk membaca panjang array
  for      : tidak sejajar dengan yang lain

  range(o,n-1) -> x=baris, y=kolom

contoh matrix A = [U11, U12, U13], [U21, U22, U23], [U31, U32, U33] agar menjadikan segitiga 0 bawah, ialah dengan langkah-langkah, seperti; 

  langkah I : 
  U21-Lam*U11=0, dengan Lamda = U21/U11
  U31-Lam*U11=0

  Langkah II :
  U32-Lam*U22=0
  dst

salah satu fungsi Eliminasi gauss dalam python adalah mencari nilai X tiap kolomnya.

Screenshot (203).png

Screenshot (204).png


Pertemuan 5 Metode Numerik

Rabu, 6 Maret 2019

Menghitung Persamaan Pada perhitungan struktural sederhana (pada pegas) | buat persamaan | pecahkan

Contoh kasus 1 : Ada bangunan dan memiliki 4 titik secara berurutan, titik 1 diatas dan titik 4 paling bawah, maka tentukan tegangan dan regangan paling tinggi.

hasil : tegangan terjadi pada titik 1 

       regangan, terjadi pada titik 4

Contoh kasus 2 : kerjakan menggunakan python persamaan berikut " 

 2x-2y=1
 4x-6y=1

hasil : tidak bisa diselesaikan karena tidak memiliki titik temu. maka pelajaran yang bisa diambil ialah bahwa sebelum mengoprasikan dengan python maka harus ditelaah terlebih dahulu apakah persamaan bisa diselesaikan atau hanya mengecoh.

Tugas 5 Metode Numerik

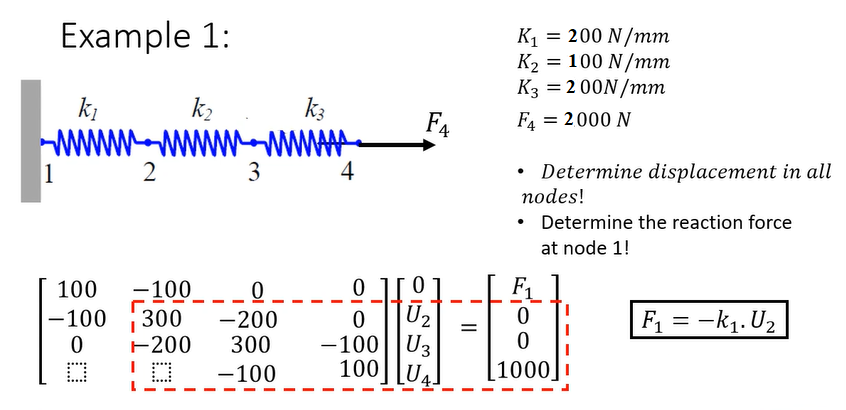
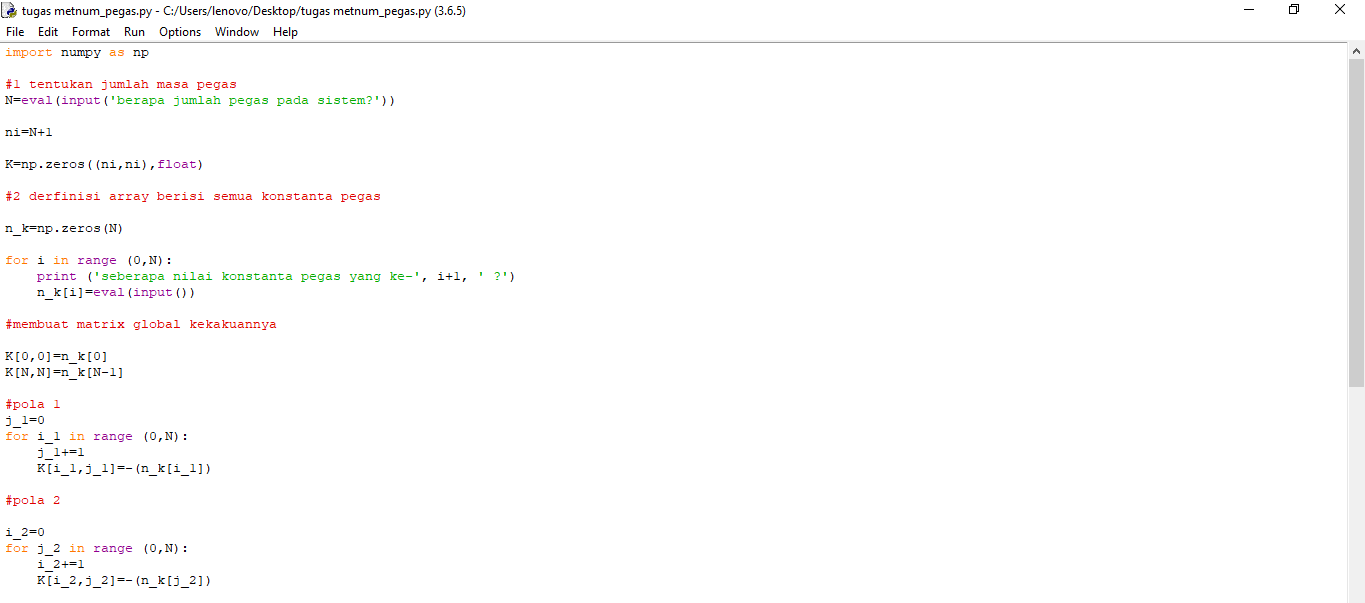
Aplikasi Eliminasi gauss pada sistem pegas seri

Jika Diketahui konstanta pegas 1,2 dan 3 serta gaya yang bekerja pada pegas :

Soalpegas.png

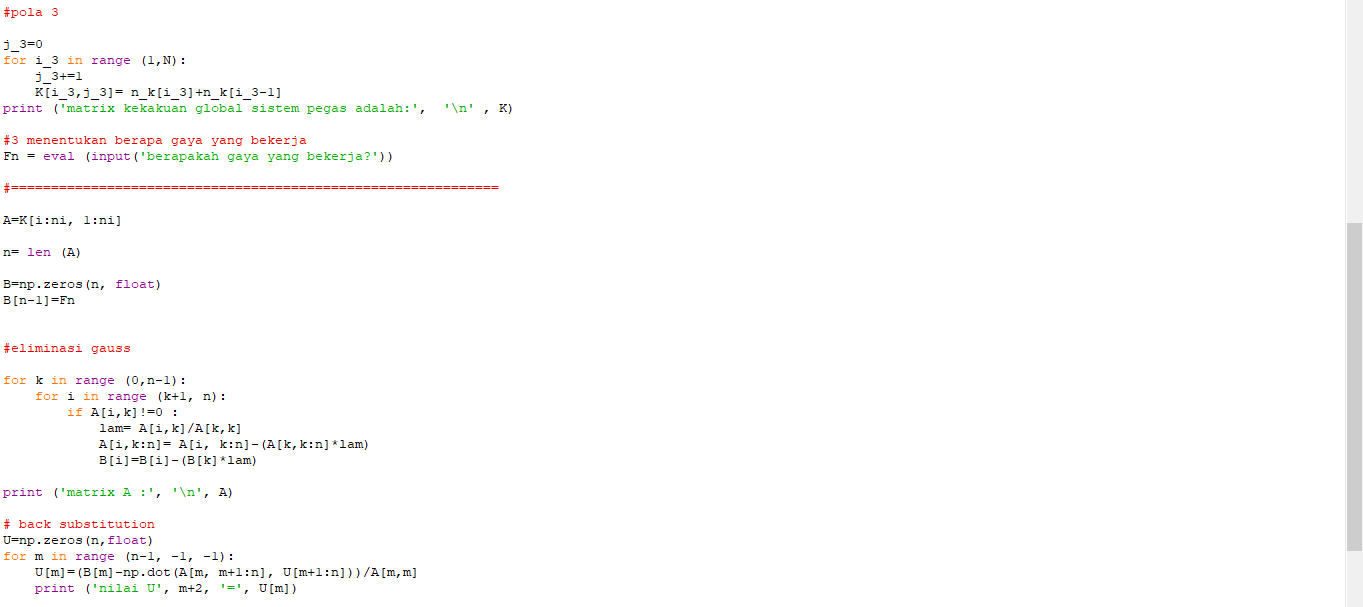
Pengaplikasian gaya pegas seri pada python :

Pegas1.0.png

Pegas2.png

Pegas3.png

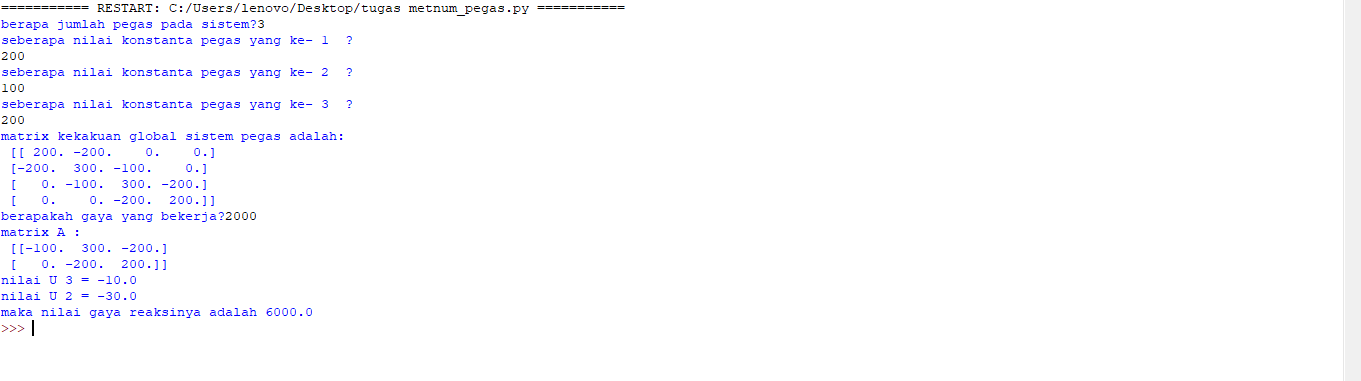
Hasil running :

Pegas4.png


Pertemuan 6 Metode Numerik

Rabu, 13 Maret 2019

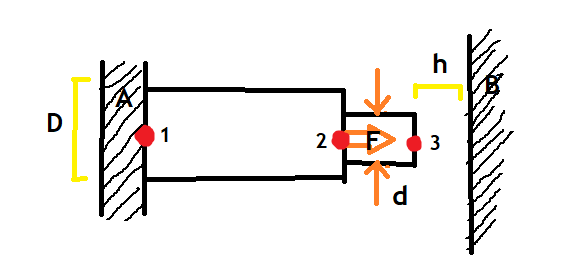
Pelajari Hal 20 Linear spring as a finite Element

"Ada gambar batang". Hitung tegangan pada titik 1,2 &3

Tugas : 1. Buat Flowchart --> Program Pegas 2. Buat program Numerik (Python) untuk analisis struktur bilangan satu dimensi

Tugas 6 Metode Numerik

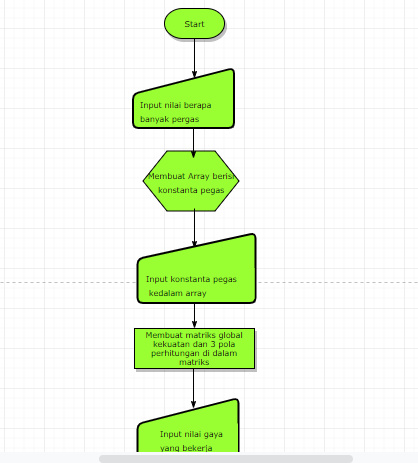
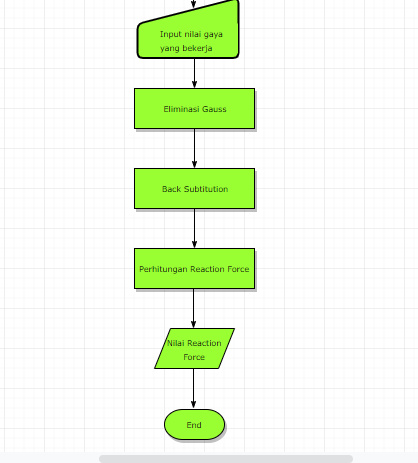
Tugas 1 : Flowchart Program Pegas Seri

Bandi1.jpg

Bandi2.jpg

Tugas 2 : Program Numerik Analisis struktur bilangan satu dimensi

PegasBatang.png

Link Video : Youtube

[1]

https://youtu.be/BUridbdiuTc


UAS METODE NUMERIK - OPTIMASI STIFFNER

Berikut adalah Video lampiran UAS Metode Numerik, dengan topik Optimasi Stiffner.

Link Video : Youtube

[2]

https://youtu.be/c6U2gKfXrr4

PPT UAS METNUM

[3]

https://drive.google.com/file/d/1hhq7qBbjTnFI_bOsfoVjOC-qkVEmx2CA/view?usp=sharing

FILE PYTHON

[4]

https://drive.google.com/file/d/1cb8PSQtaU0u31ffIYywwmsNJOnu8JX4A/view?usp=sharing

CODING :

import math def bracket(f,x1,h): 

   c = 1.618033989
   f1 = f(x1)
   x2 = x1 + h; f2 = f(x2)
   if f2 > f1:
       h = -h
       x2 = x1 + h; f2 = f(x2)
       if f2 > f1: return x2,x1 - h
   for i in range (100):
       h = c*h
       x3 = x2 + h; f3 = f(x3)
       if f3 > f2: return x1,x3
       x1 = x2; x2 = x3
       f1 = f2; f2 = f3
   print("Bracket did not find a minimum")

def search(f,a,b,tol=1.0e-9): 

   nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
   print(nIter)
   
   R = 0.618033989
   C = 1.0 - R
   x1 = R*a + C*b; x2 = C*a + R*b
   f1 = f(x1); f2 = f(x2)
   for i in range(nIter):
       if f1 > f2:
           a = x1
           x1 = x2; f1 = f2
           x2 = C*a + R*b; f2 = f(x2)
       else:
           b = x2
           x2 = x1; f2 = f1
           x1 = R*a + C*b; f1 = f(x1)
   if f1 < f2: return x1,f1
   else: return x2,f2

print("Aplikasi Optimasi tinggi komponen vertikal I stiffner") b2 = eval(input("Nilai lebar tampak bawah :")) b1 = eval(input("Nilai lebar tampak atas :")) H = eval(input("Nilai tinggi I Stiffner :")) def f(x): 

   A1 = b1*(H-x)/2
   A2 = b2*x
   A3 = b1*(H-x)/2
   d1 = 1/2*(H-x)/2
   d2 = 1/2*x+(H-x)
   d3 = 3/2*(H-x)+x
   I1 = 1/12*b1*(H-x)**3
   I2 = 1/12*b2*x**3
   I3 = 1/12*b1*(H-x)**3
   dc = (d1*A1+d2*A2+d3*A3)/(A1+A2+A3)
   I = I1-A1*(dc-d1)**2+I2-A2*(dc-d2)**2+I3-A3*(dc-d3)**2
   Z = I/dc          
   return Z

xStart = 0.0 h = 1.0 x1,x2 = bracket(f,xStart,h) x,fMin = search(f,x1,x2) print("x =",x) print("optional sectional area =",-fMin) print("sectional area awal" , f(H)) A = (-fMin/f(H))*100 print("Efisiensi yang didapat sebesar =",A,"%")

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Abdul_Aziz_Ananta&oldid=8424"