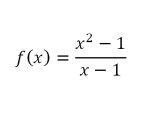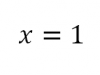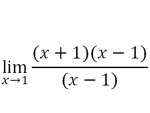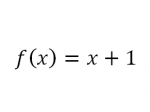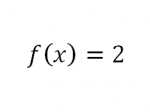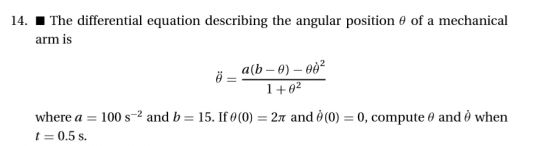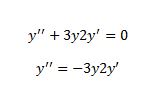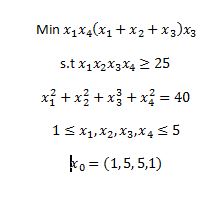Difference between revisions of "Muhammad akbar"
(→Laporan Asistensi) |
(→Tugas UTS) |
||
| (29 intermediate revisions by the same user not shown) | |||
| Line 162: | Line 162: | ||
mencari D terkecil untuk menentukan F(x) paling mendekati | mencari D terkecil untuk menentukan F(x) paling mendekati | ||
| + | |||
| + | Kemudian menggunakan python dirumuskan sebagai berikut | ||
| + | [[File:Metnum_Akbar_IV_VI.jpg|540px|center|alt text]] | ||
| + | Didapatkan f(x)=5.04915909x² - 0.24425303x + 0.80800909 dalam memiliki orde 2 | ||
| + | |||
| + | ==Pertemuan Minggu Kelima== | ||
| + | Pada minggu ini kami mengevaluasi kembali mengenai materi Initial Value Problem dan Boundary Value Problem. Mencari tahu perbedaan antara Initial Value Problem dan Boundary Value Problem. Perbedaan paling mencolok dari Initial Value Problem dan Boundary Value Problem adalah dengan ada tidaknya batas nilai input fungsi yang dipakai. Jika didalam fungsi tersebut memiliki nilai batas atas dan batas bawah, maka itu merupakan contoh dari Boundary Value Problem. Atau jika komponen nilai yang diketahui hanya satu titik nilai pada kondisi Awal, maka itu termasuk kedalam Initial Value Problem. | ||
| + | |||
| + | ===Laporan Asistensi=== | ||
| + | *Selasa, 10 Maret 2020 | ||
| + | [[File:Metnum_Akbar_V_I.jpg|540px|center|alt text]] | ||
| + | [[File:Metnum_Akbar_V_II.jpg|540px|center|alt text]] | ||
| + | [[File:Metnum_Akbar_V_III.jpg|540px|center|alt text]] | ||
| + | [[File:Metnum_Akbar_V_IV.jpg|540px|center|alt text]] | ||
| + | |||
| + | ===Tugas Metnum=== | ||
| + | [[File:Metnum_Akbar_V_V.jpg|540px|center|alt text]] | ||
| + | [[File:Metnum_Akbar_V_VI.jpg|540px|center|alt text]] | ||
| + | [[File:Metnum_Akbar_V_VII.jpg|540px|center|alt text]] | ||
| + | [[File:Metnum_Akbar_V_VIII.jpg|540px|center|alt text]] | ||
| + | |||
| + | == Pertemuan Minggu Keenam== | ||
| + | Pada minggu ini kami dijelaskan materi oleh asisten dosen dikarenakan Pak DAI sakit. Semoga pak DAI diberikan kesehatan kembali. Kami mempelajari tentang optimasi. Jadi optimasi adalah tentang bagaimana cara kita untuk meminimalkan nilai suatu fungsi atau memaksimalkan nilai suatu fungsi. Optimasi biasa berkaitan dengan desain. Terdapat komponen-komponen yang ada jika melakukan optimasi | ||
| + | |||
| + | a. Fungsi Objektif merupakan fungsi yang akan kita optimasi nilainya menjadi optimal | ||
| + | |||
| + | b. Constraint merupakan halangan atau batasan terhadap nilai fungsi objektif. Terbagi 2; | ||
| + | |||
| + | 1. equality constraint atau batasan berupa persamaan (=) | ||
| + | |||
| + | 2. inequality constraint atau batasan berupa pertidaksamaan atau berupa (<,<=,>,>=) | ||
| + | |||
| + | c. Variable keputusan atau nilai-nilai yang sudah dimiliki atau ada | ||
| + | |||
| + | Sebenarnya optimasi itu sangat banyak komponennya dalam area ke teknikan, bahkan ini menjadi jurusan pada S2. Sekarang kami hanya perlu mengenal sedikit tentang optimasi. | ||
| + | |||
| + | Saya lampirkan contoh soal optimasi yang dibahas pada pertemunan minggu keenam | ||
| + | [[File:Metnum_Akbar_VI_II.jpg|540px|center|alt text]] | ||
| + | |||
| + | disini fungsi pertama merupakan fungsi objektif | ||
| + | |||
| + | fungsi kedua merupakan inequality constraint | ||
| + | |||
| + | fungsi ketiga merupakan equality constraint | ||
| + | |||
| + | fungsi keempat merupakan nilai variabel kebputusannya, dan | ||
| + | |||
| + | fungsi kelima perkiraan nilai yang kita tentukan | ||
| + | |||
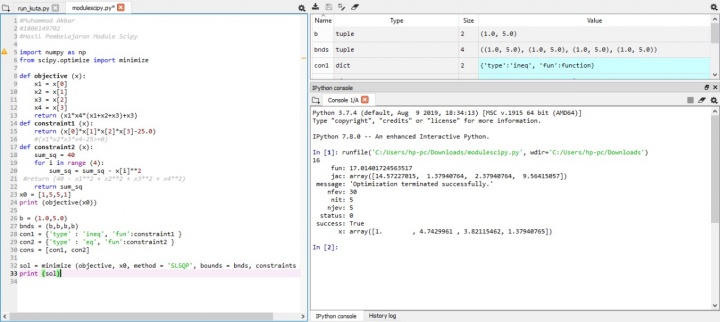
| + | [[File:Metnum_Akbar_VI_I.jpg|720px|center|alt text]] | ||
| + | |||
| + | |||
| + | Contoh optimasi adalah misalkan pemilik kayu meminta enginer untuk membuatkan pagar dari kayu yang dia miliki sepanjang 20 meter. Nilai luas area dari daerah yang ditutupi pagar kayu harus maksimal. Dan agar anak sang pemilik bisa bermain didalamnya maka panjang dari daerah di dalam pagar harus sama atau lebih dari 8 meter. Dari permasalahan tersebut kita menentukan nilai masing-masing komponennya | ||
| + | |||
| + | Fungsi Objektifnya adalah luas daerah | ||
| + | |||
| + | equality constrainnya adalah panjang kayu yang berdampak pada panjang keliling pagar | ||
| + | |||
| + | inequality constrainnya adalah p>=8 agar anaknya bisa bermain di dalam area pagar. | ||
| + | |||
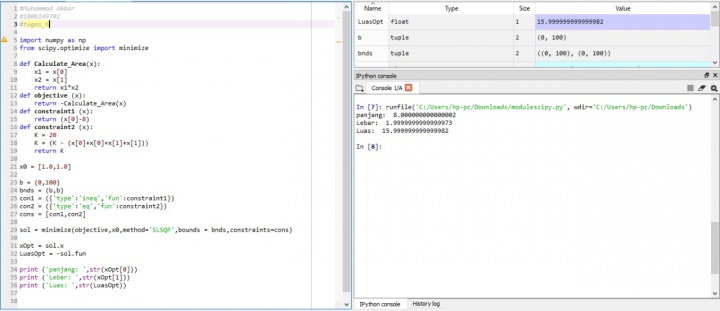
| + | Soal area luas dari pagar berikut nilai hasilnya | ||
| + | |||
| + | [[File:Metnum_Akbar_VI_III.jpg|720px|center|alt text]] | ||
| + | |||
| + | |||
| + | ===Tugas Optimasi Video=== | ||
| + | [[File:Metnum_Akbar_VII_I.jpg|720px|center|alt text]] | ||
| + | |||
| + | Berikut video penyelesaian dari soal diatas saya sambungkan ke Youtube | ||
| + | https://youtu.be/01PitWgeT4s | ||
| + | |||
| + | ==Tugas UTS== | ||
| + | 1. (i) Membuat Model AUV untuk simulasi CFDSOF, (ii) Melakukan simulasi hambatan dengan CFDSOF | ||
| + | |||
| + | 2. Membuat persamaan dari data-data hambatan dan kecepatan (Curve Fitting) | ||
| + | |||
| + | 3. Model matematis untuk memperkirakan propulsi yang dibutuhkan untuk berbagai kecepatan | ||
| + | |||
| + | 4. Waktu yang dibutuhkan untuk mencapai kecepatan maksimal (Runge Kutta). | ||
| + | |||
| + | === Pembuatan model AUV === | ||
| + | Dengan meniru KRI alugoro dibuaut model sederhananya menggunakan Solid Work. | ||
| + | https://youtu.be/M40H-Gqhoik | ||
| + | |||
| + | ===Simulasi CFDSOF=== | ||
| + | Menggunakan Software CFDSOF untuk mendapatkan hambatan kapal berbagai kecepatan | ||
| + | https://www.youtube.com/watch?v=ww1RNkMpMCM | ||
| + | |||
| + | ===Membuat Persamaan Regresi=== | ||
| + | Menggunakan curve fitting untuk mendapatkan hubungan persamaan kecepatan dengan hambatan | ||
| + | https://www.youtube.com/watch?v=30rmJNHyO2Y | ||
Latest revision as of 18:50, 3 April 2020
Contents
Tentang saya
Nama: Muhammad Akbar
Tempat Tanggal Lahir: Jakarta, 4 Juli 2000
Tempat Tinggal : Padang Panjang
Status: Belum menikah
Saya merupakan mahasiswa teknik perkapalan fakultas teknik universitas indonesia angkatan 2018.
sebelumnya saya belum mengerti apapun tentang metode numerik, saya tidak tahu apapun tentang pemograman dan lain sebagainya Pertemuan pertama mata kuliah metode numerik terjadi pada tanggal 7 Februari 2020. mata kuliah ini diajar oleh dua orang dosen yaitu, pak Dai dan pak harinaldi.
Pertemuan Minggu Pertama ( 7 Februari 2020 )
Pada minggu pertama mata kuliah Metode Numerik bapak Dr. Ir. Ahmad Indra Siswantara atau dikenal dengan sebutan Pak DAI memberikan pengenalan tentang metode numerik dan manfaat yang di peroleh dengan mempelajari metode numerik. Metode numerik digunakan digunakan untuk permodelan kejadian-kejadian yang ada di dunia perkapalan yang tidak bisa dilakukan secara laboraturium atau biaya melakukan percobaan yang mahal, dapat diatasi dengan menggunakan metode numerik.
Tugas Pertama Mencari Nilai Fungsi f(x)
Diketahui suatu fungsi
dimana karena jika memasukan nilai x=1 nilai yang didapat adalah 0/0 atau undefinedMaka digunakan pendekatan untuk menemukan nilai fungsi f(x) dimana x=1 dengan cara menggunakan limit
Sehingga fungsi berubah menjadi
kemudian dimasukan nilai
nilai fungsi menjadi
Dan jika ditulis dalam bahasa phyton menjadi
dalam bahasa bahasa phyton, kita menggunakan fungsi if, maksudnya adalah jika nilai input yang kita masukan 1 maka persamaannya akan beralih ke persamaan g, dan jika nilai x tidak sama dengan 1 maka persamaan yang berjalan adalah f.
Output
Mengerjakan tugas mencari nilai fungsi f(x) saya menjadi sedikit paham mengenai algoritma saya menjadi sedikit tertarik dengan metode numerik.
Pertemuan Minggu Kedua ( 14 Februari 2020 )
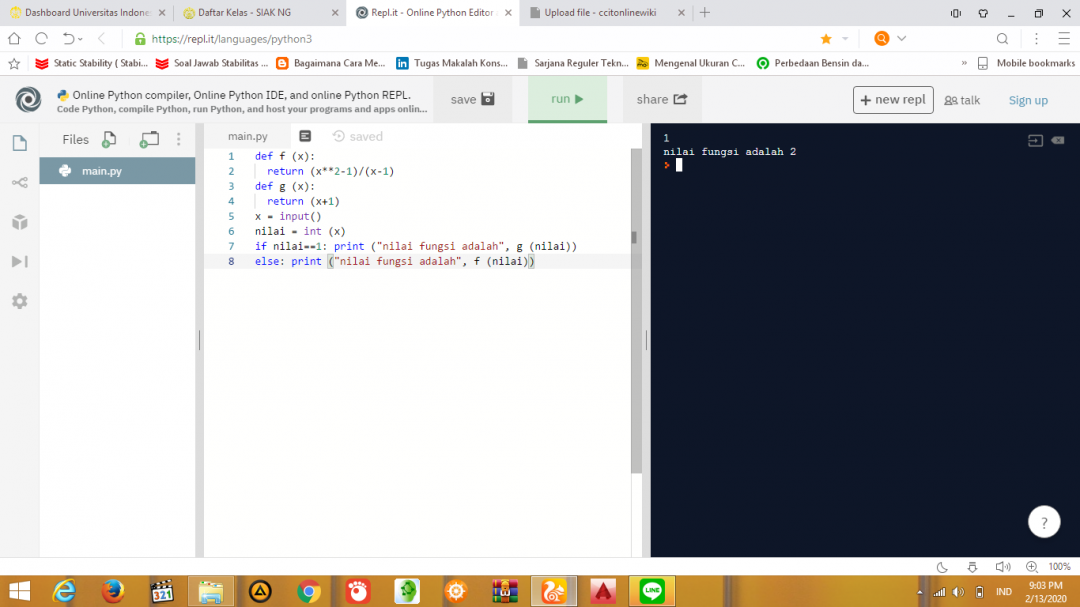
pada pertemuan minggu kedua, kami kelas metode numerik teknik perkapalan 2020 disuruh pak DAI untuk memilih soal yang menurut kami menarik. Soal yang menurut saya menarik adalah pada soal halaman 79 nomor 8.
Pada soal tersebut kita disuruh mencari masing-masing nilai x. Ada banyak cara yang dapat digunakan, yaitu dengan persamaan linear dan dengan persamaan matrix. Karena persamaan yang ada pada sooal telah disusun menjadi suatu matrix maka cara penyelesaiannya yang paling efisien adalah dengan cara matrix. Menyelesaikan persamaan matris Ax=b dimana kita disuruh untuk mencari nilai semua bilangan x maka diperlukan step agar dapat menyelesaikan persamaan tersebut. Ketika saya mempelajari aljabar linear ada banyak metode numerik yang digunakan untuk menyelesaikan permasalahan tersebut. ada metode invers dan metode Gauss-Jordan. Menggunakan metode invers, kita melakukan invers terhadap nilai A. Ax=b maka untuk mencari nilai x=A**-1 * B. dan pada saat melakukan invers juga ada banyak cara lain dilakukan untuk mencari invers suatu matrix ada metode sarrus, metode +, -, +. Sedangkan untuk metode gaus jordan kita perlu membuat persamaan matematikanya Ax=B, kemudian kita harus merubah nilai A menjadi matrix satu utama dengan metode Gauss-Jordan. dengan melakukan operasi penjumlahan dan pengurangan suatu baris dengan baris lainnya sehingga matrix yang A menjadi matrix satu utama sedangkan matrix B berubah menjadi nilai-nilai dari matrix X.
Data -> Informasi -> Pengetahuan -> Ilmu yang bermanfaat -> hikmah -> hidayah
Soal Pertama menggunakan Metode Manual
Pada metode manual saya menggunakan metode Gauss-Jordan dalam menyelesaikan permasalahan Matrix diatas. Penyelesaian permasalahan matrix menggunakan Gauss-Jordan mengharuskan kita untuk menjadikan Matrix A menjadi matrix satu utama dengan cara-cara mengoperasikan matrixnya.
Berikut saya lampirkan hasil dari pekerjaan saya menggunakan metode manual
Soal Pertama menggunakan Metode Phyton
Pada metode phyton saya menggunakan dokumen sympy yang merupakan bagian dari phyton. Di dalam dokumen sympy terdapat kumpulan program matematika. sehingga program matematika menjadi bisa dijalankan.
Berikut saya lampirkan kerjaan saya menggunakan dokumen sympy pada python.
Soal Kedua dengan menggunakan Metode Manual dan Metode Phyton
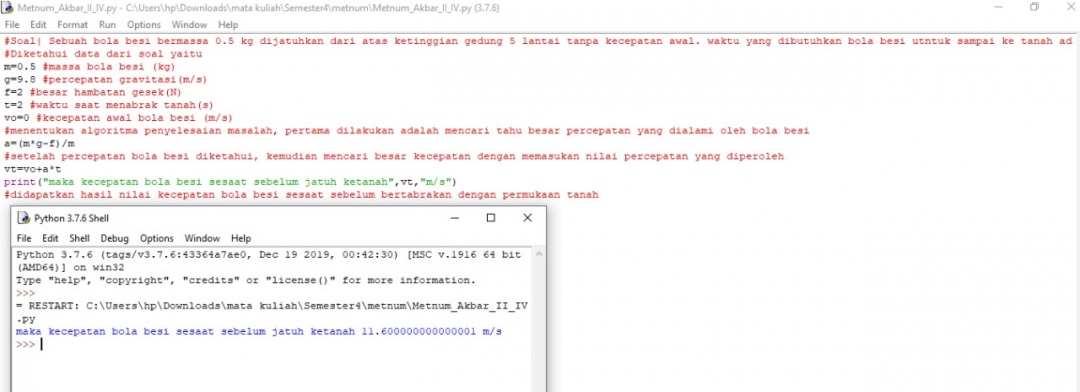
Sebuah bola besi dijatuhkan dari gedung 5 lantai bermassa 5 kg. bola jatuh ke permukaan tanah setelah 2 sekon. Ternyata pada saat dijatuhkan, bola besi diketahui terkena gaya gesek angin sebesar 2 Newton. Hitunglah berapa besar kecepatan bola besi, sesaat sebelum jatuh ke permukaan tanah.
Menyelesaikan permasalahan tersebut, yang pertama dilakukan adalah menentukan variable-variabel yang memengaruhi gerak jatuh bola. Hal yang memengaruhi tersebut adalah kecepatan awal benda, besar percepatan dan waktu bola besi tersebut jatuh. Karena gerak jatuh bebas, maka kecepatan awal dari bola besi di definisikan 0. Waktu bola jatuh sudah diketahui dari pengukuran. Kemudian percepatan dipengaruhi oleh gaya berat bola dan gaya gesek antara bola dan udara. Gaya berat merupakan fungsi dari massa benda dikali dengan percepatan gravitasi dan gaya gesek adalah fungsi dari massa benda dikali koefesien gaya gesek. Setelah dilakukan operasi jumlah gaya yang ada sebanding dengan massa dan percepatan. maka nilai percepatan yang diperoleh adalah 5.8 m/s^2. kemudian fungsi kecepatan adalah fungsi percepatan dikali dengan waktu. Akhinya nilai kecepatan benda sesaat sebelum menyentuh tanah adalah 11.6 m/s.
Kemudian saya melakukan pada phyton algoritma-algoritma yang telah ditentukan diatas.Berikut tampilan dari menggunakan phyton dalam menyelesaikan permasalahan tersebut
Progeres Belajar Metode Numerik
Pertemuan Minggu Ketiga ( 21 Februari 2020 )
Pegas massa Misalkan ada sebuah pegas yang ditahan oleh sebuah benda bermassa. Kemudian benda tersebut ditarik kebawah, maka benda tersebut akan naik turun, bahkan lebih tinggi dari posisi semula. Hal ini terjadi karena pegas bersifat lembam. pertanyaannya adalah bagaimana bentuk model matematis yang bisa mewakili atau menggambarkan gerakan dinamis pegas massa tersebut.
Ada 3 prinsip dasar didalam ilmu teknik
1. Prinsip konservasi massa.
Artinya jumlah massa dalam suatu sistem adalah konstan/tidak dapat diciptakan atau dimusnahkan (dM/dt)=0. contoh rumus pada Q=V*A=konstan, rumus tersebut merupakan turunan dari fungsi dM/dt=0 pada aliran air, tetapi rumus tersebut tidak dapat dilakukan pada fluida yang mampu mampat(dapat mengalami perubahan massa jenis.
2. Prinsip konservasi momentum(kesetimbangan gaya)
F=M*a=M*dv/dt
3. Prinsip konservasi energi.
Artinya energi tidak dapat hilang dan tidak dapat dibentuk, akan tetapi dapat berubah bentuk
Laporan Asistensi
- Selasa, 25 Februari 2020
- Michael Ahli
Tugas Initial Value Problem
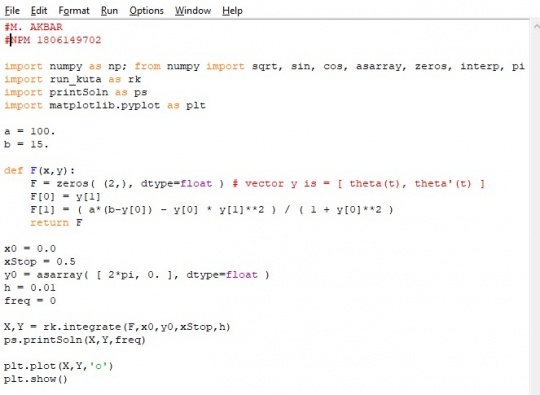
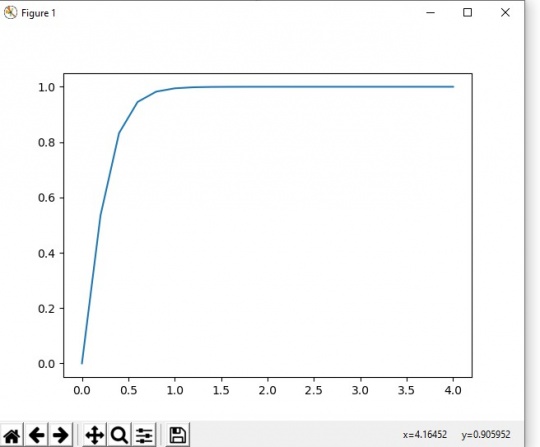
Saya mengerjakan soal nomor 14 dengan menggunakan metode runge kutta
Pada soal diketahui persamaan posisi angular dari lengan mekanik
Pada saat dibuat kedalam pemograman menjadi
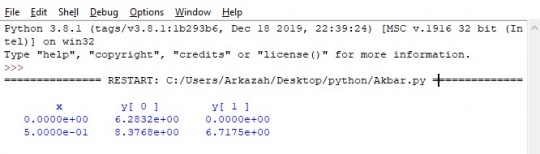
kemudian keluar nilai matrix
kemudian di plot dalam posisi titik-titik menjadi
Pertemuan Minggu Keempat ( 28 Februari 2020 )
Pada minggu keempat ini kami mempelajari boundary value problem. selain memberikan kondisi awal, yang diperlukan untuk mencari nilai akhir, terkadang kita perlu memberikan batas-batas agar nilai output dari input yang kita hasilkan menjadi lebih mudah untuk dianalisis, sebagai contoh perumpamaan nilai batas adalah batas nilai maksimum atau batas minimum.
Laporan Asistensi
- Jumat, 25 Februari 2020
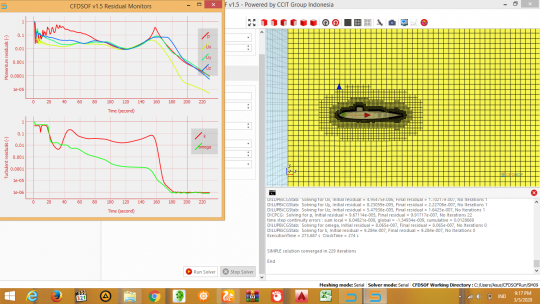
Pada asistensi ini, sebelumnya kami disuruh untuk mengintstal aplikasi CFDSOF untuk melakukan simulasi kapal selam. Kemudian diberikan lagi dalam bentuk video yang diupload di wiki. Pada aplikasi CFDSOF kami mencari nilai hambatan pada kecepatan tertentu dengan cara memasukan kondisi-kondisi di dalam software CFDSOF
Setelah selesai akan muncul grafik menunjukan residual dari perhitungan. Ketika grafik residual turun berarti menunjukan kekonvergenan.
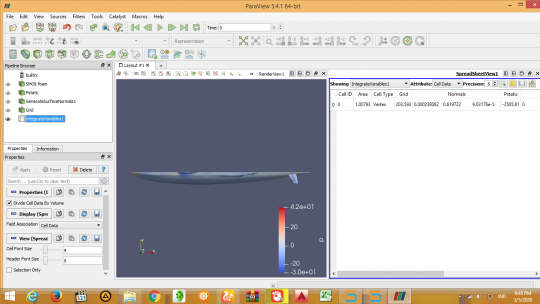
Kemudian perhitungan hambatan dilakukan pada aplikasi paraview, dengan mengedit ketentuan-ketentuan sesuai dengan yang diberikan asdos.
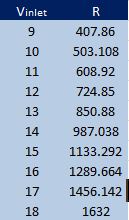
Setelah selesai melakukan operasi hitung maka akan keluar nilai hambatan pada kolom Grid
Setelah itu saya mencari nilai hambatan untuk 10 variasi kecepatan yang di input pada boundary condition nilai kecepatannya berapa. Berikut data dari pengukuran besar kecepatan terhadap tekanan.
- Selasa, 3 Maret 2020
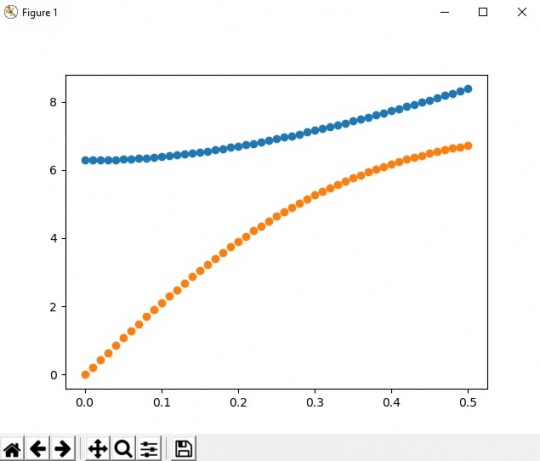
Data yang didapatkan pada simulasi uji hambatan kapal selam akan dilakukan regresi linearnya menggunakan bahasa pemograman. Kemudian Asdos memberikan pemahaman singkat tentang metode melakukan regresi linear.
Pertama adalah dengan metode newton. Jika menggunakan 5 data yang telah didapatkan saat uji hambatan maka menggunakan metode newton hasilnya akan menjadi.
Kemudian menggunakan least square caranya menjadi
mencari D terkecil untuk menentukan F(x) paling mendekati
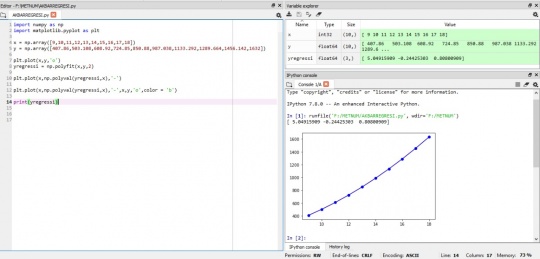
Kemudian menggunakan python dirumuskan sebagai berikut
Didapatkan f(x)=5.04915909x² - 0.24425303x + 0.80800909 dalam memiliki orde 2
Pertemuan Minggu Kelima
Pada minggu ini kami mengevaluasi kembali mengenai materi Initial Value Problem dan Boundary Value Problem. Mencari tahu perbedaan antara Initial Value Problem dan Boundary Value Problem. Perbedaan paling mencolok dari Initial Value Problem dan Boundary Value Problem adalah dengan ada tidaknya batas nilai input fungsi yang dipakai. Jika didalam fungsi tersebut memiliki nilai batas atas dan batas bawah, maka itu merupakan contoh dari Boundary Value Problem. Atau jika komponen nilai yang diketahui hanya satu titik nilai pada kondisi Awal, maka itu termasuk kedalam Initial Value Problem.
Laporan Asistensi
- Selasa, 10 Maret 2020
Tugas Metnum
Pertemuan Minggu Keenam
Pada minggu ini kami dijelaskan materi oleh asisten dosen dikarenakan Pak DAI sakit. Semoga pak DAI diberikan kesehatan kembali. Kami mempelajari tentang optimasi. Jadi optimasi adalah tentang bagaimana cara kita untuk meminimalkan nilai suatu fungsi atau memaksimalkan nilai suatu fungsi. Optimasi biasa berkaitan dengan desain. Terdapat komponen-komponen yang ada jika melakukan optimasi
a. Fungsi Objektif merupakan fungsi yang akan kita optimasi nilainya menjadi optimal
b. Constraint merupakan halangan atau batasan terhadap nilai fungsi objektif. Terbagi 2;
1. equality constraint atau batasan berupa persamaan (=)
2. inequality constraint atau batasan berupa pertidaksamaan atau berupa (<,<=,>,>=)
c. Variable keputusan atau nilai-nilai yang sudah dimiliki atau ada
Sebenarnya optimasi itu sangat banyak komponennya dalam area ke teknikan, bahkan ini menjadi jurusan pada S2. Sekarang kami hanya perlu mengenal sedikit tentang optimasi.
Saya lampirkan contoh soal optimasi yang dibahas pada pertemunan minggu keenam
disini fungsi pertama merupakan fungsi objektif
fungsi kedua merupakan inequality constraint
fungsi ketiga merupakan equality constraint
fungsi keempat merupakan nilai variabel kebputusannya, dan
fungsi kelima perkiraan nilai yang kita tentukan
Contoh optimasi adalah misalkan pemilik kayu meminta enginer untuk membuatkan pagar dari kayu yang dia miliki sepanjang 20 meter. Nilai luas area dari daerah yang ditutupi pagar kayu harus maksimal. Dan agar anak sang pemilik bisa bermain didalamnya maka panjang dari daerah di dalam pagar harus sama atau lebih dari 8 meter. Dari permasalahan tersebut kita menentukan nilai masing-masing komponennya
Fungsi Objektifnya adalah luas daerah
equality constrainnya adalah panjang kayu yang berdampak pada panjang keliling pagar
inequality constrainnya adalah p>=8 agar anaknya bisa bermain di dalam area pagar.
Soal area luas dari pagar berikut nilai hasilnya
Tugas Optimasi Video
Berikut video penyelesaian dari soal diatas saya sambungkan ke Youtube https://youtu.be/01PitWgeT4s
Tugas UTS
1. (i) Membuat Model AUV untuk simulasi CFDSOF, (ii) Melakukan simulasi hambatan dengan CFDSOF
2. Membuat persamaan dari data-data hambatan dan kecepatan (Curve Fitting)
3. Model matematis untuk memperkirakan propulsi yang dibutuhkan untuk berbagai kecepatan
4. Waktu yang dibutuhkan untuk mencapai kecepatan maksimal (Runge Kutta).
Pembuatan model AUV
Dengan meniru KRI alugoro dibuaut model sederhananya menggunakan Solid Work. https://youtu.be/M40H-Gqhoik
Simulasi CFDSOF
Menggunakan Software CFDSOF untuk mendapatkan hambatan kapal berbagai kecepatan https://www.youtube.com/watch?v=ww1RNkMpMCM
Membuat Persamaan Regresi
Menggunakan curve fitting untuk mendapatkan hubungan persamaan kecepatan dengan hambatan https://www.youtube.com/watch?v=30rmJNHyO2Y