Difference between revisions of "Muhammad Rais Habibie"
Mraishabibie (talk | contribs) |
Mraishabibie (talk | contribs) (→TUGAS AKHIR) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 71: | Line 71: | ||
| − | if a == p : | + | |
| + | if a == p == 0 : | ||
| + | y = (c-r)/(b-q) | ||
| + | x = 0 | ||
| + | print("nilai y =",y,"nilai x =",x) | ||
| + | elif b == q == 0: | ||
| + | x = (c-r)/(a-p) | ||
| + | y = 0 | ||
| + | print("nilai y =", y, "nilai x =", x) | ||
| + | elif a == p : | ||
i = b - q | i = b - q | ||
j = c - r | j = c - r | ||
y = j/i | y = j/i | ||
x = (c -(b*y))/a | x = (c -(b*y))/a | ||
| − | print("nilai y=",y,"nilai x =",x) | + | print("nilai y =",y,"nilai x =",x) |
| − | |||
elif a == 0: | elif a == 0: | ||
y = c / b | y = c / b | ||
x = (r - (q * y)) / p | x = (r - (q * y)) / p | ||
| − | print("nilai y=", y, "nilai x =", x) | + | print("nilai y =", y, "nilai x =", x) |
elif b == 0: | elif b == 0: | ||
x = c / a | x = c / a | ||
y = (r - (p * x)) / q | y = (r - (p * x)) / q | ||
| − | print("nilai y=", y, "nilai x =", x) | + | print("nilai y =", y, "nilai x =", x) |
elif p == 0: | elif p == 0: | ||
y = r / q | y = r / q | ||
x = (c - (a * y)) / b | x = (c - (a * y)) / b | ||
| − | print("nilai y=", y, "nilai x =", x) | + | print("nilai y =", y, "nilai x =", x) |
elif q == 0: | elif q == 0: | ||
x = r / p | x = r / p | ||
y = (c - (a * x)) / b | y = (c - (a * x)) / b | ||
| − | print("nilai y=", y, "nilai x =", x) | + | print("nilai y =", y, "nilai x =", x) |
elif a != p : | elif a != p : | ||
a2= a*p | a2= a*p | ||
| Line 106: | Line 114: | ||
y = j2 / i2 | y = j2 / i2 | ||
x = (c - (b * y))/a | x = (c - (b * y))/a | ||
| − | print("nilai y=", y, "nilai x =", x) | + | print("nilai y =", y, "nilai x =", x) |
input() | input() | ||
| − | |||
== FLOWCHART == | == FLOWCHART == | ||
| Line 118: | Line 125: | ||
== ALGORITMA == | == ALGORITMA == | ||
1. Start | 1. Start | ||
| + | ---- | ||
2. Input berupa float a,b,c,p,q,r | 2. Input berupa float a,b,c,p,q,r | ||
| + | ---- | ||
3. Jika a =p lakukan langkah | 3. Jika a =p lakukan langkah | ||
| + | ---- | ||
4. i = b - q | 4. i = b - q | ||
| + | ---- | ||
j = c - r | j = c - r | ||
| + | ---- | ||
y = j/i | y = j/i | ||
| + | ---- | ||
x = (c -(b*y))/a | x = (c -(b*y))/a | ||
| + | ---- | ||
5. Setelah itu lakukan langkah 17 | 5. Setelah itu lakukan langkah 17 | ||
| − | + | ---- | |
6. Jika tidak lakukan langkah dibawah | 6. Jika tidak lakukan langkah dibawah | ||
| − | + | ---- | |
7. Jika a = 0 lakukan | 7. Jika a = 0 lakukan | ||
| + | ---- | ||
8. y = c / b | 8. y = c / b | ||
| + | ---- | ||
x = (r - (q * y)) / p | x = (r - (q * y)) / p | ||
| + | ---- | ||
9. Jika b = 0 lakukan | 9. Jika b = 0 lakukan | ||
| + | ---- | ||
10. x = c / a | 10. x = c / a | ||
| + | ---- | ||
y = (r - (p * x)) / q | y = (r - (p * x)) / q | ||
| + | ---- | ||
11. Jika p = 0 lakukan | 11. Jika p = 0 lakukan | ||
| + | ---- | ||
12. y = r / q | 12. y = r / q | ||
| + | ---- | ||
x = (c - (a * y)) / b | x = (c - (a * y)) / b | ||
| + | ---- | ||
13. Jika q = 0 lakukan | 13. Jika q = 0 lakukan | ||
| + | ---- | ||
14. y = r / q | 14. y = r / q | ||
| + | ---- | ||
x = (c - (a * y)) / b | x = (c - (a * y)) / b | ||
| + | ---- | ||
15. Jika a != p lakukan | 15. Jika a != p lakukan | ||
| + | ---- | ||
16. a2= a*p | 16. a2= a*p | ||
| + | ---- | ||
b2=b*p | b2=b*p | ||
| + | ---- | ||
c2=c*p | c2=c*p | ||
| + | ---- | ||
p2=p*a | p2=p*a | ||
| + | ---- | ||
q2=q*a | q2=q*a | ||
| + | ---- | ||
r2=r*a | r2=r*a | ||
| + | ---- | ||
i2 = b2 - q2 | i2 = b2 - q2 | ||
| + | ---- | ||
j2 = c2 - r2 | j2 = c2 - r2 | ||
| + | ---- | ||
y = j2 / i2 | y = j2 / i2 | ||
| + | ---- | ||
x = (c - (b * y))/a | x = (c - (b * y))/a | ||
| + | ---- | ||
17. Print nilai X dan print nilai Y | 17. Print nilai X dan print nilai Y | ||
| + | ---- | ||
18. Input () | 18. Input () | ||
| + | ---- | ||
19. Stop | 19. Stop | ||
| + | ---- | ||
| + | line 1 :import numpy as np | ||
| + | line 2 :from numpy import array | ||
| + | line 3 : # define the matrix [A] | ||
| + | line 4 : A=array([[3, -4, 3], [-4, 3, -5], [5, -7, 1]], float) | ||
| + | line 5 : # define matrix b | ||
| + | line 6 : b = array ([[6], [-7], [ 10]], float) | ||
| + | line 7 : #matrix nya menjadi | ||
| + | line 8 : c=array([[3, -4, 3, 6], [-4, 3, -5, -7], [5, -7, 1, 10]], float) | ||
| + | line 9 : print ('Matrix dari persamaan adalah : | ||
| + | line 10 : print (c) | ||
| + | line 11 : #define rows column | ||
| + | line 12 : n=len(b) #number of rows and colomn, due too the matrix that is square matrix | ||
| + | line 13 : print ('n adalah ' + str(n)) | ||
| + | line 14 : x=np.zeros((3), float) | ||
| + | line 15 : for k in range (0,n-1): | ||
| + | line 16 : for i in range (k+1,n): | ||
| + | line 17 : if A[i,k] != 0.0 : #perintah jika sebuah baris yang akan di eliminasi, ada bagiannya yang tidak 0, maka akan di substract dengan pivot | ||
| + | line 18 : lam = A[i,k]/A[k,k] | ||
| + | line 19 : A[i, k+1:n] = A[i, k+1:n] - lam*A[k, k+1:n] | ||
| + | line 20 : b[i]=b[i] - lam*b[k] | ||
| + | line 21 : for k in range (n-1,-1,-1): | ||
| + | line 22 : x[k]=(b[k]-np.dot(A[k,k+1:n], x[k+1:n]))/A[k,k] | ||
| + | line 23 : print (x[k]) | ||
| + | |||
| + | == FEM == | ||
| + | import numpy as np | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | A1 = float(input("Masukkan Luas Permukaan Bidang Sambung Material 1 :")) | ||
| + | |||
| + | L1 = float(input("Masukkan Panjang Material 1 :")) | ||
| + | |||
| + | E1 = float(input("Masukkan Modulus Young Material 1 :")) | ||
| + | |||
| + | k1 = A1*E1/L1 | ||
| + | |||
| + | print ("k1 =", k1) | ||
| + | |||
| + | |||
| + | A2 = float(input("Masukkan Luas Permukaan Bidang Sambung Material 2 :")) | ||
| + | |||
| + | L2 = float(input("Masukkan Panjang Material 2 :")) | ||
| + | |||
| + | E2 = float(input("Masukkan Modulus Young Material 2 :")) | ||
| + | |||
| + | k2 = A2*E2/L2 | ||
| + | |||
| + | print ("k2 =", k2) | ||
| + | |||
| + | |||
| + | A3 = float(input("Masukkan Luas Permukaan Bidang Sambung Material 3 :")) | ||
| + | |||
| + | L3 = float(input("Masukkan Panjang Material 3 :")) | ||
| + | |||
| + | E3 = float(input("Masukkan Modulus Young Material 3 :")) | ||
| + | |||
| + | k3 = A3*E3/L3 | ||
| + | |||
| + | print ("k3 =", k3) | ||
| + | |||
| + | |||
| + | F2 = float(input("Masukkan Gaya di sebelah kiri (vektor) :")) | ||
| + | |||
| + | F3 = float(input("Masukkan Gaya di sebelah kanan (vektor) :")) | ||
| + | |||
| + | |||
| + | ka = k1+k2 | ||
| + | |||
| + | kb = k2+k3 | ||
| + | |||
| + | |||
| + | a = np.array([[ka,-k2],[-k2,kb]],float) | ||
| + | |||
| + | b = np.array([F2,F3],float) | ||
| + | |||
| + | c = np.array([[ka,-k2],[-k2,kb],[F2,F3]],float) | ||
| + | |||
| + | n = len(b) | ||
| + | |||
| + | x=np.zeros((3), float) | ||
| + | |||
| + | for k in range (0,n-1): | ||
| + | |||
| + | for i in range (k+1,n): | ||
| + | if a[i,k] != 0.0 : | ||
| + | lam = a[i,k]/a[k,k] | ||
| + | a[i, k+1:n] = a[i, k+1:n] - lam*a[k, k+1:n] | ||
| + | b[i]=b[i] - lam*b[k] | ||
| + | for k in range (n-1,-1,-1): | ||
| + | |||
| + | x[k]=(b[k]-np.dot(a[k,k+1:n], x[k+1:n]))/a[k,k] | ||
| + | |||
| + | x2 = x[0] | ||
| + | |||
| + | x3 = x[1] | ||
| + | |||
| + | |||
| + | F1 = x2*(-k1) | ||
| + | |||
| + | F4 = x3*(-k3) | ||
| + | |||
| + | |||
| + | print ("Kalkulasi deformasi antara material 1 dan 2 sebesar :", x2) | ||
| + | |||
| + | print ("Kalkulasi deformasi antara material 2 dan 3 sebesar :", x3) | ||
| + | |||
| + | print ("Gaya pada ujung kiri struktur sebesar :", F1) | ||
| + | |||
| + | print ("Gaya pada ujung kanan struktur sebesar :", F4) | ||
| + | |||
| + | |||
| + | |||
| + | == TUGAS AKHIR == | ||
| + | |||
| + | import math | ||
| + | def bracket(f,x1,h): | ||
| + | c = 1.618033989 | ||
| + | f1 = f(x1) | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | h = -h | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | return x2,x1 - h | ||
| + | for i in range (100): | ||
| + | h = c*h | ||
| + | x3 = x2 + h | ||
| + | f3 = f(x3) | ||
| + | if f3 > f2: | ||
| + | return x1,x3 | ||
| + | x1 = x2 | ||
| + | x2 = x3 | ||
| + | f1 = f2 | ||
| + | f2 = f3 | ||
| + | print ("Bracket did not find a minimum") | ||
| + | def search(f,a,b,tol=1.0e-9): | ||
| + | nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a)))) | ||
| + | R = 0.618033989 | ||
| + | C = 1.0 - R | ||
| + | x1 = R*a + C*b | ||
| + | x2 = C*a + R*b | ||
| + | f1 = f(x1) | ||
| + | f2 = f(x2) | ||
| + | for i in range(nIter): | ||
| + | if f1 > f2: | ||
| + | a = x1 | ||
| + | x1 = x2 | ||
| + | f1 = f2 | ||
| + | x2 = C*a + R*b | ||
| + | f2 = f(x2) | ||
| + | else: | ||
| + | b = x2 | ||
| + | x2 = x1 | ||
| + | f2 = f1 | ||
| + | x1 = R*a + C*b | ||
| + | f1 = f(x1) | ||
| + | if f1 < f2: | ||
| + | return x1,f1 | ||
| + | else: | ||
| + | return x2,f2 | ||
| + | print("Aplikasi Optimasi Section Modulus L Stiffner") | ||
| + | print("Kondisi Terikat : lebar alas > lebar atas > lebar tengah") | ||
| + | b1 = eval(input("Nilai lebar bangun alas :")) | ||
| + | b3 = eval(input("Nilai lebar bangun atas :")) | ||
| + | b2 = eval(input("Nilai lebar bangun tengah :")) | ||
| + | H = eval(input("Nilai tinggi T stiffner :")) | ||
| + | def f(x): | ||
| + | A1 = b1*(H-x)/2 | ||
| + | A2 = b2*x | ||
| + | A3 = b3*(H-x)/2 | ||
| + | d1 = 1/2*(H-x)/2 | ||
| + | d2 = 1/2*x+(H-x)/2 | ||
| + | d3 = 3/4*(H-x)+x | ||
| + | I1 = 1/12*b1*((H-x)/2)**3 | ||
| + | I2 = 1/12*b2*x**3 | ||
| + | I3 = 1/12*b3*((H-x)/2)**3 | ||
| + | dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) | ||
| + | I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 | ||
| + | Z = I/dc | ||
| + | return Z | ||
| + | xStart = 0.0 | ||
| + | h = 1.0 | ||
| + | x1,x2 = bracket(f,xStart,h) | ||
| + | y,fMin = search(f,x1,x2) | ||
| + | print("optimal sectional area =",-fMin) | ||
| + | print("sectional area awal" , f(H)) | ||
| + | A = -fMin/f(H)*100 | ||
| + | print ("efisiensi",A,"%") | ||
| + | input ("\nPress return to exit") | ||
| + | |||
| + | ---- | ||
| + | https://youtu.be/RTNXpbZNp_g (link video) | ||
| + | ---- | ||
| + | |||
| + | https://drive.google.com/open?id=1cJQoWBNAnUdzxgaydOQoFOrAUURMxQU1 (link power point) | ||
| + | |||
| + | ---- | ||
Latest revision as of 21:49, 29 May 2019
Tujuan perkuliahan metode numerik : 1.Memahami konsep atau prinsip dan mampu menerapkannya 2.Menjadi orang yang lebih mengenal siapa dirinya(berakal)
Metode numerik berisi tentang :
-Flowchart
-Algoritma
-Pemprograman
-Metode literative
Dapat digunakan untuk menyelesaikan persamaan-persamaan aljabar seperti diferensial ataupun integral. Dapat dikembangkan menjadi optimasi dan menyelesaikan studi kasus.
Matematika, Matematika bisa membantu tapi juga bisa menyesatkan. Berakal, Akal adalah tali yang mengikat kita terhadap konsep hidup sebagai manusia. Karena tidak semua hal dapat kita ketahui sebagai manusia, ada hal-hal yang tidak dapat kita definisikan dan itu hanya tuhan yang tau, jadi berakal adalah syarat untuk menjaga diri kita tetap pada koridor manusia sebaga mana mestinya, sesuai apa yang sebagaimana tuhan ciptakan.
RESUME
Hubungan mata kuliah metode numerik bisa dihubungkan dengan tiga hal:
1. Metnum dan Strutkur pada kapal
2. Metnum dan Propulsi
3. Metnum dan Agama (menghitung zakat)
Terdapat tiga dimensi, yaitu satu dimensi,dua dimensi dan tiga dimensi. Contoh perhitungan pada satu dimensi ialah Bernouli. Langkah langkah dalam menyelesaikan masalah di teknik ialah,masalah di teknik,model matematis,metode numerik,algoritma(flow chart),program komputer,hasil numerik,visual,interpretasi/analisa,solusi engineering (teknik).
Contoh menyelesaikan masalah diteknik adalah kekuatan rangka badan kapal terhadap keadaan laut tertentu Tahap penyelesaiian masalah adalah Metode teoritis,metode percobaan dan yang terakhir adalah metode komputasi. Metode komputasi adalah pendekatan dengan ilmu matematika dan dasar dasar fisika.
Algoritma adalah Langkah langkah penyelesaian masalah terdapat satu set instruksi untuk dikerjakan komputer. Terdapat juga program komputer. Salah satu contoh program komputer sendiri adalah python yang dapat mengcoding sebuah program dan dapat mensumulasikannya.
Setelah itu terdapat hasil numerik yaitu hasil dari pemograman berupa angka angka. Selanjutnya interpretasi dapat berupa hasil visualisasi seperti perbedaan warna yang dianalisa oleh engineer.
PROGRAM
print ('Persamaan linear dua variabel \n ax + by = c\n px + qy = r ')
a = float(input(" masukan nilai a =")) b = float(input(" masukan nilai b =")) c = float(input(" masukan nilai c =")) p = float(input(" masukan nilai p =")) q = float(input(" masukan nilai q =")) r = float(input(" masukan nilai r ="))
if a == p == 0 :
y = (c-r)/(b-q)
x = 0
print("nilai y =",y,"nilai x =",x)
elif b == q == 0:
x = (c-r)/(a-p)
y = 0
print("nilai y =", y, "nilai x =", x)
elif a == p :
i = b - q
j = c - r
y = j/i
x = (c -(b*y))/a
print("nilai y =",y,"nilai x =",x)
elif a == 0:
y = c / b
x = (r - (q * y)) / p
print("nilai y =", y, "nilai x =", x)
elif b == 0:
x = c / a
y = (r - (p * x)) / q
print("nilai y =", y, "nilai x =", x)
elif p == 0:
y = r / q
x = (c - (a * y)) / b
print("nilai y =", y, "nilai x =", x)
elif q == 0:
x = r / p
y = (c - (a * x)) / b
print("nilai y =", y, "nilai x =", x)
elif a != p :
a2= a*p
b2=b*p
c2=c*p
p2=p*a
q2=q*a
r2=r*a
i2 = b2 - q2
j2 = c2 - r2
y = j2 / i2
x = (c - (b * y))/a
print("nilai y =", y, "nilai x =", x)
input()
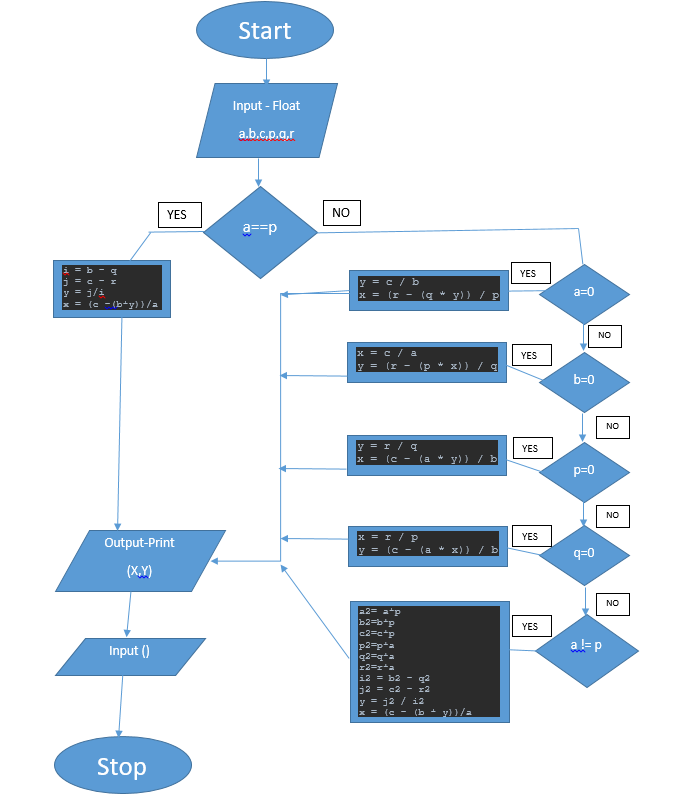
FLOWCHART
ALGORITMA
1. Start
2. Input berupa float a,b,c,p,q,r
3. Jika a =p lakukan langkah
4. i = b - q
j = c - r
y = j/i
x = (c -(b*y))/a
5. Setelah itu lakukan langkah 17
6. Jika tidak lakukan langkah dibawah
7. Jika a = 0 lakukan
8. y = c / b
x = (r - (q * y)) / p
9. Jika b = 0 lakukan
10. x = c / a
y = (r - (p * x)) / q
11. Jika p = 0 lakukan
12. y = r / q
x = (c - (a * y)) / b
13. Jika q = 0 lakukan
14. y = r / q
x = (c - (a * y)) / b
15. Jika a != p lakukan
16. a2= a*p
b2=b*p
c2=c*p
p2=p*a
q2=q*a
r2=r*a
i2 = b2 - q2
j2 = c2 - r2
y = j2 / i2
x = (c - (b * y))/a
17. Print nilai X dan print nilai Y
18. Input ()
19. Stop
line 1 :import numpy as np line 2 :from numpy import array line 3 : # define the matrix [A] line 4 : A=array([[3, -4, 3], [-4, 3, -5], [5, -7, 1]], float) line 5 : # define matrix b line 6 : b = array ([[6], [-7], [ 10]], float) line 7 : #matrix nya menjadi line 8 : c=array([[3, -4, 3, 6], [-4, 3, -5, -7], [5, -7, 1, 10]], float) line 9 : print ('Matrix dari persamaan adalah : line 10 : print (c) line 11 : #define rows column line 12 : n=len(b) #number of rows and colomn, due too the matrix that is square matrix line 13 : print ('n adalah ' + str(n)) line 14 : x=np.zeros((3), float) line 15 : for k in range (0,n-1): line 16 : for i in range (k+1,n): line 17 : if A[i,k] != 0.0 : #perintah jika sebuah baris yang akan di eliminasi, ada bagiannya yang tidak 0, maka akan di substract dengan pivot line 18 : lam = A[i,k]/A[k,k] line 19 : A[i, k+1:n] = A[i, k+1:n] - lam*A[k, k+1:n] line 20 : b[i]=b[i] - lam*b[k] line 21 : for k in range (n-1,-1,-1): line 22 : x[k]=(b[k]-np.dot(A[k,k+1:n], x[k+1:n]))/A[k,k] line 23 : print (x[k])
FEM
import numpy as np
A1 = float(input("Masukkan Luas Permukaan Bidang Sambung Material 1 :"))
L1 = float(input("Masukkan Panjang Material 1 :"))
E1 = float(input("Masukkan Modulus Young Material 1 :"))
k1 = A1*E1/L1
print ("k1 =", k1)
A2 = float(input("Masukkan Luas Permukaan Bidang Sambung Material 2 :"))
L2 = float(input("Masukkan Panjang Material 2 :"))
E2 = float(input("Masukkan Modulus Young Material 2 :"))
k2 = A2*E2/L2
print ("k2 =", k2)
A3 = float(input("Masukkan Luas Permukaan Bidang Sambung Material 3 :"))
L3 = float(input("Masukkan Panjang Material 3 :"))
E3 = float(input("Masukkan Modulus Young Material 3 :"))
k3 = A3*E3/L3
print ("k3 =", k3)
F2 = float(input("Masukkan Gaya di sebelah kiri (vektor) :"))
F3 = float(input("Masukkan Gaya di sebelah kanan (vektor) :"))
ka = k1+k2
kb = k2+k3
a = np.array([[ka,-k2],[-k2,kb]],float)
b = np.array([F2,F3],float)
c = np.array([[ka,-k2],[-k2,kb],[F2,F3]],float)
n = len(b)
x=np.zeros((3), float)
for k in range (0,n-1):
for i in range (k+1,n):
if a[i,k] != 0.0 :
lam = a[i,k]/a[k,k]
a[i, k+1:n] = a[i, k+1:n] - lam*a[k, k+1:n]
b[i]=b[i] - lam*b[k]
for k in range (n-1,-1,-1):
x[k]=(b[k]-np.dot(a[k,k+1:n], x[k+1:n]))/a[k,k]
x2 = x[0]
x3 = x[1]
F1 = x2*(-k1)
F4 = x3*(-k3)
print ("Kalkulasi deformasi antara material 1 dan 2 sebesar :", x2)
print ("Kalkulasi deformasi antara material 2 dan 3 sebesar :", x3)
print ("Gaya pada ujung kiri struktur sebesar :", F1)
print ("Gaya pada ujung kanan struktur sebesar :", F4)
TUGAS AKHIR
import math def bracket(f,x1,h):
c = 1.618033989
f1 = f(x1)
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
h = -h
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
return x2,x1 - h
for i in range (100):
h = c*h
x3 = x2 + h
f3 = f(x3)
if f3 > f2:
return x1,x3
x1 = x2
x2 = x3
f1 = f2
f2 = f3
print ("Bracket did not find a minimum")
def search(f,a,b,tol=1.0e-9):
nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
R = 0.618033989
C = 1.0 - R
x1 = R*a + C*b
x2 = C*a + R*b
f1 = f(x1)
f2 = f(x2)
for i in range(nIter):
if f1 > f2:
a = x1
x1 = x2
f1 = f2
x2 = C*a + R*b
f2 = f(x2)
else:
b = x2
x2 = x1
f2 = f1
x1 = R*a + C*b
f1 = f(x1)
if f1 < f2:
return x1,f1
else:
return x2,f2
print("Aplikasi Optimasi Section Modulus L Stiffner") print("Kondisi Terikat : lebar alas > lebar atas > lebar tengah") b1 = eval(input("Nilai lebar bangun alas :")) b3 = eval(input("Nilai lebar bangun atas :")) b2 = eval(input("Nilai lebar bangun tengah :")) H = eval(input("Nilai tinggi T stiffner :")) def f(x):
A1 = b1*(H-x)/2 A2 = b2*x A3 = b3*(H-x)/2 d1 = 1/2*(H-x)/2 d2 = 1/2*x+(H-x)/2 d3 = 3/4*(H-x)+x I1 = 1/12*b1*((H-x)/2)**3 I2 = 1/12*b2*x**3 I3 = 1/12*b3*((H-x)/2)**3 dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 Z = I/dc return Z
xStart = 0.0 h = 1.0 x1,x2 = bracket(f,xStart,h) y,fMin = search(f,x1,x2) print("optimal sectional area =",-fMin) print("sectional area awal" , f(H)) A = -fMin/f(H)*100 print ("efisiensi",A,"%") input ("\nPress return to exit")
https://youtu.be/RTNXpbZNp_g (link video)
https://drive.google.com/open?id=1cJQoWBNAnUdzxgaydOQoFOrAUURMxQU1 (link power point)